Combining an Extended SMAA-2 Method with Integer Linear Programming for Task Assignment of Multi-UCAV under Multiple Uncertainties
Abstract
1. Introduction
2. Related Work
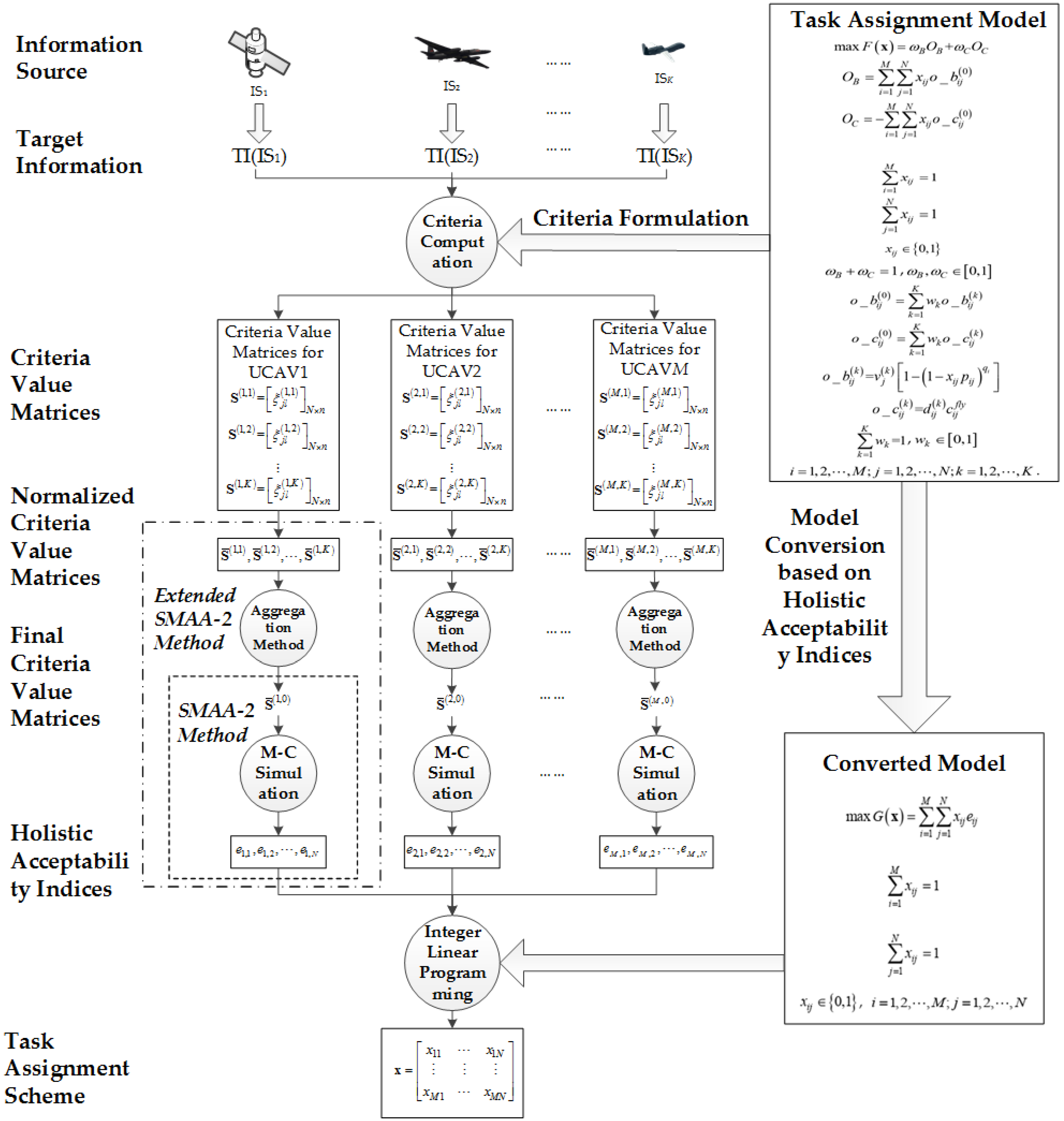
- We propose a novel method to aggregate multiple criteria value matrices from different information sources (ISs) under the condition that the criteria weight information is unavailable and the weight information about ISs is partially available.
- We integrate the aggregation method into the original SMAA-2 method. Thus, we propose an extended SMAA-2 method.
- We propose to convert the task assignment model for multi-UCAV with a variety of uncertain parameters into an integer linear programming model to maximize the holistic acceptability index of the task assignment scheme according to the meaning of holistic acceptability indices, and then apply integer linear programming to achieve task assignment.
3. Problem Formulation
4. The Stochastic Multicriteria Acceptability Analysis-2 (SMAA-2) Method
5. The Extended SMAA-2 Method
5.1. Normal Distribution Interval Number and Weighted Arithmetic Averaging Operator
5.2. Aggregation Method of Criterion Value Matrices from Different Information Sources
5.2.1. WAA Operator-Based Criteria Value Matrices Aggregation
5.2.2. Iterative Algorithm for Computing Objective Weights
| Algorithm 1: Pseudo-code of the aggregation method | |
| Input: | number of alternatives, criteria, and information sources: , , ; |
| criteria value matrices: ; | |
| subjective weight vector and initial objective weight vector, ; | |
| criteria weight vector ; | |
| error margin used in computing the objective weight vector: . | |
| Output: | final criteria value matrix . |
| Procedures: | |
| whiledo | |
| compute by (33) | |
| for to do | |
| compute by (22), (23), (31), (32) and (34) | |
| end for | |
| update by (35) | |
| update by (36) | |
| end while | |
| return | |
5.3. Integrating the Aggregation Method into the Original SMAA-2 Method
| Algorithm 2: Pseudo-code of the extended SMAA-2 method | ||
| Symbols: | , number of times alternative is evaluated into rank j in the Monte Carlo simulation; | |
| , number of iterations, set as 10000; | ||
| , vector of ranks of alternatives; | ||
| , utility value vector of alternatives; | ||
| , function returning the final criteria value matrix based on the criteria weight vector (details are presented in Algorithm 1) | ||
| , function returning a random criteria value matrix from criteria distribution ; | ||
| , function returning a random weight vector from weight distribution ; | ||
| , function returning a vector of ranks corresponding to . | ||
| Input: | number of alternatives, criteria, and decision-makers: , , ; | |
| criteria value matrices: ; | ||
| subjective weight vector and initial objective weight vector , ; | ||
| error margin used in computing the objective weight vector: ; | ||
| number of iterations of the Monte Carlo simulation: . | ||
| Output: | rank acceptability index ; | |
| central weight vector ; | ||
| confidence factor ; | ||
| holistic acceptability index . | ||
| Procedures: | // Initialize , and for to do for to do end for end for // Phase 1, compute , and // Main loop for to do //produce by // is the generated random criteria value matrix for to do end for for to do if then end if end for end for // Compute , and for to do if then end if for to do end for end for | // Phase 2, compute // Initialize , and generate the final criteria value matrix corresponding to for to do end for // Main loop for to do for to do for to and do if then go to worse end if end for worse: end for end for for to do end for |
6. Converting the Task Assignment Model Based on Holistic Acceptability Indices
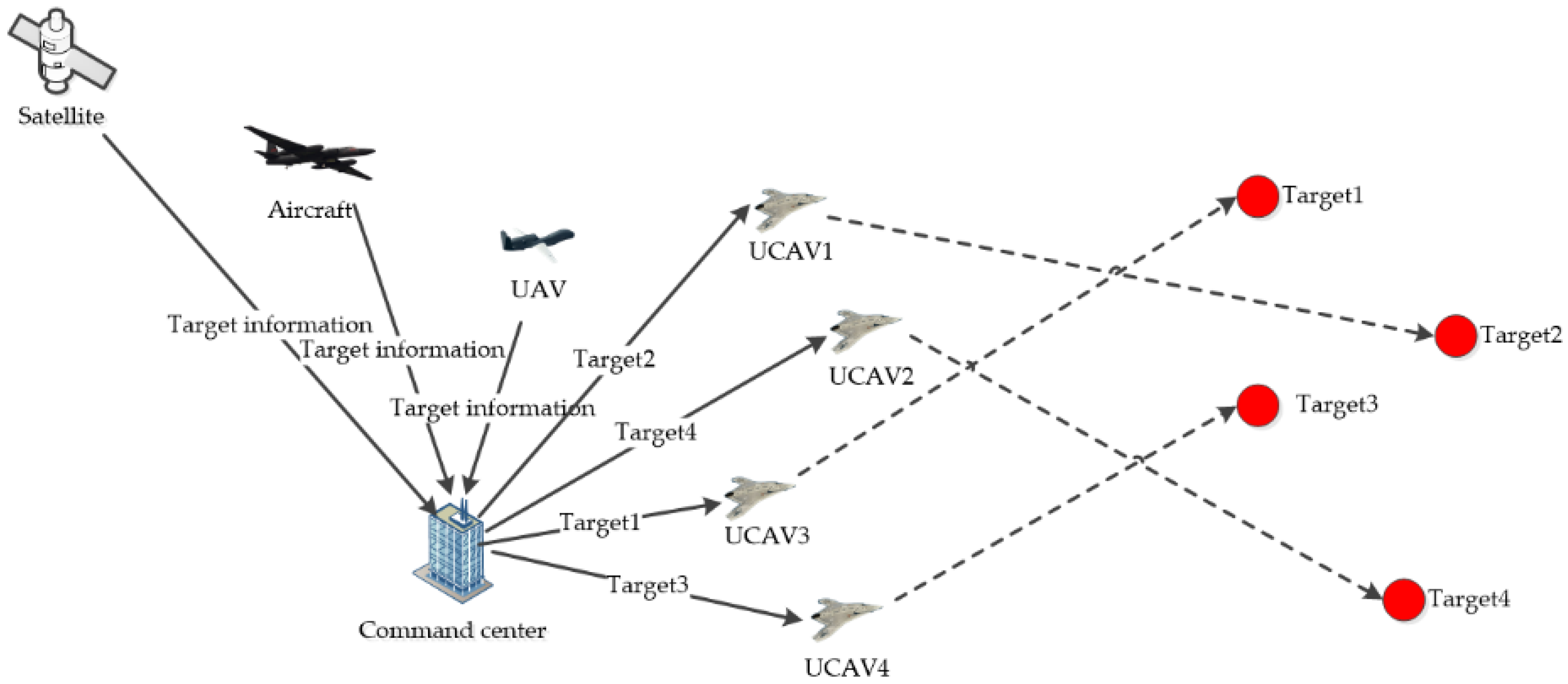
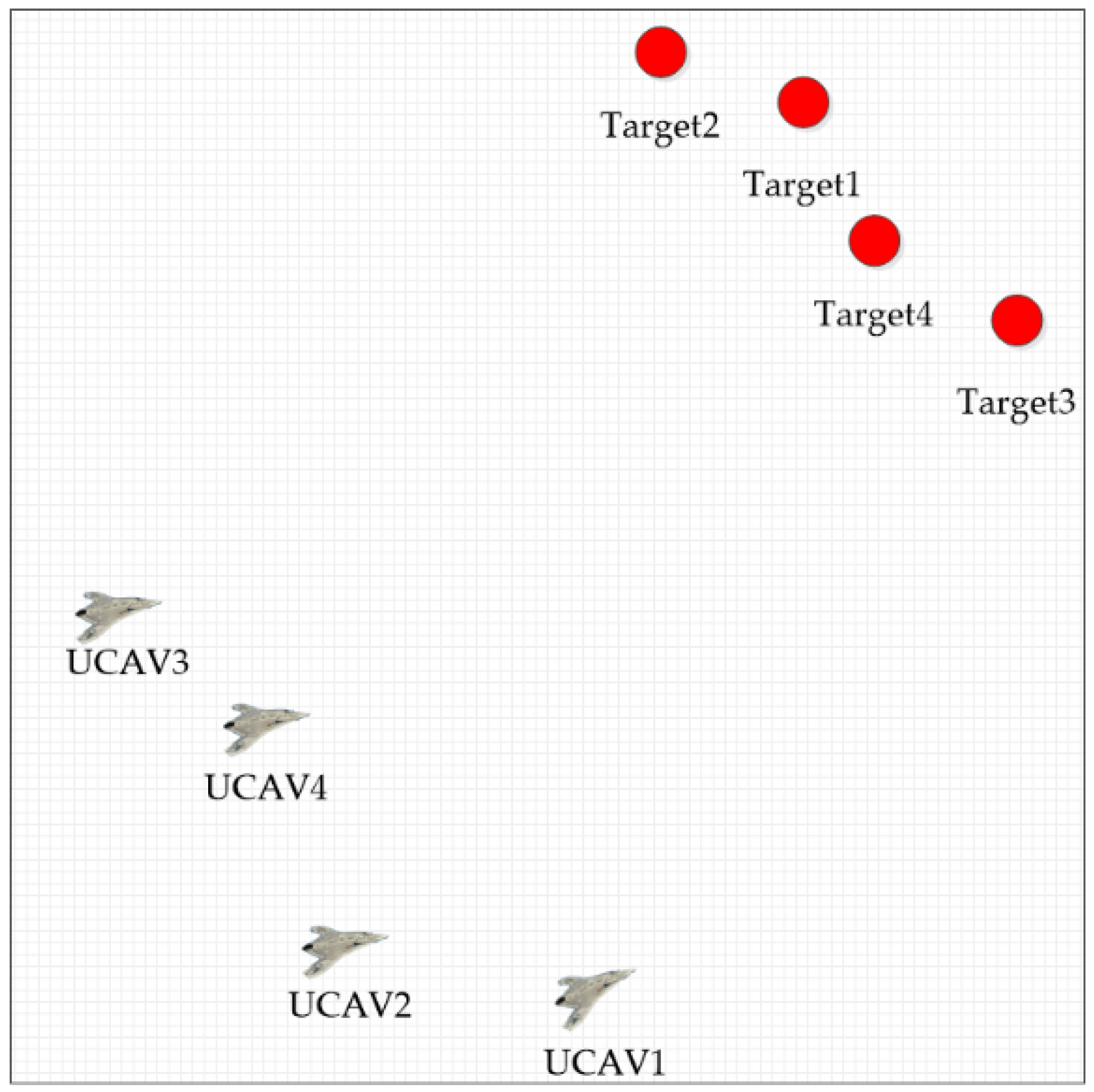
7. Case Study
8. Conclusions
- Due to the integration of the WAA operator-based aggregation method, the extended method is able to perform stochastic multicriteria acceptability analysis under circumstances of multiple criteria value matrices. This is also the most prominent advantage of the extended method over the original SMAA-2 method.
- The extended method employs the iterative algorithm to compute the objective weight of a sensor based on the accuracy and credibility of the target information it provides so as to minimize the subjective judgment errors of experts on the sensor performance. By this means, the actual importance of a sensor can be reflected to the greatest extent so that the final criteria value matrix obtained could be as accurate as possible. Through these measures, the credibility and accuracy of task assignment schemes can be further increased.
- The foundation of the extended method is the stochastic multicriteria acceptability analysis, so it inherits the advantage of the SMAA technique in that it does not require decision-makers to express their preferences explicitly [30]. This property is particularly useful in operational planning because the commander could only express implicit preferences for multiple operational objectives most of the time.
- The extended method is based on the assumption that the uncertain target information can be represented by normal distribution interval numbers. This assumption may limit the application of the method. When the uncertain target information is represented by fuzzy sets or rough sets, the extended method cannot be applied.
- The extended method employs a linear utility value function to map criteria values to utility values. Although Lahdelma et al. have proved it may often be safe to apply a linear utility value function, they also mentioned that when the convexity or concavity of the utility value function is severe, the results would be slightly different [45]. This means that in some special cases, the linear utility value function may not be the best choice, and we would need to construct a more appropriate one.
Author Contributions
Funding
Conflicts of Interest
Abbreviation
| The ith UCAV | |
| The jth target | |
| , | Operational benefit and corresponding weight |
| , | Operational cost and corresponding weight |
| Decision variables. If is assigned to , and otherwise | |
| Operational benefit of attacking | |
| Operational cost of attacking | |
| Weight of the kth sensor | |
| Value of , provided by the kth senor | |
| Lethality probability of missiles loaded on against | |
| The number of missiles loaded on | |
| Distance between and , provided by the kth senor | |
| Flight cost per unit distance from and |
References
- Zhang, Y.; Chen, J.; Shen, L.C. Real-Time Trajectory Planning for UCAV Air-to-Surface Attack Using Inverse Dynamics Optimization Method and Receding Horizon Control. Chin. J. Aeronaut. 2013, 26, 1038–1056. [Google Scholar] [CrossRef]
- Austin, R. Characteristics of Aircraft Types. In Unmanned Aircraft Systems: UAVs Design, Development and Deployment, 1st ed.; Moic, I., Seabridge, A., Langton, R., Eds.; John Wiley & Sons Ltd.: Chichester, UK, 2010; pp. 70–71. ISBN 978-0-470-05819-0. [Google Scholar]
- Jia, Z.Y.; Yu, J.Q.; Ai, X.L.; Xu, X.; Yang, D. Cooperative Multiple Task Assignment Problem with Stochastic Velocities and Time Windows for Heterogeneous Unmanned Aerial Vehicles Using a Genetic Algorithm. Aerosp. Sci. Technol. 2018, 76, 112–125. [Google Scholar] [CrossRef]
- Schumacher, C.; Chandler, P.; Pachter, M.; Pachter, L. UAV Task Assignment with Timing Constraints via Mixed-Integer Linear Programming. In Proceedings of the AIAA 3rd “Unmanned Unlimited” Technical Conference, Workshop and Exhibit, Chicago, IL, USA, 20–23 September 2004; pp. 2004-5352:1–2004-5352:10. [Google Scholar]
- Schumacher, C.; Chandler, P.; Pachter, M.; Pachter, L. Constrained Optimization for UAV Task Assignment. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; pp. 2004-5352:1–2004-5352:14. [Google Scholar]
- Darrah, M.A.; Niland, W.M.; Stolarik, B.M. Multiple UAV Dynamic Task Allocation using Mixed Integer Linear Programming in a SEAD Mission. In Proceedings of the Infotech@Aerospace Conference, Arlington, VA, USA, 26–29 September 2005; pp. 2005-7164:1–2005-7164:11. [Google Scholar]
- Rasmussen, S.J.; Shima, T. Branch and bound tree search for assigning cooperating UAVs to multiple tasks. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 2171–2176. [Google Scholar]
- Rasmussen, S.J.; Shima, T. Tree Search Algorithm for Assigning Cooperating UAVs to Multiple Tasks. Int. J. Robust Nonlinear Control 2008, 18, 135–153. [Google Scholar] [CrossRef]
- Alighanbari, M.; How, J.P. Cooperative Task Assignment of Unmanned Aerial Vehicles in Adversarial Environments. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 4661–4666. [Google Scholar]
- Diaz, J.A.; Fernandez, E. A Tabu Search Heuristic for the Generalized Assignment Problem. Eur. J. Oper. Res. 2001, 132, 22–38. [Google Scholar] [CrossRef]
- Sun, X.L.; Qi, N.M.; Yao, W.R. Boolean Networks-Based Auction Algorithm for Task Assignment of Multiple UAVs. Math. Probl. Eng. 2015. [Google Scholar] [CrossRef]
- Ramirez-Atencia, C.; Bello-Orgaz, G.; R-Moreno, M.D.; Camacho, D. Solving Complex Multi-UAV Mission Planning Problems using Multi-Objective Genetic Algorithms. Soft Comput. 2017, 21, 4883–4900. [Google Scholar] [CrossRef]
- Darrah, M.; Fuller, E.; Munasinghe, T.; Duling, K.; Gautam, M.; Wathen, M. Using Genetic Algorithms for Tasking Teams of Raven UAVs. J. Intell. Robot. Syst. 2013, 70, 361–371. [Google Scholar] [CrossRef]
- Edison, E.; Shima, T. Integrated Task Assignment and Path Optimization for Cooperating Uninhabited Aerial Vehicles using Genetic Algorithms. Comput. Oper. Res. 2011, 38, 340–356. [Google Scholar] [CrossRef]
- Deng, Q.B.; Yu, J.Q.; Wang, N.F. Cooperative Task Assignment of Multiple Heterogeneous Unmanned Aerial Vehicles using a Modified Genetic Algorithm with Multi-Type Genes. Chin. J. Aeronaut. 2013, 26, 1238–1250. [Google Scholar] [CrossRef]
- Zhong, Y.; Yao, P.Y.; Sun, Y.; Yang, J. Cooperative Task Allocation Method of MCAV/UCAV Formation. Math. Probl. Eng. 2016. [Google Scholar] [CrossRef]
- Han, B.W.; Yao, P.Y.; Sun, Y. UAVS Cooperative Task Allocation Based on Multi-objective MSQPSO Algorithm. Acta Electron. Sin. 2017, 45, 1856–1863. [Google Scholar] [CrossRef]
- Duan, H.B.; Li, P.; Yu, Y.X. A Predator-prey Particle Swarm Optimization Approach to Multiple UCAV Air Combat Modeled by Dynamic Game Theory. IEEE/CAA J. Autom. Sin. 2015, 2, 11–18. [Google Scholar] [CrossRef]
- Mataric, M.; Sukhatme, G.; Østergaard, E. Multi-Robot Task Allocation in Uncertain Environments. Auton. Robot. 2003, 14, 255–263. [Google Scholar] [CrossRef]
- Hooshangi, N.; Alesheikh, A.A. Agent-based Task Allocation under Uncertainties in Disaster Environments: An Approach to Interval Uncertainty. Int. J. Disast. Risk Reduct. 2017, 24, 160–171. [Google Scholar] [CrossRef]
- Kim, M.H.; Baik, H.; Lee, S. Resource Welfare Based Task Allocation for UAV Team with Resource Constraints. J. Intell. Robot. Syst. 2015, 77, 611–627. [Google Scholar] [CrossRef]
- Fu, X.W.; Wang, H.; Li, B.; Gao, X.G. An Efficient Sampling-Based Algorithms using Active Learning and Manifold Learning for Multiple Unmanned Aerial Vehicle Task Allocation under Uncertainty. Sensors 2018, 18, 2645. [Google Scholar] [CrossRef] [PubMed]
- Capitan, J.; Spaan, M.; Merino, L.; Ollero, A. Decentralized Multi-Robot Cooperation with Auctioned POMDPs. Int. J. Robot. Res. 2013, 32, 650–671. [Google Scholar] [CrossRef]
- Capitan, J.; Merino, L.; Ollero, A. Cooperative Decision-Making under Uncertainties for Multi-Target Surveillance with Multiples UAVs. J. Intell. Robot. Syst. 2016, 84, 371–386. [Google Scholar] [CrossRef]
- Ji, X.T.; Niu, Y.F.; Shen, L.C. Robust Satisficing Decision Making for Unmanned Aerial Vehicle Complex Missions under Severe Uncertainty. PLoS ONE 2016, 11, 1–35. [Google Scholar] [CrossRef] [PubMed]
- Ure, N.K.; Chowdhary, G.; How, J.P.; Vavrina, M.A.; Vian, J. Health Aware Planning Under Uncertainty for UAV Missions with Heterogeneous Teams. In Proceedings of the European Control Conference (ECC), Zürich, Switzerland, 17–19 July 2013; pp. 3312–3319. [Google Scholar]
- Wang, X.L.; Wu, J.B.; Huang, H.B.; Deng, S. Multiple Tasks Scheduling Algorithm for UAV Attacking in Uncertain Environment. In Proceedings of the International Conference on Systems and Informatics (ICSAI), Yantai, China, 19–20 May 2012; pp. 735–739. [Google Scholar]
- Liu, L.T.; Shell, D.A. Assessing Optimal Assignment under Uncertainty: An Interval-based Algorithm. Int. J. Robot. Res. 2011, 30, 936–953. [Google Scholar] [CrossRef]
- Liu, L.T.; Shell, D.A. Tackling Task Allocation Uncertainty via a Combinatorial Method. In Proceedings of the IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), College Station, TX, USA, 5–8 November 2012; pp. 1–6. [Google Scholar]
- Lahdelma, R.; Hokkanen, J.; Salminen, P. SMAA-Stochastic Multiobjective Acceptability Analysis. Eur. J. Oper. Res. 1998, 106, 137–143. [Google Scholar] [CrossRef]
- Hu, X.X.; Cheng, J.; He, L. Task Assignment for Multi-UAV under Severe Uncertainty by Using Stochastic Multicriteria Acceptability Analysis. Math. Probl. Eng. 2015. [Google Scholar] [CrossRef]
- Lahdelma, R.; Salminen, P. SMAA-2: Stochastic Multicriteria Acceptability Analysis for Group Decision Making. Oper. Res. 2001, 49, 444–454. [Google Scholar] [CrossRef]
- Zhu, F.L.; Zhong, P.A.; Wu, Y.N.; Sun, Y.M.; Chen, J.; Jia, B.Y. SMAA-based Stochastic Multi-Criteria Decision Making for Reservoir Flood Control Operation. Stoch. Environ. Res. Risk Assess. 2017, 31, 1485–1497. [Google Scholar] [CrossRef]
- Tervonen, T.; Lahdelma, R. Implementing Stochastic Multicriteria Acceptability Analysis. Eur. J. Oper. Res. 2007, 178, 500–513. [Google Scholar] [CrossRef]
- Wang, H.C.; Jiao, W.L.; Lahdelma, R.; Zhu, C.Z.; Zou, P.H. Stochastic Multicriteria Acceptability Analysis for Evaluation of Combined Heat and Power Units. Energies 2015, 8, 59–78. [Google Scholar] [CrossRef]
- Kangasa, A.; Kangasb, J.; Lahdelma, R.; Salminen, P. Using SMAA-2 Method with Dependent Uncertainties for Strategic Forest Planning. For. Policy Econ. 2006, 9, 113–125. [Google Scholar] [CrossRef]
- Yang, F.; Song, S.L.; Huang, W.; Xia, Q. SMAA-PO: Project Portfolio Optimization Problems Based on Stochastic Multicriteria Acceptability Analysis. Ann. Oper. Res. 2015, 233, 535–547. [Google Scholar] [CrossRef]
- Wang, X.F.; Xiao, M.S. Approach of Group Decision Making Based on Normal Distribution Interval Number with Incomplete Information. Control Decis. 2010, 25, 1494–1498. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Y.X.; Ge, Z.H. Probability Measure of Interval-Number Based on Normal Distribution and Multi-Attribute Decision Making. Syst. Eng. Electron. 2008, 30, 652–654. [Google Scholar] [CrossRef]
- Lehmann, R. 3 sigma-Rule for Outlier Detection from the Viewpoint of Geodetic Adjustment. J. Surv. Eng. 2013, 139, 157–165. [Google Scholar] [CrossRef]
- Tran, L.; Duckstein, L. Multiobjective Fuzzy Regression with Central Tendency and Possibilistic Properties. Fuzzy Set. Syst. 2002, 130, 21–31. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.L.; Zhang, M.; Liu, H. Ranking interval numbers based a new distance measure. J. Xihua Univ. 2008, 27, 87–90. [Google Scholar] [CrossRef]
- Zhang, L.E.; Wang, X.F. Approach to Stochastic Multi-Criteria Group Decision Making Based on Normal Distribution Prioritized Aggregation Operator. J. Hunan Univ. Technol. 2014, 28. [Google Scholar] [CrossRef]
- Chen, X.H.; Liu, Y.F. Expert Weights Determination Method and Realization Algorithm Based on Interval Numbers Group Decision Matrices. Syst. Eng. Electron. 2010, 32, 2128–2131. [Google Scholar] [CrossRef]
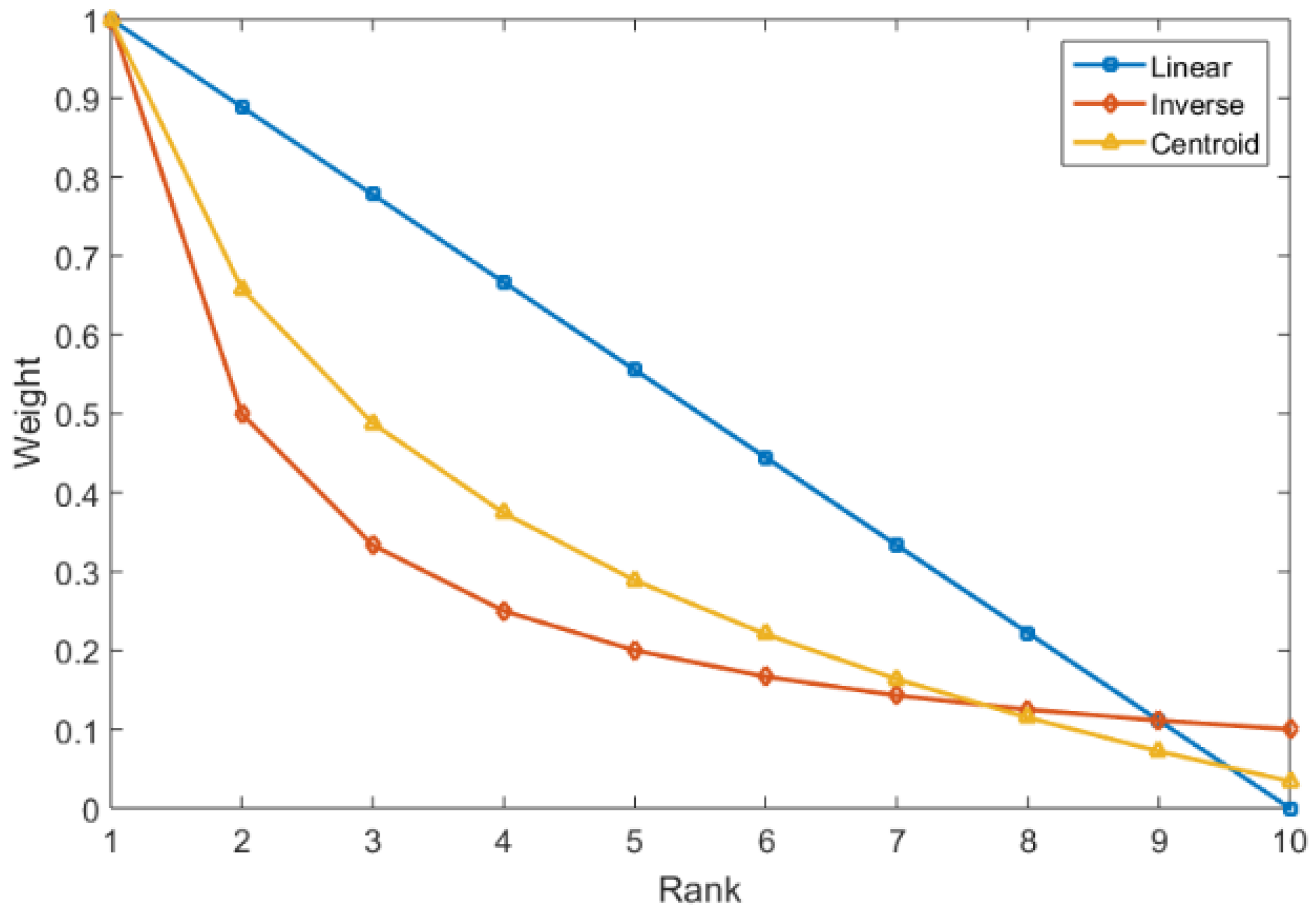
- Lahdelma, R.; Salminen, P. The Shape of the Utility or Value Function in Stochastic Multicriteria Acceptability Analysis. Oper. Res. Spectr. 2012, 34, 785–802. [Google Scholar] [CrossRef]
| Sensors | Target Value | |
|---|---|---|
| Sensor 1 | ||
| Sensor 2 | ||
| Sensor 3 | ||
| Sensor 4 |
| UCAVs | |||
|---|---|---|---|
| 6 | |||
| 8 | |||
| 6 | |||
| 6 |
| Parameters | Subjective Weight Vector of Sensors | Initial Objective Weight Vector of Sensors | Error Margin | Adjustment Factor |
|---|---|---|---|---|
| Value | [0.20, 0.10, 0.35, 0.35] | [0.25, 0.25, 0.25, 0.25] | 10−8 | 0.5 |
| Sensors | Target Value | |
|---|---|---|
| Sensor 1 | ||
| Sensor 2 | ||
| Sensor 3 | ||
| Sensor 4 |
| Sensor 1 | Sensor 2 | Sensor 3 | Sensor 4 | |
|---|---|---|---|---|
| UCAV1 | ||||
| UCAV2 | ||||
| UCAV3 | ||||
| UCAV4 |
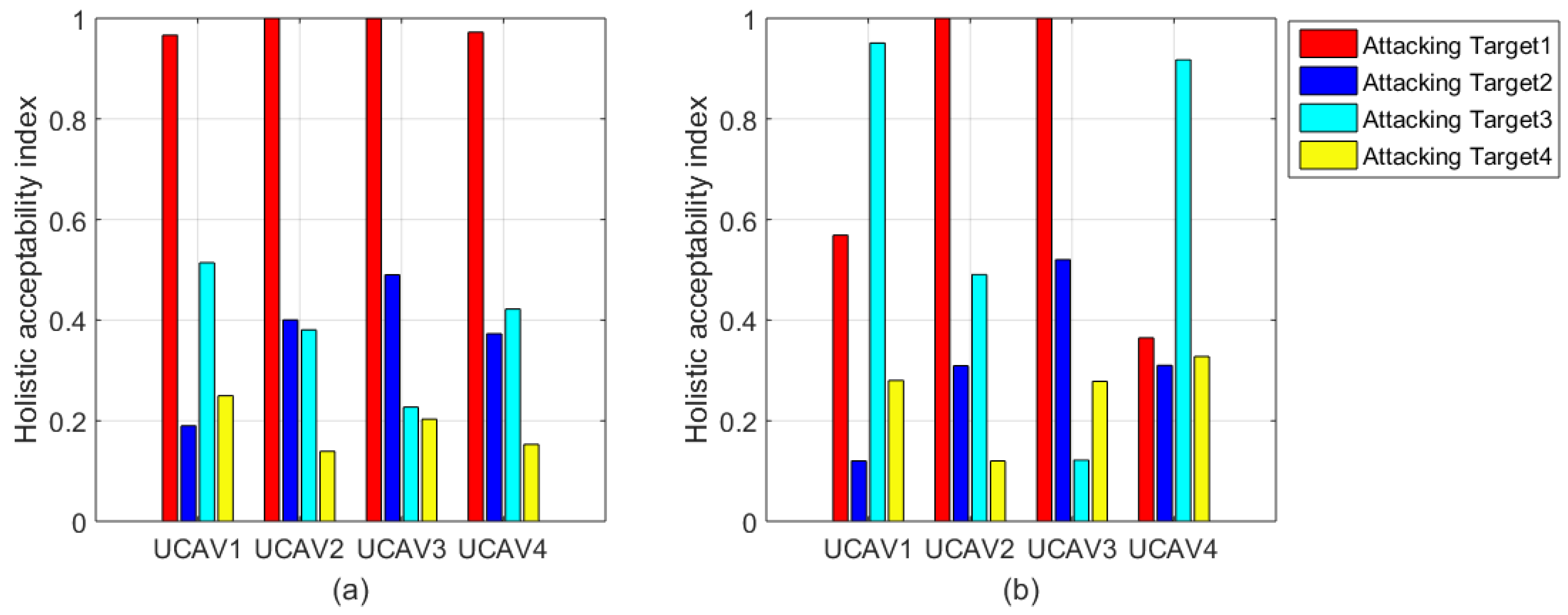
| 0.9664 | 0.1899 | 0.5141 | 0.2496 | 0.5689 | 0.1200 | 0.9511 | 0.2800 | ||
| 0.9999 | 0.4003 | 0.3808 | 0.1390 | 1.0000 | 0.3094 | 0.4906 | 0.1200 | ||
| 0.9996 | 0.4901 | 0.2272 | 0.2031 | 1.0000 | 0.5200 | 0.1216 | 0.2784 | ||
| 0.9724 | 0.3728 | 0.4219 | 0.1530 | 0.3646 | 0.3100 | 0.9176 | 0.3278 | ||
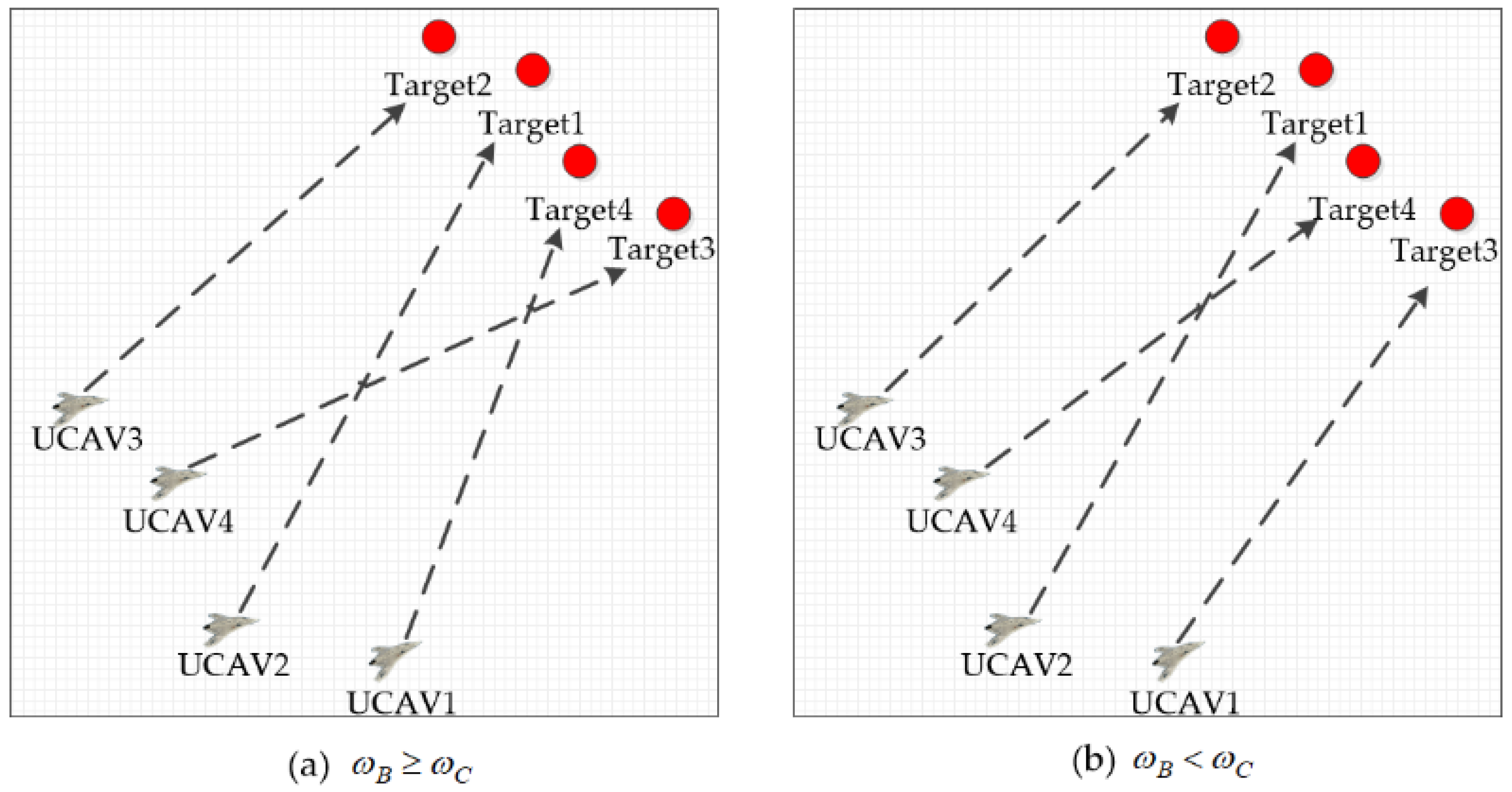
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | ||
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Luo, P.; Hu, X.; Zhang, X. Combining an Extended SMAA-2 Method with Integer Linear Programming for Task Assignment of Multi-UCAV under Multiple Uncertainties. Symmetry 2018, 10, 587. https://doi.org/10.3390/sym10110587
Wang J, Luo P, Hu X, Zhang X. Combining an Extended SMAA-2 Method with Integer Linear Programming for Task Assignment of Multi-UCAV under Multiple Uncertainties. Symmetry. 2018; 10(11):587. https://doi.org/10.3390/sym10110587
Chicago/Turabian StyleWang, Jun, Pengcheng Luo, Xinwu Hu, and Xiaonan Zhang. 2018. "Combining an Extended SMAA-2 Method with Integer Linear Programming for Task Assignment of Multi-UCAV under Multiple Uncertainties" Symmetry 10, no. 11: 587. https://doi.org/10.3390/sym10110587
APA StyleWang, J., Luo, P., Hu, X., & Zhang, X. (2018). Combining an Extended SMAA-2 Method with Integer Linear Programming for Task Assignment of Multi-UCAV under Multiple Uncertainties. Symmetry, 10(11), 587. https://doi.org/10.3390/sym10110587




