Abstract
In this study, we apply a robust optimization approach to a p-center facility location problem under uncertainty. Based on a symmetric interval and a multiple allocation strategy, we use three types of uncertainty sets to formulate the robust problem: box uncertainty, ellipsoidal uncertainty, and cardinality-constrained uncertainty. The equivalent robust counterpart models can be solved to optimality using Gurobi. Comprehensive numerical experiments have been conducted by comparing the performance of the different robust models, which illustrate the pattern of robust solutions, and allocating a demand node to multiple facilities can reduce the price of robustness, and reveal that alternative models of uncertainty can provide robust solutions with different conservativeness.
1. Introduction
The facility location problem addresses facility locations intended to serve a set of given demands. In reality, facility location is often a long-term decision and is vital in building a logistics network, so firms must consider the uncertainties in its life-span in the initial design. Uncertainties can be even more drastic in emergency circumstances, in which firms need to serve demand quickly and fairly. In such cases, decision-makers have to solve location problems under uncertain input data.
Facility locations under uncertainty received decades of research attention, with different approaches to embedding uncertain information in location models. These modeling techniques are classified mainly as robust approaches and stochastic approaches, depending on whether decision makers can acquire probabilistic information. For emergency situations such as natural disasters, it is difficult to acquire distributional information in advance, which motivates our study of the robust optimization (RO) approach in this work. Most existing studies on facility locations under uncertainty focus on optimizing the total cost or profit. However, the p-center location model, which minimizes the maximum cost between a client and its closest facility in a network, focuses on clients “who are poorest served” and is more suitable for emergency services. A multiple allocation strategy is practical and may improve the price of robustness of a location plan.
This study presents robust p-center facility location models based on three types of cost uncertainty: box uncertainty, ellipsoid uncertainty and, cardinality-constrained uncertainty. Along with a multiple allocation strategy, we can develop robust solutions with different structures from our models. We present the tractable formulations and compare the performance of three RO approaches through a series of numerical experiments.
The paper proceeds as follows: in Section 2, we review the relevant literature on the facility location problem under uncertainty and RO approaches. In Section 3, we adopt three RO approaches to formulate robust p-center models and present their tractabilities, and illustrate the causes and robustness of the multiple allocation strategy. In Section 4, we conduct a series of numerical experiments to illustrate the pattern of the robust solutions and compare the performance of different RO models. In Section 5, we provide conclusions and discuss future research directions.
2. Literature Review
The facility location problem is a classic area with many years of research. The fundamental concepts of location research include p-median problems, fixed-charge problems, covering problems, and p-center problems. The first two problems are widely studied and focus on minimizing the total cost, though overall performance may not be a priority during emergency situations, in which case the last two problems are applicable. Among these models, the goal of the p-center model is to minimize the worst performance (cost) of a network, and is suitable when service equity for every client is very important. Jia et al. [1] studies the p-center problem for locating medical services in a large-scale emergency. Calik [2] is the first to study a multiple allocation strategy for the p-center problem with capacitated facilities by presenting a branch-and-cut algorithm to solve the model. However, for the standard uncapacitated p-center problem, multiple allocation is meaningless since it can only produce a single allocation result [3]. Sarkar and Majumder [4] propose three facility location problems with different dimensions. They extend a two-dimensional problem by considering commodity type and transportation mode. We only consider a two-dimensional p-center problem, but in an uncertain environment with no probabilistic information, in which case robust optimization is the most appropriate method. Daskin [5] and Laporte et al. [6] provide more comprehensive discussions of facility location research.
Facility location problems under uncertainty received considerable attention in recent years. Snyder [7] provide detailed reviews. This line of study uses three categories of methods: RO, stochastic programming (SP), and chance constraints. The last two approaches require probabilistic information in advance [8,9]. We choose the RO approach to model uncertainty due to the low availability of distributional information in circumstances such as emergencies.
RO is an attractive optimization method with an increasing amount of recent research. The fundamental element of RO is various uncertainty sets, such as interval and finite sets of scenarios by Kouvelis and Yu [10], box uncertainty by Soyster [11], ellipsoidal uncertainty by Ben-Tal and Nemirovski [12,13], cardinality-constrained uncertainty by Bertsimas and Sim [14], and so on, each with distinct tractability and conservativeness. Normally, an uncertain problem is transformed to its equivalent or approximate tractable robust counterpart. Apart from the classic RO approaches, Bösing and D’Andreagiovanni [15] extend cardinality-constrained uncertainty by introducing multiple deviations bands, developing a cutting-plane method to solve the robust model. Gabrel et al. [16] introduce a robustness criterion, which optimizes partial scenarios and guarantees the worst performance for any scenario. Goh and Sim [17] develop a distributionally RO approach for uncertain problems with partial distribution information. More recently, RO has been applied to multi-stage problems. Zeng and Zhao [18] present an exact column-and-constraint algorithm for the two-stage RO models. Hanasusanto et al. [19] study approximate solution methods for the robust two-stage binary program. For systematic RO theories and applications, we refer to Ben-Tal et al. [20], Bertsimas et al. [21], Gabrel et al. [22], Gorissen et al. [23].
RO applications to the facility location problem have emerged in the last decade. Baron et al. [24] apply RO to the facility location problem by modeling demand uncertainty as box and ellipsoid in the fixed-charge problem. Nikoofal and Sadjadi [25] propose a robust p-median model with edge length uncertainty using an “uncertainty budget” to limit the total scaled variation of the uncertainty parameters. Lu and Sheu [26] present a robust vertex p-center model for locating urgent relief centers. Lu [27] models demand and time uncertainty in intervals, minimizing the worse-case deviation of the objective for a weighted vertex p-center problem. Gülpinar et al. [28] combine chance constraint, stochastic programming and RO methods to formulate robust facility location models, using Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR) to represent the decision maker’s risk preference. D’Andreagiovanni et al. [29] propose a connected facility location model for hybrid wired-wireless network design problem, using cardinality-constrained uncertainty to model wireless propagation, a primal heuristic method based on variable fixing and large neighborhood search is designed to solve the robust model. Some studies apply two-stage RO to facility location problems. Atamturk and Zhang [30] is the first to propose a two-stage RO model for network flow and design problems. Hervet et al. [31] introduce a two-stage robust network design problem under scenario-based demand uncertainty, solving it with a column-and-constraints generation algorithm. Gabrel et al. [32] propose a two-stage robust location-transportation model with a cardinality-constrained demand uncertainty set. An et al. [33] present a two-stage RO model for a reliable p-median problem using a cardinality-constrained set to model facility disruption uncertainty. Álvarez-Miranda et al. [34] propose a two-stage recoverable fixed-charge facility location problem with a finite uncertainty set of scenarios, in which both the location and allocation decisions are made in two stages. Peng et al. [35] present a multiplicative cardinality-constrained uncertainty, considering a two-stage facility location problem with disruptions. Furthermore, Lu et al. [36] is the first to apply the distributionally RO method to model disruption uncertainty in the context of facility location. We compare this paper with the related references in Table 1, the column “CC” stands for cardinality-constrained uncertainty and “2SRO” represents the two-stage robust optimization model. To the best of our knowledge, we present the first robust p-center facility location model applying set-based RO approach, modelling uncertain cost as box, ellipsoidal and cardinality-constrained uncertainty.

Table 1.
Contribution to the literature.
3. A Robust Multiple Allocation p-Center Facility Location Problem
The deterministic p-center problem is proved to be NP-hard by Kariv and Hakimi [37], aiming to locate p facilities to serve given demand while minimizing the maximum cost to serve a demand node. We assume that in our models:
- (i)
- The capacity of all open facilities can satisfy all the demands. The uncapacitated facility location problem (UFLP) is one of the fundamental location problems described in Laporte et al. [6];
- (ii)
- The demand is infinitely divisible and can be fulfilled by one or multiple facilities as addressed in Calik [2].
Based on the formulation of the deterministic p-center problem in Section 3.1, we assume the cost is uncertain and contained in an uncertainty set, applying three RO approaches to formulate robust models for the multiple allocation p-center problem under cost uncertainty in Section 3.2, Section 3.3 and Section 3.4. We implement a box uncertainty set and an ellipsoidal uncertainty set using an approach similar to that of Baron et al. [24]. We introduce the cardinality-constrained uncertainty set following Bertsimas and Sim [14].
3.1. Deterministic Problem Formulation
Assume all data are known in advance in the problem. Sets I and J are on a connected graph G, where I is the set of demand nodes and J is the set of potential facility nodes. For every , , suppose that we know the unit cost between node i and node j, , and the demand for node i, . and are decision variables: if facility in node j is open and , otherwise. Unlike the classic p-center model, we relax to , so x is the proportion of i’s demand a facility in node j serves. We further explain this multiple allocation strategy in Section 3.5. Following Daskin [5], we formulate the multiple allocation uncapacitated p-center problem as follows:
PCENTER
The objective function (1) and constraints (2) minimize the maximum cost to serve a demand node. Constraint (3) limits the total number of open facilities. Constraints (4) and (5) guarantee that demand can be assigned only to open facilities and all demand must be served.
When the problem in PCENTER remains deterministic, we can solve it as a mixed integer linear program (MILP). However, in an uncertain environment without probabilistic information, the original solution may no longer be optimal. Let be the uncertain cost between nodes i and j. We can apply the RO approaches in the following sections to reformulate the problem based on different uncertainty sets.
3.2. The Robust Problem: Box Uncertainty
We consider the case that all unit costs , , for serving a demand node i are uncertain and bounded in a symmetric interval. L is the maximum cost under box uncertainty for serving all demand nodes. Let be the nominal value of . Under box uncertainty, we choose from a symmetric box: with mean , determines the uncertain scale, and . Let , be the box uncertainty set.
We can augment constraints (2) such that
Because , the robust counterparts of constraints (7) are
Therefore, the robust counterpart of PCENTER, which we can solve using an MILP solver, is as follows:
3.3. The Robust Problem: Ellipsoid Uncertainty
For the case of ellipsoid uncertainty, we assume that all unit costs , , for serving a demand node i are bounded in an ellipsoid. L is the maximum cost under ellipsoid uncertainty for serving all demand nodes. We consider a total-normalized-squared deviation to define an ellipsoid uncertainty set:
where is a parameter that controls the robustness in for constraint i.
Let , be a order diagonal matrix with non-zero entries ; then,
The augmented counterpart of constraints (2) are
According to the Karush–Kuhn–Tucker condition, the robust counterparts of constraints (11) are
Let , so we can linearize constraints (12) such that
The robust counterpart of PCENTER with ellipsoidal uncertainty is
is a conic quadratic program that we can solve using a mixed-integer quadratic constrained program (MIQCP) solver, such as Gurobi.
3.4. The Robust Problem: Cardinality-Constrained Uncertainty
Under the cardinality-constrained uncertainty, we give a budget , which limits the number of unit costs (, ) that can vary from their nominal values. L is the maximum cost under cardinality-constrained uncertainty for serving all demand nodes. The robust formulation of the constraints (2) becomes
Let vector be a feasible solution for constraints (15). The protection function of the ith constraint (15) is
which is equivalent to
Let , be the dual value corresponding to constraints (18) and (19); then, the dual of the Problem (17)–(19) is
According to strong duality, we can formulate the robust counterpart of PCENTER under cardinality-constrained uncertainty as an MILP such that
3.5. Robustness of the Multiple Allocation Strategy
According to Nemhauser and Wolsey [3], we can relax all allocation variables to in PCENTER, which means that only single allocation solutions can be derived from deterministic uncapacitated p-center problem. Because each client is always served by its “closest” facility to minimize the cost, unless more than one facility has the same cost for a demand node. However, this conclusion is invalid when the “closest” facility is unclear. Our robust problems are able to provide mulitiple allocation solutions under uncertain circumstances.
In Figure 1 and Figure 2, we illustrate the impact of the three uncertainty sets on the choice of facilities for a single demand node i. Due to the constraints in (8), (12) and (15), every cost varies in the range of . Suppose that demand node i can be allocated to four open facilities, 1 to 4 along the y-axis, with the cost of each facility to serve demand node i varying in the four intervals above the x axis. Both facilities 1 and 2 may provide the lowest cost for i. Figure 1 shows that box uncertainty considers only the worst unit cost between every demand node and facility, and thus solving the robust problem is equivalent to solving a deterministic one. The best choice is obviously facility 1.
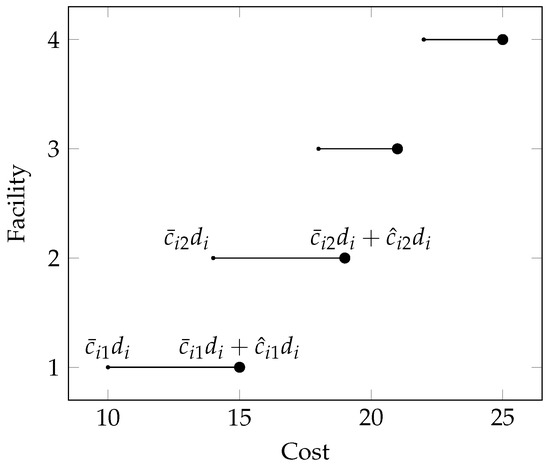
Figure 1.
The choice of facilities to serve demand node i: Box uncertainty.
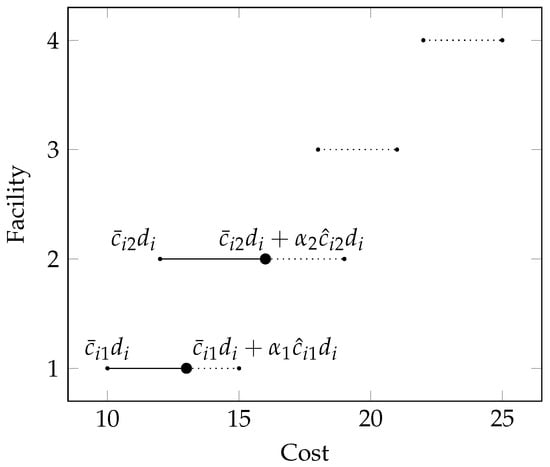
Figure 2.
The choice of facilities to serve demand node i: Ellipsoidal and Cardinality-constrained uncertainty.
For the other two robust problems, both the ellipsoidal uncertainty set and cardinality-constrained uncertainty set can prevent all uncertain unit costs from reaching their worst value simultaneously. In this case, the optimal choice of facility for demand node i may be unclear when more than one facility can provide the minimum unit cost. Figure 2 provides an example of choosing multiple facilities to serve demand node i. Instead of applying a single allocation strategy, which may lead to a poor solution, the robust problems under ellipsoidal and cardinality-constrained uncertainty can provide multiple allocation solutions, resulting in choosing facilities 1 and 2 together, which are both possible optimal choices with a single allocation strategy, but it requires that the robust parameters and be within a certain range (e.g., ).
For any demand node i, we have the following proposition:
Proposition 1.
In the robust p-center problems with ellipsoidal uncertainty and cardinality-constrained uncertainty:
(i) In the optimal solution, a demand node i can possibly be served by multiple facilities.
(ii) When a demand node i is allocated to multiple facilities, the optimal solution under ellipsoidal uncertainty is related to , the optimal solution under cardinality-constrained uncertainty is fixed and not related to .
Proof of Proposition 1.
Choosing optimal facilities for serving demand node i ( are under cardinality-constrained uncertainty) is equivalent to solving:
where is the deviation variable, and is the set of open facilities. Let , , , , , , . The Model (28)–(34) is a convex program, which can be solved applying the Karush–Kuhn–Tucker condition in Equations (36)–(47), the Lagrange function is in Equation (35):
Let , so that, for all . Immediately, we know for all , because of Equations (34) and (47); otherwise, for all , , . For all, due to Equations (32) and (43). Then, consider the following cases:
- case 1: . Due to Equations (29) and (45), , meaning only one facility is selected to serve i, only when .
- case 2: . Due to Equations (33), (34), (36) and (45), for all , , meaning multiple facilities are choosen to serve demand node i, only when all , , are equal.
- case 3: , . Due to Equation (37), for all , . Therefore, is only related to , , which is fixed.
- case 4: , . Due to Equations (36) and (41), , so that all , , are equal. This requires all are identical, we assume this is a special case that cannot occur.
Furthermore, we can evaluate the robust problem under ellipsoidal uncertainty by replacing constraint (30) with , let . Similar conclusions can be derived as under cardinality-constrained uncertainty, except that the multiple solutions require that, for all , . Due to Equation (30), varies with as well as . □
The multiple allocation solution to the problem with ellipsoidal and cardinality-constrained uncertainty will lower the maximum cost to serve a demand node because it does not consider the worst value of every uncertain costs, as box uncertainty does. Therefore, for the multiple allocation p-center problem under uncertain cost, ellipsoidal and cardinality-constrained uncertainty is less conservative than box uncertainty is, but may lead to a higher maximum cost to serve a demand node when all uncertain costs vary to their worst value. We further study how the three RO models affect the objective values and solutions in the next section.
4. Numerical Study
In this section, we provide an illustrative example in Section 4.1 to show the pattern of solutions for the three RO models under different robustness levels. We study how the overlapping uncertain costs affect the solutions in Section 4.2. We also conduct a set of experiments to compare the performance of the three RO approaches in Section 4.3.
All of the experiments are based on artificial data. For the experiments in Section 4.1 and Section 4.2, we give a simple three-node network and set . All data are designed by ourself for illustration purpose, we assume , for computational ease. In Section 4.3, we generate a random 10-node network for each instance and set . We described the detailed method for generating input data and assume , . We solve all robust counterpart models using Gurobi 7.5.
4.1. Effect of Robustness Parameters
We compare different solutions from the three RO models in Section 3. A simple instance is as follows: , , ; , , where and are overlapping. We test the change in solutions as a function of the robustness parameter in Section 3.3 and in Section 3.4. Figure 3 and Figure 4 show the objective values and solutions with respect to or , respectively. In the following figures, “box”, “ell”, and “cc” represent the models with box, ellipsoidal, and cardinality-constrained uncertainty, respectively.
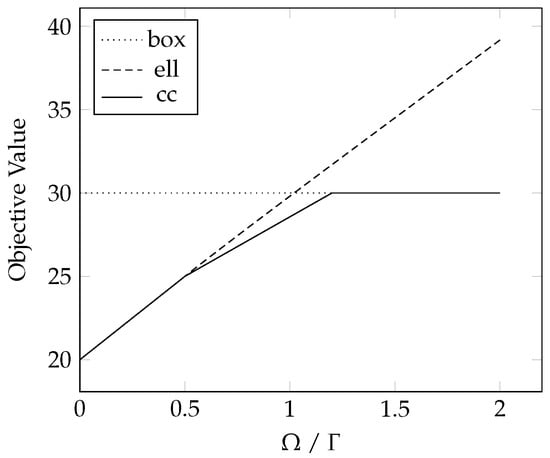
Figure 3.
Objective values of the example with respect to and .
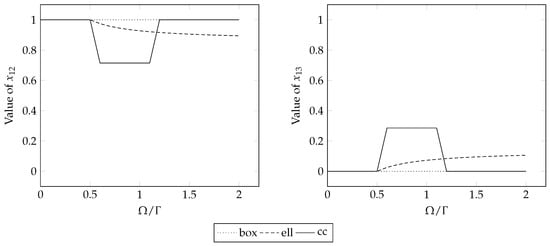
Figure 4.
Solutions to the example with respect to and : (, , , , , , and constantly).
From Figure 3, we see that, when the value of or is within a certain range, the robust problems with ellipsoidal and cardinality-constrained uncertainty produce solutions in which and are non-binary, meaning that the facilities in nodes 2 and 3 can simultaneously serve the demand from node 1. However, in the cardinality-constrained case, and is fixed when we produce multiple allocation solutions, while, for the ellipsoidal case, and vary with . Figure 3 and Figure 4 show that, when using a multiple allocation strategy, the objective values of the models with ellipsoidal and cardinality-constrained uncertainty are not as conservative as for box uncertainty. Note that, for the ith constraint, when , is the largest ellipsoid contained in , so, if , the solution to the corresponding model may be the same as in the box case, which means that the objective value of ellipsoidal case has no practical meaning when it is larger than that in the box case.
4.2. Effect of Overlapping Uncertain Cost
As we mentioned in Section 3.5, we can derive multiple allocation solutions from the problem with ellipsoidal and cardinality-constrained uncertainty. Because overlapping cost intervals serve a demand node means that we cannot find a single optimal facility, we test how the overlapping scale affects the solutions in this subsection. For this illustration, , , ; , , and . is a value that controls how much overlaps with . Let . In Figure 5 and Figure 6, we plot the objective values and solutions of the RO models, respectively, as the value of changes.
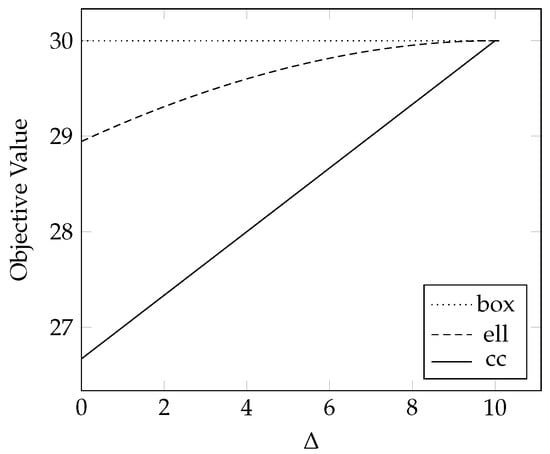
Figure 5.
Objective values of the example with respect to .
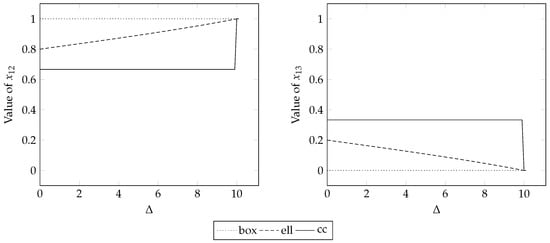
Figure 6.
Solutions to the example with respect to : (, , , , , , and constantly).
Figure 5 verifies that the overlapping cost intervals that determine the objective value leads to the multiple allocation solution. When , and do not overlap, and the three RO models produce identical solutions. When , the objective value of the cardinality-constrained case increases linearly with and stays lower than that in the ellipsoidal case, as in Section 4.1, until they converge when . In Figure 6, we note that affects the solution to the ellipsoidal case; for and , the ellipsoidal case values change nonlinearly as increases, while the solutions to the cardinality-constrained case maintain the same value as long as and overlap.
4.3. Comparison of RO Approaches
We regard as the scale of cost uncertainty, and choose a data range as cost diversity. We generate every from 1 to 100 randomly (uniformly), and , and randomly from . Letting , , we generate randomly and uniformly from , , , and . We generate 100 instances for each combination of and a data range of . Set . Table 2 and Figure 7 report the results. In Table 2, columns “”, “”, and “” report the mean objective values of robust problems with box, ellipsoidal and cardinality-constrained uncertainty, respectively. Each cell in the table report the results for 100 experiments. The column “SA” shows the number of experiments that provide only single allocation solutions. Figure 7 is the graphical representation of Table 2, and we plot the comparison between the three RO methods group by .

Table 2.
Comparison of the three models under different scales of cost uncertainty and diversity.
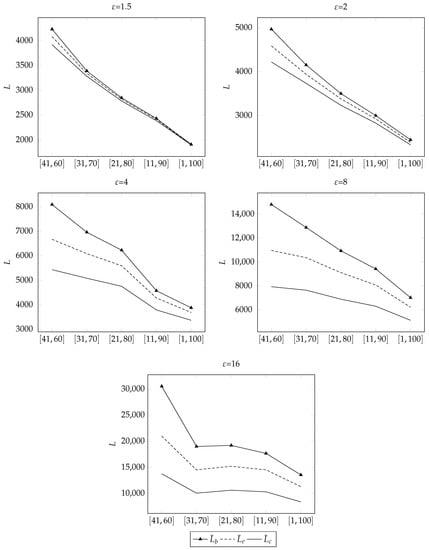
Figure 7.
Comparison of the three models under different scales of cost uncertainty and diversity.
From the table, we see that the number of single allocation cases decreases with the scale of cost uncertainty and increases as the cost range of expands. Thus, as an example, with lower cost uncertainty and higher cost diversity, box uncertainty is more suitable because the other two models will probably give the same solution, especially when solving the model of ellipsoidal uncertainty requires dealing with a quadratic problem. However, with higher cost uncertainty and less cost diversity, the robust solutions of ellipsoidal and cardinality-constrained uncertainty can provide multiple allocation solutions that are not totally conservative. We observed from Table 2 and Figure 7 that, as grows, the difference between , , increases. With the same , the gap between the three RO methods decreases with the width of data range. This is because larger and a narrower data range may lead to more deeply overlapping uncertain costs. We also observe this from Figure 5 because the gap between the three objective values narrows as increases.
5. Conclusions
In this study, we apply three classic RO modeling techniques to formulate a multiple allocation p-center facility location problem. Previous works in this area all focus on minimizing the total cost or maximizing profit. The comparison between three RO methods indicates that, between the deterministic problem with no robustness and the box uncertainty case, which is completely conservative, the cardinality-constrained uncertainty model is less conservative than the ellipsoidal uncertainty model overall. We also find that different RO methods are suited for different scales of cost uncertainty and diversity.
We are the first to apply set-based RO approaches modeling the uncertain cost in the p-center problem. Since p-center is widely applied in emergency services, and uncertainties with no distributional information are common in emergencies like natural disaster, our models are practical for locating an urgent distribution relief center or medical unit. Moreover, allocating the demand to multiple facilities is meaningful and this strategy can provide robust solutions that are not totally conservative.
We will further study the practical applications of our robust models, and the capacitated p-center model is a natural start. Combining with multiple dimensional location models (Sarkar and Majumder [4]) can also make our work more realistic. We consider only static decision-making in this study. Future work can apply robust adaptable optimization (Bertsimas et al. [21]) and other multi-stage RO methods (Hanasusanto et al. [19]) to formulate dynamic problems, which usually split the decision process into a here-and-now, wait-and-see procedure.
Author Contributions
Methodology, B.D. and H.Z.; Software, B.D.; Supervision, H.Z.; Writing—Original Draft, B.D.; Writing—Review and Editing, H.Z.
Funding
This work is supported by the National Natural Science Foundation of China under Grant No. 71471007.
Acknowledgments
We would like to thank the associate editor and the two reviewers for their helpful comments to improve the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jia, H.; Ordóñez, F.; Dessouky, M.M. A modeling framework for facility location of medical services for large-scale emergencies. IIE Trans. 2007, 39, 41–55. [Google Scholar] [CrossRef]
- Calik, H. Exact Solution Methodologies for the p-Center Problem Under Single and Multiple Allocation Strategies. Ph.D. Thesis, Bilkent University, Ankara, Turkey, 2013. [Google Scholar]
- Nemhauser, G.L.; Wolsey, L.A. Integer and Combinatorial Optimization; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Sarkar, B.; Majumder, A. A study on three different dimensional facility location problems. Econ. Model. 2013, 30, 879–887. [Google Scholar] [CrossRef]
- Daskin, M.S. Network and Discrete Location: Models, Algorithms, and Applications; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Laporte, G.; Nickel, S.; da Gama, F.S. Location Science; Springer: Berlin, Germany, 2015. [Google Scholar]
- Snyder, L.V. Facility location under uncertainty: A review. IIE Trans. 2006, 38, 547–564. [Google Scholar] [CrossRef]
- Louveaux, F.V. Discrete stochastic location models. Ann. Oper. Res. 1986, 6, 23–34. [Google Scholar] [CrossRef]
- Louveaux, F.V.; Peeters, D. A dual-based procedure for stochastic facility location. Oper. Res. 1992, 40, 564–573. [Google Scholar] [CrossRef]
- Kouvelis, P.; Yu, G. Robust Discrete Optimization and Its Applications; Kluwer Academic Publishers: Boston, MA, USA, 1997. [Google Scholar]
- Soyster, A.L. Convex programming with set-inclusive constraints and applications to inexact linear programming. Oper. Res. 1973, 21, 1154–1157. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust solutions of uncertain linear programs. Oper. Res. Lett. 1999, 25, 1–13. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust solutions of linear programming problems contaminated with uncertain data. Math. Programm. 2000, 88, 411–424. [Google Scholar] [CrossRef]
- Bertsimas, D.; Sim, M. The price of robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Büsing, C.; D’Andreagiovanni, F. New results about multi-band uncertainty in robust optimization. In Proceedings of the 11th International Symposium on Experimental Algorithms, Bordeaux, France, 7–9 June 2012; pp. 63–74. [Google Scholar]
- Gabrel, V.; Murat, C.; Thiele, A. Portfolio optimization with pw-robustness. EURO J. Comput. Optim. 2018, 6, 267–299. [Google Scholar] [CrossRef]
- Goh, J.; Sim, M. Distributionally robust optimization and its tractable approximations. Oper. Res. 2010, 58, 902–917. [Google Scholar] [CrossRef]
- Zeng, B.; Zhao, L. Solving two-stage robust optimization problems using a column-and-constraint generation method. Oper. Res. Lett. 2013, 41, 457–461. [Google Scholar] [CrossRef]
- Hanasusanto, G.A.; Kuhn, D.; Wiesemann, W. K-adaptability in two-stage robust binary programming. Oper. Res. 2015, 63, 877–891. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Ghaoui, L.E.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Bertsimas, D.; Brown, D.B.; Caramanis, C. Theory and applications of robust optimization. SIAM Rev. 2011, 53, 464–501. [Google Scholar] [CrossRef]
- Gabrel, V.; Murat, C.; Thiele, A. Recent advances in robust optimization: An overview. Eur. J. Oper. Res. 2014, 235, 471–483. [Google Scholar] [CrossRef]
- Gorissen, B.L.; Yanıkoğlu, İ.; den Hertog, D. A practical guide to robust optimization. Omega 2015, 53, 124–137. [Google Scholar] [CrossRef]
- Baron, O.; Milner, J.; Naseraldin, H. Facility location: A robust optimization approach. Prod. Oper. Manag. 2011, 20, 772–785. [Google Scholar] [CrossRef]
- Nikoofal, M.E.; Sadjadi, S.J. A robust optimization model for p-median problem with uncertain edge lengths. Int. J. Adv. Manuf. Technol. 2010, 50, 391–397. [Google Scholar] [CrossRef]
- Lu, C.C.; Sheu, J.B. Robust vertex p-center model for locating urgent relief distribution centers. Comput. Oper. Res. 2013, 40, 2128–2137. [Google Scholar] [CrossRef]
- Lu, C.C. Robust weighted vertex p-center model considering uncertain data: An application to emergency management. Eur. J. Oper. Res. 2013, 230, 113–121. [Google Scholar] [CrossRef]
- Gülpinar, N.; Pachamanova, D.; Çanakoglu, E. Robust strategies for facility location under uncertainty. Eur. J. Oper. Res. 2013, 225, 21–35. [Google Scholar] [CrossRef]
- D’Andreagiovanni, F.; Mett, F.; Nardin, A.; Pulaj, J. Integrating LP-guided variable fixing with MIP heuristics in the robust design of hybrid wired-wireless FTTx access networks. Appl. Soft Comput. 2017, 61, 1074–1087. [Google Scholar] [CrossRef]
- Atamturk, A.; Zhang, M. Two-stage robust network flow and design under demand uncertainty. Oper. Res. 2007, 55, 662–673. [Google Scholar] [CrossRef]
- Hervet, C.; Faye, A.; Costa, M.C.; Chardy, M.; Francfort, S. Solving the two-stage robust FTTH network design problem under demand uncertainty. Electron. Notes Discrete Math. 2013, 41, 335–342. [Google Scholar] [CrossRef]
- Gabrel, V.; Lacroix, M.; Murat, C.; Remli, N. Robust location transportation problems under uncertain demands. Discrete Appl. Math. 2014, 164, 100–111. [Google Scholar] [CrossRef]
- An, Y.; Zeng, B.; Zhang, Y.; Zhao, L. Reliable p-median facility location problem: Two-stage robust models and algorithms. Transp. Res. Part B Methodol. 2014, 64, 54–72. [Google Scholar] [CrossRef]
- Álvarez-Miranda, E.; Fernández, E.; Ljubić, I. The recoverable robust facility location problem. Transp. Res. Part B Methodol. 2015, 79, 93–120. [Google Scholar] [CrossRef]
- Peng, C.; Li, J.; Wang, S. Two-stage robust facility location problem with multiplicative uncertainties and disruptions. In Proceedings of the 14th International Conference on Services Systems and Services Management (ICSSSM 2017), Dalian, China, 16–18 June 2017; pp. 1–6. [Google Scholar]
- Lu, M.; Ran, L.; Shen, Z.j.M. Reliable facility location design under uncertain correlated disruption. Manuf. Serv. Oper. Manag. 2015, 17, 445–455. [Google Scholar] [CrossRef]
- Kariv, O.; Hakimi, S.L. An algorithmic approach to network location problems. I: The p-centers. SIAM J. Appl. Math. 1979, 37, 513–538. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).