1. Introduction
In the study of t-norm based fuzzy logic systems [
1,
2,
3,
4,
5,
6,
7,
8,
9], algebraic systems (such as residuated lattices, BL-algebras, MTL-algebras, pseudo-BL algebras, pseudo-MTL algebras, et al.) play an important role. In this paper, we discuss pseudo-BCI/BCK algebras which are connected with non-commutative fuzzy logic systems (such that non-commutative residuared lattices, pseudo-BL/pseudo-MTL algebras).
BCK-algebras and BCI-algebras were introduced by Is
ki [
10] as algebras induced by Meredith’s implicational logics BCK and BCI. The name of BCK-algebra and BCI-algebra originates from the combinatories B, C, K, I in combinatory logic. The notion of pseudo-BCK algebra was introduced by G. Georgescu and A. Iorgulescu in [
11] as a non-commutative extension of BCK-algebras. Then, as common generalization of pseudo-BCK algebras and BCI-algebras, W.A. Dudek and Y.B. Jun introduced the concept of pseudo-BCI algebra in [
12]. In fact, there are many other non-classical logic algebraic systems related to BCK- and BCI-algebras, such as BCC-algebra, BZ-algebra and so forth, some monographs and papers on these topics can be found in [
7,
8,
9,
13,
14,
15,
16,
17,
18].
Pseudo-BCI-algebras are algebraic models of some extension of a noncommutative version of the BCI-logic, the corresponding logic is called pseudo-BCI logic [
19]. P. Emanovský and J. Kühr studied some properties of pseudo-BCI algebras, X.L. Xin et al. [
20] investigated monadic pseudo BCI-algebras and corresponding logics and some authors discussed the filter (ideal) theory of pseudo-BCI algebras [
21,
22,
23,
24,
25,
26,
27,
28]. Moreover, some notions of period, state and soft set are applied to pseudo-BCI algebras [
29,
30,
31].
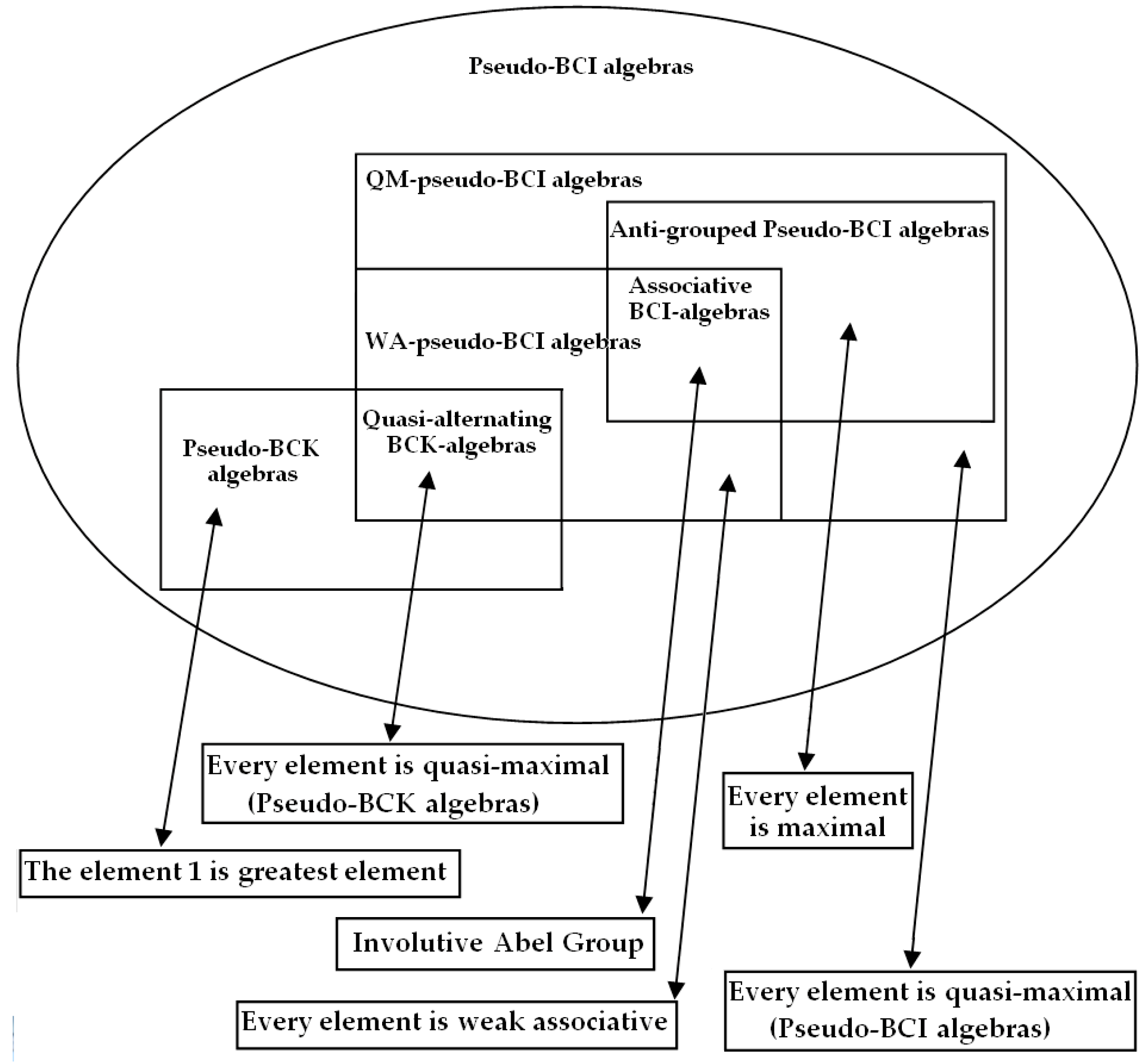
In this paper, we further study the structure characterizations of pseudo-BCI algebras. By using the notions of quasi-maximal element, quasi-left unit element, KG-union and direct product, we give the structure theorem of the class of pseudo-BCI algebras in which every element is quasi-maximal (call they QM-pseudo-BCI algebras). Moreover, we introduce weak associative property in pseudo-BCI algebras, discuss basic properties of weak associative pseudo-BCI algebra (WA-pseudo-BCI algebra) and establish the structure theorem of WA-pseudo-BCI algebra.
It should be noted that the original definition of pseudo-BCI/BCK algebra is different from the definition used in this paper. They are dual. We think that the logical semantics of this algebraic structure can be better represented by using the present definition.
2. Preliminaries
Definition 1 ([
10,
16])
. An algebra (A; →, 1) of type (2,0) is called a BCI-algebra if the following conditions are satisfied for all x, y, z from A:- (1)
- (2)
- (3)
- (4)
wheremeans . An algebra (A; →, 1) of type (2,0) is called a BCK-algebra if it is a BCI-algebra and satisfies:
- (5)
∀x ∈ A.
Definition 2 ([
10,
16])
. A BCK-algebra (A; →, 1) is called bounded if there exists unique element 0 such that 0 x = 1 for any x A. Definition 3 ([
13,
14])
. A BCK-algebra (A; →, 1) is called quasi-alternating BCK-algebra if it satisfies the following axiom: x, y X, x y implies x y =
y. Definition 4 ([
9,
11])
. A pseudo-BCK algebra is a structure (A; , , , 1
), where “” is a binary relation on A, “” and “” are binary operations on A and “1
” is an element of A, verifying the axioms: for all x, y, z A,- (1)
()(),()(),
- (2)
- (3)
- (4)
- (5)
x = y,
- (6)
If (A; , , , 1) is a pseudo-BCK algebra satisfying for all x, y A, then (A; , 1) is a BCK-algebra.
Proposition 1 ([
9,
11])
. Let (A; , , , 1) be a pseudo-BCK algebra, then A satisfy the following properties ():- (1)
- (2)
xz,
- (3)
- (4)
- (5)
- (6)
- (7)
- (8)
- (9)
Definition 5 ([
12)
. A pseudo-BCI algebra is a structure (A; , , , 1), where “” is a binary relation on A, “” and “” are binary operations on A and “1” is an element of A, verifying the axioms: for all x, y, z A,- (1)
- (2)
- (3)
- (4)
ifand , then x = y,
- (5)
iffiff
Note that, every pseudo-BCI algebra satisfying for all x, y A is a BCI-algebra.
Proposition 2 ([
12,
22,
24])
. Let (A; , , , 1) be a pseudo-BCI algebra, then A satisfy the following properties ():- (1)
ifthen
- (2)
ifthenand
- (3)
ifandthen ,
- (4)
- (5)
iff
- (6)
- (7)
ifthenand
- (8)
- (9)
- (10)
- (11)
(x → y) → 1 = (x → 1) ⇝ (y → 1),(x ⇝ y) ⇝ 1 = (x ⇝ 1) → (y → 1)
- (12)
.
Definition 6 ([
10,
24])
. A pseudo-BCI algebra A is said to be an anti-grouped pseudo-BCI algebra if it satisfies the following identities: Proposition 3 ([
24])
. A pseudo-BCI algebra A is anti-grouped if and only if it satisfies:(G1) for all x, y, z ∈ A, (x y) (x z) = y z and
(G2) for all x, y, z ∈ A, (x y) (x z) = y z.
Proposition 4 ([
24])
. Let A = (A; , , , 1) be an anti-grouped pseudo-BCI algebra. Define Φ(A) = (A; +, −, 1) byThen Φ(A) is a group. Conversely, let G = (G; +, −, 1) be a group. Define Ψ(G) = (G;,, , 1), where Then,Ψ(G) is an anti-grouped pseudo-BCI algebra. Moreover, the mapping Φ and Ψ are mutually inverse.
Definition 7 ([
27])
. Let (A; , , , 1) be a pseudo-BCI algebra. DenoteWe say that K(A) is the pseudo-BCK part of A andis the anti-grouped part of A.
Definition 8 ([
28])
. A pseudo-BCI algebra A is said to be a T-type if it satisfies the following identities:(T1) for all x ∈ A, (x ) = x , or (x ) = x
Proposition 5 ([
28])
. A pseudo-BCI algebra A is T-type if and only if it satisfies:(T2) for all x ∈ A, x (x ) = , or x (x ) =
3. Some New Concepts and Results
By the definition of pseudo-BCI/BCK algebra, we know that the direct product of two pseudo-BCI/BCK algebras is a pseudo-BCI/BCK algebra. That is, we have the following lemma.
Lemma 1 ([
20])
. Let (X; , ) and (Y; , ) be two pseudo-BCI algebras. Define two binary operators , on as follwos: for any (x1, y1), (x2, y2) ∈ and denote 1 = (1X, 1Y). Then (; , , 1) is a pseudo-BCI algebra. By the results in [
18,
20], we can easy to verify that the following lemma (the proof is omitted).
Lemma 2. Let (K;,, 1) be a pseudo-BCK algebra, (G;,, 1) an anti-grouped pseudo-BCI algebra and KG = {1}. DenoteA =b and define the operations,on A as follows: Then (A;,, 1) is a pseudo-BCI algebra.
Definition 9. Let K be a pseudo-BCK algebra and G be an anti-grouped pseudo-BCI algebra, KG = {1}. If the operators,are defined on A = KG according to Lemma 2, then (A;,, 1) is a pseudo-BCI algebra, we call A to be a KG-union of K and G and denote by A = KG.
Definition 10. Letis a partial ordered set with 1 as a constant element. For x in X, we call x a quasi-maximal element of X, if for any,
Definition 11. Let (G,*) be a grouoid, . Then x is called a quasi-left unit element of G, if it satisfies: Theorem 1. Let (A;,,, 1) be pseudo-BCK algebra. Then the following conditions are equivalent:
- (a1)
, x is a quasi-maximal element;
- (a2)
,implies ;
- (a3)
x is a quasi-left unit elemen w.r.t, that is,impliesand ;
- (a4)
,implies ;
- (a5)
implies .
Proof. : Suppose that , .
Case 1: If , it is follows that , that is,
Case 2: If , by (a1) and Definition 10, from and , we have . Therefore, (a2) hold.
: For any x, y in A, by Proposition 1 (6) and Definition 4 (2), we have , . Assume If , then (since, if , then form and we get x = y, this is contradictory to the hypothesis . Thus, from and using (a2) we have .
If , from this and applying (a2), we have . Thus,
- (i)
when , we can get , that is, ;
- (ii)
when
, from this and
using (a2) we have
Combine the aforementioned conclusion
, we can get
It follows that .
Therefore, based on the above cases we know that implies .
Similarly, we can prove that implies .
(a3) ⇒ (a4): Obviously.
(a4) ⇒ (a5): Suppose . Applying (a4), Also, by Definition 4 (2), , thus .
Case 1: If
, using (a4),
Hence,
= 1. Moreover,
Therefore, Case 2: If , then . In fact, if , using (a4), it follows that x = y, this is a contradiction with .
By above results we know that (a5) hold.
(a5) ⇒ (a1): Assume that , and Then . If , by (a5), , then . This means that implies x = a or a = 1. ☐
By Theorem 1 and Definition 3 we get
Corollary 1. Let (A;,, , 1) be a pseudo-BCK algebra. Then every element of A is quasi-maximal if and only if A is a quasi-alternating BCK-algebra.
4. The Class of Pseudo-BCI Algebras in Which Every Element is Quasi-Maximal
Example 1. Let A = {a, b, c, d, e, f, g, 1}. Define operationsandon A as following Cayley Table 1 and Table 2. Then A is pseudo-BCI algebra in which every element is quasi-maximal. Definition 12. A pseudo-BCI/BCK algebra A is said to be a QM-pseudo-BCI/BCK algebra if every element of A is quasi-maximal.
Theorem 2. Let (A;,,,
1) be a pseudo-BCI algebra. Then A is a QM-pseudo-BCI algebra if and only if it satisfies: Proof. If A is a QM-pseudo-BCI algebra, by Definitions 10 and 12, the above condition is satisfied.
Conversely, assume that If then 1 = it follows that by Proposition 2 (1). If then by the condition. This means that is a quasi- maximal element in A, hence, A is a QM-pseudo-BCI algebra. ☐
By Theorem 1 we know that a pseudo-BCK algebra is a QM-pseudo-BCK algebra if and only if it is a quasi-alternating BCK-algebra. It will be proved that any QM-pseudo-BCI algebra is constructed by the combination of a quasi-alternating BCK-algebra and an anti-grouped pseudo- BCI algebra (a group-like algebra).
Lemma 3 ([
27])
. Let A be a pseudo-BCI algebra, K(A) the pseudo-BCK part of A. If AG(A) = (A − K(A)){1} is subalgebra of A, then ()- (1)
Ifandthen
- (2)
Ifandthen
Applying the results in [
24,
27] we can easy to verify that the following lemma is true (the proof is omitted).
Lemma 4. Let A be an anti-grouped pseudo-BCI algebra. Then
- (1)
for any x, y in A, y implies x = y;
- (2)
for any x, y in A,
Theorem 3. Let A be a pseudo-BCI algebra, K(A) the pseudo-BCK part of A and AG(A) the anti-grouped part of A. The following statements are equivalent:
- (1)
A is a QM-pseudo-BCI algebra;
- (2)
K(A) is quasi-alternating BCK-algebras and AG(A) = (A − K(A)){1};
- (3)
implies
- (4)
implies
- (5)
implies
- (6)
implies
Proof. (1) ⇒ (2): Suppose that A is a QM-pseudo-BCI algebra. Then, for all , by Corollary 1, we can know K(A) is quasi-alternating BCK-algebras. If , then and Since , by Definition 12 we have . Thus, (A − K(A)){1} ⊆ AG(A). On the other hand, obviously, AG(A) ⊆ (A − K(A)){1}. Hence AG(A) = (A − K(A)){1}.
(2) ⇒ (3): Assume that (2) hold. For any x, y in A, ,
Case 1:
Then
Because
K(
A) is quasi-alternating BCK-algebra, using Theorem 1,
. Thus
Case 2:
. Since
AG(
A) is an anti-grouped pseudo-BCI subalgebra of
A, then by Lemma 4 we get
Case 3:
,
. Then
Applying Lemma 3 (1),
Then
Case 4:
,
Then
Applying Lemma 3 (2),
When
x = 1, then
; when
then
using Lemma 3 (2),
(3) ⇒ (1): Assume that
and
. We will prove that
y = 1. By (3), we have
Case 1: when , then , so Case 2: when , then , so , this is a contradiction with .
Therefore, for all , x is a quasi-maximal element of A.
(4) ⇒ (2): Suppose (4) hold. For any x, y in A.
If
,
by (4),
Then, Since K(A) is a pseudo-BCK subalgebra of A, using Proposition 1 (6), . It follows that , that is, . Thus, applying Theorem 1, K(A) is a quasi- alternating BCK-algebra.
If
, we prove that
. Assume
by (4), we have
Using Proposition 2 (9) and (12),
Moreover, applying Proposition 2 (9), (11) and (12) we have
This means that
By Lemma 3 (1),
Hence, . This is contraction with Therefore, and . It follows that (A − K(A)){1} ⊆ AG(A). Obviously, AG(A) ⊆ (A − K(A)){1}. So AG(A) = (A − K(A)){1}.
(2) ⇒ (4): It is similar to (2) ⇒ (3). It follows that (4) (2).
Similarly, we can prove (5) (2), (6) (2). ☐
Theorem 4. Let (A;,, , 1) be a pseudo-BCI algebra, AG(A) the anti-grouped part of A, K(A) the pseudo-BCK part of A. Then A is a QM-pseudo-BCI algebra if and only if K(A) is a quasi-alternating BCK-algebra and A = K(A)AG(A).
Proof. If A is a QM-pseudo-BCI algebra, then K(A) is a quasi-alternating BCK-algebra and A = K(A)AG(A), by Lemma 3 and Theorem 3.
Conversely, if K(A) is a quasi-alternating BCK-algebra, then every element in K(A) is quasi-maximal; if A = K(A)AG(A), then AG(A) = (A − K(A)){1}, it follows that every element in A − K(A) is quasi-maximal. By Definition 12, we know that A is a QM-pseudo-BCI algebra. ☐
5. Weak Associative Pseudo-BCI Algebras
Definition 13. A pseudo-BCI/BCK algebra A is said to be weak associative, if it satisfies: Example 2 Let A = {a, b, c, d, e, f, 1}. Define operation on A as following Cayley Table 3. Then A is a weak associative pseudo-BCI algebra, where . Theorem 5. Let (A;,, , 1) be a weak associative pseudo-BCI algebra. Then A is a QM-pseudo-BCI algebra and a T-type pseudo-BCI algebra.
Proof. For any
x,
y in
A,
then (by Definition 13)
Thus, if then Obviously, when Hence, from Definition 13 we get that for any x, y in A, Applying Theorem 3 (5) we know that A is a QM-pseudo-BCI algebra.
Moreover, we already prove that for any x in A, by Definition 8 we know that A is a T-type pseudo-BCI algebra. ☐
The inverse of Theorem 5 is not true. Since (d ) so the QM-pseudo-BCI algebra in Example 1 is not weak associative. The following example shows that a T-type pseudo-BCI algebra may be not a QM-pseudo-BCI algebra.
Example 3. Let A = {a, b, c, d, 1}. Define operations on A as following Cayley Table 4 and Table 5. Then A is a T-type pseudo-BCI algebra but it is not a QM-pseudo-BCI algebra, since Lemma 5 ([
16,
24])
. Let (A; →, 1) be a BCI-algebra. Then the following statements are equivalent:- (1)
A is associative, that is,for any x, y, z in A;
- (2)
for any x in A,
- (3)
for all x, y in A,x
Theorem 6. Let (A;,, , 1) be a weak associative pseudo-BCI algebra, AG(A) the anti-grouped part of A, K(A) the pseudo-BCK part of A. Then
- (1)
K(A) is quasi-alternating BCK-algebra andAG(A) = (A − K(A)){1};
- (2)
For any x in AG(A), x;
- (3)
For any x, y in A, x that is, A is a BCI-algebra;
- (4)
AG(A) is an Abel group, that is, AG(A) is associative BCI-algebra.
Proof. (1) It follows from Theorems 5 and 3.
(2) For any x in AG(A), then We will prove that
If obviously,
If
then
by Definition 13. Thus,
Applying Proposition 2 (12) we have
(3) For any x, y in A,
- (i)
when x, y in K(A), by (1), K(A) is a BCK-algebra, so x
- (ii)
when
x, y in (
A − K(
A)), by (1) and (2), applying Proposition 2 (11),
- (iii)
when x in K(A), y in (A − K(A)), using Lemma 3 (1), x
- (iv)
when y in K(A), x in (A − K(A)), using Lemma 3 (2), x
Therefore, for all x, y in A, x It follows that A is a BCI-algebra.
(4) Applying (2), by Lemma 5 we know that AG(A) is an Abel group, that is, AG(A) is associative BCI-algebra. ☐
From Theorems 6 and 4 we immediately get
Theorem 7. Let (A;,, , 1) be a pseudo-BCI algebra, AG(A) the anti-grouped part of A, K(A) the pseudo-BCK part of A. Then A is a weak associative pseudo-BCI algebra if and only if K(A) is a quasi-alternating BCK-algebra, AG(A) is an Abelian group and A = K(A)AG(A).
Theorem 8. Let (A;,,, 1) be a pseudo-BCI algebra. Then the following conditions are equivalent:
- (1)
for anywhen
- (2)
for anywhen
- (3)
for anywhen
- (4)
for anywhen
Proof. : It follows from Definition 13 and Theorem 6.
: Similar to the discussion process from Definition 13 to Theorem 6, we can obtain a result similar to Theorem 6. That is, from (2) we can get that A is a BCI-algebra. Hence, (2) implies (1).
Similarly, (3) ⇔ (1) and (4) ⇔ (1). ☐
Finally, we discuss the relationships among general pseudo-BCI algebras, QM-pseudo-BCI algebras and weak associative pseudo-BCI algebras (WA-pseudo-BCI algebras).
In fact, in every T-type pseudo-BCI algebra, there is a maximal WA-pseudo-BCI subalgebra. That is, if (A; , , , 1) is a T-type pseudo-BCI algebra, AG(A) the anti-grouped part of A, K(A) the pseudo-BCK part of A, then Kqm(A)∪AG(A) is a WA-pseudo-BCI subalgebra of A, where Kqm(A) is the set of all quasi-maximal element in K(A). For example, {c, d, 1} is a WA-pseudo-BCI subalgebra of the pseudo-BCI algebra A in Example 3.
In general, in every pseudo-BCI algebra, there is a maximal QM-pseudo-BCI subalgebra. That is, if (A; , , , 1) is a pseudo-BCI algebra, AG(A) the anti-grouped part of A, K(A) the pseudo-BCK part of A, then Kqm(A)∪AG(A) is a QM-pseudo-BCI subalgebra of A, where Kqm(A) is the set of all quasi-maximal element in K(A).