A Multi-Granularity 2-Tuple QFD Method and Application to Emergency Routes Evaluation
Abstract
:1. Introduction
2. Preliminaries
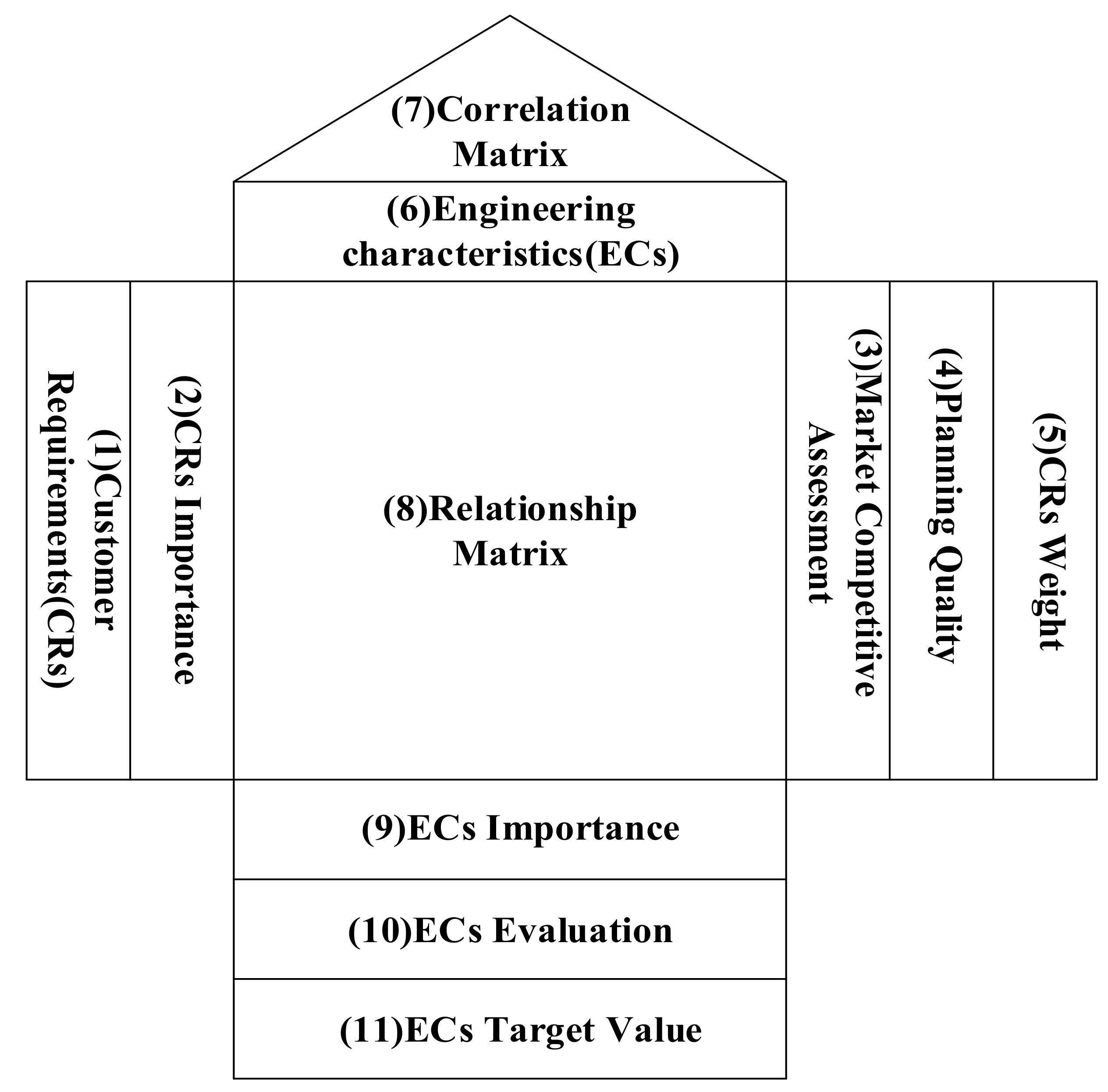
2.1. The Basic Knowledge on QFD
2.2. The 2-Tuple Linguistic Representation
2.3. The 2TLWGBM Operator
3. A Group Decision-Making Approach to Prioritize ECs
3.1. Determine the Importance of CRs Based on BWM
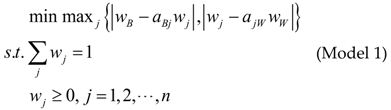
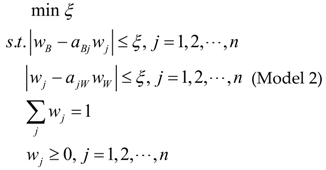
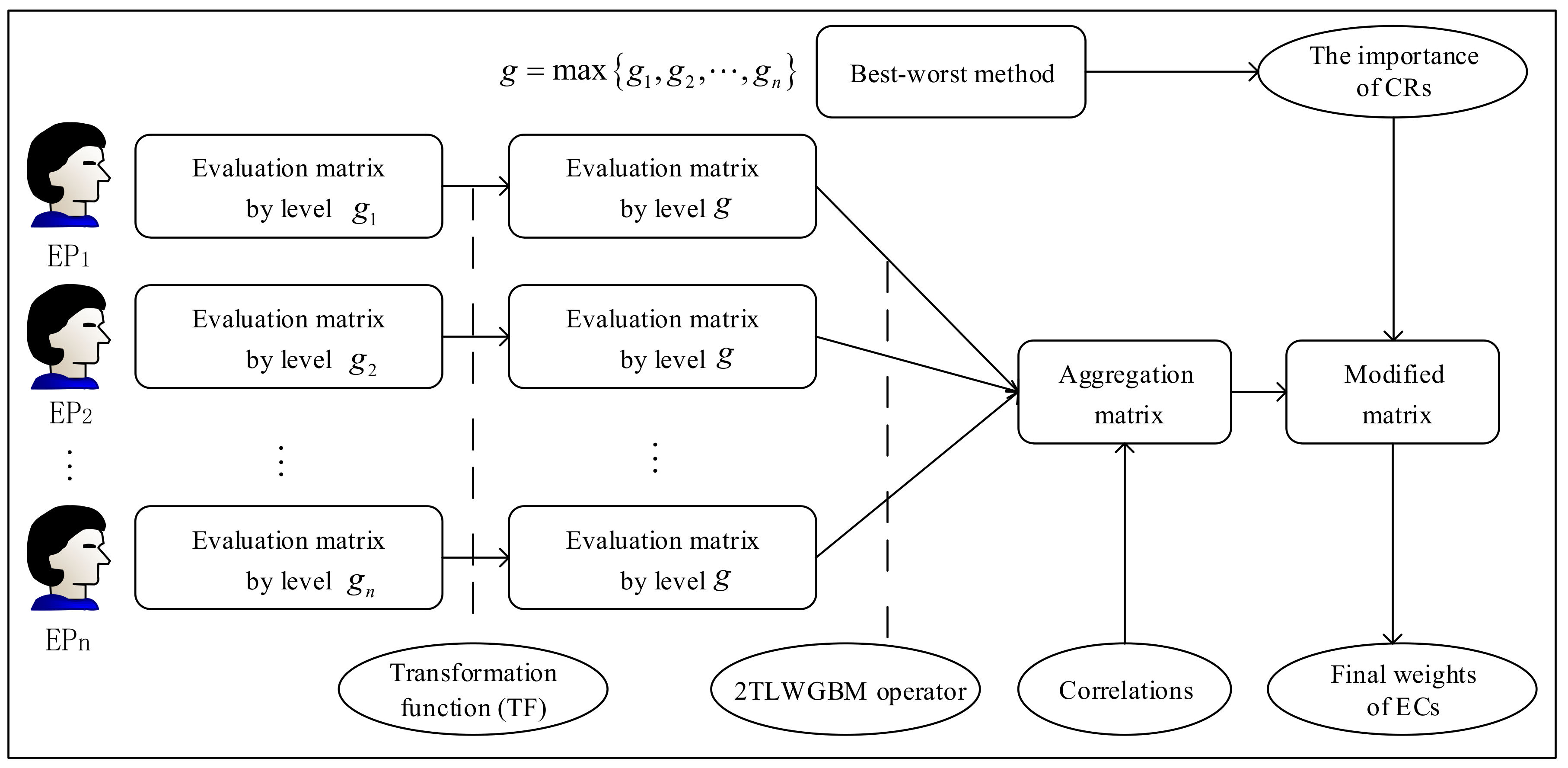
3.2. A Group Decision-Making Approach to Prioritize ECs
4. Case Study
4.1. Background
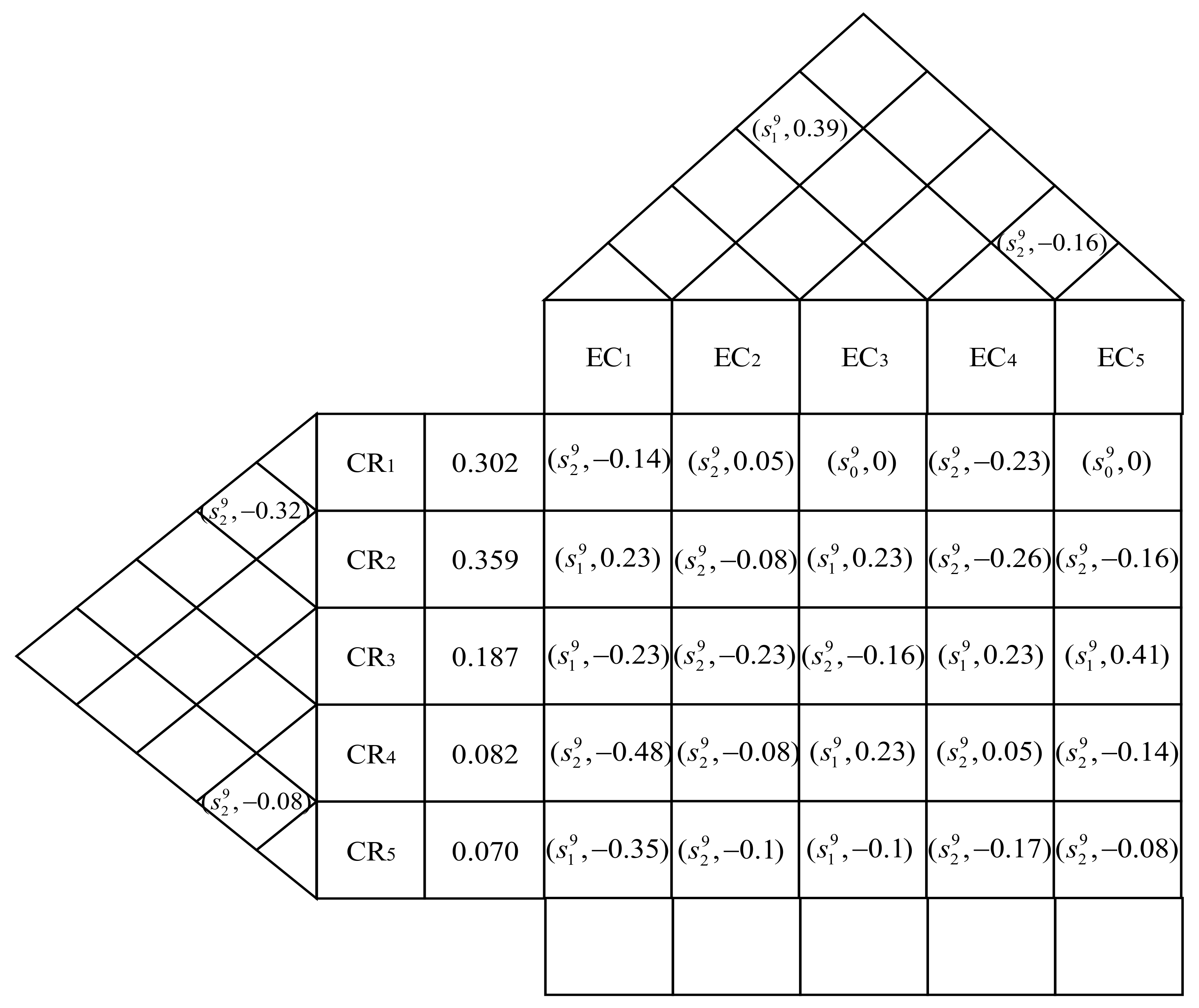
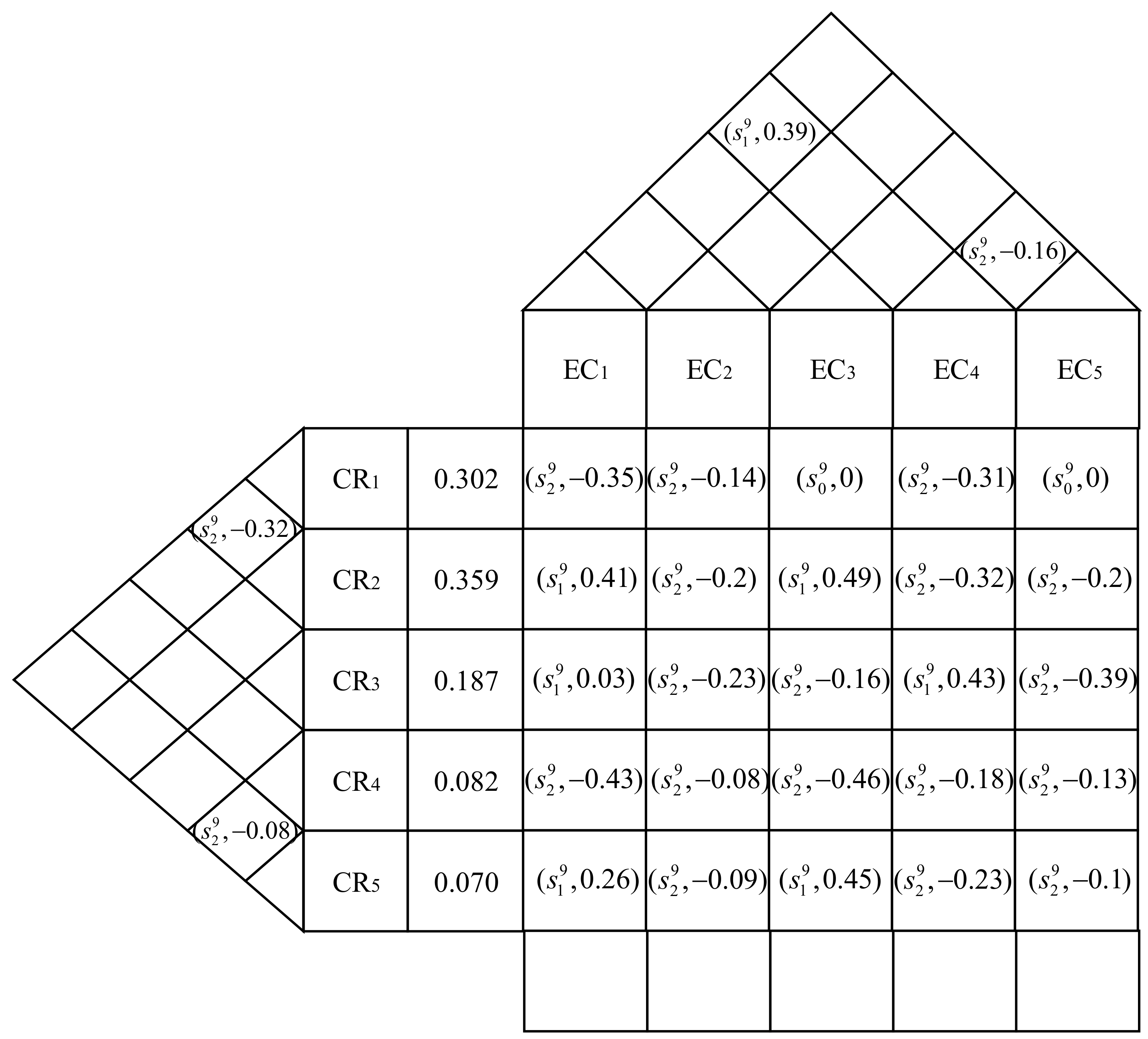
4.2. Implementation
4.3. Managerial Tips
5. Conclusions and Future Research
Author Contributions
Fundings
Acknowledgments
Conflicts of Interest
References
- Yan, H.B.; Ma, T.J.; Huynh, V.N. Coping with group behaviors in uncertain quality function deployment. Decis. Sci. 2014, 456, 1025–1052. [Google Scholar] [CrossRef]
- Ignatius, J.; Rahman, A.; Yazdani, M.; Aparauskas, J. Å.; Haron, S. H. An integrated fuzzy ANP–QFD approach for green building assessment. J. Civ. Eng. Manag. 2016, 224, 551–563. [Google Scholar] [CrossRef]
- Franceschini, F.; Galetto, M.; Maisano, D.; Mastrogiacomo, L. Prioritisation of engineering characteristics in QFD in the case of customer requirements orderings. Int. J. Prod. Res. 2015, 5313, 3975–3988. [Google Scholar] [CrossRef]
- Yan, H.B.; Ma, T.J. A group decision-making approach to uncertain quality function deployment based on fuzzy preference relation and fuzzy majority. Eur. J. Oper. Res. 2015, 2413, 815–829. [Google Scholar] [CrossRef]
- Liu, C.H.; Wu, H.H. A fuzzy group decision-making approach in quality function deployment. Qual. Quant. 2008, 424, 527–540. [Google Scholar] [CrossRef]
- Kwong, C.K.; Ye, Y.; Chen, Y.; Choy, K.L. A novel fuzzy group decision-making approach to prioritising engineering characteristics in QFD under uncertainties. Int. J. Prod. Res. 2011, 4919, 5801–5820. [Google Scholar] [CrossRef]
- Karsak, E.E. Fuzzy multiple objective programming framework to prioritize design requirements in quality function deployment. Comput. Ind. Eng. 2004, 472, 149–163. [Google Scholar] [CrossRef]
- Chen, L.H.; Weng, M.C. An evaluation approach to engineering design in QFD processes using fuzzy goal programming models. Eur. J. Oper. Res. 2006, 1721, 230–248. [Google Scholar] [CrossRef]
- Kwong, C.K.; Chen, Y.; Bai, H.; Chan, D.S.K. A methodology of determining aggregated importance of engineering characteristics in QFD. Comput. Ind. Eng. 2007, 534, 667–679. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.Z.; Zhou, J.; Yi, X.J. An exact expected value-based method to prioritize engineering characteristics in fuzzy quality function deployment. Int. J. Fuzzy Syst. 2016, 184, 630–646. [Google Scholar] [CrossRef]
- Geng, X.L.; Chu, X.N.; Xue, D.Y.; Zhang, Z.F. An integrated approach for rating engineering characteristics’ final importance in product-service system development. Comput. Ind. Eng. 2010, 594, 585–594. [Google Scholar] [CrossRef]
- Wang, Y.M. A fuzzy-normalisation-based group decision-making approach for prioritising engineering design requirements in QFD under uncertainty. Int. J. Prod. Res. 2012, 5023, 6963–6977. [Google Scholar] [CrossRef]
- Chen, L.H.; Ko, W.C.; Tseng, C.Y. Fuzzy approaches for constructing house of quality in QFD and its applications: A group decision-making method. IEEE Trans. Eng. Manag. 2013, 601, 77–87. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Chu, X.N. Fuzzy group decision-making for multi-format and multi-granularity linguistic judgments in quality function deployment. Expert Syst. Appl. 2009, 365, 9150–9158. [Google Scholar] [CrossRef]
- Wang, X.T.; Xiong, W. An integrated linguistic-based group decision-making approach for quality function deployment. Expert Syst. Appl. 2011, 3812, 14428–14438. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Fung, R.Y.K.; Li, Y.L.; Pu, Y. A group multi-granularity linguistic-based methodology for prioritizing engineering characteristics under uncertainties. Comput. Ind. Eng. 2016, 91, 178–187. [Google Scholar] [CrossRef]
- Bo, C.; Zhang, X.; Shao, S.; Smarandache, F. Multi-granulation neutrosophic rough sets on a single domain and dual domains with applications. Symmetry 2018, 10, 296. [Google Scholar] [CrossRef]
- Xu, Z.S. Multiple-attribute group decision making with different formats of preference information on attributes. IEEE Trans. Syst. Man Cybern. Part B 2007, 376, 1500–1511. [Google Scholar]
- Xu, Z.S. Group decision making based on multiple types of linguistic preference relations. Inf. Sci. 2008, 1782, 452–467. [Google Scholar] [CrossRef]
- Martínez, L.; Herrera, F. An overview on the 2-tuple linguistic model for computing with words in decision making: Extensions, applications and challenges. Inf. Sci. 2012, 207, 1–18. [Google Scholar] [CrossRef]
- Ju, Y.B.; Liu, X.Y.; Wang, A.H. Some new Shapley 2-tuple linguistic Choquet aggregation operators and their applications to multiple attribute group decision making. Soft Comput. 2010, 20, 4037–4053. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Martı́nez, L. A fusion approach for managing multi-granularity linguistic term sets in decision making. Fuzzy Set. Syst. 2000, 114, 43–58. [Google Scholar] [CrossRef] [Green Version]
- Herrera, F.; Martínez, L. A model based on linguistic 2-tuples for dealing with multigranular hierarchical linguistic contexts in multi-expert decision-making. IEEE Trans. Syst. Man Cybern. Part B 2001, 312, 227–234. [Google Scholar] [CrossRef] [PubMed]
- Espinilla, M.; Liu, J. Martinez, L. An extended hierarchical linguistic model for decision-making problems. Comput. Intell. 2011, 27, 489–512. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Kazimieras Zavadskas, E.; Ćirović, G.; Prentkovskis, O. The selection of wagons for the internal transport of a logistics company: A novel approach based on rough BWM and rough SAW methods. Symmetry 2017, 9, 264. [Google Scholar] [CrossRef]
- Herrera, F.; Martinez, L. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2000, 86, 746–752. [Google Scholar]
- Wei, G.W.; Zhao, X.F. Some dependent aggregation operators with 2-tuple linguistic information and their application to multiple attribute group decision making. Expert Syst. Appl. 2012, 395, 5881–5886. [Google Scholar] [CrossRef]
- Qin, J.D.; Liu, X.W.; Pedrycz, W. Hesitant fuzzy Maclaurin symmetric mean operators and its application to multiple-attribute decision making. Int. J. Fuzzy Syst. 2015, 174, 509–520. [Google Scholar] [CrossRef]
- Qin, J.D.; Liu, X.W. 2-tuple linguistic Muirhead mean operators for multiple attribute group decision making and its application to supplier selection. Kybernetes 2016, 451, 2–29. [Google Scholar] [CrossRef]
- Wang, J.; Wei, G.; Wei, Y. Models for green supplier selection with some 2-tuple linguistic neutrosophic number Bonferroni mean operators. Symmetry 2018, 10, 131. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Liu, X. Prioritized aggregation operators and correlated aggregation operators for hesitant 2-tuple linguistic variables. Symmetry 2018, 10, 39. [Google Scholar] [CrossRef]
- Jiang, X.P.; Wei, G.W. Some Bonferroni mean operators with 2-tuple linguistic information and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2014, 275, 2153–2162. [Google Scholar]
| αBW | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Consistency index | 0.00 | 0.44 | 1.00 | 1.63 | 2.30 | 3.00 | 3.73 | 4.47 | 5.23 |
| Passengers | Best | |||||
|---|---|---|---|---|---|---|
| 1 | 3 | 1 | 5 | 9 | 7 | |
| 2 | 5 | 1 | 4 | 9 | 8 | |
| 3 | 1 | 2 | 7 | 5 | 9 | |
| 4 | 4 | 3 | 1 | 7 | 9 | |
| 5 | 1 | 3 | 9 | 6 | 8 |
| Passengers | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Worst | |||||
| 6 | 4 | 9 | 4 | 9 | |
| 9 | 9 | 8 | 7 | 7 | |
| 5 | 7 | 2 | 9 | 1 | |
| 1 | 1 | 5 | 2 | 6 | |
| 4 | 3 | 1 | 1 | 3 |
| Priority |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, Y.; Liang, Y.; Tu, Y. A Multi-Granularity 2-Tuple QFD Method and Application to Emergency Routes Evaluation. Symmetry 2018, 10, 484. https://doi.org/10.3390/sym10100484
Mei Y, Liang Y, Tu Y. A Multi-Granularity 2-Tuple QFD Method and Application to Emergency Routes Evaluation. Symmetry. 2018; 10(10):484. https://doi.org/10.3390/sym10100484
Chicago/Turabian StyleMei, Yanlan, Yingying Liang, and Yan Tu. 2018. "A Multi-Granularity 2-Tuple QFD Method and Application to Emergency Routes Evaluation" Symmetry 10, no. 10: 484. https://doi.org/10.3390/sym10100484
APA StyleMei, Y., Liang, Y., & Tu, Y. (2018). A Multi-Granularity 2-Tuple QFD Method and Application to Emergency Routes Evaluation. Symmetry, 10(10), 484. https://doi.org/10.3390/sym10100484




