The Structure Theorems of Pseudo-BCI Algebras in Which Every Element is Quasi-Maximal

Abstract

For mathematical fuzzy logic systems, the study of corresponding algebraic structures plays an important role. Pseudo-BCI algebra is a class of non-classical logic algebras, which is closely related to various non-commutative fuzzy logic systems. The aim of this paper is focus on the structure of a special class of pseudo-BCI algebras in which every element is quasi-maximal (call it QM-pseudo-BCI algebras in this paper). First, the new notions of quasi-maximal element and quasi-left unit element in pseudo-BCK algebras and pseudo-BCI algebras are proposed and some properties are discussed. Second, the following structure theorem of QM-pseudo-BCI algebra is proved: every QM-pseudo-BCI algebra is a KG-union of a quasi-alternating BCK-algebra and an anti-group pseudo-BCI algebra. Third, the new notion of weak associative pseudo-BCI algebra (WA-pseudo-BCI algebra) is introduced and the following result is proved: every WA-pseudo-BCI algebra is a KG-union of a quasi-alternating BCK-algebra and an Abel group.

1. Introduction

In the study of t-norm based fuzzy logic systems [1,2,3,4,5,6,7,8,9], algebraic systems (such as residuated lattices, BL-algebras, MTL-algebras, pseudo-BL algebras, pseudo-MTL algebras, et al.) play an important role. In this paper, we discuss pseudo-BCI/BCK algebras which are connected with non-commutative fuzzy logic systems (such that non-commutative residuared lattices, pseudo-BL/pseudo-MTL algebras).

BCK-algebras and BCI-algebras were introduced by Is$\acute{\mathbf{e}}$ki [10] as algebras induced by Meredith’s implicational logics BCK and BCI. The name of BCK-algebra and BCI-algebra originates from the combinatories B, C, K, I in combinatory logic. The notion of pseudo-BCK algebra was introduced by G. Georgescu and A. Iorgulescu in [11] as a non-commutative extension of BCK-algebras. Then, as common generalization of pseudo-BCK algebras and BCI-algebras, W.A. Dudek and Y.B. Jun introduced the concept of pseudo-BCI algebra in [12]. In fact, there are many other non-classical logic algebraic systems related to BCK- and BCI-algebras, such as BCC-algebra, BZ-algebra and so forth, some monographs and papers on these topics can be found in [7,8,9,13,14,15,16,17,18].

Pseudo-BCI-algebras are algebraic models of some extension of a noncommutative version of the BCI-logic, the corresponding logic is called pseudo-BCI logic [19]. P. Emanovský and J. Kühr studied some properties of pseudo-BCI algebras, X.L. Xin et al. [20] investigated monadic pseudo BCI-algebras and corresponding logics and some authors discussed the filter (ideal) theory of pseudo-BCI algebras [21,22,23,24,25,26,27,28]. Moreover, some notions of period, state and soft set are applied to pseudo-BCI algebras [29,30,31].

In this paper, we further study the structure characterizations of pseudo-BCI algebras. By using the notions of quasi-maximal element, quasi-left unit element, KG-union and direct product, we give the structure theorem of the class of pseudo-BCI algebras in which every element is quasi-maximal (call they QM-pseudo-BCI algebras). Moreover, we introduce weak associative property in pseudo-BCI algebras, discuss basic properties of weak associative pseudo-BCI algebra (WA-pseudo-BCI algebra) and establish the structure theorem of WA-pseudo-BCI algebra.

It should be noted that the original definition of pseudo-BCI/BCK algebra is different from the definition used in this paper. They are dual. We think that the logical semantics of this algebraic structure can be better represented by using the present definition.

2. Preliminaries

Definition 1

([10,16]). An algebra (A; →, 1) of type (2,0) is called a BCI-algebra if the following conditions are satisfied for all x, y, z from A:

(1) 

$x\to y\le \left(y\to z\right) \to \left(x\to z\right),$

(2) 

$x\le \left(x\to y\right) \to y,$

(3) 

$x\le x,$

(4) 

$x\le y, y\le x imply x=y,$where$x\le y$means $x\to y=1$. An algebra (A; →, 1) of type (2,0) is called a BCK-algebra if it is a BCI-algebra and satisfies:

(5) 

$x\to 1=1,$∀x ∈ A.

Definition 2

([10,16]). A BCK-algebra (A; →, 1) is called bounded if there exists unique element 0 such that 0 $\to$ x = 1 for any x $\in$ A.

Definition 3

([13,14]). A BCK-algebra (A; →, 1) is called quasi-alternating BCK-algebra if it satisfies the following axiom: $\forall$ x, y $\in$ X, x $\ne$ y implies x $\to$ y = y.

Definition 4

([9,11]). A pseudo-BCK algebra is a structure (A; $\le$, $\to$, $⇝$, 1), where “$\le$” is a binary relation on A, “$\to$” and “$⇝$” are binary operations on A and “1” is an element of A, verifying the axioms: for all x, y, z $\in$ A,

(1) 

$x\to y\le$($y\to z$)$⇝$($x\to z$),$x⇝y\le$($y⇝z$)$\to$($x⇝z$),

(2) 

$x\le \left(x\to y\right)⇝y, x\le \left(x⇝y\right)\to y$

(3) 

$x\le x,$

(4) 

$x\le 1,$

(5) 

$x\le y,$$y\le x\Rightarrow$x = y,

(6) 

$x\le y⇝x\to y=1\iff x⇝y=1.$

If (A; $\le$, $\to$, $⇝$, 1) is a pseudo-BCK algebra satisfying $x\to y=x⇝y$ for all x, y $\in$ A, then (A; $\to$, 1) is a BCK-algebra.

Proposition 1

([9,11]). Let (A; $\le$, $\to$, $⇝$, 1) be a pseudo-BCK algebra, then A satisfy the following properties ($\forall x, y,z\in A$):

(1) 

$x\le y\Rightarrow y\to z \le$$x\to z,$$y⇝z \le$$x⇝z$

(2) 

$x\le y,$$y\le z$$\Rightarrow$x$\le$z,

(3) 

$x⇝\left(y\to z\right)=y\to \left(x⇝z\right),$

(4) 

$x\le y\to z\iff y\le x⇝z,$

(5) 

$x\to y\le \left(z\to x\right)\to \left(z\to y\right),$$x⇝y\le \left(z⇝x\right)⇝\left(z⇝y\right),$

(6) 

$x\le y\to x, x\le y⇝x,$

(7) 

$1\to x=x,1⇝x=x,$

(8) 

$x\le y\Rightarrow z\to x \le$$z\to y,$$z⇝x \le$$z⇝y,$

(9) 

$\left(\left(y\to x\right)⇝x\right)\to x=y\to x,$$\left(\left(y⇝x\right)\to x\right)⇝x=y⇝x.$

Definition 5

([12). A pseudo-BCI algebra is a structure (A; $\le$, $\to$, $⇝$, 1), where “$\le$” is a binary relation on A, “$\to$” and “$⇝$” are binary operations on A and “1” is an element of A, verifying the axioms: for all x, y, z $\in$ A,

(1) 

$x\to y\le \left(y\to z\right)⇝\left(x\to z\right),$$x⇝y\le \left(y⇝z\right)\to \left(x⇝z\right),$

(2) 

$x\le \left(x\to y\right)⇝y, x\le \left(x⇝y\right)\to y,$

(3) 

$x\le x,$

(4) 

if$x\le y$and $y\le x$, then x = y,

(5) 

$x\le y$iff$x\to y=1$iff$x⇝y=1.$

Note that, every pseudo-BCI algebra satisfying $x\to y=x⇝y$ for all x, y $\in$ A is a BCI-algebra.

Proposition 2

([12,22,24]). Let (A; $\le$, $\to$, $⇝$, 1) be a pseudo-BCI algebra, then A satisfy the following properties ($\forall x, y,z\in A$):

(1) 

if$1\le x,$then$x=1,$

(2) 

if$x\le y,$then$y\to z \le$$x\to z$and$y⇝z \le$$x⇝z,$

(3) 

if$x\le y$and$y\le z,$then $x\le z$,

(4) 

$x⇝\left(y\to z\right)=y\to \left(x⇝z\right),$

(5) 

$x\le y\to z,$iff$y\le x⇝z$

(6) 

$x\to y\le \left(z\to x\right)\to \left(z\to y\right),$$x⇝y\le \left(z⇝x\right)⇝\left(z⇝y\right),$

(7) 

if$x\le y,$then$z\to x\le$$z\to y$and$z⇝x \le$$z⇝y,$

(8) 

$1\to x=x, 1⇝x=x,$

(9) 

$\left(\left(y\to x\right)⇝x\right)\to x=y\to x,$$\left(\left(y⇝x\right)\to x\right)⇝x=y⇝x,$

(10) 

$x\to y\le \left(y\to x\right)⇝1,$$x⇝y\le \left(y⇝x\right)\to 1,$

(11) 

(x → y) → 1 = (x → 1) ⇝ (y → 1),(x ⇝ y) ⇝ 1 = (x ⇝ 1) → (y → 1)

(12) 

$x\to 1=x⇝1$.

Definition 6

([10,24]). A pseudo-BCI algebra A is said to be an anti-grouped pseudo-BCI algebra if it satisfies the following identities:

$$for anyx\in A,\left(x\to 1\right)\to 1=xor\left(x⇝1\right)⇝1=x.$$

Proposition 3

([24]). A pseudo-BCI algebra A is anti-grouped if and only if it satisfies:

• (G1) for all x, y, z ∈ A, (x $\to$ y) $\to$ (x $\to$ z) = y $\to$ z and
• (G2) for all x, y, z ∈ A, (x $⇝$ y) $⇝$ (x $⇝$ z) = y $⇝$ z.

Proposition 4

([24]). Let A = (A; $\le$, $\to$, $⇝$, 1) be an anti-grouped pseudo-BCI algebra. Define Φ(A) = (A; +, −, 1) by

$$x+y=\left(x\to 1\right)\to y = \left(y⇝1\right)⇝x, \forall x, y\in A;$$

$$-x=x\to 1=x⇝1, \forall x\in A.$$

Then Φ(A) is a group. Conversely, let G = (G; +, −, 1) be a group. Define Ψ(G) = (G;$\le$,$\to$, $⇝$, 1), where

$$x\to y=\left(-x\right)+y, x⇝y=y+\left(-x\right), \forall x, y\in G;$$

$$x\le y if and only if \left(-x\right)+y=1 \left(or y+\left(-x\right)=1\right), \forall x, y\in G.$$

Then,Ψ(G) is an anti-grouped pseudo-BCI algebra. Moreover, the mapping Φ and Ψ are mutually inverse.

Definition 7

([27]). Let (A; $\le$, $\to$, $⇝$, 1) be a pseudo-BCI algebra. Denote

$$K\left(A\right)=\{x\in A|x\le 1\};$$

$$AG\left(A\right)=\{x\in A|\left(x\to 1\right)\to 1=x\}.$$

We say that K(A) is the pseudo-BCK part of A and$AG\left(A\right)$is the anti-grouped part of A.

Definition 8

([28]). A pseudo-BCI algebra A is said to be a T-type if it satisfies the following identities:

(T1) for all x ∈ A, (x $\to 1$) $\to 1$ = x $\to 1$, or (x $⇝1$) $⇝1$ = x $⇝1.$

Proposition 5

([28]). A pseudo-BCI algebra A is T-type if and only if it satisfies:

(T2) for all x ∈ A, x$\to$ (x $\to 1$) = $1$, or x $⇝$ (x $⇝1$) = $1.$

3. Some New Concepts and Results

By the definition of pseudo-BCI/BCK algebra, we know that the direct product of two pseudo-BCI/BCK algebras is a pseudo-BCI/BCK algebra. That is, we have the following lemma.

Lemma 1

([20]). Let (X; ${\to }_X$, $⇝{ }_X,1_X$) and (Y; ${\to }_Y$, $⇝{ }_Y,1_Y$) be two pseudo-BCI algebras. Define two binary operators $\to$, $⇝$ on $X\times Y$ as follwos: for any (x₁, y₁), (x₂, y₂) ∈ $X\times Y,$

$$(x_1,y_1)\to (x_2,y_2)=(x_1{\to }_{ X}{x}_2,y_1 \to { }_Y{y}_2);$$

$$(x_1,y_1)⇝ (x_2,y_2)=( x_1{⇝}_X{x}_2{y}_1 {⇝}_Y{y}_2);$$

and denote 1 = (1_X, 1_Y). Then ($X\times Y$; $\to$, $⇝$, 1) is a pseudo-BCI algebra.

By the results in [18,20], we can easy to verify that the following lemma (the proof is omitted).

Lemma 2.

Let (K;$\to$,$⇝$, 1) be a pseudo-BCK algebra, (G;$\to$,$⇝$, 1) an anti-grouped pseudo-BCI algebra and K$\cap$G = {1}. DenoteA =$KG$b and define the operations$\to$,$⇝$on A as follows:

$$x\to y=\{\begin{array}{cc}x\to y& if x,y\in K or x,y\in G\\ y& if x\in K, y\in G\\ x\to 1& if y\in K\left\{1\right\}, x\in G\end{array}$$

$$x⇝y=\{\begin{array}{cc}x⇝y& if x,y\in K or x,y\in G\\ y& if x\in K, y\in G\\ x⇝1& if y\in K\left\{1\right\}, x\in G\end{array}$$

Then (A;$\to$,$⇝$, 1) is a pseudo-BCI algebra.

Definition 9.

Let K be a pseudo-BCK algebra and G be an anti-grouped pseudo-BCI algebra, K$\cap$G = {1}. If the operators$\to$,$⇝$are defined on A = K$\cup$G according to Lemma 2, then (A;$\to$,$⇝$, 1) is a pseudo-BCI algebra, we call A to be a KG-union of K and G and denote by A = K${\oplus }_{KG}$G.

Definition 10.

Let$\left(X, \le \right)$is a partial ordered set with 1 as a constant element. For x in X, we call x a quasi-maximal element of X, if for any$a\in X$,$x\le a\Rightarrow x=a or a=1.$

Definition 11.

Let (G,*) be a grouoid, $x\in G$. Then x is called a quasi-left unit element of G, if it satisfies:

$$\forall y\in G, x\ast y = y when x\ne y.$$

Theorem 1.

Let (A;$\le$,$\to$,$⇝$, 1) be pseudo-BCK algebra. Then the following conditions are equivalent:

(a1) 

$\forall x\in A$, x is a quasi-maximal element;

(a2) 

$\forall x\in A$,$y\in A-\left\{1\right\},$$x\le y$implies $x=y$;

(a3) 

$\forall x\in A,$x is a quasi-left unit elemen w.r.t$\to ,⇝$, that is,$x\ne y$implies$x\to y=y$and $x⇝y=y$;

(a4) 

$\forall x,y\in A$,$x\ne y$implies $x\to y=y$;

(a5) 

$\forall x,y\in A, x\ne y$implies $x⇝y=y$.

Proof. 

$\left(\mathrm{a}1\right)\Rightarrow \left(\mathrm{a}2\right)$: Suppose that $x\in A$, $y\in A-\left\{1\right\} and x\le y$.

Case 1: If $x=1$, it is follows that $1=x\le y\le 1$, that is, $x=y=1.$

Case 2: If $x\ne 1$, by (a1) and Definition 10, from $x\le y$ and $y\ne 1$, we have $x=y$. Therefore, (a2) hold.

$\left(\mathrm{a}2\right)\Rightarrow \left(\mathrm{a}3\right)$: For any x, y in A, by Proposition 1 (6) and Definition 4 (2), we have $x\le y\to x$, $y\le x\to y,x\le \left(x\to y\right)⇝y$. Assume $x\ne y.$ If $y\to x=1$, then $x\to y\ne 1$ (since, if $x\to y=1$, then form $y\to x=1$ and $x\to y=1$ we get x = y, this is contradictory to the hypothesis $x\ne y)$. Thus, from $y\le x\to y$ and $x\to y\ne 1,$ using (a2) we have $y=x\to y$.

If $y\to x\ne 1$, from this and $x\le y\to x and$ applying (a2), we have $x=y\to x$. Thus,

(i)

when $\left(x\to y\right)⇝y=1$, we can get $x\to y\le y\le x\to y$, that is, $y=x\to y$;

(ii)

when $\left(x\to y\right)⇝y\ne 1$, from this and $x\le \left(x\to y\right)⇝y,$ using (a2) we have $x=\left(x\to y\right)⇝y.$ Combine the aforementioned conclusion $x=y\to x$, we can get

$$x=y\to x=y\to \left(\left(x\to y\right)⇝y\right)=\left(x\to y\right)⇝\left(y\to y\right)=\left(x\to y\right)⇝1=1,$$

It follows that $y=1\to y=x\to y$.

Therefore, based on the above cases we know that $x\ne y$ implies $y=x\to y$.

Similarly, we can prove that $x\ne y$ implies $y=x⇝y$.

(a3) ⇒ (a4): Obviously.

(a4) ⇒ (a5): Suppose $x\ne y$. Applying (a4), $x\to y=y.$ Also, by Definition 4 (2), $x\le \left(x⇝y\right)\to y$, thus $x\to \left[\left(x⇝y\right)\to y\right]=1$.

Case 1: If $x\ne \left(x⇝y\right)\to y$, using (a4), $x\to \left[\left(x⇝y\right)\to y\right]=\left[\left(x⇝y\right)\to y\right].$ Hence, $\left(x⇝y\right)\to y$ = 1. Moreover,

$$y\to \left(x⇝y\right)=x⇝\left(y\to y\right)=x⇝1=1.$$

Therefore, $y=x⇝y.$ Case 2: If $x=\left(x⇝y\right)\to y$, then $x⇝y=y$. In fact, if $x⇝y\ne y$, using (a4), $\left(x⇝y\right)\to y=y,$ it follows that x = y, this is a contradiction with $x\ne y$.

By above results we know that (a5) hold.

(a5) ⇒ (a1): Assume that $x\in X$, $a\in X$ and $x\le a.$ Then $x⇝a=1$. If $x\ne a$, by (a5), $x⇝a=a$, then $a=x⇝a=1$. This means that $x\le a$ implies x = a or a = 1. ☐

By Theorem 1 and Definition 3 we get

Corollary 1.

Let (A;$\le$,$\to$, $⇝$, 1) be a pseudo-BCK algebra. Then every element of A is quasi-maximal if and only if A is a quasi-alternating BCK-algebra.

4. The Class of Pseudo-BCI Algebras in Which Every Element is Quasi-Maximal

Example 1.

Let A = {a, b, c, d, e, f, g, 1}. Define operations$\to$and$⇝$on A as following Cayley Table 1 and Table 2. Then A is pseudo-BCI algebra in which every element is quasi-maximal.

Table 1. The Cayley table of operation $\to$.

→	a	b	c	d	e	f	g	1
a	1	b	c	d	e	f	g	1
b	a	1	c	d	e	f	g	1
c	c	c	1	f	g	d	e	c
d	d	d	e	1	c	g	f	d
e	f	f	g	c	1	e	d	f
f	e	e	d	g	f	1	c	e
g	g	g	c	d	e	f	1	g
1	a	b	c	d	e	f	g	1

Table 2. The Cayley table of operation ⇝.

⇝	a	b	c	d	e	f	g	1
a	1	b	c	d	e	f	g	1
b	a	1	c	d	e	f	g	1
c	c	c	1	f	g	d	e	c
d	d	d	e	1	c	g	f	d
e	f	f	g	c	1	e	d	f
f	e	e	d	g	f	1	c	e
g	g	g	c	d	e	f	1	g
1	a	b	c	d	e	f	g	1

Definition 12.

A pseudo-BCI/BCK algebra A is said to be a QM-pseudo-BCI/BCK algebra if every element of A is quasi-maximal.

Theorem 2.

Let (A;$\le$,$\to$,$⇝$, 1) be a pseudo-BCI algebra. Then A is a QM-pseudo-BCI algebra if and only if it satisfies:

$$for any x, y\in A-\left\{1\right\}, x\le y\Rightarrow x=y.$$

Proof. 

If A is a QM-pseudo-BCI algebra, by Definitions 10 and 12, the above condition is satisfied.

Conversely, assume that $x, y\in A,$ $x\le y.$ If $x=1,$ then 1 = $x\le y,$ it follows that $x=y=1,$ by Proposition 2 (1). If $x\ne 1,y\ne 1,$ then $x=y$ by the condition. This means that $x$ is a quasi- maximal element in A, hence, A is a QM-pseudo-BCI algebra. ☐

By Theorem 1 we know that a pseudo-BCK algebra is a QM-pseudo-BCK algebra if and only if it is a quasi-alternating BCK-algebra. It will be proved that any QM-pseudo-BCI algebra is constructed by the combination of a quasi-alternating BCK-algebra and an anti-grouped pseudo- BCI algebra (a group-like algebra).

Lemma 3

([27]). Let A be a pseudo-BCI algebra, K(A) the pseudo-BCK part of A. If AG(A) = (A − K(A))$\cup${1} is subalgebra of A, then ($\forall x,y\in A$)

(1) 

If$x\in K\left(A\right)$and$y\in A-K\left(A\right),$then$x\to y=x⇝y=y.$

(2) 

If$x\in A-K\left(A\right)$and$y\in K\left(A\right),$then$x\to y=x⇝y=x\to 1.$

Applying the results in [24,27] we can easy to verify that the following lemma is true (the proof is omitted).

Lemma 4.

Let A be an anti-grouped pseudo-BCI algebra. Then

(1) 

for any x, y in A, $x\le$ y implies x = y;

(2) 

for any x, y in A,$x=\left(x\to y\right)⇝y=\left(x⇝y\right)\to y.$

Theorem 3.

Let A be a pseudo-BCI algebra, K(A) the pseudo-BCK part of A and AG(A) the anti-grouped part of A. The following statements are equivalent:

(1) 

A is a QM-pseudo-BCI algebra;

(2) 

K(A) is quasi-alternating BCK-algebras and AG(A) = (A − K(A))$\cup${1};

(3) 

$\forall x,y\in A,$$x\ne y$implies$\left(x\to y\right)⇝y=\left(x\to 1\right)\to 1;$

(4) 

$\forall x,y\in A,$$x\ne y$implies$\left(x⇝y\right)\to y=\left(x\to 1\right)\to 1;$

(5) 

$\forall x,y\in A,$$x\ne y$implies$\left(x\to y\right)\to y=\left(x\to 1\right)\to 1;$

(6) 

$\forall x,y\in A,$$x\ne y$implies$\left(x⇝y\right)⇝y=\left(x\to 1\right)\to 1.$

Proof. 

(1) ⇒ (2): Suppose that A is a QM-pseudo-BCI algebra. Then, for all $x,y\in K\left(A\right)$, by Corollary 1, we can know K(A) is quasi-alternating BCK-algebras. If $x\in A-K\left(A\right)$, then $x\to 1\ne 1$ and $\left(x\to 1\right)\to 1\ne 1.$ Since $x\le \left(x\to 1\right)\to 1$, by Definition 12 we have $x=\left(x\to 1\right)\to 1$. Thus, (A − K(A))$\cup${1} ⊆ AG(A). On the other hand, obviously, AG(A) ⊆ (A − K(A))$\cup${1}. Hence AG(A) = (A − K(A))$\cup${1}.

(2) ⇒ (3): Assume that (2) hold. For any x, y in A, $x\ne y$,

Case 1: $x,y\in K\left(A\right).$ Then $x\to 1=y\to 1=1.$ Because K(A) is quasi-alternating BCK-algebra, using Theorem 1, $x\to y=y$. Thus

$$\left(x\to y\right)⇝y=y⇝y=1=1\to 1= \left(x\to 1\right)\to 1.$$

Case 2: $x,y\in AG\left(A\right)$. Since AG(A) is an anti-grouped pseudo-BCI subalgebra of A, then by Lemma 4 we get

$$\left(x\to y\right)⇝y=x=\left(x\to 1\right)\to 1.$$

Case 3: $x\in K\left(A\right)$, $y\in AG\left(A\right)$. Then $x\to 1=1.$ Applying Lemma 3 (1), $x\to y=y.$ Then

$$\left(x\to y\right)⇝y=y⇝y=1=1\to 1=\left(x\to 1\right)\to 1.$$

Case 4: $x\in AG\left(A\right)$, $y\in K\left(A\right).$ Then $x=\left(x\to 1\right)\to 1,y\to 1=1.$ Applying Lemma 3 (2), $x\to y=x\to 1.$ When x = 1, then $\left(x\to y\right)⇝y=\left(x\to 1\right)\to 1$; when $x\ne 1,$ then $x\to 1\in A-K\left(A\right),$ using Lemma 3 (2),

$$\left(x\to 1\right)⇝y=\left(x\to 1\right)\to 1$$

Hence,

$$\left(x\to y\right)⇝y=\left(x\to 1\right)⇝y=\left(x\to 1\right)\to 1.$$

(3) ⇒ (1): Assume that $x\le y$ and $x\ne y$. We will prove that y = 1. By (3), we have

$$y=1⇝y=\left(x\to y\right)⇝y=\left(x\to 1\right)\to 1.$$

Case 1: when $x\in K\left(A\right)$, then $x\to 1=1$, so $y=1.$ Case 2: when $x\in X-K\left(A\right)$, then $\left(x\to 1\right)\to 1=x$, so $y=x$, this is a contradiction with $x\ne y$.

Therefore, for all $x\in A$, x is a quasi-maximal element of A.

(4) ⇒ (2): Suppose (4) hold. For any x, y in A.

If $x,y\in K\left(A\right)$, $x\ne y,$ by (4),

$$\left(x⇝y\right)\to y=\left(x\to 1\right)\to 1=1.$$

Then, $x⇝y\le y.$ Since K(A) is a pseudo-BCK subalgebra of A, using Proposition 1 (6), $y\le x⇝y$. It follows that $y\le x⇝y\le y$, that is, $x⇝y=y$. Thus, applying Theorem 1, K(A) is a quasi- alternating BCK-algebra.

If $x\in A-K\left(A\right)$, we prove that $\left(x\to 1\right)\to 1=x$. Assume $\left(x\to 1\right)\to 1\ne x,$ by (4), we have

$$\left\{\left[\left(x\to 1\right)\to 1\right]⇝x\right\}\to x=\left\{\left[\left(x\to 1\right)\to 1\right]\to 1\right\}\to 1.$$

Using Proposition 2 (9) and (12),

$$\left\{\left[\left(x\to 1\right)\to 1\right]\to 1\right\}\to 1=\left(x\to 1\right)\to 1.$$

Thus

$$\left\{\left[\left(x\to 1\right)\to 1\right]⇝x\right\}\to x=\left(x\to 1\right)\to 1.$$

Moreover, applying Proposition 2 (9), (11) and (12) we have

$$\begin{array}{cc}& \left\{\left[\left(x\to 1\right)\to 1\right]⇝x\right\}\to 1\hfill \\ \hfill =& \left\{\left[\left(x\to 1\right)\to 1\right]⇝1\right\}\to \left(x⇝1\right)\hfill \\ \hfill =& \left\{\left[\left(x\to 1\right)⇝1\right]\to 1\right\}\to \left(x⇝1\right)\hfill \\ \hfill =& \left(x\to 1\right)\to \left(x⇝1\right)\hfill \\ \hfill =& 1.\hfill \end{array}$$

This means that $\left(\left(x\to 1\right)\to 1\right)\to x\in K\left(A\right).$ By Lemma 3 (1),

$$\left\{\left[\left(x\to 1\right)\to 1\right]⇝x\right\}\to x=x.$$

Hence, $\left(x\to 1\right)\to 1=x$. This is contraction with $\left(x\to 1\right)\to 1\ne x.$ Therefore, $\left(x\to 1\right)\to 1=x$ and $x\in AG\left(A\right)$. It follows that (A − K(A))$\cup${1} ⊆ AG(A). Obviously, AG(A) ⊆ (A − K(A))$\cup${1}. So AG(A) = (A − K(A))$\cup${1}.

(2) ⇒ (4): It is similar to (2) ⇒ (3). It follows that (4) $\iff$ (2).

Similarly, we can prove (5) $\iff$ (2), (6) $\iff$ (2). ☐

Theorem 4.

Let (A;$\le$,$\to$, $⇝$, 1) be a pseudo-BCI algebra, AG(A) the anti-grouped part of A, K(A) the pseudo-BCK part of A. Then A is a QM-pseudo-BCI algebra if and only if K(A) is a quasi-alternating BCK-algebra and A = K(A)${\oplus }_{KG}$AG(A).

Proof. 

If A is a QM-pseudo-BCI algebra, then K(A) is a quasi-alternating BCK-algebra and A = K(A)${\oplus }_{KG}$AG(A), by Lemma 3 and Theorem 3.

Conversely, if K(A) is a quasi-alternating BCK-algebra, then every element in K(A) is quasi-maximal; if A = K(A)${\oplus }_{KG}$AG(A), then AG(A) = (A − K(A))$\cup${1}, it follows that every element in A − K(A) is quasi-maximal. By Definition 12, we know that A is a QM-pseudo-BCI algebra. ☐

5. Weak Associative Pseudo-BCI Algebras

Definition 13.

A pseudo-BCI/BCK algebra A is said to be weak associative, if it satisfies:

$$for any, y,z\in A, \left(x\to y\right)\to z=x\to \left(y\to z\right)when\left(x\ne y, x\ne z\right).$$

Example 2

Let A = {a, b, c, d, e, f, 1}. Define operation $\to$ on A as following Cayley Table 3. Then A is a weak associative pseudo-BCI algebra, where $⇝ = \to$.

Table 3. The Cayley table of the operation →.

→	a	b	c	d	e	f	1
a	1	b	c	d	e	f	1
b	a	1	c	d	e	f	1
c	a	b	1	d	e	f	1
d	d	d	d	1	f	e	d
e	e	e	e	f	1	d	e
f	f	f	f	e	d	1	f
1	a	b	c	d	e	f	1

Theorem 5.

Let (A;$\le$,$\to$, $⇝$, 1) be a weak associative pseudo-BCI algebra. Then A is a QM-pseudo-BCI algebra and a T-type pseudo-BCI algebra.

Proof. 

For any x, y in A, $x\ne y,$ then (by Definition 13)

$$\left(x\to y\right)\to y=x\to \left(y\to y\right)=x\to 1.$$

Thus, if $x\ne 1,$ then $\left(x\to 1\right)\to 1=x\to 1.$ Obviously, when $x=1,$ $\left(x\to 1\right)\to 1=x\to 1.$ Hence, from Definition 13 we get that for any x, y in A, $x\ne y \Rightarrow \left(x\to y\right)\to y=\left(x\to 1\right)\to 1.$ Applying Theorem 3 (5) we know that A is a QM-pseudo-BCI algebra.

Moreover, we already prove that $\left(x\to 1\right)\to 1=x\to 1$ for any x in A, by Definition 8 we know that A is a T-type pseudo-BCI algebra. ☐

The inverse of Theorem 5 is not true. Since (d $\to c$) $\to c\ne d\to 1,$ so the QM-pseudo-BCI algebra in Example 1 is not weak associative. The following example shows that a T-type pseudo-BCI algebra may be not a QM-pseudo-BCI algebra.

Example 3.

Let A = {a, b, c, d, 1}. Define operations $\to and⇝$ on A as following Cayley Table 4 and Table 5. Then A is a T-type pseudo-BCI algebra but it is not a QM-pseudo-BCI algebra, since

$$\left(b\to c\right)\to a=a\ne 1=b\to \left(c\to a\right).$$

Table 4. The operation → in the T-type pseudo-BCI algebra.

→	a	b	c	d	1
a	1	1	1	d	1
b	b	1	1	d	1
c	b	b	1	d	1
d	d	d	d	1	d
1	a	b	c	d	1

Table 5. The operation ⇝ in the T-type pseudo-BCI algebra.

⇝	a	b	c	d	1
a	1	1	1	d	1
b	c	1	1	d	1
c	a	b	1	d	1
d	d	d	d	1	d
1	a	b	c	d	1

Lemma 5

([16,24]). Let (A; →, 1) be a BCI-algebra. Then the following statements are equivalent:

(1) 

A is associative, that is,$\left(x\to y\right)\to z=x\to \left(y\to z\right)$for any x, y, z in A;

(2) 

for any x in A,$x\to 1=x;$

(3) 

for all x, y in A,x$\to y= y\to x.$

Theorem 6.

Let (A;$\le$,$\to$, $⇝$, 1) be a weak associative pseudo-BCI algebra, AG(A) the anti-grouped part of A, K(A) the pseudo-BCK part of A. Then

(1) 

K(A) is quasi-alternating BCK-algebra andAG(A) = (A − K(A))$\cup${1};

(2) 

For any x in AG(A), x$\to 1=x⇝1=x$;

(3) 

For any x, y in A, x$\to y=x⇝y,$ that is, A is a BCI-algebra;

(4) 

AG(A) is an Abel group, that is, AG(A) is associative BCI-algebra.

Proof. 

(1) It follows from Theorems 5 and 3.

(2) For any x in AG(A), then $\left(x\to 1\right)\to 1=x.$ We will prove that $x\to 1=x.$

If $x=1,$ obviously, $x\to 1=x.$

If $x\ne 1,$ then $\left(x\to 1\right)\to 1=x\to 1$ by Definition 13. Thus,

$$x\to 1=\left(x\to 1\right)\to 1=x.$$

Applying Proposition 2 (12) we have

$$x⇝1= x\to 1=x.$$

(3) For any x, y in A,

(i)

when x, y in K(A), by (1), K(A) is a BCK-algebra, so x $\to y=x⇝y;$

(ii)

when x, y in (A − K(A)), by (1) and (2), applying Proposition 2 (11),

$$x\to y=\left(x\to y\right)\to 1=\left(x\to 1\right)⇝\left(y\to 1\right)=x⇝y;$$

(iii)

when x in K(A), y in (A − K(A)), using Lemma 3 (1), x $\to y=x⇝y;$

(iv)

when y in K(A), x in (A − K(A)), using Lemma 3 (2), x $\to y=x⇝y;$

Therefore, for all x, y in A, x$\to y=x⇝y.$ It follows that A is a BCI-algebra.

(4) Applying (2), by Lemma 5 we know that AG(A) is an Abel group, that is, AG(A) is associative BCI-algebra. ☐

From Theorems 6 and 4 we immediately get

Theorem 7.

Let (A;$\le$,$\to$, $⇝$, 1) be a pseudo-BCI algebra, AG(A) the anti-grouped part of A, K(A) the pseudo-BCK part of A. Then A is a weak associative pseudo-BCI algebra if and only if K(A) is a quasi-alternating BCK-algebra, AG(A) is an Abelian group and A = K(A)${\oplus }_{KG}$AG(A).

Theorem 8.

Let (A;$\le$,$\to$,$⇝$, 1) be a pseudo-BCI algebra. Then the following conditions are equivalent:

(1) 

for any$x, y,z\in A,$$\left(x\to y\right)\to z=x\to \left(y\to z\right)$when$\left(x\ne y, x\ne z\right);$

(2) 

for any$x, y,z\in A,$$\left(x⇝y\right)⇝z=x⇝\left(y⇝z\right)$when$\left(x\ne y, x\ne z\right);$

(3) 

for any$x, y,z\in A,$$\left(x\to y\right)⇝z=x\to \left(y⇝z\right)$when$\left(x\ne y, x\ne z\right);$

(4) 

for any$x, y,z\in A,$$\left(x⇝y\right)\to z=x⇝\left(y\to z\right)$when$\left(x\ne y, x\ne z\right).$

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$: It follows from Definition 13 and Theorem 6.

$\left(2\right)\Rightarrow \left(1\right)$: Similar to the discussion process from Definition 13 to Theorem 6, we can obtain a result similar to Theorem 6. That is, from (2) we can get that A is a BCI-algebra. Hence, (2) implies (1).

Similarly, (3) ⇔ (1) and (4) ⇔ (1). ☐

Finally, we discuss the relationships among general pseudo-BCI algebras, QM-pseudo-BCI algebras and weak associative pseudo-BCI algebras (WA-pseudo-BCI algebras).

In fact, in every T-type pseudo-BCI algebra, there is a maximal WA-pseudo-BCI subalgebra. That is, if (A; $\le$, $\to$, $⇝$, 1) is a T-type pseudo-BCI algebra, AG(A) the anti-grouped part of A, K(A) the pseudo-BCK part of A, then K_qm(A)∪AG(A) is a WA-pseudo-BCI subalgebra of A, where K_qm(A) is the set of all quasi-maximal element in K(A). For example, {c, d, 1} is a WA-pseudo-BCI subalgebra of the pseudo-BCI algebra A in Example 3.

In general, in every pseudo-BCI algebra, there is a maximal QM-pseudo-BCI subalgebra. That is, if (A; $\le$, $\to$, $⇝$, 1) is a pseudo-BCI algebra, AG(A) the anti-grouped part of A, K(A) the pseudo-BCK part of A, then K_qm(A)∪AG(A) is a QM-pseudo-BCI subalgebra of A, where K_qm(A) is the set of all quasi-maximal element in K(A).

6. Conclusions

In the study of pseudo-BCI algebras, the structures of various special pseudo-BCI algebras are naturally an important problem. At present, the structures of several subclasses such as quasi-alternating pseudo-BCI algebras and anti-grouped pseudo-BCI algebras are clear. In this paper, we have studied an important subclass of pseudo-BCI algebras, that is, QM-pseudo-BCI algebras in which every element is quasi-maximal. We obtain a very clear structure theorem of this subclass. At the same time, we have studied a class of more special pseudo-BCI algebras, that is, weak associative (WA) pseudo-BCI algebras in which every element is weak associative and obtained the structure theorem of this subclass. These results enrich the research content of pseudo-BCI algebras and clearly presented the relationships between various subclasses, which can be illustrated as Figure 1. Finally, we show that the two types of pseudo-BCI algebras are very important, since (1) every pseudo-BCI algebra contains a subalgebra which is QM-pseudo-BCI algebra, (2) every T-type pseudo-BCI algebra contains a subalgebra which is WA-pseudo-BCI algebra. As a further study direction, we will discuss the integration of related topics in the light of some new research findings in [32,33,34].

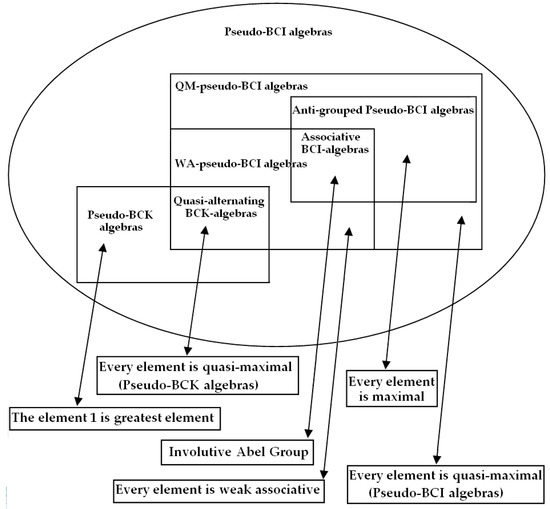
Figure 1. Main results in this paper.