3.1. Classical Description
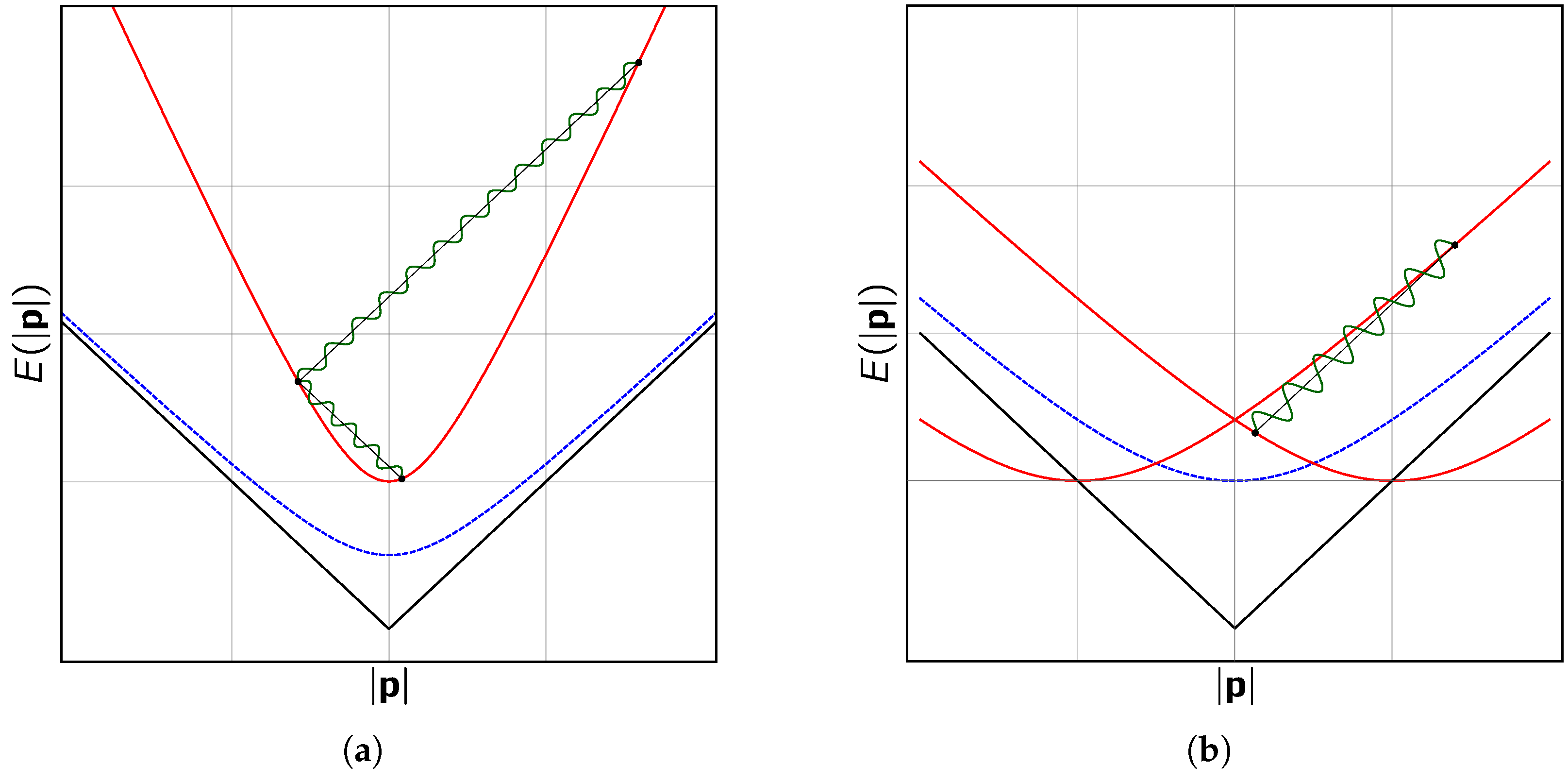
The presumably first detailed study of vacuum Cherenkov radiation was carried out by Coleman and Glashow in [
12]. Amongst other things, they consider an isotropic modification of the speed of light such that
. They find that massive particles start emitting photons once their energy lies above a certain threshold energy. The rate of energy loss
is stated in the paper as well, and it goes to 0 when the particle energy approaches the threshold energy from above. Since they do not state a modified action, it is, first of all, not clear how they obtained
. A calculation of the energy loss requires knowledge of the dynamics of the process that can be inferred from a theory only. As will be explained later, the authors most probably considered the standard Feynman rules of a scalar quantum electrodynamics and a phase space modified due to Lorentz violation.
The first articles on vacuum Cherenkov radiation in the realm of the SME were written by Lehnert and Potting in 2004 [
13,
14]. They are based on a spacelike MCS electromagnetism coupled to standard massive particles. MCS theory is characterized by a dimensionless preferred direction
and a mass scale
. This framework is birefringent, i.e., it provides two distinct modified propagation modes ⊖ and ⊕ of electromagnetic waves. Independently of the observer frame chosen,
. The properties of the dispersion laws are quite obscure in a purely timelike frame. For example, in such a frame, the mode ⊕ has a cusp for a vanishing momentum and a gap exists where the energy of ⊖ becomes complex.
To simplify the analysis, the authors study the vacuum Cherenkov process in the rest frame of the massive particle, which is possible due to observer Lorentz invariance. In the rest frame, the four-current
is stationary. The solution to the four-potential can be written as an integral over momentum space involving a product of the Green’s function of MCS theory and the Fourier transform
of the four-current:
where
is an appropriate contour in the complex
plane and
is a tensor structure characteristic for MCS theory. The Green’s function involves the inverse of the MCS dispersion equation
for
. The contour integral in the complex plane picks up contributions from the poles inside the contour only. If these poles are purely imaginary, the integrand will be exponentially damped for large distances from the trajectory. This means that the far-field vanishes whereupon there is no radiation far away from the source, which is the situation in standard electrodynamics. Hence, vacuum Cherenkov radiation occurs once there are real solutions of
(corresponding to spacelike dispersion relations) such that the exponential function is oscillatory. From the brief discussion of the modes of MCS theory above, we already know that such solutions exist indeed. They are given by the modes ⊖. The condition of real, spacelike solutions of the dispersion equation is equivalent to the existence of a refractive index
of the vacuum. A boost to an arbitrary observer frame provides the condition on the Cherenkov angle:
where
is the three-velocity of the particle.
Furthermore, Lehnert and Potting found that the emitted radiation can be right-handed or left-handed polarized, dependent on the emission direction with respect to and the spacelike preferred direction . Using the energy-momentum tensor, it can be shown that there is no net radiated energy in the rest frame of a localized source. Furthermore, the radiated three-momentum vanishes due to the symmetry of the integrand as long as the integrand itself is regular. For real solutions of , the integrand is singular, in fact, and there are nonvanishing contributions to the radiated three-momentum. The latter has a backreaction on the radiating particle. Due to such recoil effects, the particle will no longer move on a geodesic, i.e., the weak equivalence principle is violated under this condition.
Further results on vacuum Cherenkov radiation at the classical level were obtained by Altschul in a series of papers. Studies on the nonbirefringent part of the
CPT-even modification of Maxwell theory were carried out in [
16]. These nine nonbirefringent coefficients are characterized by a symmetric, traceless matrix
. Altschul finds that there exists a coordinate transformation between the
coefficients in the fermion sector and the
coefficients in the photon sector. Hence, investigating vacuum Cherenkov radiation in both sectors should produce equivalent results at first order in Lorentz violation. The possible problem of a missing frequency cutoff is identified in the computation of the total radiated energy. Therefore, integrating the radiated-energy spectrum
over the photon frequency
may produce infinite results, as the modified theory allows for arbitrarily high
. A hypothetical cutoff is introduced via the argument that there are possible causality problems of the theory in the vicinity of the threshold. However, we will see below that such a cutoff is obsolete when taking into account recoil effects. In the subsequent paper [
17], Altschul studies additional properties of vacuum Cherenkov radiation for both MCS theory and modified Maxwell theory. He points out that MCS theory allows for a single subluminal mode only, whereas two such modes can arise in modified Maxwell theory dependent on the propagation direction. A consequence is that there is always a single Cherenkov cone only for MCS theory, whereas in modified Maxwell theory there may be two distinct cones for certain directions.
Timelike MCS theory is plagued by several problems. The energy density for the timelike sector is known to be unbounded from below. Thus, there exist runaway modes whose amplitudes increase exponentially as a function of the distance from the source. The possible origin of these issues is the gap of complex energies for the mode ⊖ indicated above. This gap exists for small momenta and long wavelengths, respectively, which is the motivation to study the power emitted by these long-wavelength modes in [
22]. The power of the short-wavelength modes is found by a phase space estimate to be proportional to
at least (with the velocity
v of the radiating particle). As radiation of long wavelengths is likely to be emitted in the nonrelativistic regime and as these contributions cannot be estimated from the phasespace, they must be of
. The timelike MCS theory leads to a modified Ampère law where the additional term
is interpreted as a current. Altschul obtains the perturbative solution of the modified Ampère law at leading order in
and
v in a clever way. Based on this solution, the outgoing Poynting vector flux
at
is shown to be an odd function of
where
is the polar angle. Hence, the total integral of
over a closed surface vanishes demonstrating that the runaway modes do not contribute to vacuum Cherenkov radiation.
The latter result is generalized in [
23] for the situation of a steady motion of the charge, i.e., recoil effects are neglected. The authors expand the electric and magnetic field
in terms of
and the particle velocity
v. They argue that each term of this expansion is either of toroidal nature,
, or of azimuthal form,
. The central finding is that the functions
,
,
for the electric field
, the magnetic field
, and the vector potential
are either even or odd with respect to
. As a result of that, each combination that contributes to the outgoing Poynting flux
provides an odd function in
. Therefore, any integral of
over a sphere vanishes and there is no net outflow of energy at all!
A possible interpretation of the latter result is that the negative energy carried away from the long-wavelength modes compensates the contributions of positive energy associated with the short-wavelength modes. Interestingly, a paper appeared very recently demonstrating this proposed cancelation explicitly [
30]. The authors work in the same framework as that developed in [
23]. They calculate the Fourier transform of the magnetic field at first order in
and
v. Based on this finding, all magnetic field terms of odd orders in
can be obtained iteratively. Summing these contributions corresponds to a geometric series whose limit is an expression that is quadratic in the photon momentum and involves a singularity for the photon momentum equal to
. When the momentum approaches the singularity from above, there is a sign change of the whole expression demonstrating the cancelation between contributions of large momentum with those of low momentum. The singularity itself is not problematic, as its principal value can be considered formally.
3.2. Quantum Effects
The presumably first studies of the vacuum Cherenkov process in the context of quantum field theory were carried out in [
15,
18]. The first paper is based on a MCS theory coupled to standard Dirac fermions. Due to the issues of timelike MCS theory, an observer frame with a purely spacelike preferred direction
is considered. The matrix element squared of the process at tree-level is obtained based on a set of modified Feynman rules. The decay rate follows from integrating the latter result over the modified phase space. As long as the fermion under consideration has a nonvanishing momentum component
parallel to
, the decay rate is found to be nonzero. For
, the decay rate depends on
in a polynomial manner, whereas for
it involves a logarithmic term. Such logarithmic dependencies are nonperturbative in Lorentz violation and they seem to be characteristic for the ultra-high energy regime of a birefringent theory. An additional example for a behavior of this kind will be encountered below. Furthermore, the authors find that the emitted photon is circularly polarized for large photon momenta and linearly polarized for vanishing photon momenta.
In their second paper [
18], Klinkhamer and Kaufhold extend their analysis of [
15]. Apart from MCS theory coupled to standard Dirac fermions, they also consider a modified scalar quantum electrodynamics, i.e., they couple MCS theory to the Lagrange density of a massive, spinless field. Including the second framework into their investigation permits them to calculate the decay rates
and radiated-energy rates
for spin-1/2 fermions and spinless bosons, respectively. For fermion momenta
, spin effects are found to be highly suppressed. However, at least for large fermion momenta, they play a certain role:
where
is the fine-structure constant.
It is interesting that these leading-order results can be obtained from a semiclassical description based on the following nontrivial refractive index of the vacuum:
with the photon energy
and the angle
between the photon momentum and
. Now, the photon spectrum for ordinary Cherenkov radiation in macroscopic media, which is provided by the Frank–Tamm formula, is reinterpreted in the context of a vacuum with the refractive index given by Equation (
3). Taking the photon momentum into account, which is a quantum effect, introduces a finite maximum energy of the emitted photon. Hence, the Frank–Tamm spectrum can be integrated over the photon frequency resulting in the first radiated-energy rate of Equation (
2). This finding makes sense, as Frank and Tamm did not consider the spin of the radiating particle. The latter leads to an extra contribution that adds up to the second rate of Equation (
2).
A further step towards a better understanding of vacuum Cherenkov radiation in the quantum regime is achieved via [
19]. In the latter reference, isotropic modified Maxwell theory based on the single coefficient
is coupled to standard Dirac fermions. The process is found to have a threshold
. Furthermore, the decay rate and radiated-energy rate are computed again using a set of modified Feynman rules for photons and a modified phase space. For comparison, a semiclassical analysis is performed in addition based on a modified refractive index
of the vacuum. Recoil effects lead to a finite radiated-energy rate that is found to be equal to the corresponding result in [
12] for large momenta. The deduction from this finding is that Coleman and Glashow also did not take into account the particle spin. By doing so, the leading-order classical result is equal to the leading-order rate of the quantum field theory analysis including Dirac fermions.
At around the same time, the paper [
20] was published. The latter also deals with isotropic modifications of both the photon and the fermion sector. In a quantum field theory analysis, the authors derive both the threshold and the decay rate for the vacuum Cherenkov process at leading order in Lorentz violation. These results are consistent with those of [
19] at leading order. A constraint on isotropic Lorentz violation in the photon and electron sector follows from the assumption that an energy loss by vacuum Cherenkov radiation hides within the uncertainty of the synchrotron losses at the Large Electron-Positron Collider (LEP).
A couple of years later, Díaz and Klinkhamer refined the study carried out in [
24]. Here, the parton model is used to understand effects related to a possible internal structure of the incoming fermion. In this approach, a Cherenkov photon can be emitted from a single parton inside a fermion, i.e., neutrons can radiate vacuum Cherenkov radiation, as well. The authors determine the emission rate by an electrically charged parton carrying the fraction
of the incoming fermion momentum
p. The maximum photon energy is found to be proportional to the fraction
x. Hence, Cherenkov emission is suppressed for small momentum fractions, which practically excludes this process for the sea quarks. Another interesting property is that emissions of very hard photons may lead to momentum transfers large enough to destroy the initial hadron and to produce new ones in the final state. Finally, the total power radiated by a composite proton and neutron, respectively, is determined based on very recent data on parton distribution functions. The rates for both an initial proton and neutron are suppressed by around one order of magnitude in comparison to the rate in [
19] for a structureless Dirac fermion. This result does not change the constraint obtained in [
19] though.
A quantum field theory analysis that complements the classical studies of [
22,
23,
30] for vacuum Cherenkov radiation in timelike MCS theory is carried out in [
27]. Complex energies of the mode ⊖ can be avoided by introducing a nonvanishing photon mass. Note that the current experimental limit on a photon mass is
[
31], which is many orders of magnitudes larger than the best constraint on the controlling coefficient under consideration, which is
[
32]. A nonzero photon mass also allows for a consistent quantization procedure whereupon the decay rate for vacuum Cherenkov radiation can be calculated in quantum field theory. The process has a threshold and the decay rate for initial fermion momenta much larger than this threshold is characterized by two different regimes. There is a range of momenta where it is suppressed quadratically by Lorentz violation and increases quadratically with the fermion momentum. For very large momenta, it is only linearly suppressed by Lorentz violation and grows linearly with momentum.
After the big amount of investigations of vacuum Cherenkov radiation with modified photons, time was ready to study the vacuum Cherenkov process for Lorentz-violating fermions in [
28]. The coordinate transformation moving Lorentz violation between the photon and fermion sector [
16] only covers the
CPT-even, nonbirefringent
c coefficients for fermions. Such a transformation is neither known for the
CPT-odd
a,
b,
e,
f, and
g coefficients nor for the
CPT-even, birefringent
d,
H coefficients, which is why such an analysis is definitely reasonable. Note also that for the birefringent
b,
d,
H, and
g coefficients, there are two fermion modes that will be denoted as
and
where the index
X stands for a controlling coefficient. This property leads to interesting new effects that do not have a counterpart in the photon sector. The base of the analysis performed in [
28] are the modified Feynman rules for external fermion legs developed in the technical work [
33]. Due to calculational complexities, decay rates and radiated-energy rates are obtained numerically for a broad range of coefficients. The essential properties are that the processes for the
c,
d,
e,
f, and
g coefficients have thresholds. Furthermore, for large incoming fermion momenta, the decay rates for the
c,
d coefficients are linearly suppressed in Lorentz violation, whereas the decay rates for
e,
f, and
g are quadratically suppressed. The processes
are allowed for a certain sign of the controlling coefficients and
occur for the opposite sign. Analog decays for the
a,
b, and
H coefficients are found to be forbidden. However, the birefringent nature of the spin-nondegenerate coefficients opens up the possibility of spin–flip processes
and the analog ones with ⊕ and ⊖ interchanged. These decays have peculiar properties. First, they do not have a threshold and, second, their decay rates are highly suppressed by several powers of the controlling coefficients in contrast to the spin-conserving decays. Furthermore, the decay rates involve logarithmic terms for large momenta similarly to the results for MCS theory obtained in [
15].
3.3. Radiation of Particles Other Than Photons
A plethora of alternative Cherenkov-type processes is conceivable in Lorentz-violating theories. The radiating particle does not necessarily have to be a massive fermion and the radiated particles need not inevitably be photons. One of the first articles in this realm was published by Altschul [
26]. Here, an effective theory for Lorentz-violating pions is considered coupled to standard photons. In this framework, high-energy photons can lose energy by radiating pions where the process involves a threshold. At leading order in Lorentz violation, the threshold has parallels with the analog expression for nonbirefringent modified Maxwell theory in [
16]. After all, both frameworks are quite similar from a merely kinematic point of view. As the direct calculation of the decay rate is cumbersome, an estimate of the rate is obtained from the prominent process
.
A further interesting Cherenkov-type process is explored in [
29]. The authors consider a Lorentz-violating modification of the free W-boson sector. Such a term enables a Cherenkov-type process in vacuo where a fermion of mass
decays into a fermion of mass
under the emission of a W boson. An analysis in the rest frame of the incoming particle is feasible. It reveals that the process is energetically possible for a quite large controlling coefficient in the rest frame showing that this frame must be strongly boosted with respect to a concordant frame where Lorentz violation is supposed to be small. Analogous to [
24], the authors perform a sophisticated parton model study based on the elementary process mentioned before. Hence, the decay rate of W-boson emission of a single quark is convoluted with appropriate parton distribution functions. As the probability of finding quarks with a large momentum fraction
steeply decreases for
, the decay rate of a proton right at the threshold region is considerably suppressed in comparison to the decay rate of the elementary process.
After the detection of superluminal neutrinos had been announced by the OPERA collaboration in 2011, Cohen and Glashow quickly published a paper studying Cherenkov-type radiation of electron-positron pairs by neutrinos via virtual Z bosons [
21]. Based on the value for Lorentz violation in the neutrino sector announced by OPERA, they showed that neutrinos would quickly lose their energy via this Cherenkov process making it impossible for them to arrive at the Gran Sasso laboratory with the energy that was measured by OPERA. Few months later, OPERA announced that errors had occurred in the course of the measurement process rendering their results incorrect.