Soil Moisture Retrieval Based on GPS Signal Strength Attenuation
Abstract
:1. Introduction
2. Measurement Setup and Data
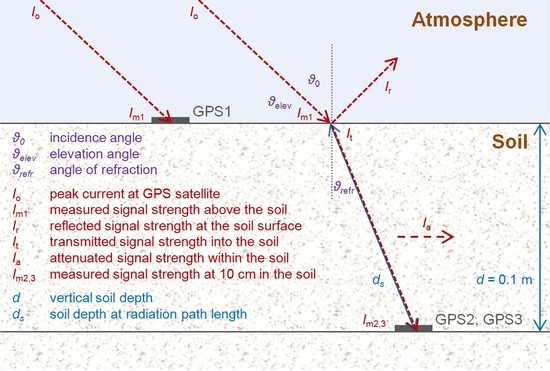
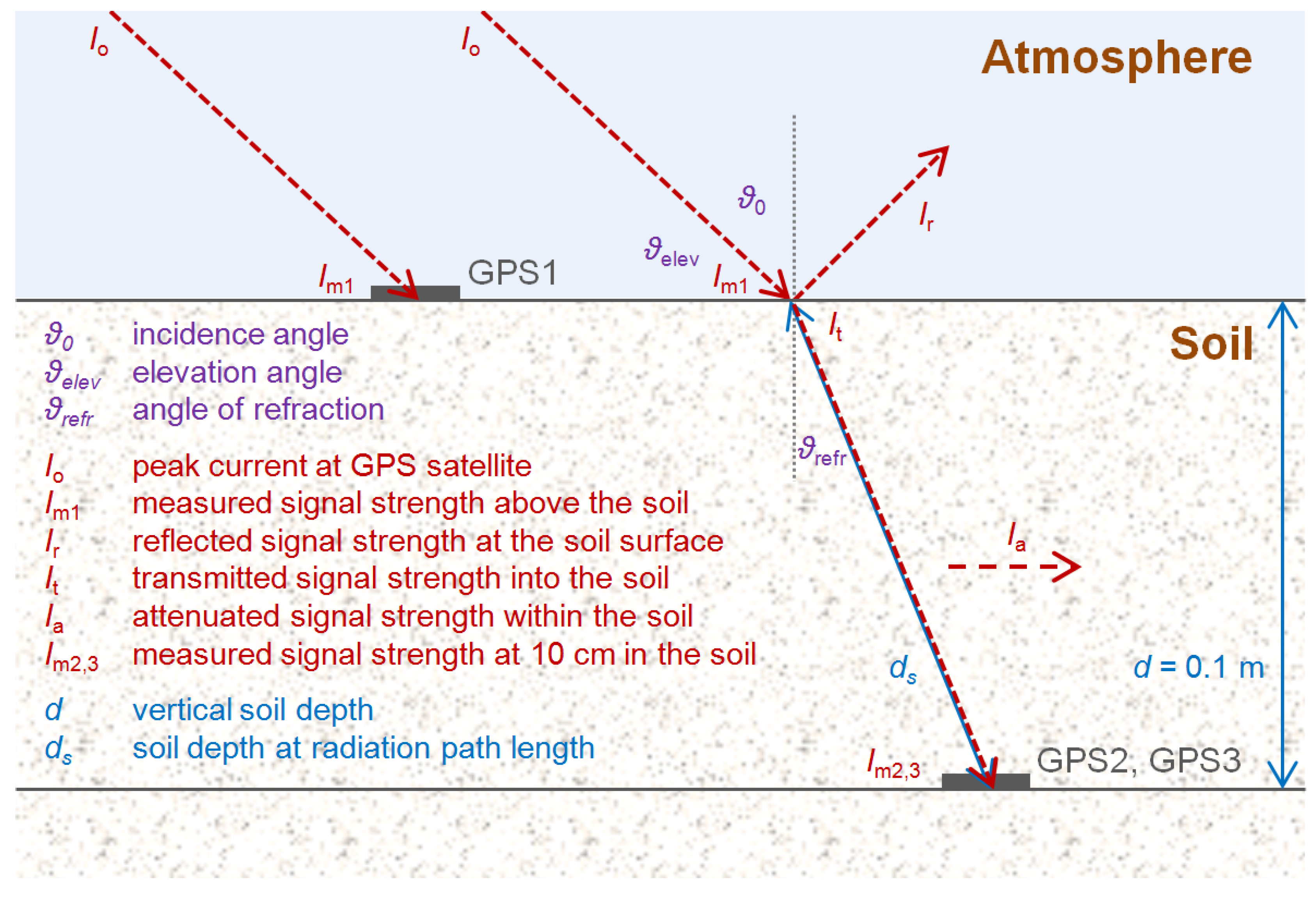
2.1. GPS Measurement Setup at the DWD Test Site Munich
2.2. Accompanying in Situ Data
2.3. Land-Surface Model PROMET
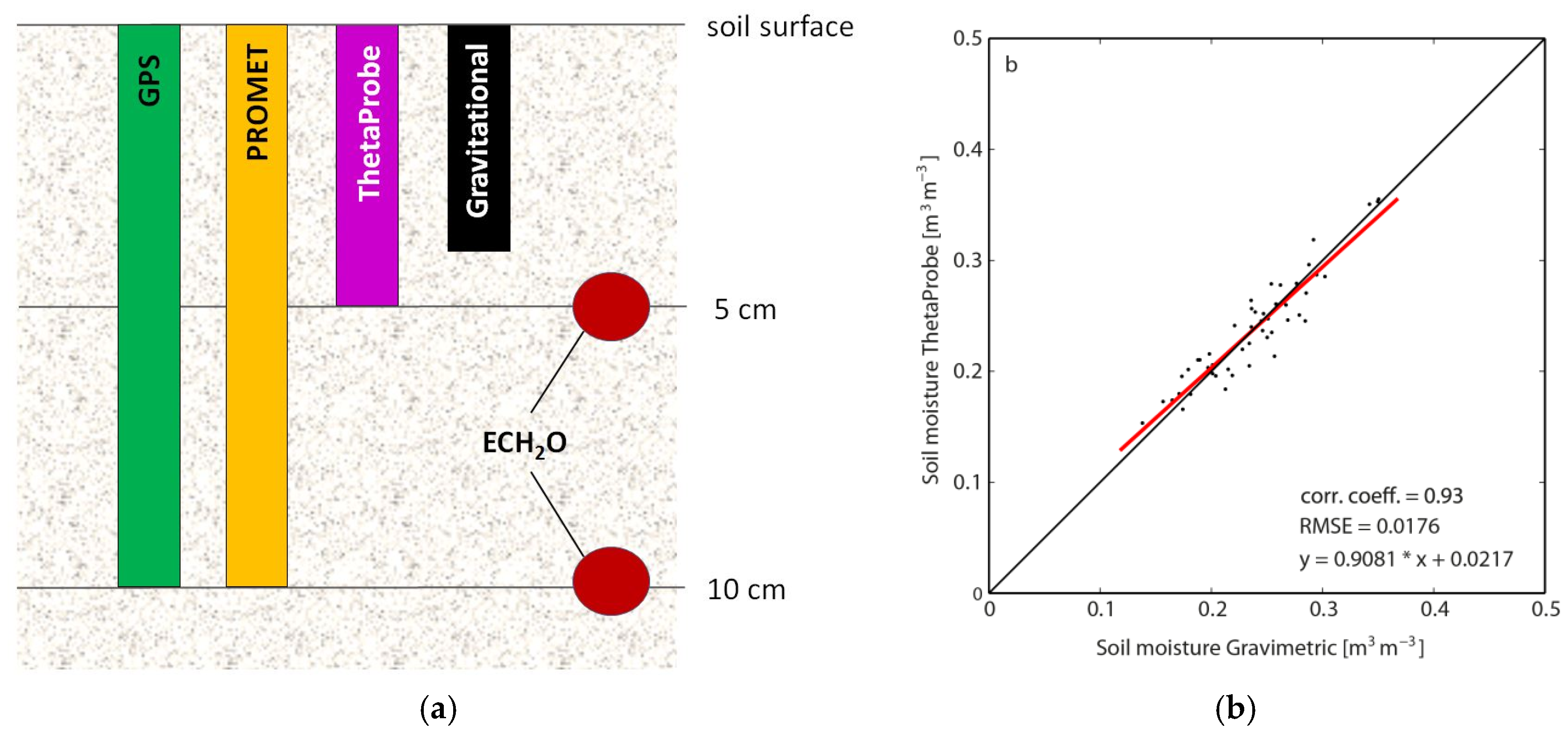
2.4. Soil Moisture Sampling Volumes and Vertical Ranges of Different Methods
3. Soil Moisture Retrieval with GPS
3.1. GPS Data Processing
3.2. GPS Signal Strength Attenuation
3.3. Dobson Four-Component Dielectric Mixing Model
3.4. Calculation of Soil Moisture and Sensitivity
4. Results
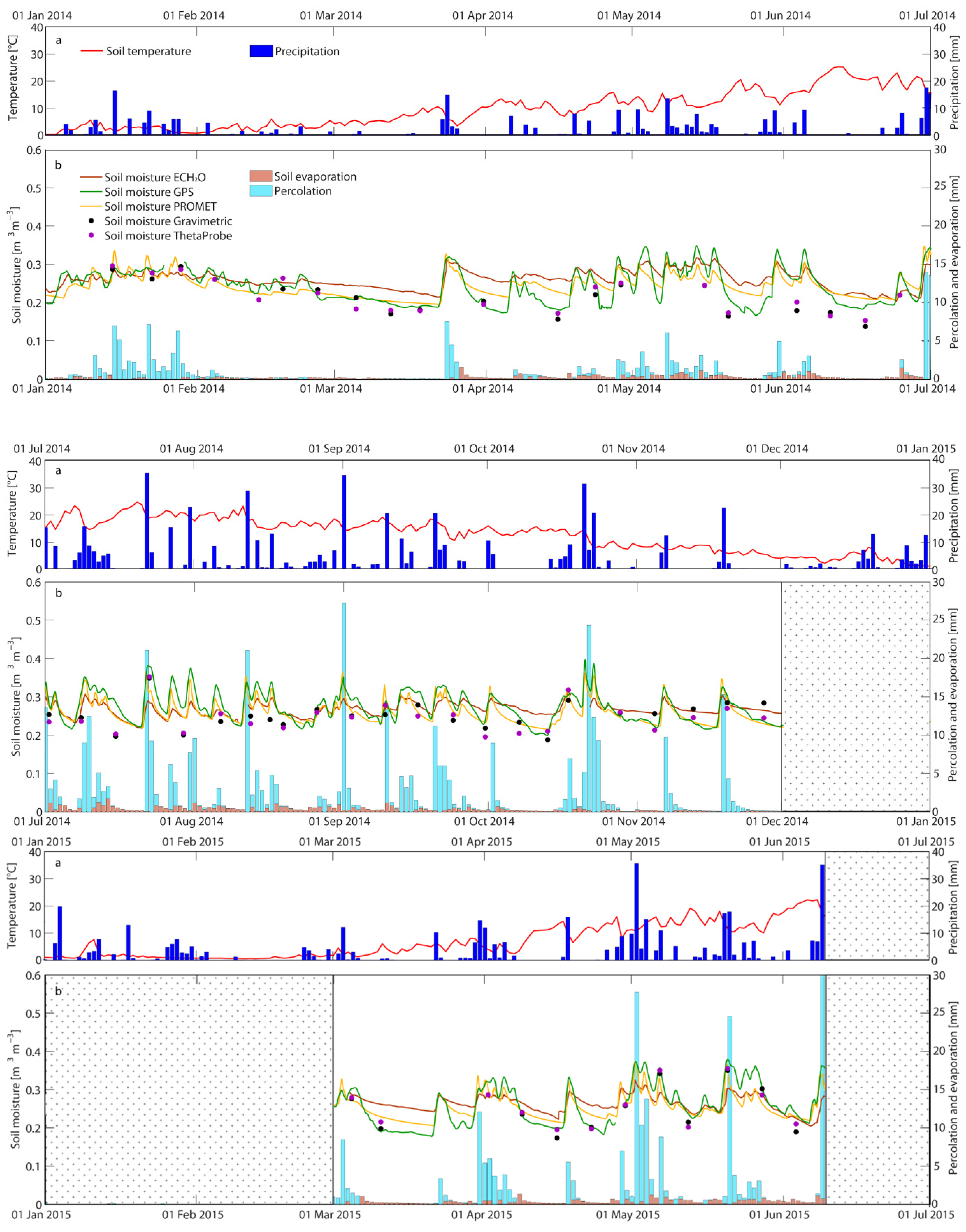
4.1. Time Series of Soil Moisture and Hydrological Data
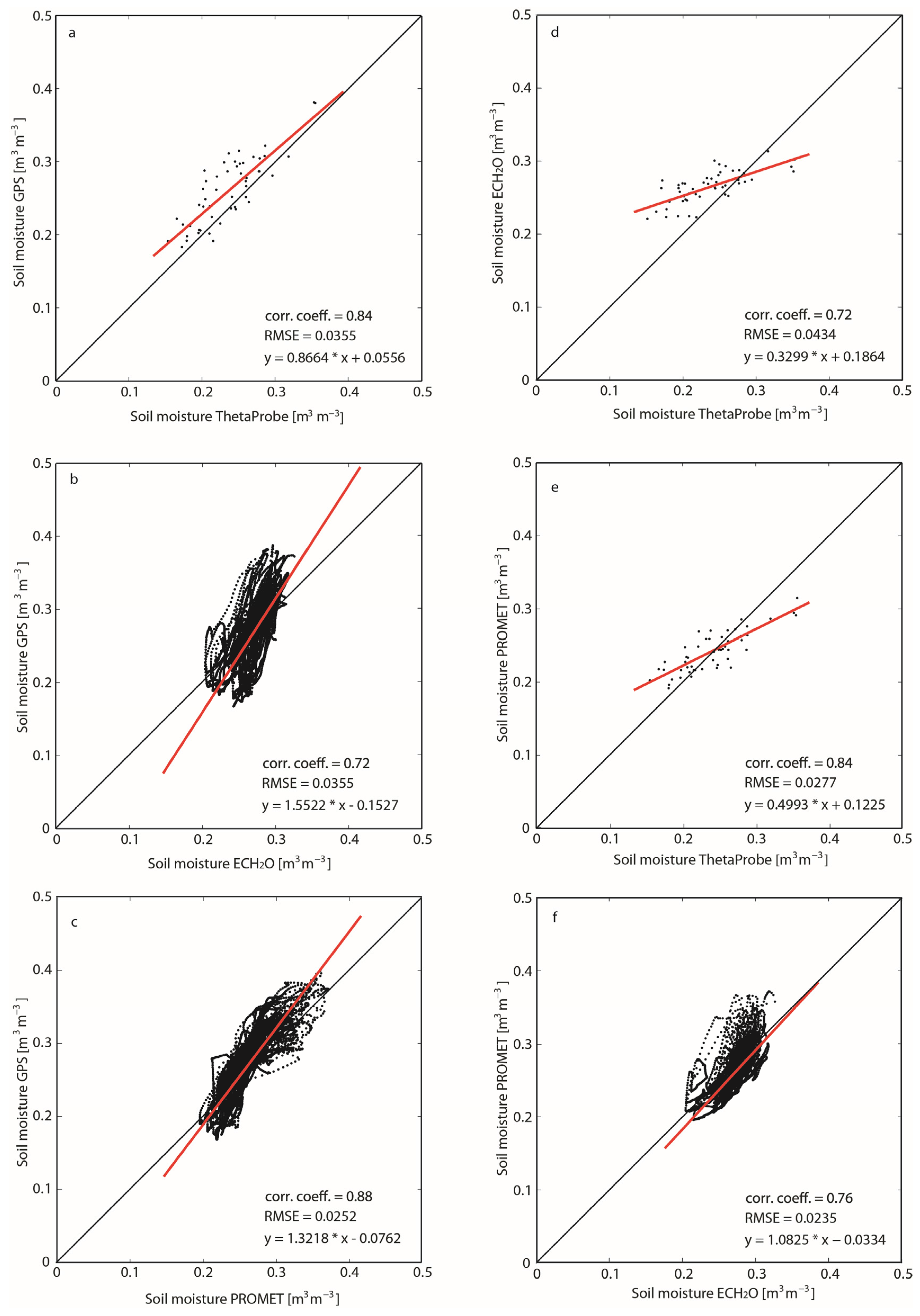
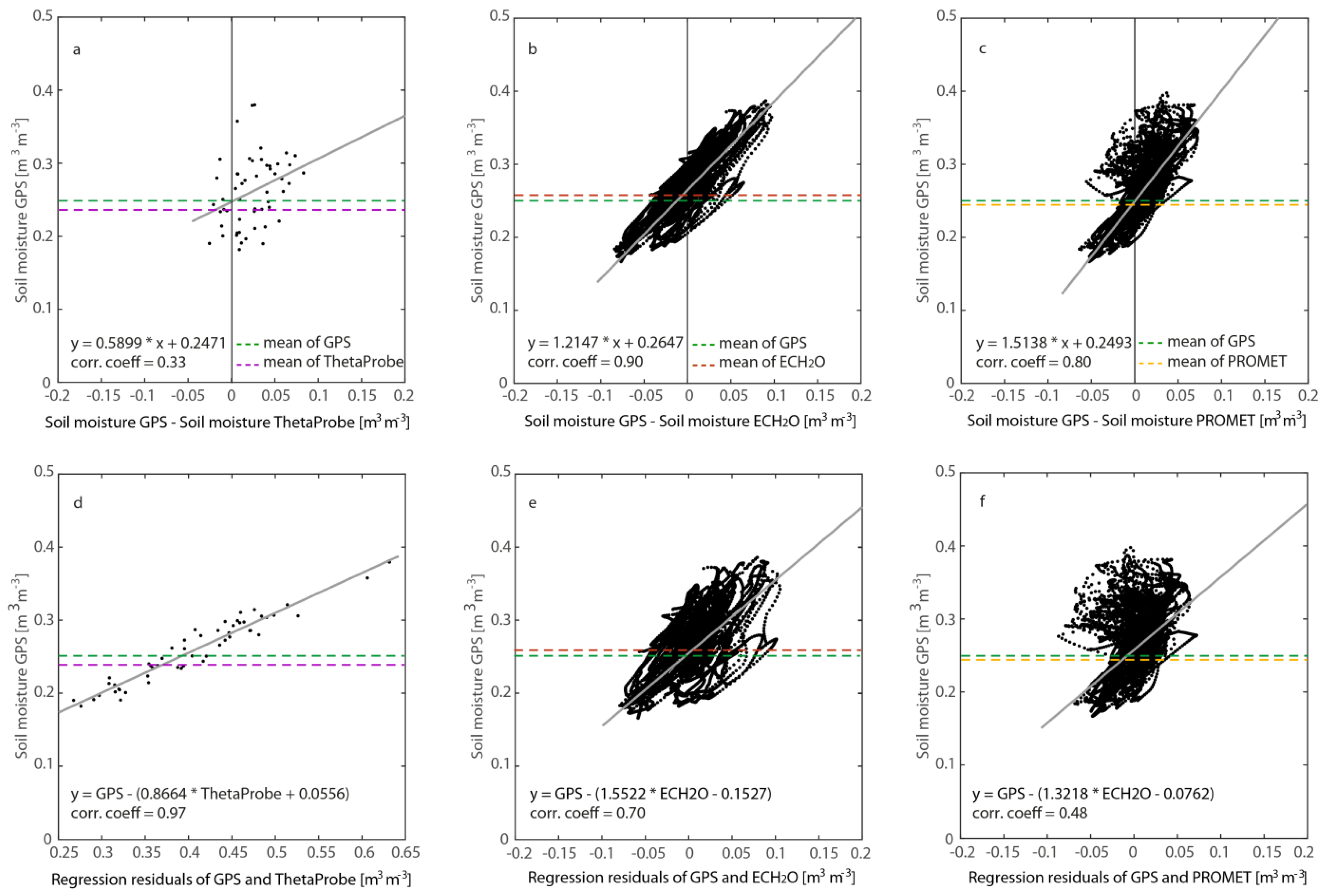
4.2. Comparison of the Different Soil Moisture Methods
5. Discussion
5.1. Conformities and Discrepancies between the Different Soil Moisture Methods
5.2. Advantages and Limitations of GPS Soil Moisture Measurements
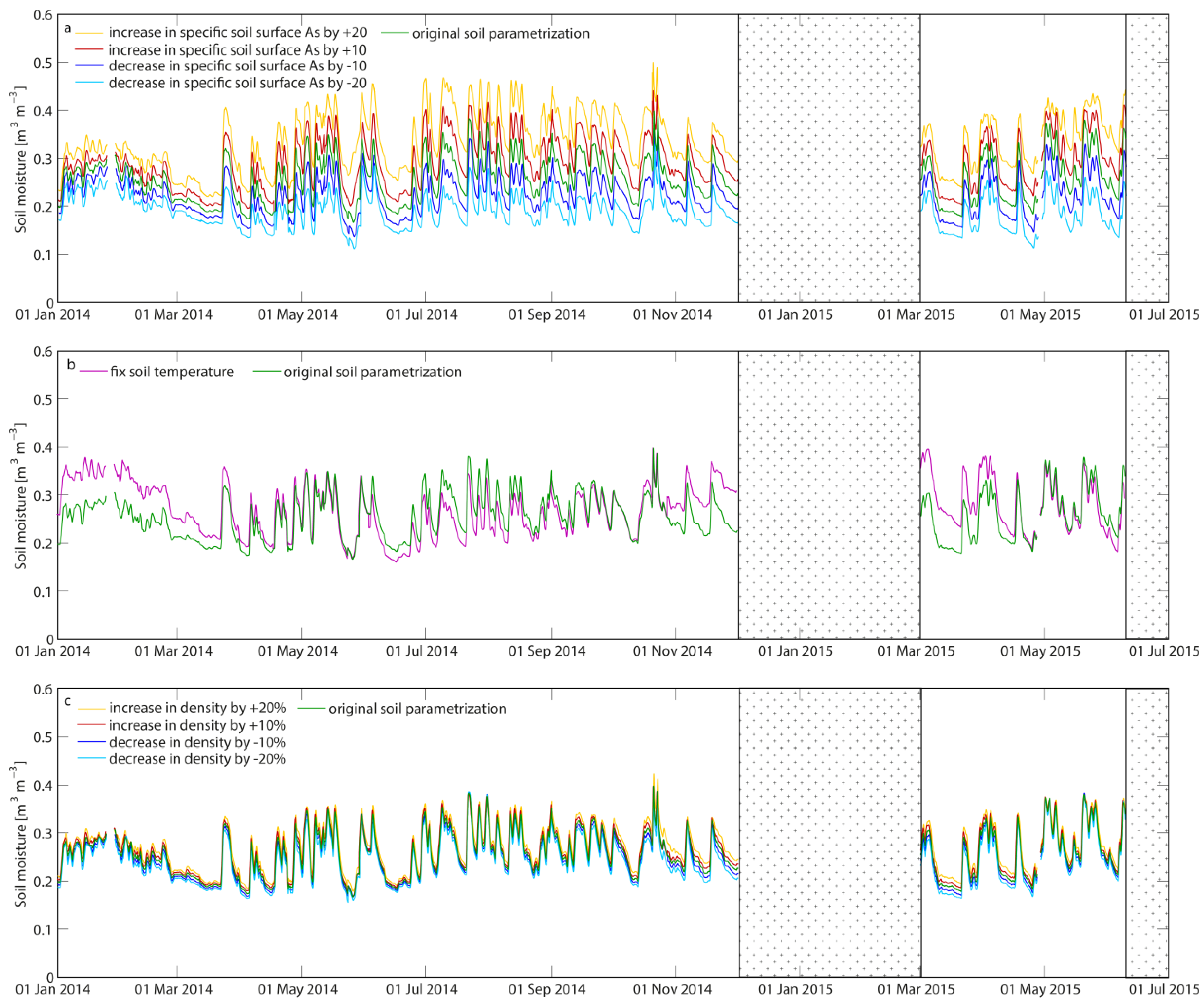
5.3. Sensitivity Analysis of GPS Soil Moisture Measurements
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dirmeyer, P.A. Using a global soil wetness dataset to improve seasonal climate simulation. J. Clim. 2000, 13, 2900–2922. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.O.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C. The SMOS mission: New tool for monitoring key elements ofthe global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.; Kanae, S.; Kowalczyk, E.; Lawrence, D. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Komma, J.; Blöschl, G.; Reszler, C. Soil moisture updating by ensemble Kalman filtering in real-time flood forecasting. J. Hydrol. 2008, 357, 228–242. [Google Scholar] [CrossRef]
- Loew, A.; Schwank, M.; Schlenz, F. Assimilation of an L-band microwave soil moisture proxy to compensate for uncertainties in precipitation data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2606–2616. [Google Scholar] [CrossRef]
- Mauser, W.; Klepper, G.; Zabel, F.; Delzeit, R.; Hank, T.; Putzenlechner, B.; Calzadilla, A. Global biomass production potentials exceed expected future demand without the need for cropland expansion. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
- Fischer, E.; Seneviratne, S.; Lüthi, D.; Schär, C. Contribution of land-atmosphere coupling to recent European summer heat waves. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Loew, A.; Holmes, T.; de Jeu, R. The European heat wave 2003: Early indicators from multisensoral microwave remote sensing? J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Long, D.G.; Blackwell, W.J.; Elachi, C.; Fung, A.K.; Ruf, C.; Sarabandi, K.; Zebker, H.A.; Van Zyl, J. Microwave Radar and Radiometric Remote Sensing; University of Michigan Press: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Ulaby, F.T.; Dubois, P.C.; van Zyl, J. Radar mapping of surface soil moisture. J. Hydrol. 1996, 184, 57–84. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T. Active microwave soil moisture research. IEEE Trans. Geosci. Remote Sens. 1986, GE-24, 23–36. [Google Scholar] [CrossRef]
- Loew, A.; Ludwig, R.; Mauser, W. Derivation of surface soil moisture from Envisat Asar wide swath and image mode data in agricultural areas. IEEE Trans. Geosci. Remote Sens. 2006, 44, 889–899. [Google Scholar] [CrossRef]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.-C.; Bizzarri, B.; Wigneron, J.-P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Hydrol. Res. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Mauser, W.; Rombach, M.; Bach, H.; Demircan, A.; Kellndorfer, J.M. Determination of Spatial and Temporal Soil-Moisture Development Using Multitemporal ERS-1 Data; Satellite Remote Sensing; International Society for Optics and Photonics: Rome, Italy, 1995; pp. 502–515. [Google Scholar]
- Barré, H.M.; Duesmann, B.; Kerr, Y.H. SMOS: The mission and the system. IEEE Trans. Geosci. Remote Sens. 2008, 46, 587–593. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Martinuzzi, J.-M.; Font, J.; Berger, M. Soil moisture retrieval from space: The soil moisture and ocean salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Katzberg, S.J.; Torres, O.; Grant, M.S.; Masters, D. Utilizing calibrated GPS reflected signals to estimate soil reflectivity and dielectric constant: Results from SMEX02. Remote Sens. Environ. 2006, 100, 17–28. [Google Scholar] [CrossRef]
- Chew, C.; Small, E.E.; Larson, K.M. An algorithm for soil moisture estimation using GPS-interferometric reflectometry for bare and vegetated soil. GPS Solut. 2016, 20, 525–537. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.D.; Bilich, A.L.; Braun, J.J.; Zavorotny, V.U. Use of GPS receivers as a soil moisture network for water cycle studies. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Larson, K.M.; Braun, J.J.; Small, E.E.; Gutmann, E.D.; Bilich, A.L. A physical model for GPS multipath caused by land reflections: Toward bare soil moisture retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 100–110. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Camps, A.; Aguasca, A.; Vall-llossera, M.; Valencia, E.; Ramos-Perez, I.; Park, H. Review of crop growth and soil moisture monitoring from a ground-based instrument implementing the interference pattern GNSS-R technique. Radio Sci. 2011, 46. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Camps, A.; Vall-Llossera, M.; Valencia, E.; Marchan-Hernandez, J.F.; Ramos-Perez, I. Soil moisture retrieval using GNSS-R techniques: Experimental results over a bare soil field. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3616–3624. [Google Scholar] [CrossRef]
- Privette, C.V., III; Khalilian, A.; Bridges, W.; Katzberg, S.; Torres, O.; Han, Y.J.; Maja, J.M.; Qiao, X. Relationship of soil moisture and reflected GPS signal strength. Adv. Remote Sens. 2016, 5, 18–27. [Google Scholar] [CrossRef]
- Dall’Amico, J.T.; Schlenz, F.; Loew, A.; Mauser, W. First results of SMOS soil moisture validation in the Upper Danube catchment. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1507–1516. [Google Scholar] [CrossRef]
- De Rosnay, P.; Calvet, J.-C.; Kerr, Y.; Wigneron, J.-P.; Lemaître, F.; Escorihuela, M.J.; Sabater, J.M.; Saleh, K.; Barrié, J.; Bouhours, G. SMOSREX: A long term field campaign experiment for soil moisture and land surface processes remote sensing. Remote Sens. Environ. 2006, 102, 377–389. [Google Scholar] [CrossRef]
- Delwart, S.; Bouzinac, C.; Wursteisen, P.; Berger, M.; Drinkwater, M.; Martin-Neira, M.; Kerr, Y.H. SMOS validation and the cosmos campaigns. IEEE Trans. Geosci. Remote Sens. 2008, 46, 695–704. [Google Scholar] [CrossRef]
- Bircher, S.; Balling, J.E.; Skou, N.; Kerr, Y.H. Validation of SMOS brightness temperatures during the hobe airborne campaign, Western Denmark. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1468–1482. [Google Scholar] [CrossRef]
- Panciera, R.; Walker, J.P.; Kalma, J.D.; Kim, E.J.; Hacker, J.M.; Merlin, O.; Berger, M.; Skou, N. The Nafe’05/Cosmos data set: Toward SMOS soil moisture retrieval, downscaling, and assimilation. IEEE Trans. Geosci. Remote Sens. 2008, 46, 736–745. [Google Scholar] [CrossRef]
- Jackson, T.J.; Bindlish, R.; Cosh, M.; Zhao, T. SMOS soil moisture validation with us in situ networks. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, USA, 24–29 July 2011; pp. 21–23.
- Rötzer, K.; Montzka, C.; Bogena, H.; Wagner, W.; Kerr, Y.H.; Kidd, R.; Vereecken, H. Catchment scale validation of SMOS and ASCAT soil moisture products using hydrological modeling and temporal stability analysis. J. Hydrol. 2014, 519, 934–946. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; Oevelen, P.V. The international soil moisture network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Kerr, Y.; Waldteufel, P.; Saleh, K.; Escorihuela, M.-J.; Richaume, P.; Ferrazzoli, P.; De Rosnay, P.; Gurney, R.; Calvet, J.-C. L-band microwave emission of the biosphere (L-meb) model: Description and calibration against experimental data sets over crop fields. Remote Sens. Environ. 2007, 107, 639–655. [Google Scholar] [CrossRef]
- Koch, F.; Prasch, M.; Schmid, L.; Schweizer, J.; Mauser, W. Measuring snow liquid water content with low-cost GPS receivers. Sensors 2014, 14, 20975–20999. [Google Scholar] [CrossRef] [PubMed]
- Schmid, L.; Koch, F.; Heilig, A.; Prasch, M.; Eisen, O.; Mauser, W.; Schweizer, J. A novel sensor combination (upGPR–GPS) to continuously and non-destructively derive snow cover properties. Geophys. Res. Lett. 2015, 42, 3397–3405. [Google Scholar] [CrossRef]
- Mauser, W.; Bach, H. PROMET–large scale distributed hydrological modelling to study the impact of climate change on the water flows of mountain watersheds. J. Hydrol. 2009, 376, 362–377. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-Rayes, M. Microwave dielectric behavior of wet soil-part II: Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- Mauser, W.; Prasch, M. Regional Assessment of Global Change Impacts: The Project GLOWA-Danube; Springer: Berlin, Germany, 2015. [Google Scholar]
- Weber, M.; Braun, L.; Mauser, W.; Prasch, M. Contribution of rain, snow-and icemelt in the Upper Danube discharge today and in the future. Geogr. Fis. Din. Quat. 2010, 33, 221–230. [Google Scholar]
- Koch, F.; Prasch, M.; Bach, H.; Mauser, W.; Appel, F.; Weber, M. How will hydroelectric power generation develop under climate change scenarios? A case study in the Upper Danube basin. Energies 2011, 4, 1508–1541. [Google Scholar] [CrossRef]
- Fastrax IT430 Data Sheet. Available online: https://upverter.com/datasheet/042ba70ed2cd4485a04760b5e6864a3cad0eca96.pdf (accessed on 12 April 2016).
- Hirschmann Car Communication. GPS Antennas—Powerful and Flexibly Combined. Available online: http://www.hirschmann-car.com/en/products/antenna-systems/gnss-satellite-positioning/gps/ (accessed on 12 April 2016).
- Bogena, H.; Huisman, J.; Oberdörster, C.; Vereecken, H. Evaluation of a low-cost soil water content sensor for wireless network applications. J. Hydrol. 2007, 344, 32–42. [Google Scholar] [CrossRef]
- Mauser, W.; Schädlich, S. Modelling the spatial distribution of evapotranspiration on different scales using remote sensing data. J. Hydrol. 1998, 212, 250–267. [Google Scholar] [CrossRef]
- Strasser, U.; Mauser, W. Modelling the spatial and temporal variations of the water balance for the weser catchment 1965–1994. J. Hydrol. 2001, 254, 199–214. [Google Scholar] [CrossRef]
- Prasch, M.; Mauser, W.; Weber, M. Quantifying present and future glacier melt-water contribution to runoff in a central Himalayan river basin. Cryosphere 2013, 7, 889–904. [Google Scholar] [CrossRef]
- Prasch, M.; Marke, T.; Strasser, U.; Mauser, W. Large scale integrated hydrological modelling of the impact of climate change on the water balance with Danubia. Adv. Sci. Res. 2011, 7, 61–70. [Google Scholar] [CrossRef]
- Philip, J. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, A. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Muerth, M.; Mauser, W. Rigorous evaluation of a soil heat transfer model for mesoscale climate change impact studies. Environ. Model. Softw. 2012, 35, 149–162. [Google Scholar] [CrossRef]
- Muerth, M. A Soil Temperature and Energy Balance Model for Integrated Assessment of Global Change Impacts at the Regional Scale, LMU. 2008. Available online: http://edoc.ub.uni-muenchen.de/8810/ (accessed on 15 April 2016).
- Schlenz, F.; Dall’Amico, J.T.; Loew, A.; Mauser, W. Uncertainty assessment of the smos validation in the Upper Danube catchment. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1517–1529. [Google Scholar] [CrossRef]
- Schlenz, F.; Mauser, W.; Loew, A. Analysis of smos brightness temperature and vegetation optical depth data with coupled land surface and radiative transfer models in Southern Germany. Hydrol. Earth Syst. Sci. 2012, 16, 3517–3533. [Google Scholar] [CrossRef]
- Loew, A.; Schlenz, F. A dynamic approach for evaluating coarse scale satellite soil moisture products. Hydrol. Earth Syst. Sci. 2011, 15, 75–90. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.D. In situ measurement of soil moisture: A comparison of techniques. J. Hydrol. 2004, 293, 85–99. [Google Scholar] [CrossRef]
- Mittelbach, H.; Casini, F.; Lehner, I.; Teuling, A.J.; Seneviratne, S.I. Soil moisture monitoring for climate research: Evaluation of a low-cost sensor in the framework of the Swiss Soil Moisture EXperiment (SwissSMEX) campaign. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Limsuwat, A.; Sakaki, T.; Illangasekare, T.H. Experimental quantification of bulk sampling volume of ECH2O soil moisture sensors. In Proceedings of the 29th Annual American Geophysical Union Hydrology Days, Collins, CO, USA, 25–27 March 2009.
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GPS; Springer: Berlin, Germany, 2008. [Google Scholar]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Lane, J.; Saxton, J. Dielectric dispersion in pure polar liquids at very high radio-frequencies. I. Measurements on water, methyl and ethyl alcohols. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences; The Royal Society: London, UK, 1952; pp. 400–408. [Google Scholar]
- Nolan, M.; Fatland, D.R. Penetration depth as a dinsar observable and proxy for soil moisture. IEEE Trans. Geosci. Remote Sens. 2003, 41, 532–537. [Google Scholar] [CrossRef]
- Hallikainen, M.T.; Ulaby, F.T.; Dobson, M.C.; El-Rayes, M.A.; Wu, L.-K. Microwave dielectric behavior of wet soil-part 1: Empirical models and experimental observations. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 25–34. [Google Scholar] [CrossRef]

| Permittivity of Medium | Real Part ε′ | Imaginary Part ε″ |
|---|---|---|
| 1.00 | 0.00 | |
| 2.44 | ~0.00 | |
| 35.00 | 15.00 |
| Soil Temperature | Real Part ε′ | Imaginary Part ε″ |
|---|---|---|
| 0.1 °C | 85.57 | 23.81 |
| 10 °C | 82.76 | 19.42 |
| 20 °C | 79.47 | 16.55 |
| 30 °C | 76.12 | 14.75 |
| 40 °C | 72.95 | 13.61 |
| Method | Mean | Std | Min | Max |
|---|---|---|---|---|
| GPS | 0.2565 | 0.0469 | 0.1667 | 0.3977 |
| ECH2O | 0.2633 | 0.0216 | 0.2044 | 0.3268 |
| PROMET | 0.2522 | 0.0314 | 0.1892 | 0.3675 |
| ThetaProbe | 0.2382 | 0.0465 | 0.1535 | 0.3553 |
| Gravimetric | 0.2380 | 0.0482 | 0.1379 | 0.3507 |
| Method | ThetaProbe | ECH2O | PROMET | GPS |
|---|---|---|---|---|
| ThetaProbe | - | 0.72 | 0.84 | 0.84 |
| ECH2O | 0.0434 | - | 0.76 | 0.72 |
| PROMET | 0.0277 | 0.0235 | - | 0.88 |
| GPS | 0.0355 | 0.0355 | 0.0252 | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koch, F.; Schlenz, F.; Prasch, M.; Appel, F.; Ruf, T.; Mauser, W. Soil Moisture Retrieval Based on GPS Signal Strength Attenuation. Water 2016, 8, 276. https://doi.org/10.3390/w8070276
Koch F, Schlenz F, Prasch M, Appel F, Ruf T, Mauser W. Soil Moisture Retrieval Based on GPS Signal Strength Attenuation. Water. 2016; 8(7):276. https://doi.org/10.3390/w8070276
Chicago/Turabian StyleKoch, Franziska, Florian Schlenz, Monika Prasch, Florian Appel, Tobias Ruf, and Wolfram Mauser. 2016. "Soil Moisture Retrieval Based on GPS Signal Strength Attenuation" Water 8, no. 7: 276. https://doi.org/10.3390/w8070276
APA StyleKoch, F., Schlenz, F., Prasch, M., Appel, F., Ruf, T., & Mauser, W. (2016). Soil Moisture Retrieval Based on GPS Signal Strength Attenuation. Water, 8(7), 276. https://doi.org/10.3390/w8070276