Development of Dynamic Ground Water Data Assimilation for Quantifying Soil Hydraulic Properties from Remotely Sensed Soil Moisture
Abstract
:1. Introduction
2. Materials and Methods
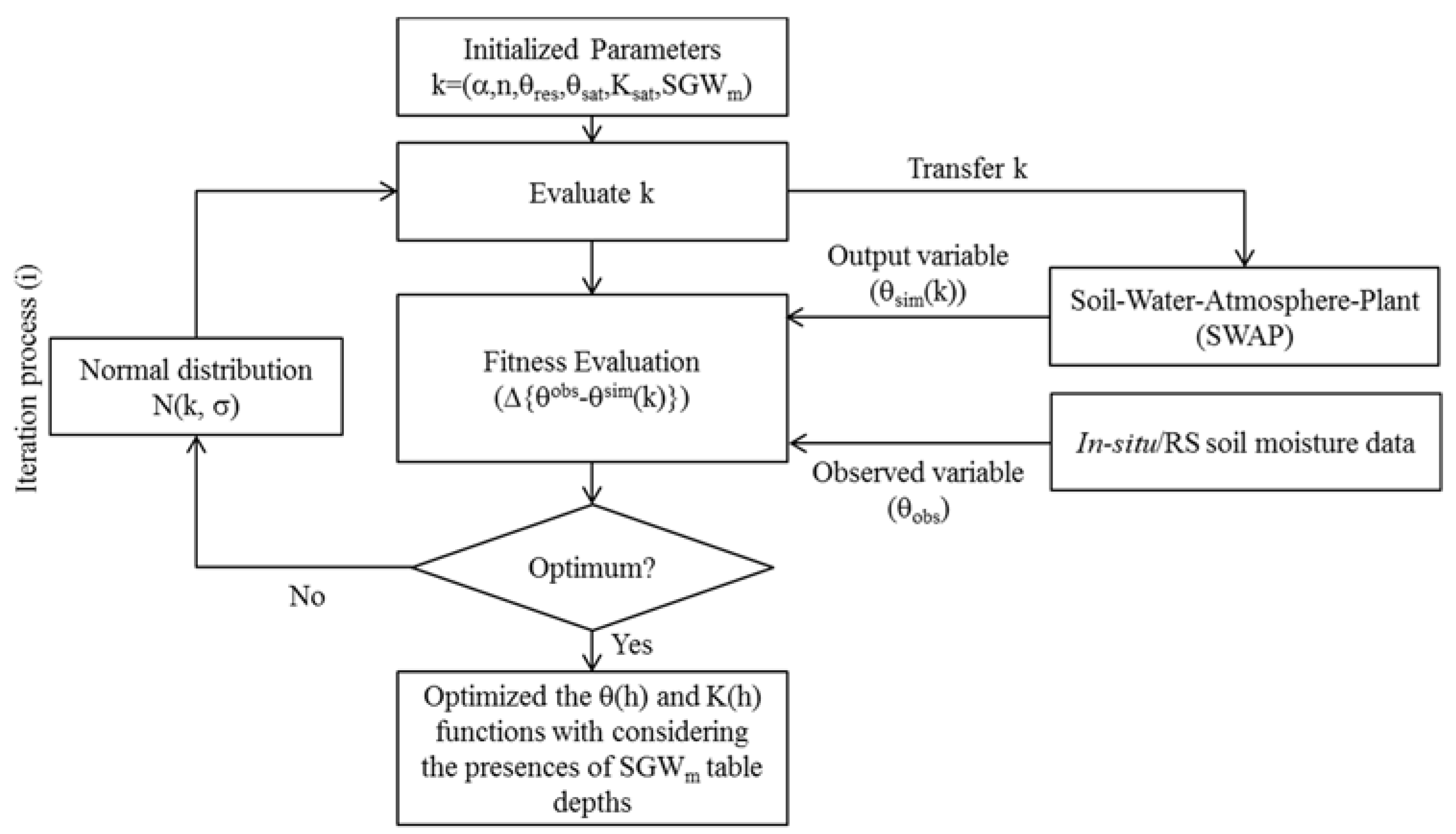
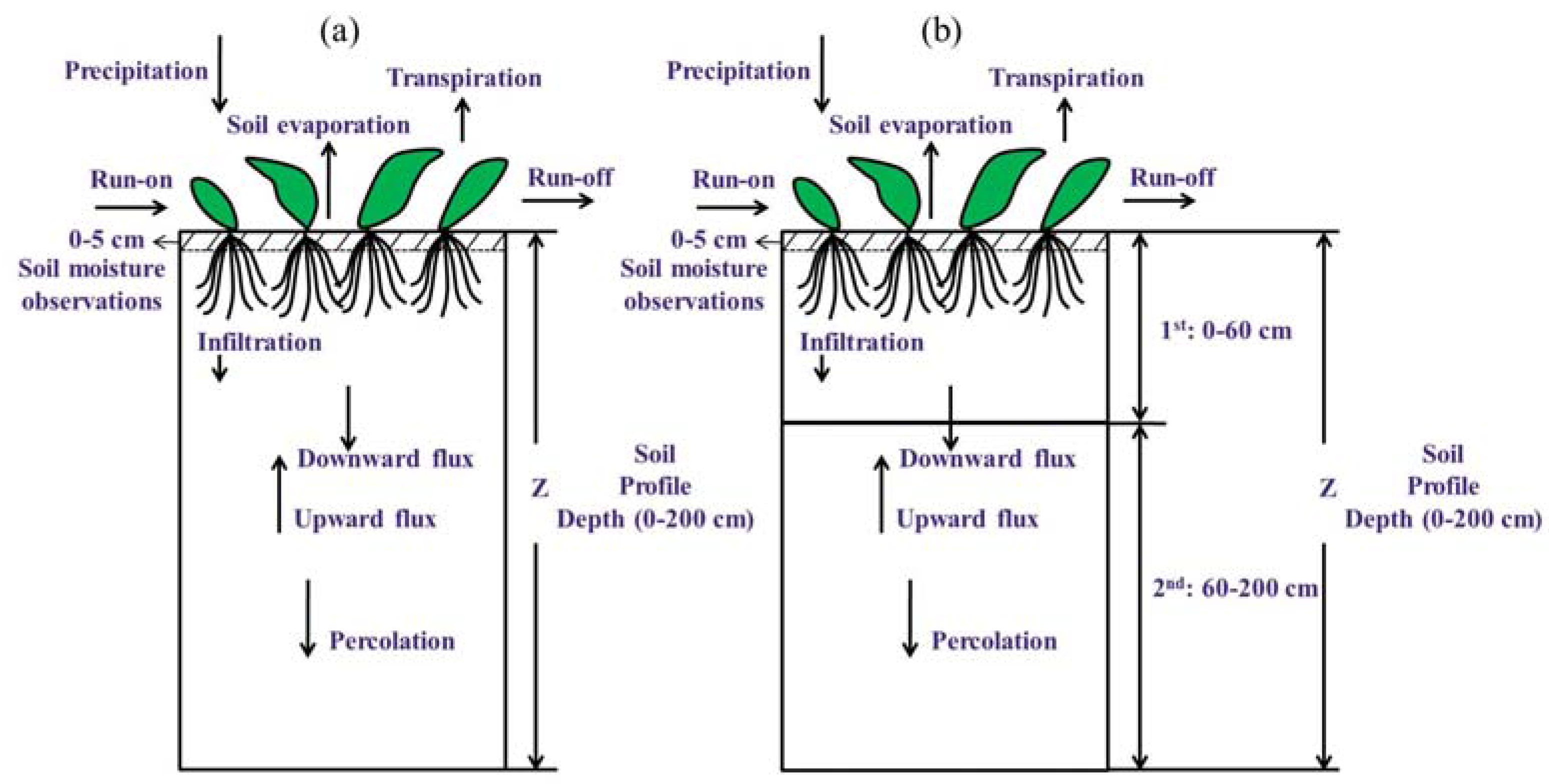
2.1. Conceptual Framework of the Dynamic Ground Water (DGW) Data Assimilation Approach
2.2. Soil–Water–Atmosphere–Plant Model
2.3. Iteration Algorithm
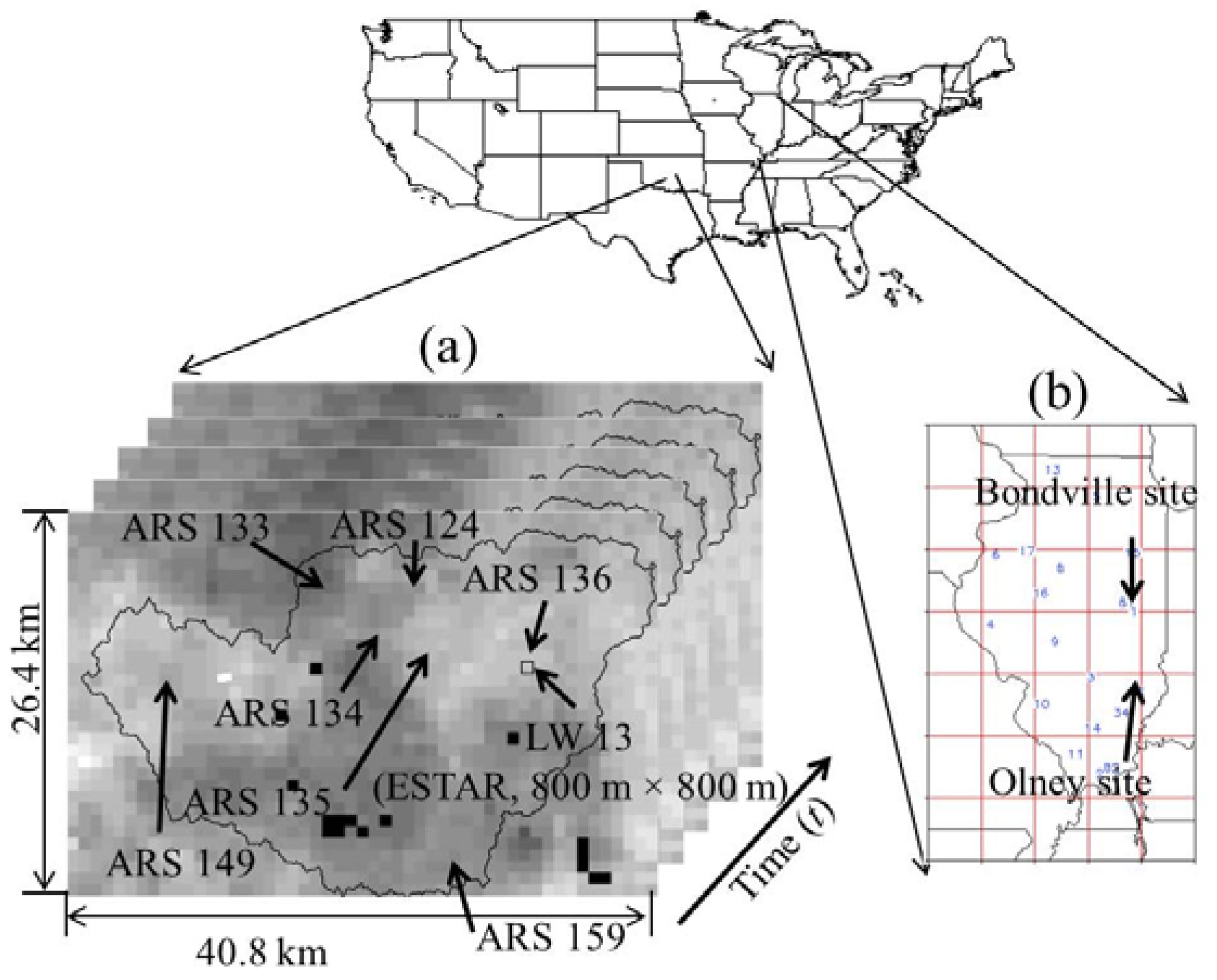
2.4. Description of Study Sites and Data
2.5. Numerical
3. Results and Discussion
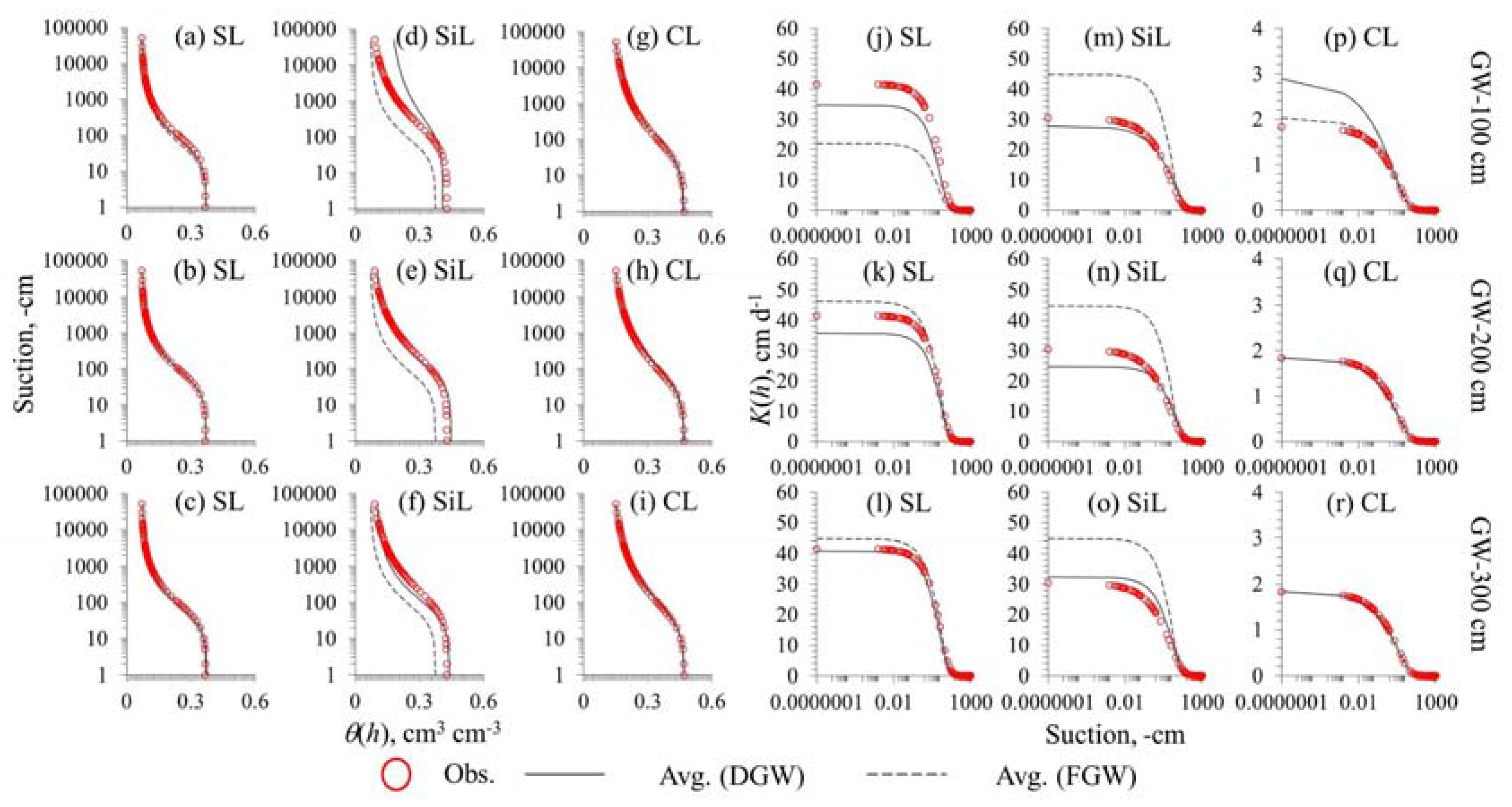
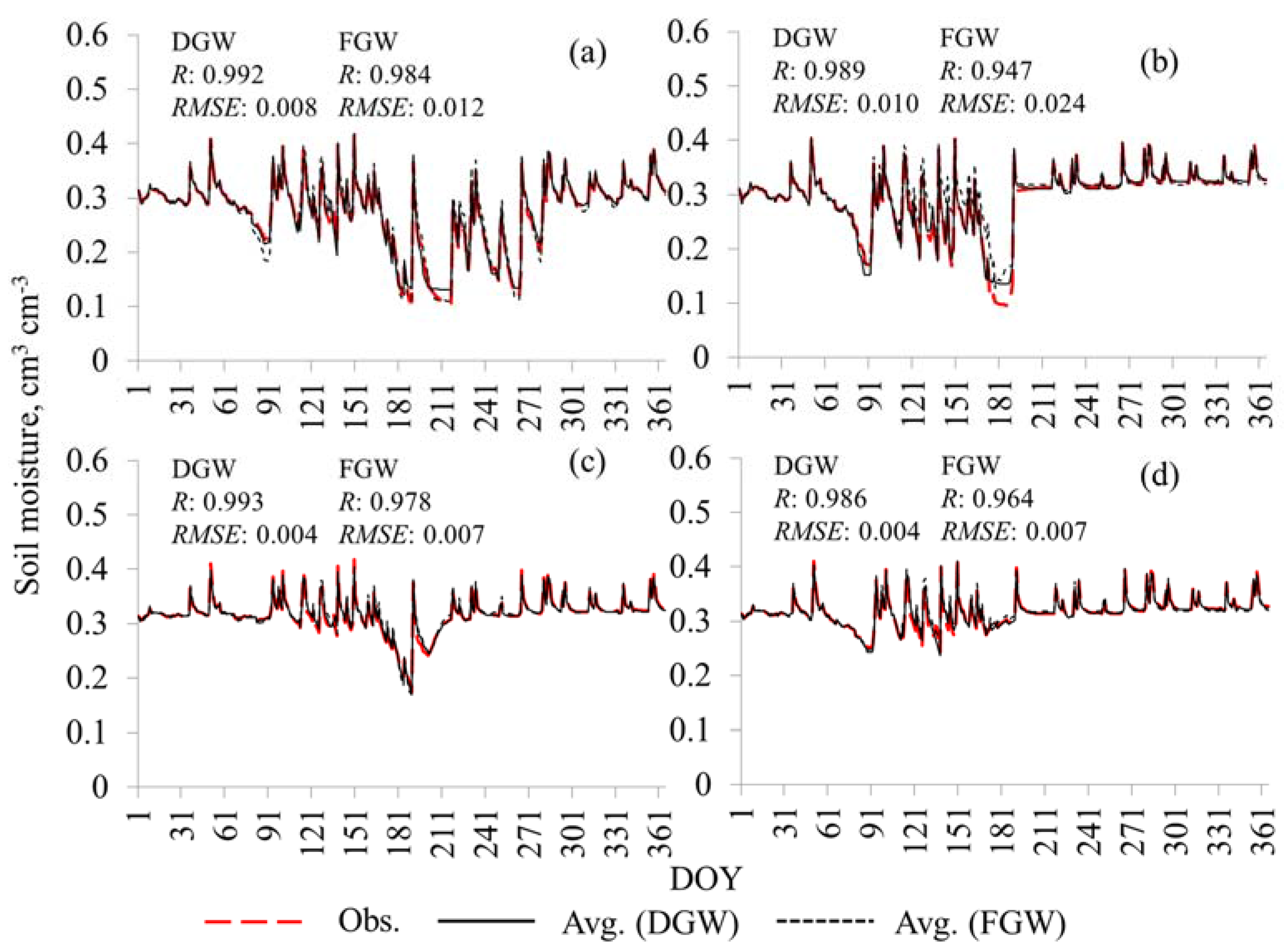
3.1. Synthetic Conditions
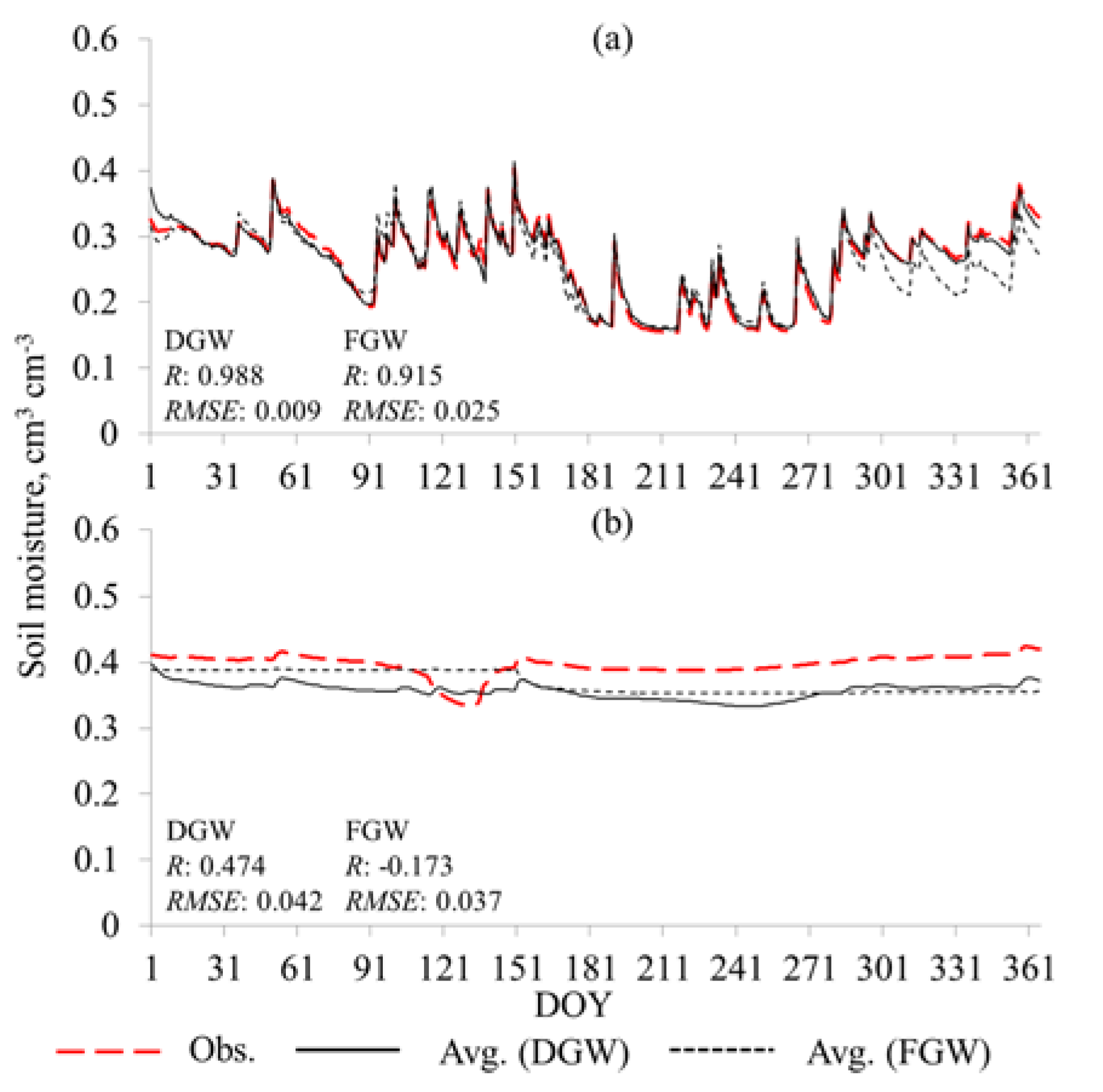
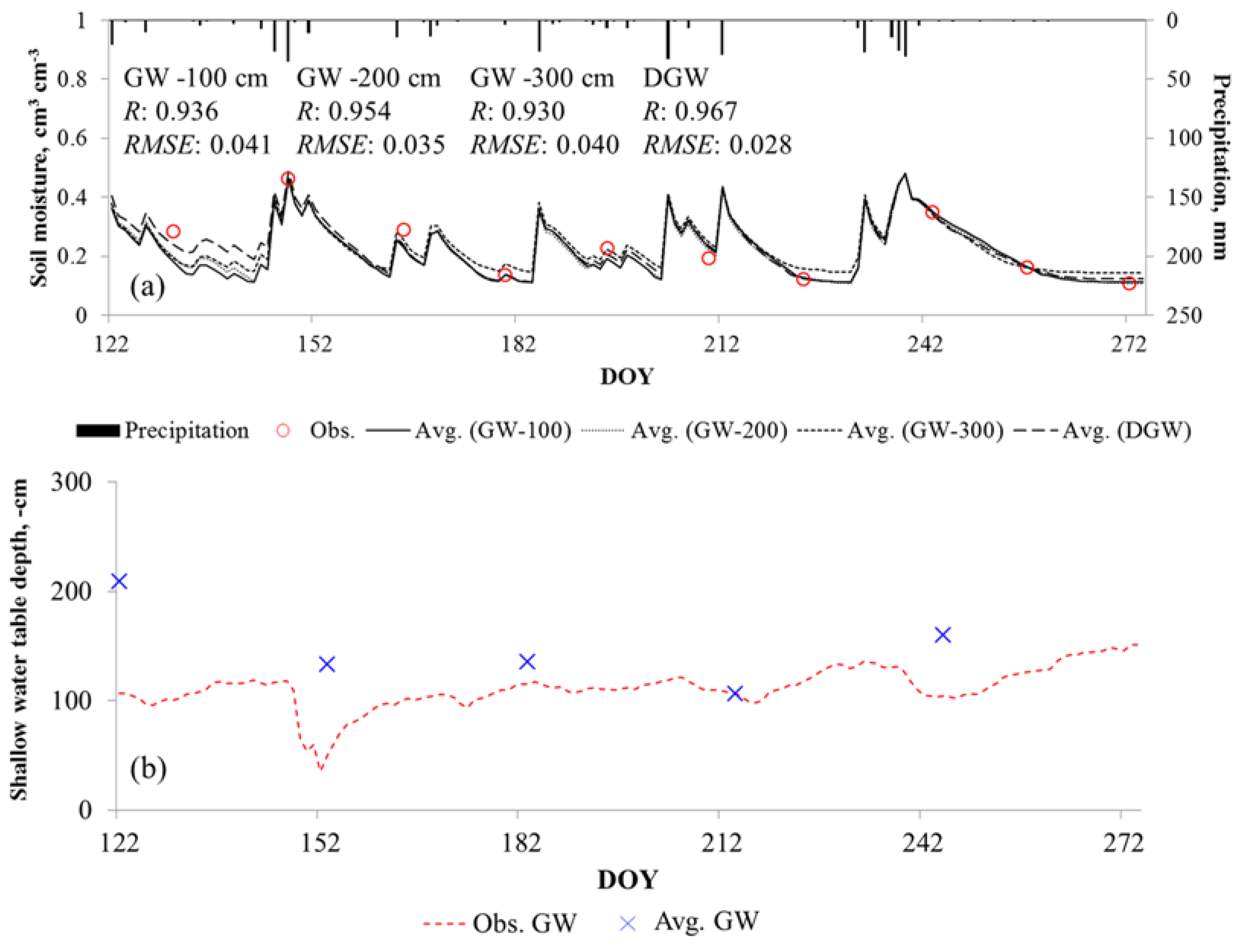
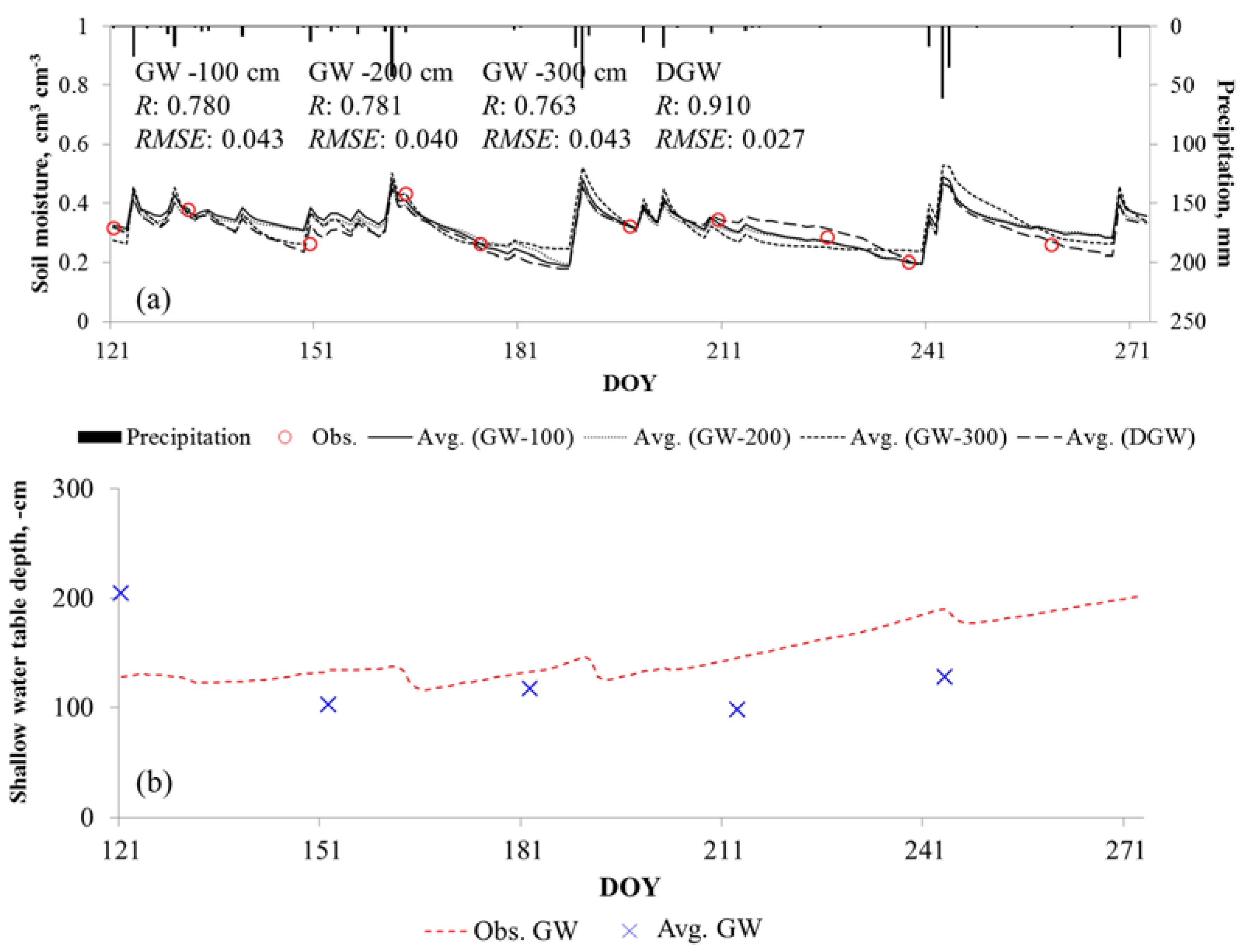
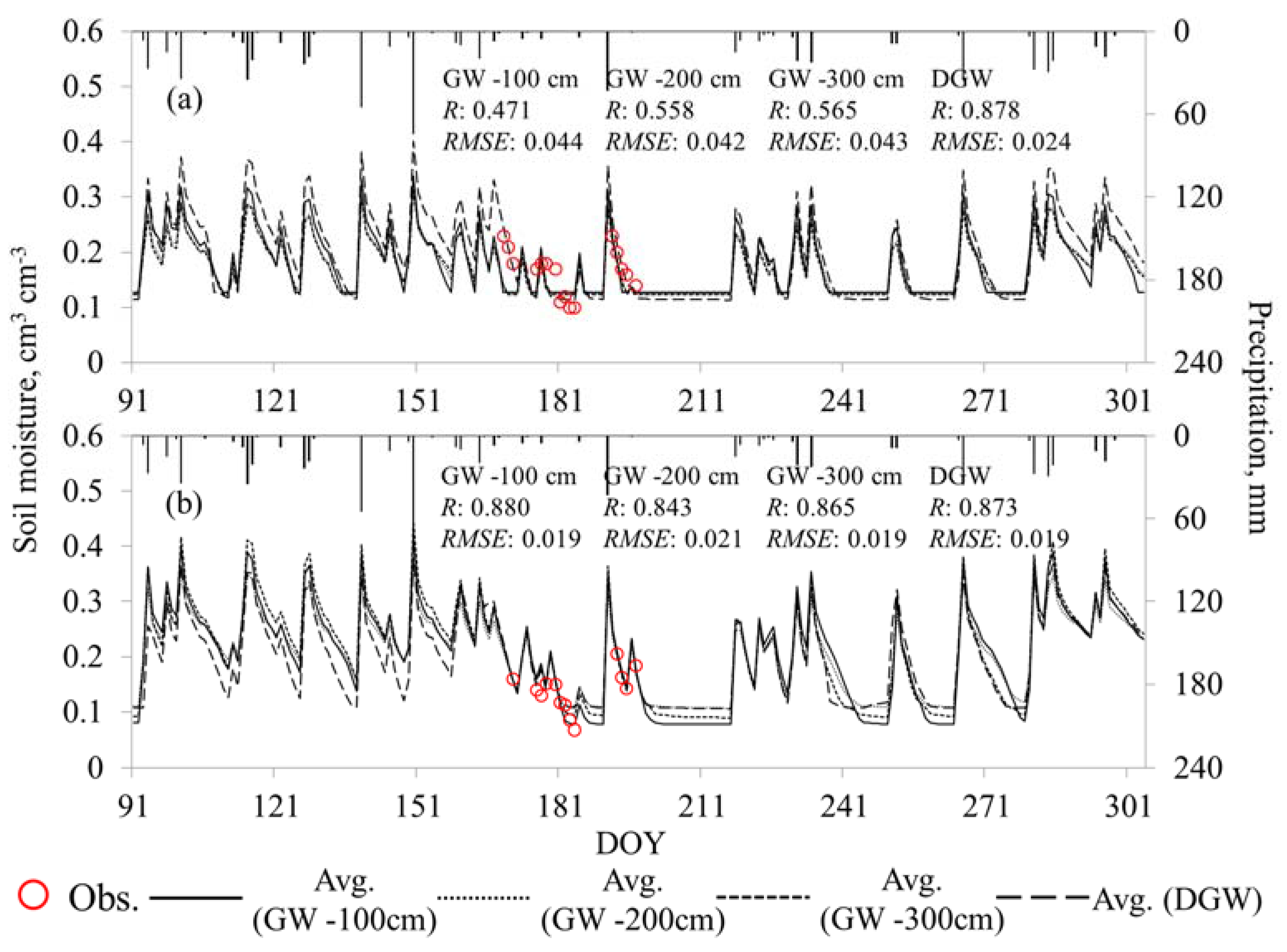
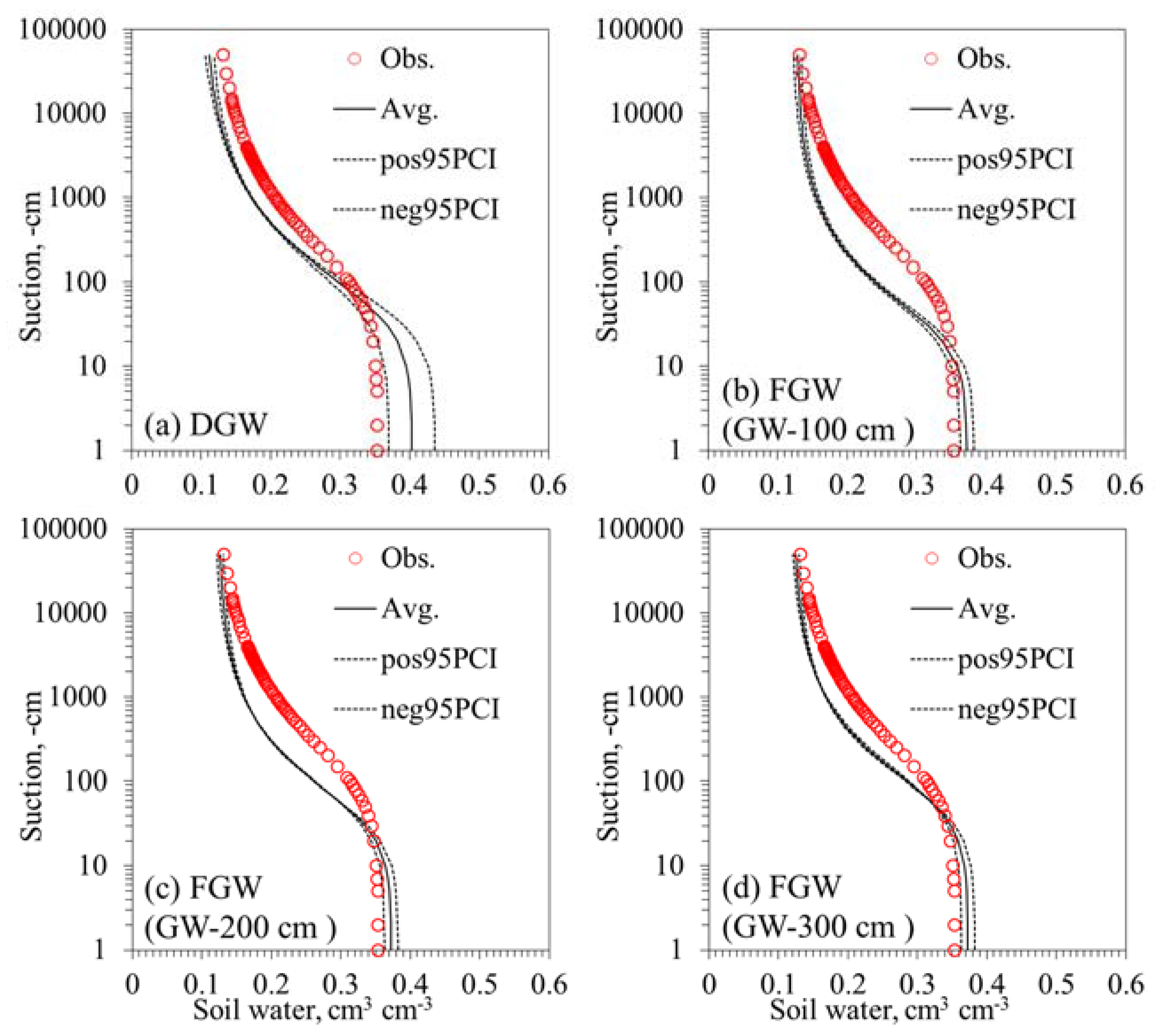
3.2. Field Validation Experiments
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Martinuzzi, J.M.; Font, J.; Berger, M. Soil moisture retrieval from space: The soil moisture and ocean salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Njoku, E.G.; Jackson, J.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; Houser, P. The Hydrosphere State (Hydros) mission: An Earth system pathfinder for global mapping of soil moisture and land freeze/thaw. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2184–2195. [Google Scholar] [CrossRef]
- Ottlé, C.; Vidal-Madjar, D. Assimilation of soil moisture inferred from infrared remote sensing in a hydrological model over the HAPEX-MOBILHY region. J. Hydrol. 1994, 158, 241–264. [Google Scholar] [CrossRef]
- Njoku, E.; Entekkabi, D. Passive microwave remote sensing of soil moisture. J. Hydrol. 1996, 184, 101–129. [Google Scholar] [CrossRef]
- Ines, A.V.M.; Mohanty, B.P. Near-surface soil moisture assimilation to quantify effective soil hydraulic properties using genetic algorithm. I. Conceptual modeling. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Ines, A.V.M.; Mohanty, B.P. Near-surface soil Moisture assimilation for quantifying effective soil hydraulic properties using genetic algorithms: II. Using airborne remote sensing dyring SGP97 and SMEX02. Water Resour. Res. 2008, 45. [Google Scholar] [CrossRef]
- Ines, A.V.M.; Mohanty, B.P. Parameter Criterioning with a Noisy Monte Carlo Genetic Algorithm for Estimating Effective Soil Hydraulic properties from Space. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Shin, Y.; Mohanty, B.P.; Ines, A.V.M. Estimating effective soil hydraulic properties using spatially distributed soil moisture and evapotranspiration. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Galantowicz, J.F.; Entekhabi, D.; Njoku, E.G. Tests of sequential data assimilation for retrieving profile soil moisture and temperature from observed L-band radiobrightness. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1860–1870. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.T. One-dimensional soil moisture profile retrieval by assimilation of near-surface observations: A comparison of retrieval methods. Adv. Water Resour. 2001, 24, 631–650. [Google Scholar] [CrossRef]
- Crow, W.T.; Wood, E.F. The assimilation of remotely sensed soil brightness temperature imagery into a land surface model using enxemble Kalman filtering: A case study based on ESTAR measurements during SGP97. Adv. Water Resour. 2003, 26, 137–149. [Google Scholar] [CrossRef]
- Dunne, S.; Entekhabi, D. An ensemble-based reanalysis approach to land data assimilation. Water Resour. Res. 2005, 41, W02013. [Google Scholar] [CrossRef]
- Oleson, K.W.; Lawrence, D.M.; Bonan, G.B.; Flanner, M.G.; Kluzek, E.; Lawrence, P.J.; Levis, S.; Swenson, S.C.; Thornton, P.E. Technical Description of Version 4.0 of the Community Land Model. Available online: http://www.cesm.ucar.edu/models/cesm1.0/clm/CLM4_tech_Note.pdf (accessed on 5 December 2015).
- Ek, M.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta Model. J. Geophys. Res. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Vazquez-Amábile, G.G.; Engel, B.A. Use of SWAT to compute groundwater table depth and streamflow in the Muscatatuck river watershed. Trans. ASAE 2005, 48, 991–1003. [Google Scholar] [CrossRef]
- Pivot, J.M.; Josien, E.; Martin, P. Farms adaptation to changes in flood risk: A management approach. J. Hydrol. 2002, 267, 12–25. [Google Scholar] [CrossRef]
- Skaggs, R.W. DRAINMOD Reference Report; USDA Soil Conservation Service: Washington, DC, USA, 1980. [Google Scholar]
- Arnold, J.G.; Srinavasan, R.; Muttiah, R.S.; Williams, J.R. Large-area hydrologic modeling and assessment: Part I. Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Van Dam, J.C.; Huygen, J.; Wesseling, J.G.; Feddes, R.A.; Kabat, P.; van Waslum, P.E.V.; Groenendijk, P.; van Diepen, C.A. Theory of SWAP Version 2.0: Simulation of Water Flow and Plant Growth in the Soil-Water-Atmosphere-Plant Environment; Technical Document 45; Wageningen Agricultural University and DLO Winand Staring Centre: Wageningen, The Netherlands, 1997. [Google Scholar]
- Kroes, J.G.; van Dam, J.C.; Huygen, J.; Vervoort, R.W. User’s Guide of SWAP Version 2.0: Simulation of Water, Solute Transport, and Plant Growth in the Soil–Atmosphere–Plant Environment; Report 81; DLO Winand Staring Centre: Wageningen, The Netherlands, 1999. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation foe predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zarandy, H. Simulation of Field Water Use and Crop Yield; John Wiley & Sons: New York, NY, USA, 1978. [Google Scholar]
- Belmans, C.; Wesseling, J.G.; Feddes, R.A. Simulation of the water balance of a cropped soil: SWATRE. J. Hydrol. 1983, 63, 271–286. [Google Scholar] [CrossRef]
- Van Dam, J.C. Field-Scale Water Flow and Solute Transport: SWAP Model Concepts, Parameter Estimation, and Case Studies. Ph.D. Thesis, Department of Soil Physics, Agricultural Hydrology and Groundwater, Wageningen University, Wageningen, The Netherlands, 2000. [Google Scholar]
- Wesseling, J.G.; Kroes, J.G. A Global Sensitivity Analysis of the Model SWAP; Report 160; DLO Winand Staring Cent.: Wageningen, The Netherlands, 1998. [Google Scholar]
- Sarwar, A.; Bastiaanssen, W.G.M.; Boers, M.T.; van Dam, J.C. Evaluating drainage design parameters for the fourth drainage project, Pakistan by using SWAP model: I. Calibration. Irrig. Drain. Syst. 2000, 14, 257–280. [Google Scholar] [CrossRef]
- Droogers, P.; Bastiaanssen, W.G.M.; Beyazgül, M.; Kayam, Y.; Kite, G.W.; Murray-Rust, H. Distributed agro-hydrological modeling of an irrigation system in western Turkey. Agric. Water Manag. 2000, 43, 183–202. [Google Scholar] [CrossRef]
- Singh, R.; Jhorar, R.K.; van Dam, J.C.; Feddes, R.A. Distributed ecohydrological modelling to evaluate irrigation system performance in Sirsa district, India: II. Impact of viable water managements scenarios. J. Hydrol. 2006, 329, 714–723. [Google Scholar] [CrossRef]
- Singh, R.; Kroes, J.G.; van Dam, J.C.; Feddes, R.A. Distributed ecohydrological modelling to evaluate the performance of irrigation system in Sirsa district, India: I. Current water management and its productivity. J. Hydrol. 2006, 329, 692–713. [Google Scholar] [CrossRef]
- International Soil Moisture Network. Available online: http://ismn.geo.tuwien.ac.at/ (accessed on 25 November 2015).
- Jackson, T.J.; Le Vine, D.M.; Hsu, A.Y.; Oldak, A.; Starks, P.J.; Swift, C.T.; Isham, J.D.; Haken, M. Soil moisture mapping at regional scales using microwave radiometry: The Southern Great Plains hydrology experiment. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2136–2151. [Google Scholar] [CrossRef]
- Njoku, E. SMEX03 AMSR-E Daily Gridded Soil Moisture and Brightness Temperatures; National Snow and Ice Data Center. Digital Media: Boulder, CO, USA, 2004. [Google Scholar]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. IEEE Proc. 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Mohanty, B.P.; Shouse, P.J.; Miller, D.A.; van Genuchten, M.T. Soil property database: Southern Great Plains 1997 Hydrology Experiment. Water Resour. Res. 2002, 38, 1047. [Google Scholar] [CrossRef]
- USDA-Agricultural Research Service. Available online: http://ars.mesonet.org/ (accessed on 10 December 2015).
- Illinois State Water Survey. Available online: http://www.isws.illinois.edu/ (accessed on 10 November 2015).
- Leij, F.J.; Alves, W.J.; van Genuchten, M.T.; Williams, J.R. The UNSODA unsaturated soil hydraulic database. In Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media; Proceeding of International Workshop; University of California: Riverside, CA, USA, 1999. [Google Scholar]
- Shin, Y.; Mohanty, B.P.; Ines, A.V.M. Soil hydraulic properties in one-dimensional layered soil profile using layer-specific soil moisture assimilation scheme. Water Resour. Res. 2012, 48, W06529. [Google Scholar] [CrossRef]
| Ranges | α | n | θres | θsat | Ksat | SGWm = 1, …, M |
|---|---|---|---|---|---|---|
| Max. | 0.006 | 1.200 | 0.061 | 0.370 | 1.840 | 50.000 |
| Min. | 0.033 | 1.610 | 0.163 | 0.550 | 130.000 | 300.000 |
| Silt Loam (Target Values) | α | n | θres | θsat | Ksat | ||
|---|---|---|---|---|---|---|---|
| 0.012 | 1.39 | 0.061 | 0.43 | 30.5 | |||
| Grass | DGW | Avg. | 0.013 | 1.456 | 0.106 | 0.431 | 27.948 |
| SD | 0.001 | 0.026 | 0.005 | 0.017 | 0.801 | ||
| FGW | Avg. | 0.015 | 1.401 | 0.075 | 0.405 | 12.85 | |
| SD | 0.001 | 0.008 | 0.002 | 0.003 | 0.810 | ||
| Wheat | DGW | Avg. | 0.014 | 1.45 | 0.115 | 0.431 | 31.81 |
| SD | 0.001 | 0.026 | 0.005 | 0.017 | 0.801 | ||
| FGW | Avg. | 0.015 | 1.42 | 0.087 | 0.402 | 14.019 | |
| SD | 0.001 | 0.008 | 0.002 | 0.003 | 0.810 | ||
| Soybean | DGW | Avg. | 0.014 | 1.384 | 0.137 | 0.411 | 29.843 |
| SD | 0.001 | 0.026 | 0.005 | 0.017 | 0.801 | ||
| FGW | Avg. | 0.021 | 1.325 | 0.13 | 0.397 | 19.894 | |
| SD | 0.001 | 0.008 | 0.002 | 0.003 | 0.810 | ||
| Maize | DGW | Avg. | 0.014 | 1.456 | 0.139 | 0.423 | 32.056 |
| SD | 0.001 | 0.026 | 0.005 | 0.017 | 0.801 | ||
| FGW | Avg. | 0.018 | 1.414 | 0.107 | 0.41 | 18.296 | |
| SD | 0.001 | 0.008 | 0.002 | 0.003 | 0.81 | ||
| Grass (Layered soil column) | DGW | Avg. | 0.009 | 1.471 | 0.064 | 0.462 | 26.914 |
| SD | 0.001 | 0.026 | 0.005 | 0.017 | 0.801 | ||
| FGW | Avg. | 0.016 | 1.41 | 0.07 | 0.394 | 11.285 | |
| SD | 0.000 | 0.008 | 0.002 | 0.003 | 0.810 | ||
| Date | Target Values (Obs. SGW, cm) | Grass | Wheat | Soybean | Maize | Grass (Layered Soil Column) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | SD | Avg. | SD | Avg. | SD | Avg. | SD | Avg. | SD | ||
| 04-01 | 160.0 | 149.9 | 7.4 | 154.4 | 7.4 | 162.9 | 7.4 | 155.5 | 7.4 | 170.0 | 7.4 |
| 05-01 | 200.0 | 208.1 | 13.2 | 200.8 | 13.2 | 202.0 | 13.2 | 186.0 | 13.2 | 196.3 | 13.2 |
| 06-01 | 170.0 | 152.4 | 5.3 | 168.8 | 5.3 | 173.4 | 5.3 | 162.2 | 5.3 | 174.3 | 5.3 |
| 07-01 | 170.0 | 171.3 | 4.3 | 159.9 | 4.3 | 151.6 | 4.3 | 171.4 | 4.3 | 186.9 | 4.3 |
| 08-01 | 170.0 | 159.3 | 5.5 | 175.1 | 5.5 | 179.3 | 5.5 | 163.8 | 5.5 | 188.0 | 5.5 |
| 09-01 | 170.0 | 157.5 | 7.6 | 176.8 | 7.6 | 181.2 | 7.6 | 169.6 | 7.6 | 211.4 | 7.6 |
| 10-01 | 160.0 | 145.2 | 6.9 | 144.9 | 6.9 | 161.8 | 6.9 | 152.1 | 6.9 | 172.3 | 6.9 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, Y.; Lim, K.J.; Park, K.; Jung, Y. Development of Dynamic Ground Water Data Assimilation for Quantifying Soil Hydraulic Properties from Remotely Sensed Soil Moisture. Water 2016, 8, 311. https://doi.org/10.3390/w8070311
Shin Y, Lim KJ, Park K, Jung Y. Development of Dynamic Ground Water Data Assimilation for Quantifying Soil Hydraulic Properties from Remotely Sensed Soil Moisture. Water. 2016; 8(7):311. https://doi.org/10.3390/w8070311
Chicago/Turabian StyleShin, Yongchul, Kyoung Jae Lim, Kyungwon Park, and Younghun Jung. 2016. "Development of Dynamic Ground Water Data Assimilation for Quantifying Soil Hydraulic Properties from Remotely Sensed Soil Moisture" Water 8, no. 7: 311. https://doi.org/10.3390/w8070311
APA StyleShin, Y., Lim, K. J., Park, K., & Jung, Y. (2016). Development of Dynamic Ground Water Data Assimilation for Quantifying Soil Hydraulic Properties from Remotely Sensed Soil Moisture. Water, 8(7), 311. https://doi.org/10.3390/w8070311







