Extreme Precipitation Dynamics and El Niño–Southern Oscillation Influences in Kathmandu Valley, Nepal
Abstract
1. Introduction
2. Materials and Methods
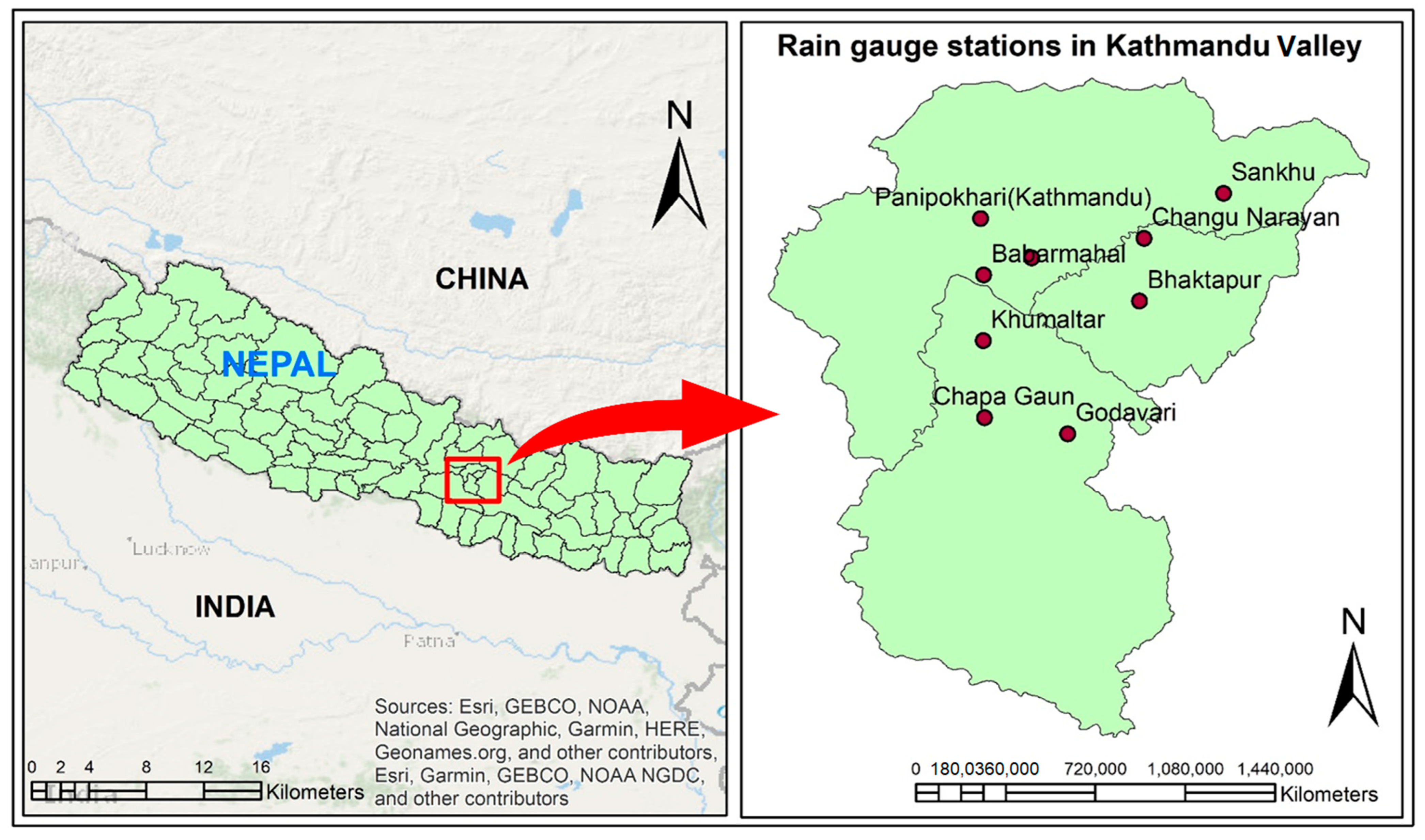
2.1. Study Area
2.2. Data Preparation
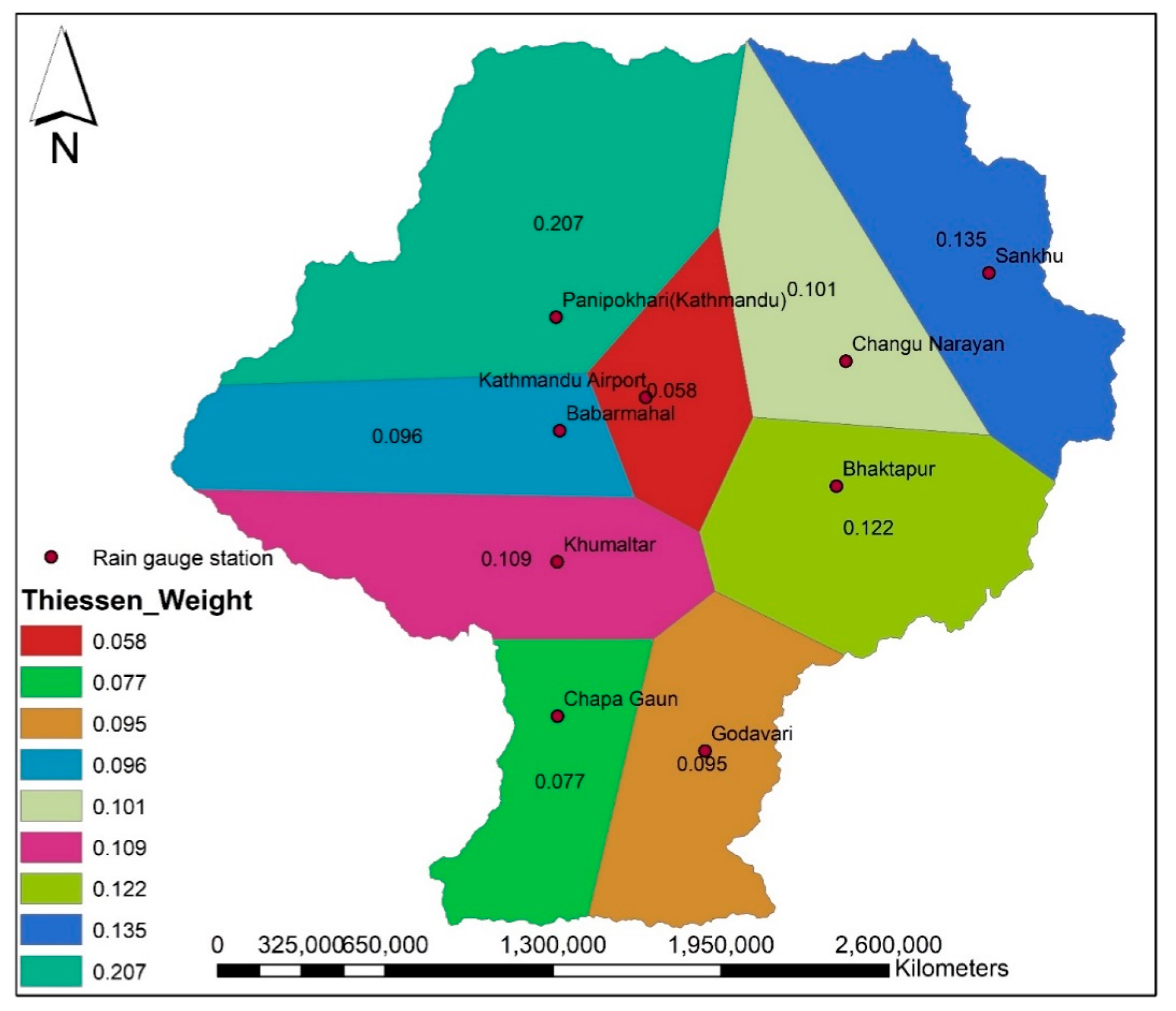
2.2.1. Observed Station Data
2.2.2. ENSO Index
2.3. Data Analysis
2.3.1. Average Precipitation
2.3.2. Precipitation Trend Analysis (Mann–Kendall Test)
2.3.3. Trend Magnitude Estimation (Sen’s Slope)
2.3.4. Extreme Precipitation Indices
2.3.5. Precipitation Concentration Index (PCI)
3. Results
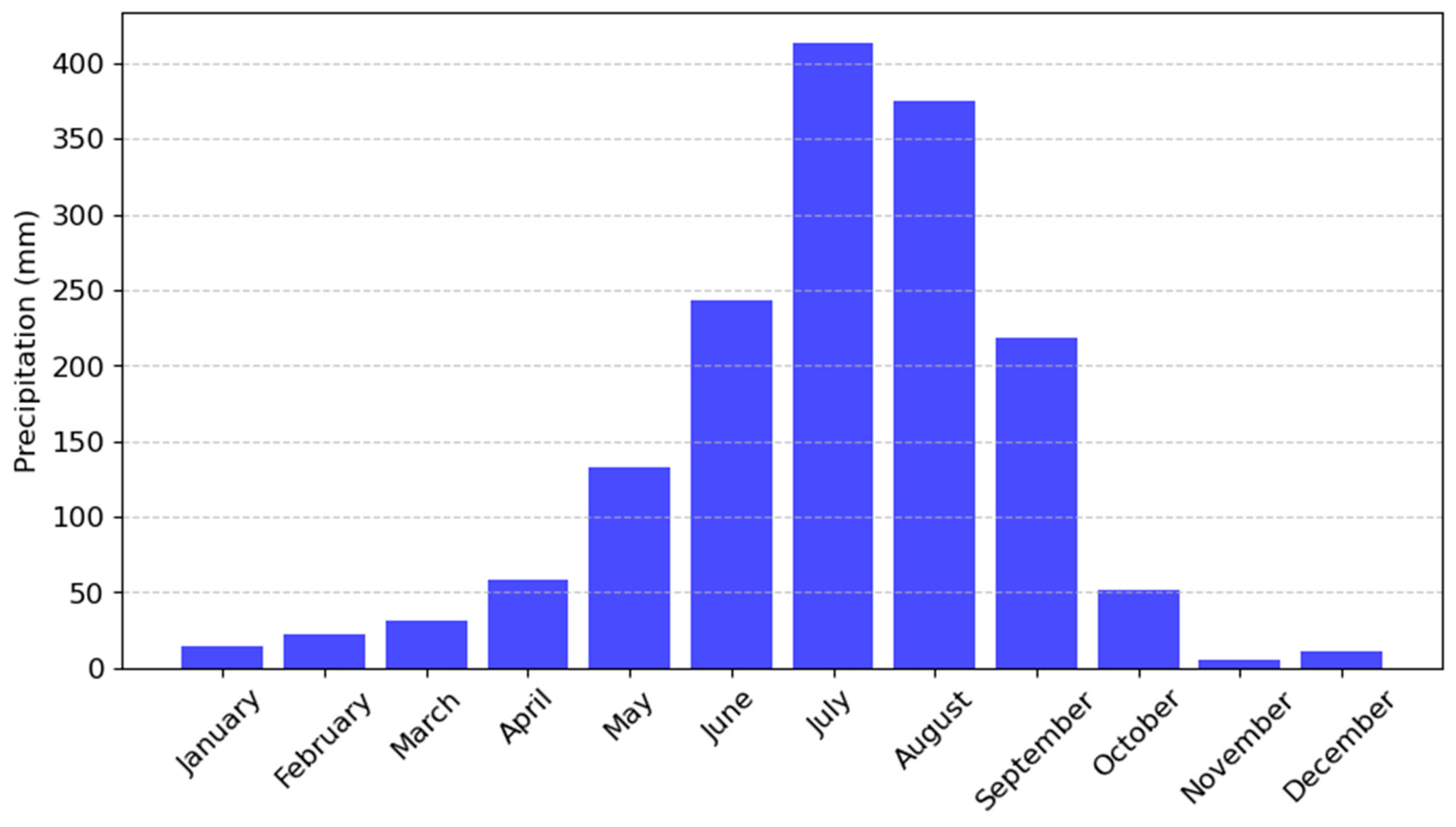
3.1. Monthly Average Precipitation
3.2. Precipitation Trends and Variability
3.3. Temporal Patterns of Extreme Precipitation Indices
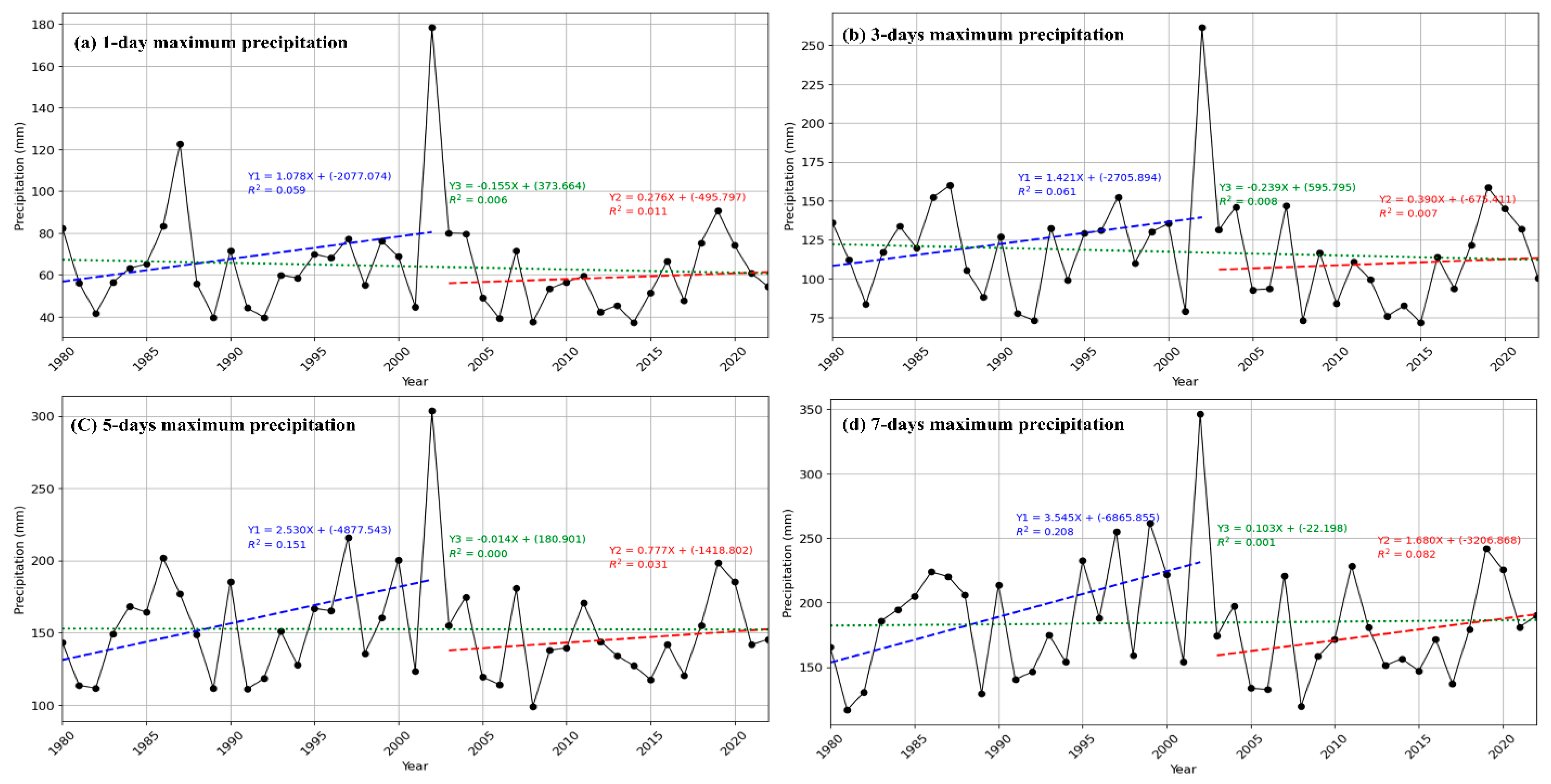
3.3.1. High-Intensity Precipitation Indices
Maximum 1-Day (RX1day), 3-Day (RX3day), 5-Day (RX5day), and 7-Day (RX7day) Precipitation
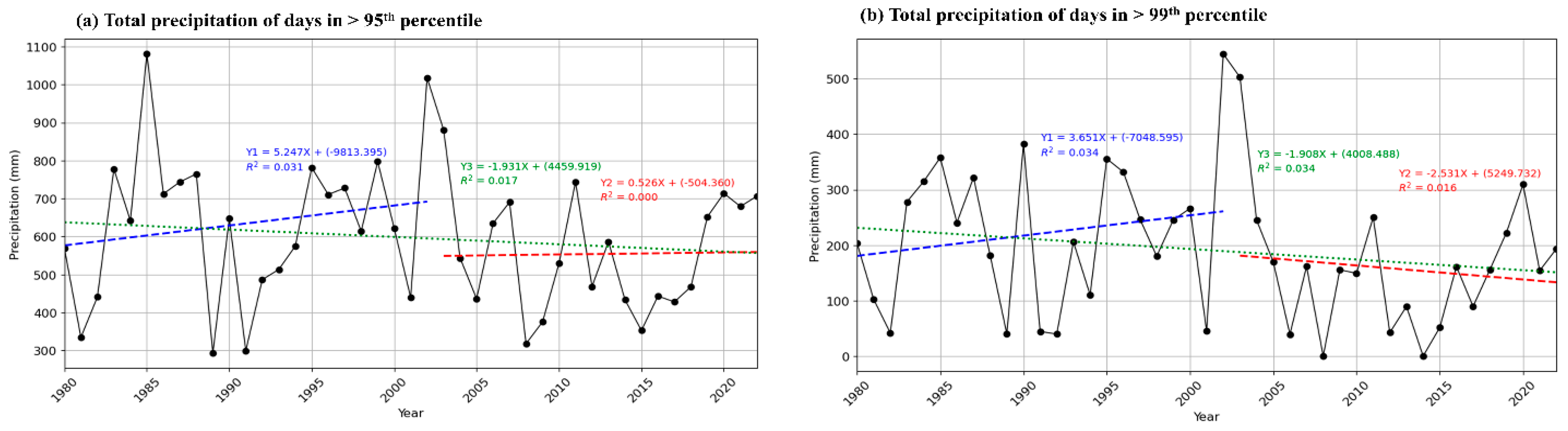
Total Precipitation in R95pTOT and R99pTOT
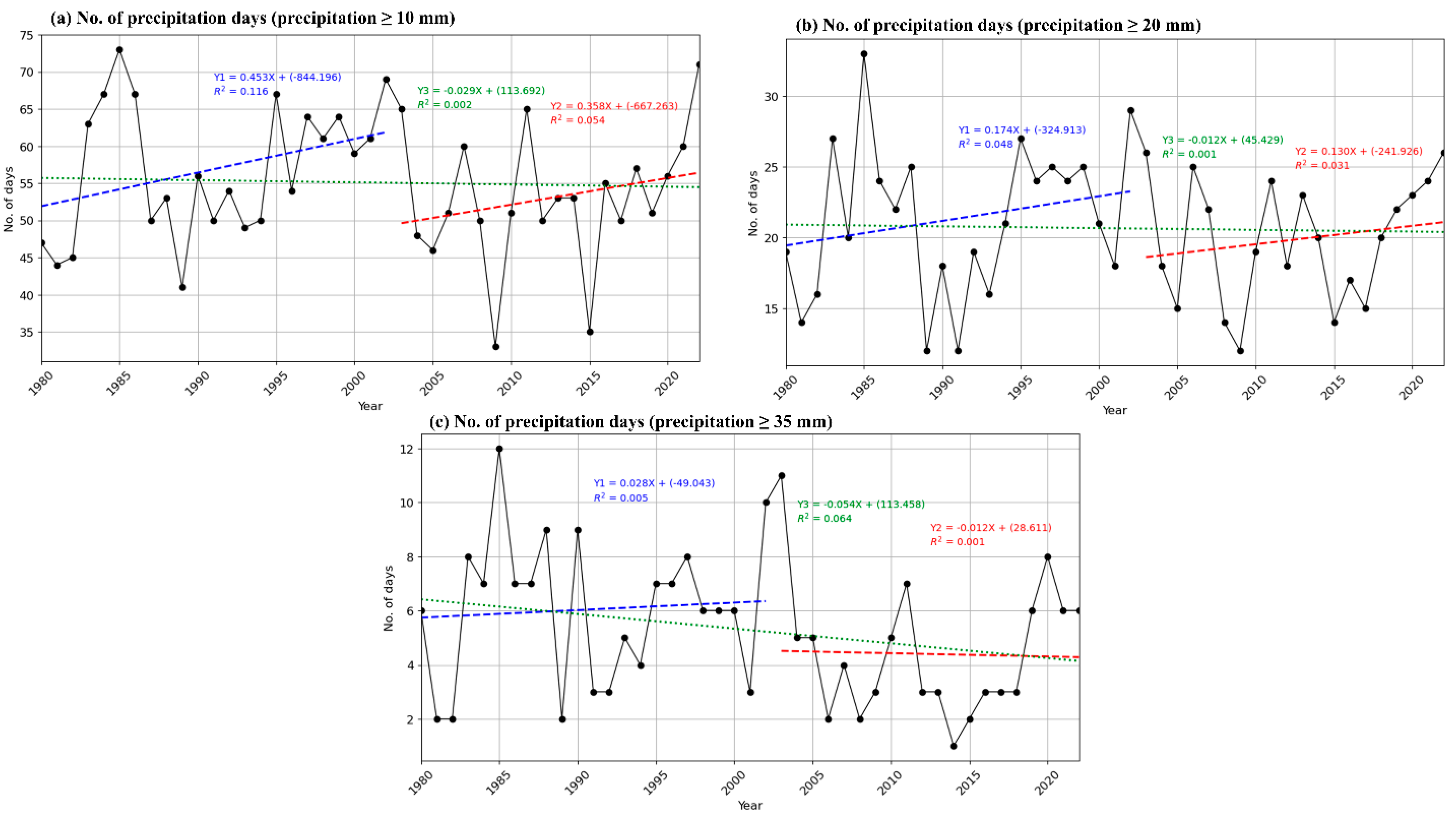
3.3.2. Precipitation Days at Different Thresholds
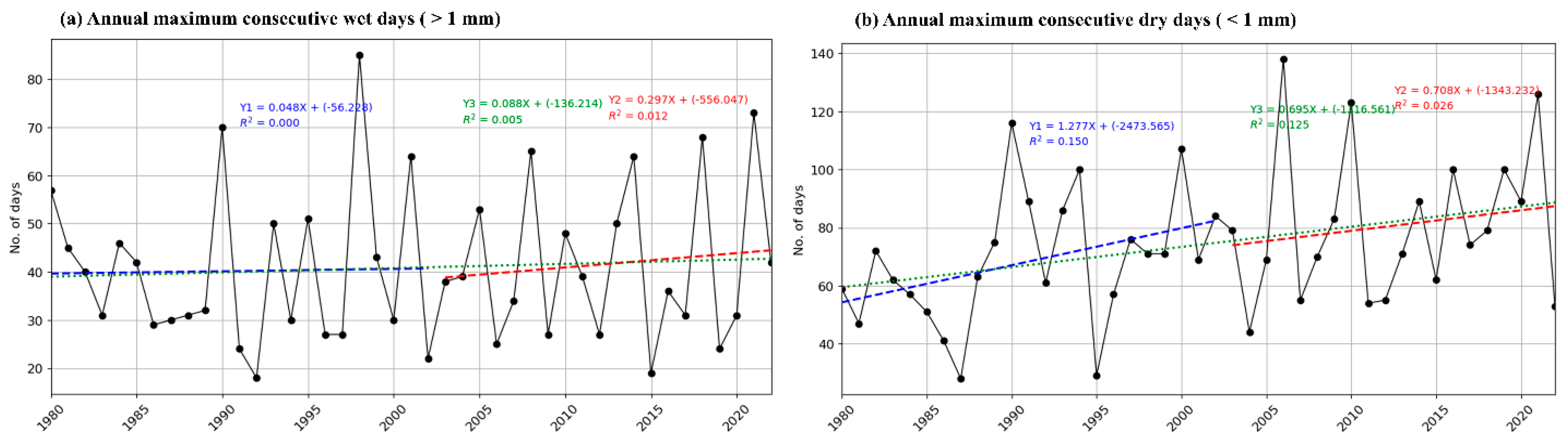
3.3.3. Annual Maximum Consecutive Wet and Dry Days
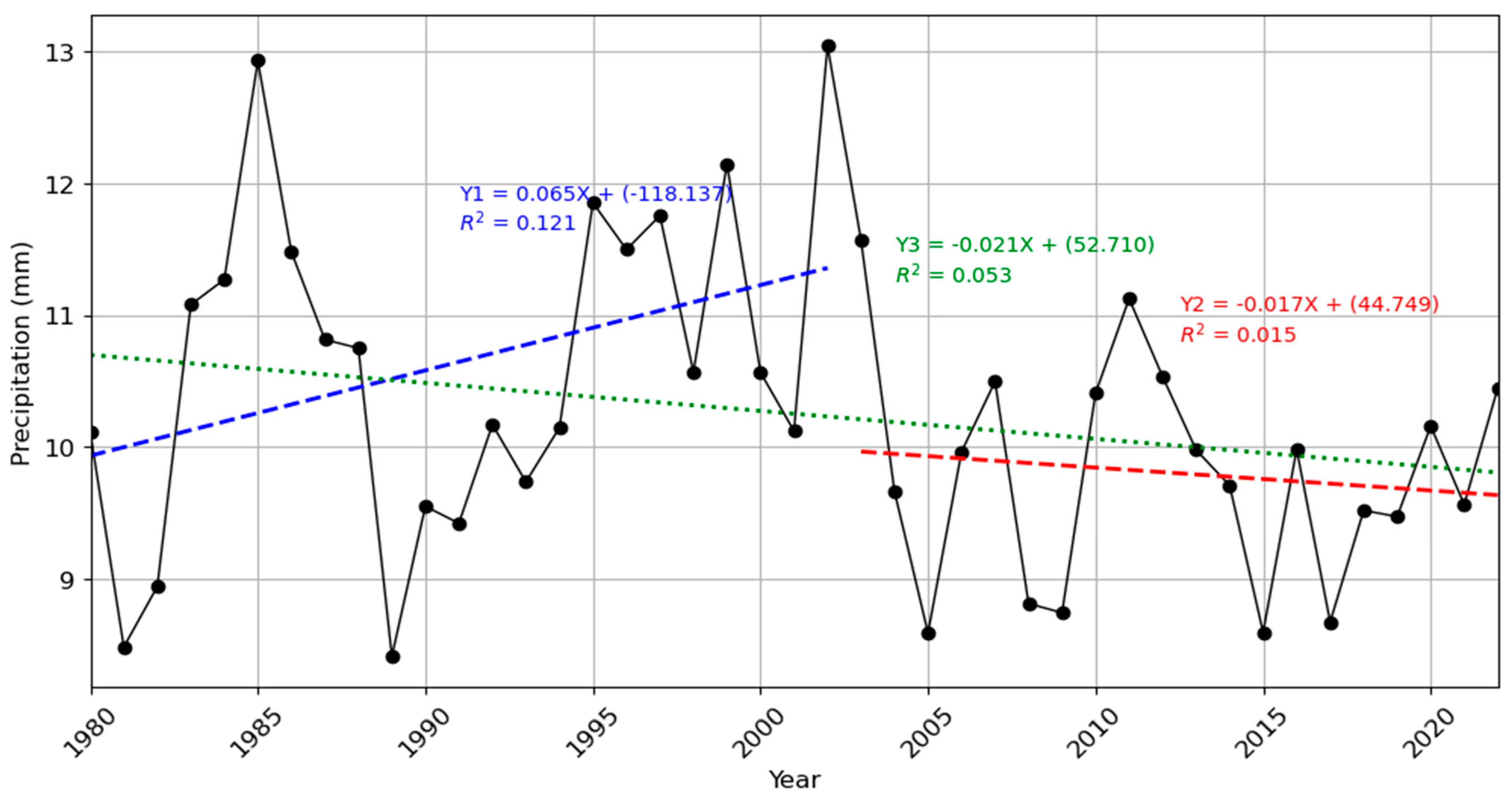
3.3.4. Average Precipitation on Wet Days
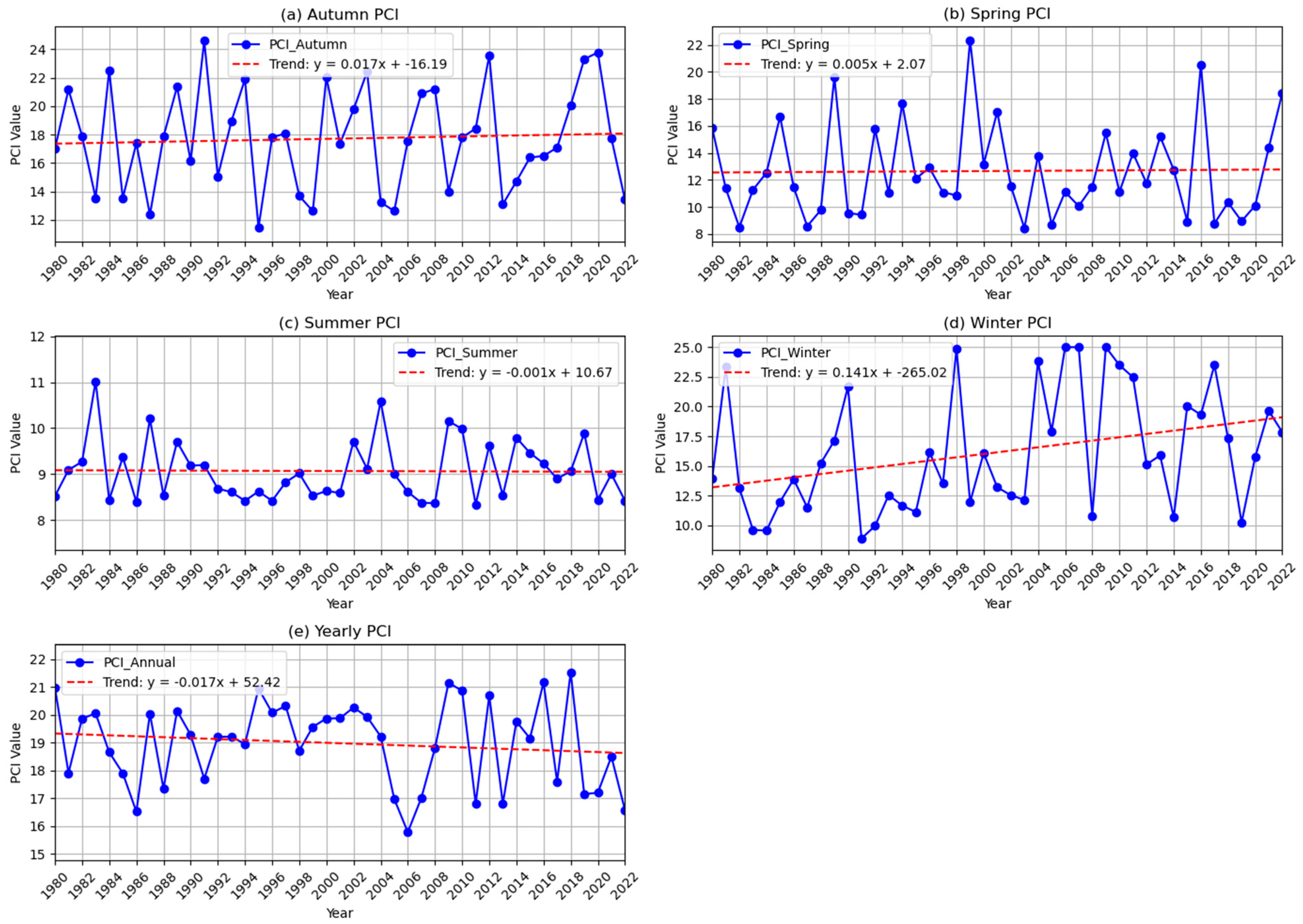
3.4. Precipitation Concentration Index
3.5. Mann–Kendall Trend Analysis of Extreme Precipitation for 1980–2022 with Decadal Segmentation (1980–2002 and 2003–2022)
3.6. Influence of ENSO on Precipitation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Summary for Policymakers. In Climate Change 2022—Impacts, Adaptation and Vulnerability; Cambridge University Press: Cambridge, UK, 2023; pp. 3–34. [CrossRef]
- An, D.; Eggeling, J.; Zhang, L.; He, H.; Sapkota, A.; Wang, Y.-C.; Gao, C. Extreme precipitation patterns in the Asia–Pacific region and its correlation with El Niño-Southern Oscillation (ENSO). Sci. Rep. 2023, 13, 11068. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Tiwari, K.R.; Hao, L.; Amatya, D.; Liu, N.; Song, C. Climate change and forest hydrology in future forests. In Future Forests: Mitigation and Adaptation to Climate Change; Elsevier: Amsterdam, The Netherlands, 2024; pp. 95–124. [Google Scholar] [CrossRef]
- Lamichhane, D.; Bao, Q.; Dhital, Y.P.; Devkota, R.; Bhattarai, U.; Nepal, B.; Pokharel, A.K.; Dawadi, B. Precipitation Concentration Variability and Its Association with Geographical Factors and ENSO Over Nepal from 1990 to 2020. Earth Syst. Environ. 2024, 8, 1–17. [Google Scholar] [CrossRef]
- Karki, R.; Hasson, S.U.; Schickhoff, U.; Scholten, T.; Böhner, J. Rising Precipitation Extremes across Nepal. Climate 2017, 5, 4. [Google Scholar] [CrossRef]
- Pandey, V.P.; Shrestha, D.; Adhikari, M. Characterizing natural drivers of water-induced disasters in a rain-fed watershed: Hydro-climatic extremes in the Extended East Rapti Watershed. J. Hydrol. 2021, 598, 126383. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, X.; Zwiers, F.; Westra, S.; Alexander, L.V. A Global, Continental, and Regional Analysis of Changes in Extreme Precipitation. J. Clim. 2021, 34, 243–258. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. Addendum: More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Change 2016, 6, 508–513. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Montanari, A. Global and Regional Increase of Precipitation Extremes Under Global Warming. Water Resour. Res. 2019, 55, 4901–4914. [Google Scholar] [CrossRef]
- Safdar, F.; Mahmood, F.; Khan, M.Z.A.; Arshad, M. Observed and predicted precipitation variability across Pakistan with special focus on winter and pre-monsoon precipitation. Environ. Sci. Pollut. Res. 2023, 30, 4510–4530. [Google Scholar] [CrossRef] [PubMed]
- Aditya, F.; Gusmayanti, E.; Sudrajat, J. Rainfall trend analysis using Mann-Kendall and Sen’s slope estimator test in West Kalimantan. IOP Conf. Ser. Earth Environ. Sci. 2021, 893, 012006. [Google Scholar] [CrossRef]
- Rahaman, M.H.; Saha, T.K.; Masroor, M.; Roshani; Sajjad, H. Trend analysis and forecasting of meteorological variables in the lower Thoubal river watershed, India using non-parametrical approach and machine learning models. Model Earth Syst. Environ. 2024, 10, 551–577. [Google Scholar] [CrossRef]
- Maharana, P.; Agnihotri, R.; Dimri, A.P. Changing Indian monsoon rainfall patterns under the recent warming period 2001–2018. Clim. Dyn. 2021, 57, 2581–2593. [Google Scholar] [CrossRef]
- Jihan, M.A.T.; Popy, S.; Kayes, S.; Rasul, G.; Maowa, A.S.; Rahman, M. Climate change scenario in Bangladesh: Historical data analysis and future projection based on CMIP6 model. Sci. Rep. 2025, 15, 7856. [Google Scholar] [CrossRef] [PubMed]
- Subba, S.; Ma, Y.-M.; Ma, W.-Q.; Han, C.-B. Extreme precipitation detection ability of four high-resolution precipitation product datasets in hilly area: A case study in Nepal. Adv. Clim. Change Res. 2024, 15, 390–405. [Google Scholar] [CrossRef]
- Bell, R.; Fort, M.; Götz, J.; Bernsteiner, H.; Andermann, C.; Etzlstorfer, J.; Posch, E.; Gurung, N.; Gurung, S. Major geomorphic events and natural hazards during monsoonal precipitation 2018 in the Kali Gandaki Valley. Geomorphology 2021, 372, 107451. [Google Scholar] [CrossRef]
- Fernando, N.S.; Shrestha, S.; Saurav, K.; Mohanasundaram, S. Investigating major causes of extreme floods using global datasets: A case of Nepal. Prog. Disaster Sci. 2022, 13, 100212. [Google Scholar] [CrossRef]
- Khatri, S.K.; Hamal, R.; Poudel, K.R.; Poudel, K.P.; Paudel, N. Rainfall patterns and hazard susceptibility analysis of Pokhara City, Nepal: Implication of climate change. Theor. Appl. Climatol. 2025, 156, 146. [Google Scholar] [CrossRef]
- Chhetri, T.B.; Dhital, Y.P.; Tandong, Y.; Devkota, L.P.; Dawadi, B. Observations of heavy rainfall and extreme flood events over Banke-Bardiya districts of Nepal in 2016–2017. Prog. Disaster Sci. 2020, 6, 100074. [Google Scholar] [CrossRef]
- Adhikari, N.; Gao, J.; Yao, T.; Yang, Y.; Dai, D. The main controls of the precipitation stable isotopes at Kathmandu. Tellus B Chem. Phys. Meteorol. 2020, 72, 1721967. [Google Scholar] [CrossRef]
- Shrestha, S.; Yao, T.; Kattel, D.B.; Devkota, L.P. Precipitation characteristics of two complex mountain river basins on the southern slopes of the central Himalayas. Theor. Appl. Clim. 2019, 138, 1159–1178. [Google Scholar] [CrossRef]
- Karki, R.; Talchabhadel, R.; Aalto, J.; Baidya, S.K. New climatic classification of Nepal. Theor. Appl. Clim. 2015, 125, 799–808. [Google Scholar] [CrossRef]
- Shrestha, S.; Yao, T.; Adhikari, T.R. Analysis of rainfall trends of two complex mountain river basins on the southern slopes of the Central Himalayas. Atmos. Res. 2019, 215, 99–115. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, L.; Hu, C.; Hao, L.; Sun, G. Changing Extreme Precipitation Patterns in Nepal Over 1971–2015. Earth Space Sci. 2024, 11, e2024EA003563. [Google Scholar] [CrossRef]
- Shrestha, M.; Acharya, S.C. Assessment of historical and future land-use–land-cover changes and their impact on valuation of ecosystem services in Kathmandu Valley. Land Degrad. Dev. 2020, 32, 3731–3742. [Google Scholar] [CrossRef]
- Chaudhary, U.; Shah, M.A.R.; Shakya, B.M.; Aryal, A. Flood Susceptibility and Risk Mapping of Kathmandu Valley Watershed. Sustainability 2024, 16, 7101. [Google Scholar] [CrossRef]
- Danegulu, A.; Karki, S.; Bhattarai, P.K.; Pandey, V.P. Characterizing urban flooding in the Kathmandu Valley, Nepal: The influence of urbanization and river encroachment. Nat. Hazards 2024, 120, 10923–10947. [Google Scholar] [CrossRef]
- Magar, B.G.; Poudel, J.M.; Paudel, B.; Pokharel, B. Climate change in outskirts of Kathmandu Valley: Local perception and narratives. Nat. Hazards 2024, 120, 8103–8120. [Google Scholar] [CrossRef]
- Kc, S.; Shrestha, S.; Ninsawat, S.; Chonwattana, S. Predicting flood events in Kathmandu Metropolitan City under climate change and urbanisation. J. Environ. Manag. 2021, 281, 111894. [Google Scholar] [CrossRef]
- Mesta, C.; Cremen, G.; Galasso, C. Urban growth modelling and social vulnerability assessment for a hazardous Kathmandu Valley. Sci. Rep. 2022, 12, 6152. [Google Scholar] [CrossRef]
- Prajapati, R.; Upadhyay, S.; Talchabhadel, R.; Thapa, B.R.; Ertis, B.; Silwal, P.; Davids, J.C. Investigating the nexus of groundwater levels, rainfall and land-use in the Kathmandu Valley, Nepal. Groundw. Sustain. Dev. 2021, 14, 100584. [Google Scholar] [CrossRef]
- Shrestha, D.; Basnyat, D.B.; Gyawali, J.; Creed, M.J.; Sinclair, H.D.; Golding, B.; Muthusamy, M.; Shrestha, S.; Watson, C.S.; Subedi, D.L.; et al. Rainfall extremes under future climate change with implications for urban flood risk in Kathmandu. Int. J. Disaster Risk Reduct. 2023, 97, 103997. [Google Scholar] [CrossRef]
- Prajapati, R.; Talchabhadel, R.; Silwal, P.; Upadhyay, S.; Ertis, B.; Thapa, B.R.; Davids, J.C. Less rain and rainy days—Lessons from 45 years of rainfall data (1971–2015) in the Kathmandu Valley, Nepal. Theor. Appl. Climatol. 2021, 145, 1369–1383. [Google Scholar] [CrossRef]
- Shrestha, S.; Semkuyu, D.J.; Pandey, V.P. Assessment of groundwater vulnerability and risk to pollution in Kathmandu Valley. Sci. Total. Environ. 2016, 556, 23–35. [Google Scholar] [CrossRef]
- Bharti, P.; Biswas, A. Predicting Urban Growth of Kathmandu Valley Using Artificial Intelligence. J. Geovisualization Spat. Anal. 2024, 8, 40. [Google Scholar] [CrossRef]
- Shrestha, S.; Neupane, S.; Mohanasundaram, S.; Pandey, V.P. Mapping groundwater resiliency under climate change scenarios: A case study of Kathmandu Valley. Environ. Res. 2020, 183, 109149. [Google Scholar] [CrossRef]
- DHM. Available online: https://www.dhm.gov.np/ (accessed on 4 March 2025).
- Ridwan, W.M.; Sapitang, M.; Aziz, A.; Kushiar, K.F.; Ahmed, A.N.; El-Shafie, A. Rainfall forecasting model using machine learning methods: Case study Terengganu. Ain Shams Eng. J. 2021, 12, 1651–1663. [Google Scholar] [CrossRef]
- Climate Prediction Center—Monitoring & Data: Current Monthly Atmospheric and Sea Surface Temperatures Index Values. Available online: https://www.cpc.ncep.noaa.gov/data/indices/ (accessed on 4 March 2025).
- Ehsan, M.A.; Tippett, M.K.; Robertson, A.W.; Singh, B.; Rahman, M.A. The ENSO Fingerprint on Bangladesh Summer Monsoon Rainfall. Earth Syst. Environ. 2023, 7, 617–627. [Google Scholar] [CrossRef]
- Lenssen, N.J.L.; Goddard, L.; Mason, S. Seasonal Forecast Skill of ENSO Teleconnection Maps. Weather. Forecast. 2020, 35, 2387–2406. [Google Scholar] [CrossRef]
- Sahoo, M.; Yadav, R.K. Teleconnection of Atlantic Nino with summer monsoon rainfall over northeast India. Glob. Planet. Change 2021, 203, 103550. [Google Scholar] [CrossRef]
- Yang, Y.-M.; Park, J.-H.; An, S.-I.; Wang, B.; Luo, X. Mean sea surface temperature changes influence ENSO-related precipitation changes in the mid-latitudes. Nat. Commun. 2021, 12, 1495. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. 1945. Available online: https://www.jstor.org/stable/1907187 (accessed on 1 January 2025).
- Ahmed, I.A.; Shahfahad; Dutta, D.K.; Baig, M.R.I.; Roy, S.S.; Rahman, A. Implications of changes in temperature and precipitation on the discharge of Brahmaputra River in the urban watershed of Guwahati. Environ. Monit. Assess. 2021, 193, 518. [Google Scholar] [CrossRef]
- Obuobie, E.; Osei, M.A.; Addi, M.; Agyekum, J.; Akurugu, B.A.; Bazaanah, P.; Gaisie-Essilfie, F.A.; Appiah, G. Analysis of spatio-temporal trends in climate extremes in the Lower Volta Basin. Theor. Appl. Clim. 2025, 156, 120. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wires Clim. Change 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Oliver, J.E. Monthly Precipitation Distribution: A Comparative Index. Prof. Geogr. 1980, 32, 300–309. [Google Scholar] [CrossRef]
- Bandar, Q.K.A.; Muslih, K.D. Spatial assessment of precipitation concentration and seasonality in Iraq. Theor. Appl. Clim. 2025, 156, 134. [Google Scholar] [CrossRef]
- Du, J.; Yu, X.; Zhou, L.; Li, X.; Ao, T. Less concentrated precipitation and more extreme events over the Three River Headwaters region of the Tibetan Plateau in a warming climate. Atmospheric Res. 2024, 303, 107311. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Sreekesh, S. Assessments of multiple gridded-rainfall datasets for characterizing the precipitation concentration index and its trends in India. Int. J. Clim. 2021, 42, 3147–3172. [Google Scholar] [CrossRef]
- Tolika, K. On the analysis of the temporal precipitation distribution over Greece using the Precipitation Concentration Index (PCI): Annual, seasonal, monthly analysis and association with the atmospheric circulation. Theor. Appl. Climatol. 2019, 137, 2303–2319. [Google Scholar] [CrossRef]
- Amiri, M.A.; Gocić, M. Analyzing the applicability of some precipitation concentration indices over Serbia. Theor. Appl. Clim. 2021, 146, 645–656. [Google Scholar] [CrossRef]
- Balling, R.C.; Kiany, M.S.K.; Roy, S.S.; Khoshhal, J. Trends in Extreme Precipitation Indices in Iran: 1951–2007. Adv. Meteorol. 2016, 2016, 2456809. [Google Scholar] [CrossRef]
- De Lima, M.I.P.; Santo, F.E.; Ramos, A.M.; Trigo, R.M. Trends and correlations in annual extreme precipitation indices for mainland Portugal, 1941–2007. Theor. Appl. Climatol. 2015, 119, 55–75. [Google Scholar] [CrossRef]
- Gocic, M.; Shamshirband, S.; Razak, Z.; Petković, D.; Ch, S.; Trajkovic, S. Long-Term Precipitation Analysis and Estimation of Precipitation Concentration Index Using Three Support Vector Machine Methods. Adv. Meteorol. 2016, 2016, 7912357. [Google Scholar] [CrossRef]
- Michiels, P.; Gabriels, D.; Hartmann, R. Using the seasonal and temporal Precipitation concentration index for characterizing the monthly rainfall distribution in Spain. CATENA 1992, 19, 43–58. [Google Scholar] [CrossRef]
- Petković, D.; Gocic, M.; Trajkovic, S.; Milovančević, M.; Šević, D. Precipitation concentration index management by adaptive neuro-fuzzy methodology. Clim. Change 2017, 141, 655–669. [Google Scholar] [CrossRef]
- Ryan, C.; Curley, M.; Walsh, S.; Murphy, C. Long-term trends in extreme precipitation indices in Ireland. Int. J. Clim. 2021, 42, 4040–4061. [Google Scholar] [CrossRef]
- Sarr, M.A.; Zoromé, M.; Seidou, O.; Bryant, C.R.; Gachon, P. Recent trends in selected extreme precipitation indices in Senegal—A changepoint approach. J. Hydrol. 2013, 505, 326–334. [Google Scholar] [CrossRef]
- Chhetri, R.; Pandey, V.P.; Talchabhadel, R.; Thapa, B.R. How do CMIP6 models project changes in precipitation extremes over seasons and locations across the mid hills of Nepal? Theor. Appl. Clim. 2021, 145, 1127–1144. [Google Scholar] [CrossRef]
- Dhital, Y.; Kayastha, R. causes and impacts of flooding in the Bagmati River Basin. J. Flood Risk Manag. 2013, 6, 253–260. [Google Scholar] [CrossRef]
- Pradhan-Salike, I.; Pokharel, J.R. Impact of Urbanization and Climate Change on Urban Flooding: A case of the Kathmandu Valley. J. Nat. Resour. Dev. 2017, 7, 56–66. [Google Scholar] [CrossRef]
- Roxy, M.K.; Ghosh, S.; Pathak, A.; Athulya, R.; Mujumdar, M.; Murtugudde, R.; Terray, P.; Rajeevan, M. A threefold rise in widespread extreme rain events over central India. Nat. Commun. 2017, 8, 708. [Google Scholar] [CrossRef]
- Society of Hydrologists and Meteorologists-Nepal. SOHAM_Newsletter_Vol-1_-No-1_October-Novermber-2002. Available online: https://soham.org.np/newsletter/soham-nepal-newsletter-8/ (accessed on 1 January 2025).
- Durbar, S. A Preliminary Loss and Damage Assessment of Flood and Landslide National Disaster Risk Reduction and Management Authority Preliminary Loss and Damage Assessment of Flood and Landslide September 2024 Published by Government of Nepal Ministry of Home Affairs National Disaster Risk Reduction and Management Authority. 2024. Available online: www.bipad.gov.np (accessed on 12 March 2025).
- Guo, E.; Wang, Y.; Jirigala, B.; Jin, E. Spatiotemporal variations of precipitation concentration and their potential links to drought in mainland China. J. Clean. Prod. 2020, 267, 122004. [Google Scholar] [CrossRef]
- Nandargi, S.S.; Aman, K. Precipitation concentration changes over India during 1951 to 2015. Sci. Res. Essays 2018, 13, 14–26. [Google Scholar] [CrossRef]
- Rahman, S.; Islam, A.R.M.T. Are precipitation concentration and intensity changing in Bangladesh overtimes? Analysis of the possible causes of changes in precipitation systems. Sci. Total. Environ. 2019, 690, 370–387. [Google Scholar] [CrossRef] [PubMed]
- Rashid, I.U.; Abid, M.A.; Almazroui, M.; Kucharski, F.; Hanif, M.; Ali, S.; Ismail, M. Early summer surface air temperature variability over Pakistan and the role of El Niño–Southern Oscillation teleconnections. Int. J. Clim. 2022, 42, 5768–5784. [Google Scholar] [CrossRef]
- Shrestha, A.; Kostaschuk, R. El Niño/Southern Oscillation (ENSO)-related variablity in mean-monthly streamflow in Nepal. J. Hydrol. 2005, 308, 33–49. [Google Scholar] [CrossRef]
- Kadel, I.; Yamazaki, T.; Iwasaki, T.; Abdillah, M.R. Projection of future monsoon precipitation over the central Himalayas by CMIP5 models under warming scenarios. Clim. Res. 2018, 75, 1–21. [Google Scholar] [CrossRef]
- Xu, Z.X.; Takeuchi, K.; Ishidaira, H. Correlation between El Niño-Southern Oscillation (ENSO) and precipitation in South-east Asia and the Pacific region. Hydrol. Process. 2003, 18, 107–123. [Google Scholar] [CrossRef]
- Izumo, T.; Lengaigne, M.; Vialard, J.; Luo, J.-J.; Yamagata, T.; Madec, G. Influence of Indian Ocean Dipole and Pacific recharge on following year’s El Niño: Interdecadal robustness. Clim. Dyn. 2013, 42, 291–310. [Google Scholar] [CrossRef]
- Leupold, M.; Pfeiffer, M.; Watanabe, T.K.; Reuning, L.; Garbe-Schönberg, D.; Shen, C.-C.; Brummer, G.-J.A. El Niño-Southern Oscillation and internal sea surface temperature variability in the tropical Indian Ocean since 1675. Clim. Past 2021, 17, 151–170. [Google Scholar] [CrossRef]


| Precipitation Indices | Abbreviation | Unit | Description |
|---|---|---|---|
| Maximum 1-day precipitation amount | RX1day | mm | Intensity of precipitation |
| Maximum 3-day precipitation amount | RX3day | mm | Intensity of precipitation |
| Maximum 5-day precipitation amount | RX5day | mm | Intensity of precipitation |
| Maximum 7-day precipitation amount | RX7day | mm | Intensity of precipitation |
| Total precipitation on days exceeding the 95th percentile (very wet days) | R95pTOT | mm | Intensity of precipitation |
| Total precipitation on days exceeding the 99th percentile (extremely wet days) | R99pTOT | mm | Intensity of precipitation |
| Count of days with precipitation ≥ 10 mm (heavy precipitation days) | R10 mm | days | Frequency of precipitation |
| Count of days with precipitation ≥ 20 mm (very heavy precipitation days) | R20 mm | days | Frequency of precipitation |
| Count of days with precipitation ≥ 35 mm (extreme precipitation days) | R35 mm | days | Frequency of precipitation |
| Maximum number of consecutive dry days (precipitation < 1 mm) | CDDs | days | Frequency of precipitation |
| Maximum number of consecutive wet days (precipitation > 1 mm) | CWDs | days | Frequency of precipitation |
| Simple Daily Intensity Index (SDII)—average precipitation on wet days | SDII | mm/day | Intensity of precipitation |
| PCI Threshold | Description |
|---|---|
| <10 | Uniform |
| 11–15 | Moderate |
| 16–20 | Irregular |
| >20 | Strongly irregular |
| Period | Min (mm) | Max (mm) | Mean (mm) | SD (mm) | CV (%) | Mann–Kendall Z-Value | Mann–Kendall p-Value | Sen’s Slope (mm/year) | Trend |
|---|---|---|---|---|---|---|---|---|---|
| January | 0 | 70.2 | 14.4 | 17.6 | 121.8 | −0.18 | 0.86 | −0.006 | NS |
| February | 0 | 83.7 | 22.4 | 21.0 | 93.8 | 0.54 | 0.59 | 0.106 | NS |
| March | 0.2 | 98.6 | 31.0 | 24.0 | 77.4 | 0.12 | 0.91 | 0.024 | NS |
| April | 2.2 | 136.4 | 58.2 | 34.0 | 58.4 | 0.95 | 0.13 | 0.361 | NS |
| May | 44.2 | 251.2 | 132.6 | 50.3 | 37.9 | 0.37 | 0.17 | 0.211 | NS |
| June | 90.4 | 559.6 | 242.7 | 97.5 | 40.2 | −0.32 | 0.75 | −0.419 | NS |
| July | 247.2 | 621.6 | 413.2 | 95.2 | 23.0 | 0.14 | 0.89 | 0.226 | NS |
| August | 260.1 | 567.1 | 375.3 | 67.2 | 17.9 | −1.37 | 0.17 | −0.866 | NS |
| September | 103.4 | 430.4 | 218.4 | 74.8 | 34.3 | −0.03 | 0.97 | −0.016 | NS |
| October | 1.3 | 201.6 | 51.9 | 50.8 | 98.0 | 0.18 | 0.86 | 0.042 | NS |
| November | 0 | 64.2 | 5.6 | 11.3 | 202.5 | −2.24 | 0.03 | −0.035 | ↓ |
| December | 0 | 78.6 | 11.4 | 19.3 | 168.4 | −2.39 | 0.02 | −0.031 | ↓ |
| Winter | 0.2 | 143.1 | 48.3 | 32.7 | 67.7 | −0.16 | 0.88 | −0.088 | NS |
| Summer | 703.3 | 1386.9 | 1031.2 | 166.0 | 16.1 | −0.83 | 0.41 | −1.661 | NS |
| Spring | 104.5 | 368.7 | 221.8 | 67.9 | 30.6 | 1.37 | 0.04 | 1.174 | ↑ |
| Autumn | 119.2 | 567.8 | 275.8 | 92.9 | 33.7 | −0.12 | 0.91 | −0.125 | NS |
| Annual | 1155.7 | 2061.6 | 1577.1 | 224.7 | 14.2 | −0.45 | 0.65 | −0.806 | NS |
| Precipitation Indices | Mean (mm) | SD (mm) | CV (%) | Mann–Kendall Z-Value | Mann–Kendall p-Value | Sen’s Slope (mm/year) |
|---|---|---|---|---|---|---|
| RX1day | 61.27 | 17.31 | 27.92 | −0.06 | 0.60 | −0.17 |
| RX3day | 113.56 | 26.16 | 22.76 | −0.08 | 0.47 | −0.26 |
| RX5day | 148.73 | 29.01 | 19.27 | 0.01 | 0.96 | −0.04 |
| RX7day | 180.45 | 38.32 | 20.98 | 0.05 | 0.03 * | 0.08 |
| R95pTOT | 586.83 | 173.51 | 29.21 | −0.08 | 0.44 | −2.00 |
| R99pTOT | 182.63 | 118.09 | 63.89 | −0.16 | 0.03 * | −1.96 |
| R10mm | 54.74 | 9.00 | 16.25 | 0.03 | 0.75 | −0.03 |
| R20mm | 20.45 | 4.82 | 23.28 | −0.01 | 0.95 | −0.01 |
| R35mm | 5.17 | 2.62 | 50.14 | −0.18 | 0.05 * | −0.05 |
| CDDs | 73.81 | 24.92 | 33.36 | 0.24 | 0.02 * | 0.69 |
| CWDs | 41.31 | 16.10 | 38.51 | 0.01 | 0.90 | 0.09 |
| PRCPTOT | 1550.62 | 215.38 | 13.72 | −0.05 | 0.67 | −1.12 |
| SDII | 10.19 | 1.08 | 10.51 | −0.17 | 0.11 | −0.02 |
| PCI—autumn | 17.72 | 3.64 | 20.32 | 0.04 | 0.68 | 0.02 |
| PCI—spring | 12.66 | 3.51 | 27.38 | 0.02 | 0.86 | 0.01 |
| PCI—summer | 9.07 | 0.66 | 7.24 | −0.01 | 0.92 | 0.00 |
| PCI—winter | 16.15 | 5.11 | 31.28 | 0.23 | 0.03 * | 0.14 |
| PCI—annual | 18.98 | 1.53 | 7.95 | −0.07 | 0.50 | −0.02 |
| 1980–2002 | 2003–2022 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Precipitation Indices | Mean (mm) | SD (mm) | CV (%) | Mann–Kendall Z-Value | Mann–Kendall p-Value | Sen’s Slope (mm/year) | Mean (mm) | SD (mm) | CV (%) | Mann–Kendall Z-Value | Mann–Kendall p-Value | Sen’s Slope (mm/year) |
| RX1day | 64.56 | 18.66 | 28.20 | 0.09 | 0.61 | 0.31 | 57.99 | 15.62 | 26.28 | 0.12 | 0.46 | 0.49 |
| RX3day | 119.21 | 24.54 | 20.09 | 0.08 | 0.65 | 0.62 | 107.91 | 27.09 | 24.50 | 0.13 | 0.42 | 0.80 |
| RX5day | 153.53 | 31.63 | 20.10 | 0.20 | 0.22 | 1.56 | 143.93 | 26.01 | 17.64 | 0.17 | 0.29 | 0.91 |
| RX7day | 186.92 | 41.97 | 21.91 | 0.33 | 0.04 * | 3.48 | 173.97 | 34.07 | 19.11 | 0.24 | 0.05 * | 1.76 |
| R95pTOT | 625.16 | 189.36 | 29.56 | 0.14 | 0.03 * | 5.07 | 548.49 | 150.91 | 26.85 | 0.10 | 0.57 | 4.45 |
| R99pTOT | 213.62 | 113.67 | 51.93 | 0.08 | 0.65 | 2.21 | 151.64 | 116.84 | 75.19 | 0.04 | 0.79 | −2.5 |
| R10mm | 56.10 | 8.97 | 15.60 | 0.20 | 0.20 | 0.50 | 53.38 | 9.05 | 16.54 | 0.18 | 0.26 | 0.40 |
| R20mm | 21.14 | 5.34 | 24.65 | 0.17 | 0.29 | 0.25 | 19.76 | 4.25 | 21.00 | 0.16 | 0.33 | 0.17 |
| R35mm | 6.00 | 2.63 | 42.72 | 0.04 | 0.81 | 0.00 | 4.33 | 2.39 | 53.92 | 0.09 | 0.58 | 0.00 |
| CDDs | 67.52 | 23.20 | 33.54 | 0.27 | 0.09 ** | 1.43 | 80.10 | 25.53 | 31.11 | 0.22 | 0.04 * | 1.00 |
| CWDs | 39.90 | 16.18 | 39.56 | −0.14 | 0.38 | −0.30 | 42.71 | 16.30 | 37.24 | −0.02 | 0.90 | 0.00 |
| PRCPTOT | 1581.39 | 210.72 | 13.00 | 0.07 | 0.70 | 2.43 | 1519.86 | 220.69 | 14.17 | 0.12 | 0.46 | 6.17 |
| SDII | 10.56 | 1.20 | 11.11 | 0.21 | 0.20 | 0.07 | 9.81 | 0.82 | 8.18 | −0.08 | 0.65 | −0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaulagain, D.; Ray, R.L.; Yakub, A.O.; Same, N.N.; Park, J.; Tangoh, A.F.; Roh, J.W.; Suh, D.; Lim, J.-O.; Huh, J.-S. Extreme Precipitation Dynamics and El Niño–Southern Oscillation Influences in Kathmandu Valley, Nepal. Water 2025, 17, 1397. https://doi.org/10.3390/w17091397
Chaulagain D, Ray RL, Yakub AO, Same NN, Park J, Tangoh AF, Roh JW, Suh D, Lim J-O, Huh J-S. Extreme Precipitation Dynamics and El Niño–Southern Oscillation Influences in Kathmandu Valley, Nepal. Water. 2025; 17(9):1397. https://doi.org/10.3390/w17091397
Chicago/Turabian StyleChaulagain, Deepak, Ram Lakhan Ray, Abdulfati Olatunji Yakub, Noel Ngando Same, Jaebum Park, Anthony Fon Tangoh, Jong Wook Roh, Dongjun Suh, Jeong-Ok Lim, and Jeung-Soo Huh. 2025. "Extreme Precipitation Dynamics and El Niño–Southern Oscillation Influences in Kathmandu Valley, Nepal" Water 17, no. 9: 1397. https://doi.org/10.3390/w17091397
APA StyleChaulagain, D., Ray, R. L., Yakub, A. O., Same, N. N., Park, J., Tangoh, A. F., Roh, J. W., Suh, D., Lim, J.-O., & Huh, J.-S. (2025). Extreme Precipitation Dynamics and El Niño–Southern Oscillation Influences in Kathmandu Valley, Nepal. Water, 17(9), 1397. https://doi.org/10.3390/w17091397








