Hybrid Optimization Approaches for Impeller Design in Turbomachinery: Methods, Metrics, and Design Strategies
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Comparative Visual Analysis of Optimization Strategies
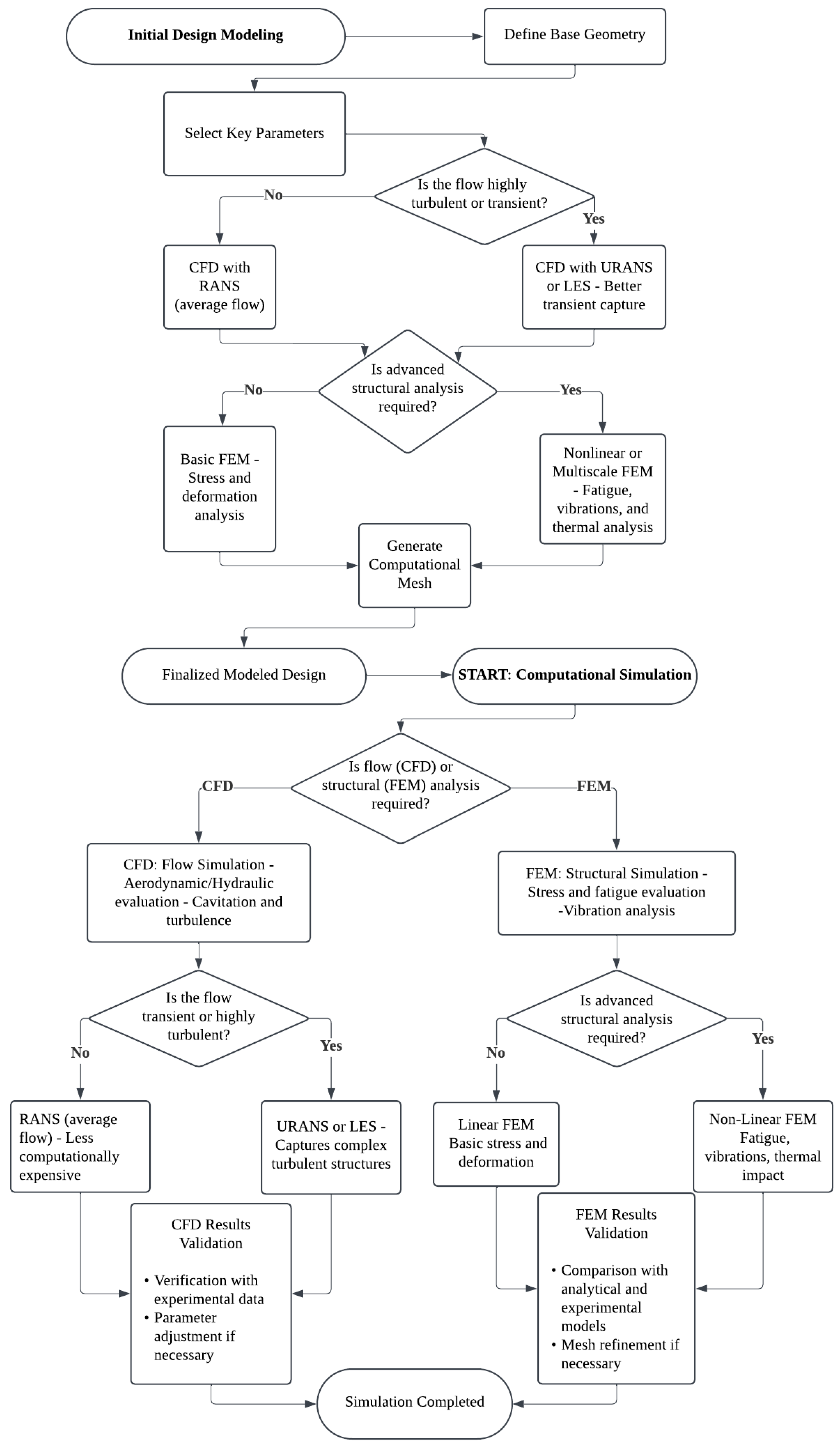
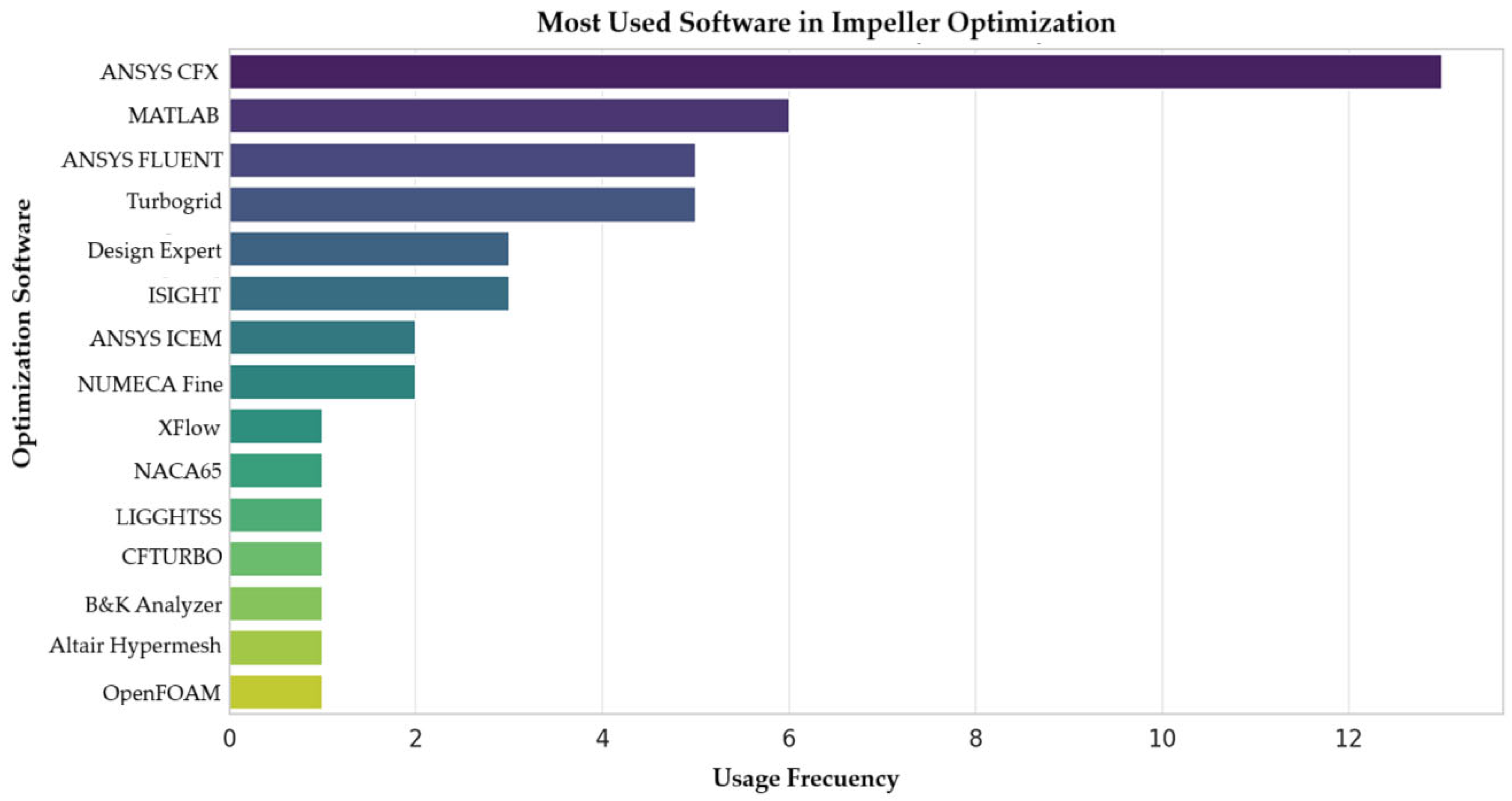
3.2. CFD-Based Simulation Models
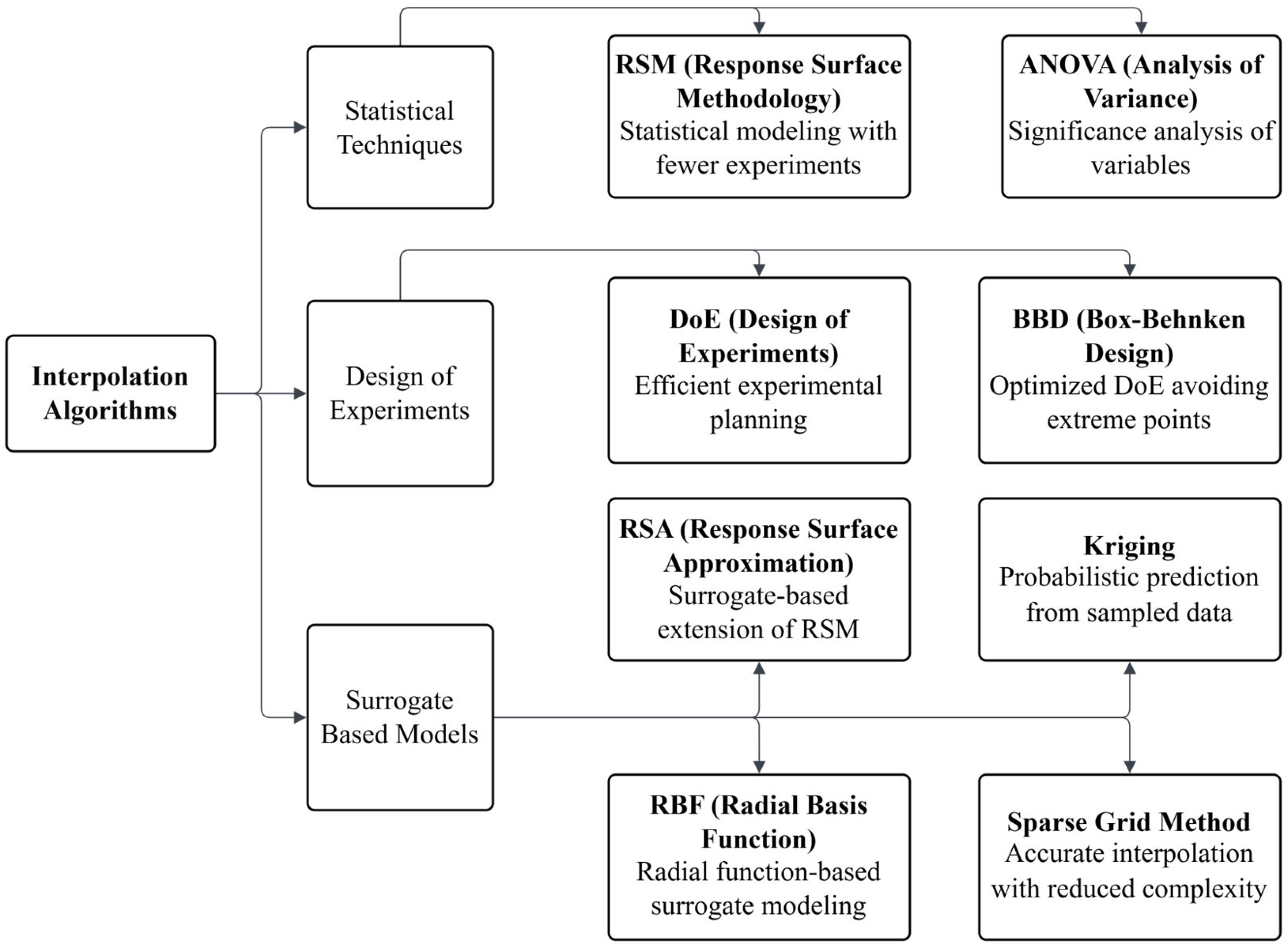
3.3. Interpolation Algorithms
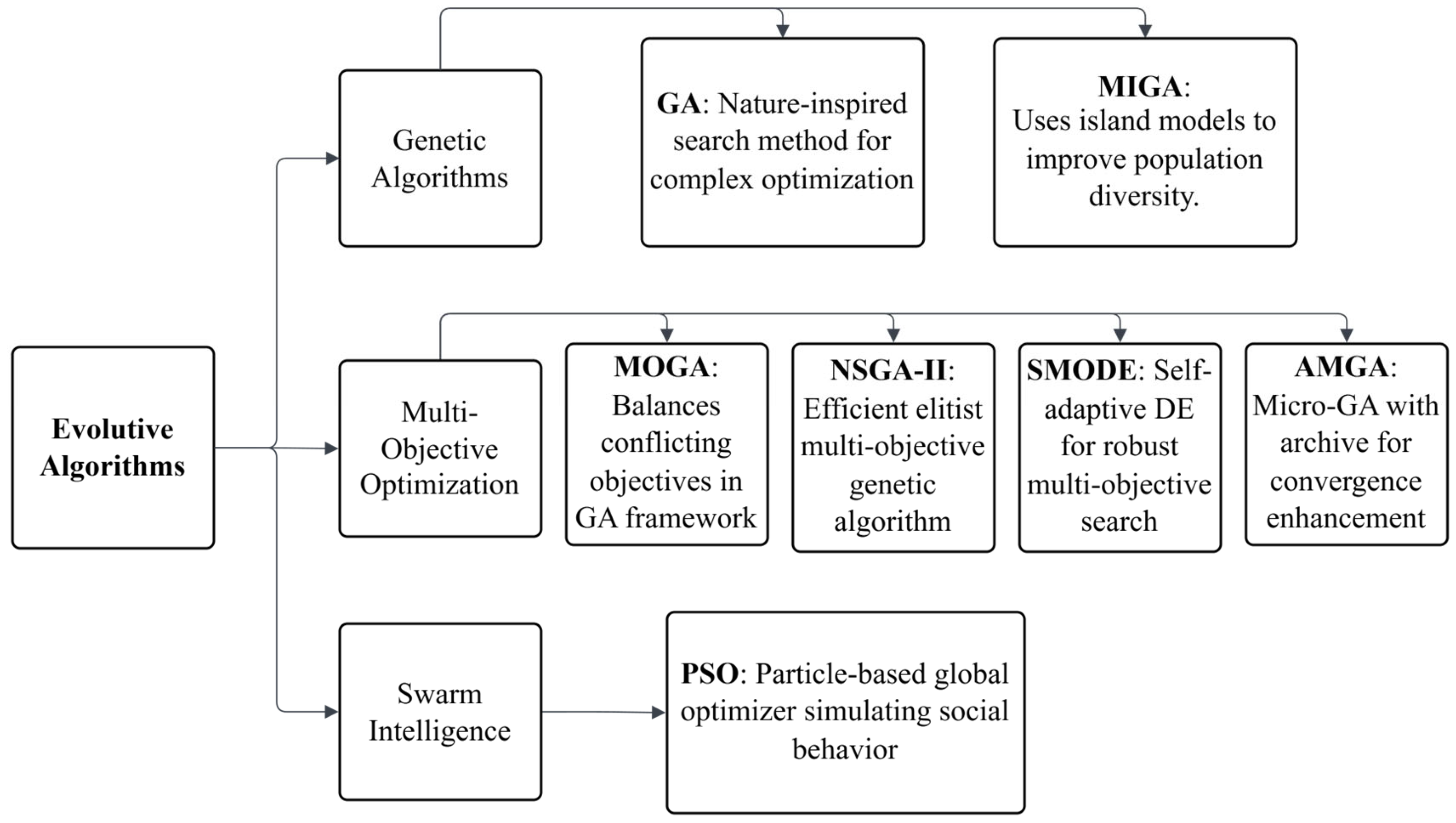
3.4. Evolutive Algorithms
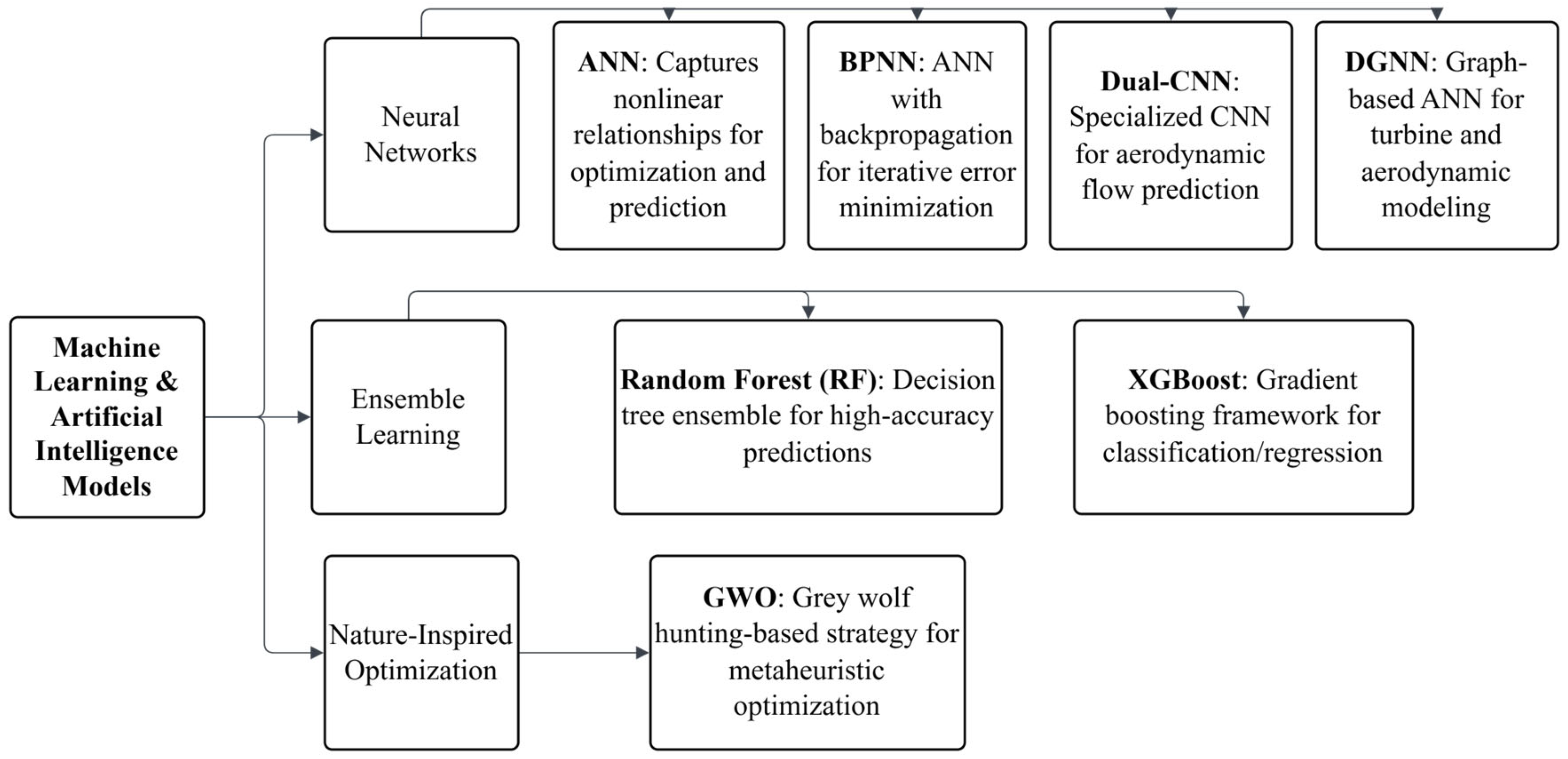
3.5. Machine Learning and AI
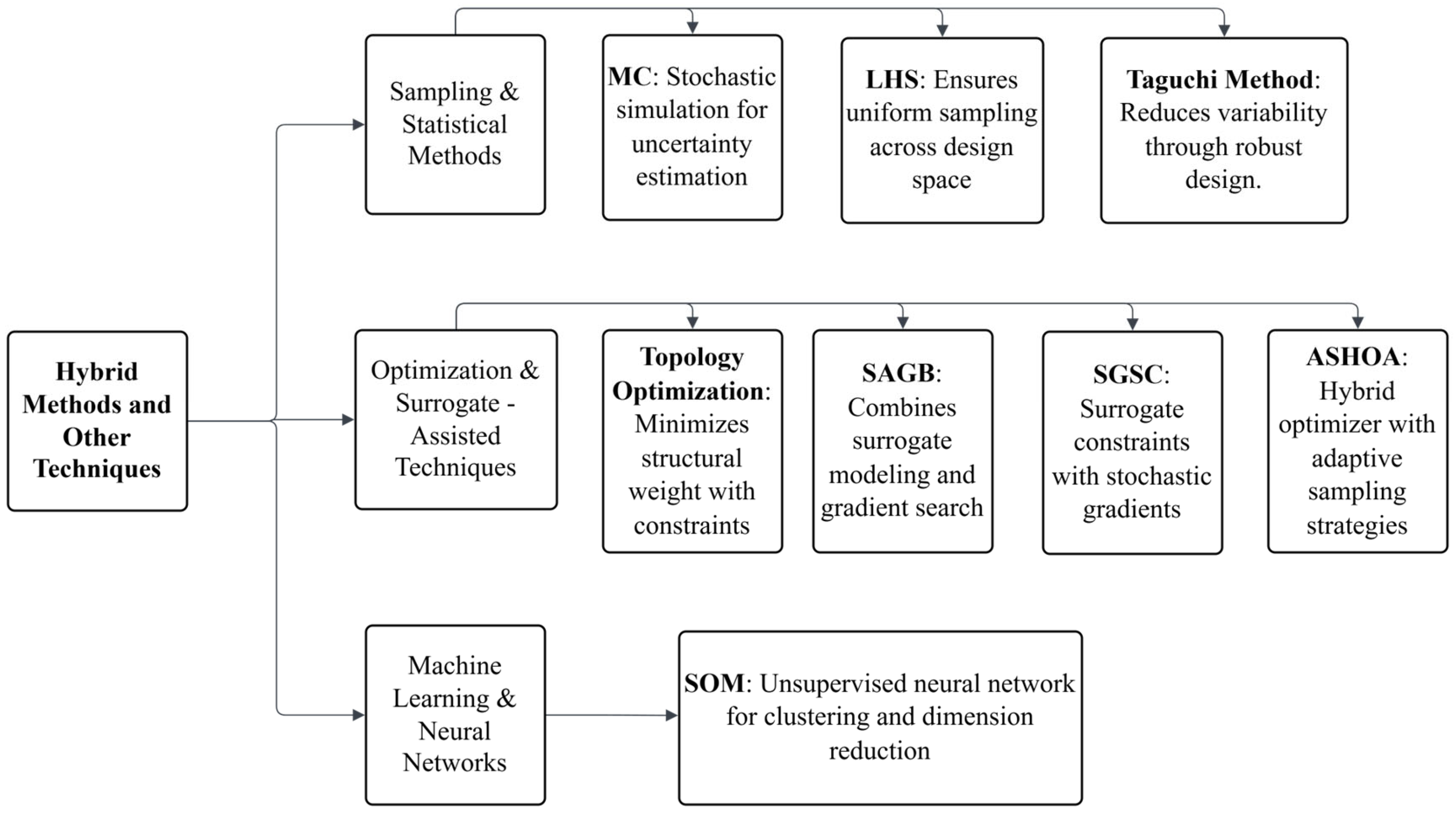
3.6. Hybrid Methods
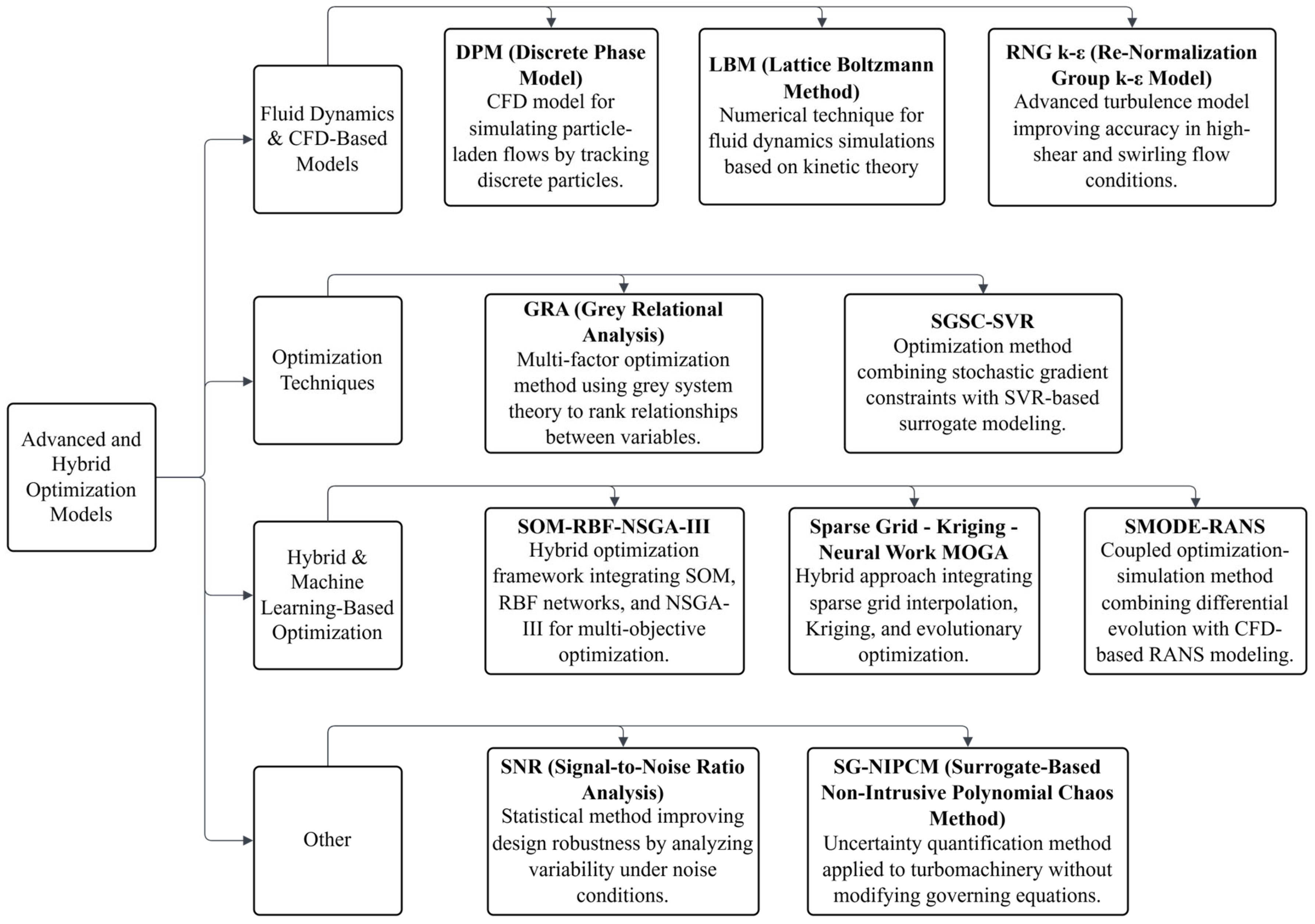
3.7. Advanced and Hybrid Optimization Models
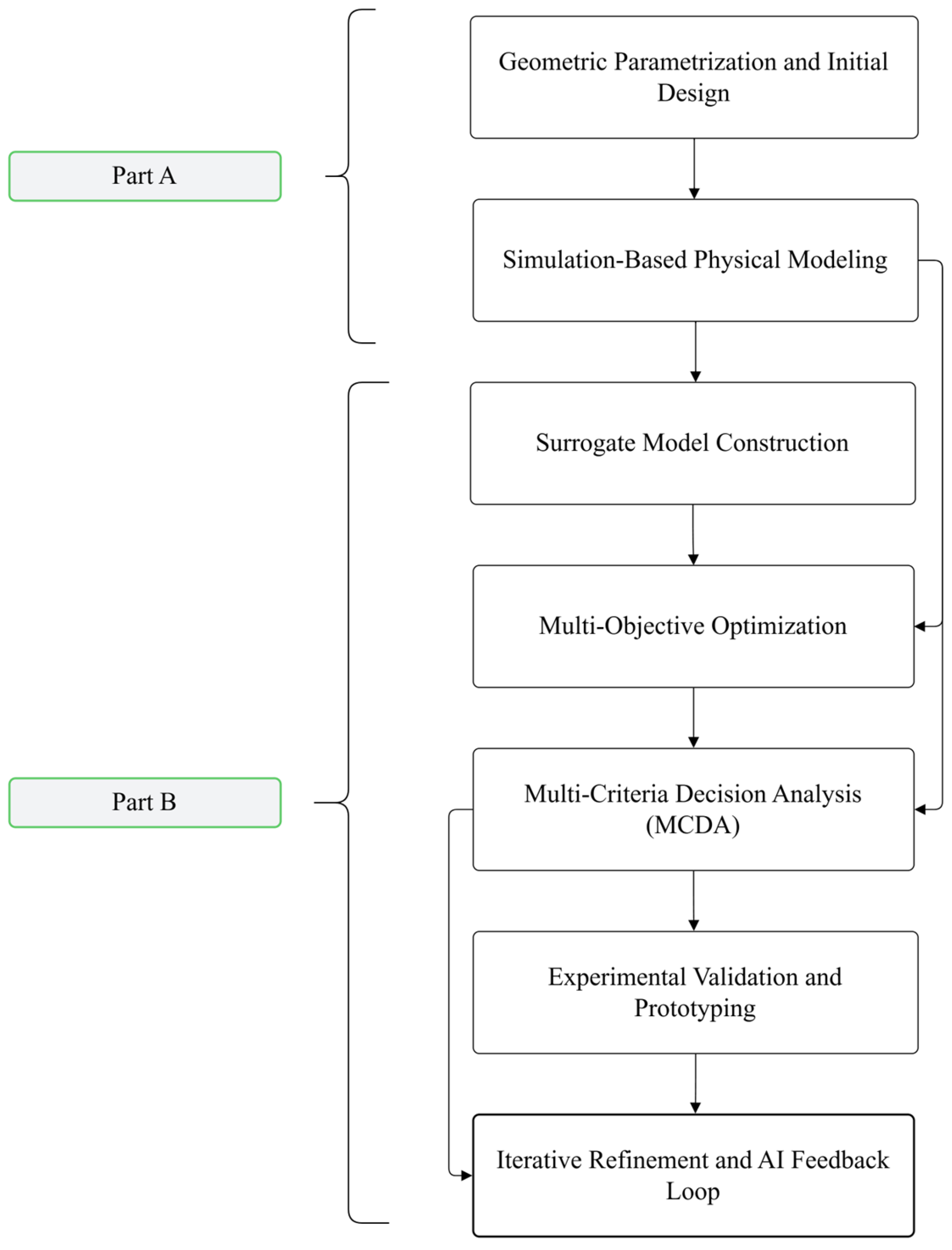
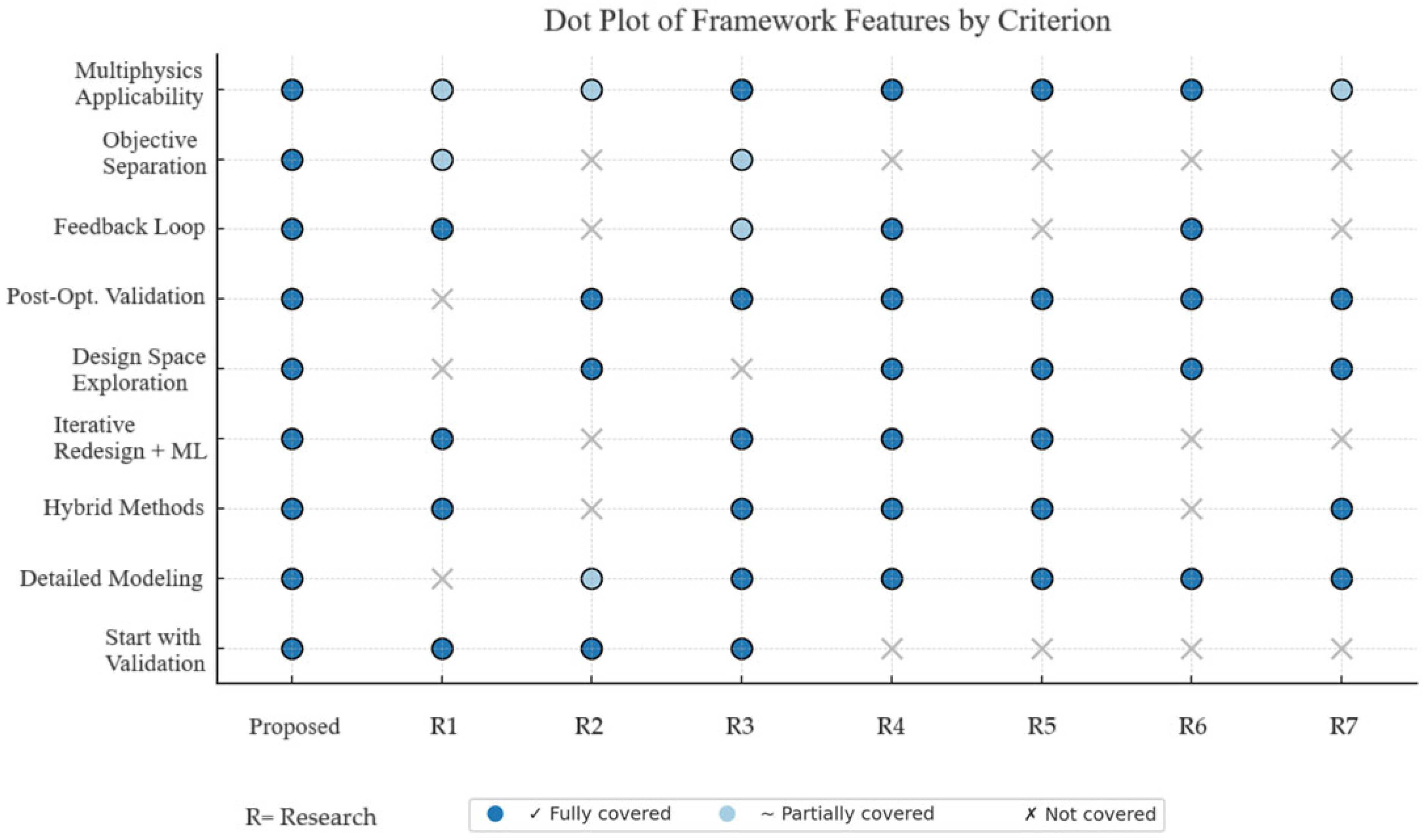
3.8. Framework Proposal
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| AMGA | Adaptive Multi-Objective Genetic Algorithm |
| ANN | Artificial Neural Network |
| ASHOA | Adaptive Sampling Hybrid Optimization Algorithm |
| BBD | Box–Behnken Design |
| BPNN | Backpropagation Neural Network |
| CFD | Computational Fluid Dynamics |
| CNN | Convolutional Neural Network |
| DADO | Deterministic Adaptive Design Optimization |
| DEM | Discrete Element Method |
| DGNN | Dual Graph Neural Network |
| DoE | Design of Experiments |
| DPM | Discrete Phase Model |
| FEM | Finite Element Method |
| GA | Genetic Algorithm |
| GRA | Grey Relational Analysis |
| GWO | Grey Wolf Optimizer |
| IDM | Inverse Design Method |
| IGWO | Improved Grey Wolf Optimizer |
| ISSA-BPNN | Improved Sparrow Search Algorithm + BPNN |
| KRG | Kriging |
| LBM | Lattice Boltzmann Method |
| LES | Large Eddy Simulation |
| LHS | Latin Hypercube Sampling |
| LMN | Local Model Network |
| MDO | Multidisciplinary Design Optimization |
| MC | Monte Carlo |
| MIGA | Modified Island Genetic Algorithm |
| ML | Machine Learning |
| MLP | Multi-Layer Perceptron |
| MOGA | Multi-Objective Genetic Algorithm |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| NUMECA | Software Suite for CFD (NUMERICAL MECHANICS Applications) |
| PSO | Particle Swarm Optimization |
| RANS | Reynolds-Averaged Navier–Stokes |
| RBF | Radial Basis Function |
| RBFNN | Radial Basis Function Neural Network |
| RF | Random Forest |
| RMS | Root Mean Square |
| RSA | Response Surface Approximation |
| RSM | Surface Methodology |
| SAGB | Surrogate-Assisted Gradient-Based |
| SGSC | Stochastic Global Sensitivity-based Calibration |
| SIS | Subset Simulation |
| SOM | Self-Organizing Map |
| SST | Shear Stress Transport |
| SVM | Support Vector Machine |
| TO | Topology Optimization |
| URANS | Unsteady Reynolds-Averaged Navier–Stokes |
| WOA | Whale Optimization Algorithm |
| XGBoost | Extreme Gradient Boosting |
| ZGB | Zwart–Gerber–Belamri (Cavitation Model) |
Appendix A
| Research | Results | Reference |
| A Study on the Multi-Objective Optimization of Impeller for High-Power Centrifugal Compressor | Structural and aerodynamic optimization of the impeller. | [11] |
| Optimization of a Centrifugal Compressor Using the Design of Experiment Technique | Efficiency and pressure-ratio optimization: +3% and +11%. | [14] |
| Optimization of Energy Recovery Turbine in Demineralized Water Treatment System of Power Station by Box–Behnken Design Method | The optimized model’s efficiency is 1.8% higher. | [53] |
| Multi-Objective Optimization of a Regenerative Pump with S-Shaped Impeller Using Response Surface Methodology | Pump efficiency +2.85% under single-objective optimization and +1.67% under double-objective optimization. | [54] |
| The Optimization of a First-Stage Liquid-Sealing Impeller Structure for a Turbopump Based on Response Surface Methodology | Pressurization coefficient +2.5%. | [23] |
| Multiobjective Optimization for the Impeller of Centrifugal Fan Based on Response Surface Methodology with Grey Relational Analysis Method | Head increased by 2.5845 m and efficiency improved by 2.88%. | [56] |
| Impeller Optimization in Crossflow Hydraulic Turbines | Reduced manufacturing costs using new impeller technology compared to conventional methods. | [124] |
| Multi-Disciplinary Optimization Design of Axial-Flow Pump Impellers Based on the Approximation model | Single-blade mass −10.47%, while efficiency +0.61%. | [6] |
| Design and Optimization of Meridional Profiles for the Impeller of Centrifugal Compressors | Elliptical curves showed acceptable performance vs. circular curves, with +2.6% at low flow rates and +3% at high flow rates. | [12] |
| Instabilities Identification Based on a New Centrifugal 3D Impeller Outflow Model | URANS simulation can reproduce the main features of rotational stall in the diffuser at 30% of the total cost. | [50] |
| Comprehensive Improvement of Mixed-Flow Pump Impeller Based on Multi-Objective Optimization | Pump efficiency +0.63%, +3.39%, and +3.77% at 0.8QDES, 1. QDES, and 1.2 QDES, respectively. | [72] |
| A General Framework for Designing 3D Impellers Using Topology Optimization and Additive Manufacturing | Total impeller mass decreased by nearly 30%. | [29] |
| Additive Manufacturing and Topology Optimization Applied to Impeller to Enhance Mechanical Performance | Stress levels reduced by 25%, impeller mass decreased by 20%, leading to higher allowable speed and better overall performance. | [30] |
| Topology Optimization Design with Addictive Manufacturing Constraints for Centrifugal Impeller | Impeller weight reduced by up to 18.5%. | [31] |
| Aerodynamic Analysis and Design Optimization of a Centrifugal Compressor Impeller Considering Realistic Manufacturing Uncertainties | Decreasing blade angles counteracts the detrimental effects of positive blade-thickness errors. | [108] |
| Robust Optimization and Uncertainty Quantification of a Micro Axial Compressor for Unmanned Aerial Vehicles | Isentropic efficiency and pressure ratio increase by 0.6% and 0.5%, while reducing their standard deviations and that of mass flow rate by 32.4%, 41.2%, and 25.1% | [117] |
| Novel Multidisciplinary Design and Multi-Objective Optimization of Centrifugal Compressor used for Hydrogen Fuel Cells | Power consumption reduced by 2.99%, with a maximum isentropic-efficiency increase of 2.16%. | [24] |
| Cavitation Performance Enhancement of a Centrifugal Pump Impeller Based on Taguchi’s Orthogonal Optimization | Cavitation performance improved by 19.3% at the best efficiency point. | [32] |
| Optimization of centrifugal pump impeller for pumping viscous fluids using direct design optimization technique | Operational stability and overall performance enhanced. | [134] |
| The Fan Design Optimization for Totally Enclosed Type Induction Motor with Experimentally Verified CFD-Based MOGA Simulations | Efficiency increased by 8%, volumetric flow rate by 18%, and winding temperature decreased by 8 °C. | [25] |
| Aerodynamic Robustness Optimization and Design Exploration of Centrifugal Compressor Impeller under Uncertainties | The average pressure ratio increased by 9.3% and average isentropic efficiency by 6.7%. Their standard deviations decreased by 7.5% and 15.4%, respectively, and the acoustic power level dropped by 11 dB. | [21] |
| Impeller Shape-Optimization of Stirred-Tank Reactor: CFD and Fluid Structure Interaction Analyses | Energy consumption decreased by 26.71%, while equivalent stress rose by 6.09%. | [26] |
| A Study on Suction Pump Impeller Form Optimization for Ballast Water Treatment System | Efficiency exceeded 12%. | [68] |
| Research on Cooperative Optimization of Multiphase Pump Impeller and Diffuser Based on Adaptive Refined Response Surface Method | Pressure increment increased by 38 kPa in the optimized model. | [63] |
| Energy-Saving Oriented Optimization Design of the Impeller and Volute of a Multi-Stage Double-Suction Centrifugal Pump using Artificial Neural Network | Efficiency increased by 2.05%, 3.56%, and 5.36% at 0.6Qd, 1.0Qd, and 1.2Qd, respectively, compared to the reference design | [8] |
| Centrifugal Pump Impeller and Volute Shape Optimization via Combined NUMECA, Genetic Algorithm, and Back Propagation Neural Network | Head and efficiency at the design flow increased by 7.69% and 4.74%. Further optimization raised head by 2.69 m and efficiency by 4.32%. | [36] |
| Impeller Optimization using a Machine Learning-Based Algorithm with Dynamic Sampling Method and Flow Analysis for an Axial Flow Pump | Optimized axial flow pump exhibits a 2% efficiency increase. | [125] |
| Machine Learning Based Design Optimization of Centrifugal Impellers | A single impeller-performance prediction with the machine-learning approach requires under 1 s. | [15] |
| Multi-Objective Optimization for Impeller Structure Parameters of Fuel Cell Air Compressor using Linear-Based Boosting Model and Reference Vector Guided Evolutionary Algorithm | For the Maxσ solution, the isentropic efficiency and pressure ratio increased by 18.7% and 70.1%, respectively. For the Maxηc solution, improved by 23.0% and 48.9%, respectively. | [34] |
| Fatigue Reliability Evaluation for Impellers with Consideration of Multi-Source Uncertainties using a WOA-XGBoost Surrogate Model | XGBoost model achieves an R2 above 0.93 in fatigue-life prediction. | [27] |
| Optimized Design of Solid–Liquid Dual-Impeller Mixing Systems for Enhanced Efficiency | Cloud height increased by 8.7%, and energy consumption decreased by 15.6%. | [58] |
| Automatic Detection of Surface Defects of Submersible Pump Impellers by Machine Learning Algorithm | High surface defect detection efficiency, high accuracy, high automation, and low cost. | [28] |
| Satellite Thermal Management Pump Impeller Design and Optimization | Efficiency rose by 3.55%, and head increased by 7.9%. | [44] |
| Modal Analysis and Structural Optimization of Integrated Bladed Disks and Centrifugal Compressor Impellers | Mass was reduced by 23%, explosion margin increased by 4.31%, and critical resonance conditions were eliminated. | [35] |
| An Improved Grey Wolf Optimizer (IGWO) Algorithm for Optimization of Centrifugal Pump With Guide Vane | Efficiency is 1.2% higher than the original pump, and the anti-cavitation performance is improved. | [96] |
| Novel Designs of Blade Mixer Impellers from the Discrete Element Method and Topology Optimization | Impeller shape can be modified to enhance mixing or reduce energy consumption. | [116] |
| Matching Optimization of a Mixed Flow Pump Impeller and Diffuser Based on the Inverse Design Method | Optimized pump’s efficiency at 1.2QDES, 1.0Q QDES, and 0.8Q QDES increased by 6.47%, 3.68%, and 0.82%, respectively. | [22] |
| Improving Centrifugal Compressor Performance by Optimizing the Design of Impellers Using Genetic Algorithm and Computational Fluid Dynamics Methods | Operational stability and overall performance enhanced. | [41] |
| Hydrodynamic Optimization of the Impeller and Diffuser Vane of an Axial-Flow Pump | Total efficiency and total head were 0.974% and 21.028% higher. After diffuser-blade optimization, total efficiency and total head increased by 3.097% and 10.205%. | [33] |
| Hydrodynamic Optimization of the Impeller and Diffuser Vane of an Axial-Flow Pump | Overall efficiency improved by 2.05%, and loss margin improved by 8.89%. | [79] |
| Optimization of Impeller Blades of an Electric Water Pump via Computational Fluid Dynamics | Q = Qd increased from 20.5 m to 21.9 m, while pump efficiency rose from 66.7% to 72.3%. | [51] |
| Optimization Design of Energy-Saving Mixed Flow Pump Based on MIGA-RBF Algorithm | Experimental results show a maximum pump-efficiency increase of 4.3%. | [42] |
| Introducing Non-Hierarchical RSM and MIGA for Performance Prediction and Optimization of a Centrifugal Pump under the Nominal Condition | Efficiency improved by 3.717% post-optimization. | [74] |
| Optimization of the Impeller for Hydraulic Performance Improvement of a High-Speed Magnetic Drive Pump | Hydraulic efficiency of the optimal impeller was 6.23% higher. | [76] |
| Uncertainty Quantification and Aerodynamic Robust Optimization of Turbomachinery Based on Graph Learning Methods | Reduced losses and improved efficiency. | [104] |
| Uncertainty Quantification-Based Optimization of Centrifugal Compressor Impeller for Aerodynamic Robustness under Stochastic Operational Conditions | Mean pressure increased by 2.3%, mean efficiency by 2.9%, and the variance of the pressure ratio decreased by 14.3%. | [21] |
| A Gradient-Based Method Assisted by Surrogate Model for Robust Optimization of Turbomachinery Blades | Blade optimization is under robust design. | [110] |
| Topology Optimization of Static Turbomachinery Components | Final weight 65% lower than the original component. | [13] |
| Liquid-Vapor Two-Phase Flow in Centrifugal Pump: Cavitation, Mass Transfer, and Impeller Structure Optimization | Enhanced cavitation performance. | [120] |
| Mixing Optimization with Inward Flow Configuration Contra-Rotating Impeller, Baffle-Free Tank | High mixing efficiency and low torque at pilot scale. | [107] |
| Optimal Design and Performance Improvement of an Electric Submersible Pump Impeller Based on Taguchi Approach | Head increased by 3.5%, and efficiency rose by 6.1%. | [45] |
| Computational Prediction of the Just-Suspended Speed, Njs, in Stirred Vessels using the Lattice Boltzmann Method (LBM) Coupled with a Novel Mathematical Approach | Efficiency increased by 2.4%. | [37] |
| Analysis of Erosion Minimization for a Slurry Pump Using Discrete Phase Model Simulations | Erosion-rate density was reduced. | [43] |
| Multi-Condition Optimization and Experimental Verification of Impeller for a Marine Centrifugal Pump | Maximum vibration intensity decreased, and efficiency improved. | [40] |
| CFD Simulation of Impeller Shape Effect on Quality of Mixing in Two-Phase Gas–Liquid Agitated Vessel | Axial gas-phase distribution for the 30° impeller is about 55% better than others. | [38] |
| Validating Impeller Geometry Optimization for Sound Quality Based on Psychoacoustics Metrics | Noise intensity reduced, while energy performance increased by 4.3%. | [39] |
| Integrated Energy-Efficient Machining of Rotary Impellers and Multi-Objective Optimization | Improved machining with respect to materials. | [127] |
| Surrogate-Based Design Optimization of a Centrifugal Pump Impeller | The optimum pump-impeller design shows >10% improvement in pump efficiency. | [69] |
| Surrogate-Based Design Optimization of a Centrifugal Pump Impeller | Isentropic efficiency and total pressure ratio improved by 1.61% and 4.13%, respectively, while maximum stress decreased by 9.68%. | [111] |
References
- Gambini, M.; Vellini, M. (Eds.) Turbomachinery Selection. In Turbomachinery: Fundamentals, Selection and Preliminary Design; Springer International Publishing: Cham, Switzerland, 2021; pp. 89–107. [Google Scholar] [CrossRef]
- Ji, Y.; Song, H.; Xue, Z.; Li, Z.; Tong, M.; Li, H. A Review of the Efficiency Improvement of Hydraulic Turbines in Energy Recovery. Processes 2023, 11, 1815. [Google Scholar] [CrossRef]
- Parisi, S.; Haglind, F. Numerical Analysis of Reversible Radial-Flow Turbomachinery for Energy Storage Applications. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2023; Volume 86991, p. V006T09A002. [Google Scholar]
- Shim, H.-S.; Kim, K.-Y. Design Optimization of the Impeller and Volute of a Centrifugal Pump to Improve the Hydraulic Performance and Flow Stability. J. Fluids Eng. 2020, 142, 101211. [Google Scholar] [CrossRef]
- Ye, W.; Zhuang, B.; Wei, Y.; Luo, X.; Wang, H. Investigation on the Unstable Flow Characteristic and Its Alleviation Methods by Modifying the Impeller Blade Tailing Edge in a Centrifugal Pump. J. Energy Storage 2024, 86, 111358. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, J.; Tang, F.; Wang, C. Multi-Disciplinary Optimization Design of Axial-Flow Pump Impellers Based on the Approximation Model. Energies 2020, 13, 779. [Google Scholar] [CrossRef]
- Wagner, F.; Kühhorn, A.; Janetzke, T.; Gerstberger, U. Multi-Objective Optimization of the Cooling Configuration of a High Pressure Turbine Blade. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51104, p. V05CT20A001. [Google Scholar]
- Zhao, J.; Pei, J.; Yuan, J.; Wang, W. Energy-Saving Oriented Optimization Design of the Impeller and Volute of a Multi-Stage Double-Suction Centrifugal Pump Using Artificial Neural Network. Eng. Appl. Comput. Fluid Mech. 2022, 16, 1974–2001. [Google Scholar] [CrossRef]
- Hammond, J.; Pepper, N.; Montomoli, F.; Michelassi, V. Machine Learning Methods in CFD for Turbomachinery: A Review. Int. J. Turbomach. Propuls. Power 2022, 7, 16. [Google Scholar] [CrossRef]
- Zou, Z.; Xu, P.; Chen, Y.; Yao, L.; Fu, C. Application of Artificial Intelligence in Turbomachinery Aerodynamics: Progresses and Challenges. Artif. Intell. Rev. 2024, 57, 222. [Google Scholar] [CrossRef]
- Kang, H.-S.; Kim, Y.-J. A Study on the Multi-Objective Optimization of Impeller for High-Power Centrifugal Compressor. Int. J. Fluid Mach. Syst. 2016, 9, 143–149. [Google Scholar] [CrossRef]
- Mojaddam, M.; Moussavi Torshizi, S.A. Design and Optimization of Meridional Profiles for the Impeller of Centrifugal Compressors. J. Mech. Sci. Technol. 2017, 31, 4853–4861. [Google Scholar] [CrossRef]
- Buonamici, F.; Meli, E.; Secciani, N.; Ridolfi, A.; Rindi, A.; Furferi, R. Topology Optimization of Static Turbomachinery Components. Manuf. Technol. J. 2023, 23, 11–24. [Google Scholar] [CrossRef]
- Mojaddam, M.; Pullen, K.R. Optimization of a Centrifugal Compressor Using the Design of Experiment Technique. Appl. Sci. 2019, 9, 291. [Google Scholar] [CrossRef]
- Zhang, A.; Liu, Y.; Yang, J.; Li, Z.; Zhang, C.; Li, Y. Machine Learning Based Design Optimization of Centrifugal Impellers. J. Glob. Power Propuls. Soc. 2022, 6, 124–134. [Google Scholar] [CrossRef]
- Yang, G.; Shen, X.; Pan, Q.; Ding, J.; Luo, W.; Meng, J.; Zhang, D. Multi-Objective Optimization Design for Broadening the High Efficiency Region of Hydrodynamic Turbine with Forward-Curved Impeller and Energy Loss Analysis. Renew. Energy 2025, 245, 122818. [Google Scholar] [CrossRef]
- Lavimi, R.; Le Hocine, B.; Alla, E.; Poncet, S.; Marcos, B.; Panneton, R. A Review on Aerodynamic Optimization of Turbomachinery Using Adjoint Method. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2024, 238, 6405–6441. [Google Scholar] [CrossRef]
- Gomersall, P.; Jain, D. Robust Design and Optimization of Turbo-Machinery Compressors. Catal. Propelling Sch. Forw. 2024, 2. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, Z.; Song, L.; Liu, T. A Panoramic Aerodynamic Performance Prediction Method for Turbomachinery Cascades Using Transformer-Enhanced Neural Operator. Chin. J. Aeronaut. 2025, 38, 103473. [Google Scholar] [CrossRef]
- Ke, Z.; Wei, W.; Guo, M.; Chen, B.; Liu, C.; Yan, Q. Collaborative Design Method for Multi-Impeller Turbomachinery Based on Variable Sectional-Area Distribution. Alex. Eng. J. 2024, 104, 150–161. [Google Scholar] [CrossRef]
- Tang, X.; Gu, N.; Wang, W.; Wang, Z.; Peng, R. Aerodynamic Robustness Optimization and Design Exploration of Centrifugal Compressor Impeller under Uncertainties. Int. J. Heat Mass Transf. 2021, 180, 121799. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y.; Yuan, J.; Osman, F.K. Matching Optimization of a Mixed Flow Pump Impeller and Diffuser Based on the Inverse Design Method. Processes 2021, 9, 260. [Google Scholar] [CrossRef]
- Liu, Q.; Zhuang, S.; Bao, H.; He, Z.; Wang, K.; Liu, H. The Optimization of a First-Stage Liquid-Sealing Impeller Structure for a Turbopump Based on Response Surface Methodology. Processes 2022, 10, 1999. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, H.; Chen, Q.; Peng, X.; Feng, J. Novel Multidisciplinary Design and Multi-Objective Optimization of Centrifugal Compressor Used for Hydrogen Fuel Cells. Int. J. Hydrogen Energy 2023, 48, 12444–12460. [Google Scholar] [CrossRef]
- Özyildiz, T.; Şentürk Lüle, S. The Fan Design Optimization for Totally Enclosed Type Induction Motor with Experimentally Verified CFD-Based MOGA Simulations. Arab. J. Sci. Eng. 2024, 49, 15597–15610. [Google Scholar] [CrossRef]
- Hoseini, S.S.; Najafi, G.; Ghobadian, B.; Akbarzadeh, A.H. Impeller Shape-Optimization of Stirred-Tank Reactor: CFD and Fluid Structure Interaction Analyses. Chem. Eng. J. 2021, 413, 127497. [Google Scholar] [CrossRef]
- Qian, C.; Li, W.; Wei, S.; Sun, B.; Ren, Y. Fatigue Reliability Evaluation for Impellers with Consideration of Multi-source Uncertainties Using a WOA-XGBoost Surrogate Model. Qual. Reliab. Eng. Int. 2024, 40, 3193–3211. [Google Scholar] [CrossRef]
- Yang, Y.; Shu, B.; Zhao, X. Automatic Detection of Surface Defects of Submersible Pump Impellers by Machine Learning Algorithm. In Proceedings of the 2023 IEEE International Conference on Image Processing and Computer Applications (ICIPCA), Changchun, China, 11–13 August 2023; pp. 518–522. [Google Scholar] [CrossRef]
- Meli, E.; Furferi, R.; Rind, A.; Ridolfi, A.; Volpe, Y.; Buonamici, F. A General Framework for Designing 3D Impellers Using Topology Optimization and Additive Manufacturing. IEEE Access 2020, 8, 60259–60269. [Google Scholar] [CrossRef]
- Corbo, S.; Iurisci, G.; Gangioli, F.; Boccini, E.; Meli, E.; Rindi, A. Additive Manufacturing and Topology Optimization Applied to Impeller to Enhance Mechanical Performance. In Proceedings of the 47th Turbomachinery Symposium; Turbomachinery Laboratory, Texas A&M Engineering Experiment Station: College Station, TX, USA, 2018. [Google Scholar]
- Liu, S.; Mi, D.; Wen, C.; Zheng, Y. Topology Optimization Design with Addictive Manufacturing Constraints for Centrifugal Impeller. J. Phys. Conf. Ser. 2022, 2252, 12026. [Google Scholar] [CrossRef]
- Dönmez, A.H.; Yumurtaci, Z.; Kavurmacioğlu, L. Cavitation Performance Enhancement of a Centrifugal Pump Impeller Based on Taguchi’s Orthogonal Optimization. Arab. J. Sci. Eng. 2024. [Google Scholar] [CrossRef]
- Nguyen, D.-A.; Ma, S.-B.; Kim, S.; Kim, J.-H. Hydrodynamic Optimization of the Impeller and Diffuser Vane of an Axial-Flow Pump. J. Mech. Sci. Technol. 2023, 37, 1263–1278. [Google Scholar] [CrossRef]
- Fu, J.; Wang, H.; Sun, X.; Bao, H.; Wang, X.; Liu, J. Multi-Objective Optimization for Impeller Structure Parameters of Fuel Cell Air Compressor Using Linear-Based Boosting Model and Reference Vector Guided Evolutionary Algorithm. Appl. Energy 2024, 363, 123057. [Google Scholar] [CrossRef]
- Lima, D.Z.; Dezan, D.J.; Gasparin, E.E.; Salviano, L.O.; Yanagihara, J.I.; Ferreira, W.G. Modal Analysis and Structural Optimization of Integrated Bladed Disks and Centrifugal Compressor Impellers. Struct. Multidiscip. Optim. 2024, 67, 40. [Google Scholar] [CrossRef]
- Han, X.; Kang, Y.; Sheng, J.; Hu, Y.; Zhao, W. Centrifugal Pump Impeller and Volute Shape Optimization via Combined NUMECA, Genetic Algorithm, and Back Propagation Neural Network. Struct. Multidiscip. Optim. 2020, 61, 381–409. [Google Scholar] [CrossRef]
- Sirasitthichoke, C.; Teoman, B.; Thomas, J.; Armenante, P.M. Computational Prediction of the Just-Suspended Speed, Njs, in Stirred Vessels Using the Lattice Boltzmann Method (LBM) Coupled with a Novel Mathematical Approach. Chem Eng Sci 2022, 251, 117411. [Google Scholar] [CrossRef]
- Heidari, A. CFD Simulation of Impeller Shape Effect on Quality of Mixing in Two-Phase Gas–Liquid Agitated Vessel. Chin J Chem Eng 2020, 28, 2733–2745. [Google Scholar] [CrossRef]
- Novaković, T.; Ogris, M.; Prezelj, J. Validating Impeller Geometry Optimization for Sound Quality Based on Psychoacoustics Metrics. Appl. Acoust. 2020, 157, 107013. [Google Scholar] [CrossRef]
- Wang, K.; Luo, G.; Li, Y.; Xia, R.; Liu, H. Multi-Condition Optimization and Experimental Verification of Impeller for a Marine Centrifugal Pump. Int. J. Nav. Archit. Ocean Eng. 2020, 12, 71–84. [Google Scholar] [CrossRef]
- Omidi, M.; Liu, S.-J.; Mohtaram, S.; Lu, H.-T.; Zhang, H.-C. Improving Centrifugal Compressor Performance by Optimizing the Design of Impellers Using Genetic Algorithm and Computational Fluid Dynamics Methods. Sustainability 2019, 11, 5409. [Google Scholar] [CrossRef]
- Lu, R.; Yuan, J.; Wei, G.; Zhang, Y.; Lei, X.; Si, Q. Optimization Design of Energy-Saving Mixed Flow Pump Based on MIGA-RBF Algorithm. Machines 2021, 9, 365. [Google Scholar] [CrossRef]
- Na, S.J.; Kim, Y.S.; Jeon, E.S. Analysis of Erosion Minimization for a Slurry Pump Using Discrete Phase Model Simulations. Appl. Sci. 2022, 12, 1597. [Google Scholar] [CrossRef]
- Drăgan, V.; Dumitrescu, O.; Dobromirescu, C.; Popa, I.F. Satellite Thermal Management Pump Impeller Design and Optimization. Inventions 2024, 9, 54. [Google Scholar] [CrossRef]
- Bai, L.; Yang, Y.; Zhou, L.; Li, Y.; Xiao, Y.; Shi, W. Optimal Design and Performance Improvement of an Electric Submersible Pump Impeller Based on Taguchi Approach. Energy 2022, 252, 124032. [Google Scholar] [CrossRef]
- Aliuly, A.; Amanzholov, T.; Seitov, A.; Momysh, N.; Jaichibekov, N.; Kaltayev, A. Hydraulic Design and CFD-Based Parametric Study for Optimizing Centrifugal Pump Impeller Performance. Appl. Sci. 2024, 14, 161. [Google Scholar] [CrossRef]
- Bamberger, K.; Carolus, T.; Belz, J.; Nelles, O. Development, Validation, and Application of an Optimization Scheme for Impellers of Centrifugal Fans Using Computational Fluid Dynamics-Trained Metamodels. J. Turbomach. 2020, 142, 111005. [Google Scholar] [CrossRef]
- Wu, M. Efficient CFD-Based Multi-Objective Optimization of Impeller Geometries for Homogenization Processes in Stirred Tanks: The Mean Age Theory Approach. 2024. Available online: https://depositonce.tu-berlin.de/items/8e77b8cf-3f2f-42b1-9128-406b6673d873 (accessed on 26 June 2025).
- Park, S.H.; Lee, G.H.; Kim, D.; Chang, K. Assessment of the Predictive Capabilities of Various Turbulence Models for the Simulation of Rotating Stall in the Centrifugal Pump Impeller. J. Vis. 2024, 27, 537–552. [Google Scholar] [CrossRef]
- Fan, M.; Dazin, A.; Bois, G.; Romanò, F. Instabilities Identification Based on a New Centrifugal 3D Impeller Outflow Model. Aerosp. Sci. Technol. 2023, 140, 108466. [Google Scholar] [CrossRef]
- Teng, S.; Tian, Y.; Li, B.; Kang, C. Optimization of Impeller Blades of an Electric Water Pump via Computational Fluid Dynamics. J. Mech. Sci. Technol. 2024, 38, 1281–1291. [Google Scholar] [CrossRef]
- Deng, L.; Long, Y.; Cheng, H.; Ji, B. Some Notes on Numerical Investigation of Three Cavitation Models through a Verification and Validation Procedure. J. Hydrodyn. 2023, 35, 185–190. [Google Scholar] [CrossRef]
- Ji, Y.; Ran, J.; Yang, Z.; Li, H.; Hao, X. Optimization of Energy Recovery Turbine in Demineralized Water Treatment System of Power Station by Box–Behnken Design Method. Energy Rep. 2022, 8, 362–370. [Google Scholar] [CrossRef]
- Salimi, A.; Rostami, H.H.; Riasi, A.; Nejadali, J. Multi-Objective Optimization of a Regenerative Pump with S-Shaped Impeller Using Response Surface Methodology. Int. Commun. Heat Mass Transf. 2023, 143, 106734. [Google Scholar] [CrossRef]
- Cao, W.; Wang, H.; Yang, X.; Leng, X. Optimization of Guide Vane Centrifugal Pumps Based on Response Surface Methodology and Study of Internal Flow Characteristics. J. Mar. Sci. Eng. 2023, 11, 1917. [Google Scholar] [CrossRef]
- Meng, F.N.; Dong, Q.L.; Wang, P.F.; Wang, Y. Multiobjective Optimization for the Impeller of Centrifugal Fan Based on Response Surface Methodology with Grey Relational Analysis Method. Adv. Mech. Eng. 2014. [Google Scholar] [CrossRef]
- Koç, M.A. A New Expert System for Active Vibration Control (AVC) for High-Speed Train Moving on a Flexible Structure and PID Optimization Using MOGA and NSGA-II Algorithms. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 151. [Google Scholar] [CrossRef]
- Xia, D.; Mao, Z.; Zhou, S.; He, X.; Wang, Y. Optimized Design of Solid–Liquid Dual-Impeller Mixing Systems for Enhanced Efficiency. ACS Omega 2023, 8, 47635–47645. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Zhao, Z.; Ouyang, H.; Wu, Z.; Han, X. An Efficient Reliability Analysis Method Based on the Improved Radial Basis Function Neural Network. J. Mech. Des. 2023, 145. [Google Scholar] [CrossRef]
- Zhao, G.; Zhao, Y.; Dong, S. The Surrogate Model for Short-Term Extreme Response Prediction Based on ANN and Kriging Algorithm. Appl. Ocean Res. 2024, 152, 104196. [Google Scholar] [CrossRef]
- Mallik, W.; Raveh, D.E. Kriging-Based Aeroelastic Gust Response Analysis at High Angles of Attack. AIAA J. 2020, 58, 3777–3787. [Google Scholar] [CrossRef]
- Borisut, P.; Nuchitprasittichai, A. Adaptive Latin Hypercube Sampling for a Surrogate-Based Optimization with Artificial Neural Network. Processes 2023, 11, 3232. [Google Scholar] [CrossRef]
- Cancan, P.; Xiaodong, Z.; Zhiguang, G.; Ju, W.; Yan, G. Research on Cooperative Optimization of Multiphase Pump Impeller and Diffuser Based on Adaptive Refined Response Surface Method. Adv. Mech. Eng. 2022, 14, 16878140211072944. [Google Scholar] [CrossRef]
- Ma, C.; Yang, Z.; Jiao, K.; Liu, Z.; Du, Q. Multi-Objective Optimization of the Centrifugal Compressor Impeller in 130 KW PEMFC through Coupling SVM with NSGA -III Algorithms. Int. J. Green Energy 2021, 18, 1383–1395. [Google Scholar] [CrossRef]
- Patil, A.S.; Agarwal, A.K.; Sharma, K.; Trivedi, M.K. Time-Cost Trade-off Optimization Model for Retrofitting Planning Projects Using MOGA. Asian J. Civil. Eng. 2024, 25, 3823–3833. [Google Scholar] [CrossRef]
- Zolpakar, N.A.; Lodhi, S.S.; Pathak, S.; Sharma, M.A. Application of Multi-Objective Genetic Algorithm (MOGA) Optimization in Machining Processes. In Optimization of Manufacturing Processes; Gupta, K., Gupta, M.K., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 185–199. [Google Scholar] [CrossRef]
- Motamedi Zokae, H.; Tabor, G.; Moxey, D.; Page, M.; Stokes, M. Multi-Point Aerodynamic Optimization of a Backward-Curved Impeller Fan. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: College Station, TX, USA, 2024; Volume 87981, p. V006T10A008. [Google Scholar]
- Lee, S.-B. A Study on Suction Pump Impeller Form Optimization for Ballast Water Treatment System. J. Korean Soc. Ind. Converg. 2022, 25, 121–129. [Google Scholar] [CrossRef]
- Jaiswal, A.K.; Siddique, M.H.; Paul, A.R.; Samad, A. Surrogate-Based Design Optimization of a Centrifugal Pump Impeller. Eng. Optim. 2022, 54, 1395–1412. [Google Scholar] [CrossRef]
- Elghazi, K.; Ramchoun, H.; Masrour, T. Enhancing CNN Structure and Learning through NSGA-II-Based Multi-Objective Optimization. Evol. Syst. 2024, 15, 1503–1519. [Google Scholar] [CrossRef]
- Arya, A.K. A Comparison of the MOGA and NSGA-II Optimization Techniques to Reduce the Cost of a Biomass Supply Network. Mater. Today Proc. 2022, 57, 1553–1558. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y.; Yuan, J.; Meng, F.; Appiah, D.; Chen, J. Comprehensive Improvement of Mixed-Flow Pump Impeller Based on Multi-Objective Optimization. Processes 2020, 8, 905. [Google Scholar] [CrossRef]
- Dilberoglu, U.M.; Gharehpapagh, B.; Yaman, U.; Dolen, M. The Role of Additive Manufacturing in the Era of Industry 4.0. Procedia Manuf. 2017, 11, 545–554. [Google Scholar] [CrossRef]
- Wang, W.; Sun, J.; Liu, J.; Zhao, J.; Pei, J.; Wang, J. Introducing Non-Hierarchical RSM and MIGA for Performance Prediction and Optimization of a Centrifugal Pump under the Nominal Condition. Processes 2022, 10, 1529. [Google Scholar] [CrossRef]
- Nie, S.; Zhang, J.; Hong, R.; Ji, H.; Ji, H. Effect of Parameter Optimization on the Flow Characteristics of Venturi-Self-Excited Oscillation Mixer Based on Response Surface Model and Multi-Island Genetic Algorithm. Phys. Fluids 2024, 36, 053308. [Google Scholar] [CrossRef]
- Xu, Z.; Kong, F.; Zhang, K.; Zhu, H.; Wang, J.; Qiu, N. Optimization of the Impeller for Hydraulic Performance Improvement of a High-Speed Magnetic Drive Pump. Adv. Mech. Eng. 2022, 14, 16878132221104576. [Google Scholar] [CrossRef]
- Almasi, S.; Ghorani, M.M.; Haghighi, M.H.S.; Mirghavami, S.M.; Riasi, A. Optimization of a Vacuum Cleaner Fan Suction and Shaft Power Using Kriging Surrogate Model and MIGA. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 236, 519–537. [Google Scholar] [CrossRef]
- Santana-Cabrera, J.; Monzón-Verona, J.M.; Santana-Martín, F.J.; García-Alonso, S.; Montiel-Nelson, J.A. Optimization of the Dimensionless Model of an Electrostatic Microswitch Based on AMGA Algorithm. In Advances in Evolutionary and Deterministic Methods for Design, Optimization and Control in Engineering and Sciences; Springer: Cham, Switzerland, 2015; pp. 501–509. [Google Scholar]
- He, Y.; Sun, J.; Song, P.; Wang, X.; Xu, D. Development of a Multi-Objective Preliminary Design Optimization Approach for Axial Flow Compressors. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: College Station, TX, USA, 2018; Volume 51012, p. V02CT42A030. [Google Scholar]
- Yang, Z.; Yan, J.; Chen, J.; Lu, Q.; Yue, Q. Multi-Objective Shape Optimization Design for Liquefied Natural Gas Cryogenic Helical Corrugated Steel Pipe. J. Offshore Mech. Arct. Eng. 2017, 139, 051703. [Google Scholar] [CrossRef]
- Ding, Y.; Li, L. Optimization Method for Digital Twin Manufacturing System Based on NSGA-II. Int. J. Adv. Comput. Sci. Appl. 2024, 15. [Google Scholar] [CrossRef]
- Saundefinedlican, E.; Afacan, E. MOEA/D vs. NSGA-II: A Comprehensive Comparison for Multi/Many Objective Analog/RF Circuit Optimization through a Generic Benchmark. ACM Trans. Des. Autom. Electron. Syst. 2023, 29, 1–23. [Google Scholar] [CrossRef]
- Hassanlouei, R.N.; Jahangiri, M.; Alsultany, F.H.; Salavati-Niasari, M. An Experimental Study on the Agitating Efficiency and Power Consumption for Viscoelastic-Based Nanofluids: Elasticity, Impeller Effects, and Artificial Neural Network Approach. Case Stud. Therm. Eng. 2025, 68, 105941. [Google Scholar] [CrossRef]
- Singh, J.; Singh, S. Neural Network Prediction of Slurry Erosion of Heavy-Duty Pump Impeller/Casing Materials 18Cr-8Ni, 16Cr-10Ni-2Mo, Super Duplex 24Cr-6Ni-3Mo-N, and Grey Cast Iron. Wear 2021, 476, 203741. [Google Scholar] [CrossRef]
- Jinlong, W.; Wenjie, P.; Yongjie, B.; Yuxing, Y.; Chen, C. VHCF Evaluation with BP Neural Network for Centrifugal Impeller Material Affected by Internal Inclusion and GBF Region. Eng Fail Anal 2022, 136, 106193. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Fei, L.; Feng, Z.; Gao, J.; Yan, W.; Zhao, S. Operational Performance Estimation of Vehicle Electric Coolant Pump Based on the ISSA-BP Neural Network. Energy 2023, 268, 126701. [Google Scholar] [CrossRef]
- Yi, X.; Wang, Z.; Liu, S.; Hou, X.; Tang, Q. An Accelerated Degradation Durability Evaluation Model for the Turbine Impeller of a Turbine Based on a Genetic Algorithms Back-Propagation Neural Network. Appl. Sci. 2022, 12, 9302. [Google Scholar] [CrossRef]
- Wang, X.D.; Hirsch, C.; Kang, S.; Lacor, C. Multi-Objective Optimization of Turbomachinery Using Improved NSGA-II and Approximation Model. Comput. Methods Appl. Mech. Eng. 2011, 200, 883–895. [Google Scholar] [CrossRef]
- Chang, K.; Park, S.H. Random Forest-Based Multi-Faults Classification Modeling and Analysis for Intelligent Centrifugal Pump System. J. Mech. Sci. Technol. 2024, 38, 11–20. [Google Scholar] [CrossRef]
- Rahimzadeh, A.; Ranjbarrad, S.; Ein-Mozaffari, F.; Lohi, A. Application of Machine Learning Models in Coaxial Bioreactors: Classification and Torque Prediction. ChemEngineering 2024, 8, 42. [Google Scholar] [CrossRef]
- Xu, B.; Deng, J.; Liu, X.; Chang, A.; Chen, J.; Zhang, D. A Review on Optimal Design of Fluid Machinery Using Machine Learning Techniques. J. Mar. Sci. Eng. 2023, 11, 941. [Google Scholar] [CrossRef]
- Huang, R.; Ni, J.; Qiao, P.; Wang, Q.; Shi, X.; Yin, Q. An Explainable Prediction Model for Aerodynamic Noise of an Engine Turbocharger Compressor Using an Ensemble Learning and Shapley Additive Explanations Approach. Sustainability 2023, 15, 3405. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, Z.; Lu, X.; Duan, P.; Zhu, J. Aerodynamic Robustness Optimization of Aeroengine Fan Performance Based on an Interpretable Dynamic Machine Learning Method. Reliab. Eng. Syst. Saf. 2025, 254, 110654. [Google Scholar] [CrossRef]
- Sha, Y.; Faber, J.; Gou, S.; Liu, B.; Li, W.; Schramm, S.; Stoecker, H.; Steckenreiter, T.; Vnucec, D.; Wetzstein, N.; et al. An Acoustic Signal Cavitation Detection Framework Based on XGBoost with Adaptive Selection Feature Engineering. Measurement 2022, 192, 110897. [Google Scholar] [CrossRef]
- Pan, J.; Jing, B.; Jiao, X.; Wang, S. Analysis and Application of Grey Wolf Optimizer-Long Short-Term Memory. IEEE Access 2020, 8, 121460–121468. [Google Scholar] [CrossRef]
- Jian, D.; Jinling, L.; Wuke, L.; Wei, W.; Gaigai, A. An Improved Grey Wolf Optimizer (IGWO) Algorithm for Optimization of Centrifugal Pump with Guide Vane. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2024; Volume 2854, p. 012061. [Google Scholar]
- Jing, T.; Sun, H.; Cheng, J.; Zhou, L. Optimization of a Screw Centrifugal Blood Pump Based on Random Forest and Multi-Objective Gray Wolf Optimization Algorithm. Micromachines 2023, 14, 406. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, T.; Zhang, D.; Xie, Y. Dual-Convolutional Neural Network Based Aerodynamic Prediction and Multi-Objective Optimization of a Compact Turbine Rotor. Aerosp. Sci. Technol. 2021, 116, 106869. [Google Scholar] [CrossRef]
- Moradihaji, K.; Ghassemi, M.; Pourbagian, M. Off-Design Performance Analysis of a Radial Fan Using Experimental, Computational, and Artificial Intelligence Approaches. Eur. J. Mech.-B/Fluids 2024, 104, 150–172. [Google Scholar] [CrossRef]
- Li, J.; Liu, T.; Wang, Y.; Xie, Y. Integrated Graph Deep Learning Framework for Flow Field Reconstruction and Performance Prediction of Turbomachinery. Energy 2022, 254, 124440. [Google Scholar] [CrossRef]
- Cui, H.; Li, Z.; Sun, B.; Fan, T.; Li, Y.; Luo, L.; Zhang, Y.; Wang, J. A New Ice Quality Prediction Method of Wind Turbine Impeller Based on the Deep Neural Network. Energies 2022, 15, 8454. [Google Scholar] [CrossRef]
- Guo, H.; Yu, X. A Survey on Blockchain Technology and Its Security. Blockchain Res. Appl. 2022, 3, 100067. [Google Scholar] [CrossRef]
- Javed, A.; Pecnik, R.; van Buijtenen, J.P. Optimization of a Centrifugal Compressor Impeller for Robustness to Manufacturing Uncertainties. J. Eng. Gas. Turbine Power 2016, 138, 112101. [Google Scholar] [CrossRef]
- Li, J.; Liu, T.; Zhu, G.; Li, Y.; Xie, Y. Uncertainty Quantification and Aerodynamic Robust Optimization of Turbomachinery Based on Graph Learning Methods. Energy 2023, 273, 127289. [Google Scholar] [CrossRef]
- Peng, G.; Ma, L.; Hong, S.; Ji, G.; Chang, H. Optimization Design and Internal Flow Characteristics Analysis Based on Latin Hypercube Sampling Method. Arab. J. Sci. Eng. 2025, 50, 2715–2754. [Google Scholar] [CrossRef]
- Ayremlouzadeh, H.; Jafarmadar, S.; Niaki, S.R.A. Investigation on the Effect of Impeller Design Parameters on Performance of a Low Specific Speed Centrifugal Pump Using Taguchi Optimization Method. Int. J. Fluid Power 2022, 161–182. [Google Scholar] [CrossRef]
- Satjaritanun, P.; Regalbuto, J.R.; Regalbuto, J.A.; Tippayawong, N.; Shimpalee, S. Mixing Optimization with Inward Flow Configuration Contra-Rotating Impeller, Baffle-Free Tank. Alex. Eng. J. 2021, 60, 3759–3779. [Google Scholar] [CrossRef]
- Ju, Y.; Liu, Y.; Jiang, W.; Zhang, C. Aerodynamic Analysis and Design Optimization of a Centrifugal Compressor Impeller Considering Realistic Manufacturing Uncertainties. Aerosp. Sci. Technol. 2021, 115, 106787. [Google Scholar] [CrossRef]
- Jamimoghaddam, M.; Sadighi, A.; Araste, Z. ESA-Based Anomaly Detection of a Centrifugal Pump Using Self-Organizing Map. In Proceedings of the 2020 6th Iranian Conference on Signal Processing and Intelligent Systems (ICSPIS), Mashhad, Iran, 23–24 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Jiaqi, L.U.O.; Zeshuai, C.; Zheng, Y. A Gradient-Based Method Assisted by Surrogate Model for Robust Optimization of Turbomachinery Blades. Chin. J. Aeronaut. 2022, 35, 1–7. [Google Scholar]
- Li, X.; Zhao, Y.; Liu, Z. A Novel Global Optimization Algorithm and Data-Mining Methods for Turbomachinery Design. Struct. Multidiscip. Optim. 2019, 60, 581–612. [Google Scholar] [CrossRef]
- Guo, T.; Wang, W.; Cao, L.; Xing, J. Experimental and Numerical Study on Erosive Wear in a Dredge Pump Impeller. J. Phys. Conf. Ser. 2024, 2752, 12136. [Google Scholar] [CrossRef]
- Yang, X.; Xi, T.; Qin, Y.; Zhang, H.; Wang, Y. Computational Fluid Dynamics–Discrete Phase Method Simulations in Process Engineering: A Review of Recent Progress. Appl. Sci. 2024, 14, 3856. [Google Scholar] [CrossRef]
- Roos Launchbury, D.; Casartelli, E.; Mangani, L. Lattice Boltzmann Simulation of the ERCOFTAC Pump Impeller. IOP Conf. Ser. Earth Environ. Sci. 2022, 1079, 012074. [Google Scholar] [CrossRef]
- Sá, L.F.N.; Romero, J.S.; Horikawa, O.; Silva, E.C.N. Topology Optimization Applied to the Development of Small Scale Pump. Struct. Multidiscip. Optim. 2018, 57, 2045–2059. [Google Scholar] [CrossRef]
- Castro, M.T.; Ocon, J.D. Novel Designs of Blade Mixer Impellers from the Discrete Element Method and Topology Optimization. Chem. Eng. J. 2024, 490, 151863. [Google Scholar] [CrossRef]
- Cheng, H.; Li, Z.; Duan, P.; Lu, X.; Zhao, S.; Zhang, Y. Robust Optimization and Uncertainty Quantification of a Micro Axial Compressor for Unmanned Aerial Vehicles. Appl. Energy 2023, 352, 121972. [Google Scholar] [CrossRef]
- Guo, Z.; Song, L.; Zhou, Z.; Li, J.; Feng, Z. Multi-Objective Aerodynamic Optimization Design and Data Mining of a High Pressure Ratio Centrifugal Impeller. J. Eng. Gas Turbine Power 2015, 137, 092602. [Google Scholar] [CrossRef]
- Li, G.; Ding, X.; Wu, Y.; Wang, S.; Li, D.; Yu, W.; Wang, X.; Zhu, Y.; Guo, Y. Liquid-Vapor Two-Phase Flow in Centrifugal Pump: Cavitation, Mass Transfer, and Impeller Structure Optimization. Vacuum 2022, 201, 111102. [Google Scholar] [CrossRef]
- Zirak, N.; Benfriha, K.; Shakeri, Z.; Shirinbayan, M.; Fitoussi, J.; Tcharkhtchi, A. Interlayer Bonding Improvement and Optimization of Printing Parameters of FFF Polyphenylene Sulfide Parts Using GRA Method. Prog. Addit. Manuf. 2024, 9, 505–516. [Google Scholar] [CrossRef]
- Arici, E.; Tuna, M.C.; Aytac, A.; Kelestemur, G.T. Multi-Objective Optimization of a Pond Aeration System Using Taguchi-Based Gray Relational Analysis. Aquac. Int. 2024, 33, 50. [Google Scholar] [CrossRef]
- Prakash, K.B.; Amarkarthik, A.; Ravikumar, M.; Manoj Kumar, P.; Jegadheeswaran, S. Optimizing Performance Characteristics of Blower for Combustion Process Using Taguchi Based Grey Relational Analysis. In Advances in Materials Research; Kumaresan, G., Shanmugam, N.S., Dhinakaran, V., Eds.; Springer Nature: Singapore, 2021; pp. 155–163. [Google Scholar]
- Sinagra, M.; Picone, C.; Aricò, C.; Pantano, A.; Tucciarelli, T.; Hannachi, M.; Driss, Z. Impeller Optimization in Crossflow Hydraulic Turbines. Water 2021, 13, 313. [Google Scholar] [CrossRef]
- Song, X.; Li, Y.; Huang, R.; Luo, X. Impeller Optimization Using a Machine Learning-Based Algorithm with Dynamic Sampling Method and Flow Analysis for an Axial Flow Pump. J. Phys. Conf. Ser. 2024, 2707, 012154. [Google Scholar] [CrossRef]
- Wu, Y.; Tao, R.; Zhu, D.; Yao, Z.; Xiao, R. A Machine-Learning Approach to Predicting the Energy Conversion Performance of Centrifugal Pump Impeller Influenced by Blade Profile. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2021, 235, 7363–7384. [Google Scholar] [CrossRef]
- Serin, G.; Ozbayoglu, M.; Unver, H.O. Integrated Energy-Efficient Machining of Rotary Impellers and Multi-Objective Optimization. Mater. Manuf. Process. 2020, 35, 478–490. [Google Scholar] [CrossRef]
- Ji, C.; Wang, Z.; Xi, G. Adaptive Batch Sampling Strategy for the Hundreds-Dimensional Aerodynamic Optimization of the Centrifugal Impeller. J. Turbomach. 2024, 146, 091003. [Google Scholar] [CrossRef]
- Iyer, S.; Deshmukh, S.M.; Tapre, R.W. Enhancing Impeller Design Parameters for Optimal Pump Efficiency and Performance in Supercritical Thermal Power Projects. Energy Technol. 2025, 2500022. [Google Scholar] [CrossRef]
- Chandrasekaran, M.; Santhanam, V.; Venkateshwaran, N. Impeller Design and CFD Analysis of Fluid Flow in Rotodynamic Pumps. Mater. Today Proc. 2021, 37, 2153–2157. [Google Scholar] [CrossRef]
- Benchikh Le Hocine, A.E.; Poncet, S.; Fellouah, H. Optimization of a Double-Intake Squirrel Cage Fan Using OpenFoam and Metamodels. Int. J. Heat Fluid Flow 2023, 101, 109129. [Google Scholar] [CrossRef]
- Li, M.; Wang, L. Characterization of the Flow through a Centrifugal Pump under Different Inflow Conditions Based on OpenFOAM and Sparsity-Promoting Dynamic Mode Decomposition. Phys. Fluids 2024, 36, 075189. [Google Scholar] [CrossRef]
- Remache, A.; Pérez-Sánchez, M.; Hidalgo, V.H.; Ramos, H.M.; Sánchez-Romero, F.-J. Towards Sustainability in Hydraulic Machinery Manufacturing by 3D Printing. Processes 2024, 12, 2664. [Google Scholar] [CrossRef]
- Qian, B.; Wu, P.; Huang, B.; Zhang, K.; Li, S.; Wu, D. Optimization of a Centrifugal Impeller on Blade Thickness Distribution to Reduce Hydro-Induced Vibration. J. Fluids Eng. 2020, 142, 021202. [Google Scholar] [CrossRef]
- Kim, B.; Siddique, M.H.; Samad, A.; Hu, G.; Lee, D.-E. Optimization of Centrifugal Pump Impeller for Pumping Viscous Fluids Using Direct Design Optimization Technique. Machines 2022, 10, 774. [Google Scholar] [CrossRef]

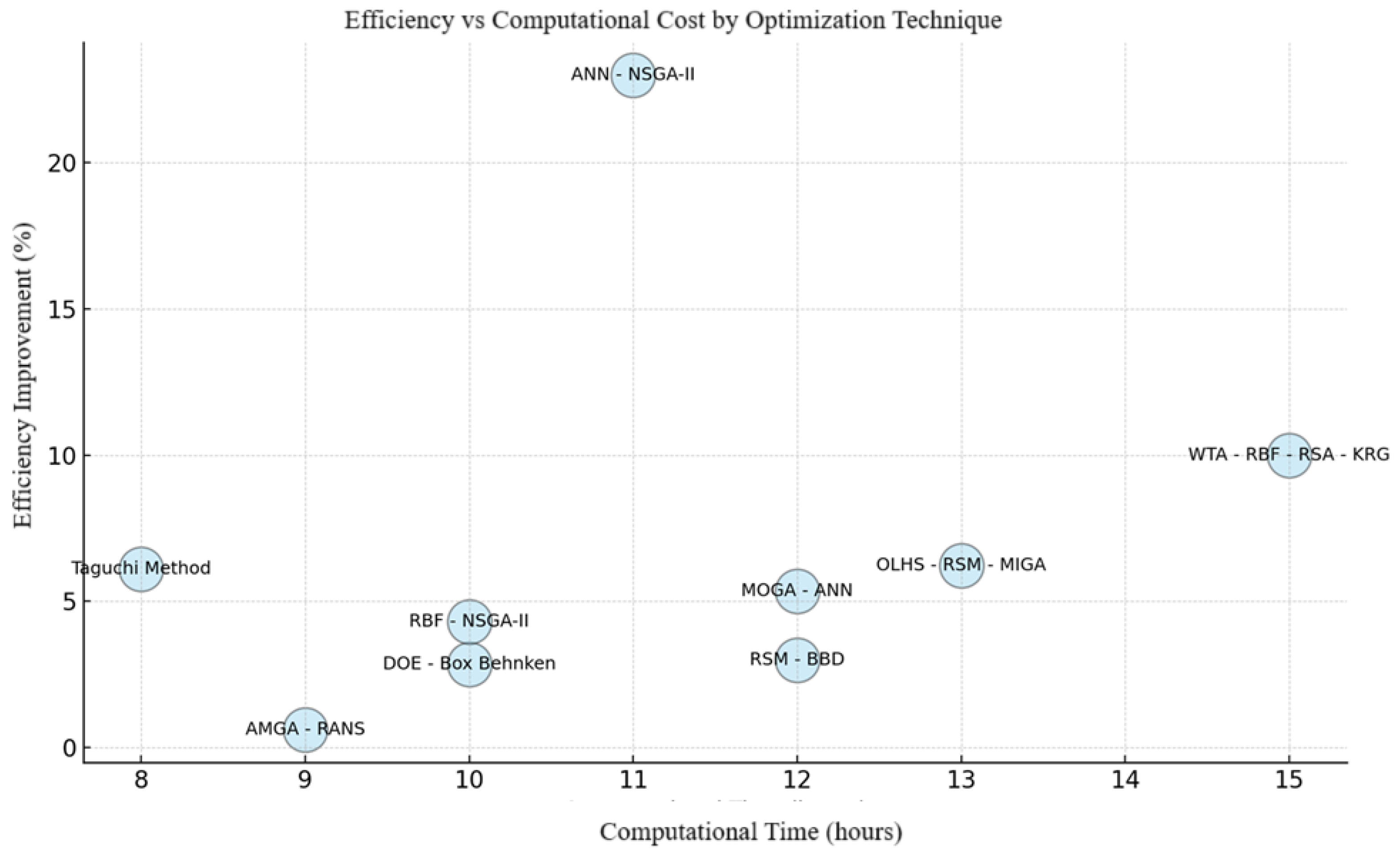


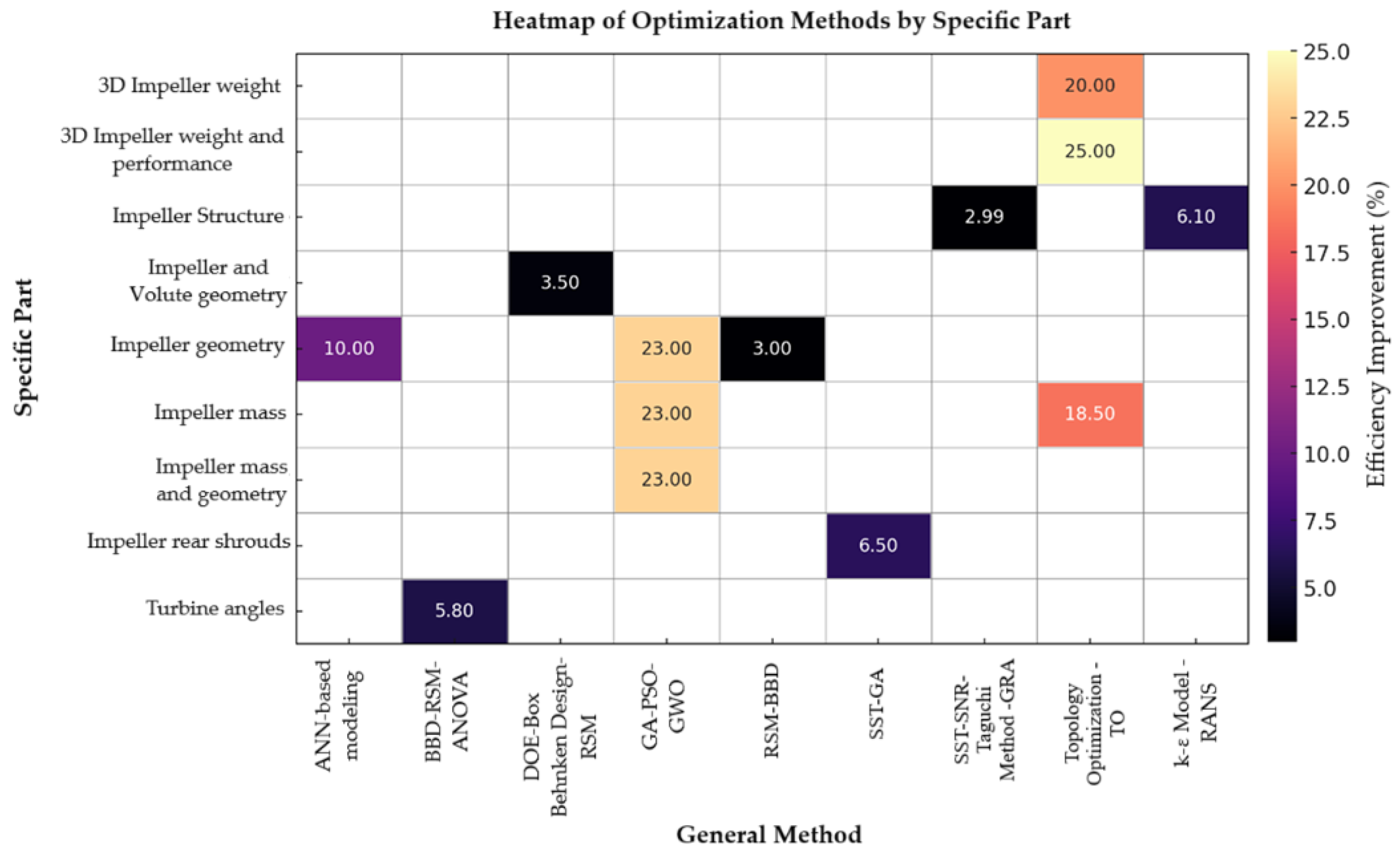

| Category | Study | Metric Improvement (%) | Optimization Approach | Reference |
|---|---|---|---|---|
| Centrifugal Compressor Optimization | Multi-objective optimization of impellers | Structural and aerodynamic optimization | CFD & RSM | [11] |
| Design of experiment (doe) technique | Efficiency +3%, pressure ratio +11% | Experimental & Statistical | [14] | |
| Meridional profile optimization | Up to +3% efficiency at high flow rates | Geometry-Based Optimization | [12] | |
| Robust optimization under uncertainties | Pressure ratio +9.3%, efficiency +6.7% | Uncertainty Quantification | [21] | |
| Axial & Mixed Flow Pumps | Multi-disciplinary axial-flow impeller design | Blade mass −10.47%, efficiency +0.61% | Approximation Model | [6] |
| Mixed-flow pump optimization | Efficiency +6.47% (1.2QDES), +3.68% (QDES) | Inverse Design Method | [22] | |
| Turbopump impeller structure | Pressurization coefficient +2.5% | Response Surface Method (RSM) | [23] | |
| Energy Efficiency & Performance Enhancement | Optimization in hydrogen fuel cell compressors | Power consumption −2.99%, isentropic efficiency +2.16% | Multi-Objective Genetic Algorithm | [24] |
| Motor cooling fan optimization | Efficiency +8%, flow rate +18% | CFD & MOGA | [25] | |
| Mixing impeller optimization | Energy consumption −26.71% | Fluid-Structure Interaction | [26] | |
| Machine Learning & AI-Driven Optimization | Ml-based impeller performance prediction | Prediction in <1 s | Machine Learning | [15] |
| Fatigue reliability modeling | XGBoost model achieves R2 > 0.93 | AI & Surrogate Modeling | [27] | |
| Automated defect detection in impellers | High accuracy & efficiency | Deep Learning | [28] | |
| Additive Manufacturing & Topology Optimization | Impeller mass reduction | Mass −30% | Topology Optimization | [29] |
| Structural enhancement for stress reduction | Stress −25%, mass −20% | Topology & Additive Manufacturing | [30] | |
| Hybrid manufacturing constraints | Weight −18.5% | Additive & Design Constraints | [31] | |
| Hydraulic & Cavitation Performance | Cavitation-resistant impeller design | Performance +19.3% | Taguchi Optimization | [32] |
| Hydrodynamic optimization of axial-flow pumps | Head +21.03%, efficiency +3.097% | CFD & Diffuser Blade Design | [33] | |
| Aerodynamic & Structural Robustness | Aerodynamic robustness in compressors | Pressure ratio +70.1%, efficiency +18.7% (Maxσ) | Response Surface & Evolutionary Algorithms | [34] |
| Aeroelastic analysis of impeller blades | Explosion margin +4.31%, mass −23% | Modal Analysis | [35] | |
| Computational Fluid Dynamics (CFD) & Genetic Algorithms | Cfd-assisted impeller shape optimization | Efficiency +4.74%, head +7.69% | NUMECA & GA | [36] |
| Computational prediction of mixing efficiency | Efficiency +2.4% | Lattice Boltzmann Method | [37] | |
| Impeller shape impact on gas-liquid mixing | Axial gas distribution improved by 55% | Two-Phase CFD Simulation | [38] | |
| Noise & Vibration Reduction | Psychoacoustic-based impeller noise reduction | Noise intensity reduced, efficiency +4.3% | Sound Quality Optimization | [39] |
| Vibration intensity reduction in marine pumps | Lower vibration, efficiency improved | Multi-Condition Optimization | [40] | |
| Multi-Objective & Genetic Algorithm-Based Optimization | Optimization of centrifugal impellers using ga | Improved efficiency & operational stability | GA & CFD | [41] |
| Energy-saving impeller design | Efficiency +4.3% | MIGA-RBF Algorithm | [42] | |
| Structural & Manufacturing Advances | Integrated blade-disk optimization | Weight −65% | Structural Optimization | [13] |
| Erosion-resistant slurry pump design | Erosion rate density reduced | Discrete Phase Modeling | [43] | |
| Miscellaneous & Novel Approaches | Satellite pump impeller optimization | Efficiency +3.55%, head +7.9% | Space Application-Specific Design | [44] |
| High-efficiency submersible pump design | Efficiency +6.1%, head +3.5% | Taguchi Method | [40,45] | |
| Cfd-based centrifugal compressor optimization | Improved performance & stability | Computational Optimization | [41] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Remache, A.; Pérez-Sánchez, M.; Hidalgo, V.H.; Ramos, H.M. Hybrid Optimization Approaches for Impeller Design in Turbomachinery: Methods, Metrics, and Design Strategies. Water 2025, 17, 1976. https://doi.org/10.3390/w17131976
Remache A, Pérez-Sánchez M, Hidalgo VH, Ramos HM. Hybrid Optimization Approaches for Impeller Design in Turbomachinery: Methods, Metrics, and Design Strategies. Water. 2025; 17(13):1976. https://doi.org/10.3390/w17131976
Chicago/Turabian StyleRemache, Abel, Modesto Pérez-Sánchez, Víctor Hugo Hidalgo, and Helena M. Ramos. 2025. "Hybrid Optimization Approaches for Impeller Design in Turbomachinery: Methods, Metrics, and Design Strategies" Water 17, no. 13: 1976. https://doi.org/10.3390/w17131976
APA StyleRemache, A., Pérez-Sánchez, M., Hidalgo, V. H., & Ramos, H. M. (2025). Hybrid Optimization Approaches for Impeller Design in Turbomachinery: Methods, Metrics, and Design Strategies. Water, 17(13), 1976. https://doi.org/10.3390/w17131976









