Iterative Solver of the Wet-Bed Step Riemann Problem
Abstract
1. Introduction
2. Step Riemann Problem
3. Solution Methodology
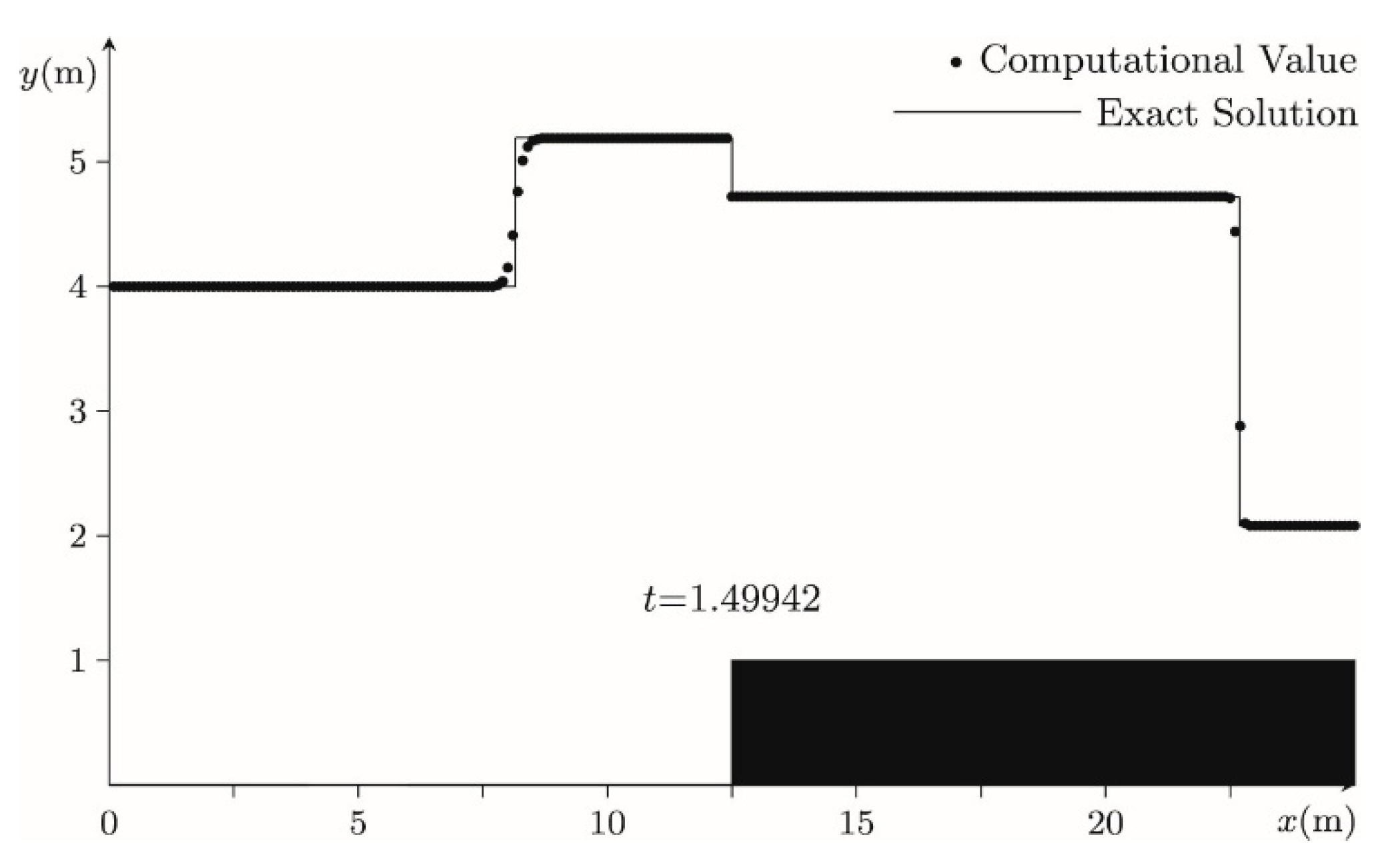
4. Results
4.1. Case 1: Rarefaction-Static Shock-Rarefaction
4.2. Case 2: Shock-Static Shock-Shock
4.3. Case 3: Rarefaction-Static Shock-Shock
4.4. Case 4: Comparison Between Present Algorithm and That of Xu et al. [38]
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abbott, M.B. Computational Hydraulics. In Elements of The Theory of Free Surface Flows; Pitman: London, UK, 1979; p. 326. [Google Scholar]
- Cunge, J.A.; Holly, F.M.; Verwey, A. Practical Aspects of Computational River Hydraulics; Pitman: London, UK, 1980; p. 416. [Google Scholar]
- Tan, W.Y. Shallow Water Hydrodynamics. In Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 1992; Volume 55, p. 433. [Google Scholar]
- Bender, J.; Öffner, P. Entropy-Conservative Discontinuous Galerkin Methods for the Shallow Water Equations with Uncertainty. Commun. Appl. Math. Comput. 2024, 6, 1978–2010. [Google Scholar] [CrossRef]
- Yao, S.; Kan, G.; Liu, C.; Tang, J.; Cheng, D.; Guo, J.; Jiang, H. A Hybrid Theory-Driven and Data-Driven Modeling Method for Solving the Shallow Water Equations. Water 2023, 15, 3140. [Google Scholar] [CrossRef]
- Li, L.; Wang, Z.; Zhao, Z.; Zhu, J. A new high order hybrid WENO scheme for hyperbolic conservation laws. Numer. Methods Partial. Differ. Equ. 2023, 39, 4347–4376. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, X.; Li, G.; Qian, S.; Niu, Q. A New Entropy Stable Finite Difference Scheme for Hyperbolic Systems of Conservation Laws. Mathematics 2023, 11, 2604. [Google Scholar] [CrossRef]
- Zahran, Y.H.; Abdalla, A.H. Central random choice methods for hyperbolic conservation laws. Ric. Di Mat. 2022, 73, 2091–2130. [Google Scholar] [CrossRef]
- Fu, L.; Hu, X.Y.; Adams, N.A. A family of high-order targeted ENO schemes for compressible-fluid simulations. J. Comput. Phys. 2016, 305, 333–359. [Google Scholar] [CrossRef]
- Liang, T.; Fu, L. A new type of non-polynomial based TENO scheme for hyperbolic conservation laws. J. Comput. Phys. 2023, 497, 112618. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, Z.-H.; Yan, C. Efficient ROUND schemes on non-uniform grids applied to discontinuous Galerkin schemes with Godunov-type finite volume sub-cell limiting. J. Comput. Phys. 2025, 522, 113575. [Google Scholar] [CrossRef]
- Leveque, R.J. Large Time Step Shock-Capturing Techniques for Scalar Conservation Laws. SIAM J. Numer. Anal. 1982, 19, 1091–1109. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P.; Brufau, P.; Burguete, J. Extension of an explicit finite volume method to large time steps (CFL>1): Application to shallow water flows. Int. J. Numer. Methods Fluids 2006, 50, 63–102. [Google Scholar] [CrossRef]
- Morales-Hernandez, M.; García-Navarro, P.; Murillo, J. A large time step 1D upwind explicit scheme (CFL> 1): Application to shallow water equations. J. Comput. Phys. 2012, 231, 6532–6557. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Hubbard, M.E.; García-Navarro, P. A 2D extension of a Large Time Step explicit scheme (CFL>1) for unsteady problems with wet/dry boundaries. J. Comput. Phys. 2014, 263, 303–327. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Lacasta, A.; Murillo, J.; García-Navarro, P. A Large Time Step explicit scheme (CFL>1) on unstructured grids for 2D conservation laws: Application to the homogeneous shallow water equations. Appl. Math. Model. 2017, 47, 294–317. [Google Scholar] [CrossRef]
- Xu, R.; Zhong, D.; Wu, B.; Fu, X.; Miao, R. A Large Time Step Godunov Scheme for Free-surface Shallow Water Equations. Chin. Sci. Bull. 2014, 59, 2534–2540. [Google Scholar] [CrossRef]
- Qian, Z.; Lee, C.-H. A class of large time step Godunov schemes for hyperbolic conservation laws and applications. J. Comput. Phys. 2011, 230, 7418–7440. [Google Scholar] [CrossRef]
- Dong, H.; Liu, F. Large time step wave adding scheme for systems of hyperbolic conservation laws. J. Comput. Phys. 2018, 374, 331–360. [Google Scholar] [CrossRef]
- Liu, F.; Dong, H. Second-order large time step wave adding scheme for hyperbolic conservation laws. J. Comput. Phys. 2020, 408, 109279. [Google Scholar] [CrossRef]
- Lindqvist, S.; Aursand, P.; Flåtten, T.; Solberg, A.A. Large Time Step TVD Schemes for Hyperbolic Conservation Laws. SIAM J. Numer. Anal. 2016, 54, 2775–2798. [Google Scholar] [CrossRef]
- Prebeg, M.; Flåtten, T.; Müller, B. Large Time Step Roe scheme for a common 1D two-fluid model. Appl. Math. Model. 2017, 44, 124–142. [Google Scholar] [CrossRef]
- Harten, A. On a Large Time-Step High Resolution scheme. Math. Comput. 1986, 46, 379–399. [Google Scholar] [CrossRef]
- Xu, R.; Borthwick, A.G.L.; Xu, B. Application of Large Time Step TVD High Order Scheme to Shallow Water Equations. Atmosphere 2022, 13, 1856. [Google Scholar] [CrossRef]
- Qian, Z.; Lee, C.-H. On large time step TVD scheme for hyperbolic conservation laws and its efficiency evaluation. J. Comput. Phys. 2012, 231, 7415–7430. [Google Scholar] [CrossRef]
- García-Navarro, P.; Cendón, E.V. On numerical treatment of the source terms in the shallow water equations. Comput. Fluids 2000, 29, 951–979. [Google Scholar] [CrossRef]
- Rogers, B.D.; Borthwick, A.G.; Taylor, P.H. Mathematical balancing of flux gradient and source terms prior to using Roe’s approximate Riemann solver. J. Comput. Phys. 2003, 192, 422–451. [Google Scholar] [CrossRef]
- Liang, Q.; Borthwick, A.G. Adaptive quadtree simulation of shallow flows with wet-dry fronts over complex topography. Comput. Fluids 2009, 38, 221–234. [Google Scholar] [CrossRef]
- Zhang, Z.; Duan, J.; Tang, H. High-order accurate well-balanced energy stable adaptive moving mesh finite difference schemes for the shallow water equations with non-flat bottom topography. J. Comput. Phys. 2023, 492, 112451. [Google Scholar] [CrossRef]
- Alcrudo, F.; Benkhaldounb, F. Exact solutions to the Riemann problem of the shallow water equations with a bottom step. Comput. Fluids 2001, 30, 643–671. [Google Scholar] [CrossRef]
- Bukreev, V.I.; Gusev, A.V.; Ostapenko, V.V. Breakdown of a discontinuity of the free fluid surface over a bottom step in a channel. Fluid Dyn. 2003, 38, 889–899. [Google Scholar] [CrossRef]
- Gallouët, T.; Hérard, J.-M.; Seguin, N. Some Approximate Godunov schemes to compute shallow-water equations with topography. Comput. Fluids 2003, 32, 479–513. [Google Scholar] [CrossRef]
- Chinnayya, A.; LeRoux, A.Y.; Seguin, N. A well-balanced numerical scheme for the approximation of the shallow-water equations with topography: The resonance phenomenon. Int. J. Finite Vol. 2004, 1, 1–33. [Google Scholar]
- Andrianov, N. Performance of numerical methods on the non-unique solution to the Riemann problem for the shallow water equations. Int. J. Num. Methods Fluids 2005, 47, 825–831. [Google Scholar] [CrossRef]
- Aleksyuk, A.I.; Belikov, V.V. The uniqueness of the exact solution of the Riemann problem for the shallow water equations with discontinuous bottom. J. Comput. Phys. 2019, 390, 232–248. [Google Scholar] [CrossRef]
- Aleksyuk, A.I.; Malakhov, M.A.; Belikov, V.V. The exact Riemann solver for the shallow water equations with a discontinuous bottom. J. Comput. Phys. 2022, 450, 110801. [Google Scholar] [CrossRef]
- Bernetti, R.; Titarev, V.; Toro, E. Exact solution of the Riemann problem for the shallow water equations with discontinuous bottom geometry. J. Comput. Phys. 2008, 227, 3212–3243. [Google Scholar] [CrossRef]
- Xu, R.; Borthwick, A.G.; Ma, H.; Xu, B. Godunov-type large time step scheme for shallow water equations with bed-slope source term. Comput. Fluids 2022, 233, 105222. [Google Scholar] [CrossRef]
- Rosatti, G.; Begnudelli, L. The Riemann Problem for the one-dimensional, free-surface Shallow Water Equations with a bed step: Theoretical analysis and numerical simulations. J. Comput. Phys. 2010, 229, 760–787. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. In A Practical Introduction, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Dold, A.; Eckmann, B. The Levenberg-Marquardt algorithm Implementation and theory. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Murillo, J.; García-Navarro, P. Weak solutions for partial differential equations with source terms: Application to the shallow water equations. J. Comput. Phys. 2010, 229, 4327–4368. [Google Scholar] [CrossRef]

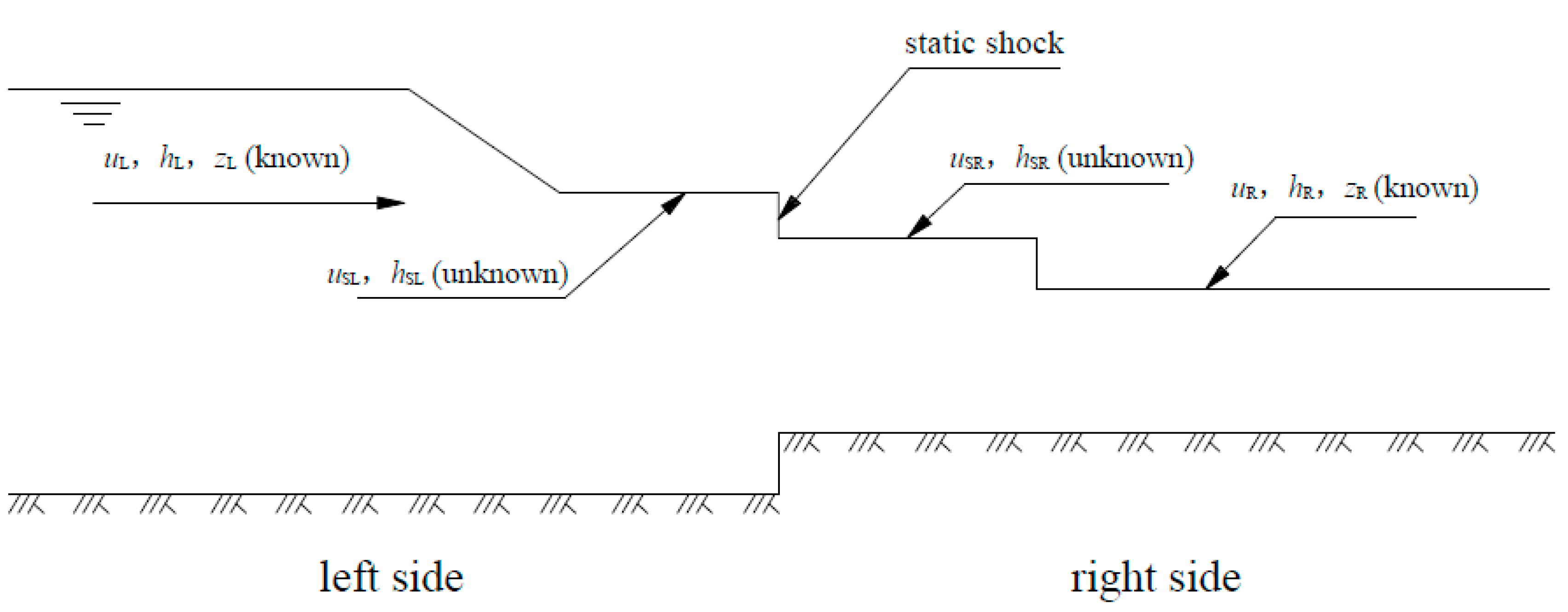


| Right-Interface-Left | Abbr. | Equations | |
|---|---|---|---|
| 1 | Rarefaction-static shock-shock | RBS | (2) (6) (7) (5) |
| 2 | Shock-static shock-shock | SBS | (3) (6) (7) (5) |
| 3 | Rarefaction-static shock-Rarefaction | RBR | (2) (6) (7) (4) |
| 4 | Shock-static shock-Rarefaction | SBR | (3) (6) (7) (4) |
| Left | Right | |||
|---|---|---|---|---|
| rarefaction | (9) | (11) | (12) | (14) |
| shock | (26) | (27) | (29) | (30) |
| Main equation | ||||
| h (m) | q (m2/s) | z (m) | |
|---|---|---|---|
| Left (12.5 > x ≥ 0 m) | 8.0 | −16.0 | 0 |
| Right (25 ≥ x > 12.5 m) | 5.0 | 35.852 | 1 |
| h (m) | q (m2/s) | z (m) | |
|---|---|---|---|
| Left (12.5 > x ≥ 0 m) | 4.0 | 19 | 0 |
| Right (25 ≥ x > 12.5 m) | 1.0838 | −2.3685 | 1 |
| h (m) | q (m2/s) | z (m) | |
|---|---|---|---|
| Left (12.5 > x ≥ 0 m) | 5.0 | 0 | 0 |
| Right (25 ≥ x > 12.5 m) | 1.0 | 0 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.; Borthwick, A.G.L. Iterative Solver of the Wet-Bed Step Riemann Problem. Water 2025, 17, 1994. https://doi.org/10.3390/w17131994
Xu R, Borthwick AGL. Iterative Solver of the Wet-Bed Step Riemann Problem. Water. 2025; 17(13):1994. https://doi.org/10.3390/w17131994
Chicago/Turabian StyleXu, Renyi, and Alistair G. L. Borthwick. 2025. "Iterative Solver of the Wet-Bed Step Riemann Problem" Water 17, no. 13: 1994. https://doi.org/10.3390/w17131994
APA StyleXu, R., & Borthwick, A. G. L. (2025). Iterative Solver of the Wet-Bed Step Riemann Problem. Water, 17(13), 1994. https://doi.org/10.3390/w17131994







