Abstract
This study employs an evolutionary game theory framework to analyze the interactive learning, imitation, and strategic evolution among multiple actors within China’s aquatic product traceability system. It focuses on four types of strategic interactions: between fishers and the government, fishers and consumers, fishers who adopt the traceability system and those who do not, and between consumers who purchase traceable aquatic products and those who do not. The evolutionarily stable strategies and equilibrium outcomes in each game depend on the net benefits obtained and the various costs borne by each party. Among these factors, transaction costs within the traceability system play a particularly critical role in shaping stakeholder behavior. The lower the transaction costs, the more likely stakeholders are to adopt strategies that support or enhance the functioning of the system. Therefore, reducing the operational and transaction costs of the traceability system should be a key policy focus for the government. This includes efforts in policy and regulatory development, platform and infrastructure construction, and the improvement of information exchange mechanisms to foster sustainable development in aquaculture.
1. Introduction
The aquatic product traceability system, as a critical institutional mechanism for enhancing food safety, increasing supply chain transparency, and fostering consumer trust, has garnered significant global attention in recent years [1]. In China, where aquatic products constitute a substantial component of daily dietary consumption—with an average daily intake of 48.0 g per person, accounting for approximately 40% of total animal protein intake—the quality and safety of these products are closely tied to public health and the sustainable development of the aquatic product market [2]. Nevertheless, the implementation of the traceability system faces substantial challenges, including the misalignment of interests among various stakeholders, the high operational costs, and persistent issues of information asymmetry. For example, small- and medium-scale fishers often face prohibitive upfront investments for equipment installation, such as digital sensors, electronic tags, and real-time data entry devices, which can exceed CNY 20,000–50,000 per unit depending on the species and scale [3]. In addition, recurring costs such as software subscription fees, staff training, and system maintenance further strain operational budgets. These cost burdens are particularly significant in regions where profit margins are already thin, discouraging voluntary adoption and weakening policy enforcement. As a result, the traceability system has not achieved the expected level of nationwide diffusion and effectiveness [4].
The interactive behaviors among multiple stakeholders play a crucial role in the operation of the system. The game relationship between fishers and the government determines the strength and effectiveness of the system implementation [5]. The interactions between fishers and consumers influence the market acceptance of traceable products. The behaviors of consumers further shape the social perception of the traceability system through network effects. Additionally, the imitation and learning behaviors within the fishers’ group have a profound impact on the overall operation of the traceability system. Therefore, from the perspective of multiple stakeholders, systematically studying the behavioral decision-making logic and evolutionary patterns of each actor in the operation of the traceability system is of significant theoretical and practical value in uncovering the operational mechanisms and optimizing policy design [6].
This paper, based on evolutionary game theory, constructs a multi-stakeholder game model to analyze the operation of China’s aquatic product traceability system. It explores four typical types of game behaviors and their evolutionarily stable strategies: the interactions between fishers and the government, fishers and consumers, between consumers, and within the fishers’ group. By examining the impact of the benefits and costs faced by each stakeholder on their strategic choices, this study reveals the critical role of transaction costs in the operation of the traceability system and offers policy recommendations for reducing these costs. The findings of this research not only enrich the application of evolutionary game theory in the field of food safety but also provide theoretical guidance and policy support for improving China’s aquatic product traceability system.
2. Literature Review
This section reviews relevant studies on the aquatic product traceability system by analyzing the existing literature in the following areas.
2.1. Aquatic Product Traceability System
The development of the system has closely followed the global rise in food safety awareness and has become a shared focus of governments, fishers, and consumers. While the construction of traceability systems varies across countries and regions, their development can generally be summarized into three main directions: policy-driven, technological innovation, and market practices.
Policy-driven initiatives serve as a foundational element in the development of the system. In recent years, the Chinese government has continuously introduced policies in the field of aquatic product traceability, aiming to promote the system’s widespread adoption by establishing nationwide traceability platforms. For instance, the “13th Five-Year National Food Safety Plan” issued by the State Council in 2017 explicitly called for the strengthening of the traceability system for aquatic product quality and safety [7]. Local governments have actively responded by implementing relevant local regulations and measures, promoting pilot projects and regional expansion of the traceability system [8]. However, the implementation of the traceability system still faces significant obstacles. In practice, inadequate regulatory enforcement, fragmented coordination between administrative departments, and the absence of unified technical standards and platforms have limited its effective rollout. These challenges contribute to substantial regional disparities in adoption and weaken the overall functionality of the system. Divergences in regional policy frameworks, regulatory enforcement intensity, and data governance practices have been widely recognized as key impediments to the coordination and integration of traceability systems across jurisdictions [9].
Technological innovation has played a significant role in advancing the development of aquatic product traceability systems, particularly through the application of emerging technologies such as the Internet of Things (IoT), big data, and blockchain [10]. These technologies provide crucial technical support for the real-time collection, storage, and transmission of traceability information [11]. IoT technology enables smart management throughout the entire production chain, from breeding and processing to transportation, ensuring the accuracy and timeliness of traceability data [12]. Blockchain technology, with its decentralized and tamper-resistant nature, ensures the transparency and security of traceability information. Particularly in international aquatic product trade, blockchain is seen as a key tool for enhancing product safety and market competitiveness [13]. Furthermore, some scholars highlight that the promotion of technological innovations requires improvements in the information technology level and management capabilities of fishers. Without sufficient investment in technology by fishers, the development of traceability systems will face significant bottlenecks [14].
From a market practice perspective, several successful cases have provided valuable experience for the promotion of the aquatic product traceability system. Shandong Province took the lead in constructing a fully traceable aquatic product quality and safety management platform using IoT and big data technologies, realizing full-chain monitoring from breeding to market. This platform not only improved product quality and safety but also enhanced consumer confidence, significantly boosting the market competitiveness of Shandong’s aquatic products [15]. Fujian Province has also built an export traceability system for aquatic products through multi-party collaboration. Notably, the establishment of the traceability system has helped increase the added value of products, especially when exporting to high-standard markets such as Japan and Europe [16]. These cases demonstrate that the effective combination of technological application and policy support can significantly promote the implementation of the system.
Despite significant achievements in the development of the aquatic product traceability system, several challenges remain. Firstly, the high cost of system construction poses a significant burden, particularly for small- and medium-sized fishers, who face substantial investment pressures related to technological equipment and management systems [17]. Secondly, the traceability systems across different regions suffer from inconsistencies in standards, with insufficient information sharing and interoperability, largely due to uneven enforcement capacity among local governments. Factors such as limited administrative resources, lack of technical expertise, and weak performance incentives contribute to inadequate policy implementation, thereby undermining the establishment of a nationwide unified traceability network [18]. Looking ahead, as global food safety standards continue to rise, the system is expected to evolve toward higher levels of standardization and intelligence. In particular, with the deeper integration of technologies such as blockchain and big data, the reliability and transparency of the system will be significantly enhanced.
2.2. Multi-Stakeholder Research on Aquatic Product Traceability System
The effective operation of the aquatic product traceability system is the result of coordinated interactions among multiple stakeholders [19]. The research in this field extends beyond the allocation of roles among the stakeholders, delving into their specific functions in information transmission and management, as well as the relationships and interactions between them [20]. In recent years, both domestic and international studies have become more refined, exploring in depth the roles and interactions of the government, fishers, consumers, and third-party organizations within the traceability system [21].
Firstly, the government’s role in the traceability system extends beyond policy and regulation formulation to include the establishment of technical standards and the construction of traceability platforms [22]. The government’s regulatory role is considered crucial for the smooth implementation of the traceability system. Some scholars argue that when promoting regional aquatic product traceability systems, the government often adopts a “government-led, fisherman-participation” model, aiming to improve the overall quality and safety level of the industry [23]. Furthermore, local government policy innovations, in alignment with central policies, have played a positive role in advancing the promotion of aquatic product traceability [24].
Secondly, as the primary implementers of the traceability system, fishers hold significant responsibility in information collection, management, and sharing [25]. Studies show that the transmission of information among fishers needs to be carried out through standardized interfaces and processes to ensure data integrity and consistency [26]. The integration of big data and blockchain technologies has greatly improved the transparency and security of information management, enhancing consumer trust in the traceability system [27]. Particularly among large-scale aquaculture fishers, the application of these advanced technologies not only optimizes production processes but also enables full-chain visual traceability [28,29].
Consumer participation is crucial for the sustainable development of the traceability system [30]. Research indicates that consumer trust and acceptance of the system directly affect market demand for traceable products [31]. Younger consumer groups, in particular, place greater emphasis on product transparency and safety and exhibit higher demand for traceability information [32,33]. Studies also show that consumers are willing to pay a premium for traceable products, providing market-driven incentives for fishers to adopt the traceability system [34].
Lastly, third-party certification agencies play a critical role in independently verifying traceability information, developing standardized systems, and promoting the integration of global traceability frameworks. Through technologies such as blockchain, these agencies further ensure the immutability and credibility of traceability data. International certification has been shown to enhance the export competitiveness of domestic aquatic products, complementing the domestic market and facilitating international market access [35,36,37]. The operations of these agencies are typically funded through service fees paid by producers or supply chain actors, with additional support in some cases from government subsidies or international cooperation programs. Regulatory oversight is generally provided by agricultural or market supervision authorities, which establish accreditation standards, conduct audits, and enforce compliance [38]. This combination of diversified funding and institutional oversight helps maintain the impartiality and accountability of third-party certification bodies within the traceability system [39].
3. Methodology
The main stakeholders involved in the operation of the aquatic product traceability system are the government, fishers, and consumers. The behaviors of these stakeholders in engaging with the traceability system are characterized by incomplete information and bounded rationality, which makes evolutionary game theory a suitable tool for analysis in such contexts. Evolutionary game theory integrates insights from classical game theory and biological evolution, with participants assumed to have bounded rationality. Using dynamic analysis, it incorporates various factors that influence participants’ behavior into the model. The aim is to examine the evolutionary trends of collective behavior from a system dynamics perspective. This approach studies how participants continuously learn, experiment, and search for optimal strategies in the game, ultimately identifying their evolutionary stable strategies (ESS) and achieving equilibrium in the game.
In the following sections, four evolutionary game models will be constructed to analyze the equilibrium of the game among the stakeholders involved in the operation of the system and the determining factors behind it. The next steps for government policy will be inferred, and corresponding policy recommendations will be proposed.
To facilitate understanding of the mathematical expressions in the following models, a summary of the main variables and parameters used in all four evolutionary game models is provided in Table 1.

Table 1.
Summary of variables and parameters in the evolutionary game models.
3.1. Evolutionary Game Analysis of Fishers’ and Government’s Behavior in the Aquatic Product Traceability System Operation
The evolutionary game model considers fishers (referring to those operating aquatic product traceability systems) and the government as the behavioral agents. The objective is to analyze the policy choices and response strategies of the government and fishers within the system, as well as the determining factors influencing these choices. The strategy space for fishers consists of (operating, not operating) the traceability system, while the government’s strategy space consists of (promoting, not promoting) the system. Suppose the probability that fishers choose to operate the traceability system is x (0 ≤ x ≤ 1), and the probability of not operating is 1 − x (0 ≤ x ≤ 1). Similarly, the probability that the government chooses to support the construction of the traceability system is y (0 ≤ y ≤ 1), and the probability of not supporting it is 1 − y (0 ≤ y ≤ 1). If the government promotes the construction of the traceability system but the fishers choose not to operate it, the fishers cannot obtain the additional benefits provided by the system, resulting in a net revenue of 0 for them. The government’s revenue is also 0, but it incurs a construction cost C, leading to a net loss of −−C for the government. When the government supports the construction of the traceability system and the fishers choose to operate it, the revenue per kilogram of sales is p, and if the sales volume is k, the total revenue is pk. In this case, the government gains a social benefit E, but it also incurs costs related to policy formulation, legal regulations, and platform construction, denoted as M. Thus, the government’s net revenue is M − C. If the government does not promote the operation of the traceability system, but fishers choose to operate it, they must bear the costs of equipment upgrades and online data entry, which are denoted as I. Since there is no government support through incentives or platform facilitation, the revenue obtained by fishers will be lower than when the government actively promotes the system. The fishers’ revenue in this case can be expressed as jpk − I, where 0 ≤ j ≤ 1. When the government does not promote the construction of the traceability system, it does not incur any costs. However, if fishers still choose to operate the system, their actions generate social benefits for the government, such as improved food safety governance, enhanced public health outcomes, and strengthened international trade credibility. Since there are no incentive policies or supportive measures, the sales volume in this scenario is expected to be lower than when the government actively promotes the system. Consequently, the government’s social benefits will also be lower, represented as a proportion of the government’s benefits under the promotion scenario, denoted as r(M − C), where 0 ≤ r ≤ 1. To correspond with the fishers’ revenue, this can also be expressed as lM − C, where 0 ≤ l ≤ 1. If neither the government promotes the system nor the fishers operate it, both parties receive a revenue of 0. In this paper, unless otherwise specified, all parameters representing benefits and costs are assumed to be positive. Based on the above assumptions, the payoff matrix for the evolutionary game between fishers and the government is constructed, as shown in Table 2.

Table 2.
Payoff matrix for the evolutionary game between fishers and the government.
To facilitate calculations, Table 2 is simplified into Table 3, with the corresponding relationships as shown below:

Table 3.
Simplified payoff matrix for the evolutionary game between fishers and the government.
From Table 3, the expected revenue for fishers choosing to operate the traceability system is as follows:
The revenue for choosing not to operate the traceability system is as follows:
Therefore, the average revenue for fishers is as follows:
The replicator dynamic equation for fishers choosing to operate the traceability system is as follows:
Similarly, the expected benefit for the government choosing to support the traceability system construction is as follows:
The expected benefit for the government choosing not to support the traceability system construction is as follows:
The average benefit for the government is as follows:
The dynamic equation for the government’s strategy of supporting the traceability system is as follows:
Let F(x) = 0 and F(y) = 0 hold simultaneously, the stable points of x are ,, ; the stable points of y are , , .
The local equilibrium points are derived as: (0,0), (0,1), (1,0), (1,1), and ().
Next, we verify the stability of the above local equilibrium points by constructing the Jacobian matrix:
The determinant and trace of the Jacobian matrix are as follows:
According to Friedman’s theory [21], if the following conditions hold ,, then the point (, ) is a stable equilibrium point, corresponding to the equilibrium strategy. Otherwise, it is not an equilibrium strategy. The stability of equilibrium points is summarized in Table 4.

Table 4.
Stability of local equilibrium points.
For ease of calculation, Table 4 has been simplified as Table 5, and the corresponding results are shown in Table 5, For the point (0, 0), when I > jpk, det.J > 0; when I > jpk − C, tr.J < 0. Therefore, if I > jpk, (0, 0) is a stable point; if I < jpk − C, (0, 0) is not a stable point. For the point (0, 1), when I < pk, det.J > 0; when I > pk + C, tr.J < 0. Since pk + C > pk, the equilibrium condition cannot be satisfied, meaning (0, 1) is not a stable point. For the point (1, 0), when I > jpk, det.J > 0; when I < jpk − M + lM, tr.J < 0. However, since jpk − M + lM < jpk, the equilibrium condition cannot be satisfied, so (1, 0) is not a stable point. For the point (1, 1), when I < pl, det.J > 0; when I < pk + M − Ml, tr.J < 0. Therefore, if I < pk, (1, 1) is a stable point; if I > pk + M − Ml, (1, 1) is not a stable point. For the point (x3, y3), tr.J = 0, meaning (x3, y3) is a saddle point or a center point.

Table 5.
Stability of local equilibrium points in the fisher-government game.
In conclusion, when I > jpk, the final equilibrium of the game between fishers and the government is (not operating, not promoting); while when I < pk, the final equilibrium of the game between fishers and the government is (operating, promoting). It can be seen that the construction cost I of the fishery traceability system and the sales revenue pk of fishers have a significant impact on the equilibrium of the game. As long as the construction cost for fishers to operate the traceability system is low enough, and the sales revenue is high enough, the equilibrium of (operating, promoting) will appear, and the equilibrium of (not operating, not promoting) will not appear. In this case, the government will choose to promote the flow, and the fishers will choose to operate the traceability system. Therefore, when fishers and the government cooperate to support the traceability system, both parties’ benefits will be optimal. Reducing the construction costs for both fishers and the government, and increasing fishers’ revenue (mainly through increased sales volume), will be key directions for the future widespread implementation of the traceability system in the aquatic products industry and its transformation.
Figure 1 illustrates the evolutionary game equilibrium analysis between government support and fishers’ participation in the traceability system. As government support increases, fishers’ participation probability also rises, indicating the significant impact of policy support on participation. The stable equilibrium points (such as (0, 0) and (1, 1)) represent the potential steady-state strategies between the government and fishers. The dashed lines highlight key equilibrium conditions, revealing critical points at which policy interventions may trigger strategic changes. Overall, the chart suggests that effective government policies can encourage fishers’ participation, leading to a stable and sustainable system.
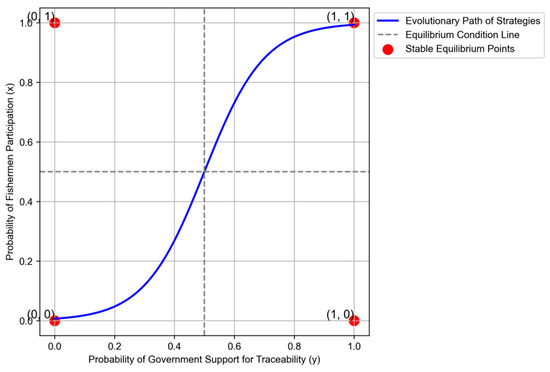
Figure 1.
Government–fishers’ game equilibrium analysis.
3.2. Evolutionary Game Analysis of Fishers and Consumers in the Operation of the Aquatic Product Traceability System
This evolutionary game model involves two key participants: fishers and aquatic product consumers, and aims to analyze the strategic interactions between them in the aquatic product sales process. The strategy space of fishers is (traceable, non-traceable), and the strategy space of consumers is (buy traceable, do not buy traceable). The probability that a consumer chooses to buy traceable aquatic products is x(0 ≤ x ≤ 1), and the probability of not buying traceable aquatic products is 1 − x. The probability that a fisherman chooses to sell traceable aquatic products is y(0 ≤ y ≤ 1), and the probability of selling non-traceable aquatic products is 1 − y. The value of x is influenced by factors such as consumers’ concerns about food safety, their perception of product quality, and their willingness to pay a premium for traceability, all of which shape their expected utility from purchasing traceable products [40].
The fisherman’s revenue depends on the weight of the aquatic products k and the per kilogram sales revenue k, so the total revenue is kr. At the same time, there are transaction costs associated with selling aquatic products, such as transportation and storage costs, which are denoted as d. The consumer’s revenue depends on the weight m of the purchased aquatic products and their actual value t, so the total revenue is kv. The consumer’s costs include the aquatic product fee paid to the fisherman, kr, and other transaction costs such as transportation fees and time costs, which are represented as d.
When both the fisherman and the consumer cooperate by choosing to sell and buy traceable aquatic products, the traceable product transaction is completed. In this case, the fisherman’s net income is kr − t, and the consumer’s net benefit is kv − kr − d. If one party adopts a non-cooperative strategy, meaning one chooses to sell or buy traceable products while the other does not, the traceable product transaction cannot be completed. The non-cooperative party gains neither revenue nor incurs any costs, so their net benefit is 0. On the other hand, the party that attempts to buy or sell traceable products but cannot complete the transaction will incur storage fees, transportation costs, etc., but will not earn any revenue from the transaction, thus resulting in negative net benefits of −d or −t. When both parties choose non-cooperation, neither party gains any revenue nor incurs any costs, and their net benefits are both 0. Based on the above assumptions, the payoff matrix between consumers and fishers in the game is constructed as shown in Table 6.

Table 6.
Payoff matrix of the game between consumers and fishers.
From Table 6, the expected benefit for consumers choosing to purchase traceable aquatic products is as follows:
The expected benefit for consumers choosing not to purchase traceable aquatic products is as follows:
Therefore, the average benefit for consumers is the following:
The replicator dynamic equation for consumers choosing to purchase traceable aquatic products is as follows:
Similarly, the expected benefit for fishers choosing to operate the traceability system is as follows:
The expected benefit for fishers choosing not to cooperate is the following:
Therefore, the average benefit for fishers is the following:
The replicator dynamic equation for fishers choosing to operate the traceability system is as follows:
By setting F(x) = 0 and F(y) = 0 simultaneously, the stable points for x and y are obtained as follows:
x stable point: ; y stable point: , . Thus, the local equilibrium points are (0, 0), (0, 1), (1, 0), (1, 1), .
Next, we verify the stability of these five local equilibrium points by constructing the Jacobian matrix:
The determinant and trace of the Jacobian matrix are expressed as follows:
According to Friedman’s theory, if det.J > 0 and tr.J < 0, then the point (x, y) is a stable equilibrium point, meaning the corresponding strategy is an evolutionarily stable equilibrium strategy. Otherwise, it is not an equilibrium strategy. The stability assessment of equilibrium points is summarized in Table 7.

Table 7.
Stability of local equilibrium points in the fisher-consumer game.
For the point (0, 0), since det.J > 0 and tr.J < 0, the point (0, 0) satisfies the stability conditions, meaning that (0, 0) is a stable evolutionary equilibrium solution.
For the point (0, 1), the condition for det.J > 0 is a < kv − kr, while the condition for tr.J < 0 is a > kv − kr + t. However, it is clear that kv − kr + t > kv − kr, meaning that the equilibrium condition cannot be satisfied. Thus, (0, 1) is not a stable point.
For the point (1, 0), the condition for det.J > 0 is c < kr, while the condition for tr.J < 0 is t > kr + d. However, since kr + d > kr, the condition cannot be satisfied. Thus, (1, 0) is also an unstable point.
For the point (1, 1), when a < kv − kr and t < kr, then det.J > 0; and when a < kv − t, then tr.J < 0. Therefore, when a < kv − kr and c < kr, (1, 1) is a stable equilibrium point.
For the point (x3, y3), since tr J = 0, no equilibrium condition exists. Thus, (x3, y3) is not a stable point.
In conclusion, the game between consumers and fishers has two evolutionarily stable equilibrium solutions under specific conditions. When d > 0 and t > 0, the final equilibrium of the game between consumers and fishers is (not purchasing, not operating). However, when d < kv − kr and t < kr, the final equilibrium is (purchasing, operating). Here, a and c represent the transaction costs for consumers and fishers, respectively.
By analyzing these two equilibrium outcomes, it is evident that when the transaction costs for both parties are zero, the only stable equilibrium in the game is (purchasing, operating), meaning that both parties will choose to cooperate, thereby completing the transaction.
In reality, transaction costs always exist and can never be entirely eliminated. However, as long as transaction costs remain sufficiently low, the (purchasing, operating) equilibrium will consistently emerge as an evolutionarily stable strategy. Therefore, similar to the insights gained from the evolutionary game between fishers and the government in the construction of the system, reducing various transaction costs in the development of the traceability system will be a crucial policy choice for ensuring its successful implementation.
3.3. Evolutionary Game Analysis Between Fishers Operating the Traceability System and Other Fishers
This evolutionary game model considers two types of agents: fishers who are willing to operate the traceability system and other fishers. The objective is to analyze the game behavior, equilibrium, and influencing factors in the sales process of aquatic products, where fishers interact and learn from each other. “Other fishers” mainly refer to those who have not adopted the traceability system or other aquatic product distributors in the supply chain. Their decision-making process regarding whether to operate the traceability system differs from that of ordinary fishers in terms of influencing factors and sequence. In addition to competition dynamics, external incentives can significantly influence cooperative behavior among fishers. Government subsidies—such as for traceability equipment, certification, or training—can effectively lower the cost of system adoption. Moreover, policy mechanisms offering exclusive access to high-end or export markets for groups of fishers complying with traceability standards can enhance the benefits of collective action. These interventions help reduce the risk of strategic defection, improve perceived fairness, and foster the emergence of mutually beneficial cooperation as an evolutionarily stable outcome. Therefore, although both groups are fishers, a symmetric evolutionary game model is not used in this analysis. The strategy space for both fishers willing to operate the traceability system and other fishers is (operate, not operate). Suppose the probability that a fisher willing to operate the traceability system chooses to do so is x (0 ≤ x ≤ 1), while the probability of not operating is 1 − x. Similarly, the probability that other fishers choose to operate the traceability system is y (0 ≤ y ≤ 1), while the probability of not operating is 1 − y. The respective revenues for fishers willing to operate the traceability system and for other fishers are denoted as T and N. The total cost of system construction, legal consultation, and information search (i.e., transaction costs) is denoted as e for fishers willing to operate and f for other fishers. When both the willing fishers and other fishers choose to operate the traceability system, they enter into a competitive relationship, leading to lower revenues for both. Assume that their earnings are reduced to a and b proportions of the original revenue, respectively (where 0 ≤ a ≤ b ≤ 1). In this case, the net revenue of the fishers operating the traceability system is aM − e, and the net revenue of other fishers is bR − f (alternatively, it could be assumed that construction costs increase, but this representation is adopted for consistency with previous sections). When fishers willing to operate the traceability system choose to do so, while other fishers choose not to operate, there is no competition, allowing the operating fishers to capture all the revenue from traceable aquatic products. Their net revenue is T − e, after deducting the construction and transaction costs. Since the other fishers do not operate the traceability system, they neither gain revenue from traceable products nor incur any costs, so their net revenue is assumed to be 0. Similarly, when fishers willing to operate the traceability system choose not to operate, but other fishers choose to operate, the net revenue of the other fishers is N − f, while the willing fishers receive 0. When neither fisher is willing to operate the traceability system nor do other fishers choose to operate, both parties receive a net revenue of 0. Based on these assumptions, the evolutionary game payoff matrix between fishers willing to operate the traceability system and other fishers is constructed, as shown in Table 8.

Table 8.
Payoff matrix for the evolutionary game between system operating fishers and other fishers.
According to Table 8, the expected payoff for fishers willing to operate the traceability system when choosing to operate is the following:
The expected payoff for choosing not to operate is as follows:
Therefore, the average payoff for operating the traceability system is as follows:
The replicator dynamic equation for the strategy of operating the traceability system among willing fishers is the following:
Similarly, the expected payoff for other fishers when choosing to operate is as follows:
The average payoff for other fishers is as follows:
The replicator dynamic equation for the strategy of operating the traceability system among other fishers is as follows:
Let F(x) = 0 and F(y) = 0 hold simultaneously, then the stable points for x are x₁ = 0, x2 = 1, ; the stable points for y are y₁ = 0, y2 = 1, .
From this, the local equilibrium points are (0, 0), (0, 1), (1, 0), (1, 1), and .
Next, we verify the stability of the five local equilibrium points by constructing the Jacobian matrix:
The determinant and trace of the Jacobian matrix are as follows:
According to Friedman’s idea, if det.J > 0 and tr.J > 0, the point (x, y) is a stable equilibrium point, and the corresponding strategy is a stable equilibrium strategy; otherwise, it is not an equilibrium strategy. The stability of the equilibrium points is determined as shown in Table 9.

Table 9.
Stability of local equilibrium points in the fisher-fisher game.
For the point (0, 0), when T < e and N < f, det.J > 0; and when T + N > e + f, tr.J < 0. Combining these two conditions, we conclude that when T < e and N < f, the stability condition is satisfied, and (0, 0) is a stable point.
For the point (0, 1), when e > aT and f < N, det.J > 0; and when aT − N < e − f, tr.J < 0. Combining these two conditions, we conclude that when e < aT and f > N, the stability condition is satisfied, and (0, 1) is a stable point.
For the point (1, 0), when T > e and f > bN, det.J > 0; and when T + f > bN + e, tr.J < 0. Combining these two conditions, we conclude that when T > e and f > bN, the stability condition is satisfied, and (1, 0) is a stable point.
For the point (1, 1), when e < aT and f < bT, det.J > 0; and when e + f > aT + bN, tr.J < 0. Combining these two conditions, we conclude that when e < aT and f < bN, the stability condition is satisfied, and (1, 1) is a stable point.
For the point (x3, y3), since tr.J = 0, there is no stability condition, so (x3, y3) is not a stable point.
In summary, the game between fishers willing to operate the traceability system and other fishers has four evolutionary equilibrium solutions under specific conditions: when T < e and N < f, the strategy pair (Not Operate, Not Operate) is an evolutionarily stable equilibrium; when e > aT and f < N, the pair (Not Operate, Operate) is an evolutionarily stable equilibrium; when T > e and f > bN, the pair (Operate, Not Operate) is an evolutionarily stable equilibrium; and when e < aT and f < bN, the pair (Operate, Operate) is an evolutionarily stable equilibrium. This shows that the final equilibrium outcome of the game depends on the relative magnitude of benefits and costs. Overall, only when the benefits of operating the traceability system outweigh the costs will operation become the optimal choice for both parties. In addition to competition dynamics, external incentives can significantly influence cooperative behavior among fishers. Government subsidies—such as for traceability equipment, certification, or training—can effectively lower the cost of system adoption. Moreover, policy mechanisms offering exclusive access to high-end or export markets for groups of fishers complying with traceability standards can enhance the benefits of collective action. These interventions help reduce the risk of strategic defection, improve perceived fairness, and foster the emergence of mutually beneficial cooperation as an evolutionarily stable outcome. The costs of operating the system include not only the expenses related to aquatic product sales but also the construction and maintenance costs of the traceability system, as well as the time costs associated with promoting it. The sale of traceable aquatic products results from bargaining between both parties in the transaction, but good infrastructure and a sound traceability system can provide more information and greater convenience, thereby reducing aquatic product expenditures and saving transaction costs. Therefore, the conclusion of this game is consistent with the previous two: facilitating the construction of traceability platforms and reducing query costs will be important policy options for the government to promote the development of traceability systems. Figure 2 shows that consumer acceptance and the price for traceable aquatic products exhibit a generally inverse relationship, indicating a trend of opposite variation between the two.
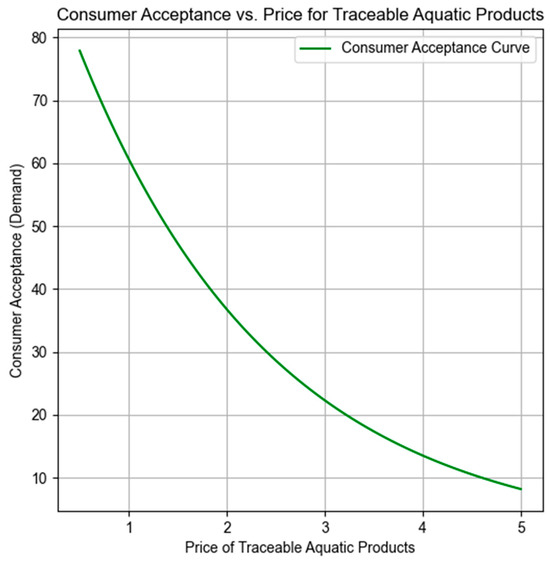
Figure 2.
Consumer acceptance curve.
3.4. Symmetric Evolutionary Game Analysis Between Consumers
This evolutionary game model considers Consumer 1 and Consumer 2 as the behavioral agents. Assuming both consumers have identical characteristics, the game is modeled as a symmetric evolutionary game, aiming to analyze how consumers influence and learn from each other, as well as to explore game behavior and equilibrium outcomes. The learning process is assumed to occur through social influence mechanisms such as word-of-mouth communication, peer behavior observation, and shared access to traceability-related information (e.g., product labels, certification platforms). These channels shape consumers’ perceived utility of traceable products and affect their probability of imitation, thereby driving the dynamic adjustment of strategy proportions in the population. The strategy space for both consumers is (Buy, Not Buy). Suppose the probability that both Consumer 1 and Consumer 2 choose to buy traceable aquatic products is x (0 ≤ x ≤ 1), and the probability of not buying is 1 − x. Both Consumer 1 and Consumer 2 receive a brand benefit E from purchasing traceable aquatic products, and the cost incurred during the purchase is g. When both consumers choose to buy, the psychological brand utility perceived by each is reduced due to the absence of exclusivity, as the symbolic value of traceable products diminishes when they are no longer perceived as scarce or status-enhancing goods. Their benefits are assumed to decrease to a proportion w of the original value (0 ≤ w ≤ 1). In this case, both consumers’ net benefits are wE − g. When Consumer 1 chooses to buy and Consumer 2 does not, Consumer 1 gains the full benefit E, minus the transaction cost g, resulting in a net benefit of E − g. Since Consumer 2 does not make a purchase, there is no additional utility or cost, and thus the net benefit is assumed to be 0. Similarly, if Consumer 1 does not buy and Consumer 2 buys, Consumer 2’s net benefit is E − g, while Consumer 1’s is 0. If neither Consumer 1 nor Consumer 2 buys traceable aquatic products, both receive a net benefit of 0. Based on these assumptions, the payoff matrix for the game between consumers is constructed as shown in Table 10.

Table 10.
Payoff matrix for the game between fishers in the traceability system.
According to the payoff matrix in Table 10, the payoff for consumers who choose to purchase traceable aquatic products is as follows:
The payoff for not purchasing is as follows:
Therefore, the average payoff for consumers is as follows:
From this, the replicator dynamic equation for consumers choosing to purchase traceable aquatic products is as follows:
Let F(x) = 0, and the solutions to the above replicator dynamic equation are as follows: .
According to the stability principle of differential equations and the properties of evolutionarily stable strategies (ESS), when F(x*) < 0, x* is an evolutionarily stable strategy of the corresponding evolutionary game.
By solving the first derivative of F(x) with respect to x, we obtain the following:
Substituting into the equation, we obtain the following:
. When E − g < 0, x₁* = 0 is an evolutionarily stable strategy. When g − wE < 0, x2* = 1 is an evolutionarily stable strategy. When g − E < 0 and wE − g < 0, that is, wE < g < E, then x3* is an evolutionarily stable strategy.
In summary, the game between consumers regarding the purchase of traceable aquatic products has three evolutionarily stable equilibrium solutions under certain conditions. When g > E, that is, when the benefit of purchasing is less than the cost, all consumers choosing not to purchase traceable aquatic products constitutes an evolutionarily stable equilibrium. When wE > g, meaning the purchase cost is lower than a certain proportion of the utility from not purchasing, all consumers choosing to purchase forms an evolutionarily stable equilibrium. When wE < g < E, a mixed strategy where consumers choose to purchase with a certain probability becomes an evolutionarily stable equilibrium. This implies that while traceable products offer some brand utility, the lack of exclusivity reduces their appeal, and not all consumers will consistently choose to purchase them. In practice, this equilibrium may be reflected in market segments where consumers alternate between traceable and non-traceable options depending on price, occasion, or perceived risk. For example, a consumer may purchase traceable seafood when shopping for family meals but switch to non-traceable options for casual or low-budget consumption. This reflects a coexistence of behavioral types, stabilizing the market at a probabilistic consumption level rather than full adoption. Moreover, the lower the purchase cost and the higher the benefit, the higher the proportion of consumers choosing to purchase in the equilibrium strategy. This indicates that reducing the cost associated with purchasing through the traceability system will strongly promote its adoption and widespread use.
Figure 3 illustrates the relationship between traceability costs and fishers’ profit, showing how profits decrease as costs rise. The shaded area under the curve emphasizes the impact of increasing traceability costs on profitability, with the orange color representing the magnitude of the profit at each cost level. This chart effectively highlights the negative effect of higher costs on fishers’ earnings, offering a clear visual representation of the cost-profit relationship.
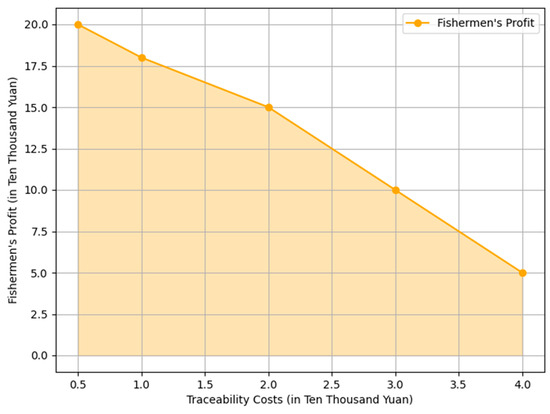
Figure 3.
Impact of traceability costs on fishers’ profit.
4. Discussion
First, the stable equilibrium outcomes of the four types of games—between fishers and the government, between fishers and consumers, among fishers themselves, and between consumers of traceable aquatic products and other consumers—are not unique. The final equilibrium results depend on the benefits each party derives from the system and the various costs they incur. These costs include not only the direct operational expenses but also the transaction costs associated with the system’s operation.
Second, the evolutionarily stable equilibria in all four types of games indicate that the construction cost of the traceability system plays a particularly important role in each party’s choice of stable strategy. Overall, when transaction costs are low—especially in the ideal scenario where transaction costs are zero—all parties tend to choose to operate or support the traceability system. Conversely, when transaction costs are high, they are more likely to choose not to operate or not to support the system.
For consumers, transaction costs associated with adopting traceable aquatic products include time spent identifying certified items, limited access to traceable options in lower-tier markets, insufficient understanding of traceability benefits, and technological barriers in digital verification systems. These costs reduce the net perceived utility of traceable products and directly influence consumer participation. Moreover, income levels and price elasticity shape consumption behavior across socioeconomic groups. Consumers in higher-income and urban regions tend to prioritize food safety and quality assurance and thus are more willing to pay for traceable certification. In contrast, consumers in lower-income or rural areas exhibit higher price sensitivity and lower adoption rates due to affordability constraints. To mitigate these obstacles, policy measures such as clear labeling, traceability education campaigns, and subsidies for traceable products are essential for expanding consumer coverage and ensuring equitable access to the traceability system.
Third, reducing the operational costs of the traceability system will be a key policy direction for the government in promoting its adoption. Lowering construction and operational expenses can significantly facilitate the development of the traceability system. The main sources of construction costs include information asymmetry, legal costs, and transaction inefficiencies. Reducing these costs will require government efforts in policy and regulatory formulation, platform development, and information exchange mechanisms.
5. Conclusions
Building on the analytical results of the four evolutionary game models, we discuss the practical implications for promoting the adoption and sustainable operation of aquatic product traceability systems. The findings highlight that stakeholders’ strategic decisions are shaped by perceived benefits, cost burdens, and institutional conditions. Accordingly, this section proposes targeted policy recommendations aimed at optimizing stakeholder incentives, reducing transaction costs, and enhancing institutional and technological support mechanisms.
First, optimize the cost-sharing mechanism and enhance the benefits for multiple stakeholders. Given the uncertainty in the game between fishers, the government, and consumers, a reasonable cost-sharing and benefit distribution mechanism should be established. On the one hand, the government can reduce the direct operational costs for fishers through financial subsidies and tax incentives, especially in the initial construction phase of the traceability system, by providing support for equipment installation and system maintenance. On the other hand, fishers should be encouraged to participate in the construction of the traceability system, achieve economies of scale to lower unit costs, and increase market gains through differentiated product pricing. Additionally, the government can introduce consumer incentives, such as discount vouchers and loyalty points for purchasing traceable seafood, to boost consumer participation and enhance the perceived benefits for all stakeholders.
To ensure the fairness and sustainability of the cost-sharing mechanism, the government should adopt a differentiated support strategy based on the financial capacity of different fishing communities. For example, small-scale or resource-constrained fishers may receive higher subsidy rates or longer-term support, while larger or vertically integrated enterprises could be subject to phased cost-sharing rules. Additionally, a gradual exit mechanism should be designed to avoid long-term dependence on subsidies by establishing clear performance benchmarks and incentivizing capacity-building. This ensures that public resources are used efficiently while empowering fishers to progressively assume operational responsibilities.
Second, reduce transaction costs and simplify the operational process of the traceability system. Transaction costs are a key factor influencing the equilibrium outcome of the game, and they should be effectively reduced through technological and process optimizations. One approach is to develop a digital traceability platform, utilizing blockchain technology to enhance information transparency and reduce trust costs caused by information asymmetry. Additionally, the standardization of operational procedures for the traceability system should be promoted to eliminate unnecessary intermediaries, simplify workflows, and improve efficiency. Promoting workflow standardization has also yielded practical insights into ongoing regional reforms. For example, the “Digital Aquatic Chain” pilot program in Zhejiang Province integrated production, certification, and logistics data into a unified blockchain-supported platform. Through standardized QR labeling and streamlined inspection procedures, the program improved coordination among supply chain actors and reduced administrative complexity. This case illustrates how aligning digital infrastructure with standardized operations can effectively lower operational burdens and enhance the overall efficiency of traceability systems. Furthermore, the government should strengthen education and awareness campaigns for both fishers and consumers to enhance their understanding and operational proficiency of the traceability system, thereby reducing the hidden costs associated with insufficient knowledge.
Third, strengthen institutional design and platform support to promote the sustainable development of the traceability system. To reduce construction costs, the government should improve relevant laws and regulations for the traceability system, clarify the rights, responsibilities, and obligations of all stakeholders, and minimize legal disputes and potential transaction risks. The government should also lead the establishment of regional or national public traceability platforms, ensuring unified data standards and standardized interfaces to lower the self-construction and operational burdens for fishers. Additionally, enhancing collaboration among agricultural, market regulation, and information technology departments is essential to ensure effective coordination in policy, technology, and resource allocation, thereby providing strong support for the long-term stable operation of the traceability system.
Author Contributions
Conceptualization, Y.J.; formal analysis, W.J. and Q.H.; investigation, C.L. and M.Z.; writing—original draft preparation, Y.J. and W.J.; writing—review and editing, Q.H. and M.Z.; visualization, Y.J. and C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (72304158), the Zhejiang Provincial Natural Science Foundation of China (LQ22G030002), and the Zhejiang Soft Science Research Program (2024C35085).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, Q.; Liu, S.; Wang, H.; Su, C.; Liu, A.; Jiang, L. Consumption of aquatic products and meats in Chinese residents: A nationwide survey. Front. Nutr. 2022, 9, 927417. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.; Parvaiz, G.S.; Dedahanov, A.T.; Abdurazzakov, O.S.; Rakhmonov, D.A. The impact of technologies of traceability and transparency in supply chains. Sustainability 2022, 14, 16336. [Google Scholar] [CrossRef]
- Zheng, J.M.; Liao, Y.H. Decision-Making Behavior of Fishery Enterprises on Traceability Systems and Its Policy Implications: Based on a Survey in Jiangsu Province. Rural Econ. 2019, 12, 122–129. [Google Scholar]
- Li, P.; Han, H.; Zhang, S.; Fang, H.; Fan, W.; Zhao, F.; Xu, C. Reviews on the development of digital intelligent fisheries technology in aquaculture. Aquac. Int. 2025, 33, 191. [Google Scholar] [CrossRef]
- Hoque, M.Z.; Akhter, N.; Chowdhury, M.S.R. Consumers’ preferences for the traceability information of seafood safety. Foods 2022, 11, 1675. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, H. Evolutionary game analysis of multi-agent cooperation strategy analysis in agricultural water conservancy PPP project under digitization background. Sci. Rep. 2024, 14, 22915. [Google Scholar] [CrossRef]
- National Development and Reform Commission. 13th Five-Year National Food Safety Plan; National Development and Reform Commission: Beijing, China, 2017. [Google Scholar]
- Freitas, J.; Vaz-Pires, P.; Câmara, J.S. From Aquaculture Production to Consumption: Freshness, Safety, Traceability and Authentication, the Four Pillars of Quality. Aquaculture 2020, 518, 734857. [Google Scholar] [CrossRef]
- Hu, Q.G.; Zhu, A.X. The Impact of Industrial Chain Collaboration on the Operation of Aquatic Product Traceability Systems: Based on a Survey of 209 Aquatic Enterprises in China. China Rural Econ. 2017, 12, 49–64. [Google Scholar]
- Wu, N.J.; Wang, D.W.; Cui, Z.G.; Qu, K.; Yu, F.; Song, Y.; Cui, H. Research Progress on Aquatic Product Traceability Systems in China. J. Guangdong Ocean Univ. 2023, 43, 113–118. [Google Scholar]
- Cromwell, J.; Turkson, C.; Dora, M.; Yamoah, F.A. Digital technologies for traceability and transparency in the global fish supply chains: A systematic review and future directions. Mar. Policy 2025, 178, 106700. [Google Scholar] [CrossRef]
- Guo, T.R.; Zhang, Y.; Ye, M.; Ke, H.; Zhang, L.; Xiao, Q.; Wu, Z. Research Progress on Quality and Safety Control of Aquatic Food in China. Meat Res. 2019, 33, 67–72. [Google Scholar]
- John, E.P.; Mishra, U. Integrated Multitrophic Aquaculture Supply Chain Fish Traceability with Blockchain Technology, Valorisation of Fish Waste and Plastic Pollution Reduction by Seaweed Bioplastic: A Study in Tuna Fish Aquaculture Industry. J. Clean. Prod. 2024, 434, 140056. [Google Scholar] [CrossRef]
- Untal, F.J.P.; Castro, M.M.C.; Sarmiento, J.M. Fishers’ preference for mobile traceability platform: Challenges in achieving a digital tuna supply chain in Davao Region, Philippines. Int. J. Logist. Manag. 2025, 36, 433–451. [Google Scholar] [CrossRef]
- Tolentino-Zondervan, F.; Ngoc, P.T.A.; Roskam, J.L. Use cases and future prospects of blockchain applications in global fishery and aquaculture value chains. Aquaculture 2023, 565, 739158. [Google Scholar] [CrossRef]
- Luna, M.; Fernandez-Vazquez, S.; Castelao, E.T.; Fernández, Á.A. A blockchain-based approach to the challenges of EU’s environmental policy compliance in aquaculture: From traceability to fraud prevention. Mar. Policy 2024, 159, 105892. [Google Scholar] [CrossRef]
- Dong, L.; Jiang, P.; Xu, F. Impact of traceability technology adoption in food supply chain networks. Manag. Sci. 2023, 69, 1518–1535. [Google Scholar] [CrossRef]
- Ficano, G. Innovative Technologies for Packaging, Preservation, Shelf-Life Extension and Traceability of the Aquaculture and Fishery Products. Ph.D. Thesis, Università degli Studi di Palermo, Palermo, Italy, 2022. [Google Scholar]
- Zhang, Y.; Liu, J.; Wang, D. Challenges in the Regional Implementation of China’s Agricultural Product Traceability System: Evidence from a Multi-Province Study. J. Agric.-Food Policy 2021, 14, 215–229. [Google Scholar]
- Fobbe, L.; Hilletofth, P. The role of stakeholder interaction in sustainable business models. A systematic literature review. J. Clean. Prod. 2021, 327, 129510. [Google Scholar] [CrossRef]
- Islam, S.; Manning, L.; Cullen, J.M. Systematic assessment of food traceability information loss: A case study of the Bangladesh export shrimp supply chain. Food Control 2022, 142, 109257. [Google Scholar] [CrossRef]
- Lin, S.; Shi, Q.; Zhou, N. Construction of a traceability system for food industry chain safety information based on internet of things technology. Front. Public Health 2022, 10, 857039. [Google Scholar] [CrossRef]
- Yue, K.; Shen, Y. An overview of disruptive technologies for aquaculture. Aquac. Fish. 2022, 7, 111–120. [Google Scholar] [CrossRef]
- Ababouch, L.; Nguyen, K.A.T.; Castro de Souza, M.; Fernandez-Polanco, J. Value chains and market access for aquaculture products. J. World Aquac. Soc. 2023, 54, 527–553. [Google Scholar] [CrossRef]
- Wang, H.Z.; Zhao, Y. Construction and countermeasures of aquatic product information traceability system: Based on the perspective of system complexity. Jiangsu Agric. Sci. 2017, 45, 336–339. [Google Scholar]
- Wang, L.J.; Sun, C.M.; Chen, Y.Y.; Tian, T.; Liu, T. Research progress on the application of agricultural product quality traceability systems in China. Food Sci. 2015, 36, 267–271. [Google Scholar]
- Kayan, H.; Nunes, M.; Rana, O.; Burnap, P.; Perera, C. Cybersecurity of industrial cyber-physical systems: A review. ACM Comput. Surv. (CSUR) 2022, 54, 1–35. [Google Scholar] [CrossRef]
- Bao, X.; Fang, Y.; Lin, F.; Huang, X. Aquatic product traceability system based on blockchain and HACCP. J. Jiangsu Univ. (Nat. Sci. Ed.) 2024, 45, 565–573. [Google Scholar]
- Aung, T.; Abdul Razak, R.; Rahiman Bin Md Nor, A. Artificial intelligence methods used in various aquaculture applications: A systematic literature review. J. World Aquac. Soc. 2025, 56, e13107. [Google Scholar] [CrossRef]
- Li, W.; Song, R.; Yu, K. Consumer adoption of food blockchain traceability: Insights from integrating TAM and TR models. Front. Sustain. Food Syst. 2025, 9, 1515188. [Google Scholar] [CrossRef]
- Liu, Z.; Fan, T.; Li, C.; Wang, S. An investigation of consumer willingness to pay for traceable pork accompanied by supplementary quality assurance information. Front. Sustain. Food Syst. 2025, 9, 1484396. [Google Scholar] [CrossRef]
- Bhusan, S.; Abuthagir Iburahim, S.; Akash, J.S.; Nathaniel, T.P.; Arisekar, U. Emerging trends in information technology with reference to fisheries and aquaculture. In Information Technology in Fisheries and Aquaculture; Springer: Singapore, 2025; pp. 251–263. [Google Scholar]
- Steinkruger, A.; Kroetz, K.; Malakoff, K.L.; Gephart, J.A.; Luque, G.; Lee, P.; Moore, K.C.; Donlan, C.J. Seafood traceability program design: Examination of the United States’ Seafood Import Monitoring Program. Ambio 2025, 54, 168–174. [Google Scholar] [CrossRef]
- Vriezen, R.; Plishka, M.; Cranfield, J. Consumer willingness to pay for traceable food products: A scoping review. Br. Food J. 2023, 125, 1631–1665. [Google Scholar] [CrossRef]
- Fong, C.R.; Gonzales, C.M.; Rennick, M.; Lahr, H.J.; Gardner, L.D.; Halpern, B.S.; Froehlich, H.E. Conflict and alignment on aquaculture among Californian communities. Aquaculture 2024, 580, 740230. [Google Scholar] [CrossRef]
- Santana, S.; Ribeiro, A. Traceability models and traceability systems to accelerate the transition to a Circular Economy: A systematic review. Sustainability 2022, 14, 5469. [Google Scholar] [CrossRef]
- Vu, N.H.; Chi, N.T.K. Stakeholders’ assessment of feed produced from nutrients recovered from aquaculture waste in an emerging economy. Aquaculture 2024, 593, 741333. [Google Scholar] [CrossRef]
- Hachicha, M.; Ben Halima, R.; Frikha, T. PreSA: An intelligent blockchain-based platform for monitoring and predicting water quality for smart aquaculture. Neural Comput. Appl. 2024, 1–12. [Google Scholar] [CrossRef]
- Hassoun, A.; Alhaj Abdullah, N.; Aït-Kaddour, A.; Ghellam, M.; Beşir, A.; Zannou, O.; Önal, B.; Aadil, R.M.; Lorenzo, J.M.; Khaneghah, A.M.; et al. Food traceability 4.0 as part of the fourth industrial revolution: Key enabling technologies. Crit. Rev. Food Sci. Nutr. 2024, 64, 873–889. [Google Scholar] [CrossRef]
- Yin, S.; Wang, J.; Han, F.; Chen, M.; Yan, Z. Consumer preference for food safety attributes of white shrimp in China: Evidence from choice experiment with stated attribute non-attendance. Food Control 2022, 137, 108938. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).