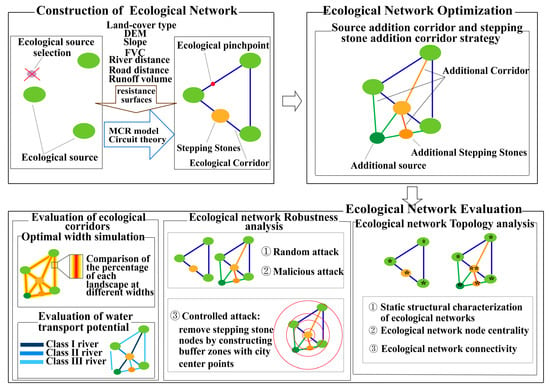
Optimization and Evaluation of Wetland Ecological Networks for Mitigating Urban Flooding
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.3. Construction of Ecological Networks
2.3.1. Identification of Ecological Source
2.3.2. Construction of Resistance Surfaces
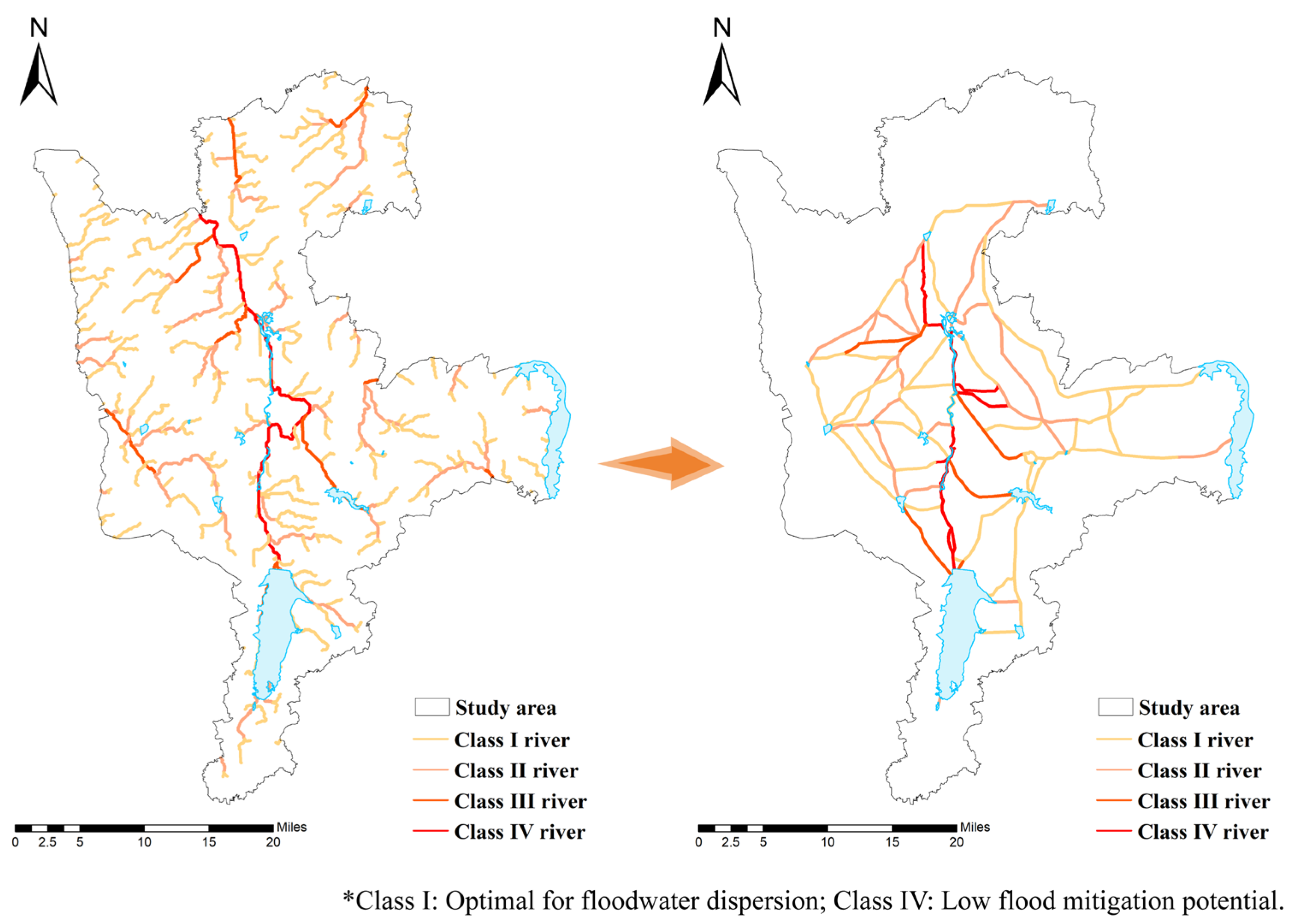
2.3.3. Extraction of Ecological Corridors
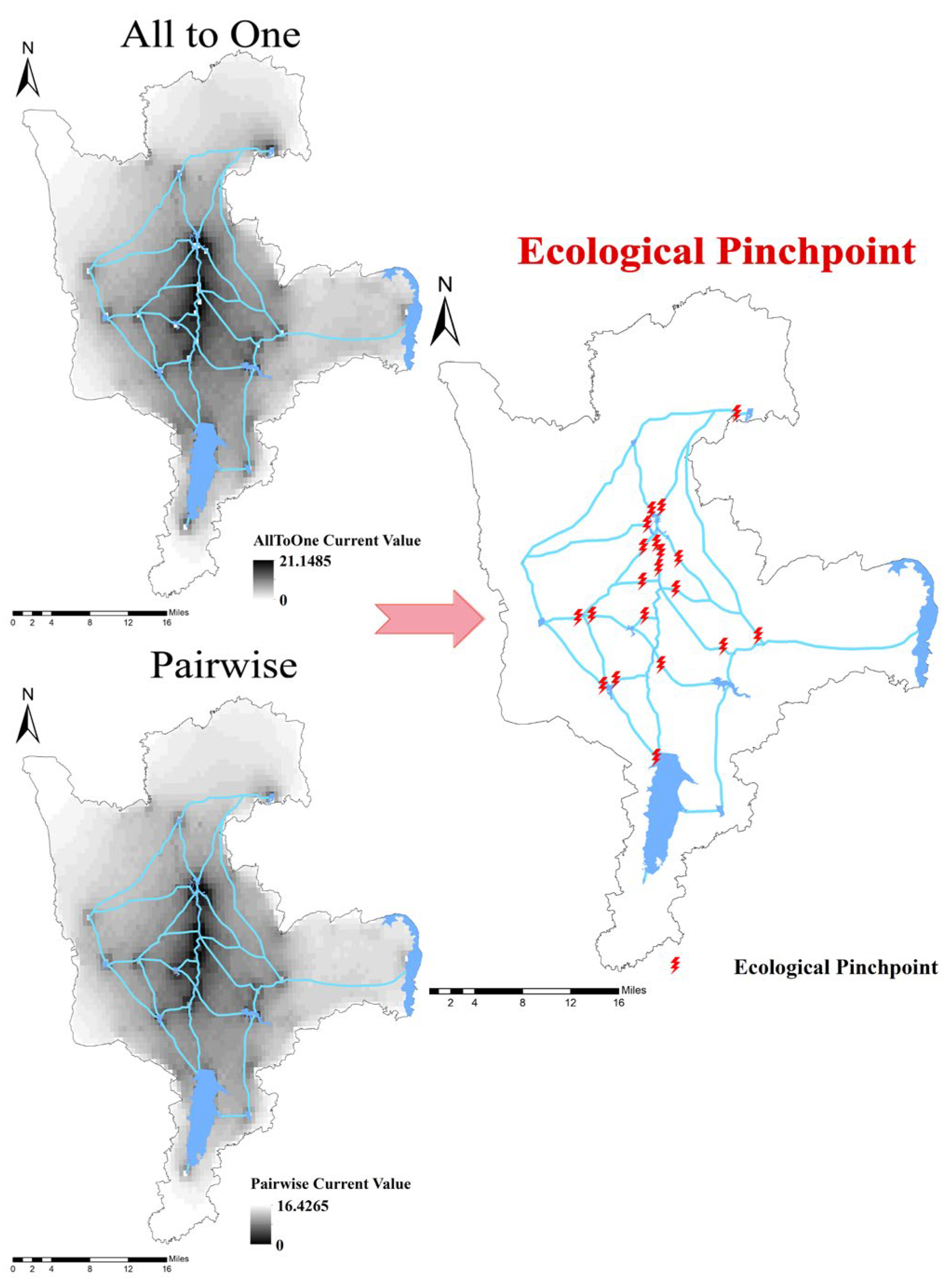
2.3.4. Extraction of Ecological Pinch Points and Stepping Stones
2.4. Ecological Network Optimization Strategies
2.5. Evaluation of Optimized Ecological Network
2.5.1. Topological Structure Analysis of the Ecological Network
2.5.2. Robustness Analysis Based on Complex Network Theory
2.5.3. Evaluation of Optimized Ecological Corridors
3. Results
3.1. Construction of the Ecological Network
3.1.1. Selection of Ecological Sources
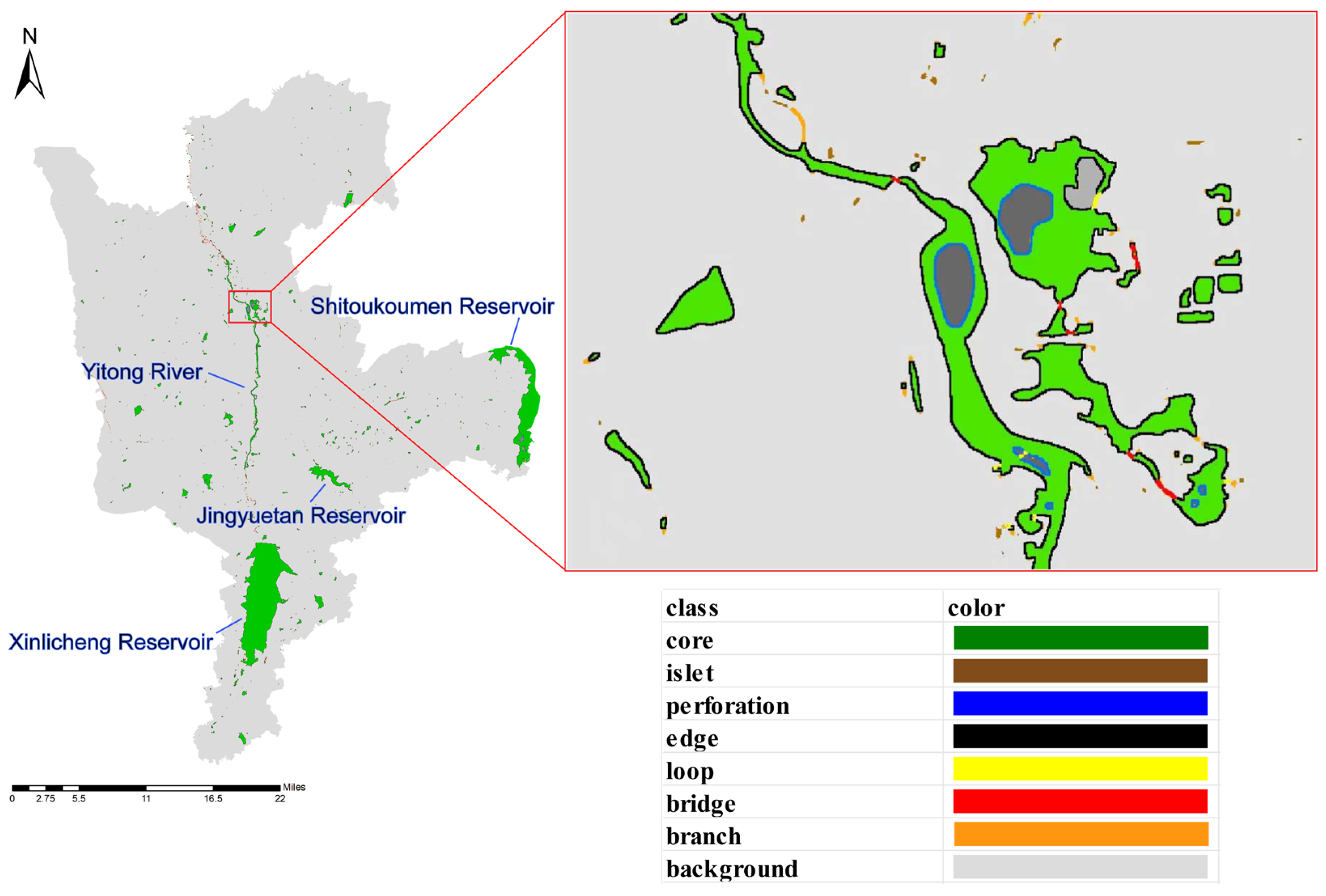
- Identification of Wetland Landscape Elements Based on MSPA
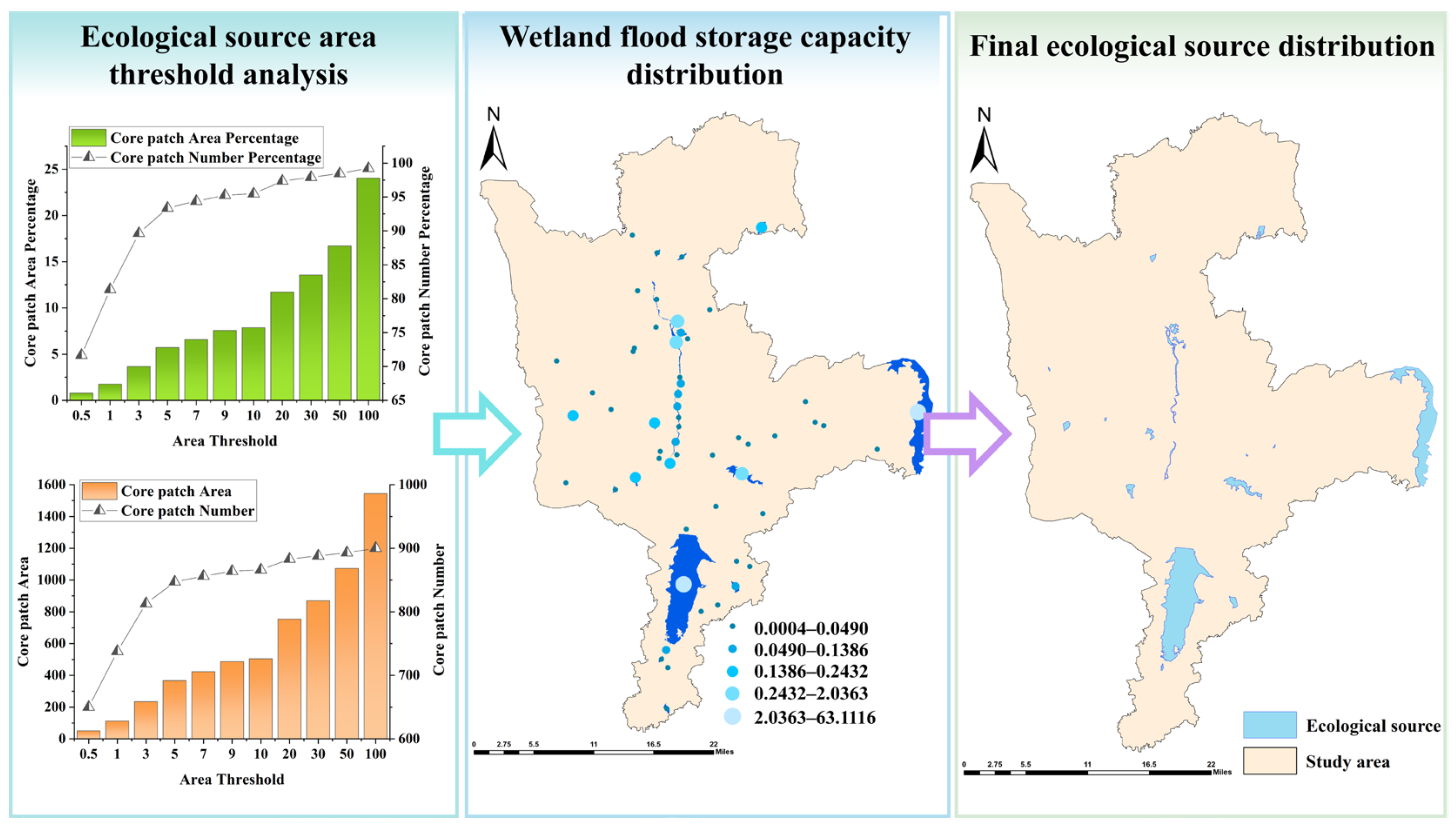
- Determination of Ecological Source Area Threshold
- Analysis of Wetland Flood Storage Capacity
- Final Determination of Ecological Sources
3.1.2. Construction of the Ecological Resistance Surface
3.1.3. Extraction of Ecological Corridors and Identification of Ecological Nodes
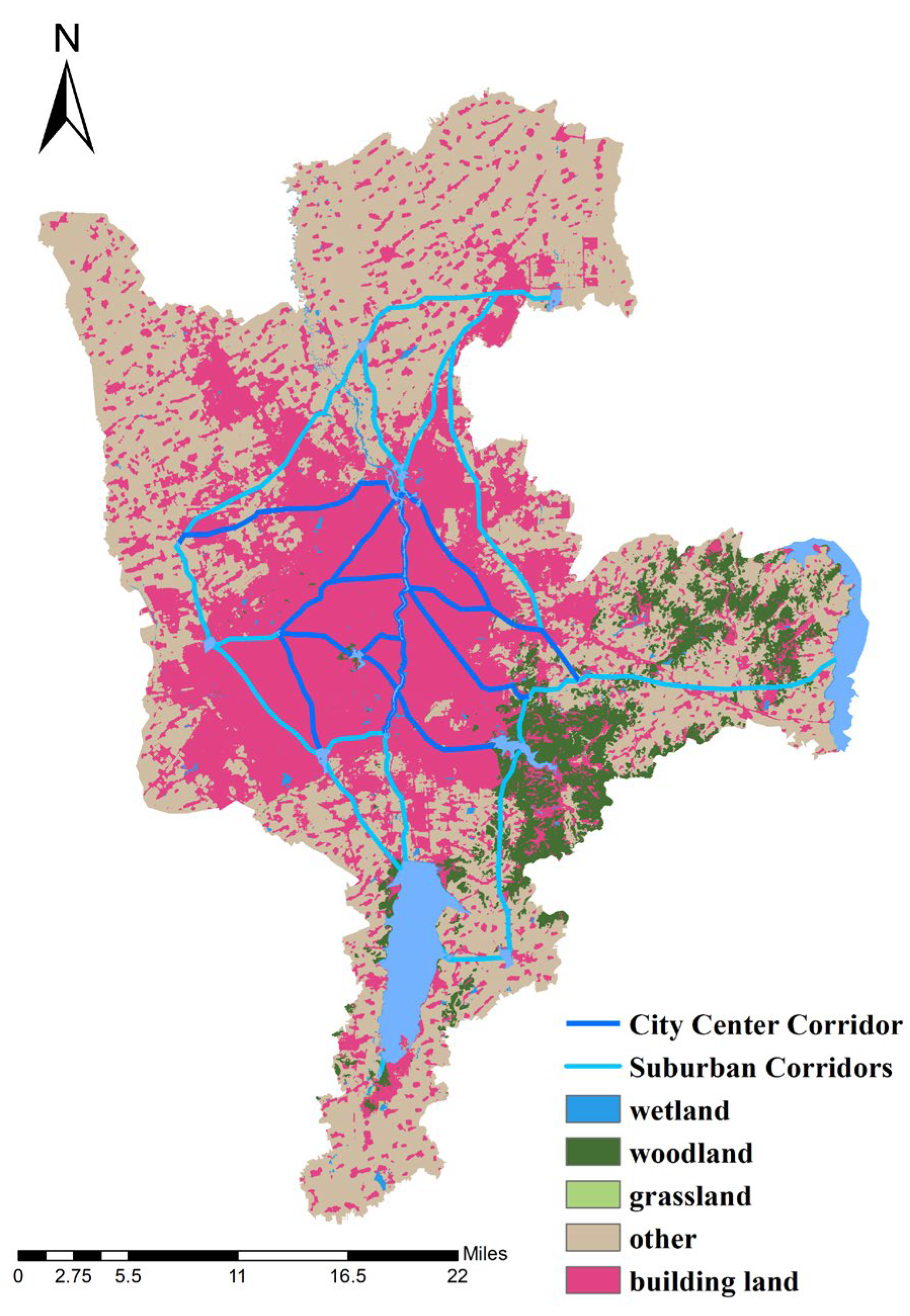
- Extraction of Ecological Corridors
- Identification of Ecological Pinch Points and Stepping Stone Patches
3.1.4. Evaluation of the Original Ecological Network’s Topological Structure
- Basic Static Structural Characteristics of the Original Ecological Network
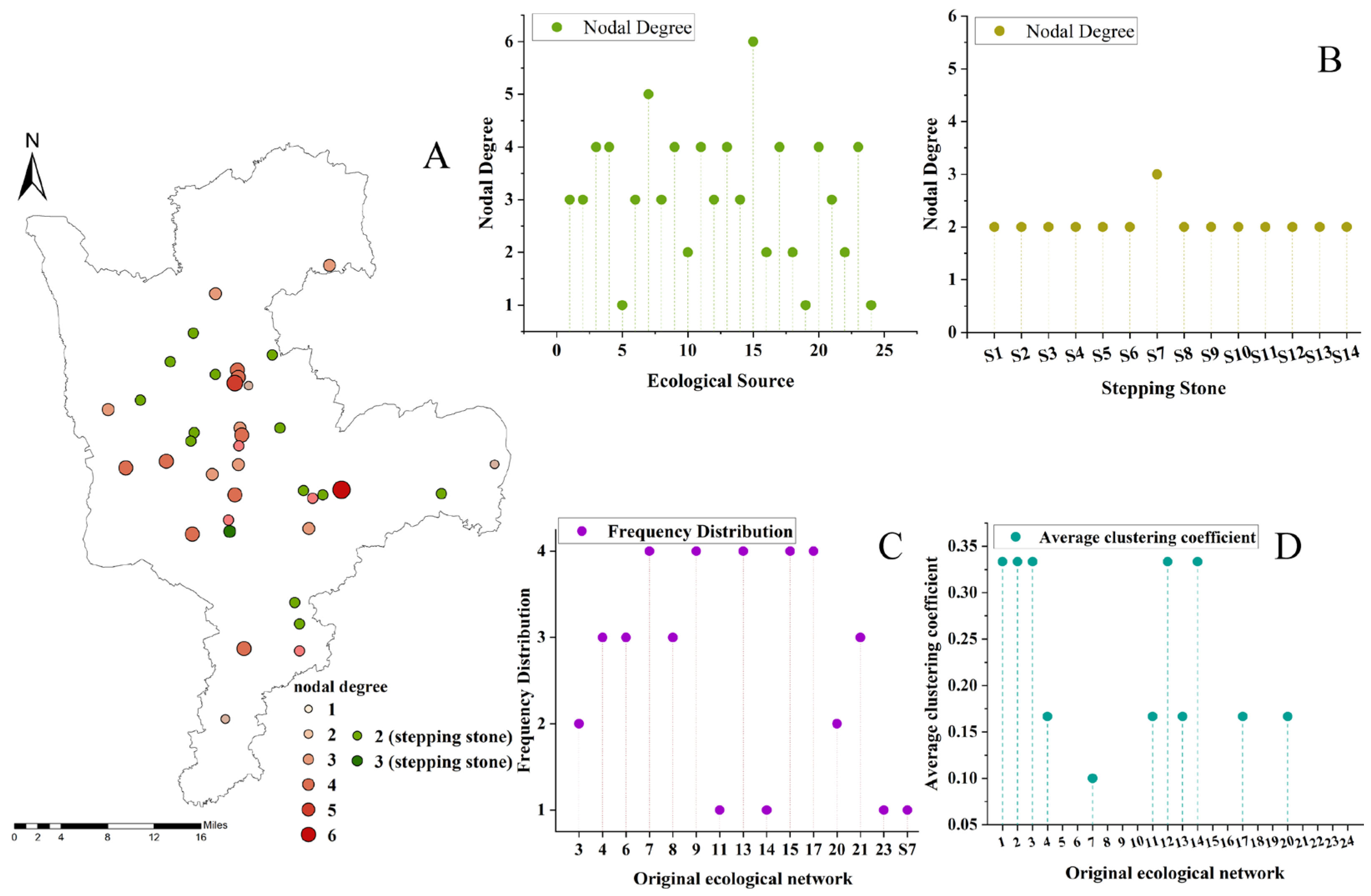
- Node Centrality in the Original Ecological Network
- Connectivity of the Original Ecological Network
3.2. Ecological Network Optimization Strategies
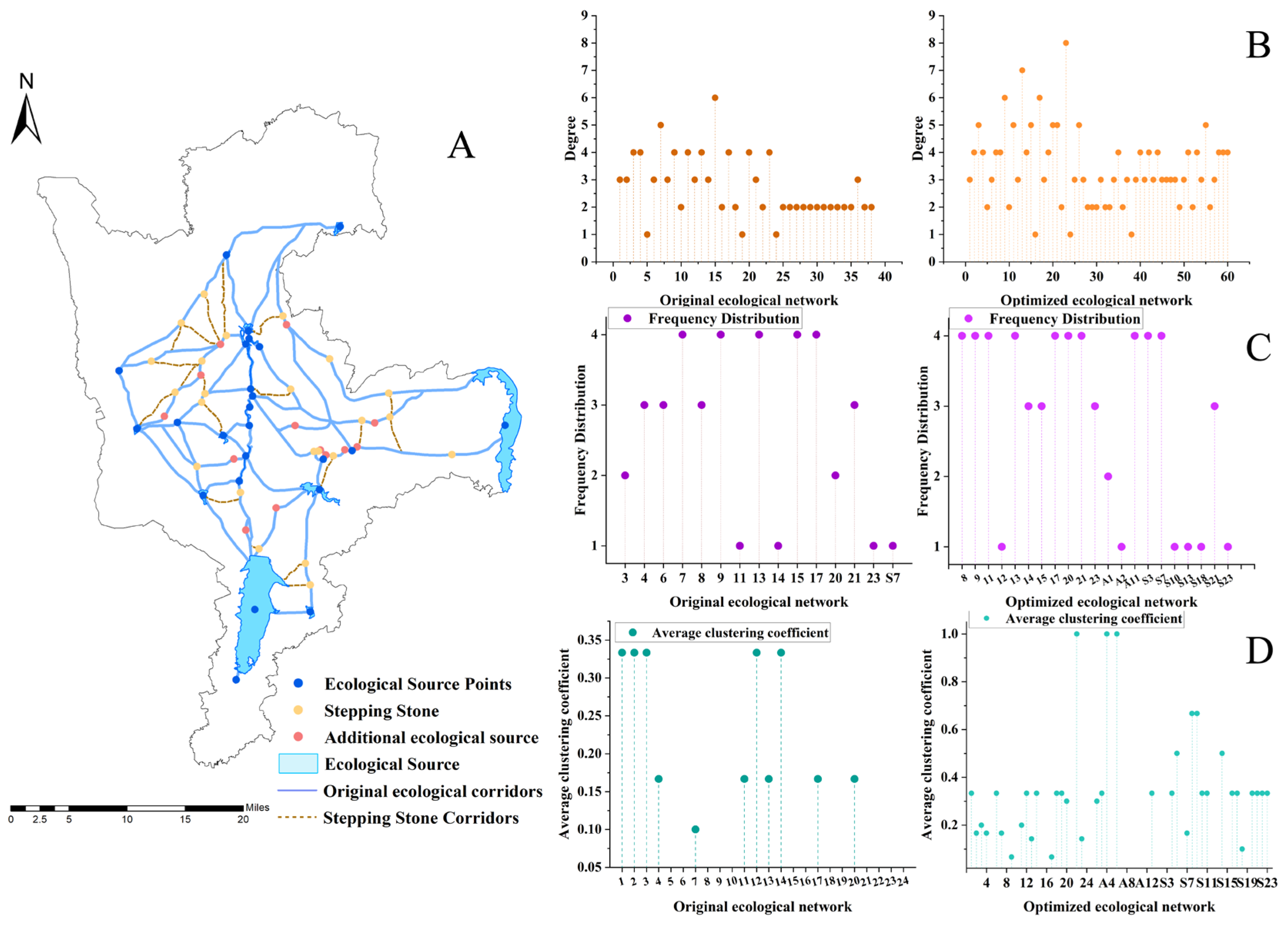
3.2.1. Source Addition Strategy
3.2.2. Stepping Stone Addition Strategy
3.3. Evaluation of the Optimized Ecological Network
3.3.1. Evaluation of Optimization Results Based on Topological Metrics
3.3.2. Robustness Analysis Based on Complex Network Theory
- Random Attack Scenario
- Malicious Attack Scenario
- Controlled Attack Scenario
3.3.3. Evaluation of Ecological Corridors
- Simulation of Optimal Ecological Corridor Width
- Assessment of Ecological Corridor Water Conveyance Potential
4. Discussion
4.1. Analysis of the Original Wetland Ecological Network
4.2. Evaluation of the Flood Mitigation Efficacy of the Optimized Network
4.2.1. Ecological Network Optimization Strategies
4.2.2. Evaluation of the Optimized Ecological Network
4.3. Policy Implications
4.4. Limitations
5. Conclusions
5.1. Enhanced Connectivity and Flood Mitigation
- The optimized network increased node degree (2.737 → 3.433) and clustering coefficient (0.074 → 0.231), significantly improving floodwater dispersion efficiency.
- Ecological corridors with 30–50 m widths were identified as optimal for peak runoff reduction, aligning with Sponge City construction standards.
5.2. Robustness Under Urban Pressures
- The network maintained 12.6–24.1% higher connectivity robustness under random, malicious, and urban expansion scenarios (Figure 11), demonstrating resilience to climate and anthropogenic disturbances.
5.3. Policy Actions
- Priority Protection: Key nodes (e.g., Source 7, 15) and stepping stone wetlands (<1 ha) require conservation to prevent fragmentation.
- Yitong River Restoration: Dredging and buffer-zone establishment are critical to sustain its role as the core corridor.
- Multi-Scale Integration: Network optimization should be embedded in the Changchun Territorial Space Master Plan (2021–2035).
5.4. Limitations and Future Work
- Seasonal wetland dynamics (e.g., water-level fluctuations) were not considered; long-term hydrological monitoring is recommended.
- Scaling the methodology to regional watersheds (e.g., Songhua River Basin) could validate broader applicability.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jenkins, K.; Surminski, S.; Hall, J.; Crick, F. Assessing surface water flood risk and management strategies under future climate change: Insights from an Agent-Based Model. Sci. Total Environ. 2017, 595, 159–168. [Google Scholar] [CrossRef] [PubMed]
- Ertan, S.; Çelik, R.N. The Assessment of Urbanization Effect and Sustainable Drainage Solutions on Flood Hazard by GIS. Sustainability 2021, 13, 2293. [Google Scholar] [CrossRef]
- Bai, T.; Mayer, A.L.; Shuster, W.D.; Tian, G.H. The Hydrologic Role of Urban Green Space in Mitigating Flooding (Luohe, China). Sustainability 2018, 10, 3584. [Google Scholar] [CrossRef] [PubMed]
- U.S. Environmental Protection Agency. Wetlands: Protecting Life and Property from Flooding; U.S. Environmental Protection Agency: Washington, DC, USA, 2006.
- Jia, H.; Ma, H.; Wei, M. Urban wetland planning: A case study in the Beijing central region. Ecol. Complex. 2011, 8, 213–221. [Google Scholar] [CrossRef]
- Uluocha, N.O.; Okeke, I.C. Implications of wetlands degradation for water resources management: Lessons from Nigeria. GeoJournal 2004, 61, 154. [Google Scholar] [CrossRef]
- Jaramillo, F.; Desormeaux, A.; Hedlund, J.; Jawitz, J.W.; Clerici, N.; Piemontese, L.; Rodríguez-Rodriguez, J.A.; Anaya, J.A.; Blanco-Libreros, J.F.; Borja, S.; et al. Priorities and Interactions of Sustainable Development Goals (SDGs) with Focus on Wetlands. Water 2019, 11, 619. [Google Scholar] [CrossRef]
- Jones-Walters, L. Pan-European ecological networks. J. Nat. Conserv. 2007, 15, 262–264. [Google Scholar] [CrossRef]
- Luo, J.L.; Zhu, L.; Fu, H. Construction of wetland ecological network based on MSPA-Conefor-MCR: A case study of Haikou City. Ecol. Indic. 2024, 166, 112329. [Google Scholar] [CrossRef]
- Xu, F.; Yin, H.; Kong, F.; Xu, J. Developing ecological networks based on mspa and the least-cost path method: A case study in bazhong western new district. Acta Ecol. Sin. 2015, 35, 6425–6434. [Google Scholar]
- Ma, J.; Yu, Q.; Wang, H.Y.; Yang, L.Z.; Wang, R.R.; Fang, M.Z. Construction and Optimization of Wetland Landscape Ecological Network in Dongying City, China. Land 2022, 11, 1226. [Google Scholar] [CrossRef]
- Yu, K.J. Landscape Ecological Security Patterns for Biological Conservation. Acta Ecol. Sin. 1999, 19, 8. [Google Scholar]
- Chi, Y.; Xie, Z.; Wang, J. Establishing archipelagic landscape ecological network with full connectivity at dual spatial scales. Ecol. Model. 2019, 399, 54–65. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Shi, Q.; Lu, J.; Han, J. Studying the spatiotemporal variations of the ecological network and carbon utilization efficiency in Southeast Tibet based on complex network theory. Ecol. Indic. 2024, 166, 112521. [Google Scholar] [CrossRef]
- Guo, H.; Yu, Q.; Pei, Y.; Wang, G.; Yue, D. Optimization of landscape spatial structure aiming at achieving carbon neutrality in desert and mining areas. J. Clean. Prod. 2021, 322, 129156. [Google Scholar] [CrossRef]
- Dou, P.; Cui, B.S. Dynamics and integrity of wetland network in estuary. Ecol. Inform. 2014, 24, 1–10. [Google Scholar] [CrossRef]
- Gao, C.; Pan, H.; Wang, M.; Zhang, T.; He, Y.; Cheng, J.; Yao, C. Identifying priority areas for ecological conservation and restoration based on circuit theory and dynamic weighted complex network: A case study of the Sichuan Basin. Ecol. Indic. 2023, 155, 111064. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, N.; Chen, A.; Qiu, J.; He, C.; Cao, Y. Identification of a wetland ecological network for urban heat island effect mitigation in Changchun, China. Ecol. Indic. 2023, 150, 110248. [Google Scholar] [CrossRef]
- Karra, K.; Kontgis, C.; Statman-Weil, Z.; Mazzariello, J.C.; Mathis, M.; Brumby, S.P. Global land use/land cover with Sentinel-2 and deep learning. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2021), Brussels, Belgium, 11–16 July 2021; IEEE: New York, NY, USA, 2021. [Google Scholar]
- Cui, L.; Wang, J.; Sun, L.; Lv, C. Construction and optimization of green space ecological networks in urban fringe areas: A case study with the urban fringe area of Tongzhou district in Beijing. J. Clean. Prod. 2020, 276, 124266. [Google Scholar] [CrossRef]
- Ding, M.; Liu, W.; Xiao, L.; Zhong, F.; Lu, N.; Zhang, J.; Zhang, Z.; Xu, X.; Wang, K. Construction and optimization strategy of ecological security pattern in a rapidly urbanizing region: A case study in central-south China. Ecol. Indic. 2022, 136, 108604. [Google Scholar] [CrossRef]
- Huang, K.; Peng, L.; Wang, X.; Deng, W. Integrating circuit theory and landscape pattern index to identify and optimize ecological networks: A case study of the Sichuan Basin, China. Environ. Sci. Pollut. Res. 2022, 29, 66874–66887. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.-H.; Chen, L.-D.; Fang, N.-F.; Qin, D.-F.; Cai, C.-F. Research on the SCS-CN initial abstraction ratio using rainfall-runoff event analysis in the Three Gorges Area, China. Catena 2009, 77, 1–7. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. SCS-CN parameter determination using rainfall-runoff data in heterogeneous watersheds—The two-CN system approach. Hydrol. Earth Syst. Sci. 2012, 16, 1001–1015. [Google Scholar] [CrossRef]
- Ye, H.; Yang, Z.; Xu, X. Ecological Corridors Analysis Based on MSPA and MCR Model-A Case Study of the Tomur World Natural Heritage Region. Sustainability 2020, 12, 959. [Google Scholar] [CrossRef]
- Kwon, O.-S.; Kim, J.-H.; Ra, J.-H. Landscape Ecological Analysis of Green Network in Urban Area Using Circuit Theory and Least-Cost Path. Land 2021, 10, 847. [Google Scholar] [CrossRef]
- McRae, B.H.; Dickson, B.G.; Keitt, T.H.; Shah, V.B. Using circuit theory to model connectivity in ecology, evolution, and conservation. Ecology 2008, 89, 2712–2724. [Google Scholar] [CrossRef]
- Dickson, B.G.; Albano, C.M.; McRae, B.H.; Anderson, J.J.; Theobald, D.M.; Zachmann, L.J.; Sisk, T.D.; Dombeck, M.P. Informing Strategic Efforts to Expand and Connect Protected Areas Using a Model of Ecological Flow, with Application to the Western United States. Conserv. Lett. 2017, 10, 564–571. [Google Scholar] [CrossRef]
- Luo, Y.; Wu, J.; Wang, X.; Wang, Z.; Zhao, Y. Can policy maintain habitat connectivity under landscape fragmentation? A case study of Shenzhen, China. Sci. Total Environ. 2020, 715, 136829. [Google Scholar] [CrossRef]
- Nie, W.; Shi, Y.; Siaw, M.J.; Yang, F.; Wu, R.; Wu, X.; Zheng, X.; Bao, Z. Constructing and optimizing ecological network at county and town Scale: The case of Anji County, China. Ecol. Indic. 2021, 132, 108294. [Google Scholar] [CrossRef]
- Wei, W.; Liu, C.; Ma, L.; Xie, B.; Zhou, J.; Nan, S. Optimization strategies of ecological security patterns through importance of ecosystem services and ecological sensitivity-A case study in the Yellow River Basin. Land Degrad. Dev. 2024, 35, 985–1001. [Google Scholar] [CrossRef]
- Goodwin, B.J.; Fahrig, L. How does landscape structure influence landscape connectivity? Oikos 2002, 99, 552–570. [Google Scholar] [CrossRef]
- Changguang, W.U.; Zhixiang, Z.; Pengcheng, W.; Wenfa, X.; Mingjun, T. The concept and measurement of landscape connectivity and its applications. Acta Ecol. Sin. 2010, 30, 1903–1910. [Google Scholar]
- Song, S.; Xu, D.; Hu, S.; Shi, M. Ecological Network Optimization in Urban Central District Based on Complex Network Theory: A Case Study with the Urban Central District of Harbin. Int. J. Environ. Res. Public Health 2021, 18, 1427. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.H.; Li, Z.H.; Wang, Y.F.; Zheng, X.Q.; Deng, X.Z. Building green infrastructure for mitigating urban flood risk in Beijing, China. Urban For. Urban Green. 2024, 93, 128218. [Google Scholar] [CrossRef]
- Ruefenacht, B.; Knight, R.L. Influences of corridor continuity and width on survival and movement of deermice Peromyscus maniculatus. Biol. Conserv. 1995, 71, 269–274. [Google Scholar] [CrossRef]
- Xie, Y.S.; Wang, Q.N.; Xie, M.Q.; Shibata, S. Construction feasibility evaluation for potential ecological corridors under different widths: A case study of Chengdu in China. Landsc. Ecol. Eng. 2023, 19, 381–399. [Google Scholar] [CrossRef]
- Kocyigit, M.B.; Akay, H. Estimation of potential flash flood risk in a basin using morphometric parameters: A case study of Akcay Basin. J. Fac. Eng. Archit. Gazi Univ. 2018, 33, 1321–1332. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Y.L.; Pu, L.J.; Jiang, B.; Yuan, S.F.; Xu, Y. A Novel Model for Detecting Urban Fringe and Its Expanding Patterns: An Application in Harbin City, China. Land 2021, 10, 876. [Google Scholar] [CrossRef]
- Wu, Y.F.; Zhang, G.X.; Rousseau, A.N.; Xu, Y.J.; Foulon, É. On how wetlands can provide flood resilience in a large river basin: A case study in Nenjiang river Basin, China. J. Hydrol. 2020, 587, 125012. [Google Scholar] [CrossRef]
- Tiner, R.W. Geographically isolated wetlands of the United States. Wetlands 2003, 23, 494–516. [Google Scholar] [CrossRef]
- Zhou, Q.; Mikkelsen, P.S.; Halsnæs, K.; Arnbjerg-Nielsen, K. Framework for economic pluvial flood risk assessment considering climate change effects and adaptation benefits. J. Hydrol. 2012, 414–415, 539–549. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, Y.; Yao, R.; Sun, P.; Zhen, N.; Xia, X. Data Uncertainty of Flood Susceptibility Using Non-Flood Samples. Remote Sens. 2025, 17, 375. [Google Scholar] [CrossRef]
- Guillen-Ludena, S.; Lopez, D.; Mignot, E.; Riviere, N. Characterization of flow resistance in a floodplain for varying building density. In Proceedings of the 4th International Association for Hydro-Environment Engineering and Research (IAHR) Congress, Liege, Belgium, 27–29 July 2016; pp. 45–48. [Google Scholar]
- Li, B.; Gan, T. Construction of water security pattern of Changsha-Zhuzhou-Xiangtan urban agglomeration based on ArcGIS and GAP analysis. Water Resour. Prot. 2019, 35, 80–88. [Google Scholar]
- Chen, H.; Liu, Y.; Hu, L.; Zhang, Z.; Chen, Y.; Tan, Y.; Han, Y. Constructing a Flood-Adaptive Ecological Security Pattern from the Perspective of Ecological Resilience: A Case Study of the Main Urban Area in Wuhan. Int. J. Environ. Res. Public Health 2023, 20, 385. [Google Scholar] [CrossRef]
- Li, C.L.; Sun, N.; Lu, Y.H.; Guo, B.Y.; Wang, Y.; Sun, X.K.; Yao, Y.K. Review on Urban Flood Risk Assessment. Sustainability 2023, 15, 765. [Google Scholar] [CrossRef]
- Yu, Q.; Yue, D.P.; Wang, Y.H.; Kai, S.; Fang, M.Z.; Ma, H.; Zhang, Q.B.; Huang, Y. Optimization of ecological node layout and stability analysis of ecological network in desert oasis: A typical case study of ecological fragile zone located at Deng Kou County (Inner Mongolia). Ecol. Indic. 2018, 84, 304–318. [Google Scholar] [CrossRef]
- Men, D.; Pan, J. Ecological network identification and connectivity robustness evaluation in the Yellow River Basin under a multi-scenario simulation. Ecol. Model. 2023, 482, 110384. [Google Scholar] [CrossRef]
- Fan, J.P.; Wang, Q.; Ji, M.; Sun, Y.J.; Feng, Y.G.; Yang, F.S.; Zhang, Z. Ecological network construction and gradient zoning optimization strategy in urban-rural fringe: A case study of Licheng District, Jinan City, China. Ecol. Indic. 2023, 150, 110251. [Google Scholar] [CrossRef]
- Chao, Y.; Yan, Y.; Yan, S.; Pan, H.; Wu, L. County Scale Ecological Security Pattern Construction Based on MCR Model A Case Study of Yongchun County, Fujian Province. Bull. Soil Water Conserv. 2023, 43, 203–210. [Google Scholar]
- Bertassello, L.E.; Jawitz, J.W.; Aubeneau, A.F.; Botter, G.; Rao, P.S.C. Stochastic dynamics of wetlandscapes: Ecohydrological implications of shifts in hydro-climatic forcing and landscape configuration. Sci. Total Environ. 2019, 694, 133765. [Google Scholar] [CrossRef]
- Schoener, G.; Stone, M.C. Impact of antecedent soil moisture on runoff from a semiarid catchment. J. Hydrol. 2019, 569, 627–636. [Google Scholar] [CrossRef]
- Giglou, A.N.; Nazari, R.; Jazaei, F.; Karimi, M. Assessing the effects of increased impervious surface on the aquifer recharge through river flow network, case study of Jackson, Tennessee, USA. Sci. Total Environ. 2023, 872, 162203. [Google Scholar] [CrossRef]


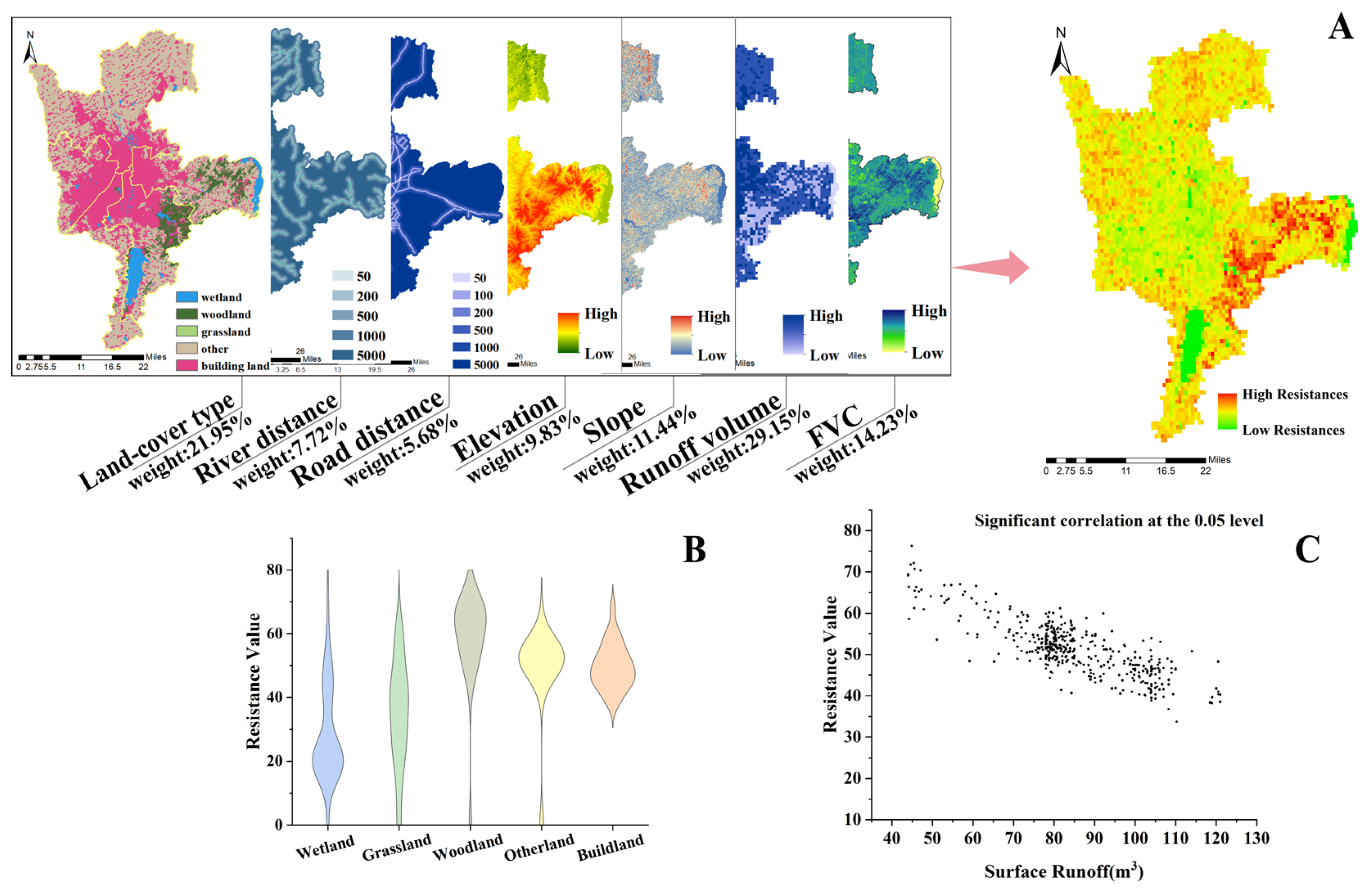


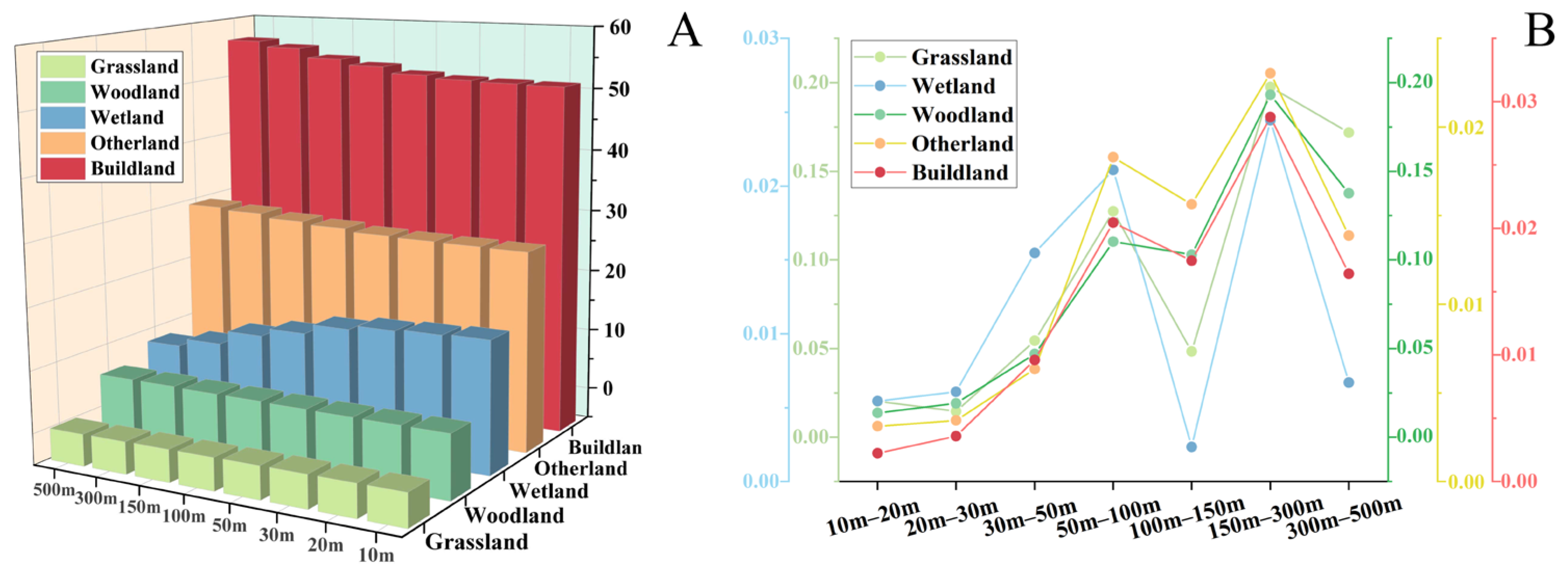
| Resistance Factor | Grading Method | Resistance Value | Weight |
|---|---|---|---|
| Land cover type | Wetland | 1 | 0.21949 |
| Grass land | 10 | ||
| Woodland | 30 | ||
| Other land | 50 | ||
| Built land | 70 | ||
| Elevation (m) | <150 | 10 | 0.09827 |
| 150–200 | 30 | ||
| 200–250 | 50 | ||
| 250–300 | 70 | ||
| >300 | 90 | ||
| Slope (°) | <5 | 10 | 0.11441 |
| 5–10 | 30 | ||
| 10–15 | 50 | ||
| 15–20 | 70 | ||
| >20 | 90 | ||
| FVC | <0.2 | 10 | 0.14227 |
| 0.2–0.4 | 30 | ||
| 0.4–0.6 | 50 | ||
| 0.6–0.8 | 70 | ||
| >0.8 | 90 | ||
| River distance (m) | <50 | 5 | 0.07724 |
| 50–100 | 10 | ||
| 100–200 | 30 | ||
| 200–500 | 50 | ||
| 500–1000 | 70 | ||
| >1000 | 90 | ||
| Road distance (m) | <50 | 5 | 0.05678 |
| 50–100 | 10 | ||
| 100–200 | 30 | ||
| 200–500 | 50 | ||
| 500–1000 | 70 | ||
| >1000 | 90 | ||
| Normalized runoff volume | <0.79 | 10 | 0.29154 |
| 0.63–0.79 | 30 | ||
| 0.47–0.63 | 50 | ||
| 0.22–0.47 | 70 | ||
| <0.22 | 90 |
| Type | Area (hm2) | Percentage |
|---|---|---|
| Core | 10,937.65 | 87.11% |
| Bridge | 76.82 | 0.61% |
| Islet | 124.6 | 0.99% |
| Edge | 1210.91 | 9.64% |
| Perforation | 33.64 | 0.27% |
| Branch | 155.32 | 1.24% |
| Loop | 17.63 | 0.14% |
| Total | 12,556.57 | 100% |
| ID | Area (hm2) | Volume (%) | SIS | ID | Area (hm2) | Volume (%) | SIS |
|---|---|---|---|---|---|---|---|
| 1 | 2922.05 | 100 | 150.945 | 13 | 40.74 | 0.18 | 0.801 |
| 2 | 5730.69 | 46.95 | 146.95 | 14 | 15.02 | 0.38 | 0.551 |
| 3 | 386.48 | 2.03 | 8.689 | 15 | 16.42 | 0.19 | 0.386 |
| 4 | 86.39 | 3.22 | 4.638 | 16 | 18.65 | 0.12 | 0.355 |
| 5 | 148.18 | 1.51 | 4.007 | 17 | 19.03 | 0.11 | 0.351 |
| 6 | 124.4 | 0.3 | 2.382 | 18 | 14.66 | 0.087 | 0.252 |
| 7 | 112.82 | 0.25 | 2.130 | 19 | 15.56 | 0.066 | 0.247 |
| 8 | 105.57 | 0.089 | 1.842 | 20 | 8.26 | 0.051 | 0.104 |
| 9 | 82.58 | 0.36 | 1.711 | 21 | 8.13 | 0.052 | 0.103 |
| 10 | 71.55 | 0.33 | 1.489 | 22 | 7.9 | 0.055 | 0.102 |
| 11 | 50.82 | 0.054 | 0.851 | 23 | 6.06 | 0.053 | 0.068 |
| 12 | 39.39 | 0.21 | 0.807 | 24 | 5.18 | 0.056 | 0.056 |
| ID | Area | dPC |
|---|---|---|
| 1 | 4.23 | 3.61551 |
| 2 | 3.57 | 3.157548 |
| 3 | 4.35 | 3.819444 |
| 4 | 4.46 | 3.627463 |
| 5 | 3.75 | 3.415335 |
| 6 | 3.46 | 3.355452 |
| 7 | 4.37 | 4.070733 |
| 8 | 4.08 | 3.871542 |
| 9 | 4.08 | 3.83618 |
| 10 | 4.51 | 4.275026 |
| 11 | 4.32 | 3.968203 |
| 12 | 3.95 | 3.510841 |
| 13 | 4.21 | 3.533849 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, H.; Cao, Y.; Zhang, Y. Optimization and Evaluation of Wetland Ecological Networks for Mitigating Urban Flooding. Water 2025, 17, 1461. https://doi.org/10.3390/w17101461
Tong H, Cao Y, Zhang Y. Optimization and Evaluation of Wetland Ecological Networks for Mitigating Urban Flooding. Water. 2025; 17(10):1461. https://doi.org/10.3390/w17101461
Chicago/Turabian StyleTong, Haoyu, Yonghong Cao, and Yue Zhang. 2025. "Optimization and Evaluation of Wetland Ecological Networks for Mitigating Urban Flooding" Water 17, no. 10: 1461. https://doi.org/10.3390/w17101461
APA StyleTong, H., Cao, Y., & Zhang, Y. (2025). Optimization and Evaluation of Wetland Ecological Networks for Mitigating Urban Flooding. Water, 17(10), 1461. https://doi.org/10.3390/w17101461