A Forecast Heuristic of Back Propagation Neural Network and Particle Swarm Optimization for Annual Runoff Based on Sunspot Number
Abstract
1. Introduction
- Formulating a BPNN model for annual runoff in training and testing stages;
- Designing a heuristic that uses PSO to solve the forecasting problem based on the proposed BPNN model in the forecasting stage.
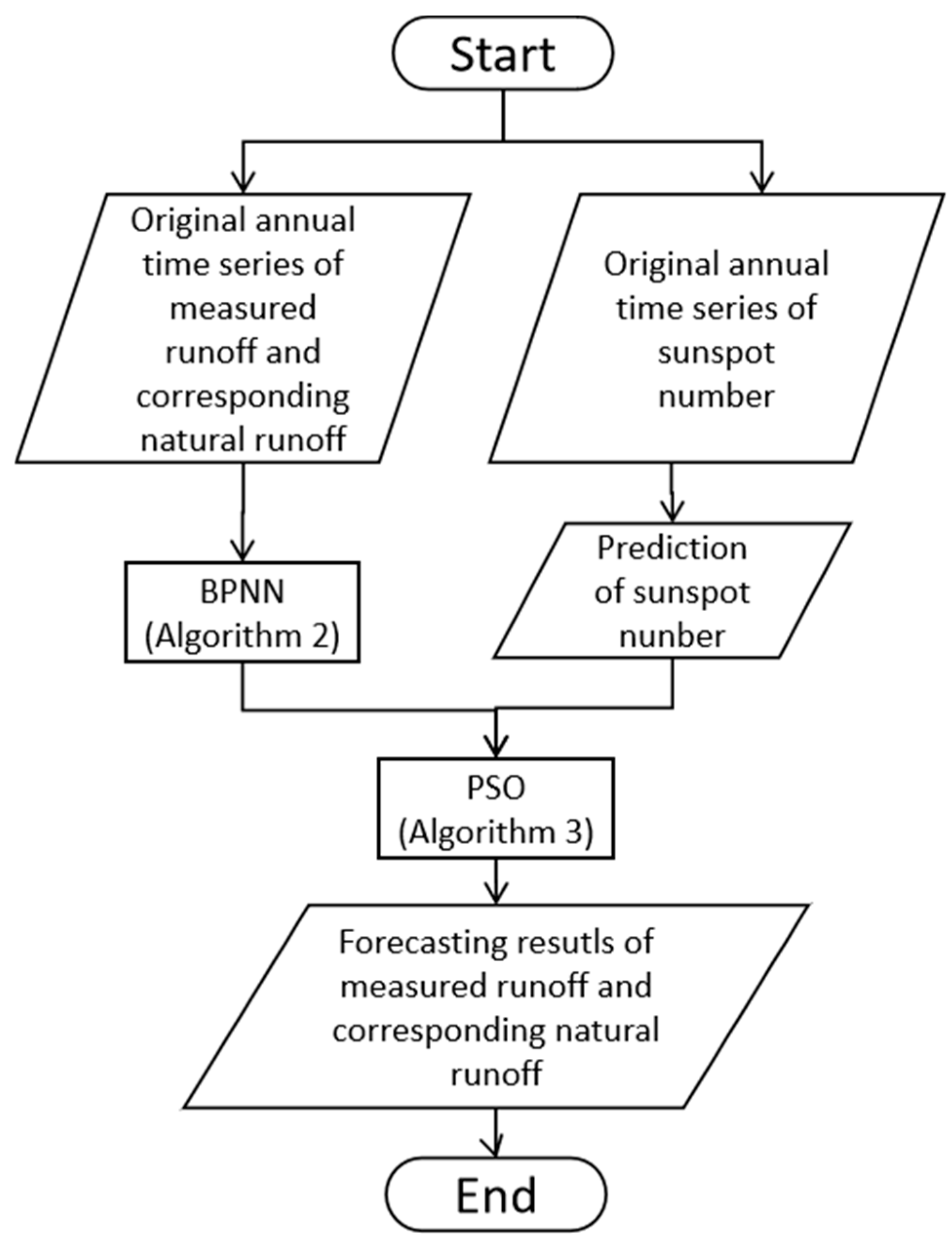
2. Forecast Heuristic of BPNN and PSO
2.1. General Framework
| Algorithm 1: Forecast heuristic |
| 1: Calculate the difference between the runoff predicted by BPNN and the runoff by the linear relationship |
| 2: Train and test the BPNN model with historical data, including the sunspot number and runoff and so on |
| 3: Set an initial value as one input of the trained BPNN model, other inputs could be predicted either on your own, or by other official organizations |
| 4: Compute based on with the trained BPNN model |
| 5: Minimize through the PSO algorithm |
| 6: repeat |
| 7: for all the targeted index do |
| 8: Calculate the step by step |
| 9: Calculate the absolute value of step by step |
| 10: Update the step by step |
| 11: end for |
| 12: Compute PSO for |
| 13: until there are no forecasting tasks |
2.2. Back Propagation Neural Network
| Algorithm 2: Back Propagation Neural Network |
| Input: Training and Testing Set |
| Learning rate η |
| 1: Data normalization (here, data preprocessing needs to be carried out according to the actual situation of the data and algorithm requirements) |
| 2: Create a network |
| 3: Training Network |
| Repeat for |
| 3.1: Positive propagation |
| 3.2: Back propagation |
| Until the end condition is met |
| 4: Using the network |
| 5: Data denormalization |
| Output: Trained BP neural network |
| 6: Test the trained network |
2.3. Particle Swarm Optimization
| Algorithm 3: PSO algorithm |
| Set particle dimension as equal to the size of Learning rate η |
| 1: Data normalization (here, data preprocessing needs to be carried out according to the actual situation of the data and algorithm requirements) |
| 2: Create a network |
| 3: Training Network |
| Repeat for |
| 3.1: Positive propagation |
| 3.2: Back propagation |
| Until the end condition is met |
| 4: Using the network |
| 5: Data denormalization |
| Output: Trained BP neural network |
| 6: Test the trained network |
3. Application in the Yellow River, China
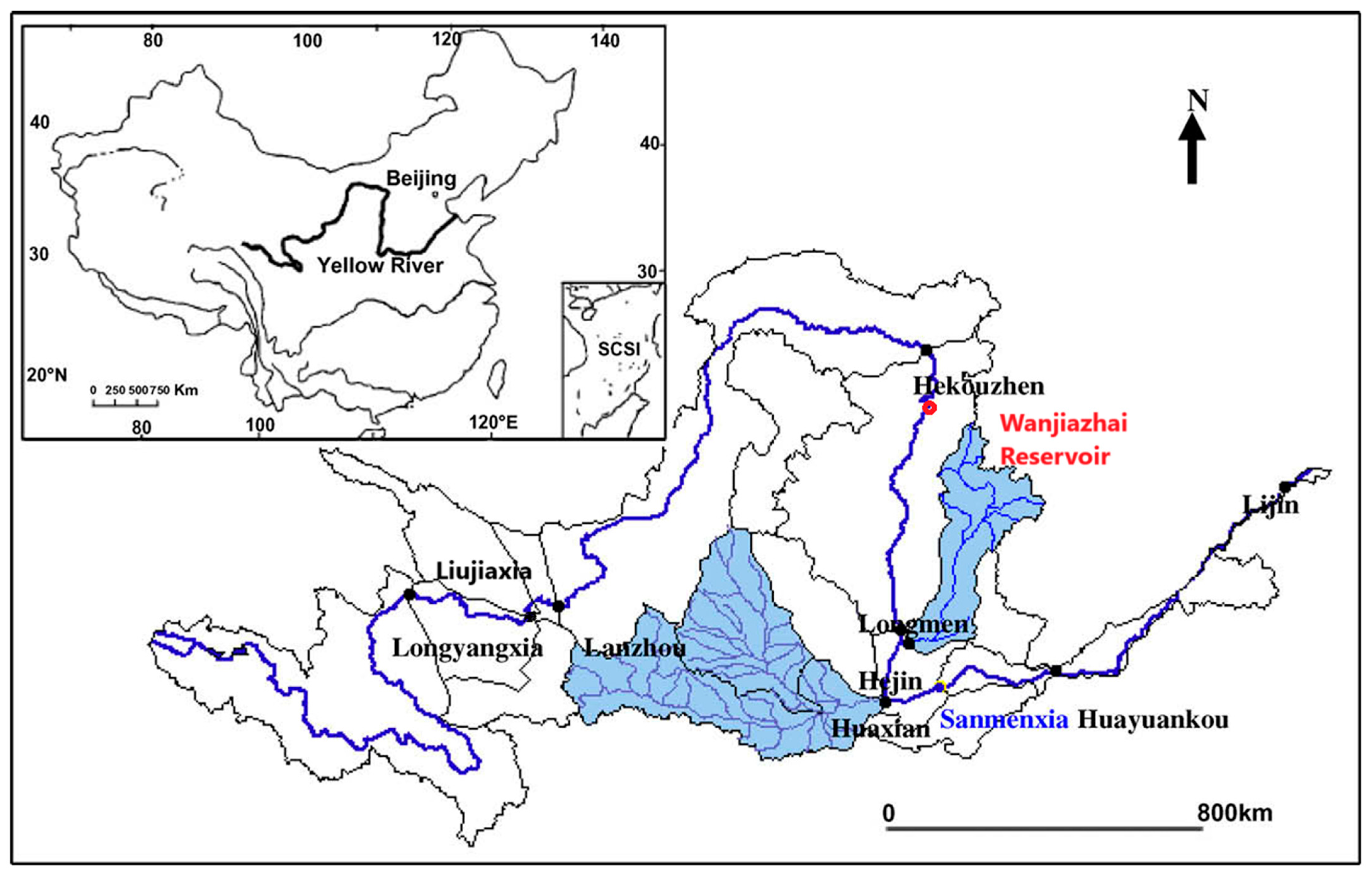
3.1. Study Region
3.2. Datasets
3.3. Study Design under the Heuristic
4. Results and Discussion
4.1. Training, Testing, and Forecasting
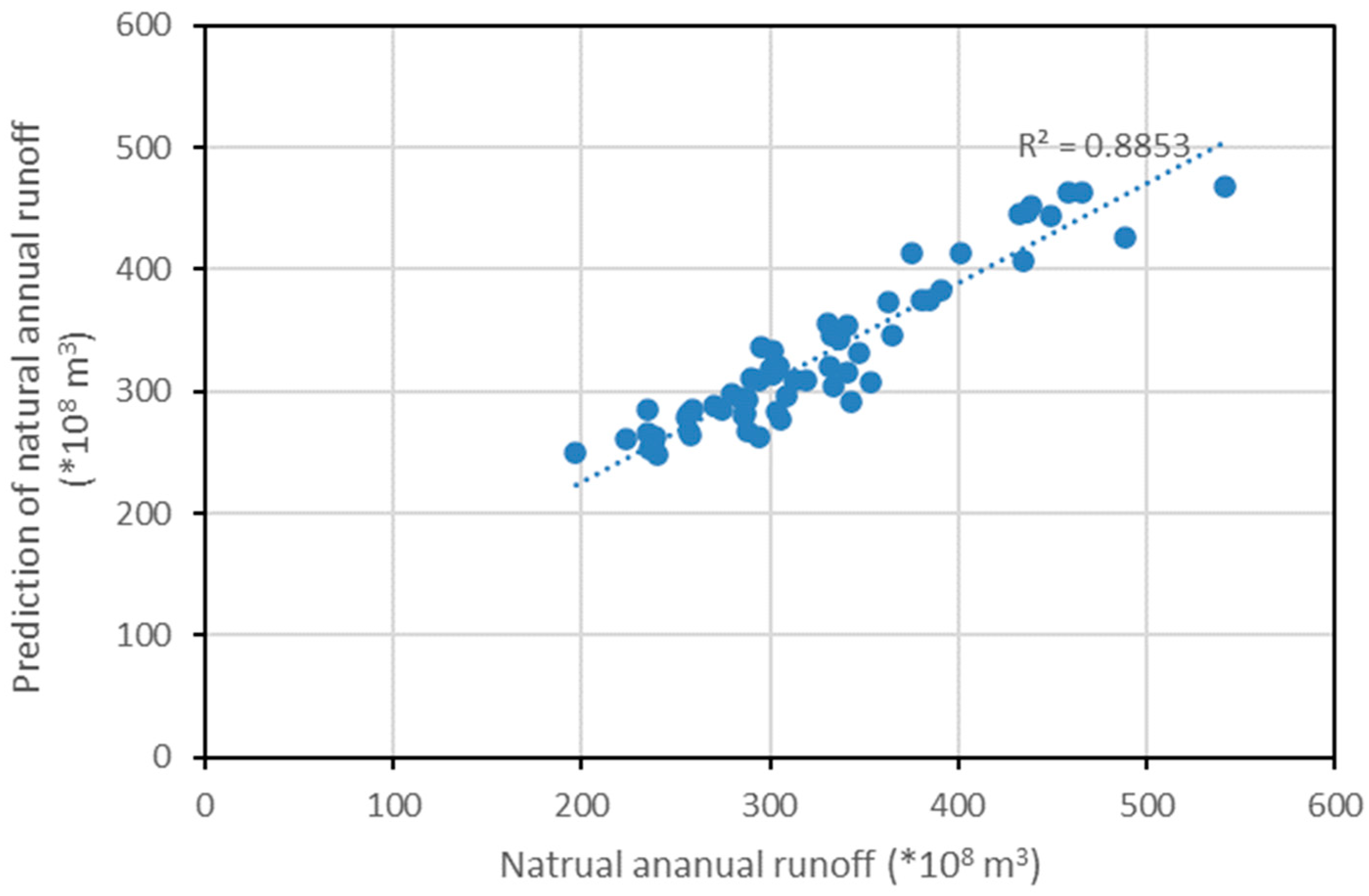
4.2. Forecasting Performs Best during the Period 2004–2014 and Extreme Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Singh, V.P.; Wang, B.; Yu, Y. CEREF: A hybrid data-driven model for forecasting annual streamflow from a socio-hydrological system. J. Hydrol. 2016, 540, 11. [Google Scholar] [CrossRef]
- Sun, F.; Sheng, D.; Ma, M.; Liu, L. Evaluation on Implementation of Water Law in China. Water Resour. Manag. 2019, 33, 2599–2613. [Google Scholar] [CrossRef]
- Sheng, D.; Yu, L.; Sun, F.; Xie, J.; Yu, Y. Reengineering and Its Reliability: An Analysis of Water Projects and Watershed Management under a Digital Twin Scheme in China. Water 2023, 15, 3203. [Google Scholar] [CrossRef]
- Lin, Z.; Zhu, J.; Wang, K. Hydrological Practice and Reflection on Promoting High Quality Development of the Yangtze River Economic Belt. Water Resour. Dev. Res. 2024, 24, 6. [Google Scholar]
- Friis-Christensen, E.; Lassen, K. Length of the Solar Cycle: An Indicator of Solar Activity Closely Associated with Climate. Science 1991, 254, 698–700. [Google Scholar] [CrossRef]
- Yonaba, R.; Mounirou, L.A.; Tazen, F.; Koita, M.; Biaou, A.C.; Zoure, C.O.; Queloz, P.; Karambiri, H.; Yacouba, H. Future cliamte or land use? Attribution of changes in surface runoff in a typical Sahelian landscape. Comput. Rendus Geosci.-Sci. Planete 2023, 355, 411–438. [Google Scholar] [CrossRef]
- Hong-Yan, L.; Li-Jun, X.; Xiao-Jun, W. Relationship between solar activity and flood/drought disasters of the Second Songhua river basin. J. Water Clim. Change 2015, 6, 8. [Google Scholar] [CrossRef]
- Xu, C.; Li, F.-w.; Feng, P. A new hybrid model for nonlinear and non-stationary runoff prediction at annual and monthly time scales. J. Hydro-Environ. Res. 2018, 20, 77–92. [Google Scholar]
- Wang, W.; Du, Y.; Chau, K.; Chen, H.; Liu, C.; Ma, Q. A Comparison of BPNN, GMDH, and ARIMA for Monthly Rainfall Forecasting Based on Wavelet Packet Decomposition. Water 2021, 13, 2871. [Google Scholar] [CrossRef]
- Li, C.H.; Yang, Z.F.; Huang, G.H.; Li, Y.P. Identification of relationship between sunspots and natural runoff in the Yellow River based on discrete wavelet analysis. Expert Syst. Appl. 2009, 36, 10. [Google Scholar] [CrossRef]
- Tian, J.; Nelson, D.M.; Hu, F.S. Possible linkages of late-Holocene drought in the North American midcontinent to Pacific Decadal Oscillation and solar activity. Geophys. Res. Lett. 2006, 33, 6. [Google Scholar] [CrossRef]
- Rind, D. The Sun’s role in climate variations. Science 2002, 296, 673–677. [Google Scholar] [CrossRef] [PubMed]
- Shindell, D.T.; Schmidt, G.A.; Mann, M.E.; Rind, D.; Waple, A. Solar Forcing of Regional Climate Change during the Maunder Minimum. Science 2001, 294, 2149–2152. [Google Scholar] [CrossRef] [PubMed]
- Kelly, P.M.; Wigley, T.L. Solar cycle length, greenhouse forcing and global climate. Nature 1992, 360, 328–330. [Google Scholar] [CrossRef]
- Labitzke, K.; Van Loon, H. Some recent studies of probable connections between solar and atmospheric variability. Ann. Geophys. 1993, 11, 11. [Google Scholar]
- Zhao, J.; Han, Y.-B.; Li, Z.-A. The effect of solar activity on the annual precipitation in the Beijing area. Chin. J. Astron. Astrophys. 2004, 4, 9. [Google Scholar] [CrossRef]
- Jones, P.D.; Jonsson, T.; Wheeler, D. Extension to the North Atlantic Oscillation using early instrumental pressure observations from Gibraltar and South-West Iceland. Int. J. Climatol. 1997, 17, 1433–1450. [Google Scholar] [CrossRef]
- Kane, R.P. Prediction of droughts in North-East Brazil: Role of ENSO and use of periodicities. Int. J. Climatol. 1997, 17, 655–665. [Google Scholar] [CrossRef]
- Pekarova, P.; Miklanek, P.; Pekar, J. Spatial and temporal runoff oscillation analysis of the main rivers of the world during the 19th-20th centuries. J. Hydrol. 2003, 274, 62–79. [Google Scholar] [CrossRef]
- Wrzesinski, D.; Sobkowiak, L.; Mares, I.; Dobrica, V.; Mares, C. Variability of River Runoff in Poland and Its Connection to Solar Variability. Atmosphere 2023, 14, 1184. [Google Scholar] [CrossRef]
- Pekarova, P.; Miklanek, P.; Pekar, J. Long-term trends and runoff fluctuations of European rivers. In Proceedings of the Fifth FRIEND World Conference, Havana, Cuba, 27 November–1 December 2006; pp. 520–525. [Google Scholar]
- Lin, Z. Seriously implement the water management concept of "water conservation priority, spatial balance, systematic governance, and dual pronged efforts" to accelerate the high-quality development of hydrology. Water Resour. Dev. Res. 2021, 21, 5. [Google Scholar]
- Li, H.Y.; Wang, Y.X.; Li, X.B. The mechanism and forecasting methods for severe droughts and floods in a river basin in China. Chin. Geogr. Sci. 2011, 21, 531–542. [Google Scholar] [CrossRef]
- Barbulescu, A.; Zhen, L. Forecasting the River Water Discharge by Artificial Intelligence Methods. Water 2024, 16, 1248. [Google Scholar] [CrossRef]
- Zhang, E.; Hou, L.; Shen, C.; Shi, Y.; Zhang, Y. Sound quality prediction of vehicle interior noise and mathematical modeling using a back propagation neural network (BPNN) based on particle swarm optimization (PSO). Meas. Sci. Technol. 2016, 27, 015801. [Google Scholar] [CrossRef]
- Pandey, S.; Wu, L.; Guru, S.M.; Buyya, R. A Particle Swarm Optimization-Based Heuristic for Scheduling Workflow Applications in Cloud Computing Environments. In Proceedings of the 24th IEEE International Conference on Advanced Information Networking and Applications, Perth, Australia, 20–23 April 2010; pp. 400–407. [Google Scholar]
- Das, G.; Pattnaik, P.K.; Padhy, S.K. Artificial Neural Network trained by Particle Swarm Optimization for non-linear channel equalization. Expert Syst. Appl. 2014, 41, 3491–3496. [Google Scholar] [CrossRef]
- Jin, C.; Jin, S.W.; Qin, L.N. Attribute selection method based on a hybrid BPNN and PSO algorithms. Appl. Soft Comput. 2012, 12, 2147–2155. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, Y.; Peng, Z.; Wang, G. Preliminary study on the relationship between sunspot activity and runoff and floods in the Yellow River, China. J. Water Resour. Water Eng. 1997, 8, 10. [Google Scholar]
- Jiang, T.; Du, Y.; Ding, Z. Exploration of the Relationship between Sunspots and Runoff. Pract. Electron. 2014, 14, 2. [Google Scholar]
- Helal, H.R.; Galal, A.A. An early prediction of the maximum amplitude of the solar cycle 25. J. Adv. Res. 2013, 4, 275–278. [Google Scholar] [CrossRef]
- Fausett, L.V. Fundamentals of Neural Networks: Architectures, Algorithms, and Applications; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- GB/T 22482—2008; Chinese Standard. Standard for Hydrological Information and Hydrological Forecasting. The Standardization Administration China: Beijing, China, 2008.



| Item | Measured Runoff | Natural Runoff | ||||
|---|---|---|---|---|---|---|
| Training | Testing | Forecasting | Training | Testing | Forecasting | |
| The ratio with <20% error | 72.4% | 50.0% | 78.3% | 56.3% | 83.7% | 78.1% |
| Average absolute error | 27.6% | 22.0% | 21.7% | 16.3% | 16.3% | 21.9% |
| Minimum error | 0.9% | 1.4% | 1.4% | 0.7% | 0.3% | 0.9% |
| Maximum error | 110.6% | 63.7% | 57.6% | 42.9% | 38.7% | 51.7% |
| R2 | 0.046 | 0.227 | 0.003 | 0.033 | 0.072 | 0.157 |
| Kling Gupta efficiency | 0.055 | 0.364 | −0.068 | -0.044 | 0.204 | −0.466 |
| Item | Measured Runoff | Natural Runoff | ||||
|---|---|---|---|---|---|---|
| Training | Testing | Forecasting | Training | Testing | Forecasting | |
| The ratio with <20% error | 90.5% | 90.7% | 89.3% | 93.3% | 93.5% | 92.3% |
| Average absolute error | 9.6% | 9.3% | 9.7% | 6.7% | 6.5% | 6.4% |
| Minimum error | 0.1% | 2.4% | 3.6% | 0.5% | 1.3% | 1.6% |
| Maximum error | 34.5% | 26.2% | 26.8% | 26.9% | 21.1% | 21.7% |
| R2 | 0.887 | 0.837 | 0.831 | 0.887 | 0.875 | 0.864 |
| Kling Gupta efficiency | 0.912 | 0.735 | 0.802 | 0.881 | 0.764 | 0.885 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, F.; Lu, X.; Yang, M.; Sun, C.; Xie, J.; Sheng, D. A Forecast Heuristic of Back Propagation Neural Network and Particle Swarm Optimization for Annual Runoff Based on Sunspot Number. Water 2024, 16, 2737. https://doi.org/10.3390/w16192737
Sun F, Lu X, Yang M, Sun C, Xie J, Sheng D. A Forecast Heuristic of Back Propagation Neural Network and Particle Swarm Optimization for Annual Runoff Based on Sunspot Number. Water. 2024; 16(19):2737. https://doi.org/10.3390/w16192737
Chicago/Turabian StyleSun, Feifei, Xinchuan Lu, Mingwei Yang, Chao Sun, Jinping Xie, and Dong Sheng. 2024. "A Forecast Heuristic of Back Propagation Neural Network and Particle Swarm Optimization for Annual Runoff Based on Sunspot Number" Water 16, no. 19: 2737. https://doi.org/10.3390/w16192737
APA StyleSun, F., Lu, X., Yang, M., Sun, C., Xie, J., & Sheng, D. (2024). A Forecast Heuristic of Back Propagation Neural Network and Particle Swarm Optimization for Annual Runoff Based on Sunspot Number. Water, 16(19), 2737. https://doi.org/10.3390/w16192737






