3.2. Surface Reservoirs in the Regulation of Water Supply and Hydrological Variability in Spain
According to MIMAM (2000) [
13], the source of all the data discussed below, the total contribution of useful rainfall in Spain is distributed as shown in
Table 4.
Of this river runoff, only 16 km3 is naturally regulated: 9 km3 for consistent demands (primarily for urban consumption) and 7 km3 for variable demands (such as irrigation). This regulation is largely due to the base flow of rivers, which originates from underground sources.
However, given the substantial gap between water demand and availability over the hydrological year, efforts have been made to enhance water regulation by constructing surface reservoirs to store excess water. Spain currently has a storage capacity of 47 km3 per year in these reservoirs, which supports a uniform demand of 36 km3 per year and a variable demand of 39 km3. This results in a total demand of 75 km3 per year, which is 1.6 times the reservoir capacity. Additionally, approximately 5.5 km3 per year is extracted from aquifers.
On the other hand, Spain is characterized by significant hydrological variability and irregularity, largely influenced by its diverse climate. This variability encompasses both temporal and spatial factors. Within the temporal aspect, it is important to differentiate between intra-annual seasonal variations and inter-annual variations.
Seasonal variations are particularly crucial for regulation plans, as reserves need only be managed for short periods, typically less than a year. Notably, disparities between inflows and demands are pronounced across different seasons. Inflows generally increase from October to February and are sustained until April, while demand, which includes a consistent year-round component, experiences a significant rise between May and August. However, variations in both inflows (e.g., snowmelt) and demand (e.g., reduced agricultural consumption) may occur, necessitating specific analysis for the area in question. As previously noted, managing intra-annual regulation tends to incur the lowest cost for storing excess water.
Surface reservoirs are primarily designed to align supply with the seasonal variations in demand for the basins or areas they serve. They typically use the average annual inflow over several years as a benchmark for resource management. However, interannual inflow distribution is highly variable and unpredictable. As a result, there are years in which the reservoir may not reach full capacity, leading to challenges in meeting demand. Conversely, in other years, inflows may exceed reservoir capacity, causing substantial volumes of water to be lost.
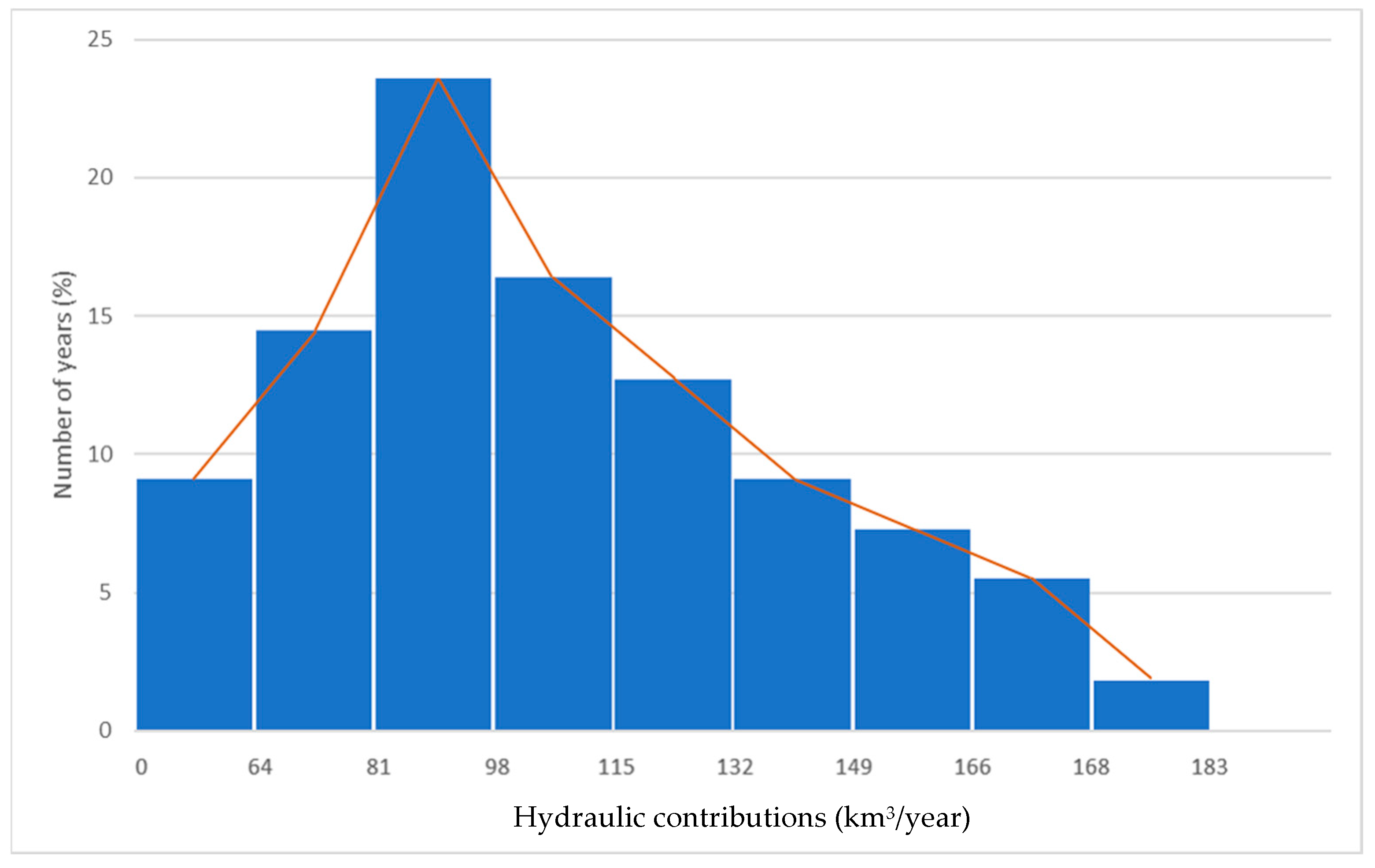
The series of annual contributions over a 55-year period, as detailed in the “Libro Blanco del Agua” (MIMAM, 2000) [
13], form the basis for the creation of
Figure 2 and
Table 5, which display the frequency distributions. The corresponding statistical parameters are outlined in
Table 6.
Regarding the mean of 111 km3/year, the notable high standard deviation of 39 km3/year and the positive skew coefficient of 0.65 indicate a departure from a normal distribution. This suggests more frequent periods of low rainfall—occurring in 60% of the years—while the remaining 40% of years experience above-average rainfall.
Consequently, a hypothetical reservoir designed to regulate 111 km3 of water annually would provide less than 90% of the demand in 47% of the years. Conversely, during 40% of the years with higher-than-average contributions, the reservoir would experience an annual excess of 12.5 km3. Over a century, the total demand would amount to 11,100 km3, while the supply would be 9849 km3 after a reduction of 1251 km3, thereby covering 89% of the total demand.
By increasing the reservoir capacity to 132 km3, which represents a 19% increase over the average contribution, the theoretical loss during the rainiest years would be reduced to 581 km3. Consequently, the supply would rise to 10,519 km3, covering 95% of the demand. This means that a 19% increase in reservoir capacity results in only a 6.8% increase in supply.
Expanding the capacity of a surface reservoir to enhance the probability of meeting a given demand involves significant economic considerations. The marginal return on substantial investments must be carefully evaluated. Surface reservoirs require design, construction, and filling. In contrast, aquifers are naturally formed and already filled (assuming they are not overexploited). Although detailed studies are necessary to understand their characteristics, aquifers do not require expansion. They can better accommodate variations in supply and demand, providing crucial support during dry years and absorbing excess water from wet years.
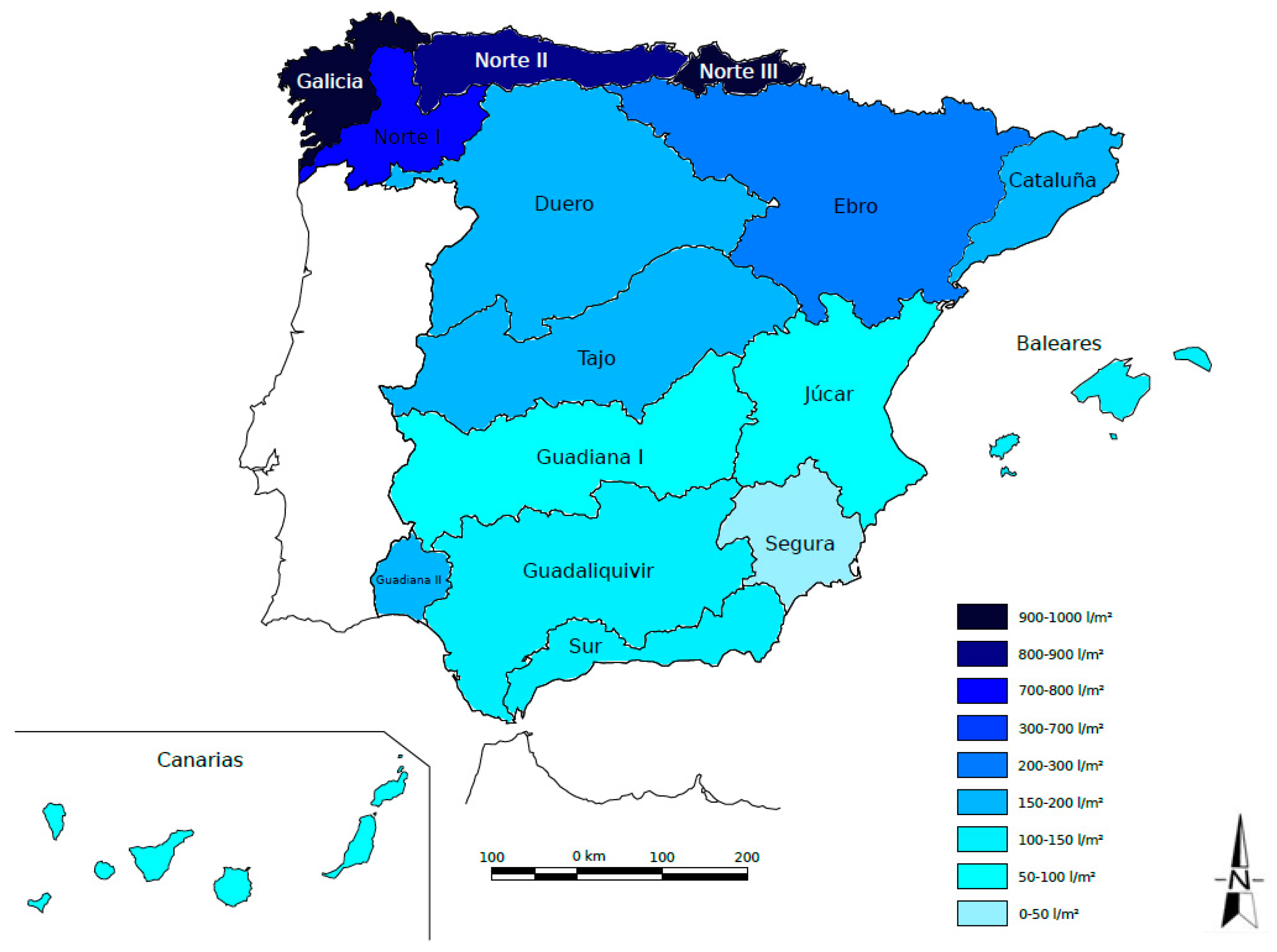
While the above values represent national annual averages, it is crucial to consider the spatial factor, which is particularly significant in Spain due to its hydrological variability.
Table 7 presents basic statistics on the average annual contributions for each of the designated territorial areas (see
Figure 3).
The irregularity of these contributions becomes evident when expressed relative to the surface area (l/m
2), ranging from 933 l/m
2 in the Galician Coast and Norte III to 42 l/m
2 in the Segura River basin. In this context, four nearly homogeneous regions with distinct statistical parameters can be identified within the Spanish Peninsula (
Table 8).
The following observations pertain to variability within each of these four regions:
On the Cantabrian coast, the variation coefficients in its four zones are generally lower than the national average, with the exception of Norte I, which is part of Lower Galicia (see
Table 7). This indicates that not only are the contributions significantly higher in this region, but they also exhibit more consistent patterns throughout the year, with a distribution that is closer to normal. This is reflected in a smaller absolute value of the skew coefficient, unlike in Norte II and III, where negative values are observed.
Additionally, the proportion of water inputs that contribute to aquifer recharge is somewhat lower than the national average, due to a higher fraction of surface runoff. This exception is found in Norte II, where the presence of carbonate lithologies results in a greater recharge of aquifers.
In the remaining northern regions (Duero, Tajo, Ebro, and Inner Basins of Catalonia), annual contributions are approximately 200 , which is higher than in the southern and Levante regions but less than a quarter of the amounts observed on the Cantabrian Coast. Additionally, the irregularity throughout the year is significantly greater, as evidenced by an average coefficient of variation of 0.70, compared to 0.35 on the Cantabrian Coast.
As one moves south, both the volume of unit input and its irregularity show a notable trend: the average annual contribution in the Guadiana, Guadalquivir, and Southern basins is 116 l/m2. Here, both the coefficient of variation (0.78) and the skew coefficient (0.91) are the highest among the four regions.
In the Levante region (Júcar and Segura rivers), the contribution is notably low at 68 , which is about one-third of the national average and one-twelfth of that on the Cantabrian Coast. Despite the annual variability in rainfall being similar to that of the southern regions, the contribution variability is markedly lower (coefficient of variation of 0.34). This reduction is attributed to the significant role of aquifers in regulating rainfall, which leads to a recharge rate of 73%—three times higher than in other zones.
3.3. Aquifers and Their Regulatory Capacity
It is generally accepted that the water resources of a geographical area include both its renewable resources (surface and groundwater). In addition to these renewable resources, aquifers often contain substantial reserves of water that may take years to replenish. Under natural conditions, these reserves are considered a form of permanent storage. However, under influenced conditions, these reserves can provide increased temporary availability, potentially enhancing long-term resource levels.
Therefore, when discussing the water in underground reservoirs or aquifers, it is important to make a distinction:
On the one hand, there are the reserves, which refer to the volume of groundwater that is readily accessible at a given time. These reserves are primarily determined by the aquifer’s total volume and its effective porosity.
On the other hand, resources refer to the volume of water that can be sustainably extracted annually, taking into account the need for conservation and protection as well as technical and economic constraints. Generally, resources represent only a portion of the reserves. However, in some aquifers with high inflow rates and permeability, the available resources may exceed the reserves.
Renewable reserves and permanent reserves can be considered separately, with their sum representing the total reserves at a given time. Distinguishing between these two types of reserves requires accounting for seasonal and inter-annual variations in the water table.
For resources, the average annual inflow over a long period—typically exceeding 10 years—is used. During this period, the mean annual recharge is assumed to be equal to the mean annual flow , implying no net change in the stock. Thus, these values () are identified as the renewable reserves () of the aquifer. It is important to note that this does not imply that such a volume of water is continuously present, as it is subject to inflows and outflows throughout the year.
In addition to the renewable reserves, there are permanent reserves (). Consequently, the total reserves () assigned to the aquifer are the sum of both types: .
The ratio of these reserves is crucial for assessing the aquifer’s regulatory capacity. This ratio is often expressed as the “Annual Renewal Rate” (
) [
18,
19], defined by the quotient
Additionally, the inverse of this ratio is known as the ‘Renewal Period in Years’ (PRA), which represents the time required to deplete all of the aquifer’s reserves while maintaining natural replenishment rates
This rate and period exhibit significant variability across different aquifers. The renewal rate can range from values close to 1 to less than one thousandth, resulting in corresponding renewal periods ranging from less than a year to several millennia. For instance, Castany (1975) [
18] provides examples of real-world cases: the greensand aquifer in the Paris Basin has a renewal rate of 0.005 and a renewal period of 2000 years; the Pliocene Meknes-Fez basin in Morocco has a rate between 0.1 and 0.5, with a renewal period of 10 to 20 years; and the Inkermann alluvial sub-flow aquifer in Russia has a rate of 0.7 and a renewal period of 1.5 years. The significance of these reserves and the regulating capacity of the aquifer, based on the renewal rate values, are described by Margat (1966) [
19], as depicted in
Table 9.
Table 10 presents estimates of annual recharge and reserves for the geographical basins of peninsular Spain, with the reserve values based on MIMAM (2000) estimates [
13].
In inland Spain, the Duero and Guadiana basins are notable for the regulatory power of their aquifers, with renewal periods exceeding 14 years. Particularly significant is the good average regulatory capacity of aquifers in regions that, despite being large water consumers, experience scarce and highly irregular recharge. This includes the Levante area (Júcar and Segura) with a renewal period of over 30 years, the Internal Basins of Catalonia with a 14-year renewal period, and the Southern basin with an average renewal period of 8 years.
For all peninsular aquifers combined, it is estimated that the total reserves (WT) amount to 219 km3 and renewable reserves (V) to 29 km3, resulting in average values of:
These averages indicate that many aquifers, except those on the Cantabrian coast, have substantial reserves, allowing for effective regulation both annually and interannually.
In Spain, under natural conditions, groundwater resources, estimated at 29 km3/year, are 1.8 times greater than surface water resources (16 km3/year). However, to meet demand, priority has traditionally been given to the use and regulation of surface water.
Besides economic considerations and factors such as underground storage and reduced evaporation losses, one significant advantage of groundwater is the ‘permanent reserve’. This reserve offers a reliable means to meet demand during years of low rainfall.
It is important to note that a key characteristic of underground reservoirs is their ‘inertia’ to recharge or discharge impulses. This is because the active reserves are those located above the outflow levels. Even during dry years, when it becomes necessary to pump a flow exceeding the natural recharge, the impact of the aquifer’s discharge will take time to manifest.