Temporal Dynamics and Predictive Modelling of Streamflow and Water Quality Using Advanced Statistical and Ensemble Machine Learning Techniques

Abstract

Changes in water quality are closely linked to seasonal fluctuations in streamflow, and a thorough understanding of how these variations interact across different time scales is important for the efficient management of surface water bodies such as rivers, lakes, and reservoirs. The aim of this study is to explore the potential connection between streamflow, rainfall, and water quality and propose an optimised ensemble model for the prediction of a water quality index (WQI). This study modelled the changes in five water quality parameters such as ammonia nitrogen (NH₃-N), phosphate (PO₄³⁻), pH, turbidity, total dissolved solids (TDS), and their associated WQI caused by rainfall and streamflow. The analysis was conducted across three temporal scales, weekly, monthly, and seasonal, using a generalised additive model (GAM) in Toowoomba, Australia. TDS, turbidity, and WQI exhibited a significant nonlinear variation with the changes in streamflow in the weekly and monthly scales. Additionally, pH demonstrated a significant linear to weakly linear correlation with discharge across the three temporal scales. For the accurate prediction of WQI, this study proposed an ensemble model integrating an extreme gradient boosting (XGBoost) and Bayesian optimisation (BO) algorithm, using streamflow as an input across the same temporal scales. The results for the three temporal scales provided the best accuracy of monthly data, based on the accuracy metrics R² (0.91), MAE (0.20), and RMSE (0.42). The comparison between the test and predicted data indicated that the prediction model overestimated the WQI at some points. This study highlights the efficiency of integrating rainfall, streamflow, and water quality correlations for WQI prediction, which can provide valuable insights for guiding future water management strategies in similar catchment areas, especially amidst changing climatic conditions.

1. Introduction

The pollution of rivers and streams resulting from both point and non-point sources is increasing due to the emerging influence of extreme rainfall events and their associated streamflow [1]. Surface water quality and ecosystem health are influenced by a complex interplay between factors such as climate variability, hydrological processes, geochemical cycles, and human activities [2,3,4]. The rapid growth of population demands increased food production, which consequently disturbs the natural land cover. The increased use of chemical fertilisers causes pollution as they are transported to surface and groundwater systems during extreme rainfall events [5]. The change in surface runoff under changing rainfall patterns induces variations in pollutant transfer to water bodies [6,7]. Rainfall, associated streamflow, and stream water quality are intimately linked; however, these three aspects are often analysed separately, and a comprehensive assessment of their combined influence on stream water quality has not been explored much [2,8].

Stream water quality encompasses three essential aspects of freshwater: its physical state (whether it is frozen or not), temperature, and the concentration of constituents. These factors significantly influence the major processes that regulate stream water quality, such as transport, exchange, storage, and the decomposition of organic matter [9,10,11]. The riverine ecosystem related to water quality is subjected to various stresses due to these processes, and streamflow patterns significantly interact with the physical and chemical composition and the state of the water [2,12]. However, there has been limited studies of how changes in streamflow patterns, influenced by varying rainfall magnitudes, interact with constituent concentrations in water bodies over different time scales [13].

There are several studies related to process-based hydrological and water quality simulation models, where streamflow variability was considered as a predictor of water quality [14]. These include the MIKE 21 and MIKE 31 models [15,16], QUAL models [17], QUAL 2 K model [18], QUASAR model [19,20], SWAT model [21], and IISDHM [22]. These models have illuminated an improved understanding of how water quality varies with streamflow variability. However, the simulation accuracy of these models is affected by spatial variations arising from hydrometeorological variability within the catchment scale. Additionally, numerous studies have demonstrated a correlation between land use change and the concentration of water constituents such as dissolved oxygen, total dissolved solids, and nutrients. Specifically, these constituents were detected to be higher in agricultural watersheds compared to forests [23]. However, in addition to land use change, stream water quality is also influenced by geology, topography, soil characteristics, and climate variability [2].

Recently, the prediction of a water quality index (WQI) has been advanced through artificial intelligence techniques such as artificial neural network (ANN), support vector machine (SVM), and adaptive neuro fuzzy inference system (ANFIS) [24,25,26]. Among them, ANN exhibits a poor prediction accuracy if the range of testing data exceeds the range of training data. Whilst SVM provides high accuracy, it requires determining the optimum values for a large number of parameters. Whereas, ANFIS is a robust algorithm which combines ANN and fuzzy logic for modelling nonlinear, complex, and dynamic systems [27]. Despite having its potency, it is computationally complex, and the accuracy is compromised by internal parameters which require a precise weight assignment in fuzzy rule membership [28]. On the other hand, hybrid models can effectively recognise the nonlinearity of input and output parameters, demonstrating enhanced robustness against data fluctuations [28].

Extreme gradient boosting (XGBoost) is recognised as a robust ensemble learning algorithm known for its effectiveness in data mining and regression tasks [29]. It stands out for its speed, robustness, and ability to deliver precise predictions, as demonstrated in its performance in major data competitions such as Kaggle and Data Castle [30]. It has been widely applied in several fields, including predicting concrete electrical resistivity for structural health monitoring and accurately mapping steel properties [31,32]. However, its utilisation in predicting streamflow and water quality is limited. We aim to showcase its potential use in predicting WQI.

Convolutional neural network (CNN) is a prevalent topic in deep learning (DL) research which has proven its effectiveness in tasks of computer vision (CV), computer-aided diagnosis (CAD), natural language processing (NLP), and pattern recognition [33]. The hyperparameters are crucial parameters to set before model training, governing its learning process and improving performance. An efficient hyperparameter optimisation algorithm can significantly enhance model performance and accuracy [34,35,36]. The most widely used hyperparameter optimisation method is grid search, which operates on the principle of exhaustive searching. However, it is limited by the high computational cost associated with exhaustive searching [34]. To mitigate this issue, the random search algorithm was introduced; however, previous studies have found it to be unreliable for training complex models [36]. Recently, Bayesian optimisation (BO) has emerged as a highly effective algorithm for addressing machine learning optimisation problems. The optimisation of artificial neural networks (ANNs), support vector machines (SVMs), and other models can be effectively carried out using this algorithm [30,37]. There have been studies on the implementation of XGBoost in hydrology [38]; however, there has been a limited investigation on its application to water quality prediction. Moreover, the estimation and optimisation of hyperparameters is one of the most important steps in the XGBoost model, and applying a BO algorithm can improve the prediction accuracy [39].

In this study, we aimed to investigate the impact of rainfall and streamflow on water quality parameters and associated WQI by applying models using advanced statistical and ensemble machine learning techniques to describe this relationship. In our previous study, five water quality parameters (NH₃-N, PO₄³⁻, pH, turbidity, total dissolved solids) were selected to compute the WQI, and we applied five machine learning and two deep learning algorithms to predict the WQI [40]. In addition to this, the trend of rainfall and water quality parameters and the correlation between rainfall and water quality were examined. Building on our previous study, this research proposed a new statistical technique, the generalised additive model (GAM), to identify the correlation between rainfall, streamflow, and water quality parameters. Further, an ensemble learning algorithm (BO–XGBoost) was used to predict the WQI across three temporal scales. The Toowoomba region of Australia consists of three major reservoirs, namely, Cooby, Cressbrook, and Perseverance [40]. The Cressbrook Reservoir was selected as the case study area, being one of the three major reservoirs for town water supply in the Toowoomba region of Australia. Due to the availability of streamflow data, this was selected as the representative case study area. The main focuses of this study are as follows:

• Simulate changes in water quality parameters and the associated WQI with variations in rainfall and streamflow across three temporal scales: weekly, monthly, and seasonal.
• Propose a novel approach combining XGBoost with a Bayesian optimisation (BO) algorithm to predict the WQI, which considers the influence of streamflow based on the same three temporal scales. The XGBoost was applied to establish the relation between the streamflow and water quality data, and the BO algorithm was used to optimise the XGBoost hyperparameters to improve the accuracy of the prediction model.

2. Materials and Methods

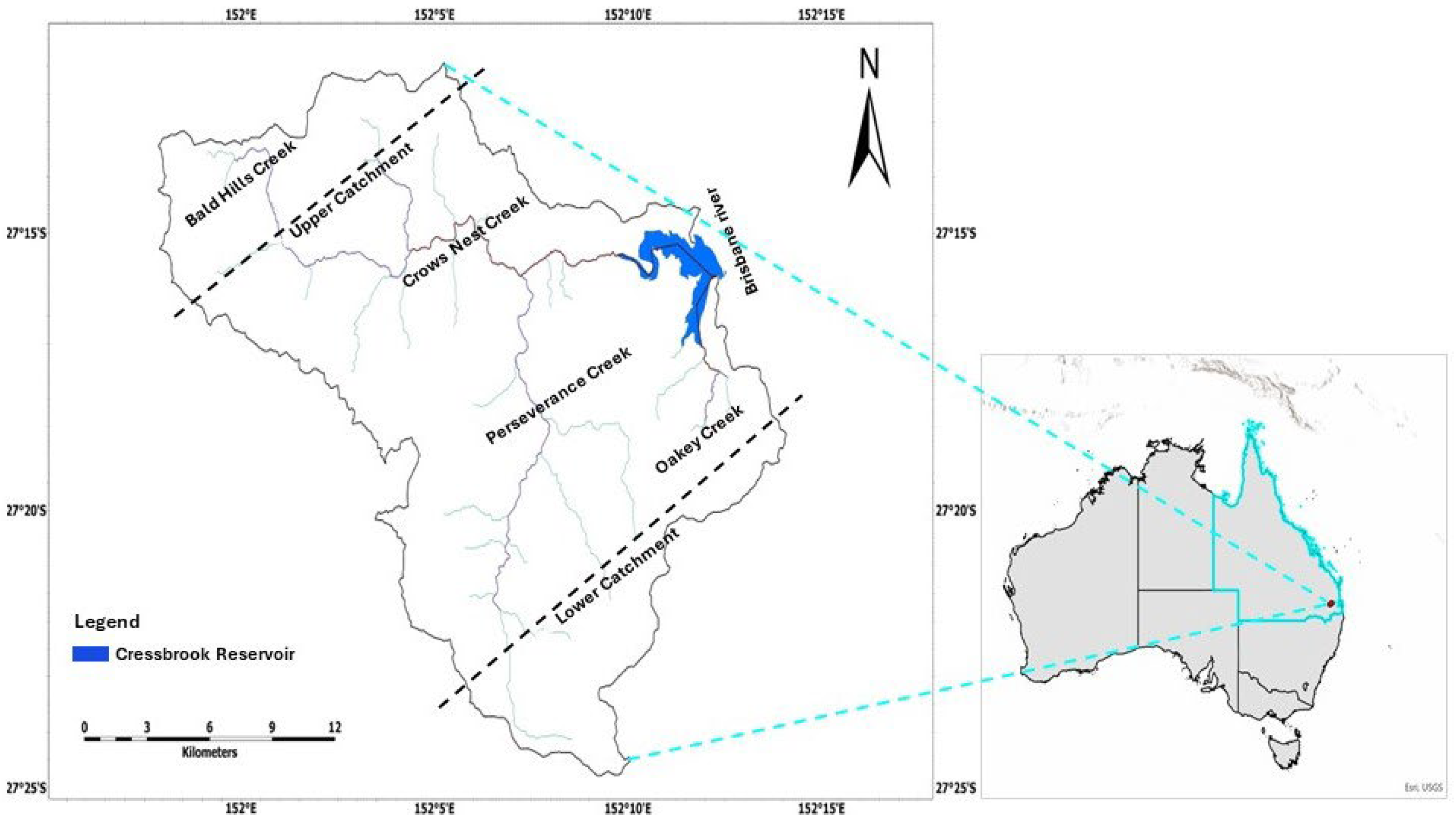
2.1. Study Area

Cressbrook Reservoir is located approximately 80 km northwest of Brisbane and 55 km northeast of Toowoomba in South East Queensland, Australia (Figure 1). It is situated at an elevation of 280 m Australian Height Datum (AHD) [41] and flows to the Brisbane River [42]. The upper Cressbrook Creek comprises Rocky Creek, Bald Hills, Old Woman’s Hut, and Crows Nest, while the lower subcatchment includes Cressbrook Reservoir and the major tributaries of Kipper and Oakey Creeks [43]. The geological features in the area are diverse and characterised by a basalt covering along the mountain range. Rainfall in the upper subcatchment is relatively higher compared to the middle (above weir and Kipper Creek) and lower catchment (below weir). The influence of the upstream dams and the lower Cressbrook weirs has substantially altered the water flow, leading to a decrease in the number of waterholes. Land use in the upper catchment includes grazing on native vegetation, animal husbandry, national park, vegetation, and irrigated perennial horticulture. In contrast, the lower catchment area is utilised for forestry, grazing on native vegetation, animal husbandry, rural residential areas, and Toogoolawah sewage treatment plant. The water quality in this area is impacted by salinity resulting due to geology and modified water flows, as well as erosion and small scalds [43]. The major challenges faced by the Cressbrook catchment include the removal and degradation of riparian vegetation, cattle grazing, deforestation, agricultural activities, and residential development [44].

2.2. Data

The relationship between water quality and local rainfall and stream discharge was analysed using daily maximum discharge data from site number 143921A (Cressbrook Creek at Rosentretars Crossing, −27.1361°, 152.33°) [45] and daily rainfall data from the Cressbrook Reservoir weather station number 040808 (−27.2641°, 152.1959°) [46]. The data were obtained from the Queensland Water Monitoring Portal (https://water-monitoring.information.qld.gov.au/, accessed on 6 March 2024) and the Bureau of Meteorology website (https://www.bom.gov.au/, accessed on 7 March 2024). The study period covered the period from 2000 to 2022 due to the availability of water quality data. Weekly water quality data were provided by the Toowoomba Regional Council (TRC) which is responsible for maintaining three water supply reservoirs in the Toowoomba region. The rationale for selecting five water quality parameters (PO₄³⁻, NH₃-N, pH, TDS, and turbidity) and the computation of the WQI were explained in the previous study [40].

2.3. Mathematical Background

2.3.1. Computation of Variation in Water Quality Parameters Using GAM

The variation in the selected water quality parameters in response to changes in rainfall and streamflow was predicted using a generalised additive model (GAM). The GAM integrates elements of both generalised linear models and additive models. It employs an additive link function to define the relationship between the response variable and the nonparametric predictor variables [47]. By applying multiple linear smooth functions, the GAM effectively addresses data nonlinearity, prevents overfitting, and obviates the requirement of prior knowledge of specific predictive function forms [48].

The GAM model, which captures the variation in the response variable using the independent variables through smooth functions, can be expressed as follows:

g(E(Y)) = β₀ + f₁ (x₁) + f₂ (x₂) + ....... + f_p (x_p) + ε

(1)

where Y is the response variable, and E(Y) is its expected value. The response distribution is not required to be normal; instead, the observations are extracted from a member of the exponential family of the distribution, to be specific Y~EF (μ, φ), where φ is the scale parameter, and μ is the mean. Similarly, g is the smooth monotonic link function (uniform, logarithmic, or transpose) that maps the mean of the distribution function to the linear predictor scale [9]. β₀ is the model intercept, and f₁, f₂...f_p are the smooth functions of the control variables x₁, x₂, ......x_p.

Smooth functions provide a flexible nonlinear illustration of covariates on the response variable by determining an appropriate basis which defines the function space to which f belongs. The components of this space are called basis functions. For instance, in the case of a second-order polynomial, the basis functions would be 1, x, and x₂ forming the set

b₀(x) = x0 = 1, b₁(x₁) = x, b₂(x) = x²

The sum of the basis functions and their corresponding regression coefficients β (weights) form the smooth function f, which can be written as

$$f(x) {\sum }_{i=1}^{k}bj\left(x\right)\beta i$$

(2)

where k denotes the fundamental dimension of the smooth function. Each basis function constitutes a column in the model matrix, allowing every smooth function f to be written in a general matrix form f_i(x_i) = X_iβ, where X_i is the model matrix [9]. Among the various types of smooth functions, a cubic spline smooth function was applied in this study.

The GAM equation in Equation (1) was modified in this study to illustrate the variation in water quality. Water quality parameters were predicted as an additive function of two covariates, rainfall and streamflow, and Equation (1) was reformed as follows.

E(Y) = β₀ + fr (Rainfall) + fq (Streamflow) + ε

(3)

Here, Y is the predicted concentration of water quality parameters, and fr and fq are the smooth functions of rainfall and streamflow, respectively. The water quality was modelled and forecasted on three temporal scales: weekly, monthly, and seasonal. A cubic spline smooth function was applied in this study, which is a smooth curve composed of segments of cubic polynomials, seamlessly connected so that the entire spline maintains continuity in both its value and the first two derivatives [9]. To fit Equation (3) for the interpretation of changes to water quality parameters, the ‘mgcv’ package of R software (4.3.2) was used. A generalised cross-validation (GCV) score was considered to check whether the model overfitted the data, and a p value was used to evaluate the model’s smoothness.

2.3.2. Prediction of WQI

In this study, an XGBoost algorithm with Bayesian optimisation was applied to predict the water quality index (WQI) using discharge data. This approach aimed to enhance model accuracy and reliability by fine-tuning hyperparameters through a systematic optimisation process. A detailed description of the algorithms is explained in the following sections.

Extreme Gradient Boosting

Extreme gradient boosting (XGBoost) is a popular and powerful machine learning model leveraging a scalable end-to-end tree boosting system capable of capturing a complex nonlinear relationship between a set of predictor and output variables. XGBoost is distinguished by two fundamental optimisation improvements based on a gradient-boosting decision tree (GBDT) algorithm. Firstly, regularisation terms are incorporated into XGBoost’s objective function which helps to mitigate overfitting. Secondly, XGBoost utilises a second-order Taylor expansion of the target function, enhancing the precision of its loss function [30].

If a dataset is assumed to have n number of variables and is denoted as A = (x_i, y_i) where i = 1,2…, n and x_i represent the input variable, while y_i represents the response variable, a tree model based on the general form of classification and regression tree-based algorithm can be generated for the following output:

$$\widehat{y_i}=\phi \left(x_i\right)=\sum _{m=1}^M{f}_{m }{\left(x_i\right), f}_m \in Ԝ$$

(4)

where M is the number of trees trained, W is the space of regression trees, (W = [f(x) = μ^lx]), and f(x) represents a single tree structure. Similarly, μ represents the leaf weight, and l_x denotes the leaf node of the xth sample.

The objective function in XGBoost incorporates both a regularisation term and a loss function as explained by Chen and Guestrin [49]:

$$\mathcal{L}(f_t)=\sum _{i=1}^{n}L (y_{i,}{\widehat{y_i}}^{t-1}+f_t\left(x_i\right)+\Omega (f_t\left)\right)$$

(5)

where L is the loss function, and Ω is the regularisation term which deals with the objective function depending on the complexity of the model, which can be expressed as follows:

$$\Omega \left(f_t\right)=\gamma . T_t+\lambda {\displaystyle \frac{1}{2}}\sum _{j=1}^T{\mu }_j^2$$

(6)

where T denotes the number of trees, and γ denotes the penalty coefficient. The objective function in Equation (5) can be simplified using a second-order Taylor series expansion as follows [50]:

$$\mathcal{L}\left(f_t\right)=\sum _{i=1}^n[L (y_{i,}{\widehat{y_i}}^{t-1}+g_i{f}_t\left(x_i\right)+{\displaystyle \frac{1}{2}} h_i{f}_t^2 (x_i)]+\Omega (f_t)$$

(7)

n for the first-order g_i and second-order h_i can be expressed as follows [30]:

$$g_i={\displaystyle \frac{\partial L (y_{i },{\widehat{y_i}}^{t-1})}{\partial {\widehat{y_i}}^{t-1}}}$$

(8)

$$h_{i }={\displaystyle \frac{{\partial }^{2 }L \left(\right(y_{i },{\widehat{y_i}}^{t-1})}{\partial {\widehat{y_i}}^{t-1}}}$$

(9)

The final form of the objective function can be derived as follows [30]:

$$\mathcal{L}\left(f_t\right)=\sum _{i=1}^n[ g_i{\mu }_l(x_i)+{\displaystyle \frac{1}{2}}{h}_i{\mu }_l^2 (x_i)]+\gamma T+\lambda {\displaystyle \frac{1}{2}} \sum _{j=1}^T{\mu }_j^2$$

(10)

Bayesian Optimisation

Hyperparameters directly influence the behaviour of training algorithms and exert a significant impact on machine learning models. Efficient optimisation of hyperparameters is important for enhancing the efficiency of machine learning models [34]. Bayesian optimisation provides an effective way to solve computationally expensive functions by identifying optimal points. It integrates previous information about the objective function with sampled points to gather updated information about the function’s distribution using a Bayesian formula. By applying this updated information, global optimum values can be assessed [34]. Bayesian optimisation involves two major steps: first, the selection of a surrogate model, typically a Gaussian process to incorporate prior information about the objective function; and second, choosing an acquisition function to propose sampling points in the search space [51].

Establishment of the Prediction Model

To predict the WQI, we introduced a XGBoost-BO model, which involved the following steps, and the methodological flow chart is illustrated in Figure 2.

(i)

Data preparation and processing:

The data were preprocessed by selecting the relevant features, specifically ‘Discharge’ and ‘WQI’. The daily time series of discharge data was converted to weekly, monthly, and seasonal values, while weekly WQI data were aggregated into monthly and seasonal values to facilitate prediction across three temporal scales. The selected features were then divided into training and testing sets, where 70% of the data were allocated for training and 30% for testing. This division ensures that the model’s performance can be effectively evaluated on unseen data.

(ii)

Definition of the objective function for Bayesian optimisation:

An objective function was defined for the Bayesian optimisation (BO) to minimise the mean absolute error (MAE) of model predictions. The primary goal was to enhance the model’s accuracy for predicting the WQI by minimising the MAE.

(iii)

Specification of hyperparameter bounds:

Defining the specification of hyperparameter bounds is fundamental for effectively optimising a machine learning model. The common hyperparameters are learning rate, maximum depth of trees, subsample ratio of training instances, column subsample ratio for constructing each tree, and regularisation parameters such as gamma and lambda. The search space for the hyperparameters of the XGBoost model was specified. These included the learning rate (0.001, 0.2), maximum depth of trees (3, 10), subsample ratio of training instances (0.8, 1.0), column subsample ratio for constructing each tree (0.3, 1.0), gamma (0, 0.3), and lambda (0, 1.0).

(iv)

Implementation of Bayesian optimisation:

In the process of optimisation, the BO algorithm was employed, which balances exploration (trying new parameter configurations) and exploitation (using known configurations that are likely to be minimal) to minimise the objective function. It iteratively updates the probabilistic model based on observed outcomes using a Gaussian process to suggest new configurations for evaluation, aiming to find the optimal set of hyperparameters. In the proposed model, the acquisition function selected was based on a Gaussian process. The number of initial points was set to 10, and the optimisation process continued for 100 consecutive iterations.

(v)

Training the XGBoost model and evaluation:

Using the optimal hyperparameters identified through Bayesian optimisation, an XGBoost model was trained on the training dataset. The trained XGBoost model was then evaluated on a separate test dataset. Three performance metrics such as coefficient of determination R², mean absolute error (MAE), and root mean square error (RMSE) were computed. These metrics provided a comprehensive evaluation of the model’s accuracy and reliability.

If y₁, y₂…., y_n are observed values and ŷ₁, ŷ₂ …, ŷ_n are the predicted values, with ӯ representing the mean of y_i, the four metrics can be calculated as follows:

$$R^2=1-{\displaystyle \frac{\sum _{i=1}^n{(ŷ-y_i)}^2}{\sum _{i=1}^n(y_i-ӯ)}}$$

(11)

$$MAE={\displaystyle \frac{1}{n}} \sum _{i=1}^n\left|ŷ-\right.\left.ӯ\right|$$

(12)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}} {(ŷ-ӯ)}^2$$

(13)

The coefficient of determination R² measured the proportion of variance in the dependent variable that was predicted from the independent variable. The MAE measured the average magnitude of the errors in a set of predictions, and the RMSE quantified the square root of the average of the squared differences between predicted and actual observations. The methodological flow chart of the proposed XGBoost-BO model is illustrated in Figure 2.

(vi)

Analysis of predicted results:

Firstly, to demonstrate the appropriate fitting of the proposed model, line plots of the actual and predicted data on the training and test sets were generated. This was conducted to indicate the suitability of the proposed model for WQI prediction on different time scales. In addition, to identify patterns in model performance, a comparative analysis of metric values across three time scales was performed. The results from this analysis were then interpreted to determine the overall efficiency and reliability of the model in forecasting WQI, conferring insights into its applicability for practical water quality management.

3. Results

3.1. Descriptive Statistics

Table 1. Descriptive statistics of water quality parameters, rainfall, and streamflow.

Time Period	Statistics	Variable
		Rainfall (mm)	Streamflow (m3/sec)	PO43− (mg/L)	NH3-N (mg/L)	pH	Turbidity (NTU)	TDS (mg/L)	WQI
Weekly	Min	0.00	0.00	0.00	0.00	6.00	0.47	106.00	4.03
	Mean	14.41	1.08	0.01	0.03	7.86	2.28	210.70	8.09
	Median	4.60	0.03	0.00	0.00	7.94	2.10	203.50	8.11
	Max	457.00	270.98	0.95	0.77	8.90	12.30	325.00	12.38
Monthly	Min	0.00	0.00	0.00	0.00	6.83	0.60	141.50	5.49
	Mean	64.22	1.08	0.01	0.03	7.86	2.28	210.70	8.09
	Median	43.70	0.04	0.01	0.002	7.88	2.11	202.90	8.12
	Max	477.60	68.90	0.21	0.67	8.55	10.45	297.00	11.17
Autumn	Min	43.30	0.00	0.00	0.00	7.19	0.66	153.60	5.99
	Mean	161.40	1.11	0.02	0.03	7.81	2.56	214.30	8.16
	Median	127.60	0.11	0.01	0.01	7.79	2.31	214.20	8.36
	Max	381.60	11.11	0.09	0.22	8.25	7.03	290.40	10.58
Winter	Min	33.20	0.00	0.00	0.00	7.15	0.75	154.40	6.46
	Mean	89.17	0.19	0.01	0.04	7.76	3.37	208.90	8.04
	Median	85.00	0.05	0.01	0.02	7.80	3.30	212.80	7.73
	Max	164.60	1.66	0.04	0.35	8.15	36.36	267.00	10.34
Spring	Min	47.00	0.00	0.00	0.00	7.27	0.96	161.20	5.96
	Mean	175.50	0.24	0.01	0.02	7.95	2.94	209.50	7.95
	Median	169.20	0.08	0.01	0.004	7.98	2.21	211.70	7.48
	Max	373.30	2.42	0.03	0.18	8.55	4.75	273.30	10.58
Summer	Min	65.40	0.00	0.00	0.00	7.36	1.56	171.70	5.86
	Mean	338.80	2.81	0.01	0.02	7.99	2.49	210.80	8.25
	Median	304.00	0.18	0.01	0.004	8.06	2.33	217.50	8.07
	Max	640.40	23.54	0.03	0.10	8.36	4.54	277.70	10.39

presents a comprehensive summary of the key hydrological and water quality parameters across three temporal scales spanning 22 years (2000–2022). WQI is a mathematical expression that transforms large and complex datasets into a single quantitative value, enhancing water quality [52]. Based on the value of the water quality indicators and assigned weightage, the WQI was calculated in our previous work related to this study. In the computation of WQI, the maximum weightage 5 (on a scale of 1–5) was assigned to NH₃-N and PO₄³⁻; TDS and pH had a given weightage of 4, and the lowest weightage was assigned to turbidity [40]. The weight assigned to the five selected water quality parameters was based on different authorised standards and their potential impact on surface water pollution [40,53,54].

Weekly rainfall averaged 14.41 mm, ranging widely from 0 to 457 mm, while weekly streamflow showed a mean of 1.08 m³/s, with a maximum value of 270.98 m³/s, indicating substantial variability. Monthly data exhibited a higher average rainfall (64.22 mm) and showed the same streamflow (1.08 m³/s), although the maximum value was notably lower compared to weekly extremes. Seasonal patterns revealed that spring and summer recorded the highest average rainfall (175.50 mm and 338.80 mm, respectively) and streamflow (0.24 m³/s and 2.81 m³/s), while the winter value was lower (0.19 m³/s). The pH of water remained consistent at an average of 7.86 across both weekly and monthly scales. The maximum pH was observed in weekly data (8.90), indicating an increase in alkalinity. The average value of PO₄³⁻ and NH₃-N ranged from 0.01 to 0.02 and 0.02 to 0.04, respectively, across the three temporal scales. The turbidity was found to be maximum at the monthly scale (10.45), while rainfall was 477.60 mm. Moreover, in the weekly data, the TDS was maximum (325), and the WQI had a mean of 8.09 with values ranging from 4.03 to 12.38, which were slightly higher in the monthly data, ranging from 5.49 to 11.17. The mean value of WQI was 8.1 with the values ranging from a minimum of 5.86 to a maximum of 10.58 across the four seasons. The seasonal statistics of WQI indicated that the WQI was generally consistent over different seasons. Overall, these descriptive statistics illustrate significant variations across different temporal scales, providing insights into the influence of rainfall volume and streamflow on water quality parameters.

3.2. Variation in Water Quality Indicators

This study did not explore and compare all possible combinations of predictors, rather it focused on using the GAM methodology to observe the influence of rainfall and streamflow on the variation in water quality parameters. Water quality parameters often exhibit profound seasonality along with temporal changes. Further, it is also recognised that within a watershed, the primary source of water (such as baseflow versus surface runoff) and its subsequent impact on water quality can fluctuate over time [9]. Therefore, this study examined these dynamics across three temporal scales, such as weekly, monthly, and seasonal, to observe the responses of water quality indicators. The response of each parameter was measured individually using the GAM model. The GAM model was applied to the raw data without altering the actual values to observe the true impact. The results derived from the GAM analysis are presented in

Table 2. Output of the GAM model for WQ parameters.

Time Scale	WQ Parameter	Model Intercept	GCV	edf (Streamflow)	edf (Rainfall)
Weekly	PO43−	0.01	0.00	1.00	1.00
	NH3-N	0.03	0.01	1.00	1.00
	pH	7.86	0.16	1.00 ***	7.06 **
	Turbidity	2.28	1.94	8.58 **	5.46
	TDS	210.65	0.13	9.00 ***	7.83 ***
	WQI	8.09	1.77	8.73 ***	1.58
Monthly	PO43−	0.01	0.00	1.00	1.00
	NH3-N	0.03	0.00	1.00	1.57
	pH	7.56	0.12	2.22 *	1.00
	Turbidity	2.29	1.65	6.36	2.05
	TDS	210.73	0.12	8.49 ***	1.65
	WQI	8.09	1.68	8.17 **	1.64
Autumn	PO43−	0.02	0.01	1.00	1.00
	NH3-N	0.02	0.00	8.79 **	5.81 ***
	pH	7.81	0.08	1.00 *	1.00
	Turbidity	2.55	0.78	8.49 **	2.73
	TDS	214.32	0.13	1.00 *	2.37
	WQI	8.16	1.87	1.00	2.53
Winter	PO43−	0.01	0.01	5.28 *	5.18 **
	NH3-N	0.04	0.00	1.00	1.00
	pH	7.76	0.05	2.86 *	1.00
	Turbidity	2.24	0.14	2.87 *	1.00
	TDS	208.93	0.12	1.86 *	1.00
	WQI	8.04	1.46	1.75	1.35
Spring	PO43−	0.01	0.01	1.00	1.00
	NH3-N	0.03	0.00	1.00	1.00
	pH	7.94	0.11	1.00 *	1.00
	Turbidity	2.21	1.04	2.23	1.11
	TDS	209.45	0.11	3.93 *	1.00
	WQI	7.94	1.72	1.00	1.00
Summer	PO43−	0.01	0.00	1.00	6.51 **
	NH3-N	0.03	0.00	5.15 **	2.08
	pH	7.99	0.08	1.00	1.00
	Turbidity	2.49	0.25	7.52 ***	1.00
	TDS	219.81	0.16	1.00	1.00
	WQI	8.25	1.81	1.00	1.00

N.B: GCV = generalised cross-validation, edf = effective degree of freedom. *** refers to p < 0.001, ** refers to p < 0.01, and * refers to p < 0.05.

.

The model intercept, which represents the baseline level assuming no influence from the predictor variables, was found to be significant (p < 0.001) across all temporal scales.

The GCV score in the ‘mgcv’ package in R can be taken into consideration for selecting the appropriate level of smoothness and serves as an estimator of prediction error, with smaller values indicating a better fit of the model [55]. The GCV scores in the developed GAM models varied across different temporal scales and water quality parameters, and the average values were 0.67, 0.59, 0.48, 0.30, 0.50, and 0.38 in the weekly, monthly, and four seasonal scales (autumn, winter, spring, and summer), respectively. These values indicated that the model fitted with appropriate smoothing to the data and minimised the risk of overfitting. In the weekly scale, the lowest GCV score was observed for the PO₄³⁻ model, which was found to be better compared to the turbidity (1.94) and WQI (1.77) models. The values on the monthly scale also achieved a good balance in capturing the underlying patterns in the data, where the PO₄³⁻ and NH₃-N models exhibited the lowest values (close to zero), and the turbidity (1.65) and WQI (1.68) models had the highest values. The values of seasonal scales indicated that the model’s performance might vary due to seasonal changes.

The smooth functions of each covariate were found to be most significant in weekly data. The effective degree of freedom (edf) for rainfall and streamflow are presented in the last two columns (five and six) in Table 2, and the significance of each edf is almost consistent for pH, turbidity, and TDS. edf is a summary statistic of GAMs which represents the degree of nonlinearity of a smooth function. An edf of 1 corresponds to a linear relationship, while an edf greater than 1 but less than or equal to 2 signifies a weakly nonlinear relationship, and an edf greater than 2 indicates a highly nonlinear relationship. Based on the edf values, highly non-linear relationships were observed between streamflow and turbidity, and TDS and WQI. However, a significant linear correlation was observed between pH and streamflow, particularly in weekly and autumn seasonal data, where the edf values ranged from 1 to 2.86.

This finding strongly agrees with the results from previous studies, where pH was found to increase significantly in surface waters adjacent to agricultural lands compared to urban and natural landscapes, as well as from paved and unpaved forest roads [56,57]. In the case of PO₄³⁻, there was a nonsignificant linear relationship between discharge and rainfall. However, during the winter season, a significant nonlinear (5.28) relationship was observed. Moreover, NH₃-N showed a nonsignificant linear relationship in the weekly and monthly scales, as well as in the winter and spring seasons, but exhibited significant nonlinear variations during the summer (5.15) and autumn (8.79) seasons. Finally, WQI showed a linear relationship in three seasons (autumn, spring, and summer) and a weakly linear relationship in the winter season.

On both the weekly and monthly scales, WQI showed a significant nonlinear variation. Short time variations often reflect the impact of storms or dry spells, leading to substantial, however, temporary changes, and the seasonal variability underscored the influence of prolonged climatic conditions on water quality parameters and associated WQI. From the analysis of weekly and monthly outputs, it was observed that the significant nonlinearity of pH, TDS, and turbidity collectively caused the significant nonlinearity of WQI, whereas NH₃-N and PO₄³⁻ exhibited a minimal influence. The notable response of pH, TDS, and turbidity to streamflow played a significant role in influencing WQI, highlighting the importance of monitoring these parameters during heavy rainfall. Storm water runoff increases turbidity levels in both surface and subsurface flows, which sometimes exceeds the upper limits as recommended in water quality guidelines. High TDS levels in surface water are often the results of agricultural runoff, unsustainable farming practices, uncontrolled animal grazing, and wildlife influences. Tourist destination places, near water sources such as recreational parks, can gradually contribute to an increase in the concentration of dissolved solids over time [58,59,60]. This analysis provides insights into the dynamic relationships between rainfall, streamflow, and various water quality parameters across different temporal scales.

3.3. Performance Analysis of the WQI Prediction Model

In this study, six models were developed to predict WQI using streamflow as input data on three temporal scales (weekly, monthly, and seasonal). Among the six prediction models, the XGBoost-BO optimised model provided the best accuracy on monthly aggregated data. The plots of observed and predicted data during both the training and testing phases of the proposed model are summarised in Figure 3 and Figure 4.

Upon examining the comparison plots of different temporal scales, it was observed that during the training phase (Figure 3), there was a strong agreement between the actual and predicted values, particularly notable in the weekly and monthly data, where the lines closely aligned. However, the seasonal data (autumn, winter, spring, and summer) also showed a satisfactory match, although slight deviations could be noted. In the subsequent set of plots (Figure 4) during the testing phase, the weekly and monthly data showed a noticeable discrepancy, with the predicted values often either underestimating or overestimating the observed values.

As described in the methodology section, Bayesian optimisation was applied to optimise the parameters to develop the XGBoost regression model to predict the WQI. BO only optimises the machine learning model during the training phase, and hyperparameter optimisation can vary with different datasets. The optimum hyperparameters identified by BO are those which perform best at the cross-validation of training data, without certainty that they perform best on the testing data [61]. The prediction performance of the model was assessed using three accuracy metrics such as R², RMSE, and MAE.

Table 3. Summary of the performance metrics of the regression models at six different temporal scales.

Performance Metrics	Phase	Time Period
		Week	Month	Autumn	Winter	Spring	Summer
R2	Training	0.75	0.91	0.92	0.86	0.75	0.96
	Testing	0.67	0.70	0.66	0.52	0.68	0.62
MAE	Training	0.58	0.20	0.14	0.15	0.23	0.08
	Testing	0.55	1.44	0.24	0.64	0.35	0.63
RMSE	Training	0.48	0.42	0.35	0.38	0.61	0.22
	Testing	0.79	1.69	1.62	1.86	1.20	0.95

shows the values of these accuracy metrics for both the training and testing phases of the proposed models.

Table 3 and Figure 5 represent a comprehensive overview of the performance metrics for the proposed WQI prediction model across different time scales during both the training and testing phases. The R² values indicate a strong correlation between the observed and predicted WQI values during the training phase, ranging from 0.75 to 0.96 across various time periods. However, the testing phase shows a moderate decline, with R² values ranging from 0.52 and 0.70, highlighting a slight reduction in model accuracy.

The mean absolute error (MAE) values further elucidate the model’s performance, where the lower MAE values during the training phase (ranging from 0.08 to 0.58) suggest a high level of accuracy in the model’s predictions. In contrast, higher MAE values were observed during the testing phase, particularly for the monthly data (1.44), indicating greater discrepancies between the observed and predicted values during this period.

The root mean squared error (RMSE) values reinforce these findings, with the training phase showcasing relatively low RMSE values (ranging from 0.22 to 0.61), reflecting the model’s robust performance. Conversely, the testing phase exhibits higher RMSE values, especially for the winter and autumn periods (1.86 and 1.62, respectively).

4. Discussion

The GAM model applies an additive link function to enumerate the relationship between the response variable and the nonparametric predictor variables [47]. In this study, each water quality parameter was considered a response variable, while rainfall and streamflow were the predictor variables. The application of the generalised additive model (GAM) proved to be an effective and insightful way of characterising the complex, nonlinear relationships between the individual water quality parameters and hydrological variables in our study. We visualised these relationship and quantified their significance, aligning with previous studies that correlated streamflow metrics, rainfall, and flow diversion with water quality variations [13]. This evaluation can facilitate easy interpretation across different covariates and models, which is particularly useful for communicating findings to nonspecialised audiences [62].

The WQI provides a standardised statistical approach to support the assessment of management strategies and the identification of areas that require reform [63]. A thorough understanding of the temporal dynamics of lake or reservoir water is crucial because it allows water quality managers to identify factors driving changes in water quality, predict future conditions, and take targeted measures [64]. The detailed analysis of the variability in water quality parameters across weekly, monthly, and seasonal scales reveals that weekly and monthly variations often imitate acute events such as storms or dry periods, which may cause temporary, but significant, changes in water quality. However, conducting a monthly analysis helps to identify the persistence of certain water quality issues which may not be evident on a weekly scale. This is because the cumulative effects of rainfall and streamflow over a month show more stable patterns. The assessment of seasonal patterns captures the impact of different climatic conditions (autumn, winter, spring, and summer) and provides insights into how prolonged periods of rainfall and dry seasons influence water quality, which is vital for developing long-term water management strategies.

Moreover, an ensemble machine learning model combining XGBoost and a BO algorithm was proposed for the first time to predict WQI, considering discharge as the input parameter, with an average accuracy of 85% (R²), MAE of 0.33, and RMSE of 0.42. The XGBoost model’s distinct advantages include mitigating overfitting, parallelised tree building, and portability [39]. The results presented by combining the statistical methods and machine learning models across different temporal scales can easily be compared and understood.

However, our approach did not account for other factors such as soil classification and flow diversion during correlation analysis, and the WQI prediction relied solely on a single dominant variable. Furthermore, the analysis and results were based on observational data, which may introduce uncertainties. The exclusion of additional variables could have underestimated the overall impact on water quality. An improvement in this approach may include considering more variables alongside streamflow for the prediction of WQI. While the proposed model performed well during the training phase, further refinement is necessary to achieve a comparable accuracy during the testing phase. Another limitation of our study was that it considered a single case study due to the unavailability of the streamflow data of other reservoirs. Future study is recommended to use remote sensing data and machine learning algorithms to estimate streamflow and WQI prediction.

5. Conclusions

Our study leveraged a generalised additive model (GAM) to explore the correlations between hydrological variables (rainfall and streamflow) and various water quality parameters (PO₄³⁻, N_NH₃, pH, turbidity, TDS, and WQI). This study introduced an optimised ensemble model XGBoost-BO designed for predicting WQI which can improve the accuracy and reliability in forecasting WQI values, offering a deeper understanding of the factors influencing water quality. The Cressbrook Reservoir was selected as the representative case, and the applicability of our method was verified at different temporal scales. The main findings of this study can be summarised as follows:

• The GAM results reveal significant correlations between streamflow and several water quality parameters. Specifically, on a weekly temporal scale, turbidity, TDS, and WQI showed a significant nonlinear relationship with discharge, which indicates that short-term variations in runoff may have pronounced effect on these parameters. On the other hand, pH, PO₄³⁻, and NH₃-N showed a linear relationship with discharge. The high sensitivity of turbidity and TDS to discharge suggests that managing flow rates and reducing runoff during storm events could be crucial in water quality management.
• On a monthly basis, streamflow exhibited smoother relationships for most parameters but still influenced TDS and WQI nonlinearly. These correlations highlight the sustained influence of hydrological variables over longer periods.
• Seasonal analysis provides further insights; in autumn and winter, NH₃-N and PO₄³⁻ displayed high edf values, respectively. However, pH showed a linear and WQI exhibited a weakly linear to linear relationship with discharge over four seasons. The seasonal interrelationship of various water quality parameters with the hydrological variables implies that management practices need to be adjusted seasonally to address the specific challenges posed in each period.
• The accuracy metrics of the WQI prediction model using XGBoost-BO, as previously discussed, are consistent with these findings. The model’s performance varies across different temporal scales, exhibiting a higher accuracy during the training phase compared to the testing phase. This variation underscores the complexity of predicting water quality, influenced by the dynamic interplay of hydrological variables.

Understanding the temporal dynamics of rainfall and streamflow and their influence on water quality is paramount for developing effective management strategies, particularly amidst climate change challenges. Surface water quality can fluctuate in response to climate disruptions such as extreme rainfall and droughts, such as the dilution and concentration of water quality parameters and physical processes like bank erosion. Additionally, water quality is influenced by the interactions of surface runoff with organic matter on the land [65,66]. Heavy precipitation causes increased runoff which may increase water contamination and public health concerns [66]. In our previous study, the water quality parameters were selected based on the fact of which parameters were being affected due to extreme rainfall events as a result of climate change [40]. The findings of this present study suggest that addressing significant climate impacts and site-specific determination and modelling with long-term precipitation, streamflow, and water quality data is essential to achieving sustainable water quality objectives. By applying a similar comprehensive analysis and modelling, the regional evaluation of climate impacts on water quality could be explored.

Additionally, understanding how water quality parameters vary across different temporal scales in response to rainfall and streamflow enables local authorities to develop more effective and targeted strategies for maintaining and improving water quality. Specifically, weekly responses can help to detect and respond to sudden or critical events swiftly, while monthly analyses provide guidance for medium-term interventions to address significant water quality issues. Seasonal observations offer valuable insights into the long-term effects of climatic variations, enabling policy makers to implement proactive measures in anticipation of seasonal changes. The proposed multi-temporal approach ensures a comprehensive understanding of the measures for the development of adaptive strategies and management practices that are responsive to both short-term and long-term fluctuations.