Abstract
The hydraulic performance of pooled stepped spillways has received less recognition compared to the traditional stepped spillways. Regarding the effectiveness of pooled stepped spillways in managing flow dynamics, previous studies have focused on investigating how different step configurations and varying chute angles can enhance energy dissipation in gravity flow over the chute. However, the potential for optimal performance and the importance of proper design have not been thoroughly explored in the existing literature. This study aims to explore new configurations of pooled stepped spillways and compare them to traditional stepped spillway designs to enhance hydraulic efficiency and maximize energy dissipation. The study examines two types of configurations of stepped spillways—two flat and two pooled configurations, each with ten steps. Using the computational Fluid Dynamics (CFD) technique, such as Volume of Fluid Method (VOF) and the realizable k-ε turbulence model for two-phase flow analysis with a 26.6° chute slope. Initially, the model was validated with experimental data by comparing various hydraulic parameters. These parameters include water depth, roller length, jump length, ratio of critical depth, and sequent depth. The hydraulic performance of both stepped geometric configurations was evaluated through numerical simulations to examine how the geometries of flat and pooled stepped spillways influence flow characteristics, energy dissipation, velocity, pressure distribution, and the Froude number at the downstream. The study analyzed downstream flow characteristics, maximum energy dissipation rates, depth-averaged velocity, static pressure, and pressure contours at the lateral direction under six different flow rates in flat and pooled stepped spillways. The findings indicate that flat-step configurations exhibit lower energy dissipation compared to pooled configurations. The relative energy loss of flow on pooled steps dissipates more energy than on flat steps. Furthermore, it is observed that the pooled configurations performed better for energy dissipation and flow stability compared to the flat configurations. The energy dissipation increased in pooled stepped spillways by 34.68% and 25.81%, respectively. Additionally, the depth-averaged flow velocity and pressure distribution decreased in case 2 and case 4 compared to the flat-step configurations.
1. Introduction
Stepped spillways are commonly constructed in dams to safely release overflow water and transfer high-energy water downstream of the dam. It plays an important role in improving energy dissipation, significantly reducing specific residual energy [1,2]. This type of spillway consists of steps that allow water to flow down from a higher elevation to a lower point, especially in mountainous regions. Effective spillway design and management are essential for minimizing the risks associated with extreme weather conditions and potential dam failures. A properly designed spillway ensures that the flow of water is safely released, reducing the risk of overflow and preventing structural damage to the dam [3]. The concept of stepped spillways dates back to ancient times, but modern engineering has significantly refined their design and functionality. Stepped spillways are particularly popular for managing high-gravity flows and ensuring the safety of dam embankments through various engineering techniques [3,4]. The stepped design can be more cost-effective regarding construction material maintenance and enhanced energy dissipation capabilities [5]. Stepped spillways can be built using various materials, including concrete, masonry, and even natural rock, depending on the site-specific requirements and the availability of resources [6]. In addition, this type of spillway is considered effective in maintaining dam wall stability and integrity due to its high gravity base and inclination towards the dam side.
Despite their potential advantages, the design and implementation of stepped spillways offer several challenges. These challenges may include cavitation, high flow velocity, and pressure distribution in which the flow profile shifts into a skimming flow condition [7,8]. The geometric design of stepped spillways significantly influences the flow patterns and the proper alignment of water flow with the design, and the pressure parameters can result in nappe flow or skimming flow. The geometry of stepped spillways directly influences flow characteristics and reduces residual energy downstream, making them an effective natural method for dissipating flow energy. Investigation is crucial to improve and safeguard the local communities and dam infrastructure from potential flood damage downstream of the structure [9]. Several researchers utilized various geometry models for stepped spillways to improve the accuracy and simplicity of flow stability and safety to minimize the risk of cavitation on the spillway surface and in the stilling basin [10,11,12]. However, proper flow resistance is crucial for assessing frictional energy losses. In skimming flows, the flow resistance depends on several factors, including stepped chute geometry, flow depth, chute slope, flow conditions, step heights, and the degree of air entrainment. Because of the complexity and interplay of these factors, it can be challenging to account for all of them comprehensively.
Computational codes and hardware technology are being utilized to employ numerical solutions. The use of technological advancement enhances the efficiency and cost-effectiveness of flow analysis and assists in the design across various fields of study [13,14]. The numerical modeling approach is also extended to more complex multiphase flows and various 3D modeling. Such techniques numerically evaluate hydraulic performance, analyze erosion and sedimentation, assess structural integrity, study air entrainment and aeration, conduct environmental impact assessments, and optimize energy dissipation [15,16,17]. Many researchers have widely employed numerical simulations in spillway design and analysis for various purposes. Several problems related to spillway fluid flow have been extensively investigated, including the dynamics of hydraulic jumps, the behavior of flow on chutes, and the effectiveness of various energy dissipation methods [17,18,19].
In addition to the numerical method, many of these researchers have employed the volume of fluid (VOF) method and the realizable k-ε turbulence model to study open channel flow. The realizable k-ε turbulence model is often considered more efficient for simulating free surface flows. It is particularly useful for understanding various stepped spillway configurations’ hydraulic properties and performance. The realizable k-ε model is especially effective in analyzing flow patterns, velocity distributions, and energy dissipation rates. Li et al. [20] conducted a study using the realizable k-ε turbulence model and the two-phase mixture model to investigate the effects of different step geometries, both rounded and trapezoidal, on air–water flows over a stepped spillway. Their findings revealed that the spillway with rounded steps exhibited higher air concentrations, whereas the trapezoidal steps resulted in higher flow velocities compared to the rounded step configuration. Ma et al. [18] investigated the interval pooled stepped spillway using a VOF method with the realizable turbulence k-ε model to evaluate energy dissipation. It was found that increasing the pool height had a limited effect on enhancing energy dissipation. Li et al. [21] used Flow-3D to study a stepped spillway with pool heights of 2 cm, 4 cm, and 6 cm under varying flow rates. The results showed that, at each flow rate, turbulent energy at the midpoint of each step decreased with increasing pool height. The energy dissipation rate decreased for a constant pool height as the flow rate increased.
Ghaderi et al. [1] tested four pool configurations and found that the notched pooled step configuration improved efficiency by approximately 5.8%. The interfacial velocities were higher in the pooled spillway than in the flat-stepped spillway. The pressure at the beginning of the steps was greater in the pooled configuration. However, the maximum pressure near the step-pool dropped for the notched pool, and the pool configuration had a minimal effect on the air entrainment site. Morovati et al. [19] found that reducing the number of steps in pooled stepped spillways decreased flow velocity and increased relative energy dissipation at the end of the spillway. Furthermore, fewer steps result in higher values of turbulent kinetic energy. The findings of Saleh et al. indicate that flat-stepped spillways generally exhibit better energy dissipation performance compared to pooled configurations in certain condition [22]. However, many studies show that pooled stepped spillways demonstrate improved aeration and energy dissipation rates under certain conditions. Studies by Morovati et al. [19], Hantoosh et al. [23], and Pandey et al. [24] also reveal that factors such as pool height, step geometry, and discharge rates significantly influence the hydraulic behavior and energy dissipation characteristics of stepped spillways. These insights contribute to the optimization of stepped spillway designs for improved hydraulic performance and energy dissipation in dam structures.
Following previous research findings, growing interest in utilizing pooled stepped spillways has been increased due to their superior energy dissipation capabilities and improved aeration performance [12,25]. Studies have shown that stepped spillways with pooled designs are more effective in dissipating flow energy compared to traditional designs; findings indicate that increasing the number of steps in the spillway enhances the energy dissipation rate [23]. The effects of steep slopes of 15°, 25°, and 45° with different inclined slopes and a maximum number of up to 50 are investigated [26]. In their study, with a constant flow rate passing over a stepped spillway, energy dissipation increases as the spillway slope and the number of steps increase [27,28]. It was investigated that the energy dissipation performance of the interval pooled stepped spillway was generally better than that of the horizontal flat stepped spillway [29]. Moreover, numerical simulations have demonstrated that the turbulent energy at the midpoint of each step decreases with an increase in pool height while the turbulent dissipation rate increases with the flow rate, but the energy dissipation rate decreases with a higher flow rate [5,12]. These spillway design and performance evaluation advancements contribute to the ongoing optimization of hydraulic structures for enhanced energy dissipation and aeration in water management systems [30]. Considering previous findings, existing studies have primarily focused on traditional stepped spillways, and pooled stepped spillways receive relatively less recognition than conventional ones. Therefore, further research is required to enhance the understanding and performance of pooled stepped spillways.
This study aims to evaluate the potential and efficiency of novel pooled stepped spillway designs compared to flat stepped spillways. It examines four geometric configurations with a chute slope of 26.6°, analyzing their effects on energy dissipation efficiency, flow patterns, velocity, pressure distributions, and Froude numbers. Additionally, the study seeks to determine which spillway design is most effective for ensuring safe operation across a range of flow conditions. It also aims to assess the reliability of the CFD technique by using the realizable k-ε turbulence model to validate its accuracy and robustness.
2. Material and Methods
2.1. Physical Model
This study integrates numerical simulations with experimental validation to understand and visualize complex flow behavior systematically. This combined approach enhances the reliability of the results by mitigating the limitations inherent in computational models. Typically, experimental setups allow for the precise observation and measurement of real-world phenomena, providing critical data for validation. In contrast, numerical simulations offer detailed insights into flow dynamics that are difficult or impossible to measure directly. Simulations generally involve the calculation of hydraulic parameters, enabling analysis and prediction under varying conditions. Numerical simulation was applied to accurately replicate the complex hydraulic phenomena occurring within fluid structures. This dual approach facilitates a full investigation of flow behavior and energy dissipation mechanisms, offering valuable insights for optimizing the design of effective and resilient spillway structures.
In this study, the experimental data used for the numerical model were collected from Daneshfaraz et al. [31]. The study utilizes laboratory experiments conducted in a flume measuring 12 m in length, 1.2 m in width, and 0.8 m in depth, with a chute angle of 26.6°. The cascade of spillways consists of 10 steps, each 0.12 m long and 0.06 m high. High flow rates of 45, 50, and 54 L per second were selected to visualize better and provide more detailed insights into the flow regime. Moreover, the experimental study also utilizes a theoretical approach to enhance understanding of flow and energy characteristics between upstream and downstream channels. We used some theoretical equations to verify our results, minimize errors, and ensure the accuracy and reliability of the simulations. Integrating these approaches enhances accuracy and reliability, improves the design, and provides a more precise representation of hydraulic parameters. The parameters examined are as follows:
where is the total energy, H is the height, is the critical depth, v0 is the velocity of the flow, and g is the acceleration due to gravity. The critical depth, yc, and velocity head can be changed, and this is expressed as follows. The difference in sequent depth ratio (y2/y1) against the normalized critical depth (yc/h) [31].
Energy loss can be calculated as , which is the difference between the energy upstream of the spillway and the downstream energy , as follows:
The Froude number (Fr) in open channel flow can be calculated to compare inertial forces to gravitational forces. In the given Equation, V is the flow velocity, g is the acceleration due to gravity, and d is the flow depth. This is expressed in Equation (5):
η is the efficiency in percentage:
2.2. Numerical Simulation
Numerical simulations became essential tools for fluid-related problems, offering advantages in promptness, safety, and cost-effective results over traditional experimental methods. This study used CFD simulations with Ansys Fluent 2023 R1 to investigate flow regimes over flat and pooled stepped spillway geometries. The VOF method utilizes free surface flows with distinct fluid phases to accurately track the fluid volume fraction in each computational cell. This approach enables detailed simulations of hydraulic behavior and energy dissipation in the spillways, providing a comprehensive framework for predicting complex flow behavior over stepped spillways. The VOF mass transfer capability enables mass exchange between phases across the interface, a crucial phenomenon for wave breaking and water splashing over the spillway steps [10,17].
The VOF method developed by Hirt and Nichols [32] effectively analyzes two-phase or multiphase flows in complex fluid dynamics and various engineering applications. This method uses a geometric reconstruction scheme to track the free surface throughout the entire domain. A single set of mass and momentum conservation equations (Equations (8) and (9)) is applied to each phase to identify the free surface. The fluid volume within each domain cell is then calculated based on these equations. The fraction of the cell volume occupied by fluid is represented by an alpha α value defined by the VOF model. In this case, α = 1 denotes a cell filled with water, while α = 0 represents a cell filled with air. In each case, the sum of the volume fractions of air and water is unity. Therefore, the volume fraction of air αa can be expressed as αa = 1 − αw, where αw represents the volume fraction of water. At each time step, the value of α is updated using the advection equation for α, Equation (7) [33]. These equations describe the conservation of mass (continuity equation) and the conservation of momentum (Navier–Stokes equation) for fluid flow, accounting for both molecular viscosity and turbulent viscosity effects.
The continuity equation is as follows:
The momentum equation is as follows:
where the variables are defined as follows: ρ is the density (kg/m3); t is time (s); ui and uj are the velocities (m/s) in the xi- and xj-direction, respectively; P is the pressure (N/m2); µ is the molecular dynamic viscosity (kg/m/s); and µt is the turbulent dynamic viscosity (kg/m/s).
2.2.1. Turbulence Model
The realizable k-ε turbulence model is a commonly used turbulence model in CFD due to its robustness and computational efficiency. It provides a semi-empirical approach to model turbulent flow characteristics, such as turbulent kinetic energy k and turbulent dissipation rate ε. The primary features in a turbulent flow over a stepped spillway are the flow recirculation zone in each step and the turbulent free surface with a highly fluctuating velocity field at the downstream steps. For flows over stepped spillways, turbulence terms in the momentum equations are crucial for defining surface friction and flow resistance [34]. Without a turbulence model, velocity distribution tends to become uniform, leading to inaccurate flow simulations. In CFD, the realizable k-ε turbulence model is an enhanced version of the standard k-ε model, incorporating modifications to better capture turbulent flow physics, especially in cases with adverse pressure gradients and swirling flows.
2.2.2. Realizable k-ε Model
The realizable k-ε model is governed by the following transport equations:
The turbulence kinetic energy (k) equation is follow as:
In the Equation, k is the turbulence kinetic energy, ρ represents the density of the fluid, uj stands for the velocity component in the jth direction, μ denotes the molecular viscosity, μt refers to the turbulent viscosity, σk is the turbulent Prandtl number for k, Gk and Gb represent terms related to the generation of turbulence kinetic energy, ε denotes the turbulence dissipation rate per unit mass, YM stands for the contribution of fluctuating dilatation in compressible turbulence to the overall dissipation rate, and Sk represents any user-defined source term that might contribute to or detract from the turbulence kinetic energy.
The turbulence dissipation rate (ε) Equation is follow as:
Model’s coefficient is equal to the following:
S is the mean rate of strain:
In the above turbulence dissipation rate equation (ε), C2 is the coefficient for the dissipation, C3 is the model constant for buoyancy-related terms, Gb is the generation of turbulence kinetic energy due to buoyancy effects, and Sε is an additional user-defined source term for the turbulence dissipation rate.
The eddy viscosity component is computed as follows:
In the model, C1ε = 1.44, C2ε = 1.9, σk = 1.0, and σε = 1.2.
The model constants used in the realizable k-ε model include σk and σε, which control the turbulent Prandtl numbers in the k and ε equations, respectively. In addition, C1ε and C2ε are parameters that influence the behavior of the dissipation rate equation. These equations and constants collectively define the realizable k-ε turbulence model, providing enhanced accuracy in predicting turbulent flows compared to the standard k-ε model.
2.3. Computational Setup
To investigate the influence of the geometries and flow characteristics of flat and pooled steps on the energy dissipation performance over a stepped spillway, the numerical spatial and temporal discretization schemes implemented for this model are listed in Table 1. The adoptions were made to ensure accuracy, stability, and convergence in the simulation of the VOF method with the realizable k-ε turbulence model using Ansys Fluent. The realizable k-ε turbulence model was implemented to accurately capture the effects of the flow recirculation, massive separation, and boundary layer separation that occur in the steps of the spillway. The discretization scheme for momentum, turbulent kinetic energy, and dissipation rate second-order methods are applied, effectively representing swirl flows. The SIMPLE algorithm was used to couple pressure and velocity. Pressure and velocity coupling, which solves the continuity and momentum equation, is achieved through a coupled scheme that enhances the stability and convergence of the solution. To achieve higher accuracy in the numerical solution, the continuity, momentum, volume fraction, turbulent kinetic energy, and turbulent dissipation rate equations are all discretized using a second-order upwind scheme [24]. This scheme reduces numerical diffusion and provides better resolution of steep gradients, which is essential for capturing the complex flow dynamics and turbulence characteristics inherent in stepped spillway flows.

Table 1.
Solver settings for CFD Model (Ansys 23.R1 Fluent).
2.3.1. Boundary Conditions
The boundary conditions for the numerical model were considered inlet, outlet, atmospheric, and wall boundary conditions. The boundary conditions did not change from one case to another except for the inlet velocity. The initial conditions at t0 consisted of water entering the domain with a depth of 0.09 m (h). The inlet flow velocity for the validation of the experimental model was set at 45, 50, and 54 L/s. For the remaining numerical models, the flow velocities were maintained between 0.45 to 0.70 m/s, with an interval of 0.05 m/s for all four cases. The outlet boundary condition for the water layer was set as a pressure outlet. Based on these boundary conditions, the goal was to achieve a flow rate difference of less than 1% between the inlet and outlet. The top boundary was modeled as atmospheric and treated as a no-slip, stationary wall. At the bottom, standard wall functions were implemented to avoid excessively fine meshes and to conserve computational resources while modeling the boundary layer. Additionally, wall functions were employed to effectively model the near-wall regions. Figure 1 depicts the boundary conditions, and the dimensions of the steps for all cases of spillways are presented in Figure 2. annotated with length (l) and height (h), points 1 and 2 represent the velocity head.
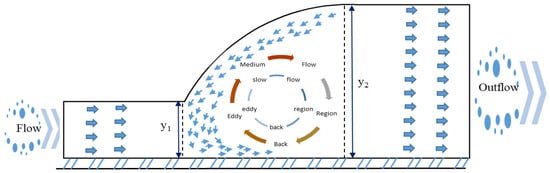

Figure 1.
Schematic view of hydraulic jump and boundary condition of pooled stepped spillway case 2.
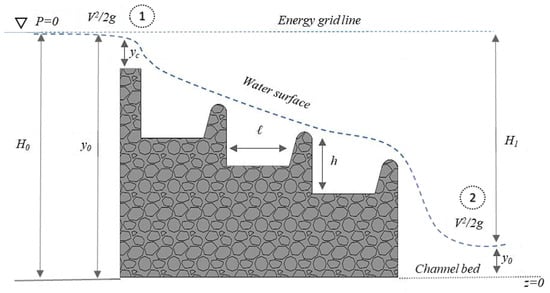
Figure 2.
Graphical representation of energy grid line and hydraulic grid line with annotations. The hydraulic grid line (HGL) is equal to the elevation head and pressure head, and the energy grid line (EGL) is equal to the hydraulic head and velocity head.
2.3.2. Gird and Mesh Assessment
In CFD numerical simulation, the choice of meshing plays a crucial role in determining the accuracy and efficiency of the model. A well-designed mesh captures the complex geometry of the flow domain and resolves the important flow features, ensuring an accurate representation of the physical phenomena. Fine meshes provide higher resolution and detail but can significantly increase computational cost and time. Conversely, coarser meshes reduce computational requirements but may fail to capture critical flow details, leading to less accurate results. The choice of meshing also affects the stability and convergence of the simulation. An inappropriate mesh can lead to unreliable results and increased computational time due to poor convergence behavior. Thus, a balanced approach that combines fine and coarse meshing in appropriate regions is essential to achieve reliable and efficient simulation results.
An optimal meshing strategy is essential for simulating flow characteristics over flat and pooled stepped spillways. Fine mesh grids are typically used in spillways near the walls and steps to accurately resolve boundary layer effects and capture the turbulence characteristics effectively. In regions with less complex flow, coarser meshes can be employed to save computational resources without compromising accuracy. To ensure the precise simulation, we set the convergence criteria for the fluent residual monitors to an absolute value of 0.001 for continuity, x,y velocity, and realizable k-ε. Additionally, we performed a mesh grid size convergence study for the transient simulation to ensure convergence based on the time step size. For a reliable simulation, we used various grid sizes to check the computational time with comparison to the accuracy of the flow pattern and vorticity as shown in Table 2.

Table 2.
Mesh quality assessment metrics and acceptable thresholds in ANSYS 23.R1 Fluent.
A grid independence study was initially conducted to ensure the mesh size’s accuracy and reliability. We utilized structured mesh algorithms known for their efficient memory usage and faster computational performance. We designed a static structured rectangular quadratic mesh and assessed three variations to ensure mesh independence: Mesh N1, with a cell size of 0.00428 m × 0.00428 m × 0.00428 m with 146,370 cells; Mesh N2, with a cell size of 0.00624 m × 0.00624 m × 0.00624 m and containing 70,007 cells; and Mesh N3, with a cell size of 0.00824 m × 0.00824 m × 0.00824 m and consisting of 40,303 cells approximately. The results did not show significant changes in Mesh N1 and N2 in the flow pattern or velocity profile near the wall and steps. However, significant changes were observed with the N3 coarse grid cells, and the fine grid results were similar to the medium size. Consequently, a medium grid size N2 0.00624 m was selected for further simulations involving four different geometrical configurations and various velocity simulations, considering computational cost and time. The details of the mesh and grid arrangements and other quality metrics are presented below in Table 2.
In the application of the realizable k-ε turbulence model, several important fluid properties are utilized to accurately simulate turbulent flows. The density of water is ρw = 998.78 kg/m3 and ρa = 1.225 kg/m3 for air. These densities are crucial for determining inertial forces in the flow and affect the momentum equations. The kinematic viscosity values are μw = 1.1094 × 10⁻6 m2/s for water and μa = 1.4657 × 10⁻5 m2/s for air. These values help calculate turbulent viscosity and dissipation rates, affecting momentum transfer and turbulence development. The surface tension value was taken as σ = 0.072 kg/s2, which is important for simulations involving free surfaces or fluid interfaces, influencing behaviors like droplet formation and wave dynamics. Including these properties in the realizable k-ε model improves the accuracy of turbulence predictions and the overall simulation of fluid dynamics and surface effects.
3. Results and Discussion
3.1. Validation of Numerical Model
The first phase in numerical simulation is to check the reliability of the model. Therefore, experimental data of three different flow rates (45, 50, and 54 L/s) were collected from a physical model to validate the reliability of the numerical model. To check the comparison between the experimental and CFD results, various hydraulic parameters were calculated including critical depth (yc), sequent depth (yc/h), the ratio of sequent to initial depth (y2/y1), hydraulic jump length and rolling length (Lj and Lr), Froude number (Fr), and Reynolds number (Re) as shown in Figure 2. These hydraulic parameters were compared with the physical model data to check their correspondence, as presented in Table 3. The numerical results showed a good resemblance with the experimental data, demonstrating that the realizable k-ε turbulence model can accurately predict various flow scenarios. The results show very small differences between the experimental and numerical CFD results. These minimal differences may be due to the influence of geometry or flow conditions.

Table 3.
Experimental and numerical realizable (k-ε) model hydraulic parameters.
3.2. Flow Behavior and Water Surface Profiles
The flow behaviors over different stepped configurations were analyzed to determine the flow dynamics at various time steps. The analysis aimed to assess the impact of the geometry configuration on the energy dissipation and flow characteristics of flat and pooled stepped spillways. Thus, four different geometries were implemented: case 1, case 2, case 3, and case 4. Among these, case and case 3 represent flat rectangular stepped configurations, while case 2 and case 4 represent pooled stepped geometry with dimensions shown in Figure 3.

Figure 3.
Flat and pooled stepped spillway configurations for numerical simulation to evaluate the flow regimes over various geometric configurations.
In stepped spillway, the interaction between the water flow and the steps plays a crucial role in energy dissipation and flow behavior. The VOF method combined with the realizable k-ε model are able to accurate capture the free surface flow. The evaluation of free surface flow conditions on a stepped spillway involves a complex interaction of aeration, cavitation, and turbulence, significantly influencing flow characteristics in high-velocity situations.
Figure 4 shows different flow regimes under different geometry configurations at various time steps. The initial flow conditions are significantly affected by aeration and high flow velocity. Free surface aeration is closely related to the flow patterns and surface velocity. As air concentration increases upstream, it interacts with the turbulent boundary layer. The effects of aeration and high flow velocity are particularly evident in the downstream flow properties of the air–water mixture, especially in scenarios with high Froude numbers. In these cases, the initial conditions notably influence the void fraction and air entrainment flux. Once the flow develops, the flow conditions change to different states.
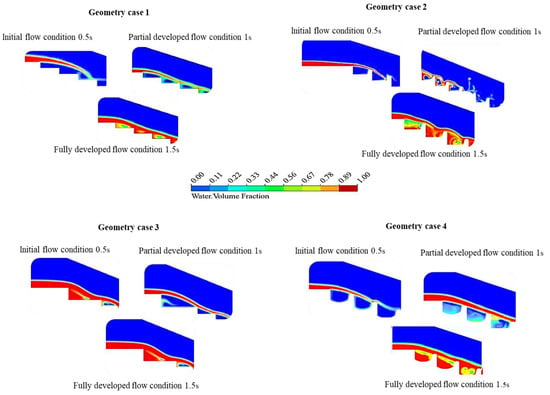
Figure 4.
Flow dynamics and regime changes across flat and pooled stepped spillways at various time steps.
3.3. Water Surface Profile for Geometry Case 1
The results for case 1 numerical simulation is illustrated in Figure 5 and summarized in Table 4 for various flow rates. The study evaluates the flow dynamics and regimes across various flow conditions. Initial velocities were varied from 0.45 to 0.70 m/s, with increments of 0.5 m/s. The impact of aeration on pressure and velocity was observed, leading to distinct flow patterns downstream of the spillway. We examined several hydraulic parameters, including downstream velocities, critical depths, sequent depths, and upstream and downstream Froude numbers, documented in Table 4. The findings indicate that an increase in initial velocity generally leads to a corresponding rise in outlet velocity, consistent with momentum and energy conservation principles. Notably, when the Froude number is leading, the flow exhibits heightened sensitivity to velocity changes. The flow variation in the stepped channel is relatively consistent; however, a strong hydraulic jump is observed downstream at flow rates of 0.65 and 0.70 m/s. Moreover, the study of supercritical flow conditions revealed that flow depth and velocity variations can induce turbulence, complicating the flow dynamics.
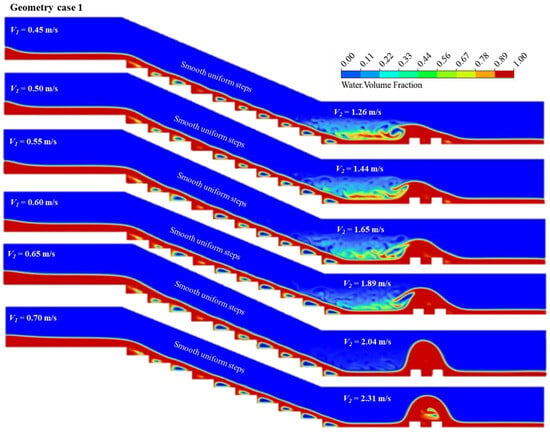
Figure 5.
Case 1: dynamic visualization of volume friction of water–air interface in a pooled stepped spillway across varying velocities.

Table 4.
Hydraulic parameters for a flat stepped spillway: geometry case 1.
3.4. Water Surface Profile for Geometry Case 2
The pooled stepped configuration in case 2 was simulated to evaluate its performance and energy dissipation at each step, with detailed results presented in Table 5. The formation of hydraulic jump, flow pattern, aeration, and the Froude number decreased substantially compared to case-1. Similarly, the flow condition in the steps changed to a transition flow regime. Moreover, while case 1 exhibited a downstream velocity of 2.32 m/s, case 2 demonstrated a significantly lower downstream velocity of 0.87 m/s, despite having the same initial velocity of 0.70 m/s. Additionally, the critical and subsequent depths did not increase compare to case 1.

Table 5.
Hydraulic parameters for a pooled stepped spillway: geometry case 2.
Similarly, the formation of turbulence and the Froude number decreased substantially from 4.76 to 2.35 at 0.70 m/s, as illustrated in Table 4 and Table 5. Regarding outlet velocity, critical and subsequent depths, and energy dissipation, case 2 represents an ideal condition for flow dynamics under certain conditions. The enhancement of energy dissipation in case 2 can be attributed to trapped water’s recirculation and continuous breakdown, as shown in Figure 6.

Figure 6.
Case 2: dynamic visualization of volume friction of water-air interface in a pooled stepped spillway across varying velocities.
3.5. Water Surface Profile for Geometry Case 3
The flat stepped configuration in case 3 in Figure 7, with an increased width, was implemented to evaluate its performance and energy dissipation at each step. Its effectiveness was compared with both the flat stepped case 1 and pooled stepped case 2 configurations. Table 6 demonstrates that case 3 showed a significant reduction in efficiency and effectiveness, with a notable increase in cavitation and velocity. Changes in geometry influenced the flow pattern and behavior, leading to variations in energy dissipation based on the flow regime. This is particularly when compared to case-1 case 1 and case-2 case 2, where downstream velocities were recorded at 2.30 m/s and Froude numbers at 4.514 m/s, respectively. Moreover, case 3 increments in critical and sequent depths are observed to be very low. However, the Froude number in case 3 downstream significantly increased compared to case-1. In terms of outlet velocity, critical and sequent depths, and energy dissipation, case 1 and case 3 exhibit similar flow dynamics under certain conditions, with no significant differences.
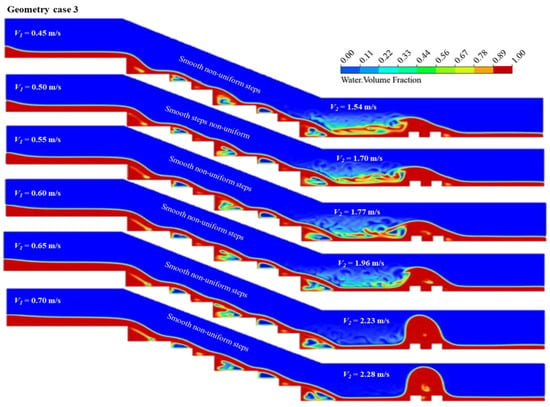
Figure 7.
Case 3: dynamic visualization of volume friction of water-air interface in a pooled stepped spillway across varying velocities.

Table 6.
Hydraulic parameters for a flat stepped spillway: geometry case 3.
3.6. Water Surface Profile for Geometry Case 4
The pooled stepped configuration in case 4, features like U-shaped steps, was evaluated with the goal of maximizing energy dissipation at each step. It was observed from Figure 8 that this configuration was significantly affected by cavitation and recirculation, particularly with a higher number of steps. Changes in geometry altered the flow pattern and behaviors with varying velocities, influenced by the flow regime, which proved helpful in energy dissipation. The downstream velocity and Froude number for case 4 were recorded at 1.30 m/s and 2.423, respectively, at an inlet velocity of 0.70 m/s, as shown in Figure 8 and Table 7. These values are notably lower than those observed in Case 1, Case 2, and Case 3. Additionally, the critical and sequent depths and the Froude number showed minimal increases and no significant changes compared to case 2. The U-shaped steps in case 4 provided better results regarding ideal hydraulic jump, velocity, and Froude number compared to the other configurations; however, further improvements are needed to enhance the flow pattern and mitigate cavitation and recirculation for structure erosion.
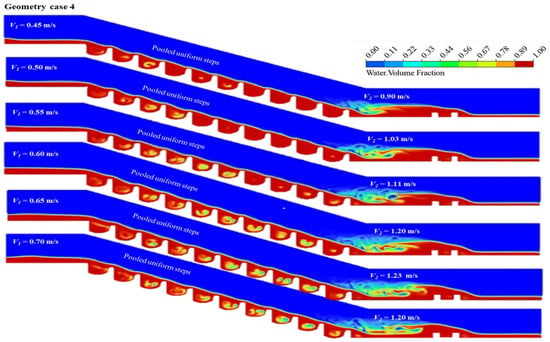
Figure 8.
Case 4: dynamic visualization of volume friction of water-air interface in a pooled stepped spillway across varying velocities.

Table 7.
Hydraulic parameters for a pooled stepped spillway: geometry case 4.
3.7. Velocity and Pressure Distribution
Investigating pressure contours on flat and pooled stepped spillways across various velocities and geometries provides crucial insights into structural integrity and potential cavitation risks. Understanding these pressure dynamics is essential for structural design and predicting areas of high stress that could lead to structural failure or damage under high pressure. Several pressure measurements were taken over the stepped spillway for all configurations. In case 1, higher pressure levels were observed at the eight, nine, and ten steps at lower velocities (0.45 to 0.55 m/s). In contrast, the highest negative pressures were recorded on the inner vertical faces of the flat stepped spillway at higher velocities (0.60 to 0.70 m/s). The pressure contours for flat steps indicate that pressure decreases as velocity increases, as observed in Figure 9. The upper half of the vertical face experienced negative pressure, while the horizontal face of the step was largely free of negative pressure, except for small fluctuations. These observations suggest that lower velocities may lead to increased pressure, but higher velocities significantly raise the risk of cavitation, particularly on the upper vertical inner faces of the step walls in flat stepped spillways. The presence of negative pressures indicates potential structural vulnerabilities, underscoring the need for careful design considerations in stepped spillway construction to mitigate cavitation risks and ensure structural safety under varying hydraulic conditions.

Figure 9.
Pressure contour within three downstream successive steps: case 1.
Overall, the findings from case 1 highlight the importance of understanding pressure dynamics in flat-stepped spillway design to prevent structural failure due to high pressure. The case 2 configuration examines pooled steps, shown in significant improvement in terms of reducing negative pressures and exhibiting lower susceptibility to cavitation compared to case 1, as depicted in Figure 10. The pressure levels on the pooled bottom face are higher, with a more uniform distribution across each face. This uniformity of flow patterns within each step of a pooled spillway contributes to better structural stability and reduced pressure and cavitation risks. Studies have shown that stepped spillways, particularly those with pooled configurations, enhance energy dissipation and reduce cavitation risks by promoting air entrainment and creating aerated flow protective layers. The uniform flow pattern and improved negative pressure are attributed to the recirculating flow within each step. Like case 1, pressure decreases with increasing velocity; however, in case 2, both pressure and velocity decrease which makes the overall behavior of the pooled steps more favorable in terms of pressure and flow dynamics.
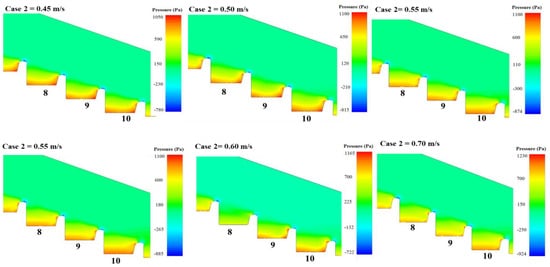
Figure 10.
Pressure contour within three downstream successive steps: case 2.
In case 3, Figure 11 illustrates very high negative pressures compared to the other three cases, leading to a substantially increased likelihood of cavitation. This elevated negative pressure suggests that the geometry of the stepped spillway in case 3 is less favourable, contributing to greater structural vulnerability. The increased risk of cavitation and less effective pressure management make the design in case 3 inadequate compared to the other cases. In contrast, case 4 in Figure 12 demonstrates maximum pressure distribution on the inner faces of the bottom steps. The geometry of this case shows that the pressure trend and uniformity change very gradually with increasing velocity. The pressure value at the beginning of the steps in the pooled configuration was higher than in the flat configuration, while in the notched pool, the maximum pressure values decreased near the step pool. The case 2 and case 4, pooled configurations whether simple or notched did not significantly influence the location of air entrainment. The pressure distribution remains uniform, which helps minimize cavitation. Moreover, the calculated pressure distribution downstream of spillway for geometry configurations case 1, case 2, case 3, and case 4 are presented in Figure 13.
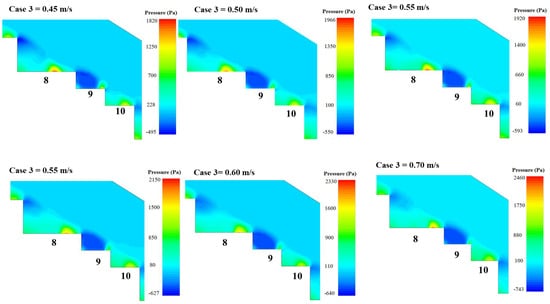
Figure 11.
Pressure contour within three downstream successive steps: case 3.
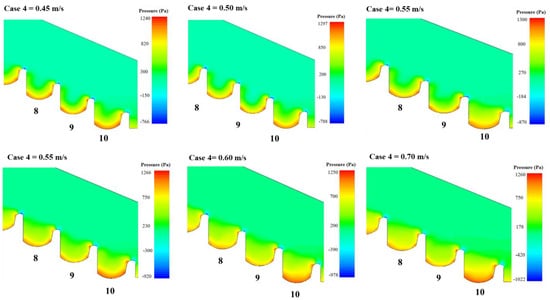
Figure 12.
Pressure contour within three downstream successive steps: case 4.
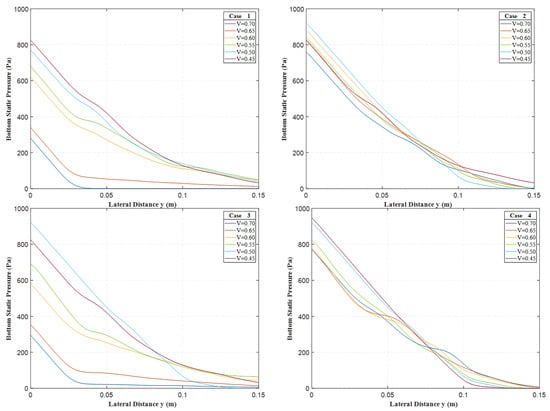
Figure 13.
Pressure distribution downstream of spillway for geometry configurations case 1, case 2, case 3, and case 4.
In spillway analysis, managing high velocity is another crucial parameter, as it directly influences the kinetic energy at the downstream end. High flow velocities can increase kinetic energy, leading to turbulence and erosion downstream of spillways. To address these challenges, various studies have focused on mitigating these issues through the use of baffle blocks in stilling basins, which reduce downstream velocity and enhance energy dissipation, thereby minimizing erosion at the toe of spillways [35].
Previously, a new methodology was introduced to predict the depth-averaged velocity along the lateral direction in open channel flow. This article applies a similar concept of depth-averaged velocity to analyze the four cases under investigation [36]. Figure 14 show the average depth velocity, showing distinct behaviors in each spillway case. Velocity fluctuations in spillways are largely attributed to kinetic turbulence, spillway geometry, and initial input velocity. The case 1 and case 3 geometries exhibit higher velocities compared to case 2 and case 4. On the other hand, the pooled stepped spillways in case 2 and case 4 promote better flow uniformity and stability at each flow rate. The analysis indicated that the pooled step geometry in case 2 performs better in terms of energy dissipation, pressure, and velocity distribution due to the characteristic height, the volume of trapped water, and the recirculating flow, which break down gravity forces in all dimensions. Energy loss in pooled stepped spillways is primarily caused by factors such as the size of recirculation zones, velocity, and vorticity.

Figure 14.
Downstream depth-averaged velocity of geometry case 1, case 2, case 3, and case 4.
To summarize, the variation in the sequent depth ratio (y2/y1) relative to the normalized critical depth (yc/h) demonstrates a notable increase in case 1 compared to case 2, case 3, and case 4. The energy dissipation (ΔE/E0) at the end of the stepped spillway is calculated as illustrated in Figure 15b. The results of the four cases, including parameters such as initial velocity (u1 m/s), downstream velocity (u2 m/s), total energy E0 (m), downstream energy E1 (m), and energy efficiency (ΔE/E0) are presented in Table 8. The findings indicate that energy dissipation is enhanced in the pooled stepped spillways of case 2 and case 4, as shown in Figure 15b. In contrast, flat-stepped spillways are less efficient in this regard. Furthermore, pooled stepped spillways with the specific configuration mentioned above significantly contribute to these improved outcomes, demonstrating superior energy dissipation compared to flat stepped spillways. However, further research is needed to fully understand the performance of pooled stepped spillways under high discharge conditions. Key areas of study should include the effects of aeration and cavitation in relation to the spillway’s slope. Additionally, it is crucial to evaluate the role of aerator systems in mitigating cavitation risks. A comprehensive examination of these factors will aid in improving spillway design and enhancing overall performance.

Figure 15.
(a) Differences of sequent depth ratio versus normalized critical depth for four different cases; (b) energy dissipation versus initial velocity.

Table 8.
Performance evaluation of flow and efficiency metrics for the four flat and pooled stepped spillways cases.
4. Conclusions
A numerical study was conducted to evaluate flat and pooled stepped spillways under four different configurations by using the realizable k-ε turbulence model with the VOF method. The experimental data of three different flow rates (45, 50, and 54 L/s) were collected from a physical model to validate the reliability of the numerical model. The numerical results showed a good resemblance with the experimental data, demonstrating that the realizable k-ε turbulence model could accurately predict various flow scenarios. Afterward, the study analyzed flow behaviors across four stepped spillway configurations and compared two flat and two pooled geometries, with velocities ranging from 0.45 to 0.70 m/s with 0.5 m/s intervals, to assess their impact on energy dissipation and flow dynamics.
Based on the results, the findings show that the pooled stepped spillways case 2 and case 4 perform better than the flat stepped spillways case 1 and case 3 regarding energy dissipation. The efficiency of case 2 and case 4 at 0.70 m/s, compared to case-1, shows an increase in relative energy loss by 34.68% and 25.81%, respectively. Moreover, case 2 and case 4 show a substantial decrease in downstream velocity of 0.87 m/s and 1.30 m/s, respectively. Similarly, the downstream depth-averaged velocity also significantly decreased, as shown in Figure 14. Additionally, the case 2 and case 4 reductions in hydraulic jump and low Froude numbers indicate improvements in energy dissipation due to the enhanced recirculation and breakdown of trapped water in pooled stepped spillways.
The pressure distribution on flat stepped spillways, especially case 3, exhibits high negative pressure values on the upper vertical faces of the steps and the horizontal steps. On the other hand, pooled stepped spillways show relatively lower negative pressure values. The turbulence kinetic energy in flat stepped case 1 and case 3 increased, while in pooled stepped spillways, it significantly decreased. Overall, pooled stepped spillways demonstrate superior performance in energy dissipation, particularly in the skimming flow regime, compared to flat stepped spillways. Further research on pooled stepped spillways is needed to address high discharge conditions, focusing on the effects of cavitation and aeration to improve spillway design and performance.
Author Contributions
U.F. conceptualization and CFD Simulation, numerical analysis investigation, methodology, writing—original draft. S.L. conceptualization, formal analysis, methodology, supervision, writing—review, and editing. J.Y. conceptualization, formal analysis, methodology, supervision, writing–review, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
As part of the research project spillway discharge safety—quality and assurance in CFD for air–water flow predictions (project no. VKU32011), the study is funded by SVC. The SVC has been established by Swedish Energy Agency, Energiforsk, and Svenska Kraftnät together with Luleå University of Technology, Royal Institute of Technology, Chalmers University of Technology, and Uppsala University. Participating companies and industry associations are AFRY, Andritz Hydro, Boliden, Fortum Generation, Holmen Energi, Jämtkraft, Karlstads Energi, LKAB, Mälarenergi, Norconsult, Rainpower, Skellefteå Kraft, Sollefteåforsens, Statkraft Sverige, Sweco Energuide, Sweco Infra-structure, Tekniska verken i Linköping, Uniper, Vattenfall R&D, Vattenfall Vattenkraft, Voith Hydro, WSP Sverige, and Zinkgruvan.
Data Availability Statement
The simulation files and data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
We are thankful to Anders Ansell for his support and resources. Additionally, the authors thank Rasoul Daneshfaraz for his dedicated efforts in utilizing experimental data to validate the model.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ghaderi, A.; Abbasi, S.; di Francesco, S. Numerical Study on the Hydraulic Properties of Flow over Different Pooled Stepped Spillways. Water 2021, 13, 710. [Google Scholar] [CrossRef]
- Ashoor, A.; Riazi, A. Stepped Spillways and Energy Dissipation: A Non-Uniform Step Length Approach. Appl. Sci. 2019, 9, 5071. [Google Scholar] [CrossRef]
- Limantara, L.M.; Malindo, D.; Juwono, P.T.; Hendrawan, A.P. Modelling Spillway for Flood Control Optimization in Embankment Dry Dam. J. Law Sustain. Dev. 2024, 12, e3277. [Google Scholar] [CrossRef]
- Matos, J.; Meireles, I. Hydraulics of Stepped Weirs and Dam Spillways: Engineering Challenges, Labyrinths of Research. In Proceedings of the Hydraulic Structures and Society—Engineering Challenges and Extremes, Brisbane, Australia, 25–27 June 2014; pp. 1–30. [Google Scholar]
- James, C.S.; Main, A.G.; Moon, J. Enhanced Energy Dissipation in Stepped Chutes. Proc. Inst. Civ. Eng.-Water Marit. Eng. 2001, 148, 277–280. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Simple Design Criterion for Residual Energy on Embankment Dam Stepped Spillways. J. Hydraul. Eng. 2016, 142, 04015062. [Google Scholar] [CrossRef]
- Mason, P.J.; Hinks, J.L. Security of Stepped Masonry Spillways: Lessons from Ulley Dam. Dams Reserv. 2008, 18, 5–8. [Google Scholar] [CrossRef]
- Souli, H.; Ahattab, J.; Bensallam, S. Influence of a Modified Weir Profile on Velocity Field and Dissipation Rate in Stepped Spillways: A Comparative Study Using Physical Models and Computational Fluid Dynamics. JAFM 2024, 17, 1874–1884. [Google Scholar] [CrossRef]
- Farooq, U.; Taha Bakheit Taha, A.; Tian, F.; Yuan, X.; Ajmal, M.; Ullah, I.; Ahmad, M. Flood Modelling and Risk Analysis of Cinan Feizuo Flood Protection Area, Huaihe River Basin. Atmosphere 2023, 14, 678. [Google Scholar] [CrossRef]
- Ghaderi, A.; Abbasi, S. Experimental and Numerical Study of the Effects of Geometric Appendance Elements on Energy Dissipation over Stepped Spillway. Water 2021, 13, 957. [Google Scholar] [CrossRef]
- Salmasi, F.; Abraham, J. Genetic Algorithms for Optimizing Stepped Spillways to Maximize Energy Dissipation. Water Supply 2022, 22, 1255–1274. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Energy Dissipation down a Stepped Spillway with Nonuniform Step Heights. J. Hydraul. Eng. 2011, 137, 1543–1548. [Google Scholar] [CrossRef]
- Bombardelli, F.A.; Meireles, I.; Matos, J. Laboratory Measurements and Multi-Block Numerical Simulations of the Mean Flow and Turbulence in the Non-Aerated Skimming Flow Region of Steep Stepped Spillways. Environ. Fluid Mech. 2011, 11, 263–288. [Google Scholar] [CrossRef]
- Alqarni, M.S.; Memon, A.A.; Anwaar, H.; Usman; Muhammad, T. The Forced Convection Analysis of Water Alumina Nanofluid Flow through a 3D Annulus with Rotating Cylinders via Κ−ε Turbulence Model. Energies 2022, 15, 6730. [Google Scholar] [CrossRef]
- Nikmehr, S.; Aminpour, Y. Numerical Simulation of Hydraulic Jump over Rough Beds. Period. Polytech. Civ. Eng. 2020, 64, 396–407. [Google Scholar] [CrossRef]
- Zabaleta, F.; Bombardelli, F.A.; Márquez Damián, S. Numerical Modeling of Self-Aerated Flows: Turbulence Modeling and the Onset of Air Entrainment. Phys. Fluids 2024, 36, 043337. [Google Scholar] [CrossRef]
- Ghaderi, A.; Dasineh, M.; Aristodemo, F.; Aricò, C. Numerical Simulations of the Flow Field of a Submerged Hydraulic Jump over Triangular Macroroughnesses. Water 2021, 13, 674. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, J.; Hu, Y. Numerical Investigation of the Flow Pattern and Energy Dissipation of Interval-Pooled Stepped Spillways. In Proceedings of the E-Proceedings of the 38th IAHR World Congress, Panama City, Panama, 1–6 September 2019; pp. 2521–2530. [Google Scholar]
- Morovati, K.; Eghbalzadeh, A.; Soori, S. Study of Energy Dissipation of Pooled Stepped Spillways. Civ. Eng. J. 2016, 2, 208–220. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Y.; Shu, Z.; Mao, X.; Xu, M.; Ye, Z.; Ye, J. A Flow-3d-Based Numerical Simulation of the Energy Dissipation Characteristics of Pooled Stepped Spillways. In Proceedings of the 2022 8th IEEE International Conference on Hydraulic and Civil Engineering: Deep Space Intelligent Development and Utilization Forum (ICHCE), Xi’an, China, 25–27 November 2022; pp. 989–994. [Google Scholar]
- Li, S.; Yang, J.; Li, Q. Numerical Modelling of Air-Water Flows over a Stepped Spillway with Chamfers and Cavity Blockages. KSCE J. Civ. Eng. 2020, 24, 99–109. [Google Scholar] [CrossRef]
- Saleh, S.M.; Muhammad, S.H.; Abo, A.A. Effect of Pooled and Flat Stepped Spillway on Energy Dissipation Using Computational Fluid Dynamics. Tikrit. J. Eng. Sci. 2022, 29, 75–79. [Google Scholar] [CrossRef]
- Hantoosh, S.H.; Shamkhi, M.S. Discharge Coefficient and Energy Dissipation on Stepped Weir. Open Eng. 2023, 13, 20220427. [Google Scholar] [CrossRef]
- Pandey, B.R.; Megh Raj, K.C.; Crookston, B.; Zenz, G. Numerical Investigation of Different Stepped Spillway Geometries over a Mild Slope for Safe Operation Using Multiphase Model. Water 2024, 16, 1635. [Google Scholar] [CrossRef]
- Guenther, P.; Felder, S.; Chanson, H. Flow Aeration, Cavity Processes and Energy Dissipation on Flat and Pooled Stepped Spillways for Embankments. Environ. Fluid Mech. 2013, 13, 503–525. [Google Scholar] [CrossRef]
- Salmasi, F.; Abraham, J. Effect of Slope on Energy Dissipation for Flow over a Stepped Spillway. Water Supply 2022, 22, 5056–5069. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, X.; Yuan, H.; Li, X.; Xie, C.; Yang, S.; Bai, Z. Energy Dissipation in Stepped Spillways with Different Horizontal Face Angles. Energies 2019, 12, 4469. [Google Scholar] [CrossRef]
- Gubashi, K.R.; Mulahasan, S.; Hacheem, Z.A.; Rdhaiwi, A.Q. Effect of the Stepped Spillway Geometry on the Flow Energy Dissipation. Civ. Eng. J. 2024, 10, 145–158. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, J.; Hu, Y. Analysis of Energy Dissipation of Interval-Pooled Stepped Spillways. Entropy 2022, 24, 85. [Google Scholar] [CrossRef]
- Hunt, S.L.; Kadavy, K.C. The Effect of Step Height on Energy Dissipation in Stepped Spillways. In Proceedings of the World Environmental and Water Resources Congress 2009, Kansas City, MO, USA, 17–21 May 2009; American Society of Civil Engineers: Kansas City, MO, USA, 2009; pp. 1–11. [Google Scholar]
- Daneshfaraz, R.; Sadeghi, H.; Ghaderi, A.; Abraham, J.P. Characteristics of Hydraulic Jump and Energy Dissipation in the Downstream of Stepped Spillways with Rough Steps. Flow Meas. Instrum. 2024, 96, 102506. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Kaouachi, A.; Carvalho, R.F.; Lopes, P.; Benmamar, S.; Gafsi, M. Numerical Investigation of Alternating Skimming Flow over a Stepped Spillway. Water Supply 2021, 21, 3837–3859. [Google Scholar] [CrossRef]
- Kositgittiwong, D.; Chinnarasri, C.; Julien, P.Y. Numerical Simulation of Flow Velocity Profiles along a Stepped Spillway. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2013, 227, 327–335. [Google Scholar] [CrossRef]
- Khuntia, J.R.; Devi, K.; Khatua, K.K. Prediction of Depth-Averaged Velocity in an Open Channel Flow. Appl. Water Sci. 2018, 8, 172. [Google Scholar] [CrossRef]
- Manogaran, T.; Mohd Arif Zainol, M.R.R.; Wahab, M.K.A.; Abdul Aziz, M.S.; Zahari, N.M. Assessment of Flow Characteristics along the Hydraulic Physical Model of a Dam Spillway. J. Civ. Eng. Sci. Technol. 2022, 13, 69–79. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).