An Assessment of the Embedding of Francis Turbines for Pumped Hydraulic Energy Storage

Abstract

In this paper, analyses of Francis turbine failures for powerful Pumped Hydraulic Energy Storage (PHES) are conducted. The structure is part of PHES Chaira, Bulgaria (HA4—Hydro-Aggregate 4). The aim of the study is to assess the structure-to-concrete embedding to determine the possible causes of damage and destruction of the HA4 Francis spiral casing units. The embedding methods that have been applied in practice for decades are discussed and compared to those used for HA4. A virtual prototype is built based on the finite-element method to clarify the influence of workloads under the generator mode. The stages of the simulation include structural analysis of the spiral casing and concrete under load in generator mode, as well as structural analysis of the spiral casing under loads in generator mode without concrete. Both simulations are of major importance. Since the failure of the surface between the turbine, the spiral casing, and the concrete is observed, the effect of the growing contact gap (no contact) is analyzed. The stresses, strains, and displacements of the turbine units are simulated, followed by an analysis for reliability. The conclusions reveal the possible reasons for cracks and destruction in the main elements of the structure.

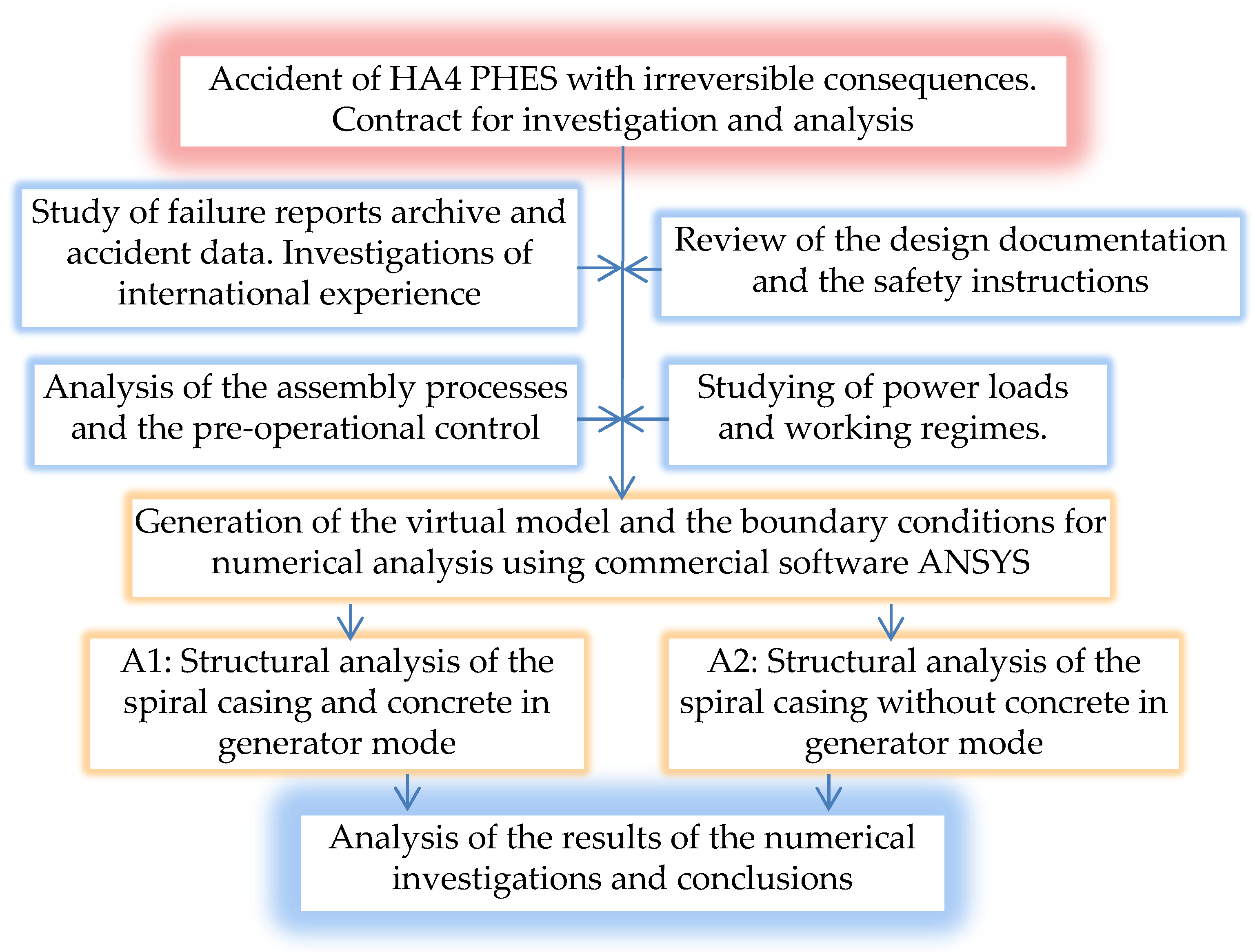
1. Introduction

The requirements for up-to-date PHESs include the development of new possibilities resulting from the need to store and regenerate unused electrical energy. The earliest PHESs were built in Switzerland, Austria, and Italy at the end of the 19th century. They include both pump and electric generators. Pumped storage systems for hydroelectric power generation have been widely applied since the middle of the 20th century [1]. The production of electricity from nuclear and hydroelectric plants and wind and solar systems requires the storage of electrical energy in the case of low electricity consumption. This is of particular importance for nuclear power plants, which should operate continuously. Recent research on the development activities in the field of hydropower technology was presented in [2]. In [3], the operational benefits of transforming cascade hydropower stations into pumped hydro energy storage systems were discussed. Worldwide, many countries are developing PHES or upgrading their existing plants. Several researchers have investigated suitable sites for pumped storage developments in their countries, such as Germany, Greece, France, the USA [4,5,6], etc.

Currently, it has been proven that PHES is an effective and attractive storage solution with fast response times and long lifetimes [7,8,9]. PHES systems store and generate electricity by exchanging water between reservoirs at different altitudes. They convert potential energy to electrical energy and vice versa, allowing for water to flow from a high altitude or by pumping water from a low altitude to a higher altitude. The pumped storage plants mainly use Francis turbines because they can act as both a hydraulic pump and a hydraulic turbine and possess a high degree of effectiveness, i.e., more than 80%. In Figure 1, a simple design scheme of a Francis turbine is presented. When it operates as a turbine, the water flow (input flow) circulates around the spiral casing while part of the flow is diverted to the turbine. So, the output flow changes its direction normal to the input flow. This is one of the main reasons for the high effectiveness of the turbine. Francis turbines used in modern power plants are more complicated and are discussed further below.

Profound investigations regarding the Francis turbine are directed towards analysis of the induced vibrations and the reasons for them. The vibrations could cause significant damage to the turbine construction and the structure as a whole, including the embedding. The vibrations could be caused by start–stop regimes, cavitation, and/or during the switching process from pumping to the generation of electricity. Favrel et al. [10] investigated the influence of discharge on the vortex rope parameters and structure and highlighted how the intensity of the excitation source is linked to vortex rope dynamics. The same authors [11] studied the cavitation and resonance effect on the draft tube of Francis turbines.

In [12], the pressure amplitude fluctuations on the Francis turbine prototype were analyzed, and measures for their avoidance were proposed for application in real turbine structures. In [13], the Francis turbine cavitation surge phenomenon in the draft tube inducing large pressure fluctuations was analyzed. A draft tube model was proposed and applied to investigate the influence of parameters on the cavitation surge.

Panov et al. [14] developed a numerical technique for the simulation of cavitation flows through the flow passage of a hydraulic turbine. The technique is based on the solution of steady 3D Navier–Stokes equations with a liquid-phase transfer equation. Numerical simulations for turbines of different specific speeds were compared with the experiment. In [15], an experimental and theoretical investigation of the flow at the outlet of a Francis turbine runner was carried out to elucidate the causes of a sudden drop in draft tube pressure.

Rudolf et al. [16] studied the spatio-temporal behavior of the draft tube of a hydraulic turbine for two partial load operating points using orthogonal decomposition. They identified the eigenmodes that compose the flow field and ranked the modes according to their energy. In [17], the response of the cavitation in the draft tube flow to a time-dependent inflow and time-dependent pressure at the draft tube exit was simulated. The results were input to a statistical identification procedure. To gain a deeper understanding of the flow behavior under high load conditions in [18], a combined 1D–3D transient two-phase numerical investigation at prototype size was carried out, and these results were compared with measured site data.

In [19], a two-phase 1D–3D model of full load surge, presented previously by the authors [14], was applied to the simulation of self-excited oscillations in the prototype power station. The model consists of 1D hydro-acoustic equations for the penstock domain and 3D two-phase unsteady RANS equations for the turbine domain, including the cavitating flow in the draft tube. In the paper of Wack and Riedelbauch [20], the occurrences of cavitating inter-blade vortices at deep part-load conditions in a Francis turbine were investigated using two-phase flow simulations.

The papers cited above show that numerical modeling of hydraulic turbines is a challenging subject since specific approaches applied to investigate an operating condition do not necessarily work for other flow phenomena. The first workshop aimed at determining the state of the art in a simulation of high-head Francis turbines under steady operations was held in Trondheim, Norway. Trivedi and Cervantes investigated the methods for simulation and some numerical results were presented in the first workshop in Trondheim in 2014 and later summarized in their paper [21]. The aim of the scientists and designers was not only to design the process and application of PHES but also to reveal the main reasons for severe incidents in conventional hydropower plants and to make recommendations on how to avoid them. The casualties could lead to tremendous economic losses and environmental disasters.

Yasuda and Watanabe [22] studied and analyzed severe incidents of conventional hydropower plants in many countries in the period of 1990–2010. In Canada, six bulb turbines of 30MW each were found to have corrosion fatigue cracking. Similar incidents were reported for power plants in Romania and Serbia. In Russia, the head cover of a 640MW Francis turbine broke away, and the power station was destroyed. In Canada, runner blades had severe cracks due to high vibration caused by guide vane failure. A Francis turbine of 88MW in the USA had severe damage because of the dropping of a link pin of a guide vane. Many cracks were found on the trailing edges of turbine blades for three Francis turbines of 200MW in Iran. The cause was vibration excited by a Von Karman Vortex Street. The same severe vibrations were the reason for the cracks found in two runners of Francis turbines of 330MW in China. In Australia, the spiral casing of a Francis turbine of 150 MW failed following excessive pressure rise due to the instant shutdown of all guide vanes [23].

The strains, stresses, and coefficient of friction are taken into account for the design of structures of concrete and steel units that are in force contact [24,25]. However, recent incidents with powerful Francis turbines and significant financial losses have imposed the necessity of a detailed analysis of the proper embedding and the reasons for such destructions. Leading investigations have been conducted by Chinese scientists who, for more than two decades, have studied the reliability of different methods for embedding spiral casing.

A very important role in the safety and accident-free work of Francis large PHES is the embedding of the spiral casing over the fundament. In Figure 2, the principal scheme of the embedding is shown [26]. Many significant casualties in powerful hydropower stations using huge Francis turbines are a result of the interaction of the structure with the fundament. The practice for the powerful Francis turbines is for the spiral casing to be placed in a concrete block, which makes the repair very complicated and often leads to the replacement of the entire turbine. In the European patent [27], a special design scheme was proposed that facilitated the repair of the power station with a Francis turbine. The scientific investigations directed toward the influence of different factors over the design scheme and structure are of significant importance since they could reveal the factors that influence structural damage. Figure 3 shows structural deformation after the accident involving concrete in the Xiluodu hydropower plant located on the Jinsha River, Southwest China [28]. The white arrow on the figure shows the concrete erosion.

In [29], the Three-Gorge Dam on the Yangtze River near Sandouping, China, was taken as an example to evaluate hydraulic forces, including water-pressure pulsation, the effect of the cracks on natural frequencies, and the vibration responses of the power station under hydraulic and earthquake forces. Yu et al. [30] applied finite-element theory to calculate a spiral casing embedded with cushion layers to study the influence of reinforcement. They analyzed the concrete frame simplification, basement simplification, and contact friction between the spiral casing and the concrete.

In [31], a hydropower station spiral casing with a nonuniform gap is simulated using the ABAQUS finite-element program system. The procedure involves the casing of a constant internal pressure, taking into account a casing contact with peripheral reinforced concrete. At the operation stage, the variation of the gap and the property of the casing–concrete contact is shown. In [32], a 3D numerical model for a hydropower plant of the Three Gorges (China) is developed, and nonlinear static and dynamic damage analysis is performed. Numerical results showed that in the casing of high water pressure and large diameter of the inlet turbine pipe, the damage is mainly located near the top of the spiral casing. The casing of the combined action of static loads and the earthquake was considered, and it was shown that the damage of the concrete surrounding the spiral casing increased insignificantly; however, some damage occurred on the side walls. Panda et al. [33] analyzed the Francis turbine of the Hydel Power Station in India. Their study was limited to the concrete around the spiral casing of the turbine. A three-dimensional simulation was performed using two software systems, i.e., the finite-element method and the three-dimensional photo-elasticity method. Both methods showed similar results.

Since 2012, several papers by Chinese scientists have been devoted to the rising deformation incident at the Xiluodu (China) hydropower stations [34] and analysis of the compressible membranes around the spiral casings of Francis turbines [35,36]. In the period to 2018, different methods of embedding Francis turbines were investigated. Zhang and Wu [35,36,37,38,39] and Wu et al. [40] performed numerical structural analysis of the Francis turbine embedding, including preloaded filling of the spiral casing with a nonuniform gap. They considered the sliding behavior of the steel on surrounding concrete, using the softened contact of the compressible membrane. In [39], the Chinese’s experience of embedding the spiral casing was reported. Wu et al. [40] studied the 15th turbine unit in the Three Gorges hydropower station (China), in which a different embedding method was used. They proved that the structure with a compressible membrane is feasible and will satisfy safety and design requirements. Guo et al. [41] performed a three-dimensional simulation algorithm of preloaded filling the spiral casing with a nonuniform gap. Zhang et al. [42] analyzed the possible methods of embedding and proposed further knowledge of two mainly applied membranes between the spiral casings and the concrete, i.e., polyurethane, cork, and polyethylene foam.

The present investigations and design solutions of the PHES step on the previous experience of the scientists and designers and are directed toward the analysis of different phenomena that improve system reliability and safety. Zhanga et al. [43] applied numerical modeling of preloaded filling spiral casing structure. They described the evolution process of the nonuniform gap and contact nonlinearity and performed an experimental investigation. They used finite-element analyses to simulate the gap and contact nonlinearity as well as the construction and operation process. Qi et al. [44] performed an optimization analysis of a giant spiral casing with combined embedding. Guo et al. [45] proposed a simulation algorithm based on contact slippage to simulate the preloading water-filled spiral casing structure problem for the Nuozhadu dam (China) hydropower project. The authors of [46] discussed pressure pulsations in the spiral casing and draft tube, from minimum power to maximum power. They performed strength calculations of the spiral casing of the Francis turbine, including two hydro units of the Ruieni hydroelectric station located on the Sebeş River in Romania. The study in [47] focuses on the complex construction-to-operation process of the spiral casing structures. An ABAQUS-based complete simulation procedure was used, taking into account contact nonlinearity.

In [28], a Chinese hydroelectric power plant with 700 MW turbines was discussed, where a structural deformation accident occurred during the construction period, causing severe loss. The study focused on two major differences in the spiral casing structures that might cause the accidents, i.e., the construction condition and the shape of the steel spiral casing. Xu et al. [48] investigated the impact of varying bedding areas on the distribution of damage in a concrete foundation and elucidated the failure mechanism and damage mode of a cushioned spiral casing under increasing water load.

The embedding of the spiral casing of the powerful PHES is a challenging task for engineers, designers, and constructors. The Francis turbine is a large hydraulic machine which, in the case of the PHES, serves as either a pump or a turbine. Different physical and natural phenomena are imposed on the whole system. High pressure and different hydraulic factors are the main reasons for vibrations and destruction. The pressure pulsations and the change in fluid flow direction, as well as the cavitation effect, have a significant influence on the reliability of the different parts of the turbine. Since the spiral casing is the largest unit experiencing extremely high pressure, its safe operation is of major importance. The casing experiences significant deformations and small translations between the steel structure and the fundament. Below, the methods will be briefly discussed using abbreviations most often used in practice. In [28], detailed explanations with profound pictures and schemes were presented. Here, we will briefly explain the essence of each of them.

N-type embedding

This is the method by which the spiral casing is entirely placed in concrete. The stages of embedding include:

-

placing inside the spiral casing of internal support that will prevent deformation because of the pressure of the surrounding concrete;

-

the spiral casing is placed on a pre-prepared foundation;

-

the casing is surrounded by reinforced concrete on several layers;

-

the internal support is removed, and the other parts of the turbine are mounted.

M-type embedding

This method is a unification of the N-type embedding for which, before the concrete, the spiral casing is wrapped in a compressible membrane. Therefore, the flexibility of the membrane ensures better conditions for contact between the casing and the concrete.

P-type embedding

P-type embedding is implemented under water-pressurized conditions. The principle consists of filling the spiral casing with water. For this purpose, to ensure the tightness of the casing, the test head and test barrel are placed, as explained in [28]. Then, pressure is applied inside the casing with a value depending on the engineering solution, for example, half of the working pressure. This way, the initial deformation of the casing is ensured before the concrete filling. The procedure continues with the aforementioned procedure with the concrete filling as it is for the N and M-type of embedding. After that, the casing is emptied, and the test head and barrel are removed. Using this method, an initial deformation of the casing is provided, and a gap between the concrete is ensured.

In many articles [28,29,30,31,32], the structures of the spiral casing and the concrete using the methods M and N types were analyzed by applying different numerical methods and software systems. The investigations of the friction process between steel structures and concrete were also studied [24,25]. Studying the experience of the scientists and the engineers in the present paper, the P-type structure is analyzed, taking into account the mutual interaction between the steel casing and the surrounding concrete. Despite the profound study of the scientific literature, the authors of the present paper were not able to find out valuable conclusions and recommendations for this type of embedding. That is why they are confident that their experience and investigations of the P-type embedding of Bulgarian PHES will be beneficial to the science and practice.

The investigations presented in this paper deal with the mechanical analysis of static components of turbine assembly. The authors of the present paper investigated the provided technical and other working documentation of the records for the working parameters of HA4 in the period of time before, during, and after the emergency. The plastic strains, the stresses, and the total deformations of the spiral casing, the stay vanes, the cover, and the supporting discs are considered. Special attention is paid to the plastic strains as the main reason for destruction. The dangerous places and units of the structure are defined. The experience of Bulgarian scientists [49,50,51] in simulation and virtual engineering is of benefit to the present investigation, analysis, and conclusions.

2. Materials and Methods

2.1. Design Geometry

The computer simulation and the consequential analyses require the compilation of a virtual prototype (computer simulation model) to clarify the mechanisms of influence of working loads and specific work casings on the structural elements.

On this basis, the possible reasons for the appearance of cracking in the fixed parts of HA4 will be analyzed. In Figure 4a, the virtual model of the design scheme of the analyzed structure is presented, which consists of the spiral casing and stator ring. The latter is composed of an upper ring, a support ring, and stay vanes (Figure 4b). The stay vanes are also called supporting columns since they ensure the support of the upper and the support rings. In Figure 4b, the part circled in red, i.e., the spiral casing and the stay vanes, will be the subject of investigation in the next section. This compound will be simulated with and without embedding in the concrete.

The spiral casing itself is built of 20 parts, including the input tube and 15 parts of the spiral casing. The material is steel HT60. The stay vanes and the rings are made of steel JIS G 3106 SM 50A. The embedding of the spiral casing (see Figure 5a) is fulfilled on two base layers. The first one (2200 mm) is fulfilled in three stages, and the second one is 2600 mm. Internal steel armature is also included in the model and is shown in Figure 5b. The mechanical and stress characteristics of the materials are presented in

Table 1. Mechanical and stress characteristics of steel and concrete.

Parameter	HT60	JIS G 3106 SM 50 A	Concrete 25
Modulus of elasticity, E, GPa	209	200	30
Coefficient of Poisson, μ	0.29	0.28	0.18
Density, ρ, kg/m3	7850	7700	2400
Yield strength Rp0,2, MPa	461	334	-
Tensile strength, Rm, MPa	620	520	-
Tangent modulus, MPa	3300	3640	-

.

Both examined models use mainly hexagonal 3D elements, with additional elements to present concrete armature (when the concrete structure is included). The mesh quality selection is an important procedure as it is needed to satisfy certain requirements.

Mesh quality was examined during analysis preparation using criteria such as skewness (distortion), aspect ratio, warping angle, etc. According to the ANSYS nCode DesignLife and ANSYS Mechanical software instructions and applications, specific control options are set to achieve allowable values for these criteria. The generated finite-element mesh is shown in general in Figure 6, including layers of the embedding (Figure 6a), generated mesh for the concrete (Figure 6b) and the turbine (Figure 6c), as well as local sectional zoom of a stay vane (Figure 6d).

The generated hexagonal 3D elements mesh has a higher quality than the generated with tetrahedral elements. The selected procedure of a high amount of elements in the range of 0.88–0.98 and distortion in the range of 0.05–0.4 proposes higher quality of the finite-element mesh of the structure, as well as higher accuracy of the numerical calculations.

2.2. Structural Loads and Operating Modes

Examined structures (with and without concrete) are subjected to different working conditions. The Francis turbine works either as an electric generator or as a pump. Additionally, there are peak loads, leakage test loads, and emergency modes. The study aims to figure out the importance of concrete structure and it is examined in generator mode only. The structure is studied under the pressure on the hydraulic unit walls. Its values are based on the records of the working situations provided by the local staff. The following pressure values are applied for the numerical simulation:

-

p1 = 6.96 MPa—applied on the internal surfaces of the spiral casing;

-

p2 = 6.26 MPa—applied on the internal surfaces of the lower and upper rings;

-

p3 = 5.57 MPa—applied on the upper and lower sealing rings.

2.3. Aim and Stages of the Investigations

On the basis of the detailed analysis of the available information about the occurrence of similar emergency casings at Chaira PHES, as well as familiarization with the testimony and analyses of the experts and those working at the hydropower plant, as well as of the repair contractor team, the following structural and mechanical analyses were performed:

• A1: Complete structural analysis of the spiral casing and concrete under loads in generator mode;
• A2: Complete structural analysis of the spiral casing under loads in generator mode but without concrete.

For the A2 procedure of the simulation, it should be noted that only the supporting basement of the turbine is considered without the enforcement of the spiral casing. This is because the gap between the spiral casing and its surrounding concrete continuously increases during the operation as a result of elastic expansion and contraction of the spiral casing due to variations in the internal pressure.

In Figure 7, the flow chart of the stages of the investigations, including the study of current destruction and construction data records of previous incidents and repairs, is presented.

3. Results

3.1. A1: Structural and Mechanical Simulation of Spiral Casing and Concrete Enclosure

This structural and mechanical analysis aims to evaluate the stresses and strains in the spiral casing. The computational results for the units indicated by a red circle in the model (Figure 4b) are presented in Figure 8 and Figure 9 as distribution fields of equivalent stresses, displacements, and strains.

In particular, the plastic strains are of interest that will indicate more clearly the difference between the two models, with and without concrete.

3.2. A2: Structural and Mechanical Analysis of Spiral Casing, without Concrete Enclosure

Again, equivalent stresses, strains, and total displacements are evaluated for important components of the spiral casing. The results are presented in Figure 10 and Figure 11 as distribution fields for a slice of the model (Figure 4b), as well as of a stay vane.

3.3. Analysis of the Numerical Simulation Results

Both models—with and without concrete structure—can be compared to outline the importance of the concrete structure and its possible influence on the overall performance of the examined hydraulic assembly. This comparison is performed on the basis of three indicators, shown in the previous section—stress, strain, and displacement. It is shown in diagrams in Figure 12, Figure 13 and Figure 14.

4. Discussion

Some comments could be stated based on the results of the simulation and the diagrams above, i.e.,:

-

the influence of the concrete structure support over the maximal stress values is insignificant, as the structure is experiencing plastic deformations in both examined casings;

-

the displacements are increased nearly twice, i.e., due to the decreased rigidity of the structure;

-

the plastic strains are increased by nearly 40%, leading to a definitive possibility for crack initiation;

-

the subject of the investigations is a critically damaged structure, and only numerical experiments and simulation could be conducted.

As stated above, for the A2 simulation (without concrete embedding), only the supporting basement of the turbine is considered without the surrounding concrete of the spiral casing. This is because the gap between the spiral casing and its surrounding concrete continuously increases. That is why the stresses in the supporting ring are a result of the weight of the turbine on the foundation (Figure 10a), while the stresses in the cover ring are negligible.

5. Conclusions

Based on the numerical experiments conducted, as well as on the consequential analysis, the major conclusions for the reasons for the accident of the HA4 in the PHES Chaira are:

-

the gap between the concrete and the spiral casing continuously increases as a result of the variable contact during operation in different modes and internal pressures, which leads to the destruction of the concrete (the same conclusion of the Chinese scientists, Figure 3 [28]);

-

although the stresses and strains in the cover ring are admissible (Figure 8a, Figure 9b, Figure 10a and Figure 11b), its total deformation (Figure 9a and Figure 11a) is significant;

-

investigation A2 shows that if the gap between the turbine and the concrete embedding is significant (no contact), the main loading as a result of the extremely high pressure is on the stay vanes;

-

the stresses and strain simulation presented in Figure 8b, Figure 9b, Figure 10b, and Figure 11b proves the aforementioned conclusion that parts of the stay vanes are imposed on critical loading during the operational mode;

-

it is proven that the contact surfaces between the support ring, the stay vanes, and the cover ring are the places with extremely high plastic stresses;

-

concentration of unacceptable stresses in the cross sections of the stay vanes along the sections of the welding are observed;

-

realization of the embedding method P (discussed in Introduction Section 1) could not be found in the scientific literature for more than 30–50 years, although some disadvantages could be observed with the other methods of embedding.

Investigations should continue on the structural behavior of the casing for other turbine working conditions, such as start–stop regime, emergencies, pumped regimes, the effect of cavitation, and other possible situations. Further investigations will be carried out on the cover ring, stay ring, and supporting columns, and possible new design solutions are to be proposed.