Dimensionless Pressure Response Analysis for Water Supply Pipeline Systems with or without Pumping Station
Abstract
:1. Introduction
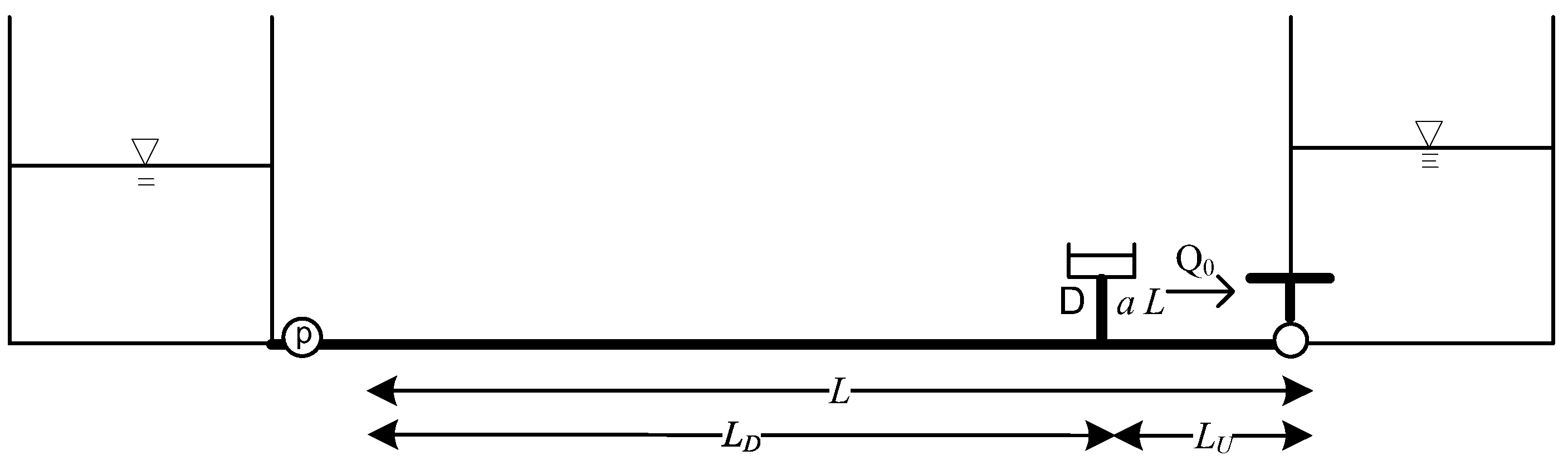
2. Materials and Methods
2.1. One-Dimensional Dimensionless Governing Equation with Steady Friction
2.2. Dimensionless Hydraulic Impedance from Surge Tank to Joining Point
2.3. Dimensionless Hydraulic Impedance from Surge Tank to Joining Point
2.4. Dimensionless Lumped Inertia
2.5. Development of Dimensionless Hydraulic Impedance for Two Different Systems
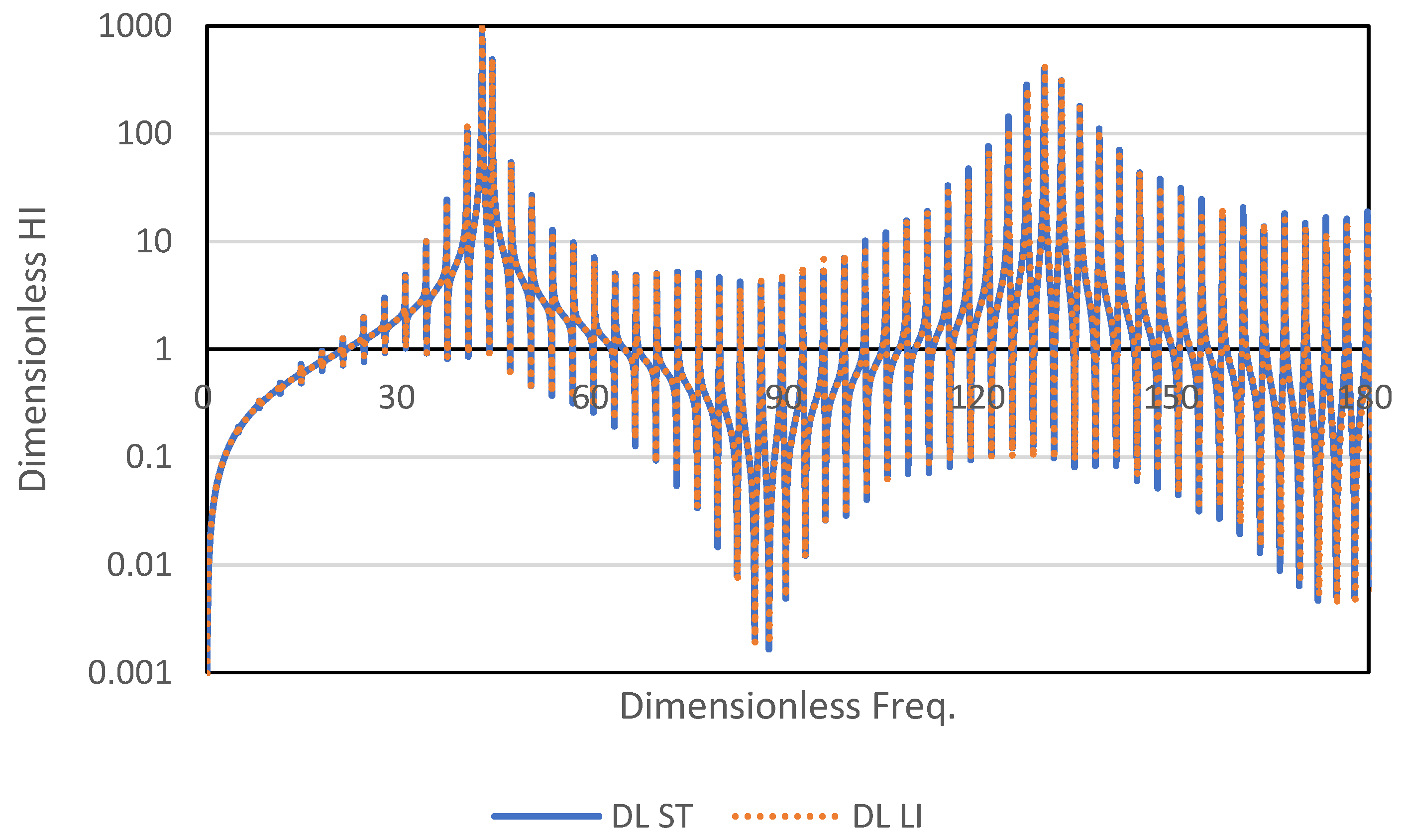
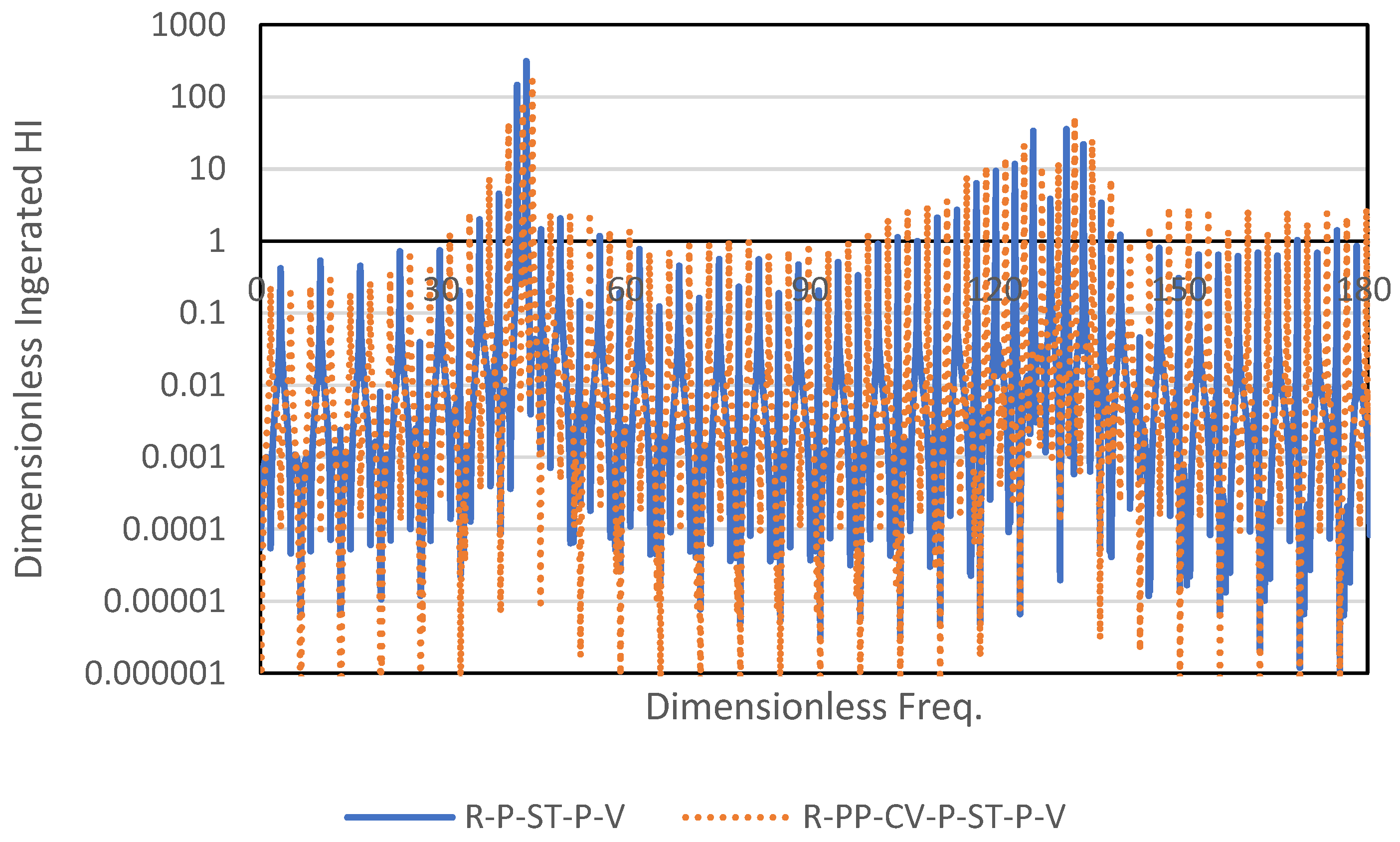
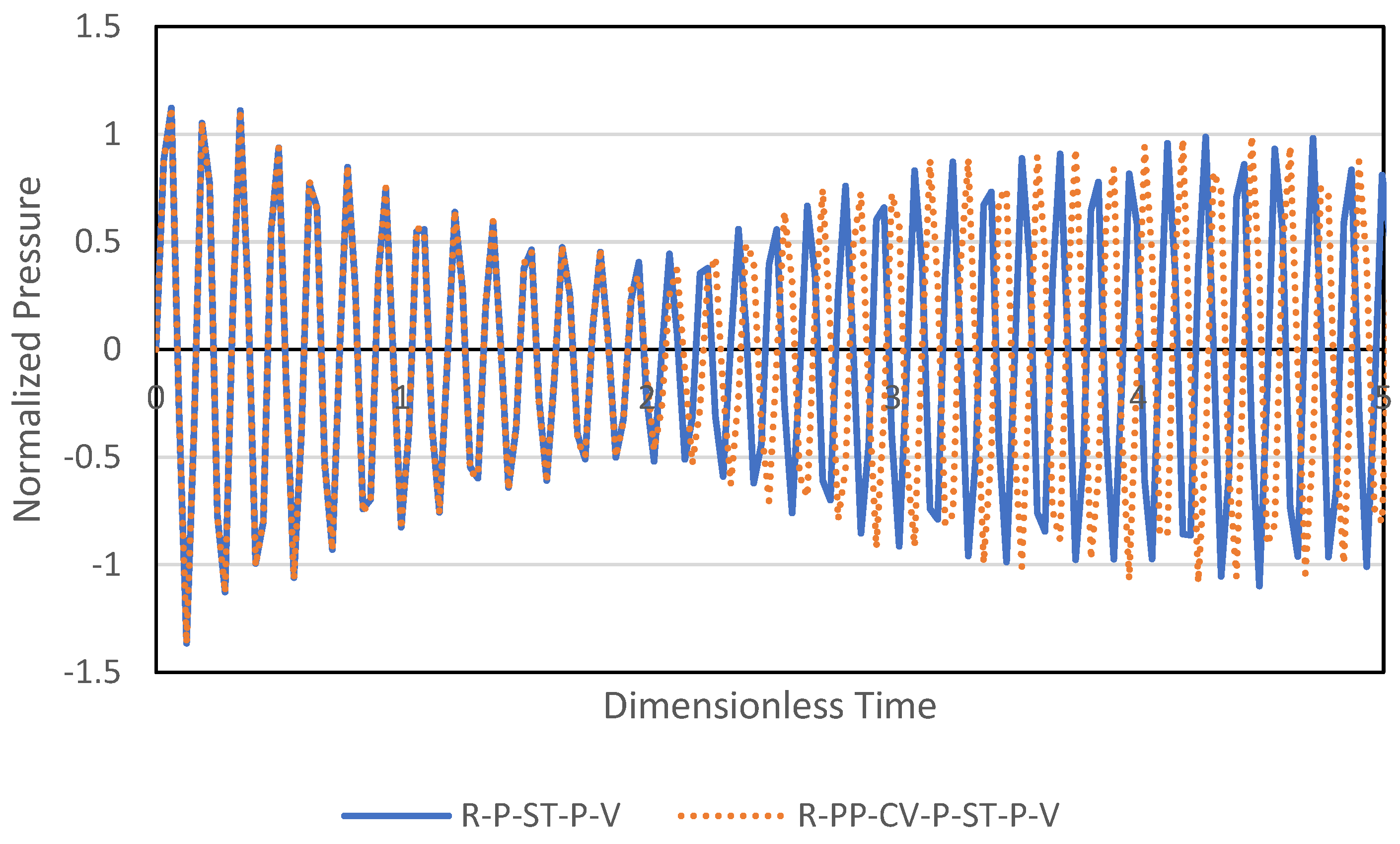
3. Results
3.1. Frequency Response Function
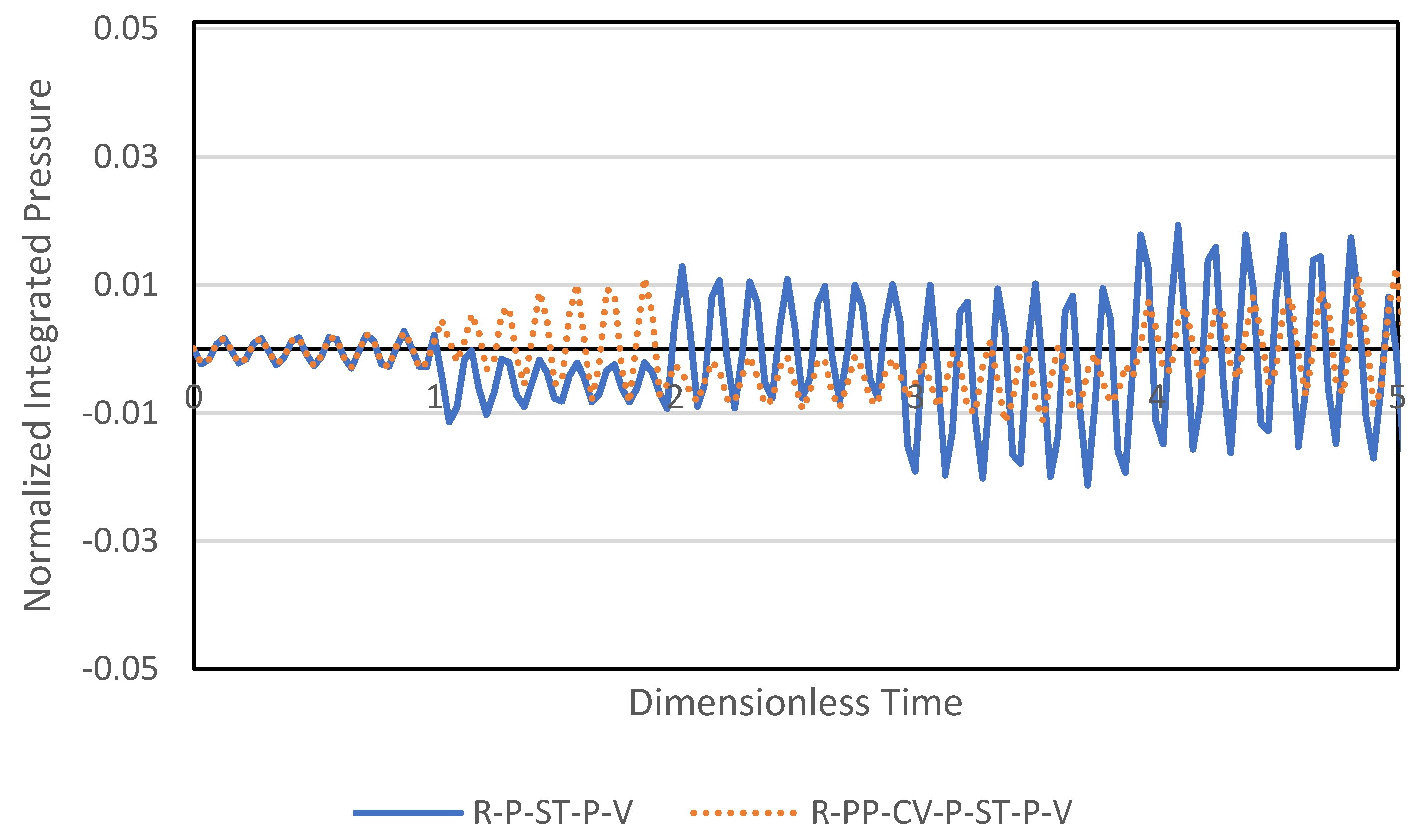
3.2. Time Domain Pressure Response
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wylie, E.B.; Streeter, V.L. Fluid Transients in Systems, 3rd ed.; Prentice-Hall International: London, UK, 1993; pp. 37–79. [Google Scholar]
- Karney, B.W.; Simpson, A.R. In-line check valves for water hammer control. J. Hydraul. Res. 2007, 45, 547–554. [Google Scholar] [CrossRef] [Green Version]
- Wan, W.; Zhang, B. Investigation of Water Hammer Protection in Water Supply Pipeline Systems Using an Intelligent Self-Controlled Surge Tank. Energies 2018, 11, 1450. [Google Scholar] [CrossRef] [Green Version]
- Triki, A. Further invetogation on water-hammer control line strategy in water-supply systems. J. Water Sup. 2018, 67, jws2017073. [Google Scholar] [CrossRef]
- Di Santo, A.R.; Fratino, U.; Iacobellis, U.V.; Piccinni, A.F. Effects of free outflow in rising mains with air chamber. J. Hydraul. Eng. 2002, 128, 992–1001. [Google Scholar] [CrossRef]
- Jung, B.S.; Karney, B.W. Systematic Surge Protection for Worst-Case Transient Loadings in Water Distribution Systems. J. Hydraul. Eng. 2009, 135, 218–223. [Google Scholar] [CrossRef] [Green Version]
- Duan, H.F.; Tung, Y.K.; Ghidaoui, M.S. Probabilistic Analysis of Transient Design for Water Supply Systems. J. Water Resour. Plan. Manag. -ASCE 2010, 136, 678–687. [Google Scholar] [CrossRef]
- Martino, G.D.; Fontana, N. Simplified approach for the optimal sizing of throttled air chambers. J. Hydraul. Eng. 2012, 138, 1101–1109. [Google Scholar] [CrossRef]
- Skulovich, O.; Bent, R.; Judi, D.; Perelman, L.S.; Ostfeld, A. Piece-wise mixed integer programming for optimal sizing of surge control devices in water distribution systems. Water Resour. Res. 2015, 51, 4391–4408. [Google Scholar] [CrossRef]
- Bhattarai, K.P.; Zhou, J.X.; Palikhe, S.; Pandey, K.P.; Suwal, N. Numerical Modeling and Hydraulic Optimization of a Surge Tank Using Particle Swarm Optimization. Water 2019, 11, 715. [Google Scholar] [CrossRef]
- Mahmoudi-Rad, M.; Najafzadeh, M. Effects of Surge Tank Geometry on the Water Hammer Phenomenon: Numerical Investigation. Sustainability 2023, 15, 2312. [Google Scholar] [CrossRef]
- Wan, W.; Wang, Y.; Chen, X.; Zhan, H.; Wang, T.; Zhang, B. Investigation of partially expanded surge tank with self-adaptive auxiliary system controlling waterhammer in pipelines. Eng. Sci. Technol. Int. J. 2023, 40, 101379. [Google Scholar] [CrossRef]
- Guo, J.; Woldeyesus, K.; Zhang, J.; Ju, X. Time evolution of water surface oscillations in surge tanks. J. Hydraul. Res. 2017, 55, 657–667. [Google Scholar] [CrossRef]
- Kim, S.H. Design of surge tank for water supply systems using the impulse response method with the GA algorithm. J. Mech. Sci. Technol. 2010, 24, 629–636. [Google Scholar] [CrossRef]
- Kim, S.H.; Choi, D. Dimensionless impedance method for general design of surge tank in simple pipeline systems. Energies 2022, 15, 3603. [Google Scholar] [CrossRef]
- Wang, C.-N.; Yang, F.-C.; Nguyen, V.T.T.; Vo, N.T.M. CFD Analysis and Optimum Design for a Centrifugal Pump Using an Effectively Artificial Intelligent Algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, V.T.T.; Vo, N.T.M. Centrifugal Pump Design: An Optimization. Eurasia Proc. Sci. Technol. Eng. Math. 2022, 17, 136–151. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S. Dimensionless Pressure Response Analysis for Water Supply Pipeline Systems with or without Pumping Station. Water 2023, 15, 2934. https://doi.org/10.3390/w15162934
Kim S. Dimensionless Pressure Response Analysis for Water Supply Pipeline Systems with or without Pumping Station. Water. 2023; 15(16):2934. https://doi.org/10.3390/w15162934
Chicago/Turabian StyleKim, Sanghyun. 2023. "Dimensionless Pressure Response Analysis for Water Supply Pipeline Systems with or without Pumping Station" Water 15, no. 16: 2934. https://doi.org/10.3390/w15162934




