Exploring the Sensitivity of the Transient Response following Power Failure to Air Valve and Pipeline Characteristics

Abstract

Air valves are protective devices often used in pressurised water pipelines, ideally admitting air to limit sub-atmospheric pressures and controlling the release of entrapped air. This work summarises a comprehensive sensitivity analysis of the transient behaviour in a rising water pipeline with an air valve following a pump trip. The paper examines the water hammer stages associated with a pump trip, namely, the initial depressurisation, followed by air admission, then air expulsion, and finally the creation of a secondary pressure wave. For each air valve location and specific set of design conditions, the relationship between the transient magnitude and air valve outflow capacity is found to be non-linear, but to roughly follow the shape of a logistic curve having a lower left plateau for attenuated (type 1) behaviour and transitioning through type 2 behaviour to a higher right plateau for water-hammer-dominated (type 3) behaviour. Through an extensive set of simulations covering a wide range of conditions, the study identifies the size of the critical outflow orifices associated with both type 1 and type 3 responses and assesses the influence of the location of the air valve on the transient magnitude and on the timing of air pocket collapse. Furthermore, the paper highlights that a non-slam air valve is capable of effectively mitigating transient magnitudes provided that its design parameters are judiciously chosen and account for both the system’s attributes and the characteristics of the transient event.

1. Introduction

The presence of air in pressurised water pipelines is often problematic. The inability to effectively manage entrapped air can lead to increased power consumption and can compromise conveyance capacity [1]. When a line is initially pressurised, the presence of entrapped air can permit rapid acceleration of the water column and can thus lead to higher transient pressures compared to lines containing water only [2]. Yet, paradoxically, the presence of sufficient air can also cushion transient events, as in the case of either an unvented system or when venting is controlled by directing air flow through a relatively small aperture [3]. Moreover, air can play a broad and beneficial role in mitigating hydraulic transients if strategically contained, as it is in hydropneumatic tanks [4].

Air valves are a frequently employed strategy for addressing air management in pressurised pipelines. Air-release valves exhaust accumulated air during regular operation, while air/vacuum valves are often selected to allow for air exchange during controlled filling and draining operations, as well as for air exchange during water hammer events [5]. Yet, in reality, air valves often underperform, with their inadequacies sometimes leading to severe consequences, including system disruption or even failure although, at other times and in other systems, their underperformance may have entirely benign outcomes [6]. Thus, a practical puzzle is created: in some systems, the presence of air valves is crucial for reliable operation, while in other systems, air valve removal may have little or no discernible effect on performance. It is to this puzzle that this paper is primarily addressed. The task of evaluating consequences raises many complexities: these include the challenge of predicting the air exchange through an air valve [7], the interaction between air and water within the pipe system [8], the often contradictory sizing criteria for different hydraulic events [9], and the non-linear impact of the air valve on transient behaviour [10].

Complications related to air exchange through the air valve include unreliable performance data from product catalogues and the unpredictability of the dynamic closure of the air valve during expulsion [11]. Accurately modelling transient air–water interactions is challenging without a CFD approach, especially for complex scenarios, such as the filling procedure of horizontal or irregular profile pipelines. Regarding air valve sizing, often the air valve must be sufficiently large to enable nearly unrestricted entry of air during drainage [12] or down-surge events [10], as well as for the efficient release of air during controlled pipeline filling [13]. However, oversizing an air valve’s outflow orifice can lead to excessive over-pressures upon air valve closure during filling operations or following a pump trip event [14]. Notably, the pipeline transient response exhibits non-linear behaviour in relation to air valve capacity [15], valve location, and system characteristics [10].

Research relating to air in pressurised pipelines can be categorised into three classes: experimental studies [16], combined experimental–numerical investigations [17], and purely numerical explorations [18]. Due to space limitations in controlled labs, experimental and experimental–numerical studies often focus on small-scale systems, which hinders their applicability to large-scale applications [19]. For instance, although the Bergant et al. (2012) study [20] conducted an experimental–numerical investigation using typical air valve and pipe sizes, the pipeline lengths employed were quite short. Regarding pipeline filling, studies often concentrate on either horizontal [21] or vertical pipes [22], which are prevalent in few large-scale systems [6]. Furthermore, the common use of orifices for air exchanges in these studies, rather than the more commonly employed air valves, introduces an added challenge when translating the findings into practical applications [3]. Certainly, numerical studies exploring the transient behaviour of large-scale pipelines influenced by the presence of air can be found in the literature. These studies include, for example, the works by Pozos et al. (2010) [23], Ramezani and Karney (2017) [10], and Li et al. (2022) [18]. The current paper is in this tradition and provides a comprehensive numerical analysis of the transient behaviour in a pressurised rising water pipeline with an air valve during a pump trip scenario.

This paper is structured as follows. A concise overview of recent related research is first provided, followed by the identification of the typical water hammer stages associated with the pump trip scenario. The two key power-loss behaviours, namely, attenuated and water-hammer-dominated events, are identified, as well as the related transitional states. A comprehensive investigation into the sensitivity of the transient response to the air valve outflow capacity and location follows. This involves analysing variations in pipeline lengths experiencing negative pressures, maximum hydraulic grade (HG) values, maximum head values, and air pocket collapse times. The timing of peak transient HGs is explored, as are the critical orifice sizes for achieving attenuated and water-hammer-dominated events. The work specifically assesses the influence of the initial steady water velocity, the elevation difference between downstream and upstream reservoirs, and the impact of changes in both wave speed and friction on the transient response. Finally, the paper investigates how non-slam air valve design parameters impact the transient response and concludes by summarising all the insights gained.

2. Overview of Related Research

Ramezani (2015) [24] studied the numerical sensitivity of transient severity to air valve capacity and pipeline configuration in a pump trip scenario. The simulations utilised an elastic model through the method of characteristics, and Monte Carlo filtering was employed to statistically evaluate the simulation results. This study found that both the air valve inflow capacity and initial steady water discharge affect the minimum transient pressures, while the air valve outflow capacity and initial steady water discharge affect the maximum transient pressures. The analysis prioritised statistical insights over the consideration of the individual physical processes that constitute the hydraulic transient phenomenon.

To complement the earlier work, Ramezani and Karney (2017) [10] developed semi-analytical formulas to elucidate the fundamental wave processes that occur following sudden depressurisation. This work emphasised the significance of air valve location to the transient response, suggesting that the downstream branch of the pipeline, in relation to the air valve, has a greater influence on severity than the upstream branch. Longer downstream branches lead to longer air pocket collapse times and more attenuated secondary pressures. The semi-analytical formulas incorporate several simplifications, including the omission of macro-cavitation, the assumption of free air inflow and outflow, and the assumption that the pressure in the air pocket is always atmospheric.

Coronado et al. (2018) [25] conducted a numerical sensitivity analysis to investigate how the air valve capacity and pipeline configuration (specifically, a single straight pipeline) can influence pipeline transient behaviour during both filling and draining procedures. The simulations used a rigid column model for the water phase and the polytropic transformation equation for the air phase. For filling, transient behaviour displayed sensitivity to pipe slope, air valve size, pipe diameter, and the friction factor. For draining, transient behaviour showed sensitivity to air valve size, air pocket size, pipe slope, and pipe diameter.

Tasca et al. (2021) [14] conducted a provisional numerical study into the impact of the air valve capacity and pipeline configuration on pipeline transient response following pump trip. While the air valve location was emphasised as significant, the importance of the air valve capacity was acknowledged, but its relevance was less apparent due to the limited range of tested air valve sizes. Tasca et al. (2021) [14] noted that the transient magnitude can be affected not only by the size of the air valve orifice but also by its discharge coefficient. Increasing the elevation of the air valve was found to attenuate the secondary waves created upon air valve closure and led to larger admitted air volumes. Tasca et al. (2022) [11] clarified the influence of the air valve outflow capacity on the pipeline transient response during the pump trip scenario; a significant finding was that the critical orifice sizes previously identified as resulting in attenuated events during pipeline filling also have considerable applicability to the pump trip scenario.

Li et al. (2022) [18] and Li et al. (2022) [15] numerically investigated the impact of air valve capacity on pipeline transient behaviour during a water hammer event resulting from the closure of the downstream valve in a gravity pipeline. It was found that restriction of the air valve outflow capacity tended to attenuate secondary pressures and that increasing an air valve’s inflow capacity tended to limit negative pressures. Li et al. (2022) [18] noted that the significance of discharge coefficients becomes less pronounced when dealing with small outflow orifices. Additionally, a ratio of 0.10 [15] or 0.05 [18] between the outflow and inflow orifice sizes was often found to be effective in simultaneously mitigating negative pressures and secondary over-pressures. The numerical simulations involved some simplifying assumptions, including the absence of macro-cavitation and isothermal air pocket evolution. In reality, small orifices often lead to attenuated transient behaviour, but may also lead to a substantial increase in air pocket temperature [26].

3. Methodology

The current paper examines a pump trip scenario in a typical rising water pipeline equipped with an air valve at a distinct high point. Figure 1 illustrates the key components of the analysed pumping system, with certain attributes allowed to vary. Similar to many operational systems, the layout includes an upstream reservoir, a pumping station (consisting of two pumps in series, each equipped with a check valve), a pipe segment featuring an air valve at a local high point, and a terminal pipe section connected to the downstream reservoir. The lengths of the two pipe segments downstream of the air valve are kept equal in this setup.

The main point of the selection of this system is not due to its universal applicability, though the configuration does typify many operational systems. Rather, this specific system is chosen as it nicely characterises the general nature of the non-linear response that even relatively simple systems can display to air valve, system, and transient attributes. Thus, the goal is to give system designers, owners, and operators an essential “sense” of where and when high sensitivity to assumed system and valve characteristics can constitute a threat to system reliability, performance, and behaviour.

3.1. Simulation Scenarios

The current study considers three sets of numerical simulations: (i) the main or foundational set of “basic” simulations, (ii) a set of simulations incorporating variations in key initial parameters, and (iii) a set of simulations involving non-slam air valves. A great many variations of the system parameters are then considered within these three cases.

The primary simulations set the initial steady water velocity to $v_0=1.5$ m/s, the elevation difference between reservoirs as $\Delta Z=50$ m, the wave speed $a=1000$ m/s, the Hazen–Williams friction coefficient $C=130$ (with corresponding absolute roughness of 0.259 mm), ratio between the air valve inflow orifice and the pipeline diameter $d_{\mathrm{in}}/D=0.20$, pipeline length $L=6000$ m, and pipe diameter $D=0.50$ m. Moreover, the simulations consider five longitudinal $L_1$ air valve locations (1000, 2000, 3000, 4000, and 5000 m), five vertical air valve locations (i.e., h value is 20, 25, 30, 35, or 40 m), and 17 $d/D$ values unequally spaced from zero to 0.40—between 0.02 and 0.10, the $d/D$ values are spaced in increments of 0.01; between 0.10 and 0.20, the $d/D$ values are spaced in increments of 0.02. The smallest $d/D$ value considered with $d/D>0$ is $d/D=0.02$. The values $d/D=0$ and $d/D=0.40$ are considered. The system response without air valve protection is also considered, to bound the results.

Significantly, the current paper explores variations in the following parameters: $v_0$, $\Delta Z$, a, and C. More specifically, three $v_0$ values are used, namely, 0.5, 1.0, and 2.0 m/s; three $\Delta Z$ values are considered, namely, 25, 75, and 100 m; and three a values are simulated, namely, 400, 600, and 800 m/s; moreover, three C values are tested, namely, 90, 110, and 150. For all these cases, $L_1=3000$ m and $h=40$ m. In scenarios where a variation in $\Delta Z$ is incorporated, the air valve is positioned at an elevation equivalent to 80% of that of the downstream reservoir. This leads to h values of 20, 60, and 80 m for $\Delta Z$ values of 25, 75, and 100 m, respectively.

This paper also investigates the effect of having a non-slam air valve at the high point instead of a regular air valve. Herein, a non-slam air valve refers to a device with a single inflow orifice but with both a small outflow orifice and a large outflow orifice, while a regular air valve refers to a device with a single inflow orifice and a single outflow orifice. Variations in the following parameters have been considered: transition head ($\Delta H_{\mathrm{transition}}$), large outflow orifice ($d_{\mathrm{large}}$), and h. The transition head refers to the threshold head that triggers the change from the large outflow orifice ($d_{\mathrm{large}}$) to the small outflow orifice ($d_{\mathrm{small}}$). Six $\Delta H_{\mathrm{transition}}$ values are considered: 0.05, 0.10, 0.15, 0.20, 0.25, and 0.30 m. Eight $d_{\mathrm{large}}/D$ values are considered: 0.06, 0.08, 0.10, 0.12, 0.14, 0.16, 0.18, and 0.20. Two h values are considered: 20 and 40 m. For all these cases, $L_1=3000$ m and $d_{\mathrm{small}}/D=0.04$.

3.2. Modelling Approach and Limitations

Each numerical simulation consists of two stages: the initial steady flow and the hydraulic transient. The initial steady flow is calculated using the Darcy–Weisbach equation, while the hydraulic transient is modelled using the 1D elastic model employing the conventional method of characteristics. The pipeline elements involved in the transient simulations include pipeline segments, upstream and downstream reservoirs, pumping station, air valve, and air pocket admitted by the air valve. Appropriately selecting the simulation time step and the simulated time is important to ensure that the numerical results capture the primary aspects of the transient.

Various numerical choices are also relevant to the transient simulation, including the calculation mesh, how short pipes are integrated into the mesh, the methodology for accounting for friction losses, and the approach used for modelling cavitation. The simulations employ the conventional method of characteristics (MOC) on a rectangular computational mesh, with the Courant number fixed at unity. Pipe reach adjustments are allowed for this purpose. Further information about the elastic model and the MOC can be found in Chaudhry (2014) [27]. Unsteady friction is incorporated into the simulations following Vitkovsky’s methodology. Additional details regarding unsteady friction methods can be found in Abdeldayem et al. (2021) [28]. The discrete vapour cavity model (DVCM) is utilised for macro-cavitation modelling. In the DVCM, vapour cavities form at specific computational nodes and remain localised. The absolute pressure in the system is constrained by the vapour pressure of water. The release of air resulting from a decrease in pressure and changes in wave speed due to the presence of vapour cavities are not taken into account. Further information about cavitation models can be found in Bergant et al. (2006) [29].

Both reservoirs are treated as constant-level reservoirs. The main set of simulations includes two pumps, each equipped with a check valve. The pump curve from the manufacturer is employed, and the simulations incorporate pump inertia with instantaneous check valve closure upon reverse flow. Further details about the simulation of turbo-machines can be found in Wylie and Streeter (1983) [30]. The air flow through the air valve is modelled according to the isentropic air flow model, considering discharge coefficients of 0.6 for both admission and expulsion. Circular air exchange orifices are assumed. More information about the isentropic air mass flow model can be found in Tasca and Karney (2023) [9]. The air pocket admitted by the air valve is assumed localised, and its evolution is modelled adiabatically, i.e., the evolution of the air pocket follows the polytropic transformation equation with a polytropic exponent of 1.4. The assumption of a stationary entrapped air pocket is reasonable since the pipe segments forming the high point with the air valve are ascending towards the air valve. When an air pocket is present in the system, the upstream and downstream branches in relation to the air valve become hydraulically separated; thus, water column separation is assumed. The current study does not consider the occurrence of air bubbles in the water phase or two-phase flows. Atmospheric pressure is assumed to be sea-level atmospheric pressure. Further details about the polytropic transformation equation in the context of hydraulic transients can be found in Fuertes et al. (2016) [31].

The time step utilised is 0.04 s. Only a slight sensitivity to the time step was observed. For the main set of simulations, a simulated time of 635 s (1.5 times the collapse time for $d/D=0.02$, $L_1=1000$ m, and $h=40$ m) is employed for $0.02\le d/D\le 0.04$; for $d/D\ge 0.05$, a simulated time of 190 s (1.5 times the collapse time for $d/D=0.05$, $L_1=1000$ m, and $h=40$ m) is employed. An analogous approach is adopted for the set of simulations incorporating variations in key initial parameters, with each variation having its own simulated time, categorised into two brackets: $0.02\le d/D\le 0.04$ and $d/D\ge 0.05$, with $h=40$ m, but $L_1=3000$ m. For the set of simulations involving a non-slam air valve, a simulated duration of 440 s is utilised (1.5 times the collapse time for $d/D=0.02$, $L_1=3000$ m, and $h=40$ m).

The numerical simulations were conducted using the application HAMMER from Bentley Systems (version 10.1.1.4).

3.2.1. Pumping System Configuration

For the main set of simulations, which considers $v_0=1.5$ m/s, $\Delta Z=50$ m, and $C=130$, the pumping system consists of two pumps in series of the model KSB ETA 250-33 330/330. For simulations with $v_0=0.5$ m/s, the pumping system consists of one pump of the model KSB ETA 125-40 395. For simulations with $v_0=1.0$ m/s, the pumping system consists of two pumps in series of the model KSB ETA 200-33 300. For simulations with $v_0=2.0$ m/s, the pumping system consists of two pumps in series that are in parallel with two other pumps in series of the model KSB ETA 200-40 340. For simulations with $\Delta Z=25$ m, the pumping system consists of one pump of the model KSB ETA 250-40 380. For simulations with $\Delta Z=75$ m, the pumping system consists of two pumps in series of the model KSB ETA 250-40 380. For simulations with $\Delta Z=100$ m, the pumping system consists of two pumps in series of the model KSB ETA 250-40 400. For simulations with $C=150$, the pumping system consists of two pumps in series of the model KSB ETA 250-33 330/300. For simulations with $C=110$, the pumping system consists of two pumps in series of the model KSB ETA 250-33 330/330. For simulations with $C=90$, the pumping system consists of two pumps in series of the model KSB ETA 250-40 380. For all these cases, the nominal rotational speed is 1760 rpm. Since the check valve is assumed to close immediately in flow reversal, and then to remain closed, Suter curves for 4-quadrant pump characterisation and for energy dissipation zones were not required.

3.2.2. Limitations of the Study

Regarding the current examination of the general transient response of pipelines in the context of a pump trip scenario, it is important to recognise that pipeline systems operate within a wide range of system configurations and environmental contexts. This complexity makes achieving a truly comprehensive reporting or results unattainable. Furthermore, real systems often exhibit a higher degree of complexity compared to the scope considered in this paper. They frequently encompass multiple points with air valve protection and a diverse array of hydraulic devices. Additionally, there are inevitably uncertainties associated with the assumed numerical and behavioural models that are necessarily simplified in order to capture unsteady flow and hydraulic element behaviour. Nonetheless, the primary goal of this study is to elucidate general relevant causal relationships in the pump trip scenario, rather than presuming high-precision simulations are practical. Despite the relative simplicity of the general pipeline layout and tested conditions under examination, the inherent limitations of numerical models, and the limited variety of data acquired from the numerical simulations, valuable engineering insights naturally emerge from the mechanistic assessment approach employed in this paper.

The current study does not account for the potential influence of a hydropneumatic tank or other specialised surge protection equipment. Indeed, the primary objective of this study is to concentrate on the distinct impact of the air valve itself and its potential in mitigating the transient event.

The main set of simulations assumes a constant wave speed of $a=1000$ m/s, a value appropriate for simulating hydraulic transients in many pipeline systems. In practice, there is some uncertainty regarding the wave speed arising from issues like temperature effects, bedding conditions, and the presence of air. Some simulations are undertaken involving lower a values, which are characteristic of viscoelastic pipes, though viscoelastic effects are not included.

The simulations assume that entrapped air remains localised near the air valve and disregard water level variations due to air pocket evolution, an assumption consistent with having relatively small air volumes. In the present study, the pipe lengths able to accommodate volumes corresponding to the maximum air pocket volumes are significantly shorter than the lengths of the pipeline segments themselves. This assumption is not universally valid [32].

The discrete vapour cavity model (DVCM) is employed for cavitation modelling. In this study, sensitivity is observed in cavitation modelling depending on the chosen size for the pipe reaches. Nonetheless, such sensitivity does not substantively alter the transient magnitudes. Moreover, the simulations do not consider wave speed reduction for pipe reaches adjacent to vapour cavities.

The pump check valves are assumed to close immediately upon reverse flow. In practice, however, the responsiveness of check valves varies based on factors such as type, age, model, and size. If the pumping system were to lack check valves, the transient behaviour could differ significantly from that presented here, and reverse flow through the pump(s) would become relevant. In rising water systems, check valves are nearly universal.

3.3. Evaluating Transient Severity

A common approach to assess the magnitude of a water hammer event involves analysing the extreme transient HG envelope obtained from a transient analysis. Agostinho et al. (2018) [33] provide an overview of 14 hydraulic transient indicators. Notably, Jung and Karney (2011) [34] introduced the negative and positive surge damage potential factors—denoted as SDPF${}^{-}$ and SDPF${}^{+}$, respectively—to facilitate the evaluation of water hammer protection strategies. These factors take into account the duration of extreme transient heads, addressing both the “how much” and “how long” aspects of the transient. For instance, Ramezani (2015) [24] utilised these factors to evaluate the role of air valves in the pump trip scenario.

This paper also addresses the important complementary aspects of “where” and “when” extreme transient heads occur. To this end, the water hammer phenomenon is divided into four sequential stages: depressurisation, air admission, air expulsion, and secondary wave. An investigation that considers the “where” and “when” aspects makes it easier to infer causal relationships. In this sense, regarding the pump trip scenario, the crucial aspects to be addressed in this paper are “where”, “when”, and “for what reason” the extreme transient heads occur.

The secondary waves resulting from the closure of the air valve at the end of the air expulsion stage are commonly discussed in the literature [15,18]. Indeed, these secondary waves should be controlled to prevent dangerous transients [35,36]. In fact, transient-critical air valves are typically situated at high points, making it rare for overall maximum transient heads to occur there. In actuality, pipeline segments situated at lower elevations are particularly susceptible to experiencing dangerous transient over-pressures.

For the pump trip scenario in a rising water pipeline, the highest transient HG occurs at the upstream section of the pipeline (i.e., at the lowest elevation region of the pipeline). The transient magnitude depends on several factors: pump(s) inertia, initial steady water velocity, pipeline layout, pipe material, diameter, and wall thickness, dynamic properties of check valve(s), air valve location, type, inflow and outflow capacities, and the occurrence of macro-cavitation. Given the intricate nature of the pump trip scenario, which involves air–water interactions within the pipe, air exchanges through the air valve, and macro-cavitation, the numerical simulation results for the maximum HG exhibit a certain degree of randomness and unpredictability.

To more comprehensively assess the extent of transient over-pressures in the system, a new parameter is introduced, providing an alternative to the maximum transient hydraulic grade line (HGL), the maximum transient HG in the system, and the magnitude of the secondary wave upon air valve closure. This parameter is referred to as the mean maximum hydraulic head and is defined as follows:

$${\overline{H}}_{\max }={\overline{\mathrm{HG}}}_{\max }-\overline{Z}=\frac{1}{N}\sum _{i=1}^N{\mathrm{HG}}_{{\max }_i}-\frac{1}{N}\sum _{i=1}^N{Z}_i$$

(1)

where ${\overline{\mathrm{HG}}}_{\max }$ is the mean maximum HG and $\overline{Z}$ is the mean pipeline elevation. These quantities are dependent on ${\overline{\mathrm{HG}}}_{{\max }_i}$ (the maximum HG at point i) and $Z_i$ (the elevation at point i). Parameter N denotes the number of pipeline reaches.

4. Water Hammer Stages in the Pump Trip Scenario

For the pump trip scenario in a rising water pipeline, depressurisation starts when power to the pumping system is cut and ends when the under-pressure wave reaches the air valve. The air admission stage starts when the under-pressure wave reaches the air valve and ends when the maximum air pocket volume is achieved. The air expulsion stage starts when the maximum air pocket volume is achieved and ends when the air valve closes (i.e., when all the air has been expelled from the line). The secondary wave stage starts when the air valve closes and ends when a peak transient pressure occurs at the upstream end of the pipeline (in case of multiple transient cycles, such a peak precedes the re-occurrence of negative pressures at the air valve with consequent re-admission of air). Collectively, these four water hammer stages comprise a water hammer cycle. For large-outflow-capacity air valves, several water hammer cycles are expected before flow in the system is arrested. Nonetheless, the extreme transient HG envelope—minimum and maximum HGLs—is generally mostly determined during the first water hammer cycle.

4.1. Stages for Reduced-Outflow-Capacity Air Valve

Figure 2 depicts the water hammer stages in the first water hammer cycle in a pipeline with an air valve with a large-inflow-capacity orifice but reduced-outflow-capacity orifice considering $L_1=3000$ m and three values for the air valve elevation (20, 30, and 40 m). In each image in Figure 2, two sets of extreme transient HGLs are represented: the overall extreme HGLs (dotted red and blue lines) and the extreme HGLs up to the end of the water hammer stage shown in the image (continuous red and blue lines). This representation allows the assessment of the timing of each part of the overall extreme transient envelope. Furthermore, each image in Figure 2 displays the HGL at the conclusion of the water hammer stage shown in the image (continuous green line). For the air expulsion stage, specifically, the continuous green line refers to the HGL four time steps after the closure of the air valve in order to display the magnitude of the secondary transient waves.

Examples of systems experiencing depressurisation are shown in Figure 2a,e,i. During the depressurisation stage, the maximum HGL does not occur. Rather the maximum HGL at the end of this stage is determined by the initial steady-state HGL, whereas the global minimum HGL for the upstream branch is primarily formed during this stage. For the downstream branch, however, the minimum HGL at the end of this stage matches the initial steady-state HGL. The depressurisation stage is short lived, spanning between the inception of the transient and the time when the reduced-pressure wave reaches the air valve.

Simulation results associated with the air admission stages are shown in Figure 2b,f,j. The overall maximum HGL does not form during the air admission stage. However, for the downstream branch, the maximum HGL at the end of this stage differs from the initial steady-state HGL. For the downstream branch, the overall minimum HGL typically occurs during the air admission stage. For $h=20$ m, the entire pipeline length experiences negative pressures by the end of this stage. In contrast, for $h=40$ m, the lower portion of the downstream branch avoids negative pressures until the end of this stage. The closure of the check valves associated with the pumps takes place during the air admission stage. The check valves close at 9.5, 10.0, and 14.4 s for the air valve elevations of 40, 30, and 20 m, respectively.

Examples of air expulsion stages are shown in Figure 2c,g,k. For $h=30$ m, the overall maximum HGL has been mostly formed by the end of the air expulsion stage. For $h=40$ m, the maximum HGL at the end of this stage closely approximates the global maximum HGL. This is not the case, though, for $h=20$ m. In Figure 2, given the reduced outflow capacity of the air valve, the secondary waves resulting from the air valve closure are mild and almost indistinguishable from the nearby HGL fluctuations. Moreover, the air pocket pressure as the air valve closes is considerably larger than atmospheric pressure (which is more pronounced for $h=20$ m). This is a consequence of the pressurisation of the entrapped air pocket during the air expulsion stage.

Examples of secondary wave stages are shown in Figure 2d,h,l. For $h=30$ m and $h=40$ m, the overall maximum HGL forms near the end of the secondary wave stage. The HGL at the end of this stage contains the maximum transient HG in the system (${\mathrm{HG}}_{\max }$) for $h=20$ m. Nonetheless, for $h=20$ m, the overall maximum HGL only occurs after $t_{{\mathrm{HG}}_{\max }}$. In contrast to the previous stages, in the secondary wave stage, the transient waves can move unimpeded across the whole pipeline as flow separation has been eliminated by the removal of the air.

Overall, the most severe HGL values occur for $h=20$ m, while the least severe ones occur for $h=40$ m. Note that for $h=40$ m, the air valve is positioned at a higher elevation, rendering it less susceptible to high pressures. The maximum transient HG in the system, which occurs at the upstream section of the pipeline, is about 145 m for $h=20$ m, 113 m for $h=30$ m, and 94 m for $h=40$ m. The maximum HGL tends to have higher values for points that are closer to the upstream reservoir.

The duration of the depressurisation stage is the same for the three air valve elevations. The duration of the other stages, however, is affected by h. The longest time for air admission and the largest admitted air pocket occur for $h=40$ m. The air pocket collapse time for $h=40$ m ($t_c=110$ s) is more than double the value for $h=30$ m ($t_c=51$ s) and almost four times the value for $h=20$ m ($t_c=31$ s). In Figure 2, the air expulsion stage persists for a longer duration than the air admission stage. This difference becomes more pronounced as h increases. For $h=40$ m, the air expulsion stage lasts 71 s, while the air admission stage lasts 36 s. On the other hand, for $h=20$ m, the air expulsion stage lasts 14 s, while the air admission stage lasts 13 s.

4.2. Stages for Large-Outflow-Capacity Air Valve

Figure 3 shows the water hammer stages in the first water hammer cycle in a pipeline with an air valve with both large-inflow-capacity and large-outflow-capacity orifices considering $L_1=3000$ m and three values for the air valve elevation (20, 30, and 40 m). Like in Figure 2, each image in Figure 3 shows the overall extreme HGLs, the extreme HGLs until the conclusion of the corresponding stage, and the HGL at the end of the corresponding stage.

The depressurisation and air admission stages in Figure 3 are similar to those in Figure 2. In these two initial stages, the outflow function of the air valve does not influence the transient response. The timings of the depressurisation and air admission stages are equivalent for corresponding air valve elevations in Figure 2 and Figure 3.

The air expulsion and secondary wave stages, however, are notably distinct between Figure 2 and Figure 3 for corresponding air valve elevations. For example, in contrast to Figure 2c,g,k, in Figure 3c,g,k, the secondary waves formed as a consequence of air valve closure are much larger in comparison to the neighbouring HGL variations. In contrast to what is shown in Figure 2c,g,k, in Figure 3c,g,k, the air pocket pressure as the air valve closes is close to the atmospheric pressure.

For $h=30$ m and $h=40$ m, in Figure 3, similar to Figure 2, most of the overall maximum HGL has been formed by the end of the secondary wave stage. In contrast, for $h=20$ m, in Figure 3, similar to Figure 2, the maximum HGL does not coincide with the end of the secondary wave stage. In Figure 3, similar to Figure 2, there is a notable tendency for larger HGL values to occur for points closer to the upstream reservoir. In contrast to Figure 2, in Figure 3, except for $h=20$ m, there is a clear discontinuity of the maximum HGL at the air valve location.

In Figure 3, similar to Figure 2, the water hammer cycle is the longest for $h=40$ m and the shortest for $h=20$ m. However, for each h value, $t_c$ is shorter in Figure 3 than in Figure 2. The air valve with a reduced-outflow-capacity orifice imposes significant resistance against air expulsion, while the air valve with a large-outflow-capacity orifice allows for the free exhaust of air. As a result, while the duration of the air expulsion stage is longer than the duration of the air admission stage in Figure 2, in Figure 3, such durations are equivalent. In Figure 3, for $h=40$ m, the duration of the air expulsion stage is 34 s, while the duration of the air admission stage is 36 s.

In Figure 3, $t_c$ is 80% longer for $h=40$ m than for $h=30$ m, and almost three times longer than the value found for $h=20$ m. A larger sensitivity of $t_c$ to h is found in Figure 2 in comparison to Figure 3. Indeed, for a small-outflow-capacity air valve, $t_c$ increases substantially as h increases.

In Figure 3, the least intense HGL values occur for $h=40$ m. The transient magnitudes for $h=20$ m and $h=30$ m, though, are quite similar—${\mathrm{HG}}_{\max }$ is about 168 m for $h=20$ m, and about 175 m for $h=30$ m. Notably, the least intense transient event shown in Figure 3 (for $h=40$ m) has a magnitude comparable to the most intense event shown in Figure 2 (for $h=20$ m).

5. Attenuated and Water-Hammer-Dominated Events

5.1. Effect of Air Valve Size on Transient Evolution

Figure 4 shows the evolution of the hydraulic head at the air valve considering $L_1=3000$ m, $h=40$ m, $d_{\mathrm{in}}/D=0.20$, and $d/D$ varying from 0.02 to 0.12. Two extreme transient behaviours can be distinguished: Figure 4a ($d/D=0.02$) shows a transient with long-period, mild, and smooth head oscillations (such behaviour can be classified as attenuated or type 1 behaviour); Figure 4j ($d/D=0.12$) shows a transient with short-period, intense, and sharp head oscillations (such behaviour can be classified as water-hammer-dominated or type 3 behaviour). In addition, the behaviour shown in Figure 4e ($d/D=0.06$) can be classified as intermediary or type 2 behaviour. Note that distinguishing between these behaviours might become a little vague for intermediate $d/D$ values.

For type 1 behaviour, the head evolution at the air valve includes at least one instance of relatively smooth head-versus-time variation with substantial compression of the air pocket before its collapse with a subsequent mitigated secondary wave (examples of type 1 behaviour are shown in Figure 4a–d). For type 2 behaviour, even though there is some compression of the air pocket before its collapse, the subsequent secondary wave is only partially mitigated (examples of type 2 behaviour are shown in Figure 4e,f). For type 3 behaviour, the air is essentially freely exhausted, resulting in a very sharp secondary wave upon air valve closure (an example of type 3 behaviour is shown in Figure 4j). The graphs in Figure 4g–i display the secondary head spike which typifies type 3 behaviour. However, note how in such cases the maximum hydraulic head increases as $d/D$ increases. This indicates that for these cases, there is still a residual air cushioning effect.

In Figure 4a, the secondary wave stage is notably absent. For this case, $t_c=423$ s, which is beyond the time range depicted in the figure. From Figure 4b onwards, however, the graphs include the secondary wave stage. The air pocket collapse time reduces as $d/D$ increases—$t_c=157$ s for $d/D=0.03$, $t_c=110$ s for $d/D=0.04$, and $t_c=86$ s for $d/D=0.05$. However, for large $d/D$ values, $t_c$ is more stable—$t_c=76$ s for $d/D=0.07$, and $t_c=73$ s for $d/D=0.12$. In Figure 4, the oscillation period decreases from $d/D=0.02$ to $d/D=0.05$. However, from $d/D=0.07$ onwards, the oscillation period becomes independent of $d/D$.

The mild and long-period head oscillations shown in Figure 4a occur due to the high resistance against air exhaust imposed by the small outflow orifice. In Figure 4j, however, air is exhausted under very reduced pressure differentials. For type 3 behaviour, sudden and large head rises are generated upon air valve closure (i.e., upon air pocket collapse). In general, for both type 1 and type 3 behaviours, the head oscillations while the air pocket is inside the pipeline are smooth, while the head oscillations after the closure of the air valve and before air re-admission are sharp and erratic. Figure 4 demonstrates the substantial variability in the fundamental nature of the transient response depending on air valve size.

The time evolution of the hydraulic conditions at the upstream section of the pipeline is also of interest. Figure 5 shows the time evolution of the HG at the upstream section of the pipeline (right downstream of the pumping station) considering $L_1=3000$, $h=40$ m, $d_{\mathrm{in}}/D=0.20$, and $d/D$ varying from 0.02 to 0.12. Type 1 behaviour is noticeable in Figure 5a, while type 3 behaviour is noticeable in Figure 5j. The upstream section (at −2 m elevation) experiences transient pressure fluctuations with a much larger amplitude than those at the air valve. For $d/D=0.07$, the HG rise after the collapse of the air pocket reaches a value of about 128 m, whereas the corresponding head rise at the air valve reaches only about 55 m.

For $d/D=0.02$, the oscillation pattern is characterised by a high frequency, while for large $d/D$ values, the oscillation pattern is divided into two consecutive periods: (i) an initial period with higher-frequency and lower-amplitude oscillations, and (ii) a posterior period with lower-frequency and higher-amplitude oscillations. In Figure 5, especially visible for the large $d/D$ values, the sudden HG rises occur slightly after the sudden head rises in Figure 4. In fact, the transient oscillations at these two locations are causally connected. While the head rise in Figure 4f occurs at about 76 s, the associated HG rise in Figure 5f occurs at about 79 s (the timing difference corresponds to $L_1/a$, i.e., the time the transient wave takes to travel from the air valve to the upstream section of the pipeline).

5.2. Evolution of Key Transient Quantities

To complement the story told in Figure 4 and Figure 5, Figure 6 and Figure 7 show the evolution of key transient quantities for type 1 and type 3 behaviours. Figure 6 shows the evolution of the HG at both the air valve and the upstream section of the pipeline, accompanied by the water velocities upstream and downstream of the air valve.

If an air valve contains entrapped air, the hydraulic head evolution is relatively smooth (type 1 behaviour) or with negligible magnitude (type 3 behaviour). The type 1 behaviour in Figure 6c is characterised by a lower-amplitude HG evolution in comparison to the type 3 behaviour in Figure 6d. The HG evolution at the upstream section, though more complex than that at the air valve, also reveals essential aspects of the transient. This difference is of particular note since monitoring pressure signals close to a pumping station is generally more convenient than at remote locations, including at air valves.

The graphs in Figure 6e–h show that, after the transient inception, the water velocity in the upstream branch ($v_{\mathrm{up}}$) varies around $v_{\mathrm{up}}=0$, while the water velocity downstream ($v_{\mathrm{ds}}$) progressively decreases. When $v_{\mathrm{ds}}$ reaches $v_{\mathrm{ds}}=0$, the maximum air pocket volume is attained. Thereafter, $v_{\mathrm{ds}}$ becomes negative (i.e., the flow reverses). The reverse flow progressively intensifies until the air pocket is fully exhausted through the air valve. Such behaviour patterns for $v_{\mathrm{up}}$ and $v_{\mathrm{ds}}$ have also been identified by Ramezani and Karney (2017) [10], implying that the main contributor to the growth of the entrapped air pocket is the downstream branch. In fact, the physical process in the downstream branch during which $v_{\mathrm{ds}}$ remains positive and which is associated with air admission through the air valve constitutes a form of draining event. Given the 1.5 m/s initial steady water velocity, the air valve should be capable of accommodating air intake for a water draining velocity of a similar magnitude, especially during the initial part of the air admission stage. As this requirement significantly exceeds the conventional range of 0.3 to 0.6 m/s for controlled line draining [5], accounting for the pump trip scenario is essential when determining the size of the air valve’s admission orifice.

As shown in Figure 6g,h, the water column in the downstream branch takes longer to be arrested for $h=40$ m than for $h=30$ m. Indeed, the velocity changes in Figure 6g are smaller than those in Figure 6h. Such a difference occurs because h is larger in Figure 6g than in Figure 6h. When the air valve is positioned at a higher elevation, a smaller portion of the initial under-pressure wave can traverse the high point and travel towards the downstream reservoir. Consequently, the initial reductions in head and water discharge in the downstream branch—along with subsequent changes in water discharge—are less pronounced for the higher-elevation air valve. Indeed, in Figure 6g,h, even when $v_{\mathrm{ds}}$ is still positive (i.e., there is no influence from the different $d/D$ assumptions), the $v_{\mathrm{ds}}$ changes are smaller for the case with higher h. Note that a decrease in $v_{\mathrm{ds}}$ occurs with a periodicity of $2(L_2+L_3)/a$. This period represents the time the wave requires to travel from the air valve to the downstream reservoir and back. Note that a reduction in $v_{\mathrm{ds}}$ occurs both when the wave reaches the downstream reservoir and when it returns to the air valve.

The dependence between the magnitude of the $v_{\mathrm{ds}}$ changes and h has also been identified by Ramezani and Karney (2017) [10]. However, by design, such work explicitly excluded the air cushioning effect that arises when a reduced-outflow-capacity air valve is used. This effect is marked by the water column’s deceleration resulting from the compression of the entrapped air pocket. In Figure 6g, the outflow orifice is small and the air cushioning effect is relevant, whereas in Figure 6h, the outflow orifice is large and the entrapped air pocket presents no resistance against the moving water column during air expulsion. In Figure 6g, $v_{\mathrm{ds}}$ reaches zero at 34 s. It then progressively reduces, reaching −0.68 m/s at 64 s. Afterwards, $v_{\mathrm{ds}}$ starts to increase, reaching 0.10 m/s at 87 s. Following this, $v_{\mathrm{ds}}$ decreases again, reaching −0.43 m/s at 107 s. Once again, $v_{\mathrm{ds}}$ starts to increase, reaching −0.13 m/s when the air valve closes at 110 s. However, in Figure 6h, the behaviour of $v_{\mathrm{ds}}$ differs, with the air valve closing when $v_{\mathrm{ds}}$ reaches its minimum value. Additionally, no deceleration of the periodic $v_{\mathrm{ds}}$ reductions is observed in this case.

Figure 7 shows the air pocket evolution for type 1 and type 3 behaviours. The graphs in Figure 7a,b show the contribution of the upstream branch to the total air pocket volume, while the graphs in Figure 7c,d show the contribution of the downstream branch. Summing the volumes from the graphs in Figure 7a,c results in the total volume shown in Figure 7e, and summing the volumes from the graphs in Figure 7b,d results in the total volume shown in Figure 7f. The air pocket volume is mainly influenced by the movement of the water column in the downstream branch, while the upstream branch has a minor impact. Water discharge in the upstream branch oscillates around zero, leading to periodic expansion and contraction of the air pocket in this branch. Conversely, in the downstream branch, the water velocity is slower to reverse, creating an opportunity for the formation of a sizeable entrapped air pocket. Note that both the upstream and downstream air pocket volumes are integral components of the resulting volume of air that is expected to accumulate at or near the air valve.

6. Maximum Air Pocket Volume

The current study maintains $d_{\mathrm{in}}/D=0.20$ throughout all simulations (such a $d_{\mathrm{in}}/D$ value allows the free entry of air into the pipeline); however, it explores a wide range of relative $d/D$ values. Given that the maximum air pocket volume ($V_{\max }$) occurs at the end of the air admission stage, unaffected by the outflow orifice, $V_{\max }$ for a given air valve inflow capacity is expected to be influenced by the initial pipeline flow conditions and the air valve location. For instance, Tasca et al. (2021) [14] mention that an air valve positioned at a higher elevation leads to a larger $V_{\max }$ value compared to a lower elevation, assuming other factors remain constant.

Figure 8 shows the relationship between $V_{\max }$ and the air valve location (determined by $L_1$ and h). For each $L_1$ value, increasing h leads to smaller $v_{\mathrm{ds}}$ reductions that occur periodically each round trip across the downstream branch during the air admission stage. Consequently, with an increase in h, the duration of the air admission stage also extends. Similarly, for each h, decreasing $L_1$ increases the time taken for a wave round trip in the downstream branch. Hence, as h increases or $L_1$ decreases, the duration of the air admission stage increases. The range of the $V_{\max }$ values spans from 0.1 m${}^3$ (for $L_1=5000$ m and $h=20$ m) to 5.5 m${}^3$ (for $L_1=1000$ m and $h=40$ m), representing a substantial difference of nearly 50 times. For $L_1=1000$ m and $h=20$ m, $V_{\max }=2.2$ m${}^3$, while for $L_1=5000$ m and $h=40$ m, $V_{\max }=1.3$ m${}^3$.

The largest $V_{\max }$ value obtained in the simulations (approximately 5.5 m${}^3$) corresponds to an air-occupied length of about 28 m, which is small relative to the pipeline length. Interestingly, the largest air pocket volume corresponds to the case with the largest descending pipe segment downstream of the air valve. Nonetheless, if the descending segment connected to the air valve were to have a mild slope, the air pocket could extend considerably farther. Since the $V_{\max }$ values found in the current study are small in relation to the length of the descending downstream segment, a metric that considered the ratio between air pocket volume and pipe volume was not used, though it might sometimes be of value.

7. Sensitivity Study

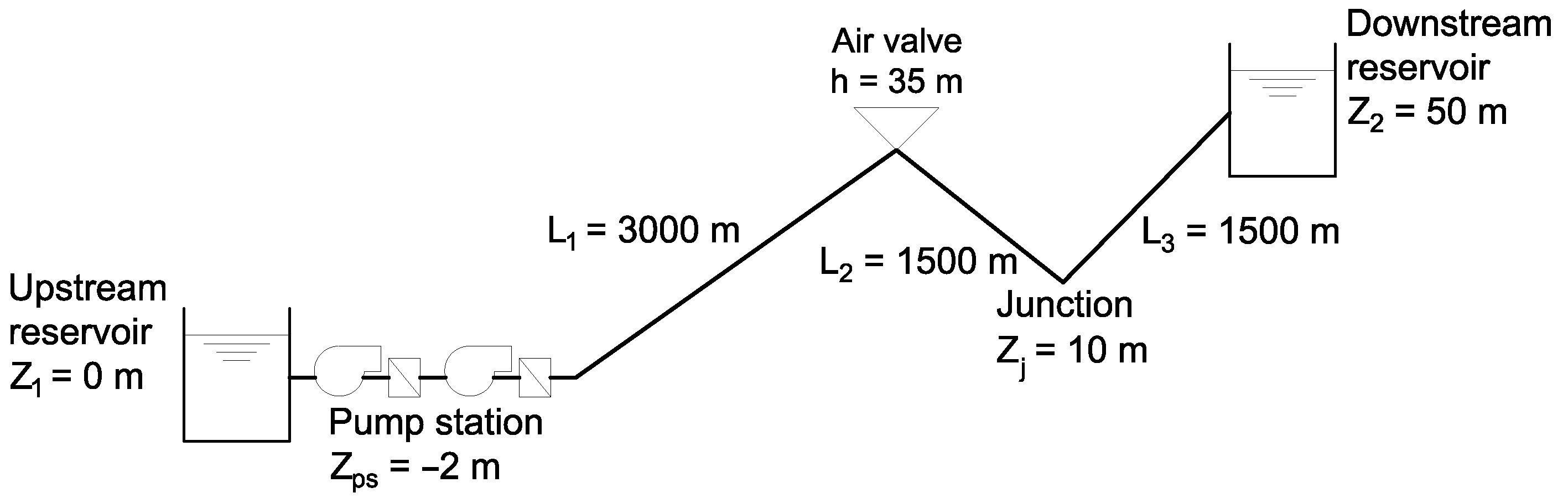
7.1. Assessing Extreme Transient Heads

The physical quantities most relevant to the study of extreme transient heads are as follows: pipeline length experiencing negative pressures ($L_s$), maximum HG in the system (${\mathrm{HG}}_{\max }$), and mean maximum hydraulic head (${\overline{H}}_{\max }$). Variations in the following parameters are considered: five values for $L_1$ (1000, 2000, 3000, 4000, and 5000 m), five values for h (20, 25, 30, 35, and 40 m), and 17 values for $d/D$ (ranging from zero to 0.40). Furthermore, the response without air valve protection is also included for comparison.

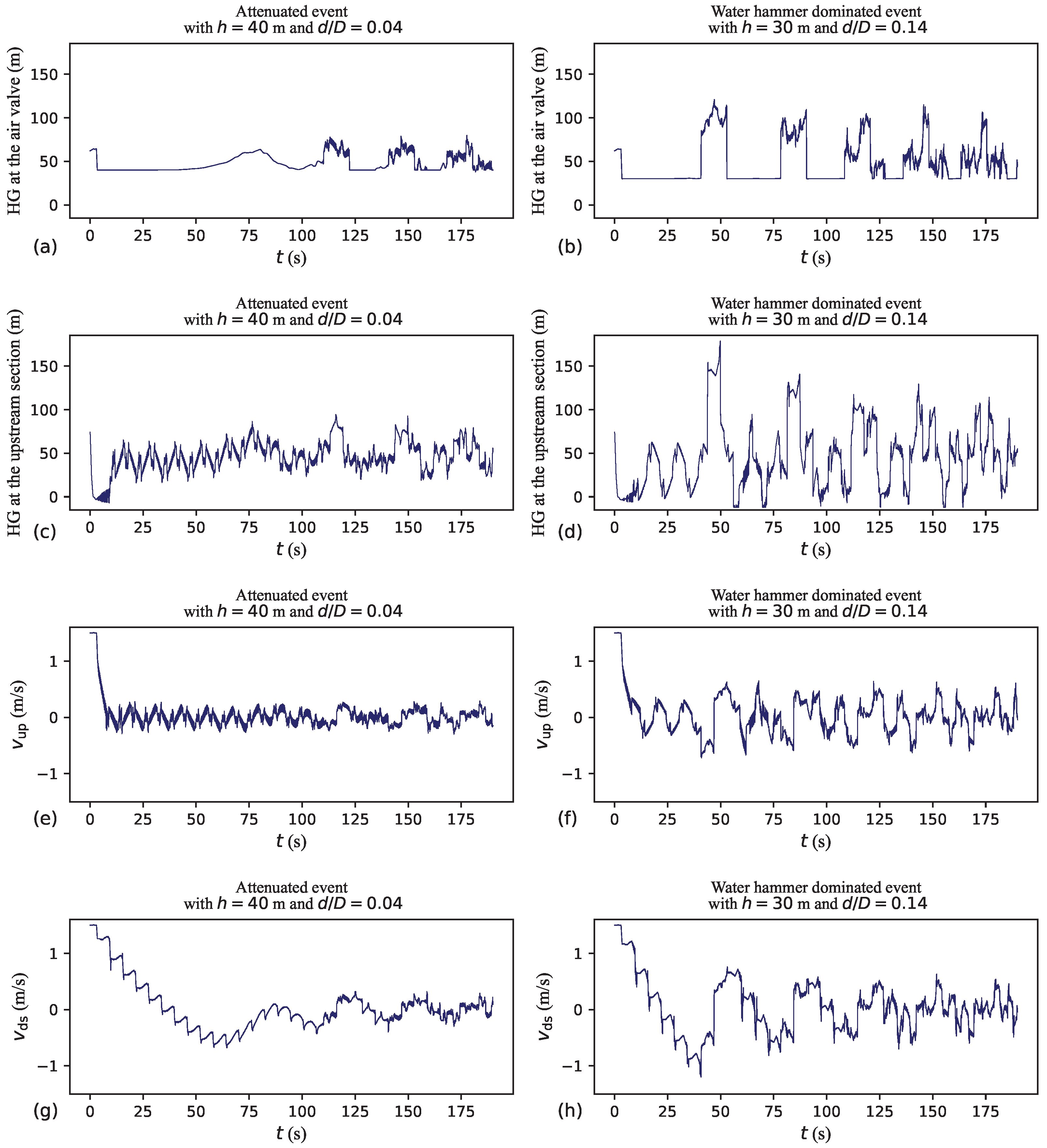
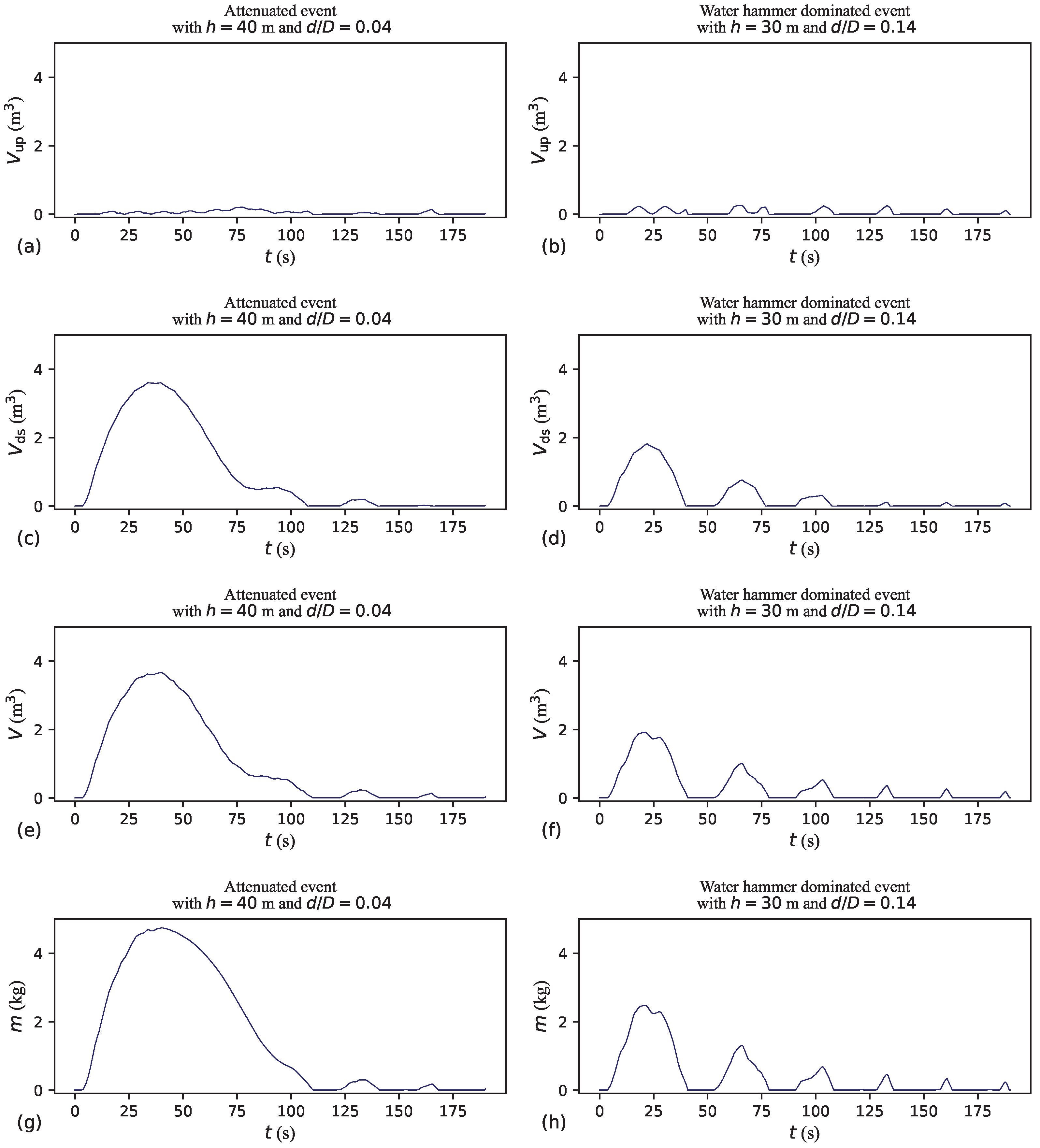
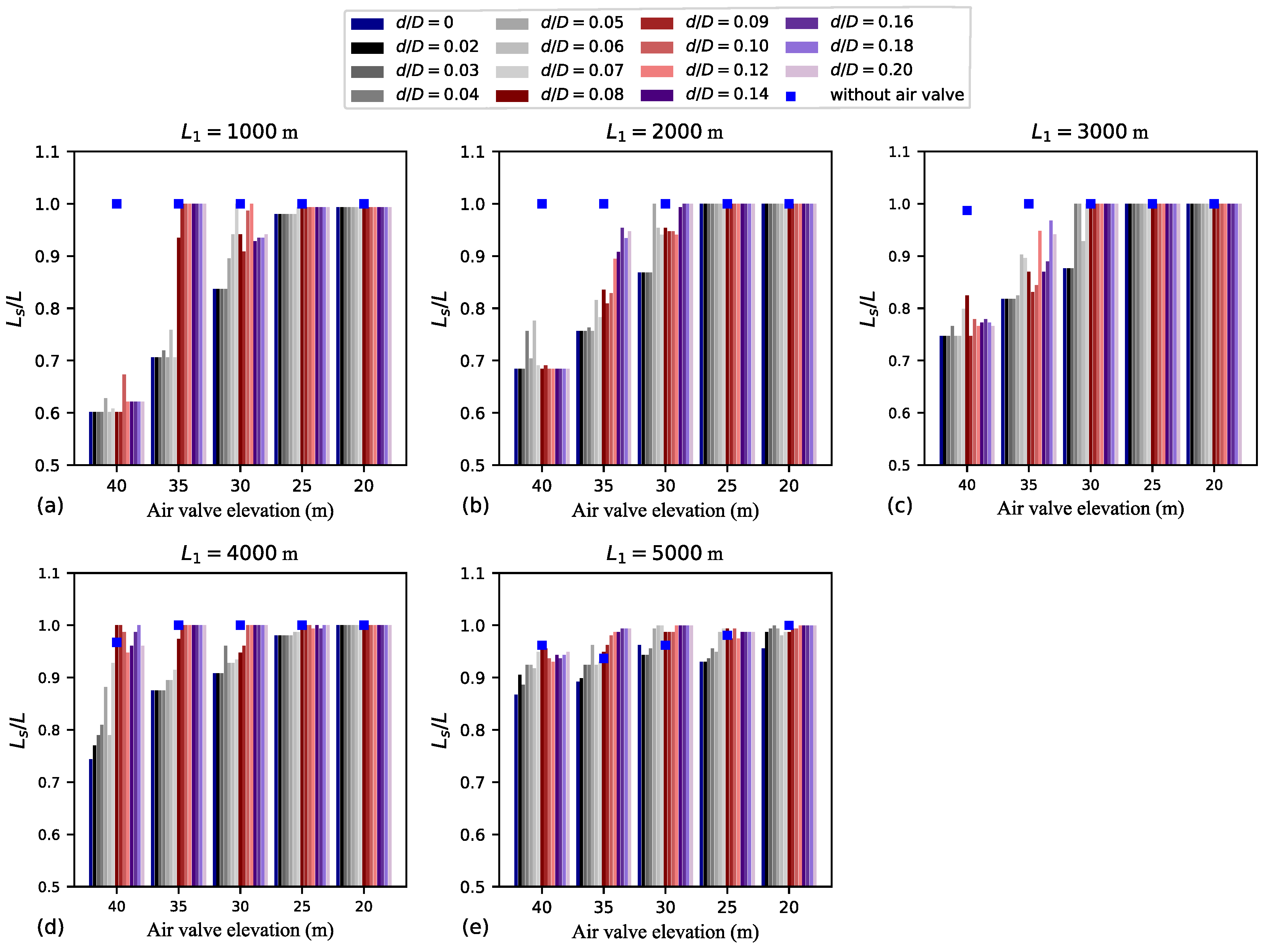
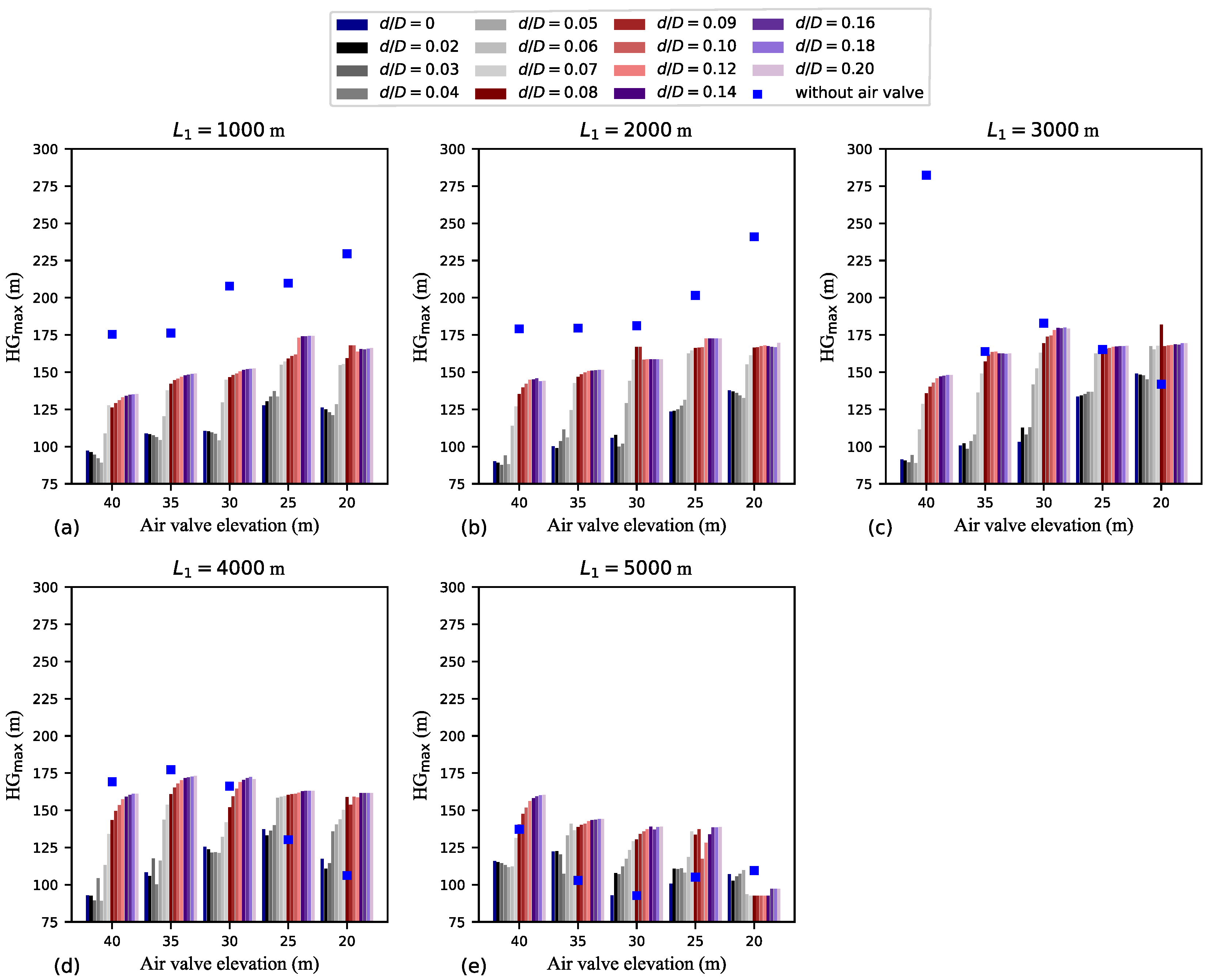
Air valves are typically thought of as devices responsible for mitigating negative pressures. However, as illustrated in Figure 2 and Figure 3, even with a system equipped with a large-inflow-capacity air valve, momentary negative pressures can still occur during the pump trip scenario. Figure 9 shows how $L_s/L$ is influenced by variations in $L_1$, h, and $d/D$. Generally, for the smallest h values (20 and 25 m), negative pressures are prevalent throughout the entire pipeline length, irrespective of $d/D$. Particularly for larger h values, smaller outflow orifices correspond to smaller $L_s/L$ values. In fact, the smallest $L_s/L$ values are those associated with $h=40$ m and $L_1=1000$ m. Interestingly, even for the cases with the smallest $L_s/L$ values, $L_s/L>0.60$. As exemplified in Figure 2a–d and Figure 3a–d, especially for the largest h values, the region of the pipeline neighbouring the low point downstream of the air valve is the least susceptible to negative pressures. Nonetheless, in the absence of air valve protection, the whole pipeline is generally subjected to negative pressures.

Having an air valve with a sufficiently small outflow orifice can help mitigate the intensity of secondary pressures upon air valve closure. Moreover, as shown in Figure 10, the presence of an air valve can also help mitigate the maximum transient HG at the upstream section of the pipeline. Figure 10 shows how ${\mathrm{HG}}_{\max }$ is influenced by variations in $L_1$, h, and $d/D$. Figure 10 reveals that, except for $L_1=5000$ m and $h=20$ m (case with the smallest $V_{\max }$ value), reducing $d/D$ leads to greater attenuation of ${\mathrm{HG}}_{\max }$ values. For every combination of $L_1$ and h (i.e., for every location of the air valve), the ${\mathrm{HG}}_{\max }$ versus $d/D$ data contains two distinct regions: a lower left region associated with smaller $d/D$ values (indicating type 1 behaviour), and a higher right region associated with larger $d/D$ values (indicating type 3 behaviour).

For $L_1=1000$ m and $L_1=2000$ m, with h ranging from 25 to 40 m, the transient magnitude tends to increase as h decreases. Similarly, for $L_1=3000$ m and $L_1=4000$ m, with h ranging from 30 to 40 m, the transient magnitude also tends to increase as h decreases. Interestingly, for the air valve location furthest from the upstream reservoir, the transient magnitude tends to decrease as h decreases. For $L_1=1000$ m and $L_1=2000$ m, ${\mathrm{HG}}_{\max }$ is larger for the cases without an air valve than for the cases with it. Pipelines with smaller h values or those located farther from the upstream reservoir are more susceptible to macro-cavitation and tend to have smaller admitted air volumes. As mentioned earlier, the effectiveness of the air valve in reducing the transient magnitude is linked to the air cushioning effect, which is less pronounced in these situations.

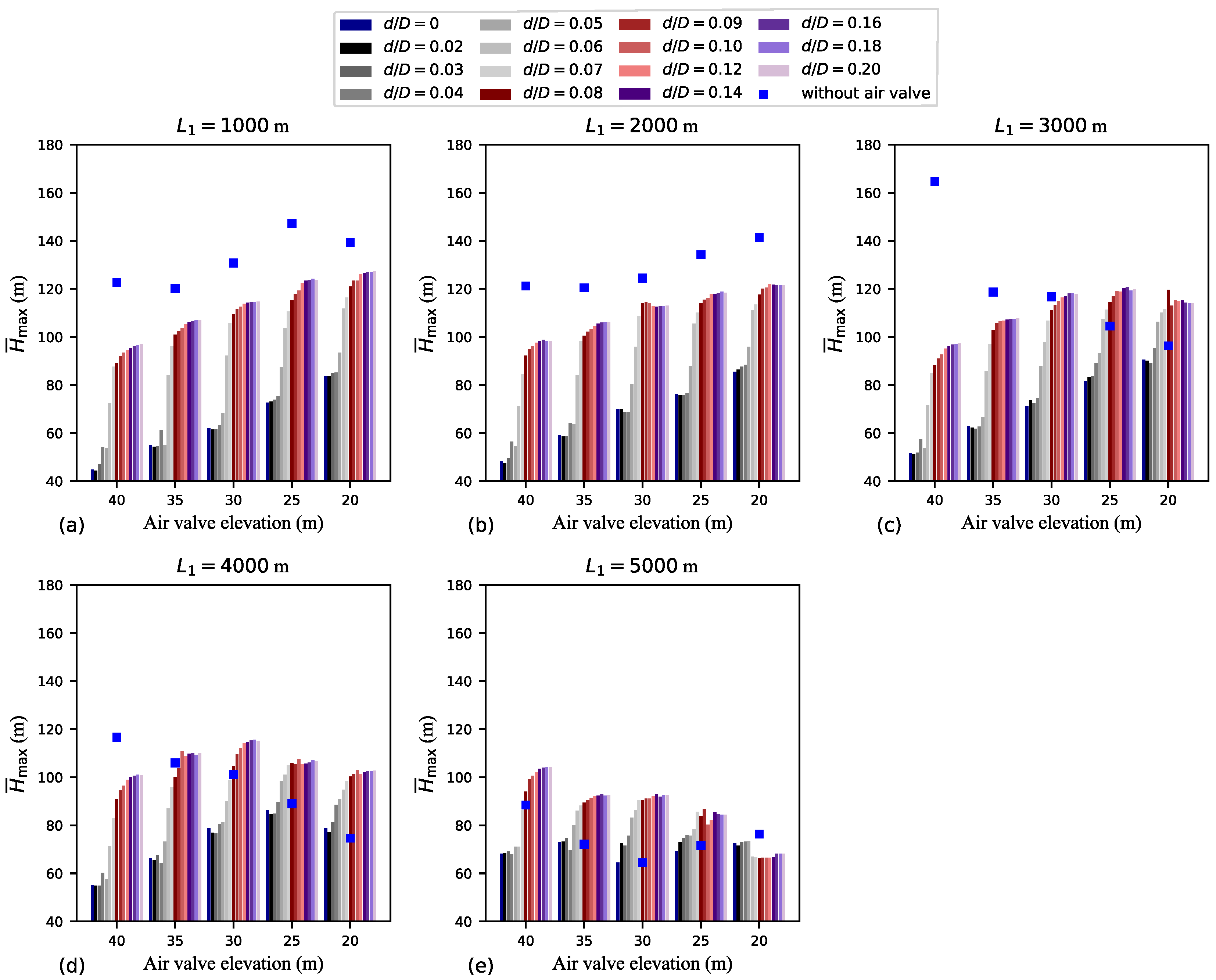
Even though ${\mathrm{HG}}_{\max }$ is an important parameter for evaluating the magnitude of the transient (since the upstream section of the pipeline must withstand the head associated with ${\mathrm{HG}}_{\max }$), the mean maximum hydraulic head (${\overline{H}}_{\max }$) offers a more comprehensive assessment of the entire transient event. Figure 11 shows how ${\overline{H}}_{\max }$ is influenced by variations in $L_1$, h, and $d/D$. The results in Figure 11 resemble those in Figure 10. However, the ${\overline{H}}_{\max }$ versus $d/D$ data in Figure 11 appear smoother and show more distinct left and right plateaus. It is important to note that if the $d/D$ ranges considered in Figure 10 and Figure 11 were narrower, the presence of the left and right plateaus could shrink or even disappear. The effectiveness of a small-outflow-capacity air valve in mitigating transient events is evident in Figure 11. For $L_1=3000$ m and $h=40$ m, ${\overline{H}}_{\max }=51$ m for $d/D=0.02$, whereas ${\overline{H}}_{\max }=93$ m for $d/D=0.10$ (a 45% difference). For $L_1=3000$ m and $h=20$ m, ${\overline{H}}_{\max }=90$ m for $d/D=0.02$, whereas ${\overline{H}}_{\max }=115$ m for $d/D=0.10$ (a 22% difference). It is important to highlight the significance of air valve elevation: e.g., for $L_1=3000$ m, the water-hammer-dominated event for $h=40$ m (with a lower driving head to induce reverse flow) displays a transient magnitude similar to that of the attenuated event for $h=20$ m.

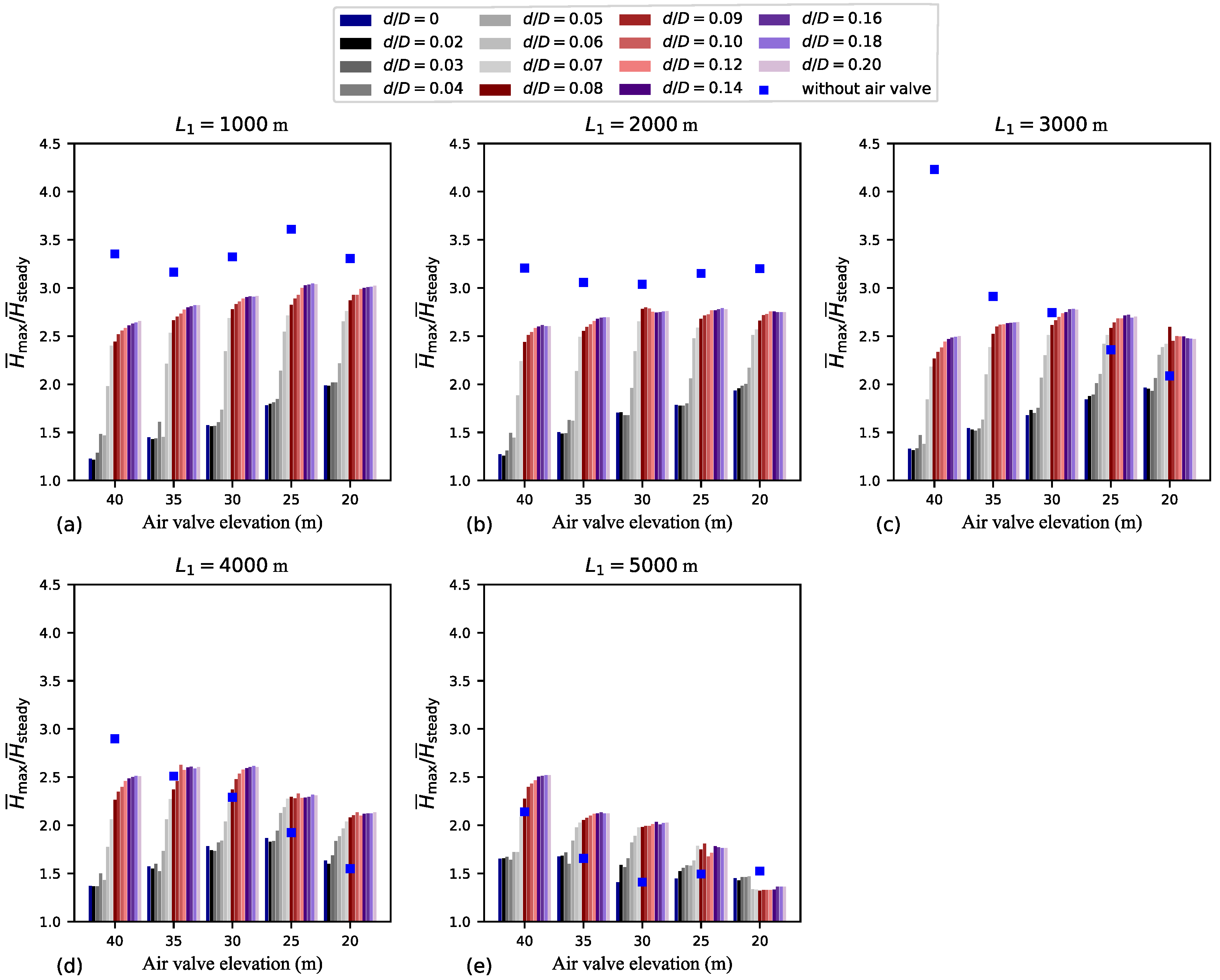
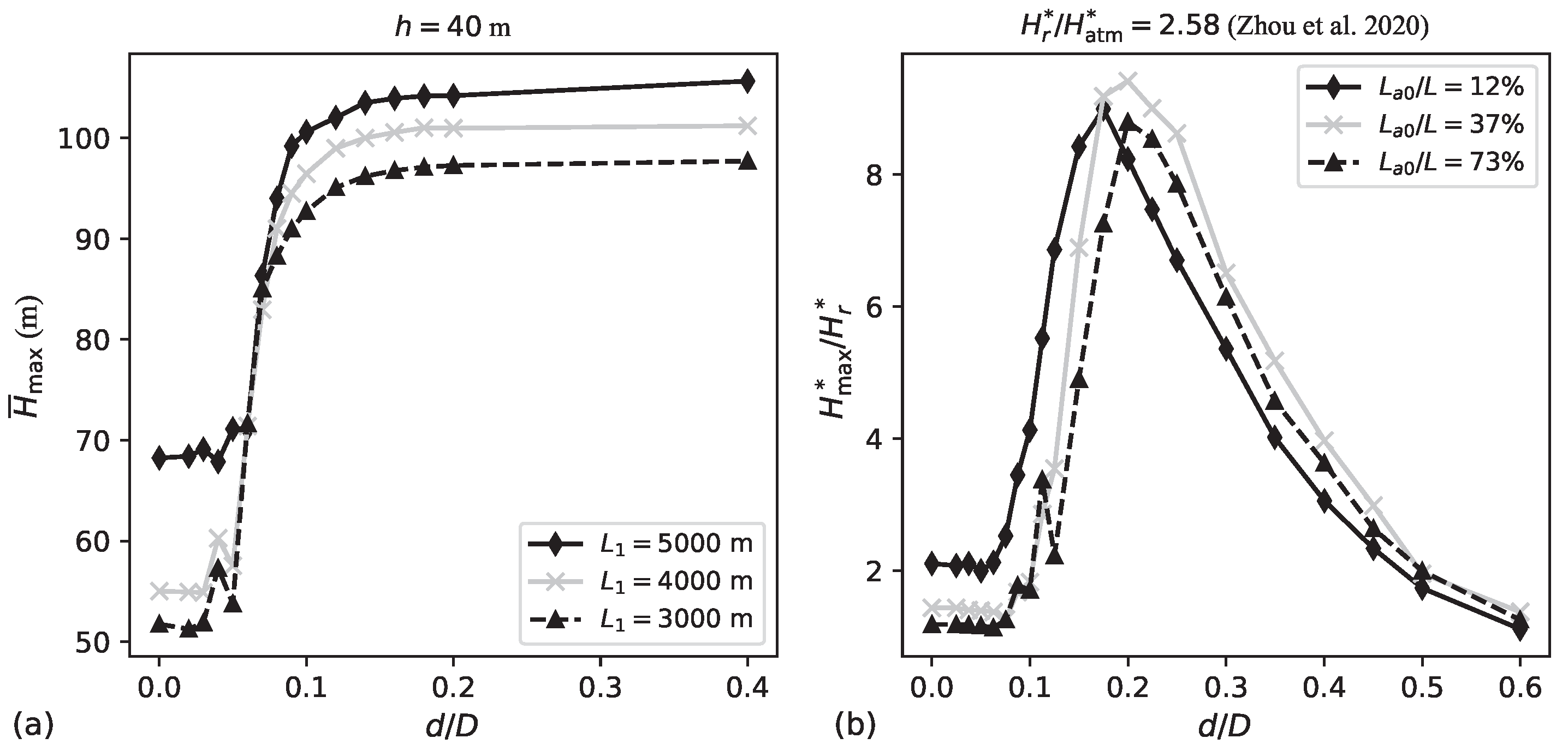
The data shown in Figure 11 are reinterpreted in Figure 12 using a dimensionless parameter denoted as ${\overline{H}}_{\max }/{\overline{H}}_{\mathrm{steady}}$, a parameter that relativises the mean maximum transient head (${\overline{H}}_{\max }$) relative to steady values (${\overline{H}}_{\mathrm{steady}}$). Note that there is a slight variation in the ${\overline{H}}_{\mathrm{steady}}$ value depending on the location of the air valve. The highest ${\overline{H}}_{\max }/{\overline{H}}_{\mathrm{steady}}$ value, approximately 3, is observed for $L_1=1000$ m, the lowest air valve elevations, and type 3 behaviour. In contrast, the smallest ${\overline{H}}_{\max }/{\overline{H}}_{\mathrm{steady}}$ value, approximately 1.2, is observed for $L_1=1000$ m, $h=40$ m, and type 1 behaviour. This implies that locating the air valve closer to the upstream reservoir results in more intense transient pressures for type 3 behaviour. However, locating the air valve near the upstream reservoir also offers the greatest potential for water hammer mitigation for type 1 behaviour.

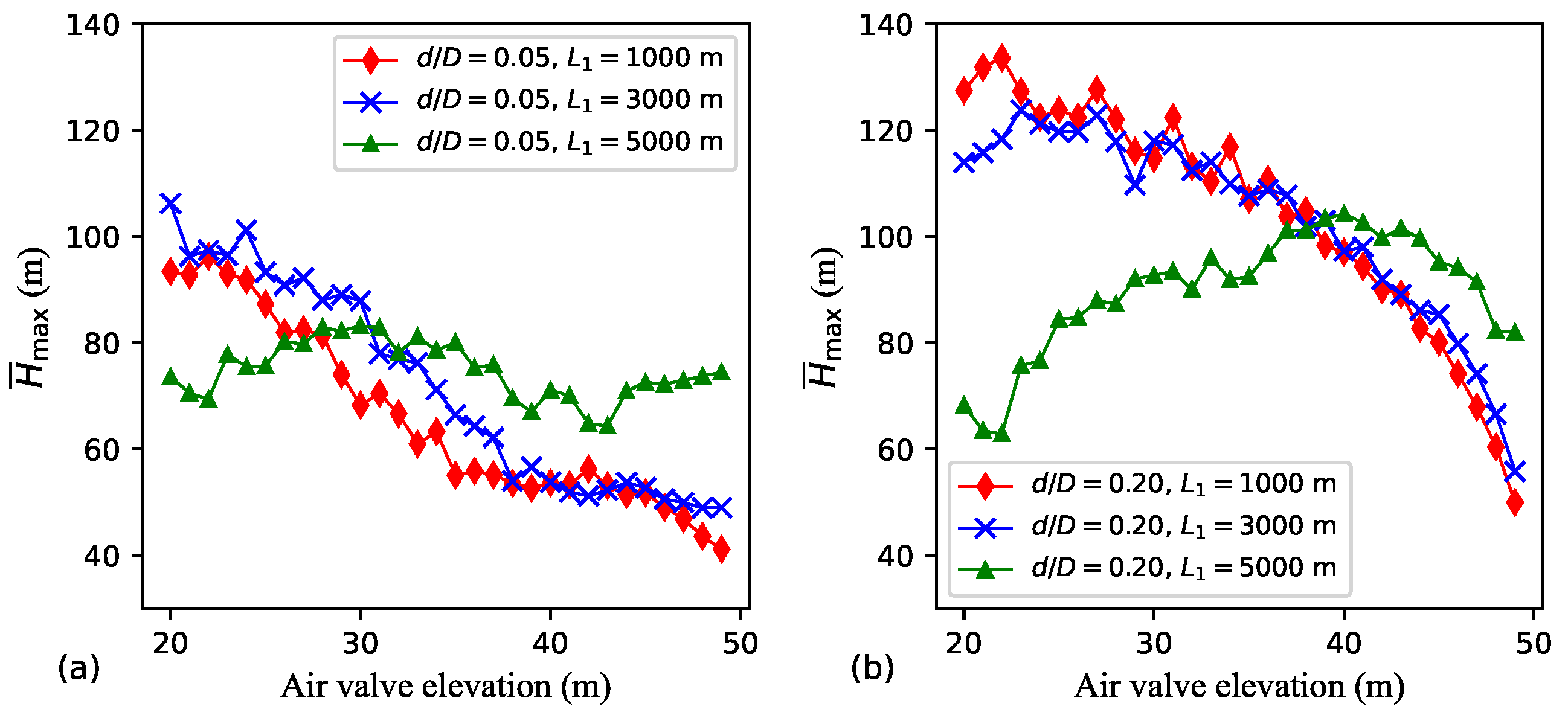
Figure 10, Figure 11 and Figure 12 show how the transient magnitude is significantly influenced by the air valve location. Figure 13 details the effect of h on ${\overline{H}}_{\max }$ for three $L_1$ values (1000, 3000, and 5000 m) and two $d/D$ values (0.05 and 0.20). For both $L_1=1000$ m and $L_1=3000$ m, ${\overline{H}}_{\max }$ tends to increase as h decreases. For $d/D=0.05$ and $L_1=5000$ m, the dependence between ${\overline{H}}_{\max }$ and h is unclear, while for $d/D=0.20$ and $L_1=5000$ m, ${\overline{H}}_{\max }$ shows some tendency to decrease as h decreases. For each air valve location, ${\overline{H}}_{\max }$ is generally smaller for $d/D=0.05$ than for $d/D=0.20$. Figure 13 reveals that, in the context of the pump trip scenario, it is the lower high points that result in more intense transient events.

7.2. Assessing the Timing of the Transient

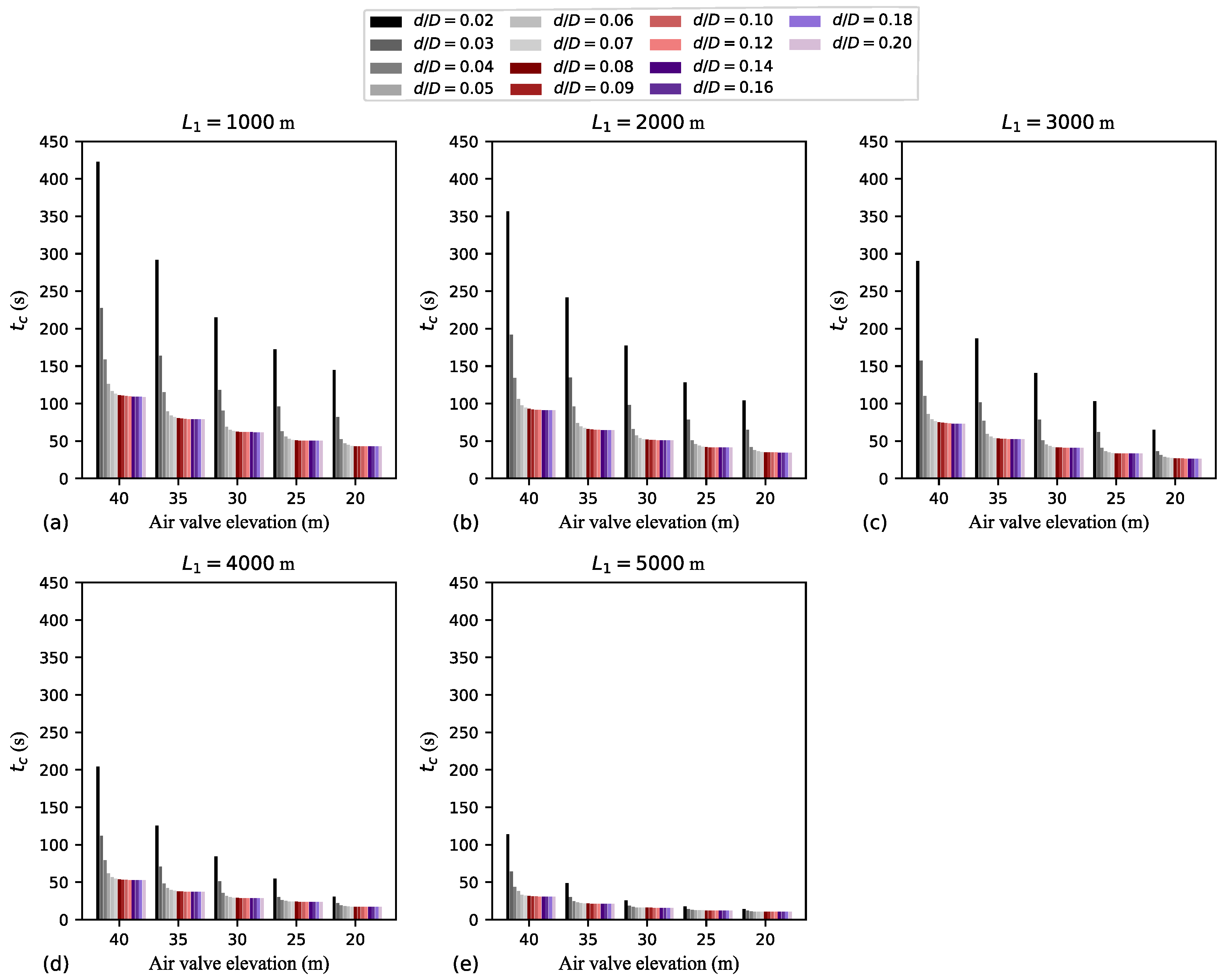
As previously discussed, the duration of the initial water hammer cycle tends to extend with decreasing values of $d/D$ and $L_1$, as well as increasing values of h. As illustrated in Figure 2 and Figure 3, the initial duration of the water hammer cycle is typically slightly longer than $t_c$, making $t_c$ a suitable proxy for this duration. Figure 14 shows how $t_c$ is influenced by variations in $L_1$, h, and $d/D$. In this figure, the case with $d/D=0$ was excluded because of the absence of air pocket collapse.

Figure 14 shows that, for each $L_1$ and $d/D$ combination, as h decreases, so does $t_c$. For each h and $d/D$ combination, as $L_1$ increases, $t_c$ decreases. For each air valve location (i.e., for each $L_1$ and h combination), as $d/D$ decreases, $t_c$ increases exponentially, while as $d/D$ increases, $t_c$ tends to a constant value. Indeed, for each air valve location, the largest $t_c$ value occurs for $d/D=0.02$. Notably, the $t_c$ value for a small outflow orifice can be several times longer than that for a large outflow orifice. For $L_1=1000$ m and $h=40$ m, $t_c=423$ s for $d/D=0.02$, whereas $t_c=109$ s for $d/D=0.20$ (a 74% reduction). For $L_1=1000$ m and $h=20$ m, $t_c=145$ s for $d/D=0.02$, whereas $t_c=43$ s for $d/D=0.20$ (a 70% reduction). For $L_1=5000$ m, $t_c$ is much smaller than for $L_1=1000$ m. For example, for $L_1=5000$ m, $h=20$ m, and $d/D=0.02$ (type 1 behaviour), $t_c=14$ s—a value much smaller than that for type 3 behaviour considering $L_1=1000$ m, $h=20$ m, and $d/D=0.20$ ($t_c=43$ s). A combined examination of Figure 11 and Figure 14 reveals a consistent trend: event intensity attenuates with increasing $t_c$, as momentum considerations would indicate.

An essential aspect regarding transient timing is the moment when the maximum hydraulic grade in the system (${\mathrm{HG}}_{\max }$) occurs. The moment when ${\mathrm{HG}}_{\max }$ occurs is referred to as $t_{{\mathrm{HG}}_{\max }}$. As discussed, a peak HG value occurs at the upstream section of the pipeline after the first instance of air pocket collapse. Yet, this peak HG does not always correspond to ${\mathrm{HG}}_{\max }$. In Figure 3, for example, the peak HG values at the upstream section of the pipeline at the conclusion of the secondary wave stage correspond to the ${\mathrm{HG}}_{\max }$ values. However, since such correspondence is not always the case, one method to assess the timing of the maximum HG in the system is by comparing it to the air pocket collapse time. Figure 15 shows how $t_{{\mathrm{HG}}_{\max }}$ minus $t_c$ is influenced by variations in $L_1$, h, and $d/D$. A negative bar in this figure indicates that ${\mathrm{HG}}_{\max }$ occurs before $t_c$, whereas a positive bar indicates the opposite.

In Figure 15, three distinct $t_{{\mathrm{HG}}_{\max }}-t_c$ patterns can be identified, which are somewhat dependent on the air valve location and outflow capacity: (i) ${\mathrm{HG}}_{\max }$ occurs much before $t_c$ (typical for small $d/D$ values); (ii) ${\mathrm{HG}}_{\max }$ occurs much after $t_c$ (sometimes observed for intermediate $d/D$ values); (iii) ${\mathrm{HG}}_{\max }$ occurs right after $t_c$ (typical for large $d/D$ values). For $L_1=5000$ m (especially for lower h values like 20, 25, and 30 m), the $t_{{\mathrm{HG}}_{\max }}-t_c$ patterns become less distinct compared to other $L_1$ values. For the smallest $d/D$ values, ${\mathrm{HG}}_{\max }$ occurs much before $t_c$, while for the largest $d/D$ values, ${\mathrm{HG}}_{\max }$ usually occurs right after $t_c$. In the context of type 3 behaviour, the usually relatively small and positive value of $t_{{\mathrm{HG}}_{\max }}-t_c$ for large $d/D$ values reinforces the connection between air valve closure and the occurrence of ${\mathrm{HG}}_{\max }$. However, for intermediate $d/D$ values, $t_{{\mathrm{HG}}_{\max }}-t_c$ can be several times the pipeline’s period.

The striking difference in transient timing between type 1 and type 3 behaviours is evident in Figure 15. For $L_1=1000$ m and $h=40$ m, $t_{{\mathrm{HG}}_{\max }}-t_c=-49$ s for $d/D=0.04$ (which is actually a non-extreme case), which is a value comparatively much larger in absolute magnitude than $t_{{\mathrm{HG}}_{\max }}-t_c=4$ s for $d/D=0.10$. In Figure 15, the number of $d/D$ cases with negative $t_{{\mathrm{HG}}_{\max }}-t_c$ values decreases as $L_1$ increases or h decreases. Negative $t_{{\mathrm{HG}}_{\max }}-t_c$ values indicate that ${\mathrm{HG}}_{\max }$ occurs while the air pocket remains. Thus, in such cases, it makes sense to infer that $t_{{\mathrm{HG}}_{\max }}$ is associated with the air expulsion stage, i.e., ${\mathrm{HG}}_{\max }$ occurs while the air pocket is being compressed by the reverse flow in the downstream branch. The transient timings associated with type 1 and type 2 behaviours occurring well before or much after $t_c$, respectively, do not necessarily rule out the possibility of a peak transient head occurring at the upstream section of the pipeline immediately after the air valve closure.

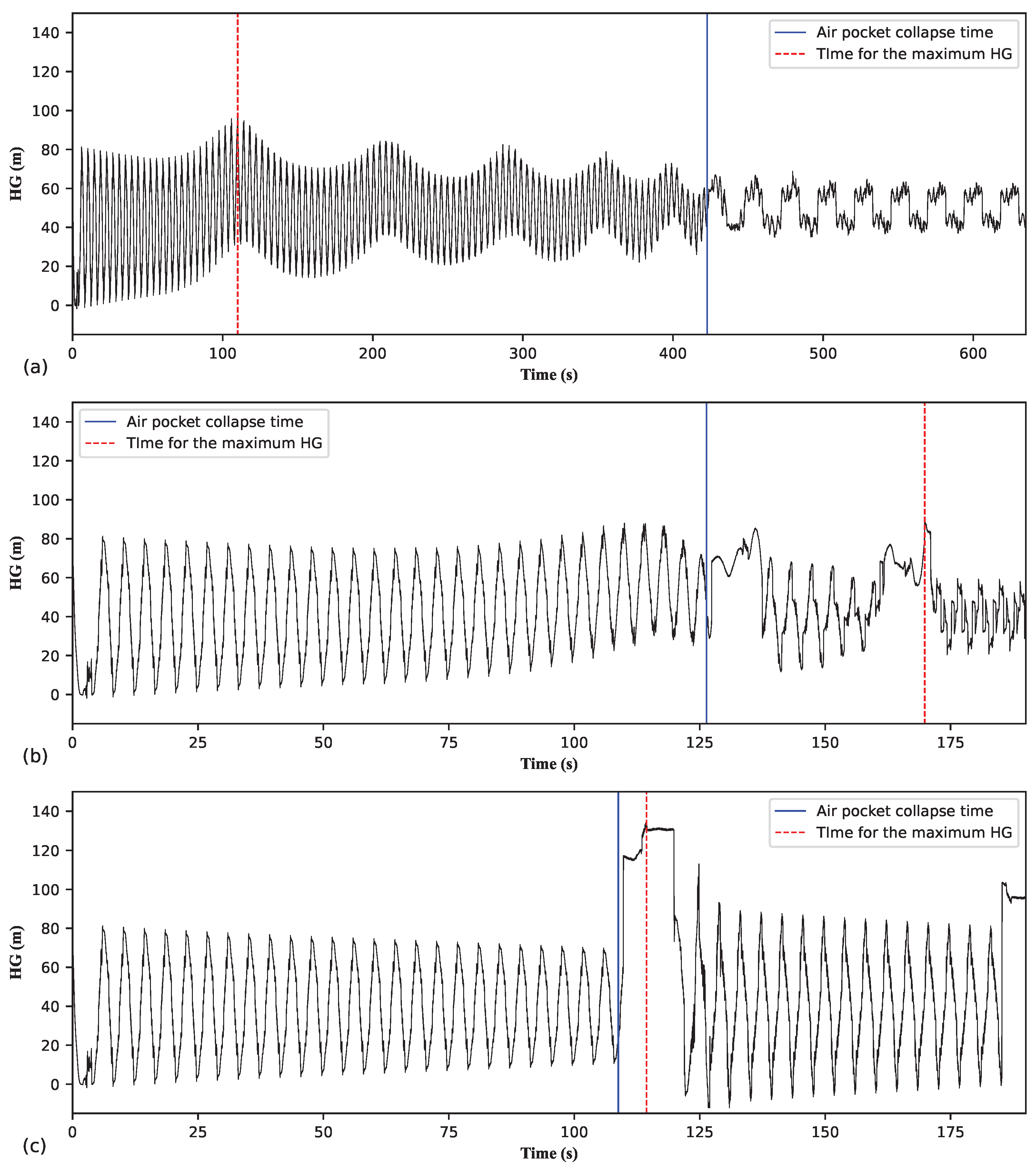
Figure 16 shows the evolution of the HG at the upstream section of the pipeline (i.e., close to the pumping station) for types 1, 2, and 3 behaviours. For $d/D=0.02$ (Figure 16a), ${\mathrm{HG}}_{\max }$ occurs much before $t_c$. For this case, $t_c$ is about four times longer than $t_{{\mathrm{HG}}_{\max }}$. For $d/D=0.05$ (Figure 16b), $t_{{\mathrm{HG}}_{\max }}$ is considerably longer than $t_c$. For this case, ${\mathrm{HG}}_{\max }$ occurs after the second instance of air pocket collapse. In Figure 16b, note the similarity in the HG signal right after $t_c$ and right before $t_{{\mathrm{HG}}_{\max }}$. This kind of HG variation is typical of the secondary wave stage. Also, note that in Figure 16b, the magnitude of the HG peak right after $t_c$ is similar to the magnitude of ${\mathrm{HG}}_{\max }$. For $d/D=0.20$ (Figure 16c), ${\mathrm{HG}}_{\max }$ occurs right after $t_c$. In general, in Figure 16, prior to $t_c$, the transient variations share the same frequency across all three cases.

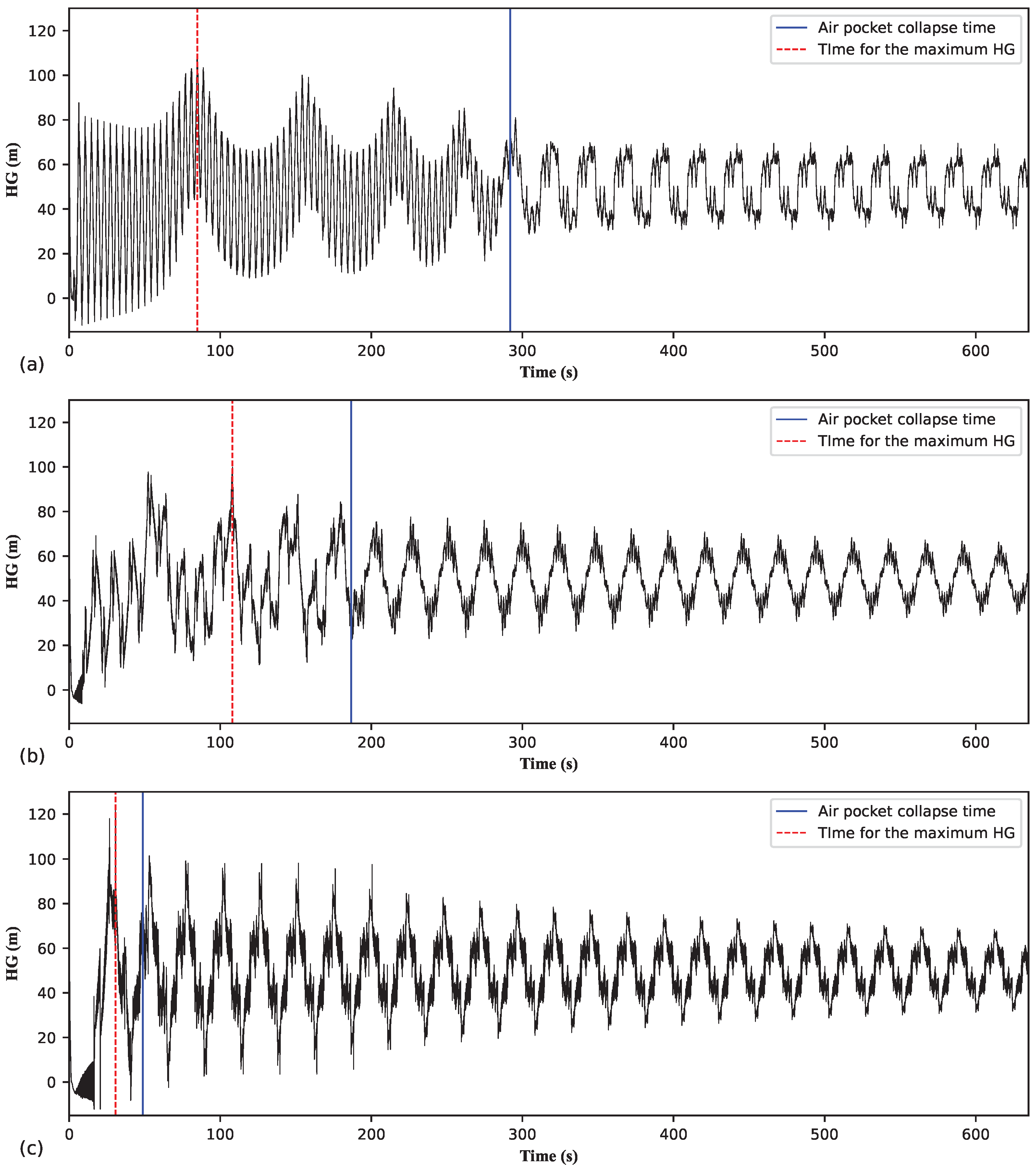
Figure 17 shows the evolution of the HG at the upstream section of the pipeline for three examples of type 1 behaviour (i.e., for three $L_1$ values) considering $h=35$ m and $d/D=0.02$. Across all three cases, $t_{{\mathrm{HG}}_{\max }}<t_c$. Prior to $t_c$, the frequency of the transient oscillations decreases as $L_1$ increases. The time it takes for the transient wave to traverse the upstream branch is directly proportional to $L_1$. The absolute value of $t_c-t_{{\mathrm{HG}}_{\max }}$ decreases as $L_1$ increases. Unlike the wave pattern depicted in Figure 16b,c, the HG oscillation in Figure 17 is not momentarily disrupted after the collapse of the air pocket. Following $t_c$, the oscillation period stabilises at $4L/a$ for all three $L_1$ cases in the figure. For $L_1=5000$ m, with its relatively short $t_c$ value, it becomes somewhat difficult to discern the period of the HG oscillation before $t_c$. In Figure 17a,b, the oscillation period before $t_c$ is determined by $4L_1/a$ (as predicted by Ramezani and Karney (2017) [10]), resulting in 4 s for $L_1=1000$ m and 12 s for $L_1=3000$ m.

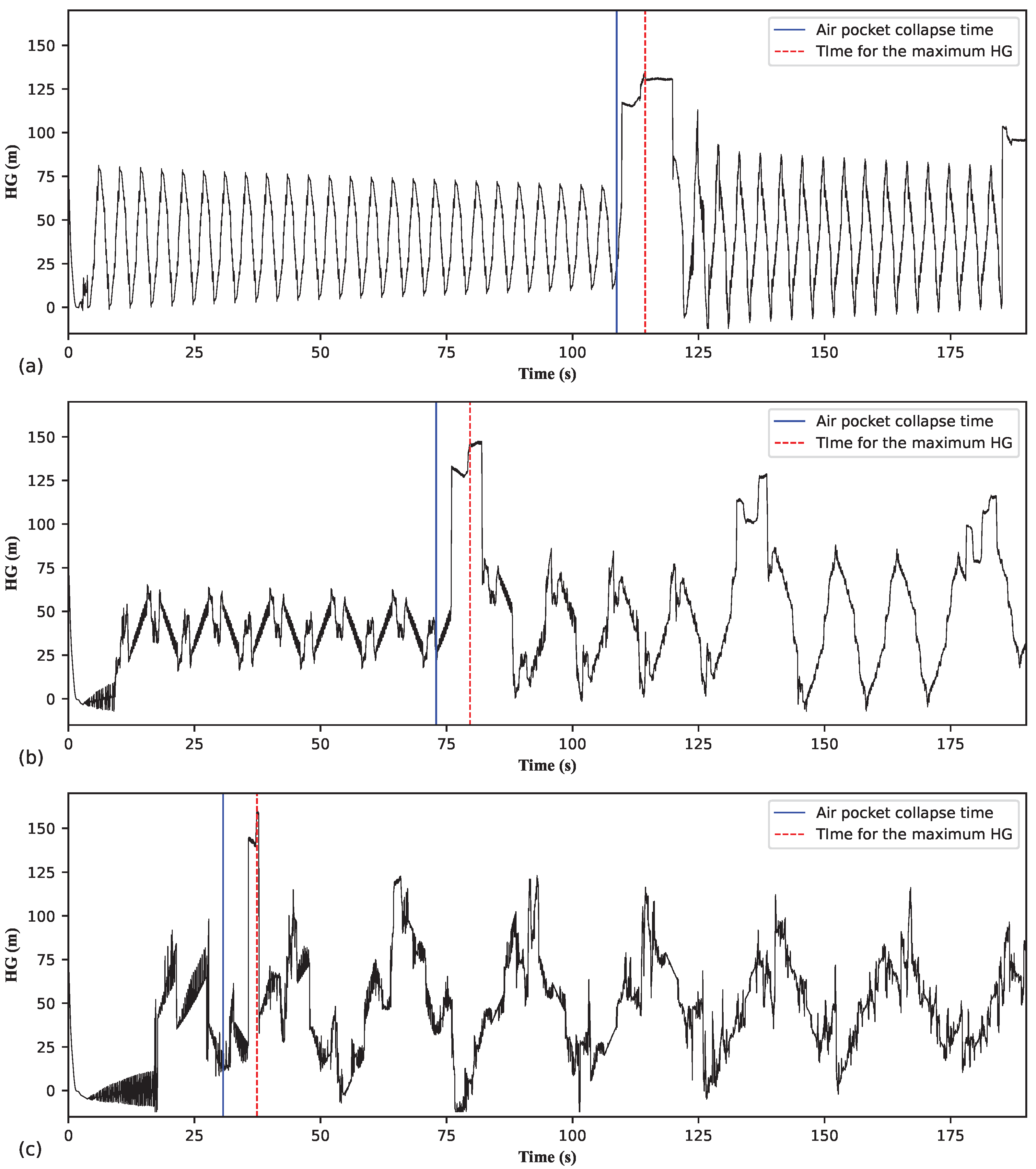
Figure 18 shows the evolution of the HG at the upstream section of the pipeline for three examples of type 3 behaviour (i.e., for three $L_1$ values) considering $h=40$ m and $d/D=0.20$. Across all three cases, $t_{{\mathrm{HG}}_{\max }}>t_c$. In contrast to Figure 17, in Figure 18, the $t_{{\mathrm{HG}}_{\max }}-t_c$ values across all three cases are similar. The frequency of the transient oscillations decreases as $L_1$ increases. Notably, the frequency of the oscillations remains the same both before and after the collapse of the air pocket. This behaviour pattern arises from the multiple instances of air admission and expulsion characteristic of type 3 behaviour, as shown in Figure 18, in contrast to the type 1 behaviour shown in Figure 17. This observation aligns with the data presented in Figure 7. The frequency of the transient oscillations in Figure 18 is determined by $4L_1/a$. In contrast to Figure 17, in Figure 18, the secondary wave stage can be easily discerned as a discontinuity in the HG oscillations. In Figure 18b, three instances of secondary wave stages can be observed, each showing progressively attenuated associated HG peaks.

7.3. Representing the Sensitivity Data

The air exchange apertures commonly examined in the literature are orifices and air valves. It is important to highlight the distinction in pipeline transient behaviour between these apertures. For the filling procedure in a pipeline with a downstream orifice, the absolute maximum transient head (often referred to as $H_{\max }^{*}$) increases with increasing $d/D$ until the maximum $H_{\max }^{*}$ value is reached. Then, $H_{\max }^{\ast }$ starts to decrease as $d/D$ increases. The $d/D$ value associated with the maximum $H_{\max }^{*}$ value is referred to as the critical $d/D$ value. The pipeline transient behaviour associated with the occurrence of the maximum $H_{\max }^{*}$ value can be classified as water-hammer-dominated and is characterised by a sudden increase in head resulting from the impact of the filling water column against the downstream orifice. References providing data on the transient magnitude versus $d/D$ for the pipeline filling procedure involving a downstream orifice include Zhou et al. (2002) [37], Lee (2005) [38], Zhou et al. (2019) [39], and Zhou et al. (2020) [3].

When filling a line with a downstream orifice, the orifice initially vents air to accommodate the incoming water. Nonetheless, as the water front reaches the orifice and in the subsequent moments, the orifice might expel not only air but also a mixture of air and water. In contrast, when filling involves a downstream air valve, only air is expected to be discharged. Even in cases where there might be a delay in air valve closure or if the last portion of the exhausted air contains moisture, the release of water or a mixture of air and water through the air valve is only momentary. Since air valves are designed to close upon contact with liquid water, the transient magnitude is anticipated to stabilise for large $d/D$ values (i.e., to remain the same for $d/D$ values for which the air cushioning effect is negligible). In fact, the air expulsion stage during the pump trip scenario represents a variation of the filling scenario, albeit within a more complex transient event. Notably, the transient magnitude during the pump trip scenario is directly influenced by the extent of the air cushioning effect during the air expulsion stage. As a result, both the pump trip and the pipeline filling scenarios share significant similarities, permitting a comparison between the physical processes involved in both situations.

Figure 19 allows a comparison between the transient responses associated with a pump trip and pipeline filling. Specifically, Figure 19a shows the relationship between ${\overline{H}}_{\max }$ and $d/D$ for the pump trip scenario involving air exchanges through an air valve. Figure 19b shows the relationship between $H_{\max }^{*}/H_r^{*}$ (ratio between the absolute maximum transient head and the absolute inlet head) and $d/D$ for the pipeline filling scenario involving air exchanges through a simple orifice. In Figure 19a,b, a strong similarity in transient response is evident between the two cases for small $d/D$ values. In both cases, if there is an increase in the maximum air pocket volume (achieved, for example, by decreasing $L_1$ in the pump trip scenario) or the initial air pocket volume, the intensity of the transient event decreases for $d/D$ values consistent with type 1 behaviour. However, a significant difference in transient response arises if the $d/D$ values are large.

The critical aperture size for type 3 behaviour (referred to as $d_{c3}$) determines the threshold $d/D$ value above which the transient can be classified as water-hammer-dominated. For the pump trip scenario, $d_{c3}$ is defined here as the $d/D$ value above which the transient magnitude stabilises. For the filling procedure, $d_{c3}$ is defined here as the $d/D$ value associated with the maximum transient magnitude. On the other hand, the critical aperture size for type 1 behaviour (referred to as $d_{c1}$) determines the $d/D$ value below which the transient can be classified as attenuated. Figure 19 compares pump trip (Figure 19a) to filling (Figure 19b), showing that the transient magnitude curves experience a sharp incline immediately after the low left plateau. However, for small $d/D$ values prior to this incline, the transient magnitude is relatively constant. The general shape of the curves in Figure 19a resembles that of a logistic curve. Each of these curves features a lower plateau to the left, followed by a steep (transitional) incline, ultimately reaching a higher plateau to the right. On the other hand, the general shape of the curves in Figure 19b resembles that of a right-skewed probability density function. Each of these curves features a lower plateau to the left, followed by a steep incline that reaches a maximum point, with a subsequent gradual descent.

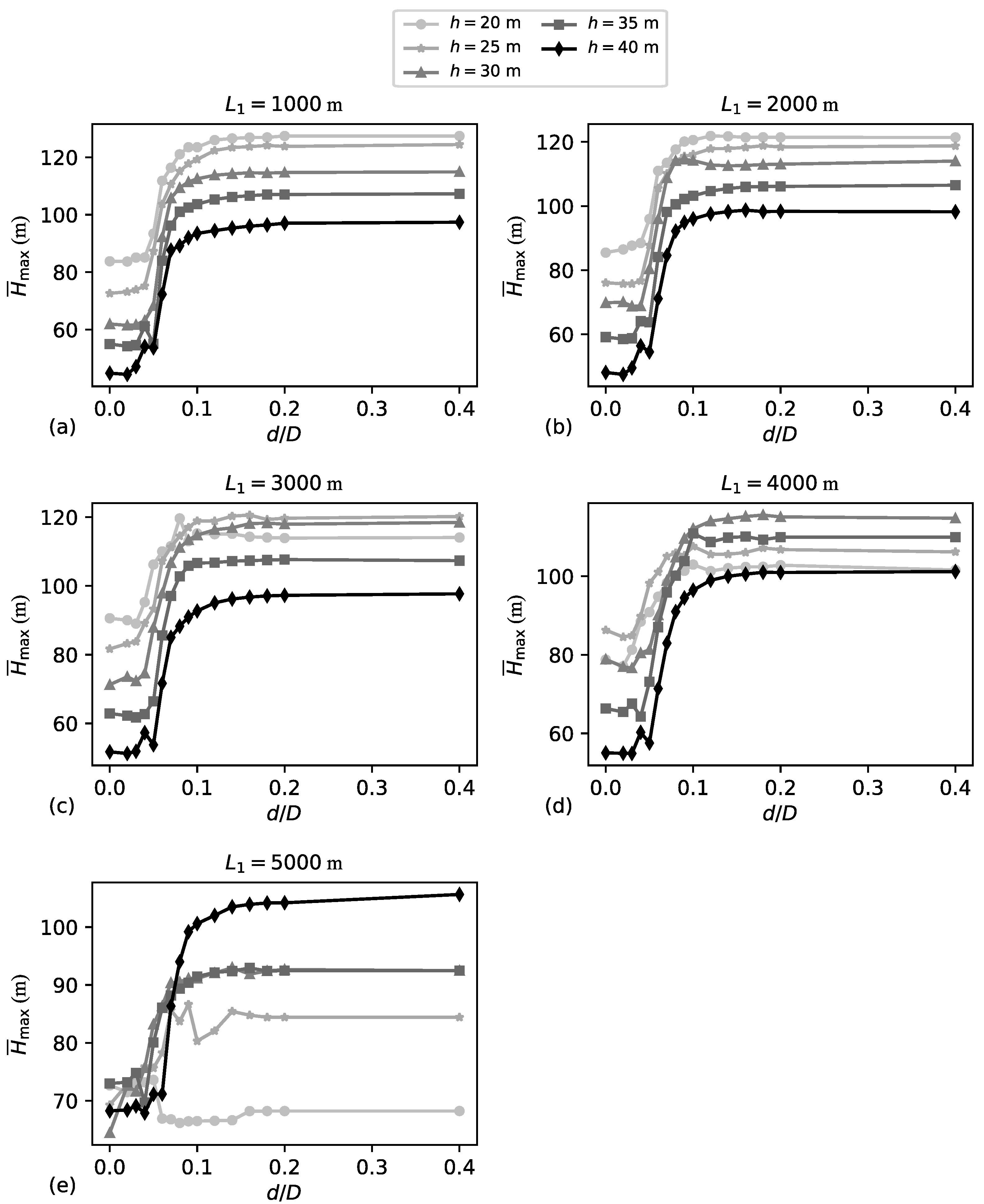
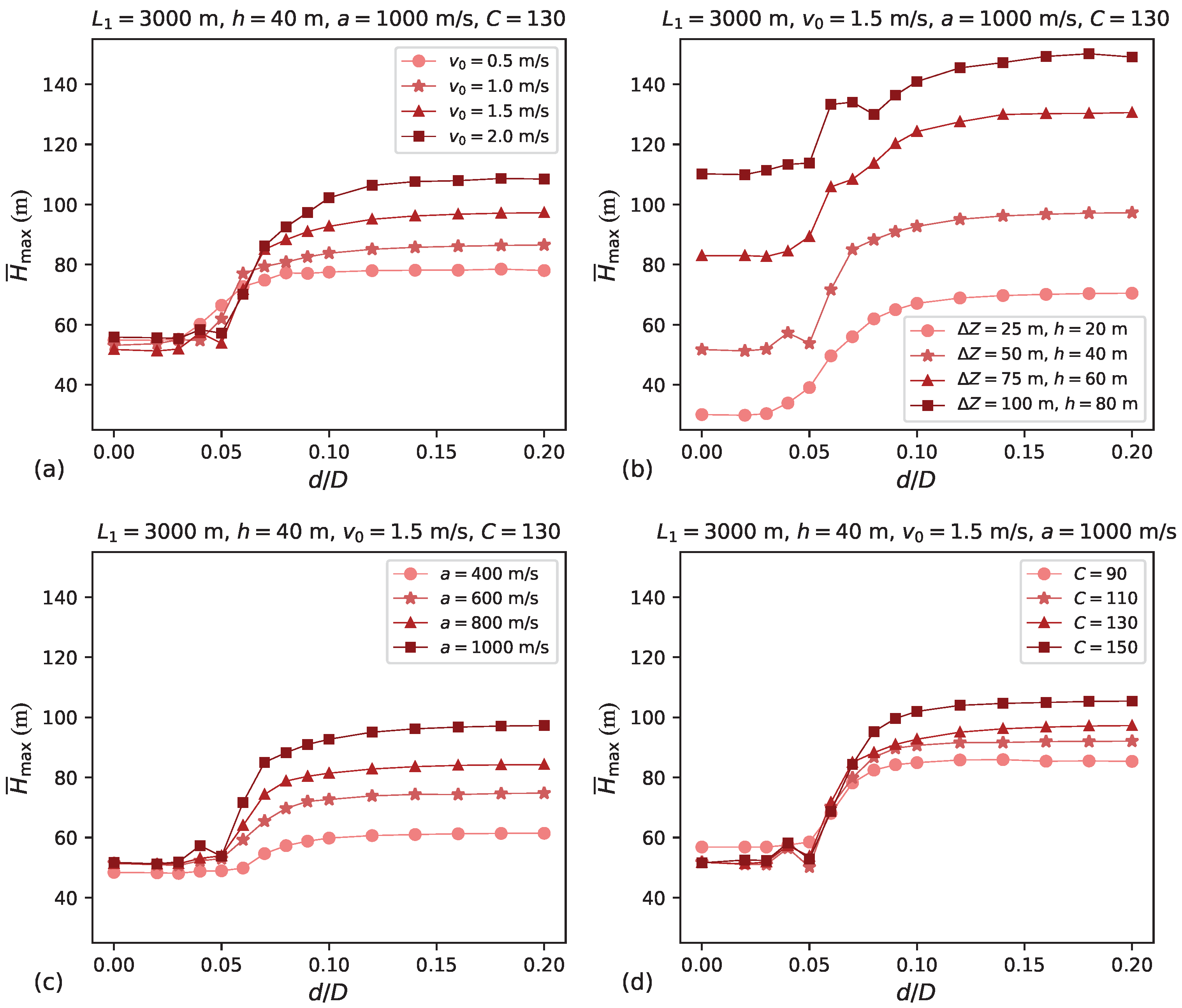
Figure 20 shows the comprehensive ${\overline{H}}_{\max }$ versus $d/D$ results obtained from the main set of numerical simulations. The curves in Figure 20 exhibit a similar shape to those in Figure 19a, except for the case with $L_1=5000$ m and $h=20$ m, which is associated with the smallest $V_{\max }$ value. As mentioned, this distinctive shape resembles the shape of a logistic curve. In Figure 20, for both $L_1=1000$ m and $L_1=2000$ m, regardless of whether it is type 1 or type 3 behaviour, the transient magnitude increases as h decreases. For $L_1$ values ranging from 1000 to 4000 m, this trend remains relatively consistent, particularly with respect to the low left plateaus. With the exception of $L_1=5000$ m, scenarios with $h=40$ m consistently exhibit the mildest transient magnitudes for both type 1 and type 3 behaviours across different $L_1$ values.

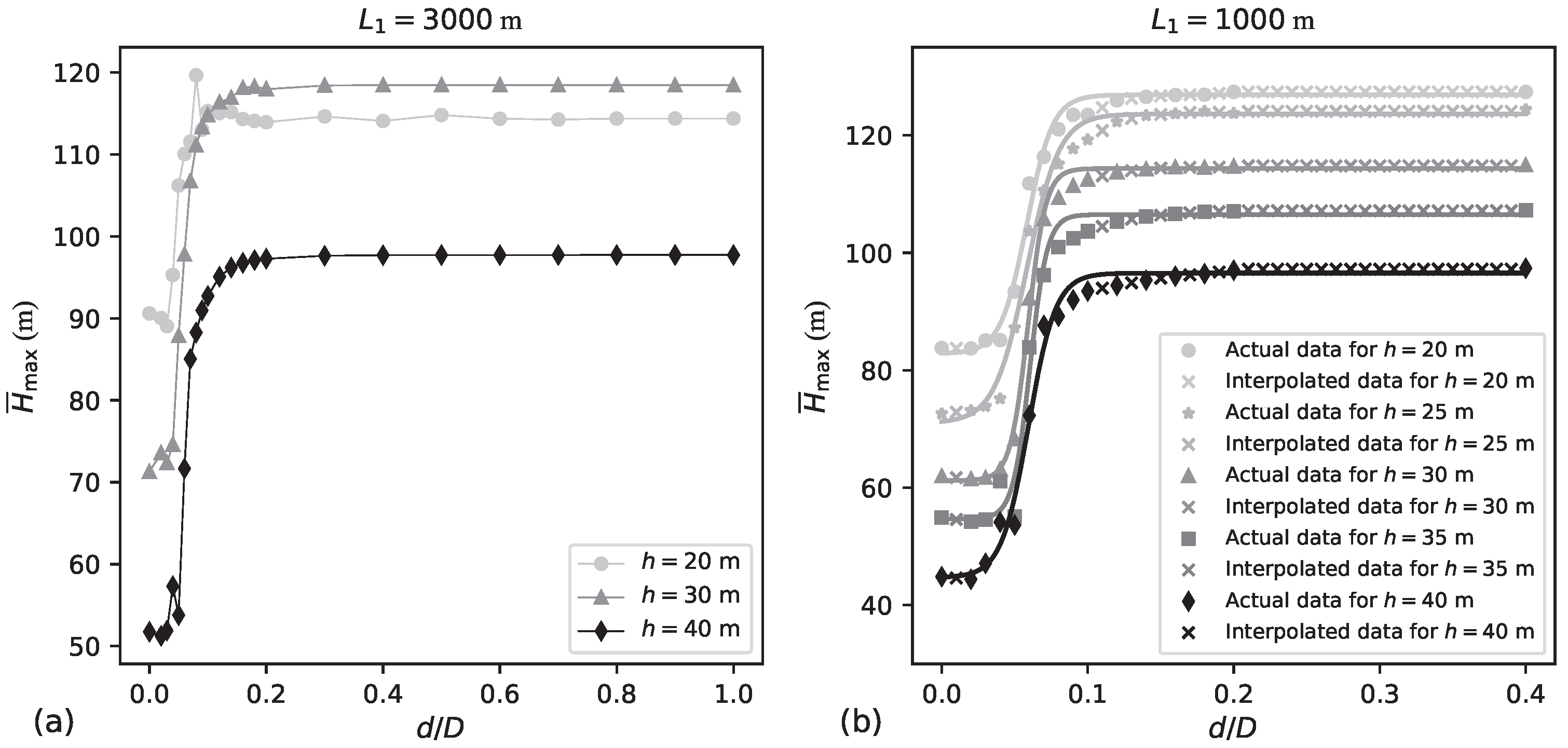
Figure 21 validates the appropriateness of fitting logistic curves to the ${\overline{H}}_{\max }$ versus $d/D$ results. In Figure 21a, ${\overline{H}}_{\max }$ remains relatively constant for large $d/D$ values. In this figure, the length of the high right plateau is significantly longer than that of the low left plateau. In fact, a significant part of the $d/D$ range in Figure 21a, specifically the largest $d/D$ values, is of limited relevance for sizing. Air valves with $d/D$ values exceeding 0.20 are typically not considered in practice. In Figure 21b, interpolated data is incorporated into the actual ${\overline{H}}_{\max }$ versus $d/D$ results to establish an evenly spaced set of ${\overline{H}}_{\max }$ versus $d/D$ pairs. These interpolated values are considered in the curve fitting process. The fitted curves shown in Figure 21b have the ability to predict the transient magnitude for both type 1 and type 3 behaviours.

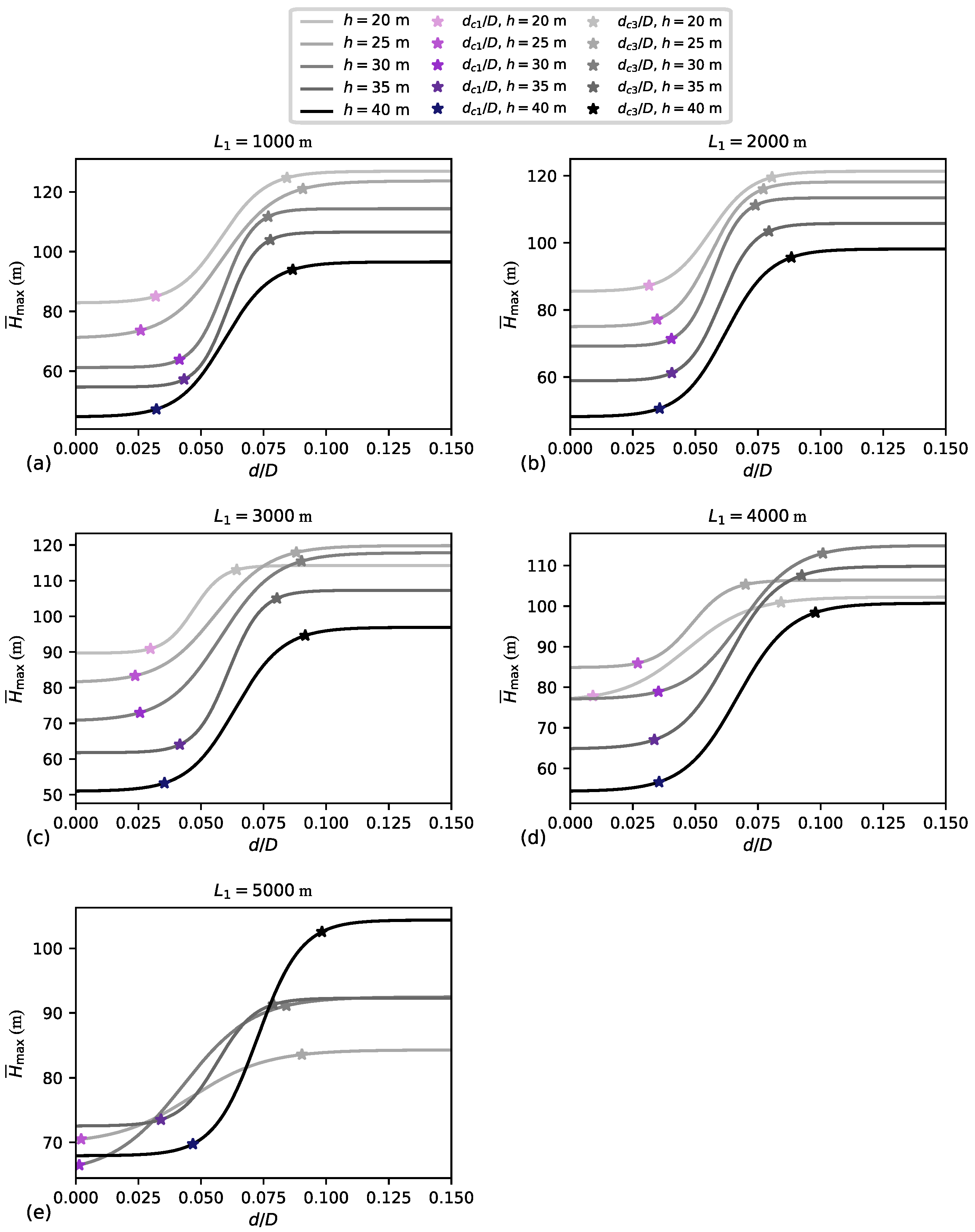
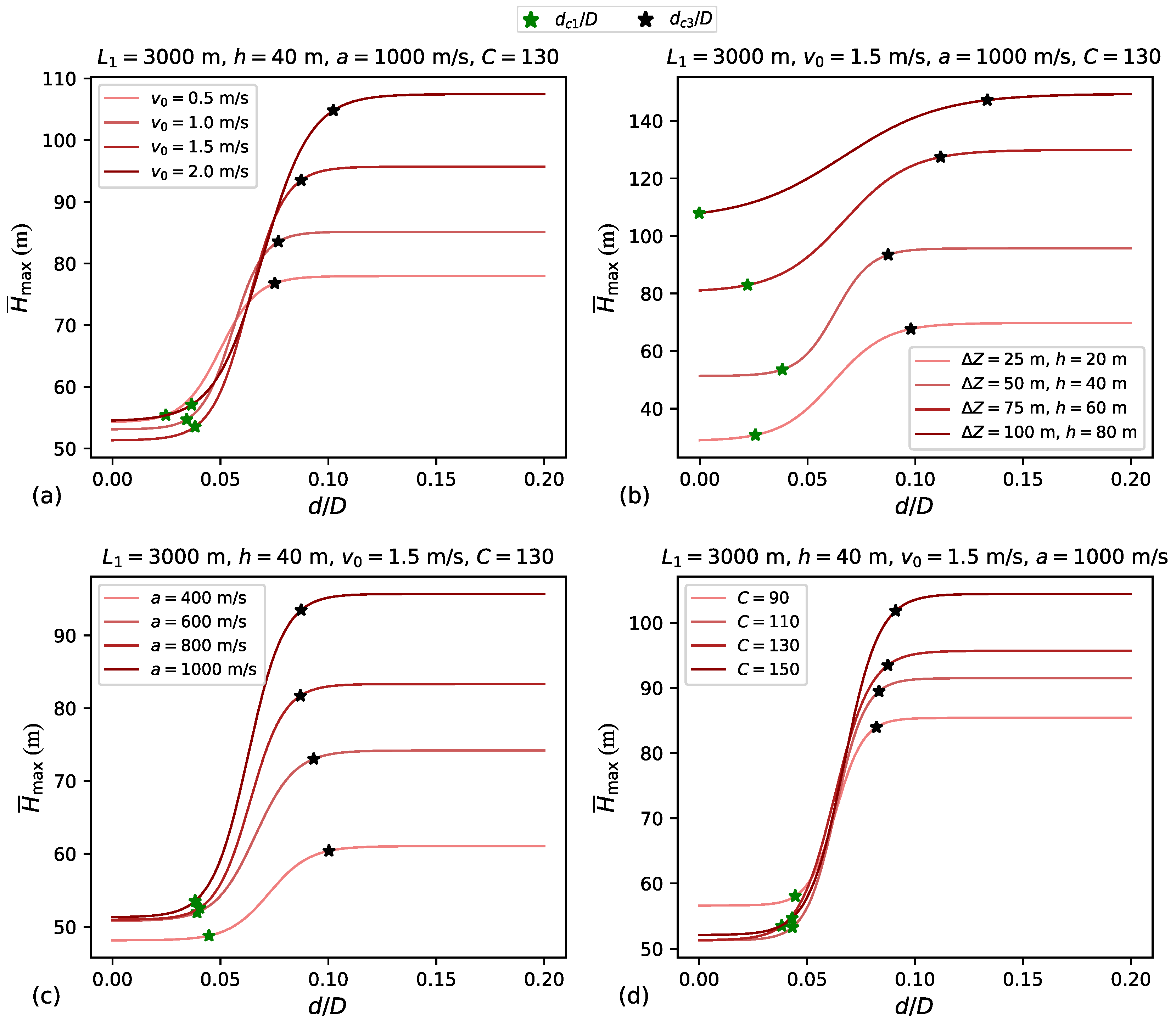
Figure 22 shows logistic curves fitted to the dataset shown in Figure 20. In Figure 22, two points along each curve are emphasised: ($d_{c1}/D$, ${\overline{H}}_{{\max }_{c1}}$), which delimits type 1 behaviour; and ($d_{c3}/D$, ${\overline{H}}_{{\max }_{c3}}$), which delimits type 3 behaviour. The $d_{c1}/D$ value is determined as the $d/D$ value corresponding to the minimum ${\overline{H}}_{\max }$ plus 5% of the logistic curve’s height, while $d_{c3}$ is determined as the $d/D$ value corresponding to the maximum ${\overline{H}}_{\max }$ minus 5% of the logistic curve’s height. These definitions for the critical air valve orifice sizes, while simple, effectively capture the transitions between the transient behaviours. Using logistic curves instead of raw data enhances the ease of comparing various scenarios and determining the critical orifice sizes.

Table 1. Critical orifice ratios for the inception of both type 1 ($d_{c1}/D$) and type 3 ($d_{c3}/D$) behaviours.

	Length of the Upstream
	Pipeline Branch
	1000 m	2000 m	3000 m	4000 m	5000 m
$d_{c1}/D$ range	0.026–0.043	0.032–0.041	0.024–0.042	0.009–0.036	0.001–0.047
$d_{c3}/D$ range	0.077–0.091	0.074–0.088	0.064–0.092	0.070–0.101	0.079–0.098
$d_{c1}/D$ for $h=20$ m	0.032	0.032	0.030	0.009	—
$d_{c3}/D$ for $h=20$ m	0.084	0.081	0.064	0.084	—
$d_{c1}/D$ for $h=25$ m	0.026	0.035	0.024	0.027	0.002
$d_{c3}/D$ for $h=25$ m	0.091	0.077	0.088	0.070	0.090
$d_{c1}/D$ for $h=30$ m	0.041	0.040	0.026	0.035	0.001
$d_{c3}/D$ for $h=30$ m	0.077	0.074	0.090	0.101	0.084
$d_{c1}/D$ for $h=35$ m	0.043	0.041	0.042	0.034	0.034
$d_{c3}/D$ for $h=35$ m	0.078	0.079	0.080	0.093	0.079
$d_{c1}/D$ for $h=40$ m	0.032	0.036	0.035	0.036	0.047
$d_{c3}/D$ for $h=40$ m	0.087	0.088	0.092	0.098	0.098

summarises the $d_{c1}/D$ and $d_{c3}/D$ values for all the cases considered in the main set of simulations, as shown in Figure 22. Significant variation is found in both the $d_{c1}/D$ and $d_{c3}/D$ values, depending on the specific combination of $L_1$ and h. For example, for the range of h values considered in this paper, for $L_1=3000$ m, the range of $d_{c1}/D$ spans from 0.024 to 0.042, while the range of $d_{c3}/D$ spans from 0.064 to 0.092. To provide greater context, consider the $d_{c1}/D$ ranges, which define type 1 behaviour, and the $d_{c3}/D$ ranges, which define type 3 behaviour, based on the data reported in Zhou et al. (2019) [39] for vertical pipe filling and in Zhou et al. (2020) [3] for horizontal pipe filling with $H_r^{*}/H_{\mathrm{atm}}^{*}=2.58$ (ratio between the absolute inlet head and the absolute atmospheric head). When filling a line with a downstream orifice, the transient magnitude versus $d/D$ data has a low left plateau for type 1 behaviour, but there is no high right plateau for type 3 behaviour, as shown in Figure 19. In a manner similar to the approach used in Figure 22 to define $d_{c1}/D$, for pipeline filling with a downstream orifice, the value of $d_{c1}/D$ is the $d/D$ value associated with the transient magnitude determined by adding 5% of the difference between the maximum value of the curve and the value of the low left plateau to the value of the low left plateau itself. Additionally, for this case, the value of $d_{c3}/D$ is the $d/D$ value associated with the maximum on the transient magnitude versus $d/D$ curve.

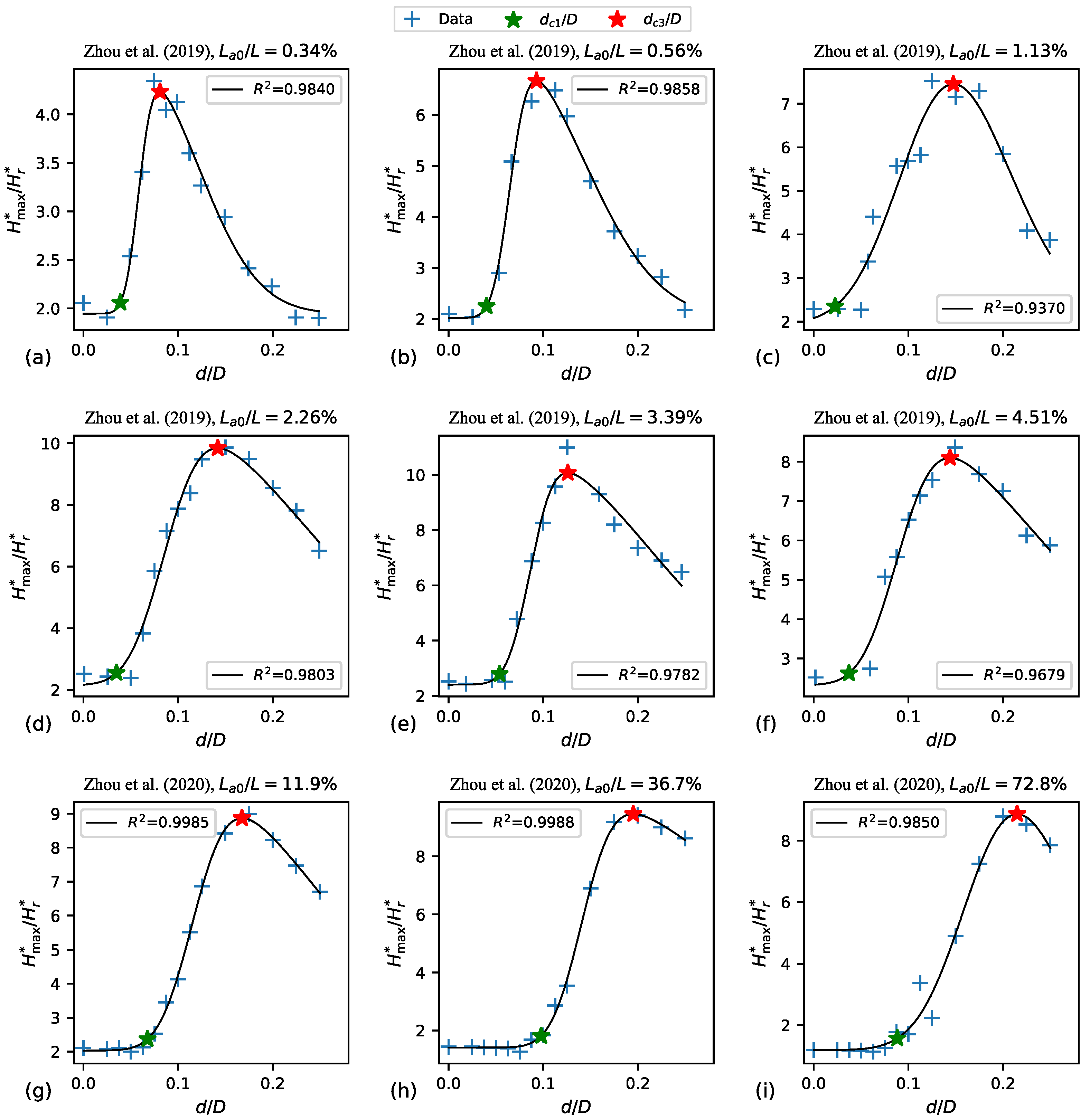
Figure 23 presents the data from Zhou et al. (2019) [39] and Zhou et al. (2020) [3] concerning the filling procedure with $H_r^{*}/H_{\mathrm{atm}}^{*}=2.58$. This figure also presents both the curves that represent the data (i.e., right-skewed probability density curves fitted to the data) and the $d_{c1}$ and $d_{c3}$ values associated with each curve. Only data within the range of $0\le d/D\le 0.25$ was considered for two main reasons. Firstly, very large $d/D$ values are generally not considered in practice. Secondly, these larger $d/D$ values sometimes correspond to transient magnitude values lower than the low left plateau of the data. This poses challenges for fitting the representational curves, as the chosen function for fitting the data assumes identical vertical axis values for both the left and right low plateaus. Not imposing this limitation on the considered $d/D$ range for curve fitting would compromise the predictive accuracy of the fitted curve for type 1 behaviour.

In Figure 23a–f (with data from Zhou et al. 2019 [39]), the $d_{c1}/D$ values range from 0.023 to 0.054, while the $d_{c3}/D$ values range from 0.081 to 0.148. In Figure 23g–i (with data from Zhou et al. 2020 [3]), the $d_{c1}/D$ values range from 0.068 to 0.098, while the $d_{c3}/D$ values range from 0.167 to 0.215. The critical $d/D$ values identified in the current study (which are presented in Table 1) exhibit greater similarity to those reported in Zhou et al. (2019) [39] than to those reported in Zhou et al. (2020) [3]. This analysis indicates that the critical $d/D$ values for both type 1 and type 3 behaviours are notably influenced by the specific characteristics of each system and the transient event. Note that the definitions used herein for type 1 and type 3 behaviours differ from those used in Zhou et al. (2019) [39] and Zhou et al. (2020) [3]. While not necessarily indicating a direct cause-and-effect relationship, similar to the current study, the experiments carried out by Zhou et al. (2019) [39] involved significantly reduced air fractions. Additionally, when compared to a horizontal filling procedure as examined in Zhou et al. (2020) [3], vertical filling procedures and the air expulsion stage with inclined pipe segments connected to the air valve are expected to exhibit a more predictable air–water interface behaviour.

7.4. Additional Intervening Parameters

The main set of numerical simulations considers $v_0=1.5$ m/s, $\Delta Z=50$ m, $a=1000$ m/s, and $C=130$. However, such parameters themselves have an effect on the ${\overline{H}}_{\max }$ versus $d/D$ results. Such an effect is explored in Figure 24. The transient magnitude, especially for type 3 behaviour, is shown to increase with $v_0$, $\Delta Z$, a, and C. It should be borne in mind that C is a conductance, so that increases in C correspond to decreased friction. In relation to $v_0$ and a, indeed, in the Joukowsky equation, the transient magnitude is proportional to the velocity variation that causes the transient and to a. In relation to $\Delta Z$, having a downstream reservoir at a higher elevation, while maintaining the water discharge, means that the necessary head at the upstream section of the pipeline must be increased. In relation to C, it is worth noting that the attenuation of the transient during the pump trip scenario can be due to the air cushioning effect (for small $d/D$ values) or due to friction (for any outflow orifice size). In scenarios with a high-outflow-capacity air valve, the transient attenuation is primarily due to friction. As the air admission and expulsion stages proceed, there is water movement in both the upstream and downstream branches. Such movement results in energy losses due to friction. Such energy dissipation in a system with water column separation due to air admission by an air valve has been investigated by Ramezani and Karney (2017) [10].

In Figure 25, logistic curves have been fitted to the ${\overline{H}}_{\max }$ versus $d/D$ data shown in Figure 24. Notably, Figure 25a shows larger $d_{c3}/D$ values for larger $v_0$ values—from 0.075 (for $v_0=0.5$ m/s) to 0.102 (for $v_0=2.0$ m/s). Similarly, in Figure 25d, $d_{c3}/D$ ranges from 0.082 (for $C=90$) to 0.091 (for $C=150$). Figure 24 and Figure 25 demonstrate that the patterns observed in the results from the main set of numerical simulations are also present in a broader spectrum of system configurations. Moreover, the outcomes of the current study corroborate and supplement the prior findings reported in Tasca et al. (2022) [11] and in Tasca et al. (2021) [14].

7.5. Non-Slam Air Valves

To implement in practice the concept of enabling unrestricted inflow while restricting outflow, a non-slam air valve can be employed. A typical non-slam air valve contains two floats, which do not hinder air inflow. With the air valve under a reduced positive head, they do not obstruct the air flow through the large orifice of the valve. However, if this positive head exceeds the transition head, the upper float closes, permitting air flow only through a small orifice. Both floats move to the closing position when the water reaches the valve, effectively sealing it. The main design parameters of a non-slam air valve are the diameter of the inflow orifice, the diameter of the large outflow orifice, the diameter of the small outflow orifice, and the transition head. Schematics of non-slam air valves can be found in Tran (2017) [40] and Li et al. (2022) [18].

Figure 26 shows the transient response of a pipeline with a non-slam air valve during the pump trip scenario. The inflow orifice ratio is set as $d_{\mathrm{in}}/D=0.20$. The small outflow orifice ratio is set as $d/D=0.04$, which is an orifice ratio found to be effective for transient attenuation. Figure 26 assesses the influence of the following parameters on the transient response: transition head ($\Delta H_{\mathrm{transition}}$), which is the threshold head for transitioning from the large outflow orifice to the small outflow orifice; large outflow orifice ratio ($d_{\mathrm{large}}/D$); and air valve elevation (h). The $\Delta H_{\mathrm{transition}}$ values considered in this figure are in line with typical values found in product catalogues.

As shown in Figure 26, in general, as $d_{\mathrm{large}}/D$ decreases, the behaviour of the non-slam air valve becomes more similar to that of the air valves with a single and small outflow orifice. This similarity becomes most pronounced when the $\Delta H_{\mathrm{transition}}$ value falls below a specific threshold for each $d_{\mathrm{large}}/D$ value. This $\Delta H_{\mathrm{transition}}$ threshold decreases as $d_{\mathrm{large}}/D$ increases. Figure 26 highlights the importance of carefully selecting both $d_{\mathrm{large}}/D$ and $\Delta H_{\mathrm{transition}}$. In this sense, inadequate selection of these parameters may render the non-slam air valve ineffective in mitigating transients. This can happen if $d_{\mathrm{large}}/D$ is oversized so that $\Delta H_{\mathrm{transition}}$ is never reached, or if $\Delta H_{\mathrm{transition}}$ is too large for a given $d_{\mathrm{large}}/D$ value.

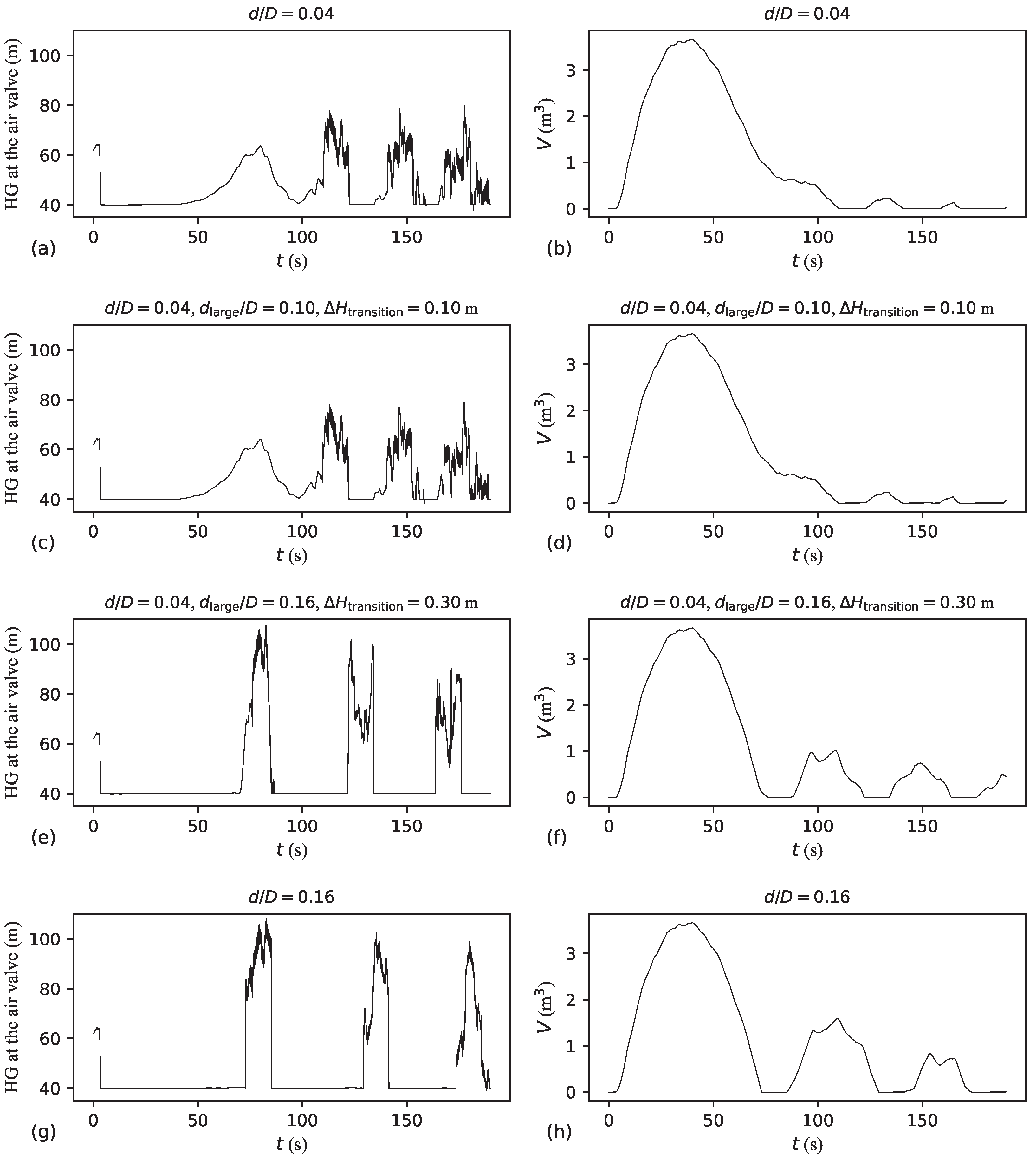
Figure 27 shows the evolution of both the HG at the air valve and the air pocket volume across four distinct situations: air valve with a single and small outflow orifice (Figure 27a,b), effective non-slam air valve (Figure 27c,d), ineffective non-slam air valve (Figure 27e,f), and air valve with a single and large outflow orifice (Figure 27g,h). For the non-slam air valve with $d_{\mathrm{large}}/D=0.10$ and $\Delta H_{\mathrm{transition}}=0.10$ m (Figure 27c,d), the transient response is similar to the case with the air valve with a single and small outflow orifice (Figure 27a,b). However, for the non-slam air valve with $d_{\mathrm{large}}/D=0.16$ and $\Delta H_{\mathrm{transition}}=0.30$ m (Figure 27e,f), the air valve fails to attenuate the transient event. In fact, the transient response for the case with the air valve with a single and large outflow orifice (Figure 27g,h) is similar to the case with the ineffective non-slam air valve (Figure 27e,f). Notably, having a small $\Delta H_{\mathrm{transition}}$ value or a small $d_{\mathrm{large}}/D$ value might render the air valve unsuitable for pipeline filling, which usually requires a high air exhaust rate.

8. Conclusions

As future conditions can never be perfectly anticipated, and real-world systems invariably deviate from numerical idealisations, it becomes crucial for design and operational engineers to gauge the potential impact of real-world variability in system parameters on anticipated system performance. This paper seeks to at least partially address this concern, aiming to comprehend through extensive simulations coupled with a physical understanding how design choices and system variations can influence the critical transient pressures. Specifically, this paper considers a key transient event, namely, the pump trip event, but also extracts a number of insights relative to pipeline filling and draining. But significantly, the sensitivity of the system’s transient response to varying conditions is shown to be remarkably diverse, demonstrating strong reactivity to changes in some cases with noticeable insensitivity in others.

In practice, the uses and specifications of air valves are vexing and problematic to many system designers and operators. This is because their behaviour is highly non-linear, sometimes showing high sensitivity to assumed conditions and sometimes displaying robust and stable results. This is at least partly because anything involving two phases is likely to be complex, but also because there is such a vast number of interacting components, including the many characteristics of the system (length, location, friction, initial state, pumping configuration), the specifics of the air valve (the absolute and relative sizes of both its admission and discharge orifices, its vertical and horizontal position, whether or not it possesses slow closing features, etc.) and of the transient itself (in this case, power failure). This work attempts the most comprehensive characterisation to date of the anticipated response of a realistic set of systems to a vast combination of characteristics. The immediate goal is to provide a systematic exploration and elucidation of the likely variation in transient response associated with a wide range of system and valve attributes. The long-term goal is to provide system owners, operators, designers, and managers a better understanding of air–system interactions so they can make better choices. This better understanding provides design engineers with a much clearer idea of what and where variations are likely to matter, and which ones do not.

Following pump trip, four stages constitute and complete a water hammer cycle: depressurisation, air admission, air expulsion, and the creation of a secondary wave. While most of the minimum hydraulic grade line (HGL) is formed during the initial two stages, the maximum HGL is often only completed after the first instance of air pocket collapse. But a key point is that each stage tends to be sensitive to different system attributes. So, for example, the smallest pipeline lengths experiencing negative pressures (i.e., smallest $L_s$ values) are associated with small $L_1$ values but with large h values. $L_s$ is found to be only slightly sensitive to $d/D$ (ratio between the outflow orifice of the air valve and the pipe diameter). Especially for large h values, there is a tendency of having smaller $L_s$ values for smaller $d/D$ values. Moreover, if the air valve is located closer to the upstream reservoir rather than farther downstream, there is a tendency to observe milder transient magnitudes for higher h values.

Three main transient behaviours have been identified: attenuated (type 1 behaviour) for small $d/D$ values, intermediate (type 2 behaviour) for moderate $d/D$ values, and water-hammer-dominated (type 3 behaviour), which typically occurs for large $d/D$ values. For type 1 behaviour, the head evolution at the air valve includes at least one instance of smooth head-versus-time variation with substantial compression of the air pocket prior to its collapse. However, for type 3 behaviour, the pressure level at the air valve remains close to the atmospheric pressure while there is still trapped air within the pipeline, i.e., there is no substantial compression of the air pocket prior to its collapse. For small $d/D$ values, prior to air pocket collapse, the transient oscillation period at the air valve decreases as $d/D$ increases. For large $d/D$ values, however, the transient oscillation, which encompasses sequential instances of air pocket admission and collapse, becomes independent of $d/D$. Importantly, in cases exhibiting type 1 behaviour, the increase in head at the air valve immediately after the collapse of the air pocket is significantly reduced compared to cases exhibiting type 3 behaviour.

For type 3 behaviour, there is a causal connection between the closure of the air valve and a subsequent pressure peak at the upstream section of the pipeline. Notably, the hydraulic head magnitude is consistently larger at the upstream section of the pipeline than at the air valve. In fact, the maximum HGL tends to be higher at locations closer to the upstream reservoir. During the transient event, the water velocity in the upstream branch of the pipeline ($v_{\mathrm{up}}$) varies around zero. In the downstream branch, though, the water velocity ($v_{\mathrm{ds}}$) progressively decreases until reaching a minimum negative value, i.e., until a maximum reverse flow is reached. The periodic $v_{\mathrm{ds}}$ changes every round trip in the downstream branch increase as h decreases. Because of this, as h increases, both the time required for reverse flow to occur and the time for air pocket collapse ($t_c$) increase. While the variation in $v_{\mathrm{ds}}$ follows a linear pattern for type 3 behaviour, the variation in $v_{\mathrm{ds}}$ for type 1 behaviour initially appears linear but transitions to a non-linear pattern during the air expulsion stage. This non-linearity occurs due to the air cushioning effect.

Regarding air pocket evolution, the water velocity variations in the upstream branch have a minimal influence, while the water velocity variations in the downstream branch have a substantial impact. In cases exhibiting type 1 behaviour, a single large air pocket typically forms within the pipeline. Conversely, in cases exhibiting type 3 behaviour, a series of air pockets forms sequentially, each with progressively smaller volumes. Maximum air pocket volume increases with h but decreases with $L_1$. The difference in maximum air pocket volume between the least favourable location for air pocket entrapment ($L_1=5000$ m and $h=20$) and the most favourable one ($L_1=1000$ m and $h=40$ m) is approximately 50 times.

The smallest $L_s$ values are found for type 1 behaviour, $L_1=1000$ m, and $h=40$ m. For type 1 behaviour, there is a tendency of having smaller $L_s$ values for larger h values. Nonetheless, in the current study, $L_s/L$ is always greater than 60%. In fact, in case the pipeline does not contain an air valve, the entire pipeline experiences negative pressures. For $L_1=1000$ m and $L_1=2000$ m, not having an air valve leads to more pronounced transient pressures compared to having an air valve, regardless of the value of $d/D$. In the transient magnitude versus $d/D$ data, for each air valve location, there is a lower left plateau (type 1 behaviour) and a higher right plateau (type 3 behaviour). Intermediate transient magnitudes correspond to type 2 behaviour. For example, for $L_1=3000$ m and $h=40$ m, the mean maximum transient head for type 1 behaviour is about 50 m, while for type 3 behaviour, it is about 100 m. Especially for small $L_1$ values, there is a tendency for the transient magnitude to be milder as h increases.

For each air valve location, $t_c$ increases exponentially as $d/D$ decreases but stabilises for large $d/D$ values. The collapse time of the air pocket is significantly affected by the location of the air valve. For example, for type 3 behaviour and $h=40$ m, $t_c=109$ s for $L_1=1000$ m, but $t_c=31$ s for $L_1=5000$ m. The timing of the maximum HG in the system ($t_{{\mathrm{HG}}_{\max }}$) can be divided into three groups: well before $t_c$ (typical of type 1 behaviour), right after $t_c$ (typical of type 3 behaviour), and well after $t_c$ (sometimes present for type 2 behaviour). Even when $t_{{\mathrm{HG}}_{\max }}$ occurs well after $t_c$, there is a pressure peak at the upstream section of the pipeline causally connected with the collapse of the air pocket. While the air pocket remains inside the pipeline, the frequency of the pressure oscillations at the upstream section of the pipeline increases as $L_1$ decreases. More specifically, the period of the pressure oscillations is given by $4L_1/a$.

Since the transient magnitude is determined during the air expulsion and secondary wave stages—with the air expulsion stage being a type of pipeline filling event—the comparison between the pump trip scenario and the filling scenario is meaningful. Previous studies concerning the filling scenario, which include a detailed assessment of transient magnitude in relation to aperture size for air exchanges, generally consider a system with a downstream end orifice instead of an air valve. For this reason, while the transient magnitude versus $d/D$ results in the current work resemble a logistic curve, the results found in the literature regarding the pipeline filling scenario with a downstream orifice resemble a skewed-to-the-right normal probability density function. If the system contains an air valve, no water is expelled through the air exchange aperture, in contrast to the case with an orifice. For each air valve location, fitting a logistic curve to the transient response data allows for defining the $d_{c1}/D$ and $d_{c3}/D$ values for the inception of type 1 and type 3 behaviours, respectively. For each air valve location, if $d/D<d_{c1}/D$, then type 1 behaviour occurs; if $d/D>d_{c3}/D$, then type 3 behaviour occurs; and if $d_{c1}/D<d/D<d_{c3}$, then type 2 behaviour occurs. For example, for $L_1=3000$ m, for the range of h values from 20 to 40 m, the $d_{c1}/D$ values range from 0.024 to 0.042, while the $d_{c3}/D$ values range from 0.064 to 0.092. The $d_{c1}/D$ and $d_{c3}/D$ values are dependent on the air valve location and the initial flow conditions.

The current study examines the impact of varying certain key initial parameters that are initially locked-in for the main set of numerical simulations. Such parameters are the initial steady water velocity ($v_0$), elevation difference between the downstream and upstream reservoirs ($\Delta Z$), wave speed (a), and friction coefficient (C). The influence of varying these parameters on the transient response is more evident in relation to type 3 behaviour compared to type 1 behaviour. Particularly in the case of type 3 behaviour, it is observed that ${\overline{H}}_{\max }$ increases with $v_0$, a, $\Delta Z$, and C. Of note, the same three transient behaviours found in the main set of transient simulations are also present when additional variations are considered for these initial parameters.

The current study assesses the impact of using a non-slam air valve with a single inflow orifice but two outflow orifices in comparison to an air valve with a single inflow orifice and a single outflow orifice. It is found that a well-sized non-slam air valve can mimic the behaviour of a large inflow orifice and small outflow orifice air valve during the pump trip scenario. For a non-slam air valve to be effective in mitigating the transient event, both the transition head ($\Delta H_{\mathrm{transition}}$) and the large outflow orifice ($d_{\mathrm{large}}/D$) should be sufficiently small. The transition head must be sufficiently small to enable the utilisation of the small outflow orifice for expulsion. It is found that the transition head threshold for ensuring the switching from the large outflow orifice to the small one during the transient event decreases as the size of the large outflow orifice increases.