Finite Volume Method for Transient Pipe Flow with an Air Cushion Surge Chamber Considering Unsteady Friction and Experimental Validation

Abstract

In various water transmission systems such as long-distance water transfer projects and hydropower stations, accurate simulation of water hammer is extremely important for safe and stable operation and the realization of intelligent operations. Previous water hammer calculations usually consider only steady-state friction, underestimating the decay of transient pressure. A second-order Finite Volume Method (FVM) considering the effect of unsteady friction factor is developed to simulate the water hammer and the dynamic behavior of air cushion surge chamber in a water pipeline system, while an experimental pipe system is conducted to validate the proposed numerical model. Two unsteady friction models, Brunone and TVB models, were incorporated into the water hammer equations, which are solved by the MUSCL–Hancock method. One virtual boundary method was proposed to realize the FVM simulation of Air Cushion Surge Chamber. Comparisons with water hammer experimental results show that, while the steady friction model only accurately predicts the first pressure peak, it seriously underestimates pressure attenuation in later stages. Incorporating an unsteady friction factor can better predict the entire pressure attenuation process; in particular, the TVB unsteady friction model more accurately reproduces the pressure peaks and the whole pressure oscillation periods. For water pipeline systems with an air cushion surge chamber, energy attenuation of the elastic pipe water hammer is primarily due to pipe friction and the air cushion. The experimental results with the air cushion surge chamber demonstrate that the proposed FVM model with the TVB unsteady friction model and the air chamber polytropic exponent near 1.0 can well reproduce the experimental pressure oscillations.

1. Introduction

Water hammer often occurs in various water pipe systems, including long-distance water transfer projects and hydropower stations. An abnormal pressure surge may lead to a pipe burst, so many water hammer protection measures are introduced to reduce the water hammer intensity. The air cushion surge chamber is a closed chamber that is partially filled with water and compressed air [1]. As compared to an open-type pressure regulating chamber, it is rarely restricted by geological or topographical features, and offers numerous advantages, such as shorter construction supply, lower excavation volume, cost-effectiveness, and minimal ecological impact [2]. The air cushion surge chamber is widely used in hydroelectric power plants for water hammer protection, ensuring the safe hydraulic operation of the water pipe system. In order to realize the safe and stable operation of water systems and the realization of intelligent operations, it is extremely important to accurately simulate the transient flow of pipe systems with an air cushion surge chamber.

The Method of Characteristics (MOC) is currently a widely used simulation tool for modeling the hydraulic transition process of hydroelectric power plants. However, there are some complicated situations, such as short pipes, T-junctions, and series pipes, in actual water delivery systems. When using MOC, interpolation or wave speed regulation is required, which reduces computational efficiency and accuracy and introduces computational errors. Moreover, most existing water hammer calculation models only adopt a steady friction model, implying that the friction inside the pipeline remains the same as the steady-state during the transient process. However, in actual transient processes, the friction inside the pipeline is influenced by multiple factors, leading to significantly different calculation results from the actual results. Additionally, they cannot accurately describe the waveform distortion and peak attenuation of pressure waves [3].

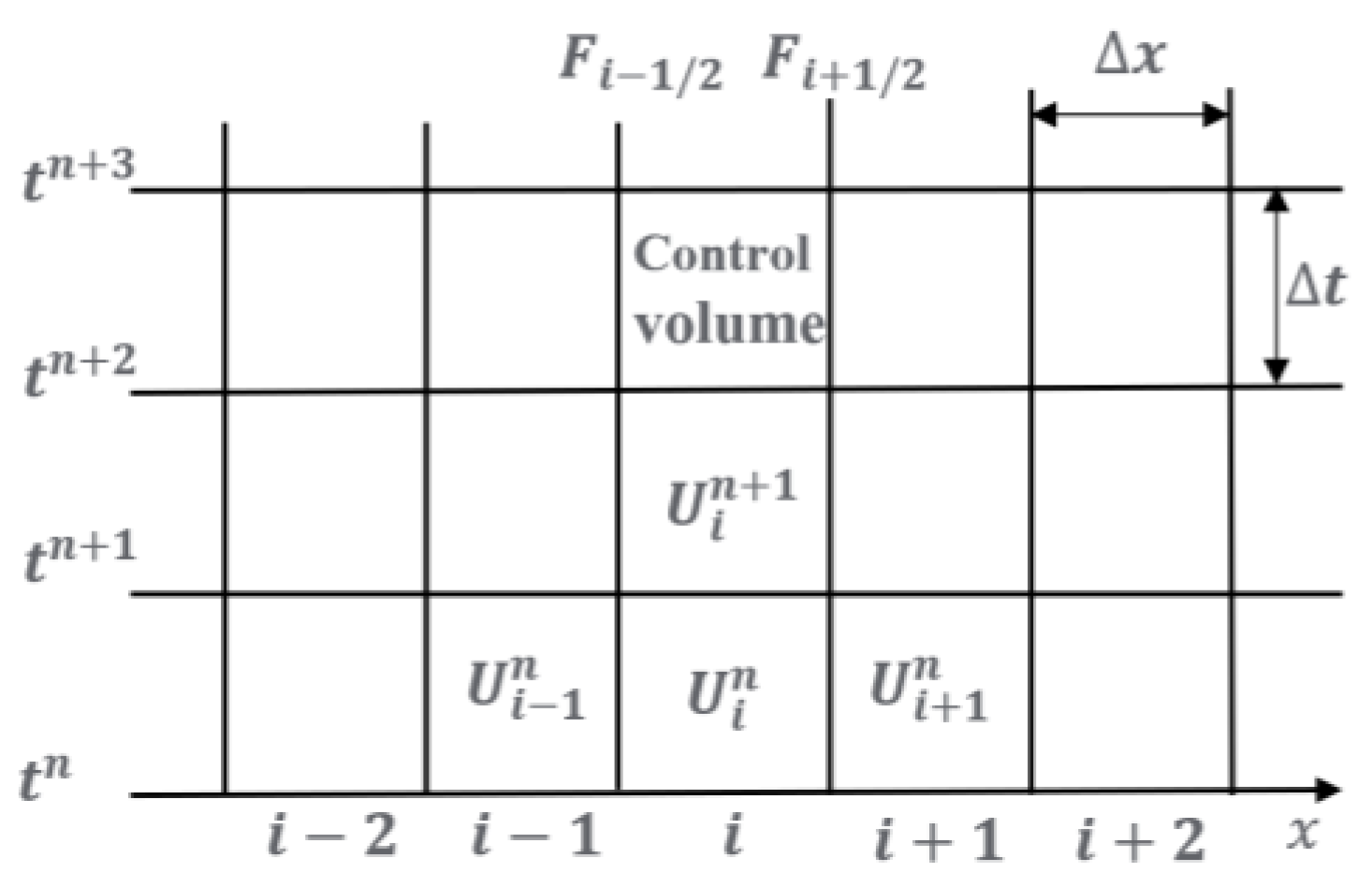
The FVM discretized the calculation area in the pipeline into independent control units, and solved the differential equations in each unit separately. Godunov et al. [4] proposed a numerical scheme for solving nonlinear Riemannian problems. This scheme is very suitable for approximating smooth solutions and discontinuous solutions. Therefore, in recent years, a large number of researchers have gradually begun to construct the Godunov scheme to solve the hydraulic transient water hammer problem.

Yazdi et al. [5] pointed out in 2007 that when calculating hydraulic transients, if the Courant number condition is not met, the second-order Godunov scheme is more stable than the MOC method. Bi Sheng et al. [6] adopted the Godunov scheme to solve the two-dimensional flow-transport equation. This model can simultaneously solve the water flux and transport flux, which is highly efficient for simulating the dynamic characteristics of water flow in complex terrain, and effectively eliminates problems such as excessive numerical damping and unstable oscillation caused by the convection term in numerical calculation. Zheng Jieheng et al. [7] used the Godunov scheme to study the hydraulic transients in sequential transmission pipelines. Based on the finite volume method, Zhao Yue et al. [8] proposed a treatment method with double virtual boundary to numerically simulate the phenomenon of water hammer and water column separation in pipelines. Zhou et al. [9,10,11] proposed a method to simulate a liquid column separation-bridging water hammer using a second-order GODUNOV scheme. Hu et al. [12] proposed the application of a second-order GODUNOV scheme to simulate non-pressurized flow.

Currently, there are two main unsteady friction models extensively utilized. These models are the weighted function model represented by the Zielke [13] and the empirical correction model represented by the Brunone [14]. According to the Zielke unsteady friction model, the instantaneous shear stress in the pipe due to transient flow is composed of a constant term and an additional term. The additional term uses the weighted function to account for the impact of historical velocity and acceleration on the current flow state. However, this method has a long calculation time and requires a large storage space. Subsequently, Zielke’s model was simplified by Trikha [15], Vardy [16], and other scholars, resulting in a weighted function class unsteady friction model with higher computational efficiency. The Brunone unsteady friction model links unsteady friction with instantaneous local acceleration and convective acceleration and proposes a new dynamic friction model. Vitkovsky [17] improved the Brunone model by predicting the direction of water flow and wave propagation, as well as the effects of specific acceleration and deceleration stages.

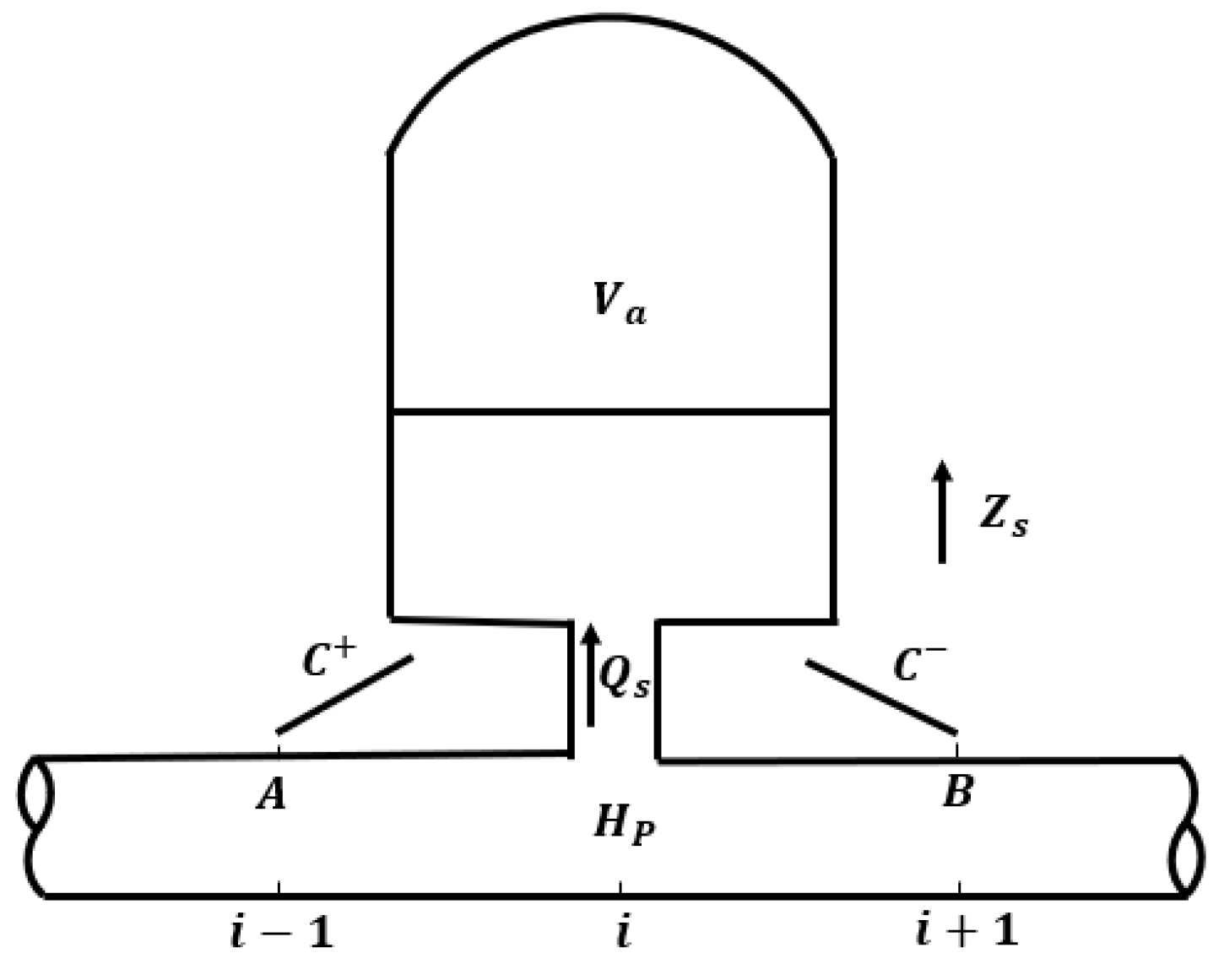
To simulate more accurately the hydraulic transient process of the pressurized delivery pipeline system with an air cushion surge chamber, this paper introduces the second-order Godunov format of FVM during the calculation process, incorporating the Trikha–Vardy–Brunone (TVB) and Brunone unsteady friction models. One virtual boundary method was proposed to realize the FVM simulation of an air cushion surge chamber. An experimental pipe system was designed and conducted to validate the proposed models in simulating the water hammer and dynamic behavior of an air cushion surge chamber.

The novelty of the paper is that a second-order FVM considering the effect of unsteady friction factor is developed to simulate the dynamic behavior of the air cushion surge chamber in a water pipeline system, while an experimental pipe system is conducted to validate the proposed numerical model. Pressure damping and energy dissipation of transient flow in a water pipeline system with air cushion surge chamber are carefully investigated and modeled, which have not been well considered in previous work.

2. Mathematical Models

2.1. Water Hammer Control Equations

Equations of motion and continuity for water hammer are [18]:

$$\mathrm{g}\frac{\partial H}{\partial x}+V\frac{\partial \mathrm{V}}{\partial \mathrm{x}}+\frac{\partial V}{\partial t}+\mathrm{g}(J_Q+J_u)=0$$

(1)

$$V\frac{\partial \mathrm{H}}{\partial \mathrm{x}}+\frac{\partial \mathrm{H}}{\partial \mathrm{t}}+\frac{a^2}{g}\frac{\partial V}{\partial x}=0$$

(2)

The matrix forms of the above two equations can be expressed as follows:

$$\frac{\partial \mathit{U}}{\partial t}+\mathit{A}\frac{\partial \mathit{U}}{\partial x}=\mathit{S}$$

(3)

where $\mathit{U}=\left(\genfrac{}{}{0pt}{}{H}{V}\right)$, $\mathit{A}=\left(\begin{array}{cc}V& a^2/g\\ g& V\end{array}\right)$, $\mathit{S}=\left(\genfrac{}{}{0pt}{}{0}{\mathit{g}{S}_0-J}\right)$, where: x is the distance along the pipe axis coordinate. H is the piezometric head; V is the flow velocity in the pipe; a is the wave velocity of the water hammer; D is the inner diameter of the pipe; J_Q and J_u represent steady friction and unsteady friction J_u; and t is time.

If V = 0, the convection term can be ignored and the classical water hammer governing equation can be changed.

$$\frac{\partial \mathit{U}}{\partial t}+\frac{\partial \mathit{F}}{\partial x}=\mathit{S}$$

(4)

where $\mathit{F}=\overline{\mathit{A}}\mathit{U}$, $\overline{\mathit{A}}=\left(\begin{array}{cc}0& a^2/g\\ g& 0\end{array}\right)$.

Brunone used instantaneous local acceleration and convective acceleration to represent the unsteady frictional component of dynamic frictional resistance, resulting in an empirically modified model. Based on Brunone’s work, Vitkovsky later added the identification of the flow direction of water and obtained an improved instantaneous acceleration model with higher calculation accuracy. The specific model forms are as follows:

$$J_u=\frac{k}{g}\left(\frac{\partial V}{\partial t}+a·\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(V\right)\left|\frac{\partial V}{\partial x}\right|\right)$$

(5)

in which the Brunone coefficient of friction $k=\sqrt{C^{*}}/2$; C* is the shear attenuation constant and the value depends on the Reynolds number. When the water flow in the pipe is laminar flow, C* = 0.00476; when the water flow in the pipe is turbulent flow,$C^{*}=7.41/\left[{Re}^{{\log }_{10}\left(14.3/{Re}^{0.05}\right)}\right]$. if V ≥ 0 then $\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(V\right)=1$; if V < 0 then $\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(V\right)=-1$.

The Zielke model simplified by Vardy and Brown (TVB model) is as follows

$$J_u=\frac{16v}{g{D}^2}\sum _{i=8}^1{\tau }_u$$

(6)

$$\begin{array}{cc}{\tau }_u\left(t+\mathsf{\Delta }t\right)=\frac{4\rho v}{D}& {\displaystyle \sum _{i=1}^N}[Y_{ai}\left(t\right)\mathit{exp}\left(-n_{i}v/R^2\mathsf{\Delta }t\right)\\ & +\frac{m_i{D}^2}{4n_{i}v\mathsf{\Delta }t}\left(1-\mathit{exp}\left(-n_{i}v/R^2\mathsf{\Delta }t\right)\right)\left(V(t+\mathsf{\Delta }t)-V\left(t\right)\right)]\end{array}$$

(7)

where τ_u is the unsteady shear stress; $\mathsf{\rho }$ is density of fluid; $\mathsf{\nu }$ is kinematic viscosity of the fluid; N is number of cells along the pipeline; Y_ai(t) is weighting function; and $\mathrm{R}$ is pipe radius; When the water flow in the pipe is laminar flow, the values of the weighted function coefficients n_i and m_i are shown below n_i {i = 1, ..., 8} = {26.3744; 10²; 10^2.5; 10³; 10⁴; 10⁵; 10⁶;10⁷} and m_i {i = 1, ..., 8} = {1; 2.1830; 2.7140; 7.5455; 39.0066; 106.8075; 359.0846; 1108.3666}.

When the water flow in the pipe is turbulent flow, the values of the weighted function coefficients n_i and m_i are shown below n_i^* ($n_i^{*}=n_i-B^{*}$) and m_i^* ($m_i^{*}=m_i/A^{*}$) n_i^*{ i = 1, ..., 13} = {10; 10^1.5; 10²; 10^2.5; 10³; 10^3.5; 10⁴; 10^4.5; 10⁵; 10^5.5; 10⁶; 10^6.5; 10⁷} and m_i^* { i = 1, ..., 13} = {9.06; −4.05; 12; 8.05; 22.7; 35.2; 65.9; 115; 206; 363; 664; 1070; 2620}.

The computational domain is discretized along both the x-axis and t-axis using the finite volume method. This results in the formation of multiple computational control volumes or cells, as shown in Figure 1. Calculations are then performed on these volumes.

Integrate Equation (4) from the control surface i − 1/2 to control surface i + 1/2. Additionally, since the control variable uniformly and continuously changes, substitute ${\mathbf{U}}_{\mathbf{i}}=\frac{1}{\mathsf{\Delta }x}{\int }_{i-1/2}^{i+1/2}udx$ to obtain the integration expression for control variable U:

$${\mathbf{U}}_i^{n+1}={\mathbf{U}}_i^n-\frac{∆t}{∆x}\left({\mathit{F}}_{\mathit{i}+\frac{1}{2}}-{\mathit{F}}_{\mathit{i}-\frac{1}{2}}\right)+\frac{∆t}{∆x}{\int }_{i-1/2}^{i+1/2}\mathbf{s}dx$$

(8)

where: F_i+1/2 and F_i−1/2 are the fluxes at i + 1/2 and i − 1/2, respectively; Δt is the time step; Δx is the length of control volume; the superscript n denotes the current time step; and n + 1 denotes the subsequent time step.

2.2. Control Equations of Air Cushion Surge Chamber

The continuity equation for node P at the bottom of the surge chamber is [18]

$$Q_T=Q+Q_S$$

(9)

where Q_T is the flow rate at the upstream pipe outlet of the surge chamber; Q is the flow rate of the downstream pipeline inlet; and Q_S is the flow into or out of the surge chamber (Figure 2).

In order to determine the pressure tube head at the bottom point P of the surge chamber, it is necessary to use the feature compatibility equation of the last calculation section of the upstream pipeline and the first calculation section of the downstream pipeline in the surge chamber.

$$C^{+}:H_P=C_P-B_P{Q}_T$$

(10)

$$C^{-}:H_P=C_M+B_M\mathrm{Q}$$

(11)

where H_p is the piezometric head at the bottom of air cushion surge chamber.

Equations (10) and (11) are substituted into continuity Equation (9) at point P, and the variables Q_T and Q are eliminated

$$\left.\genfrac{}{}{0pt}{}{H_P=C_2-C_1{Q}_s}{C_1=\frac{1}{\frac{1}{B_{P1}}+\frac{1}{B_{M2}}};C_2=C_1\left(\frac{C_{P1}}{B_{P1}}+\frac{C_{M2}}{B_{M2}}\right)}\right\}$$

(12)

where C_P1, B_P1, C_M2, and B_M2 are known variables at time t.

$$C_{P1}=H_{i-1}+B{Q}_{i-1}$$

(13)

$$C_{M2}=H_{i+1}-B{Q}_{i+1}$$

(14)

$$B_{P1}=B+R\left|Q_{i-1}\right|$$

(15)

$$B_{M2}=B+R\left|Q_{i+1}\right|$$

(16)

in which B is a function of the physical properties of the fluid and the pipeline, often called the pipeline characteristic impedance, and B = a/gA; R is the pipeline resistance coefficient R = f∆x/(2gDA²); f is the Darcy–Weisbach friction factor; D is pipe diameter; and A is the cross-section area.

Neglecting the water flow inertia and frictional head loss in the air cushion surge chamber, a relationship can be found between the pressure at the center point of the bottom and the water level in the air cushion surge chamber:

$$H_a=H_P-Z_s+H_{atm}-\left(R_S+\frac{1}{2\mathrm{g}{A}_S^2}\right)\left|Q_S\right|Q_S$$

(17)

where H_a is the absolute head equal to the gauge plus barometric pressure heads; Z_s is the elevation of the air–water interface in air chamber; H_atm is the absolute barometric pressure head; R_s is the head loss coefficient of the impedance hole of the air chamber; and A_s is the cross-section area of the air chamber.

The air was assumed to follow the reversible polytropic relation [18]

$$P{V}_a^n=P_0{V}_0^n=Constant$$

(18)

where V_a is the volume of the air within the air chamber, and n is the polytropic exponent.

After combining Equations (12)–(18), the flow rate, pressure head, and water level at the air chamber can be obtained.

3. Second order Godunov Solution Scheme

3.1. Computation of Flux Term

The Riemann problem-solving method can be applied to obtain the flux values at the i + 1/2 and i + 1/2 boundary interfaces. The average value of the control variable U on the left side of the i + 1/2 interface is represented by ${\mathbf{U}}_L^n$, and the average value of the control variable U on the right side of the i + 1/2 interface is represented by ${\mathbf{U}}_R^n$.

$$U_x^n=\left\{\begin{array}{c}{U}_L^n x<x_{i+1/2}\\ U_R^n x>x_{i+1/2}\end{array}\right.$$

(19)

The flux values at i + 1/2 can be calculated by:

$${\mathit{F}}_{i+1/2}={\overline{\mathbf{A}}}_{i+1/2}{\mathit{u}}_{i+1/2}=\frac{1}{2}{\overline{\mathbf{A}}}_{i+1/2}\left\{\left(\begin{array}{cc}1& a/g\\ g/a& 1\end{array}\right){\mathbf{U}}_L^n-\left(\begin{array}{cc}-1& a/g\\ g/a& -1\end{array}\right){\mathbf{U}}_R^n\right\}$$

(20)

The MUSCL-Hancock method for second-order linear reconstruction is used to realize the second-order accuracy of computation results.

First step: Data Reconstruction.

$$U_{i,L}=U_{i,n}-0.5∆x\mathrm{M}\mathrm{I}\mathrm{N}\mathrm{M}\mathrm{O}\mathrm{D}\left({\sigma }_i^n,{\sigma }_{i-1}^n\right)$$

(21)

$$U_{i,R}=U_{i,n}-0.5∆x\mathrm{M}\mathrm{I}\mathrm{N}\mathrm{M}\mathrm{O}\mathrm{D}\left({\sigma }_i^n,{\sigma }_{i-1}^n\right)$$

(22)

Second step: Advance time calculation

$${\overline{\mathit{U}}}_i^L={\mathit{U}}_i^L+\frac{1}{2}\frac{∆t}{∆x}\left(\overline{\mathit{A}}{\mathit{U}}_i^L-\overline{\mathit{A}}{\mathit{U}}_i^R\right)$$

(23)

$${\overline{\mathit{U}}}_i^R={\mathit{U}}_i^R+\frac{1}{2}\frac{∆t}{∆x}\left(\overline{\mathit{A}}{\mathit{U}}_i^L-\overline{\mathit{A}}{\mathit{U}}_i^R\right)$$

(24)

Third step: Solve the Riemann problem. To compute intercell flux f_i+1/2, the conventional Riemann problem with data can be calculated by

$${\mathbf{U}}_L^n\equiv {\overline{\mathbf{U}}}_i^R,{\mathbf{U}}_R^n\equiv {\overline{\mathbf{U}}}_{i+1}^L$$

(25)

By inserting the solved Equations (24) and (25) into the Equation (20), the fluxes in the second-order Godunov scheme at the boundary of each element can be obtained.

3.2. Time Integral

To advance the solution of the Godunov flux calculation at the n + 1 time step with second-order accuracy, time integration of Equation (8) is necessary. In the absence of friction, the following formula can be derived:

$${\mathit{U}}_i^{n+1}={\mathit{U}}_i^n-\frac{\mathsf{\Delta }t}{\mathsf{\Delta }x}\left({\mathit{F}}_{i+(1/2)}^n-{\mathit{F}}_{i-(1/2)}^n\right)$$

(26)

The second-order Runge–Kutta method is used to obtain explicit results with a second-order calculation accuracy when pipe friction is taken into account. The specific calculation process is shown as follows:

First step:

$${\overline{\mathit{U}}}_i^{n+1}={\mathit{U}}_i^n-\frac{\mathsf{\Delta }t}{\mathsf{\Delta }x}\left({\mathbf{f}}_{i+(1/2)}^n-{\mathbf{f}}_{i-(1/2)}^n\right)$$

(27)

Second step:

$${\stackrel{̿}{\mathit{U}}}_i^{n+1}={\overline{\mathit{U}}}_i^{n+1}+\frac{\mathsf{\Delta }t}{2}\mathit{S}\left({\overline{\mathit{U}}}_i^{n+1}\right)$$

(28)

Last step:

$${\mathit{U}}_i^{n+1}={\overline{\mathit{U}}}_i^{n+1}+\mathsf{\Delta }t\mathit{S}\left({\stackrel{̿}{\mathit{U}}}_i^{n+1}\right)$$

(29)

3.3. Boundary Condition

The virtual boundary method is used to process the boundary. To implement this method, virtual cells numbered 0, −1, N + 1, and N + 2 are added to the upstream and downstream boundaries, respectively. The condition that the upstream boundary is and the downstream boundary is $U_{-1}=U_0=U_{1/2},U_{N+1}=U_{N+2}=U_{N+1/2}$ enable the determination of the flux value at the boundary using the Riemann invariant equation. Solving the Riemann invariant equation at the upstream boundary of the reservoir yields [10]:

$$H_{1/2}-\frac{a}{\mathrm{g}}{V}_{1/2}=H_1^n-\frac{a}{\mathrm{g}}{V}_1^n$$

(30)

where $V_1^n$ and $H_1^n$ are the velocity and pressure head of the first control volume, and V_1/2 and H_1/2 are the velocity and pressure head at 1/2 interface at the upstream boundary.

Solving the Riemann invariant equation at the upstream boundary of the reservoir yields [10]:

$$H_N^n+\frac{a}{\mathrm{g}}{V}_N^n=H_{N+1/2}+\frac{a}{\mathrm{g}}{V}_{N+1/2}$$

(31)

where $V_N^n$ and $H_N^n$ are the velocity and pressure head of the last control volume, and $V_{N+1/2}$ and $H_{N+1/2}$ are the velocity and pressure head at N + 1/2 interface at the downstream boundary.

The physical variable values at each transient moment of the air cushion surge chamber can be determined by calculating the physical variable values of the virtual units at the upstream and downstream sides of the chamber based on the control equation. Thus, in combination with the Riemann invariant equation, C_P1, B_P1, C_M2, and B_M2 are known variables at time t, which can conclude that:

$$C_{P1}=H_{Nu}^n+\frac{a}{\mathrm{g}}{V}_{Nu}^n$$

(32)

$$B_{P1}=\frac{a}{\mathrm{g}{A}_1}$$

(33)

$$C_{M2}=H_{1d}^n+\frac{a}{\mathrm{g}}{V}_{1d}^n$$

(34)

$$B_{M2}=\frac{a}{\mathrm{g}{A}_2}$$

(35)

where $V_{Nu}^n$ and $H_{Nu}^n$ represent the flow rate and the water head of the last control domain of the air cushion surge chamber on the upstream side pipeline, while $V_{1d}^n$ and $H_{1d}^n$, respectively, represent the flow rate and water head of the first control domain of the air cushion surge chamber on the downstream side pipeline. A₁ and A₂ are the pipe cross-section areas at the upstream and downstream of the air chamber.

By substituting Equations (32)–(35) into Equation (8), the relation between the water level in the piezometric head at the bottom of the air cushion surge chamber and the flow rate into the air cushion surge chamber under virtual boundary conditions can be solved.

4. Results and Discussion

4.1. Experimental Setup

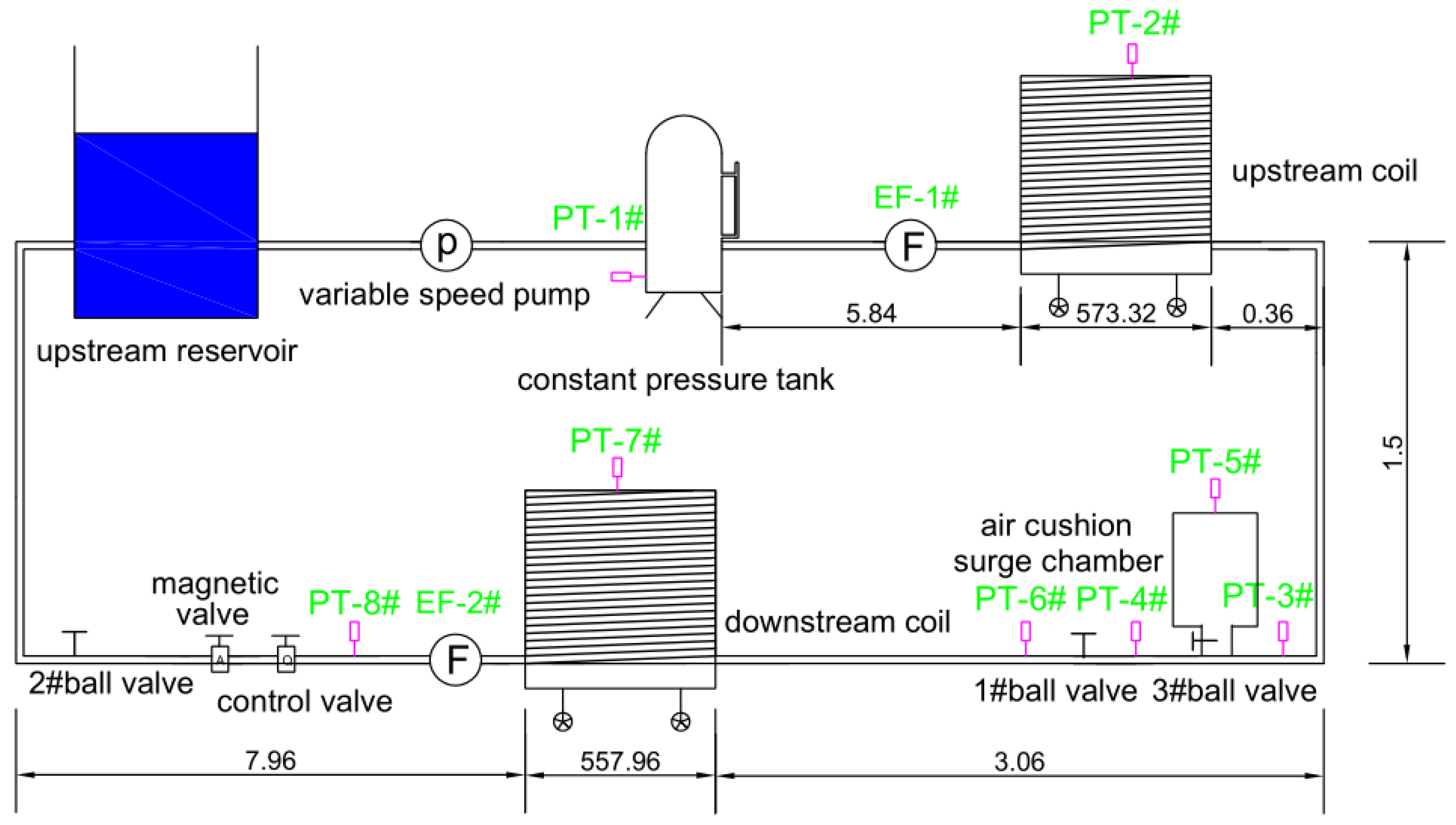
An experimental pipe system was designed and conducted to validate the proposed models in simulating the water hammer and dynamic behavior of the air cushion surge chamber. Figure 3 displays the experimental setup. The system consists of an upstream reservoir, variable frequency pump, constant pressure tank, upstream pipe, upstream electromagnetic flowmeter, and 1# ball valve. After the 1# ball valve, the pipeline serves as a return pipe. The water hammer experimental pipeline is 582 m long and is made of copper tubes, which have a wall thickness of 2 mm and an inner diameter of 21 mm. Along the pipeline, one 1/4 ball valve (1# ball valve) is arranged at the end, which is 582 m away from the upstream constant pressure tank. Additionally, five pressure sensors have been installed on the pipeline, with PT-1# measuring the pressure at the bottom of the constant pressure tank, PT-2# measuring 270 m downstream, PT-3# measuring 581.22 m downstream, PT-4# measuring 581.82 m downstream of the constant pressure tank, and PT-5# installed on the top of the air cushion surge chamber and used to measure the pressure of the gas in the gas chamber.

4.2. Water Hammer Problem in a Simple Reservoir–Pipe–Valve System

Four experimental conditions were conducted. The relevant parameters are shown in

Table 1. Water hammer case.

Case	V0 (m/s)	H0 (m)
1	0.08	31
2	0.08	57
3	0.27	31
4	0.27	57

. H₀ is constant pressure head in the upstream pressure tank.

Cases 1 and 2 exhibit laminar flow with Re = 1284, while cases 3 and 4 demonstrate low Reynolds number turbulence with Re = 4334.

The wave velocity of the water hammer in this experiment is calculated according to the experimental data measured by the pressure sensor. According to the pressure experimental data, the time difference between any two adjacent wave peaks is recorded as 2T, and then, according to the pipeline length L, water hammer wave a = 2L/T can be obtained. In addition, many factors can affect the water hammer wave velocity. In order to eliminate the interference, repeated tests were carried out on different experimental conditions and many times. Finally, the average value of multiple tests was taken as the value of the water hammer wave velocity in the subsequent numerical simulation. The wave velocity of the water hammer measured by the experiment is between 1260 m/s and 1360 m/s. In the numerical simulations, the wave speed is a = 1290 m/s and the experimentally observed range of the average resistance coefficient for the pipeline system under stable flow conditions is 0.0312~0.0356. Valve closing times ranged between 0.012 s and 0.026 s. The experimental results show that the valve closing time is much less than half of the pressure fluctuation period. Therefore, it is believed that the valve is closed instantaneously.

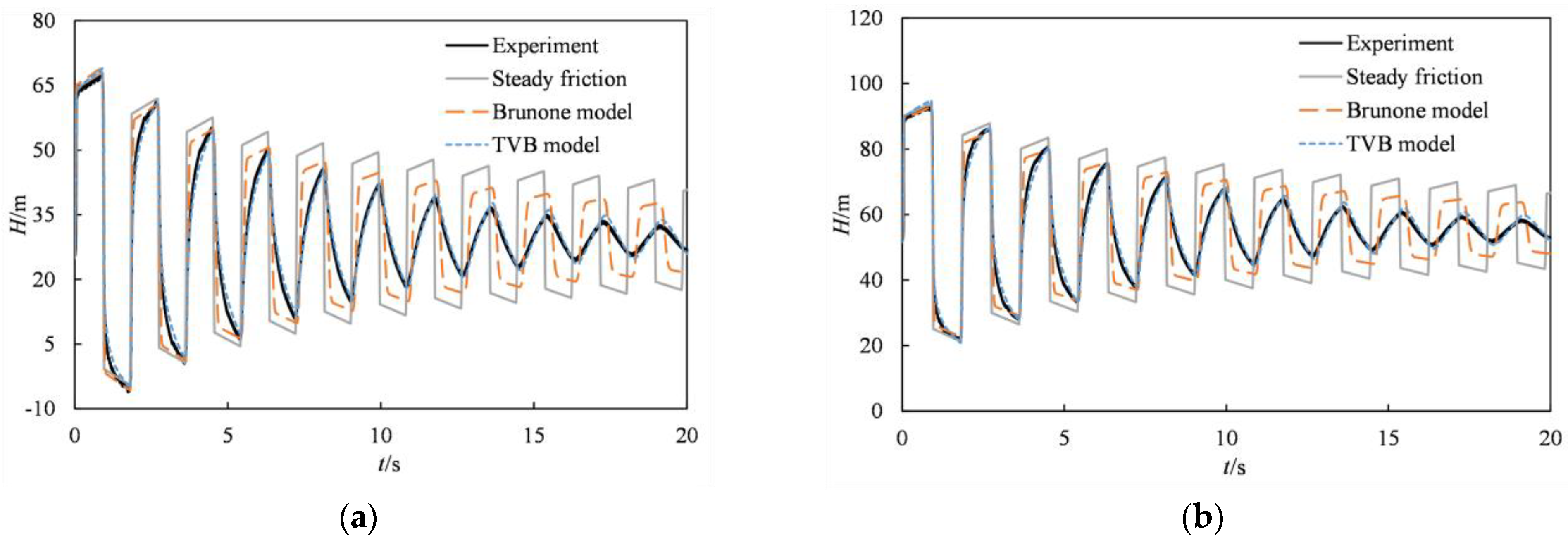
As shown in Figure 4, Cases 1 and 2 can produce a similar trend for experimental pressure oscillations, although with different reference values. This is because Cases 1 and 2 have the same Reynolds number Re = 1284, but different driving pressure heads (H₀ = 31 and 57). When the initial steady condition is under laminar flow in Case 1 and Case 2, the steady friction water hammer model can only accurately predict the first pressure peak, but fail to calculate well the subsequent pressure oscillations. The reason should be that, during the fast transient flow event, the pressure damping is mainly caused by the dynamic shear force near the pipe wall. However, the traditional water hammer model assumes that the dynamic shear force coefficient is constant. In order to verify this, the unsteady friction factor is considered in the water hammer events. Figure 4a,b show that, compared to the steady friction water hammer model, the TVB and Brunone unsteady friction models can provide the much better simulation results. Meanwhile, it can be found that the TVB model shows the highest consistency with experimental results, while the Brunone unsteady friction model still produces the differences in simulating the later pressure peaks and the pressure oscillations. The main reason is that, as described above, the Brunone unsteady friction model is an empirically modified model, and the TVB model is a mechanism model which is derived from the physical equations.

Figure 5 shows the calculated and experimental results under the turbulence flow condition in Case 3 and Case 4. Cases 3 and 4 still produce a similar trend for experimental pressure oscillations, although with reference values. Similar to laminar flow cases, the comparisons still demonstrate that, under turbulence flow condition, the steady friction model can accurately predict only the first pressure peak, and significantly underestimates the pressure damping in the later pressure oscillations. In contrast to the steady friction model, the TVB and Brunone unsteady friction models can accurately predict the entire pressure attenuation process. Among these models, the TVB model can most accurately reproduce the experimental results.

It can also be found from Figure 4 and Figure 5 that, as the Reynolds number increases, the steady friction water hammer model can give better simulation results.

Overall, the TVB model can accurately reproduce the experimental results, regardless of the presence of laminar or turbulent flow, and is recommended to simulate the water hammer events.

4.3. Water Hammer Problem with Air Cushion Surge Chamber

Figure 1 demonstrates that, by opening ball valve #3 on the connection pipe of the air cushion surge chamber, the experimental device transforms into a pressurized pipeline water supply system equipped with an air cushion surge chamber. Furthermore, a pressure sensor PT-5# is placed on top of the air cushion chamber to monitor the gaseous pressure inside it, and the steady-state gas pressure of the cushion surge chamber is also measured by this pressure sensor. The velocity of pressure wave in the air cushion surge chamber experiment is consistent with that of the above water hammer experiment without air cushion surge chamber, i.e., the wave speed is a = 1290 m/s.

Table 2. Air cushion surge chamber case.

Case	V0 (m/s)	H0 (m)	Gas Volume (mL)
1	0.27	31	475 mL
2	0.08	43	275 mL
3	0.20	57	775 mL

presents the experimental conditions of the air cushion surge chamber.

The gas polytropic index, n, is varied to 1.0, 1.2 and 1.4, where n = 1.0 corresponds to an isothermal process, n = 1.4 corresponds to an adiabatic process, and n = 1.2 for the two in between, respectively, and the simulation results are depicted in Figure 6.

Figure 6a,b display the results calculated by steady friction model and experimental results in Case 1 (laminar flow) and Case 3 (turbulent flow). Results show that a value of n = 1.0 can simulate the pressure transient process of the gas in its first cycle more effectively than n = 1.2 and n = 1.4, although it still does not reproduce well the subsequent pressure oscillations.

Compared to n = 1.2 and n = 1.4, why is the result of n = 1.0 closer to the experimental data? The main reasons are: (1) during the transient flow, air in the chamber experiences an expansion and deceleration process, which involves complicated heat transfer and thermodynamics; (2) in the existing numerical models, the air was assumed to follow the reversible polytropic relation [18]; (3) the gas polytropic index, n, is varied to 1.0, 1.2 and 1.4, where n = 1.0 corresponds to an isothermal process, n = 1.4 corresponds to an adiabatic process, and n = 1.2 for middle process; (3) in this work, the heat transfer is serious, which makes the thermal process close to the isothermal process (n = 1.0).

Meanwhile, why, even for n = 1.0, do the calculated pressure oscillations attenuate lower than the measured ones? The reasons are that: (1) in the transient event in this work, the pressure damping (namely energy dissipation) is attributed to two aspects, in which one is energy loss due to heat transfer during air compression and expansion of air chamber, and another is hydraulic loss caused by the pipe friction; (2) results in Figure 6 only consider the effect of the steady friction factor, neglecting the effect of unsteady friction.

Therefore, in the following section, the effect of unsteady friction will be included in the numerical simulation to enhance the numerical accuracy, as well as to verify the above explanation.

Figure 7 gives the results calculated by numerical models (steady and unsteady friction water hammer model) and experimental results in Case 1 (laminar flow) and Case 3 (turbulent flow). According to Section 4.2, the TVB unsteady friction model performs better simulations for water hammer pressure of the pipeline in this experimental system. Therefore, the TVB unsteady friction model is adopted for this section. Additionally, examination of the simulation results from steady friction models indicated that n = 1.0 provides the optimal simulation effect. Consequently, when using unsteady friction simulation, n is set to 1.0.

As shown in Figure 7, the results of Case 1 (laminar flow) and Case 3 (turbulent flow) both show that introduction of the unsteady friction model causes the first peak pressure to slightly increase, compared to the steady friction model. This is because air in the chamber experiences an expansion and deceleration process when the valve is quickly closed, and the unsteady friction model suppresses its deceleration, which results in the first pressure peak value increasing. However, in comparison to the steady friction model, the peak and cycle of the first period align more closely with experimental data. The peak value and cycle of the pressure decay process also exhibits better agreement with experimental data, indicating that the use of the unsteady friction model can more accurately simulate the hydraulic transient process of the pressurized pipeline water supply system. The difference between the peak pressure of the numerical simulation and the experimental results becomes larger, which is caused by the absence of wall heat exchange in the mathematical model. In future work, we will also take into account the energy loss caused by the heat exchange of the tube wall.

5. Conclusions

A second-order FVM considering the effect of unsteady friction factor is developed to simulate the water hammer and the dynamic behavior of air cushion surge chamber in a water pipeline system, while an experimental pipe system is conducted to validate the proposed numerical model. Two unsteady friction models, Brunone and TVB models, were incorporated into the water hammer equations, and the virtual boundary method was proposed to realize the FVM simulation of the air cushion surge chamber.

Comparisons with water hammer experimental results show that, while the steady friction model only accurately predicts the first pressure peak, it seriously underestimates pressure attenuation in later stages. Incorporating the unsteady friction factor can better predict the entire pressure attenuation process; in particular, the TVB unsteady friction model more accurately reproduces the pressure peaks and the whole pressure oscillation periods.

For water pipeline systems with an air cushion surge chamber, energy attenuation of the elastic pipe water hammer is primarily due to pipe friction and air cushion. The experimental results for the air cushion surge chamber demonstrate that the proposed FVM model with TVB unsteady friction model and the air chamber polytropic exponent near 1.0 can well reproduce the experimental pressure oscillations.

However, the difference between the peak pressures of the numerical simulation and the experimental results becomes larger, which is caused by the absence of wall heat exchange in the mathematical model. In the future, we will also take into account the energy loss caused by the heat exchange of the tube wall.