Spatially Consistent Drought Hazard Modeling Approach Applied to West Africa
Abstract
1. Introduction
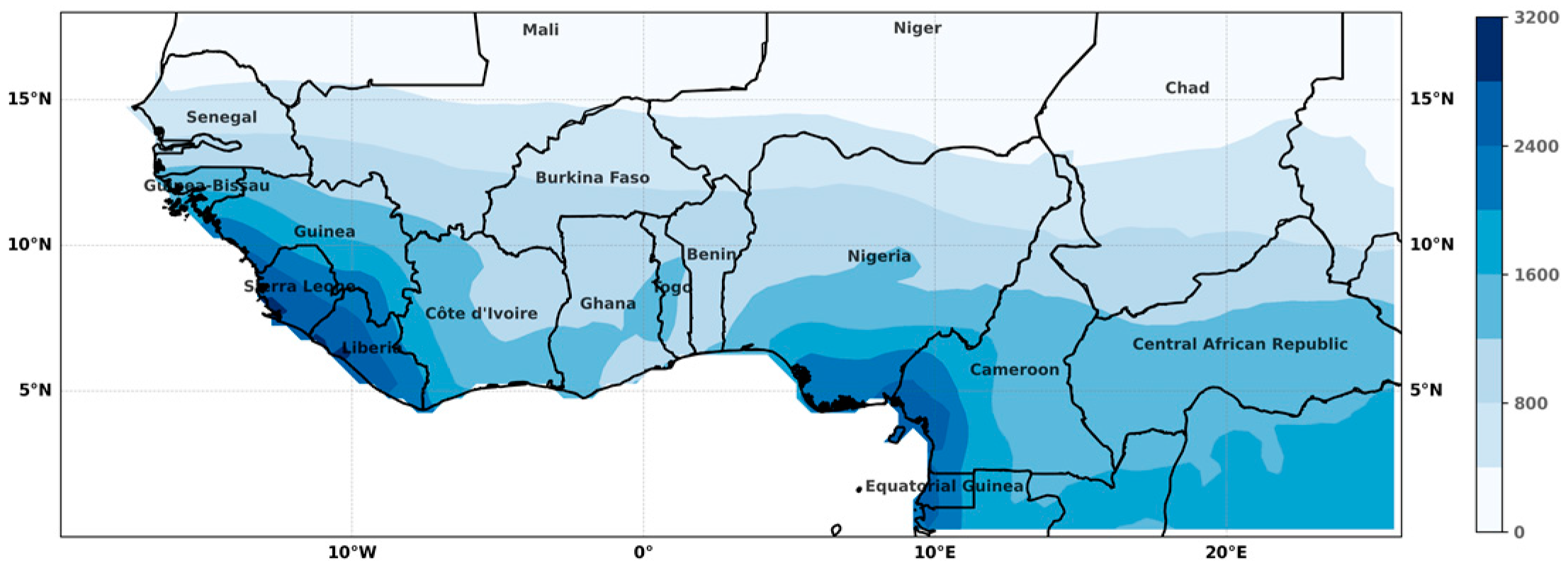
2. Data and Study Area
3. The Extreme Value Mixture Model
4. Results
4.1. Main Results from the Mixture Model
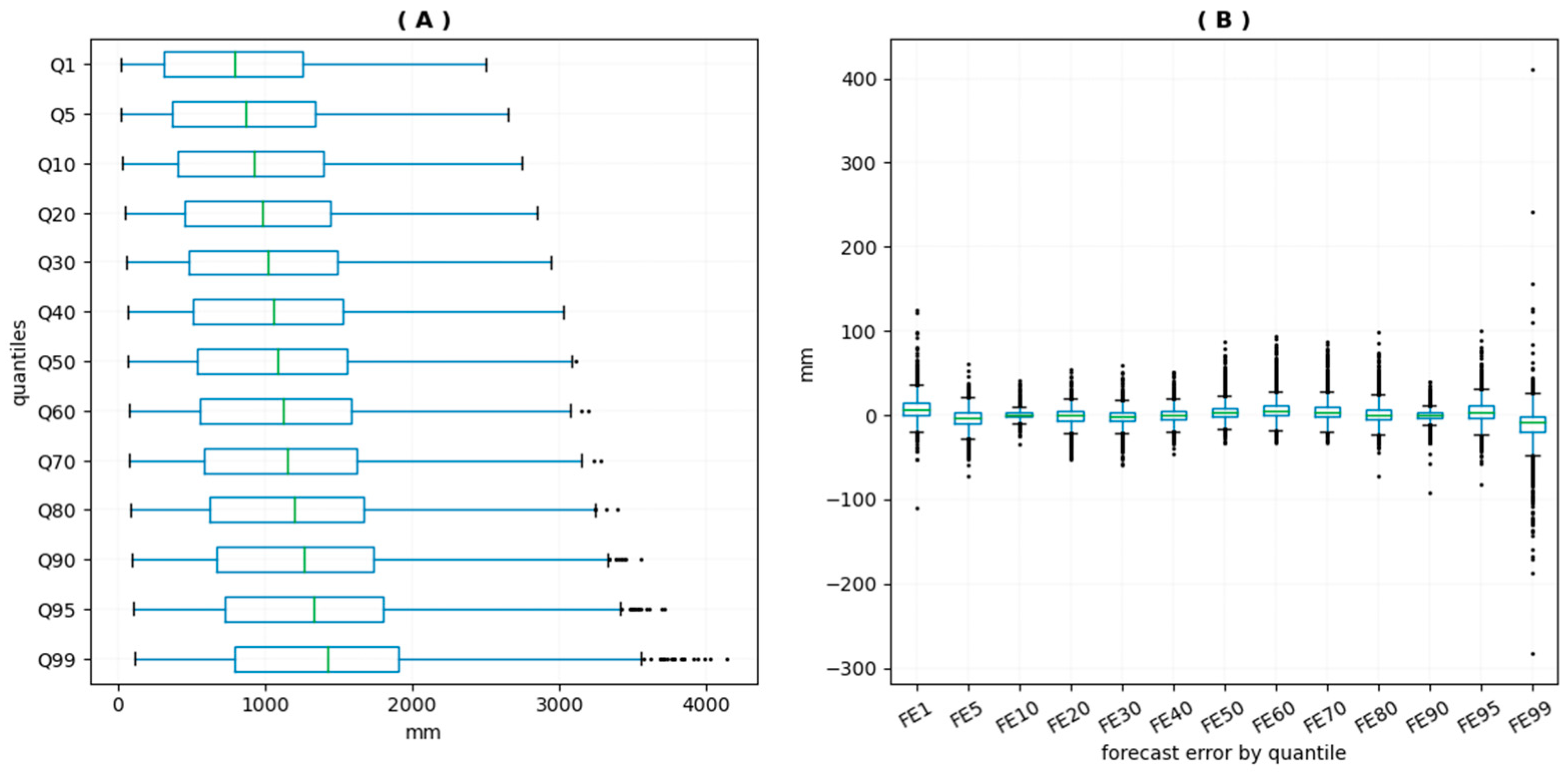
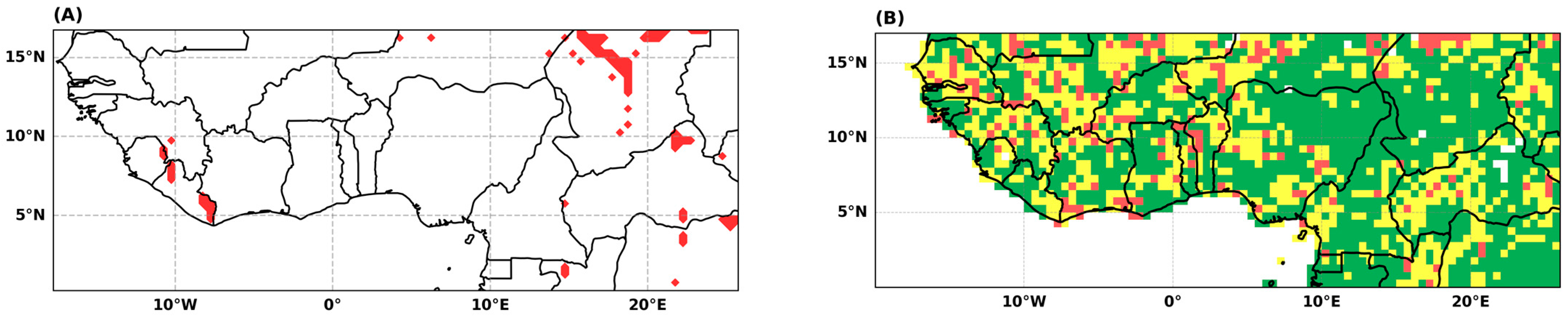
4.1.1. Stationarity Tests
4.1.2. Goodness-of-Fit Assessments
4.1.3. The GPD Parameters
4.2. The Drought Hazard Measurement
4.2.1. The Standard Approach of Drought Hazard
4.2.2. An Alternative Definition of the Drought Hazard Index
4.2.3. Extreme Drought Hazard Index
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B

References
- Carrão, H.; Naumann, G.; Barbosa, P. Mapping Global Patterns of Drought Risk: An Empirical Framework Based on Sub-National Estimates of Hazard, Exposure and Vulnerability. Glob. Environ. Change 2016, 39, 108–124. [Google Scholar] [CrossRef]
- Vogt, J.V.; Naumann, G.; Masante, D.; Spinoni, J.; Cammalleri, C.; Erian, W.; Pischke, F.; Pulwarty, R.; Barbosa, P. Drought Risk Assessment and Management—A Conceptual Framework; EUR 29464 EN; Publications Office of the European Union: Luxembourg, 2018. [Google Scholar] [CrossRef]
- Hagenlocher, M.; Meza, I.; Anderson, C.C.; Min, A.; Renaud, F.G.; Walz, Y.; Siebert, S.; Sebesvari, Z. Drought vulnerability and risk assessments: State of the art, persistent gaps, and research agenda. Environ. Res. Lett. 2019, 14, 083002. [Google Scholar] [CrossRef]
- Mens, M.J.P.; van Rhee, G.; Schasfoort, F.; Kielen, N. Integrated drought risk assessment to support adaptive policymaking in the Netherlands. Nat. Hazards Earth Syst. Sci. 2022, 22, 1763–1776. [Google Scholar] [CrossRef]
- Ó Gráda, C. Making Famine History. J. Econ. Lit. 2007, 45, 5–38. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Sivakumar, M.V.K.; Pulwarty, R. Managing Drought Risk in a Changing Climate: The Role of National Drought Policy. Weather Clim. Extrem. 2014, 3, 4–13. [Google Scholar] [CrossRef]
- Tadesse, T. Strategic Framework for Drought Risk Management and Enhancing Resilience in Africa; White Paper; UNCCD: Bonn, Germany, 2018. [Google Scholar]
- Hayes, M.J.; Wilhelmi, O.V.; Knutson, C.L. Reducing Drought Risk: Bridging Theory and Practice. Nat. Hazards Rev. 2004, 5, 106–113. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; Gimeno, L.; Eklundh, L.; Giuliani, G.; Weston, D.; El Kenawy, A.; López-Moreno, J.I.; Nieto, R.; Ayenew, T.; et al. Challenges for drought mitigation in Africa: The potential use of geospatial data and drought information systems. Appl. Geogr. 2012, 34, 471–486. [Google Scholar] [CrossRef]
- World Bank. Assessing Drought Hazard and Risk: Principles and Implementation Guidance; World Bank: Washington, DC, USA, 2019; Available online: http://documents.worldbank.org/curated/en/989851589954985863/Assessing-Drought-Hazard-and-Risk-Principles-and-Implementation-Guidance (accessed on 21 June 2022).
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Field, C.B., Barros, V., Stocker, T.F., Qin, D., Dokken, D.J., Ebi, K.L., Mastrandrea, M.D., Mach, K.J., Plattner, G.-K., Allen, S.K., et al., Eds.; A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012; Available online: https://www.ipcc.ch/site/assets/uploads/2018/03/SREX_Full_Report-1.pdf (accessed on 8 January 2020).
- Rajsekhar, D.; Singh, V.P.; Mishra, A.K. Integrated Drought Causality, Hazard, and Vulnerability Assessment for Future Socioeconomic Scenarios: An Information Theory Perspective. J. Geophys. Res. Atmos. 2015, 120, 6346–6378. [Google Scholar] [CrossRef]
- Dracup, J.A.; Lee, K.S.; Paulson, E.G. On the definition of droughts. Water Resour. Res. 1980, 16, 297–302. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The Drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- WMO; GWP. Handbook of Drought Indicators and Indices; Svoboda, M., Fuchs, B.A., Eds.; Integrated Drought Management Tools and Guidelines Series 2; Integrated Drought Management Programme (IDMP): Geneva, Switzerland, 2016. [Google Scholar]
- Wilhite, D.A. Drought as a natural hazard: Concepts and definitions. In Drought: A Global Assessment; Wilhite, D.A., Ed.; Routledge Publishers: London, UK, 2000; Volume I, Chapter 1; pp. 3–18. [Google Scholar]
- McKee, T.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.L. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; Research Paper, No. 45; US Weather Bureau: Washington, DC, USA, 1965; Available online: https://www.droughtmanagement.info/literature/USWB_Meteorological_Drought_1965.pdf (accessed on 11 August 2023).
- Guttman, N.B. Accepting the Standardized Precipitation Index: A Calculation Algorithm1. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- Edwards, D.; McKee, T. Characteristics of 20th Century Drought in The United States at Multiple Time Scales; Climatology Report No 97-2; Department of Atmospheric Science, Colorado State University: Fort Collins, CL, USA, 1997; Volume 97-2. [Google Scholar]
- Shahid, S.; Behrawan, H. Drought Risk Assessment in the Western Part of Bangladesh. Nat. Hazards 2008, 46, 391–413. [Google Scholar] [CrossRef]
- He, B.; Lü, A.; Wu, J.; Zhao, L. Drought hazard assessment and spatial characteristics analysis in China. J. Geogr. Sci. 2011, 21, 235–249. [Google Scholar] [CrossRef]
- Svoboda, M.D.; LeComte, D.; Hayes, M.; Heim, R.; Gleason, K.; Angel, J.; Rippey, B.; Tinker, R.; Palecki, M.; Stooksbury, D.; et al. The drought monitor. Bull. Am. Meteorol. Soc. 2002, 83, 1181–1190. [Google Scholar] [CrossRef]
- Şen, Z.; Almazroui, M. Actual Precipitation Index (API) for Drought classification. Earth Syst. Env. 2021, 5, 59–70. [Google Scholar] [CrossRef]
- Carrão, H.; Singleton, A.; Naumann, G.; Barbosa, P.; Vogt, J. An optimized system for the classification of meteorological drought intensity with applications in frequency analysis. J. Appl. Meteorol. Climatol. 2014, 53, 1943–1960. [Google Scholar] [CrossRef]
- Pickands, J. Statistical inference using extreme order statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar] [CrossRef]
- Balkema, A.A.; de Haan, L. Residual Life Time at Great Age. Ann. Probab. 1974, 2, 792–804. [Google Scholar] [CrossRef]
- Leadbetter, M.R. On a basis for ‘Peaks over Threshold’ modeling. Stat. Probab. Lett. 1991, 12, 357–362. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar] [CrossRef]
- Gharib, A.; Davies, E.G.R.; Goss, G.G.; Faramarzi, M. Assessment of the Combined Effects of Threshold Selection and Parameter Estimation of Generalized Pareto Distribution with Applications to Flood Frequency Analysis. Water 2017, 9, 692. [Google Scholar] [CrossRef]
- Pan, X.; Rahman, A.; Haddad, K.; Ourda, T.B.M.J. Peaks-over-threshold model in flood frequency analysis: A scoping review. Stoch. Environ. Res. Risk Assess. 2022, 36, 2419–2435. [Google Scholar] [CrossRef]
- Kim, J.E.; Yoo, J.; Chung, G.H.; Kim, T.-W. Hydrologic Risk Assessment of Future Extreme Drought in South Korea Using Bivariate Frequency Analysis. Water 2019, 11, 2052. [Google Scholar] [CrossRef]
- Burke, E.J.; Perry, R.H.J.; Brown, S.J. An extreme value analysis of UK drought and projections of change in the future. J. Hydrol. 2010, 388, 131–143. [Google Scholar] [CrossRef]
- Scarrott, C.; MacDonald, A. A review of extreme value threshold estimation and uncertainty quantification. REVSTAT-Stat. J. 2012, 10, 33–59. [Google Scholar] [CrossRef]
- Langousis, A.; Mamalakis, A.; Puliga, M.; Deidda, R. Threshold detection for the generalized Pareto distribution: Review of representative methods and application to the NOAA NCDC daily rainfall database. Water Resour. Res. 2016, 52, 2659–2681. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Solari, S.; Losada, M.A. A unified statistical model for hydrological variables including the selection of threshold for the peak over threshold method. Water Resour. Res. 2012, 48, 1–15. [Google Scholar] [CrossRef]
- MacDonald, A.; Scarrott, C.J.; Lee, D.; Darlow, B.; Reale, M.; Russell, G. A flexible extreme value mixture model. Comput. Stat. Data Anal. 2011, 55, 2137–2157. [Google Scholar] [CrossRef]
- Behrens, C.N.; Lopes, H.F.; Gamerman, D. Bayesian analysis of extreme events with threshold estimation. Stat. Model. 2004, 4, 227–244. [Google Scholar] [CrossRef]
- Mendes, B.; Lopes, H.F. Data driven estimates for mixtures. Comput. Stat. Data Anal. 2004, 47, 583–598. [Google Scholar] [CrossRef]
- Zhao, X.; Scarrott, C.J.; Reale, M.; Oxley, L. Extreme value modelling for forecasting the market crisis. Appl. Financ. Econ. 2010, 20, 63–72. [Google Scholar] [CrossRef]
- Tukey, J.W. A Survey of Sampling from Contaminated Distributions. In Contribution to Probability and Statistics, Essays in Honor of Herald Hotelling; Olkin, I., Goraye, S.G., Hoeffding, W., Madow, W.G., Mann, H.B., Eds.; Stanford University Press: Stanford, CA, USA, 1960. [Google Scholar]
- Hu, Y.; Scarrott, C. Evmix: Extreme Value Mixture Modelling, Threshold Estimation and Boundary Corrected Kernel Density Estimation. R package Version 2.10. J. Stat. Softw. 2018, 84, 1–27. [Google Scholar] [CrossRef]
- Hubert, P.; Carbonnel, J.P.; Chaouche, A. Segmentation des séries hydrométéorologiques—Application à des séries de précipitations et de débits de l’afrique de l’ouest. J. Hydrol. 1989, 110, 349–367. [Google Scholar] [CrossRef]
- Ali, A.; Lebel, T. The Sahelian standardized rainfall index revisited. Int. J. Climatol. 2009, 29, 1705–1714. [Google Scholar] [CrossRef]
- Panthou, G.; Vischel, T.; Lebel, T. Recent trends in the regime of extreme rainfall in the Central Sahel. Int. J. Climatology 2014, 34, 3998–4006. [Google Scholar] [CrossRef]
- Descroix, L.; Diongue Niang, A.; Panthou, G.; Bodian, A.; Sane, Y.; Dacosta, H.; Malam Abdou, M.; Vandervaere, J.P.; Quantin, G. Évolution récente de la pluviométrie en Afrique de l’ouest à travers deux régions: La Sénégambie et le Bassin du Niger Moyen. Climatologie 2015, 12, 25–43. [Google Scholar] [CrossRef]
- Biasutti, M. Rainfall trends in the African Sahel: Characteristics, processes, and causes. WIREs Clim. Change 2019, 10, e591. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Society. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Heidari, H.; Arabi, M.; Ghanbari, M.; Warziniack, T. A probabilistic approach for characterization of sub-annual socioeconomic drought intensity-duration-frequency (IDF) relationships in a changing environment. Water 2020, 12, 1522. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 2002, 20, 134–144. [Google Scholar] [CrossRef]
- Harvey, D.; Leybourne, S.J.; Newbold, N. Tests for Forecast Encompassing. J. Bus. Econ. Stat. 1998, 16, 254–259. [Google Scholar] [CrossRef]
- Helton, J.C.; Bean, J.E.; Economy, K.; Garner, J.W.; MacKinnon, R.J.; Miller, J.; Schreiber, J.D.; Vaughn, P. Uncertainty and sensitivity analysis for two-phase flow in the vicinity of the repository in the 1996 performance assessment for the Waste Isolation Pilot Plant: Undisturbed conditions. Reliab. Eng. Syst. Saf. 2000, 69, 227–261. [Google Scholar] [CrossRef]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storli, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef]






| Drought Category | Weight Wi | Threshold Values for the SPI | Thresholds in Percentiles | Prob. of Occurrence (ϕi) | Empirical Frequency (fi): SPI | Empirical Frequency (fi): GNG |
|---|---|---|---|---|---|---|
| 1. Mild drought | 0 | 0.341 | 0.354 | 0.356 | ||
| 2. Moderate drought | 1 | [6.68%; 15.87%] | 0.92 | 0.079 | 0.096 | |
| 3. Severe drought | 2 | 0.04 | 0.040 | 0.041 | ||
| 4. Extreme drought | 3 | ≤−2 | 0.0227 | 0.029 | 0.0227 | |
| DHI (Equation (5)) | 0.24 | 0.243 | 0.246 |
| Drought Category (USDA) | Percentiles | Theoretical Prob. of Occurrence (ϕi) | Empirical Frequency: GNG (fi) |
|---|---|---|---|
| 1. Abnormally dry | 10% | 0.096 | |
| 2. Moderate drought | 10% | 0.099 | |
| 3. Severe drought | 5% | 0.053 | |
| 4. Extreme drought | 3% | 0.027 | |
| 5. Exceptional drought | 2% | 0.021 | |
| Total | 30% | 0.295 |
| SPI | GNG | |||
|---|---|---|---|---|
| Value | Count | Percent | Count | Percent |
| 0 | 286 | 12.45 | 6 | 0.26 |
| 1 | 758 | 32.99 | 1406 | 61.18 |
| 2 | 715 | 31.11 | 791 | 34.42 |
| 3 | 424 | 18.45 | 89 | 3.87 |
| 4 | 95 | 4.13 | 6 | 0.26 |
| 5 | 19 | 0.83 | 0 | 0 |
| 6 | 1 | 0.04 | 0 | 0 |
| Total | 2298 | 100 | 2298 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Araujo Bonjean, C.; Sy, A.; Dury, M.-E. Spatially Consistent Drought Hazard Modeling Approach Applied to West Africa. Water 2023, 15, 2935. https://doi.org/10.3390/w15162935
Araujo Bonjean C, Sy A, Dury M-E. Spatially Consistent Drought Hazard Modeling Approach Applied to West Africa. Water. 2023; 15(16):2935. https://doi.org/10.3390/w15162935
Chicago/Turabian StyleAraujo Bonjean, Catherine, Abdoulaye Sy, and Marie-Eliette Dury. 2023. "Spatially Consistent Drought Hazard Modeling Approach Applied to West Africa" Water 15, no. 16: 2935. https://doi.org/10.3390/w15162935
APA StyleAraujo Bonjean, C., Sy, A., & Dury, M.-E. (2023). Spatially Consistent Drought Hazard Modeling Approach Applied to West Africa. Water, 15(16), 2935. https://doi.org/10.3390/w15162935











