Monthly Streamflow Prediction by Metaheuristic Regression Approaches Considering Satellite Precipitation Data
Abstract
:1. Introduction
2. Methods and Materials
2.1. CatBoost
2.2. eXtreme Gradient Boosting (XGBoost)
2.3. Random Forest (RF)
2.4. Case Study
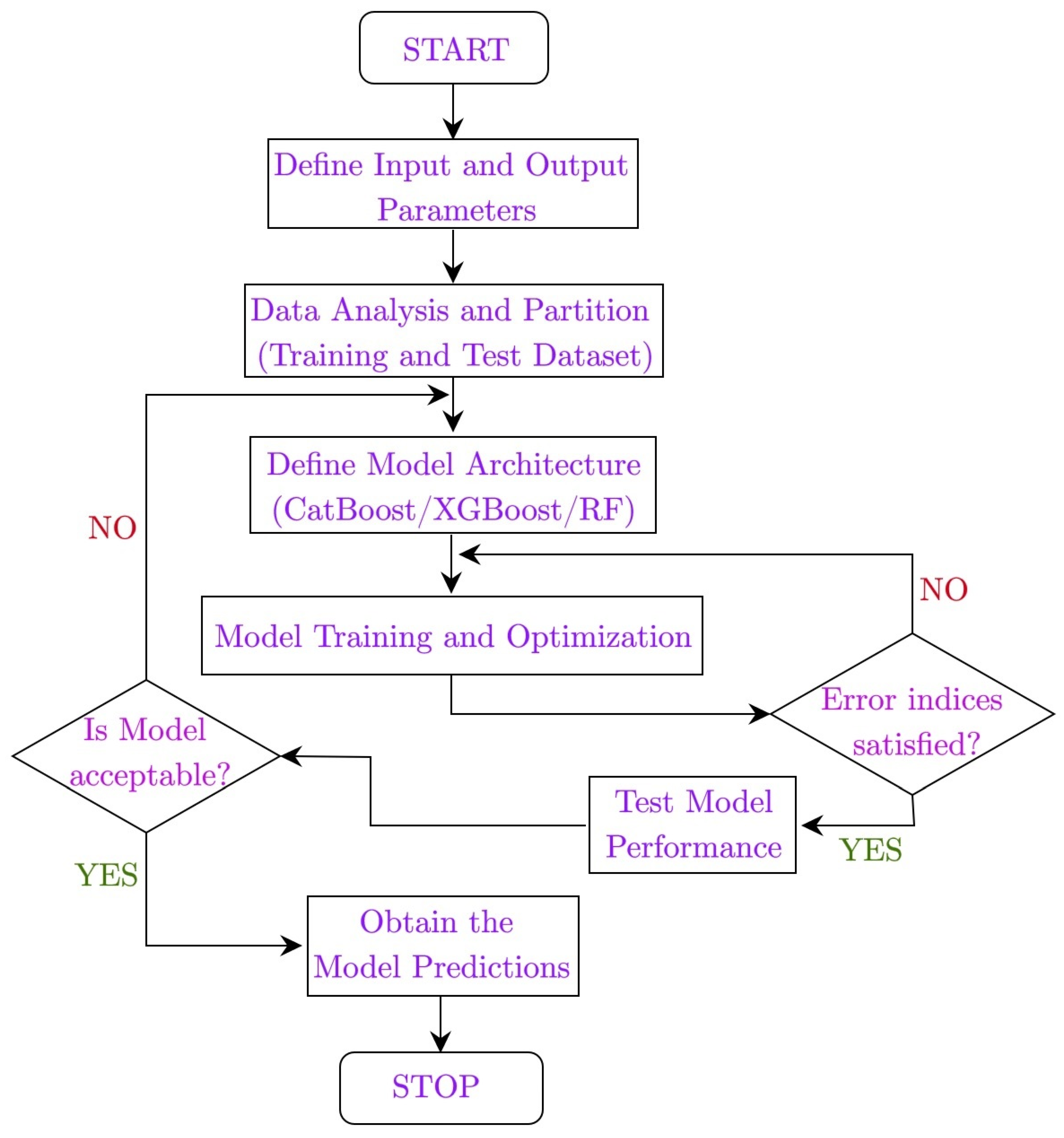
2.5. Application and Evaluation of the Methods
3. Application and Results
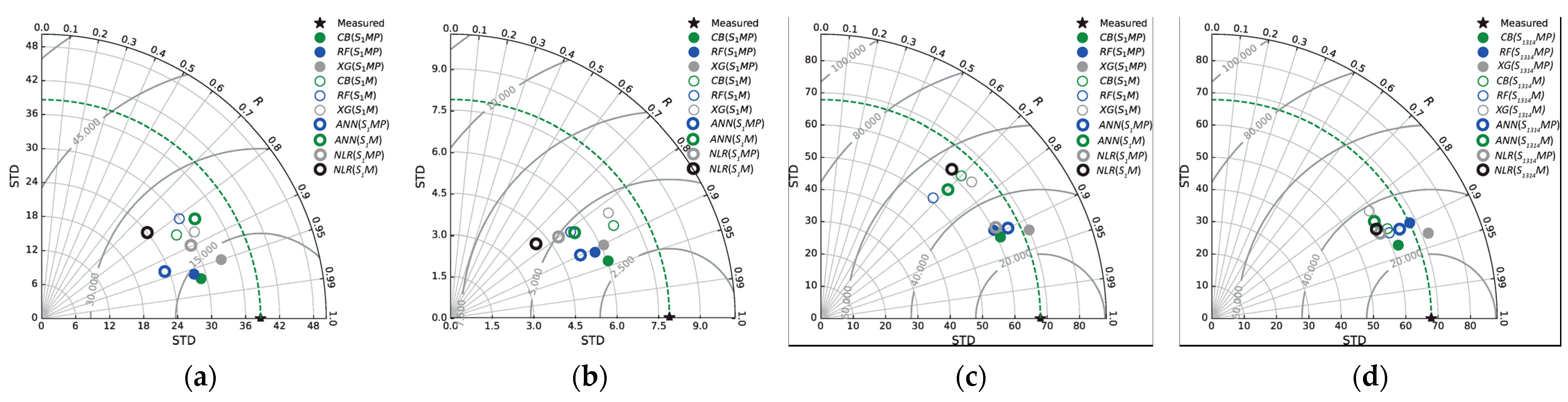
3.1. Predicting Monthly Streamflow of Durucasu Station
3.2. Predicting Monthly Streamflow at Sutluce Station
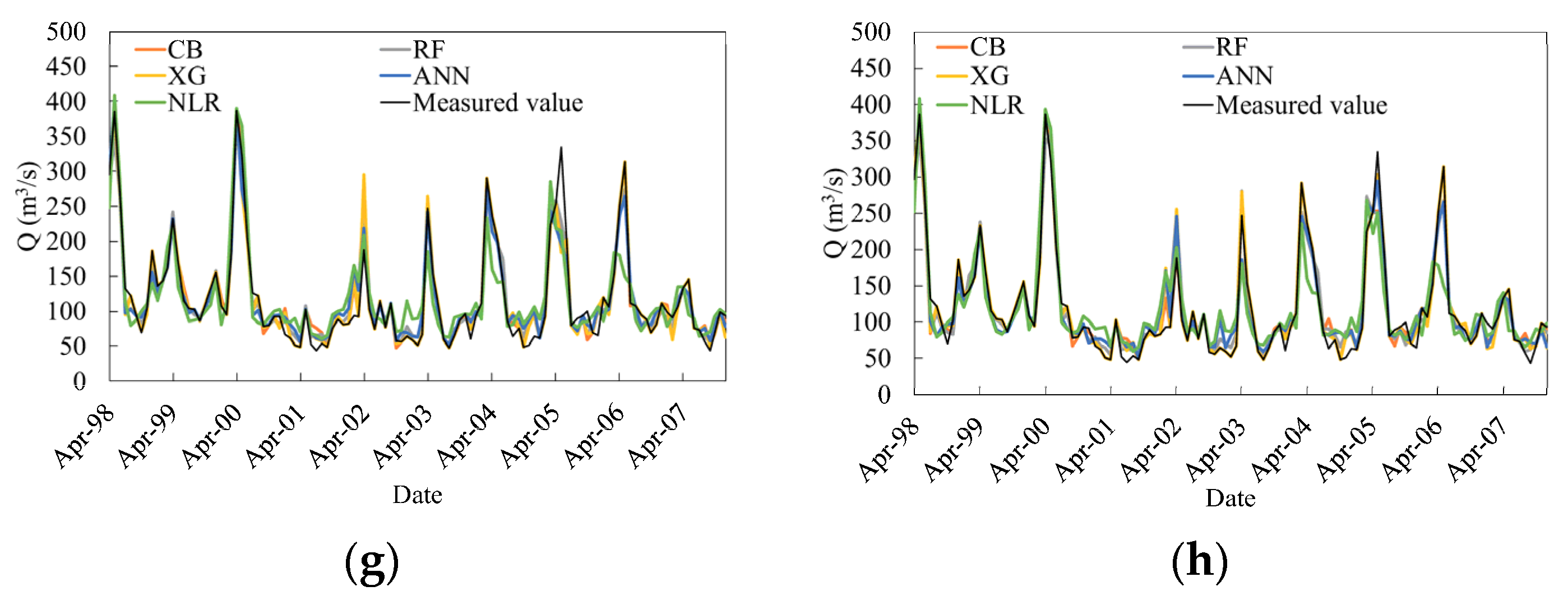
3.3. Predicting Monthly Streamflow at the Kale Station
3.4. Predicting Monthly Streamflow at the Kale Station Using Upstream Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Edwards, P.J.; Williard, K.W.; Schoonover, J.E. Fundamentals of watershed hydrology. J. Contemp. Water Res. Educ. 2015, 154, 3–20. [Google Scholar] [CrossRef]
- Davie, T. Fundamentals of Hydrology, 2nd ed.; Routledge: London, UK, 2019. [Google Scholar]
- Chegwidden, O.S.; Rupp, D.E.; Nijssen, B. Climate change alters flood magnitudes and mechanisms in climatically-diverse headwaters across the northwestern United States. Environ. Res. Lett. 2020, 15, 094048. [Google Scholar] [CrossRef]
- Goeking, S.A.; Tarboton, D.G. Forests and water yield: A synthesis of disturbance effects on streamflow and snowpack in western coniferous forests. J. For. 2020, 118, 172–192. [Google Scholar] [CrossRef] [Green Version]
- Naz, B.S.; Kao, S.C.; Ashfaq, M.; Gao, H.; Rastogi, D.; Gangrade, S. Effects of climate change on streamflow extremes and implications for reservoir inflow in the United States. J. Hydrol. 2019, 556, 359–370. [Google Scholar] [CrossRef]
- Valenzuela-Aguayo, F.; McCracken, G.R.; Manosalva, A.; Habit, E.; Ruzzante, D.E. Human-induced habitat fragmentation effects on connectivity, diversity, and population persistence of an endemic fish, Percilia irwini, in the Biobío River basin (Chile). Evol. Appl. 2020, 13, 794–807. [Google Scholar] [CrossRef] [Green Version]
- Allen, G.H.; Pavelsky, T.M. Global extent of rivers and streams. Science 2018, 361, 585–588. [Google Scholar] [CrossRef] [Green Version]
- Lu, S.; Dai, W.; Tang, Y.; Guo, M. A review of the impact of hydropower reservoirs on global climate change. Sci. Total Environ. 2020, 711, 134996. [Google Scholar] [CrossRef]
- Marques, C.A.F.; Ferreira, J.A.; Rocha, A.; Castanheira, J.M.; Melo-Gonçalves, P.; Vaz, N.; Dias, J.M. Singular spectrum analysis and forecasting of hydrological time series. Phys. Chem. Earth Parts A/B/C 2006, 31, 1172–1179. [Google Scholar] [CrossRef]
- Karran, D.J.; Morin, E.; Adamowski, J. Multi-step streamflow forecasting using data-driven non-linear methods in contrasting climate regimes. J. Hydroinform. 2014, 16, 671–689. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.Y.; Qiu, J.; Li, F.F. Hybrid models combining EMD/EEMD and ARIMA for Long-term streamflow forecasting. Water 2018, 10, 853. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Singh, V.P. Univariate streamflow forecasting using commonly used data-driven models: Literature review and case study. Hydrol. Sci. J. 2018, 63, 1091–1111. [Google Scholar] [CrossRef]
- Fatichi, S.; Rimkus, S.; Burlando, P.; Bordoy, R. Does internal climate variability overwhelm climate change signals in streamflow? The upper Po and Rhone basin case studies. Sci. Total Environ. 2014, 493, 1171–1182. [Google Scholar] [CrossRef] [PubMed]
- Adombi, A.V.D.P.; Chesnaux, R.; Boucher, M.A. Theory-guided machine learning applied to hydrogeology—State of the art, opportunities and future challenges. Hydrogeol. J. 2021, 29, 2671–2683. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Oliveto, G. Riprap incipient motion for overtopping flows with machine learning models. J. Hydroinform. 2020, 22, 749–767. [Google Scholar] [CrossRef]
- Kisi, O.; Mirboluki, A.; Naganna, S.R.; Malik, A.; Kuriqi, A.; Mehraein, M. Comparative evaluation of deep learning and machine learning in modelling pan evaporation using limited inputs. Hydrol. Sci. J. 2022, 67, 1–19. [Google Scholar] [CrossRef]
- Wang, W.; Van Gelder, P.H.; Vrijling, J.K.; Ma, J. Forecasting daily streamflow using hybrid ANN models. J. Hydrol. 2006, 324, 383–399. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W. Data-driven models for monthly streamflow time series prediction. Eng. Appl. Artif. Intell. 2010, 23, 1350–1367. [Google Scholar] [CrossRef] [Green Version]
- Freire, P.K.D.M.M.; Santos, C.A.G.; da Silva, G.B.L. Analysis of the use of discrete wavelet transforms coupled with ANN for short-term streamflow forecasting. Appl. Soft Comput. 2019, 80, 494–505. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Du, Y.; Zhuang, Y.; Yan, C. Anthropogenic impacts on streamflow-compensated climate change effect in the Hanjiang River Basin, China. J. Hydrol. Eng. 2020, 25, 04019058. [Google Scholar] [CrossRef]
- Malik, A.; Tikhamarine, Y.; Souag-Gamane, D.; Kisi, O.; Pham, Q.B. Support vector regression optimized by meta-heuristic algorithms for daily streamflow prediction. Stoch. Environ. Res. Risk Assess. 2020, 34, 1755–1773. [Google Scholar] [CrossRef]
- Wang, L.; Li, X.; Ma, C.; Bai, Y. Improving the prediction accuracy of monthly streamflow using a data-driven model based on a double-processing strategy. J. Hydrol. 2019, 573, 733–745. [Google Scholar] [CrossRef]
- Ren, K.; Wang, X.; Shi, X.; Qu, J.; Fang, W. Examination and comparison of binary metaheuristic wrapper-based input variable selection for local and global climate information-driven one-step monthly streamflow forecasting. J. Hydrol. 2021, 597, 126152. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Q.; Shao, J.; Wang, G. Dynamic streamflow simulation via online gradient-boosted regression tree. J. Hydrol. Eng. 2019, 24, 04019041. [Google Scholar] [CrossRef]
- Rice, J.S.; Emanuel, R.E.; Vose, J.M.; Nelson, S.A. Continental US streamflow trends from 1940 to 2009 and their relationships with watershed spatial characteristics. Water Resour. Res. 2015, 51, 6262–6275. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. Super ensemble learning for daily streamflow forecasting: Large-scale demonstration and comparison with multiple machine learning algorithms. Neural Comput. Appl. 2021, 33, 3053–3068. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J.; Liu, J. Streamflow forecasting using extreme gradient boosting model coupled with Gaussian mixture model. J. Hydrol. 2020, 586, 124901. [Google Scholar] [CrossRef]
- Sahour, H.; Gholami, V.; Torkaman, J.; Vazifedan, M.; Saeedi, S. Random forest and extreme gradient boosting algorithms for streamflow modeling using vessel features and tree-rings. Environ. Earth Sci. 2021, 80, 1–14. [Google Scholar] [CrossRef]
- Zhang, D.; Qian, L.; Mao, B.; Huang, C.; Huang, B.; Si, Y. A data-driven design for fault detection of wind turbines using random forests and XGboost. IEEE Access 2018, 6, 21020–21031. [Google Scholar] [CrossRef]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Niu, D.; Diao, L.; Zang, Z.; Che, H.; Zhang, T.; Chen, X. A machine-learning approach combining wavelet packet denoising with Catboost for weather forecasting. Atmosphere 2021, 12, 1618. [Google Scholar] [CrossRef]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Yu, X.; Zhou, H. Evaluation of CatBoost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- CatBoost. Available online: https://catboost.ai/ (accessed on 30 October 2022).
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 1–45. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Brownlee, J. XGBoost with Python: Gradient Boosted Trees with XGBoost and Scikit-Learn; Association for Computing Machinery: New York, NY, USA, 2016. [Google Scholar]
- Chen, R.C.; Caraka, R.E.; Arnita, N.E.G.; Pomalingo, S.; Rachman, A.; Toharudin, T.; Pardamean, B. An end to end of scalable tree boosting system. Sylwan 2020, 164, 1–11. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Pavlov, Y.L. Random Forests; De Gruyter: Boston, MA, USA, 2000; Available online: https://www.degruyter.com/document/doi/10.1515/9783110941975/html (accessed on 30 October 2022).
- Louppe, G. Understanding Random Forests: From Theory to Practice. Ph.D Thesis, University of Liège, Liège, Belgium, 2014. [Google Scholar]
- Scornet, E. Learning with Random Forests. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2015. [Google Scholar]
- Sensoy, S.; Demircan, M.; Ulupinar, Y.; Balta, Z. Climate of Turkey. Available online: https://mgm.gov.tr/FILES/genel/makale/31_climateofturkey.pdf (accessed on 30 September 2022).
- Yang, U.; Sheng-tian, Y.; Ming-yong, C.; Qiu-wen, Z.; Guo-tao, D. The Applicability Analysis of TRMM Precipitation Data in the Yarlung Zangbo River Basin. J. Nat. Resour. 2013, 28, 1414–1425. [Google Scholar]
- Santos, C.A.G.; Brasil Neto, R.M.; da Silva, R.M.; Passos, J.S.D.A. Integrated spatiotemporal trends using TRMM 3B42 data for the Upper São Francisco River basin, Brazil. Environ. Monit. Assess 2018, 190, 175. [Google Scholar] [CrossRef]
- Medhioub, E.; Bouaziz, M.; Achour, H.; Bouaziz, S. Monthly assessment of TRMM 3B43 rainfall data with high-density gauge stations over Tunisia. Arab. J. Geosci. 2019, 12, 15. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Parmar, K.S.; Soni, K.; Kisi, O. Modeling monthly streamflow in mountainous basin by MARS, GMDHNN and DENFIS using hydroclimatic data. Neural Comput. Appl. 2021, 33, 2853–2871. [Google Scholar] [CrossRef]
- Shi, J.; Guo, J.; Zheng, S. Evaluation of hybrid forecasting approaches for wind speed and power generation time series Renewable and Sustainable. Energy Rev. 2012, 16, 3471–3480. [Google Scholar]
- Zhang, D.; Peng, X.; Pan, K.; Liu, Y. A novel wind speed forecasting based on hybrid decomposition and online sequential outlier robust extreme learning machine. Energy Convers. Manag. 2019, 180, 338–357. [Google Scholar] [CrossRef]
- Kisi, O. River flow forecasting and estimation using different artificial neural network techniques. Hydrol. Res. 2008, 39, 27–40. [Google Scholar] [CrossRef]
- Sanikhani, H.; Kisi, O. River flow estimation and forecasting by using two different adaptive neuro-fuzzy approaches. Water Resour Manag. 2012, 26, 1715–1729. [Google Scholar] [CrossRef]





| Station | Station No | Phase | Streamflow Data | |||||
|---|---|---|---|---|---|---|---|---|
| Qmax | Qmin | Qmean | Sk | CV | STD | |||
| Durucasu | 1413 | Test | 173 | 9 | 40.1 | 2.11 | 0.96 | 38.3 |
| Train | 169 | 4.6 | 32.5 | 2.43 | 0.9 | 28.6 | ||
| Sutluce | 1414 | Test | 39.6 | 5.9 | 14.1 | 1.54 | 0.56 | 7.7 |
| Train | 37.5 | 4.5 | 12.2 | 1.87 | 0.53 | 6.42 | ||
| Kale | 1402 | Test | 334 | 43.5 | 104.2 | 2.38 | 0.65 | 68.6 |
| Train | 387 | 47.7 | 126.7 | 1.6 | 0.60 | 76.4 | ||
| Without TRMM Data | With TRMM Data | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model (Scenario) | Model Inputs | RMSE | rRMSE | MAE | MAPE | Model (Scenario) | Model Inputs | RMSE | rRMSE | MAE | MAPE | ||
| CB (S1) | Qt−1 | 24.11 | 0.60 | 16.48 | 0.40 | 48.12 | CB (S1P) | Qt−1, P | 18.32 | 0.46 | 11.71 | 0.58 | 45.35 |
| CB (S12) | Qt−1, Qt−2 | 26.08 | 0.65 | 15.90 | 0.42 | 47.5 | CB (S12P) | Qt−1, Qt−2, P | 24.24 | 0.60 | 13.55 | 0.51 | 46.15 |
| CB (S123) | Qt−1, Qt−2, Qt−3 | 26.76 | 0.67 | 17.18 | 0.38 | 48.19 | CB (S123P) | Qt−1, Qt−2, Qt−3, P | 27.63 | 0.69 | 15.59 | 0.43 | 46.12 |
| RF (S1) | Qt−1 | 23.19 | 0.58 | 16.21 | 0.41 | 50.2 | RF (S1P) | Qt−1, P | 15.03 | 0.37 | 10.63 | 0.61 | 46.15 |
| RF (S12) | Qt−1, Qt−2 | 26.99 | 0.67 | 17.74 | 0.36 | 53.2 | RF (S12P) | Qt−1, Qt−2, P | 17.60 | 0.44 | 11.43 | 0.59 | 48.26 |
| RF (S123) | Qt−1, Qt−2, Qt−3 | 24.85 | 0.62 | 15.78 | 0.43 | 52.1 | RF (S123P) | Qt−1, Qt−2, Qt−3, P | 17.41 | 0.43 | 11.64 | 0.58 | 47.15 |
| XGB (S1) | Qt−1 | 25.33 | 0.63 | 17.60 | 0.36 | 46.12 | XGB (S1P) | Qt−1, P | 20.16 | 0.50 | 14.13 | 0.49 | 45.19 |
| XGB (S12) | Qt−1, Qt−2 | 26.02 | 0.65 | 19.73 | 0.28 | 48.2 | XGB (S12P) | Qt−1, Qt−2, P | 15.73 | 0.39 | 10.28 | 0.63 | 46.15 |
| XGB (S123) | Qt−1, Qt−2, Qt−3 | 24.97 | 0.62 | 17.46 | 0.37 | 49.78 | XGB (S123P) | Qt−1, Qt−2, Qt−3, P | 16.35 | 0.41 | 11.64 | 0.58 | 48.12 |
| ANN (S1) | Qt−1 | 27.86 | 0.69 | 19.18 | 0.39 | 53.2 | ANN (S1P) | Qt−1, P | 22.18 | 0.55 | 15.40 | 0.53 | 50.23 |
| ANN (S12) | Qt−1, Qt−2 | 28.10 | 0.70 | 21.31 | 0.31 | 55.45 | ANN (S12P) | Qt−1, Qt−2, P | 16.99 | 0.42 | 11.31 | 0.68 | 52.13 |
| ANN (S123) | Qt−1, Qt−2, Qt−3 | 26.72 | 0.66 | 18.86 | 0.40 | 57.8 | ANN (S123P) | Qt−1, Qt−2, Qt−3, P | 17.49 | 0.44 | 12.45 | 0.64 | 52.14 |
| NLR (S1) | Qt−1 | 30.65 | 0.76 | 20.71 | 0.42 | 55.18 | NLR (S1P) | Qt−1, P | 24.40 | 0.61 | 16.32 | 0.58 | 53.14 |
| NLR (S12) | Qt−1, Qt−2 | 30.35 | 0.75 | 23.44 | 0.34 | 58.49 | NLR (S12P) | Qt−1, Qt−2, P | 18.35 | 0.46 | 12.44 | 0.71 | 55.12 |
| NLR (S123) | Qt−1, Qt−2, Qt−3 | 28.59 | 0.71 | 20.37 | 0.43 | 56.4 | NLR (S123P) | Qt−1, Qt−2, Qt−3, P | 18.71 | 0.47 | 13.70 | 0.69 | 52.15 |
| CB (S1M) | Qt−1, MN | 20.69 | 0.52 | 13.74 | 0.50 | 42.2 | CB (S1MP) | Qt−1, MN, P | 13.05 | 0.33 | 8.79 | 0.68 | 25 |
| CB (S12M) | Qt−1, Qt−2, MN | 23.16 | 0.58 | 14.26 | 0.48 | 45.35 | CB (S12MP) | Qt−1, Qt−2, MN, P | 24.04 | 0.60 | 13.11 | 0.51 | 24.5 |
| CB (S123M) | Qt−1, Qt−2, Qt−3, MN | 22.04 | 0.55 | 13.20 | 0.52 | 45.21 | CB (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 25.11 | 0.63 | 13.83 | 0.50 | 25.6 |
| RF (S1M) | Qt−1, MN | 22.09 | 0.55 | 13.81 | 0.50 | 43.24 | RF (S1MP) | Qt−1, MN, P | 14.48 | 0.36 | 9.33 | 0.66 | 25.23 |
| RF (S12M) | Qt−1, Qt−2, MN | 21.95 | 0.55 | 13.36 | 0.52 | 48.26 | RF (S12MP) | Qt−1, Qt−2, MN, P | 15.63 | 0.39 | 9.87 | 0.64 | 25.48 |
| RF (S123M) | Qt−1, Qt−2, Qt−3, MN | 22.35 | 0.56 | 13.02 | 0.53 | 48.97 | RF (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 16.16 | 0.40 | 10.42 | 0.62 | 26.5 |
| XGB (S1M) | Qt−1, MN | 18.65 | 0.51 | 14.70 | 0.47 | 40.23 | XGB (S1MP) | Qt−1, MN, P | 12.33 | 0.31 | 8.77 | 0.68 | 29.12 |
| XGB (S12M) | Qt−1, Qt−2, MN | 18.07 | 0.45 | 12.69 | 0.54 | 41.24 | XGB (S12MP) | Qt−1, Qt−2, MN, P | 14.26 | 0.36 | 9.26 | 0.66 | 28.45 |
| XGB (S123M) | Qt−1, Qt−2, Qt−3, MN | 18.1 | 0.45 | 11.54 | 0.58 | 43.5 | XGB (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 14.02 | 0.35 | 10.22 | 0.63 | 28.75 |
| ANN (S1M) | Qt−1, MN | 21.28 | 0.53 | 14.29 | 0.48 | 42.12 | ANN (S1MP) | Qt−1, MN, P | 16.01 | 0.15 | 22.21 | 0.47 | 31.12 |
| ANN (S12M) | Qt−1, Qt−2, MN | 22.34 | 0.52 | 13.58 | 0.48 | 43.15 | ANN (S12MP) | Qt−1, Qt−2, MN, P | 16.33 | 0.15 | 23.10 | 0.47 | 31.15 |
| ANN (S123M) | Qt−1, Qt−2, Qt−3, MN | 21.92 | 0.51 | 14.29 | 0.47 | 44.12 | ANN (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 15.53 | 0.14 | 21.54 | 0.46 | 32.12 |
| NLR (S1M) | Qt−1, MN | 24.40 | 0.61 | 15.14 | 0.45 | 47.35 | NLR (S1MP) | Qt−1, MN, P | 30.26 | 0.29 | 23.38 | 0.45 | 32.14 |
| NLR (S12M) | Qt−1, Qt−2, MN | 23.67 | 0.58 | 15.29 | 0.46 | 48.2 | NLR (S12MP) | Qt−1, Qt−2, MN, P | 29.05 | 0.29 | 22.44 | 0.43 | 32.17 |
| NLR (S123M) | Qt−1, Qt−2, Qt−3, MN | 24.64 | 0.61 | 14.38 | 0.45 | 47.65 | NLR (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 29.96 | 0.29 | 23.85 | 0.47 | 35.14 |
| Without TRMM Data | With TRMM Data | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model (Scenario) | Model Inputs | RMSE | rRMSE | MAE | MAPE | Model (Scenario) | Model Inputs | RMSE | rRMSE | MAE | MAPE | ||
| CB (S1) | Qt−1 | 7.83 | 0.56 | 5.18 | 0.12 | 53.2 | CB (S1P) | Qt−1, P | 5.02 | 0.36 | 3.71 | 0.37 | 45.2 |
| CB (S12) | Qt−1, Qt−2 | 4.91 | 0.35 | 3.46 | 0.41 | 54.8 | CB (S12P) | Qt−1, Qt−2, P | 5.14 | 0.37 | 3.41 | 0.42 | 46.5 |
| CB (S123) | Qt−1, Qt−2, Qt−3 | 4.96 | 0.35 | 3.41 | 0.42 | 55.4 | CB (S123P) | Qt−1, Qt−2, Qt−3, P | 5.59 | 0.4 | 3.56 | 0.40 | 46.8 |
| RF (S1) | Qt−1 | 5.77 | 0.41 | 4.01 | 0.32 | 55.2 | RF (S1P) | Qt−1, P | 4.47 | 0.32 | 3.16 | 0.46 | 48.5 |
| RF (S12) | Qt−1, Qt−2 | 4.98 | 0.35 | 3.35 | 0.43 | 55.6 | RF (S12P) | Qt−1, Qt−2, P | 4.20 | 0.3 | 3.05 | 0.48 | 48.9 |
| RF (S123) | Qt−1, Qt−2, Qt−3 | 5.17 | 0.37 | 3.63 | 0.38 | 56 | RF (S123P) | Qt−1, Qt−2, Qt−3, P | 4.69 | 0.33 | 3.32 | 0.44 | 47.5 |
| XGB (S1) | Qt−1 | 7.84 | 0.56 | 5.18 | 0.12 | 52.32 | XGB (S1P) | Qt−1, P | 6.91 | 0.49 | 4.94 | 0.16 | 43.5 |
| XGB (S12) | Qt−1, Qt−2 | 6.12 | 0.43 | 4.46 | 0.24 | 53.6 | XGB (S12P) | Qt−1, Qt−2, P | 4.88 | 0.35 | 3.40 | 0.42 | 42.9 |
| XGB (S123) | Qt−1, Qt−2, Qt−3 | 5.30 | 0.38 | 3.88 | 0.34 | 53.87 | XGB (S123P) | Qt−1, Qt−2, Qt−3, P | 5.39 | 0.38 | 3.61 | 0.39 | 44.5 |
| ANN (S1) | Qt−1 | 8.62 | 0.62 | 5.59 | 0.13 | 57.2 | ANN (S1P) | Qt−1, P | 7.60 | 0.54 | 5.38 | 0.18 | 52.3 |
| ANN (S12) | Qt−1, Qt−2 | 6.61 | 0.47 | 4.77 | 0.26 | 58.9 | ANN (S12P) | Qt−1, Qt−2, P | 5.27 | 0.38 | 3.67 | 0.46 | 53.2 |
| ANN (S123) | Qt−1, Qt−2, Qt−3 | 5.67 | 0.41 | 4.27 | 0.36 | 57.4 | ANN (S123P) | Qt−1, Qt−2, Qt−3, P | 5.77 | 0.41 | 3.86 | 0.43 | 54.1 |
| NLR(S1) | Qt−1 | 9.48 | 0.68 | 5.98 | 0.14 | 57.6 | NLR (S1P) | Qt−1, P | 8.36 | 0.60 | 5.92 | 0.19 | 51.6 |
| NLR (S12) | Qt−1, Qt−2 | 7.14 | 0.51 | 5.20 | 0.28 | 58.2 | NLR (S12P) | Qt−1, Qt−2, P | 5.69 | 0.41 | 4.00 | 0.49 | 53.1 |
| NLR (S123) | Qt−1, Qt−2, Qt−3 | 6.07 | 0.43 | 4.65 | 0.39 | 58.4 | NLR (S123P) | Qt−1, Qt−2, Qt−3, P | 6.17 | 0.44 | 4.09 | 0.46 | 52.6 |
| CB (S1M) | Qt−1, MN | 3.80 | 0.27 | 2.91 | 0.51 | 42.15 | CB (S1MP) | Qt−1, MN, P | 3.10 | 0.22 | 2.16 | 0.63 | 15.8 |
| CB (S12M) | Qt−1, Qt−2, MN | 3.37 | 0.24 | 2.58 | 0.56 | 43.15 | CB (S12MP) | Qt−1, Qt−2, MN, P | 4.08 | 0.29 | 2.82 | 0.52 | 16.3 |
| CB (S123M) | Qt−1, Qt−2, Qt−3, MN | 4.49 | 0.32 | 2.91 | 0.51 | 42.18 | CB (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 4.50 | 0.32 | 2.86 | 0.51 | 15.8 |
| RF (S1M) | Qt−1, MN | 4.63 | 0.33 | 3.15 | 0.51 | 43.32 | RF (S1MP) | Qt−1, MN, P | 3.60 | 0.26 | 2.58 | 0.63 | 18 |
| RF (S12M) | Qt−1, Qt−2, MN | 4.43 | 0.31 | 2.94 | 0.50 | 44.18 | RF (S12MP) | Qt−1, Qt−2, MN, P | 3.78 | 0.27 | 2.59 | 0.56 | 19.5 |
| RF (S123M) | Qt−1, Qt−2, Qt−3, MN | 4.56 | 0.32 | 2.99 | 0.49 | 45.78 | RF (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 3.88 | 0.28 | 2.63 | 0.55 | 18.9 |
| XGB (S1M) | Qt−1, MN | 4.37 | 0.31 | 3.59 | 0.51 | 40.59 | XGB (S1MP) | Qt−1, MN, P | 3.65 | 0.26 | 2.75 | 0.53 | 20.8 |
| XGB (S12M) | Qt−1, Qt−2, MN | 4.38 | 0.31 | 2.98 | 0.50 | 39.18 | XGB (S12MP) | Qt−1, Qt−2, MN, P | 3.67 | 0.25 | 2.76 | 0.59 | 21.5 |
| XGB (S123M) | Qt−1, Qt−2, Qt−3, MN | 4.17 | 0.3 | 2.86 | 0.52 | 40.12 | XGB (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 3.77 | 0.27 | 2.52 | 0.59 | 22.6 |
| ANN (S1M) | Qt−1, MN | 27.86 | 1.97 | 5.28 | 0.42 | 42 | ANN (S1MP) | Qt−1, MN, P | 3.92 | 0.28 | 1.03 | 0.54 | 21.1 |
| ANN (S12M) | Qt−1, Qt−2, MN | 27.30 | 1.95 | 5.28 | 0.42 | 43.5 | ANN (S12MP) | Qt−1, Qt−2, MN, P | 3.80 | 0.27 | 1.08 | 0.54 | 21.6 |
| ANN (S123M) | Qt−1, Qt−2, Qt−3, MN | 26.75 | 1.91 | 5.49 | 0.43 | 42.26 | ANN (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 4.12 | 0.29 | 1.05 | 0.53 | 23.5 |
| NLR(S1M) | Qt−1, MN | 5.41 | 0.38 | 3.59 | 0.39 | 43 | NLR (S1MP) | Qt−1, MN, P | 5.01 | 0.36 | 3.34 | 0.43 | 25.3 |
| NLR (S12M) | Qt−1, Qt−2, MN | 5.46 | 0.39 | 3.45 | 0.39 | 43.6 | NLR (S12MP) | Qt−1, Qt−2, MN, P | 4.81 | 0.34 | 3.37 | 0.43 | 24.2 |
| NLR (S123M) | Qt−1, Qt−2, Qt−3, MN | 5.25 | 0.37 | 3.70 | 0.37 | 42.5 | NLR (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 4.81 | 0.34 | 3.27 | 0.43 | 25.6 |
| Without TRMM Data | With TRMM Data | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model (Scenario) | Model Inputs | RMSE | rRMSE | MAE | MAPE | Model (Scenario) | Model Inputs | RMSE | rRMSE | MAE | MAPE | ||
| CB (S1) | Qt−1 | 71.88 | 0.69 | 53.03 | −0.26 | 42.3 | CB (S1P) | Qt−1, P | 51.41 | 0.49 | 36.7 | −16.83 | 39.5 |
| CB (S12) | Qt−1, Qt−2 | 61.36 | 0.59 | 44.83 | −0.06 | 45.2 | CB (S12P) | Qt−1, Qt−2, P | 50.26 | 0.48 | 37.09 | 0.12 | 38.6 |
| CB (S123) | Qt−1, Qt−2, Qt−3 | 63.89 | 0.61 | 49.82 | −0.18 | 44.8 | CB (S123P) | Qt−1, Qt−2, Qt−3, P | 56.25 | 0.54 | 44.09 | −0.05 | 37.6 |
| RF (S1) | Qt−1 | 66.98 | 0.64 | 50.21 | −0.19 | 45.3 | RF (S1P) | Qt−1, P | 47.51 | 0.46 | 34.15 | −17.23 | 43.5 |
| RF (S12) | Qt−1, Qt−2 | 59.93 | 0.57 | 44.52 | −0.06 | 48.5 | RF (S12P) | Qt−1, Qt−2, P | 51.04 | 0.49 | 37.66 | 0.11 | 42.5 |
| RF (S123) | Qt−1, Qt−2, Qt−3 | 63.25 | 0.61 | 46.81 | −0.11 | 46.8 | RF (S123P) | Qt−1, Qt−2, Qt−3, P | 55.60 | 0.53 | 40.59 | 0.04 | 43.8 |
| XGB (S1) | Qt−1 | 83.01 | 0.8 | 60.21 | −0.43 | 43.4 | XGB (S1P) | Qt−1, P | 50.49 | 0.48 | 37.83 | −17.53 | 40.5 |
| XGB (S12) | Qt−1, Qt−2 | 66.86 | 0.64 | 50.37 | −0.20 | 43.5 | XGB (S12P) | Qt−1, Qt−2, P | 56.27 | 0.54 | 40.95 | 0.03 | 40.15 |
| XGB (S123) | Qt−1, Qt−2, Qt−3 | 66.67 | 0.64 | 48.71 | −0.16 | 44.8 | XGB (S123P) | Qt−1, Qt−2, Qt−3, P | 58.15 | 0.56 | 42.81 | −0.02 | 41.5 |
| ANN (S1) | Qt−1 | 91.31 | 0.88 | 64.42 | −0.46 | 48.9 | ANN (S1P) | Qt−1, P | 55.54 | 0.54 | 41.23 | −19.11 | 43.5 |
| ANN (S12) | Qt−1, Qt−2 | 72.21 | 0.70 | 55.41 | −0.22 | 50.2 | ANN (S12P) | Qt−1, Qt−2, P | 60.77 | 0.59 | 44.64 | 0.03 | 44.8 |
| ANN (S123) | Qt−1, Qt−2, Qt−3 | 71.34 | 0.69 | 53.09 | −0.18 | 49.5 | ANN (S123P) | Qt−1, Qt−2, Qt−3, P | 62.22 | 0.60 | 46.66 | −0.02 | 44.9 |
| NLR (S1) | Qt−1 | 100.44 | 0.97 | 68.93 | −0.50 | 50.2 | NLR (S1P) | Qt−1, P | 61.09 | 0.59 | 44.94 | −20.83 | 44.32 |
| NLR (S12) | Qt−1, Qt−2 | 77.99 | 0.75 | 60.40 | −0.24 | 53.2 | NLR (S12P) | Qt−1, Qt−2, P | 65.63 | 0.63 | 48.66 | 0.03 | 43.9 |
| NLR (S123) | Qt−1, Qt−2, Qt−3 | 76.33 | 0.74 | 56.81 | −0.20 | 54.9 | NLR (S123P) | Qt−1, Qt−2, Qt−3, P | 66.58 | 0.64 | 50.39 | −0.02 | 43.72 |
| CB (S1M) | Qt−1, MN | 49.68 | 0.48 | 35.86 | 0.15 | 38.1 | CB (S1MP) | Qt−1, MN, P | 29.11 | 0.28 | 24.87 | 0.41 | 30.6 |
| CB (S12M) | Qt−1, Qt−2, MN | 49.78 | 0.48 | 37.32 | 0.11 | 36.5 | CB (S12MP) | Qt−1, Qt−2, MN, P | 44.30 | 0.43 | 33.19 | 0.21 | 31.2 |
| CB (S123M) | Qt−1, Qt−2, Qt−3, MN | 50.17 | 0.48 | 37.45 | 0.11 | 38.9 | CB (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 44.84 | 0.43 | 36.02 | 0.15 | 30.8 |
| RF (S1M) | Qt−1, MN | 49.68 | 0.48 | 36.20 | 0.14 | 38 | RF (S1MP) | Qt−1, MN, P | 33.41 | 0.32 | 26.79 | 0.41 | 32.35 |
| RF (S12M) | Qt−1, Qt−2, MN | 53.77 | 0.52 | 40.00 | 0.05 | 40.3 | RF (S12MP) | Qt−1, Qt−2, MN, P | 46.99 | 0.45 | 34.55 | 0.18 | 33.54 |
| RF (S123M) | Qt−1, Qt−2, Qt−3, MN | 58.40 | 0.56 | 42.03 | 0.00 | 39.5 | RF (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 51.63 | 0.5 | 36.86 | 0.13 | 35.6 |
| XGB (S1M) | Qt−1, MN | 47.71 | 0.46 | 36.29 | 0.14 | 40.1 | XGB (S1MP) | Qt−1, MN, P | 29.32 | 0.28 | 23.80 | 0.41 | 28.5 |
| XGB (S12M) | Qt−1, Qt−2, MN | 44.00 | 0.42 | 30.03 | 0.29 | 40.3 | XGB (S12MP) | Qt−1, Qt−2, MN, P | 45.25 | 0.43 | 31.59 | 0.25 | 28.4 |
| XGB (S123M) | Qt−1, Qt−2, Qt−3, MN | 45.36 | 0.44 | 33.94 | 0.19 | 42.8 | XGB (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 42.30 | 0.41 | 30.22 | 0.28 | 26.5 |
| ANN (S1M) | Qt−1, MN | 33.58 | 0.32 | 36.20 | 0.14 | 43.4 | ANN (S1MP) | Qt−1, MN, P | 31.21 | 0.29 | 24.74 | 0.44 | 35.8 |
| ANN (S12M) | Qt−1, Qt−2, MN | 32.24 | 0.31 | 36.20 | 0.14 | 45.2 | ANN (S12MP) | Qt−1, Qt−2, MN, P | 30.27 | 0.29 | 25.98 | 0.43 | 35.3 |
| ANN (S123M) | Qt−1, Qt−2, Qt−3, MN | 32.57 | 0.31 | 37.29 | 0.14 | 43.5 | ANN (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 29.65 | 0.29 | 24.25 | 0.46 | 35.7 |
| NLR (S1M) | Qt−1, MN | 50.66 | 0.49 | 36.08 | 0.14 | 41.3 | NLR (S1MP) | Qt−1, MN, P | 32.13 | 0.30 | 26.51 | 0.37 | 37.2 |
| NLR (S12M) | Qt−1, Qt−2, MN | 52.69 | 0.51 | 35.36 | 0.13 | 43.5 | NLR (S12MP) | Qt−1, Qt−2, MN, P | 32.45 | 0.31 | 27.31 | 0.35 | 37.8 |
| NLR (S123M) | Qt−1, Qt−2, Qt−3, MN | 52.18 | 0.50 | 36.44 | 0.14 | 44.4 | NLR (S123MP) | Qt−1, Qt−2, Qt−3, MN, P | 33.42 | 0.32 | 25.18 | 0.36 | 38.9 |
| Without TRMM Data | With TRMM Data | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model (Scenario) | Model Inputs | RMSE | rRMSE | MAE | MAPE | Model (Scenario) | Model Inputs | RMSE | rRMSE | MAE | MAPE | ||
| CB (S1314) | Q1413, Q1414 | 33.51 | 0.32 | 22.84 | 0.46 | 23.5 | CB (S1314P) | Q1413, Q1414, P | 31 | 0.3 | 23.76 | 0.44 | 18.5 |
| CB (S1314M) | Q1413, Q1414, MN | 30.48 | 0.29 | 22.72 | 0.46 | 21 | CB (S1314MP) | Q1413, Q1414, MN, P | 25.8 | 0.25 | 20.39 | 0.52 | 15.3 |
| RF (S1314) | Q1413, Q1414 | 32.60 | 0.31 | 21.30 | 0.49 | 26.8 | RF (S1314P) | Q1413, Q1414, P | 27.7 | 0.27 | 20.44 | 0.52 | 23.1 |
| RF (S1314M) | Q1413, Q1414, MN | 29.04 | 0.27 | 18.85 | 0.55 | 25 | RF (S1314MP) | Q1413, Q1414, MN, P | 28.7 | 0.28 | 21.68 | 0.52 | 18.8 |
| XGB (S1314) | Q1413, Q1414 | 48.59 | 0.47 | 30.38 | 0.28 | 23.5 | XGB (S1314P) | Q1413, Q1414, P | 28.2 | 0.27 | 21.67 | 0.49 | 18.5 |
| XGB (S1314M) | Q1413, Q1414, MN | 38.63 | 0.37 | 25.03 | 0.41 | 21 | XGB (S1314MP) | Q1413, Q1414, MN, P | 27.1 | 0.26 | 21.22 | 0.52 | 15.65 |
| ANN (S1314) | Q1413, Q1414 | 53.45 | 0.52 | 33.42 | 0.31 | 29.5 | ANN (S1314P) | Q1413, Q1414, P | 31.02 | 0.30 | 23.62 | 0.52 | 18.5 |
| ANN (S1314M) | Q1413, Q1414, MN | 41.72 | 0.40 | 27.53 | 0.45 | 27.5 | ANN (S1314MP) | Q1413, Q1414, MN, P | 29.27 | 0.28 | 23.34 | 0.56 | 25.45 |
| NLR (S1314) | Q1413, Q1414 | 58.80 | 0.57 | 36.09 | 0.34 | 33.2 | NLR (S1314P) | Q1413, Q1414, P | 34.12 | 0.33 | 25.51 | 0.56 | 29.5 |
| NLR (S1314M) | Q1413, Q1414, MN | 45.06 | 0.43 | 29.46 | 0.48 | 30.3 | NLR (S1314MP) | Q1413, Q1414, MN, P | 31.61 | 0.30 | 24.97 | 0.61 | 27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehraein, M.; Mohanavelu, A.; Naganna, S.R.; Kulls, C.; Kisi, O. Monthly Streamflow Prediction by Metaheuristic Regression Approaches Considering Satellite Precipitation Data. Water 2022, 14, 3636. https://doi.org/10.3390/w14223636
Mehraein M, Mohanavelu A, Naganna SR, Kulls C, Kisi O. Monthly Streamflow Prediction by Metaheuristic Regression Approaches Considering Satellite Precipitation Data. Water. 2022; 14(22):3636. https://doi.org/10.3390/w14223636
Chicago/Turabian StyleMehraein, Mojtaba, Aadhityaa Mohanavelu, Sujay Raghavendra Naganna, Christoph Kulls, and Ozgur Kisi. 2022. "Monthly Streamflow Prediction by Metaheuristic Regression Approaches Considering Satellite Precipitation Data" Water 14, no. 22: 3636. https://doi.org/10.3390/w14223636