Uncertainties in Riverine and Coastal Flood Impacts under Climate Change
Abstract
:1. Introduction
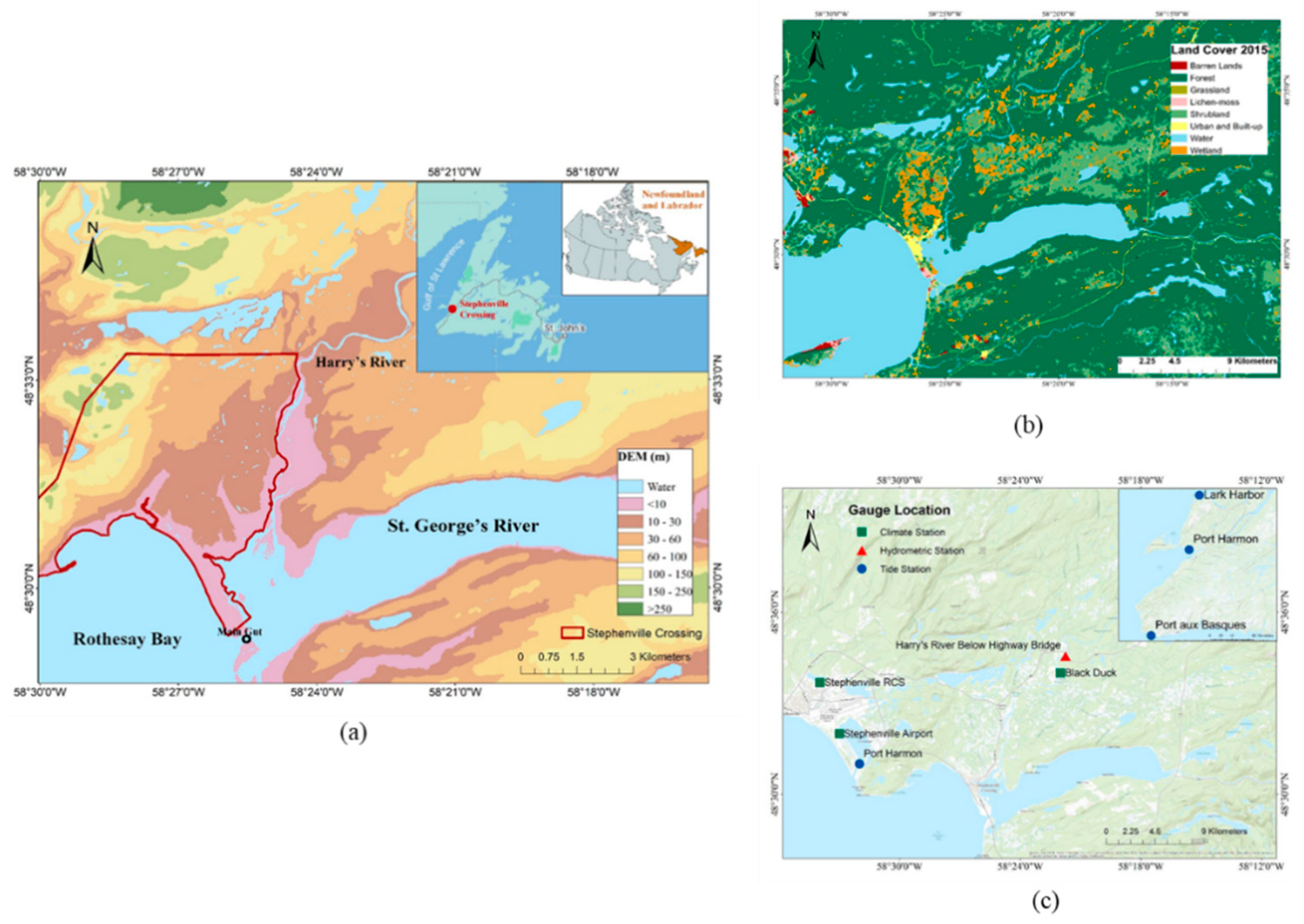
2. Study Area and Data
2.1. Data
2.1.1. Climate Projections
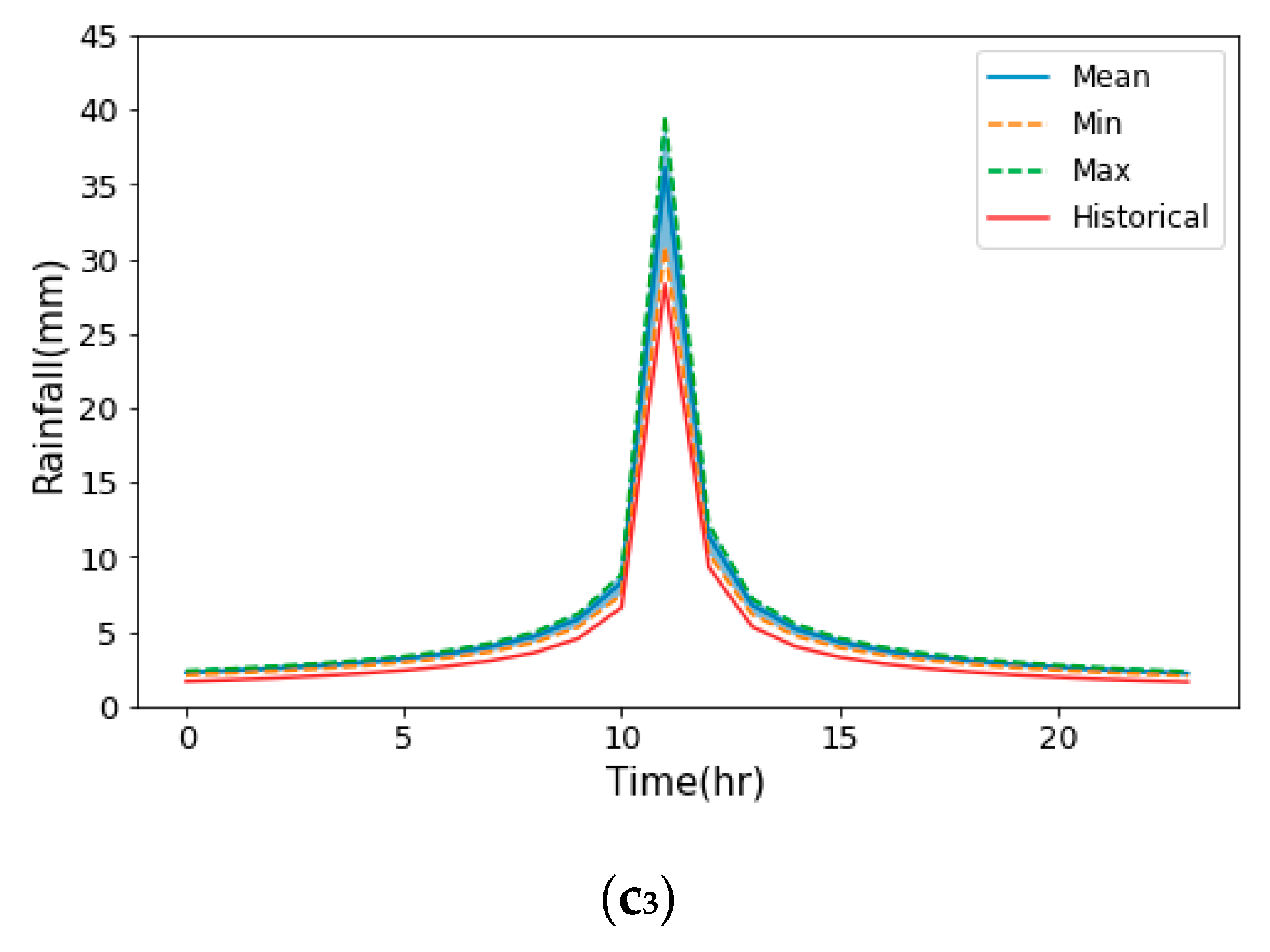
2.1.2. Intensity–Duration–Frequency (IDF) Curves
2.1.3. Projected IDF Curves
2.1.4. Coastal Components
2.1.5. Satellite Imagery
3. Methodology
3.1. Design Storms
3.1.1. Method of SCS
3.1.2. Method of Huff
3.1.3. Alternating Block Method (ABM)
3.2. Hydrologic and Hydraulic Model Setup and Calibration
3.2.1. HEC-HMS
3.2.2. HEC-RAS
4. Results and Discussion
4.1. Model Performance
4.2. GCM-IDF vs. WRF-IDF Simulations
4.2.1. Uncertainties in Storm Patterns
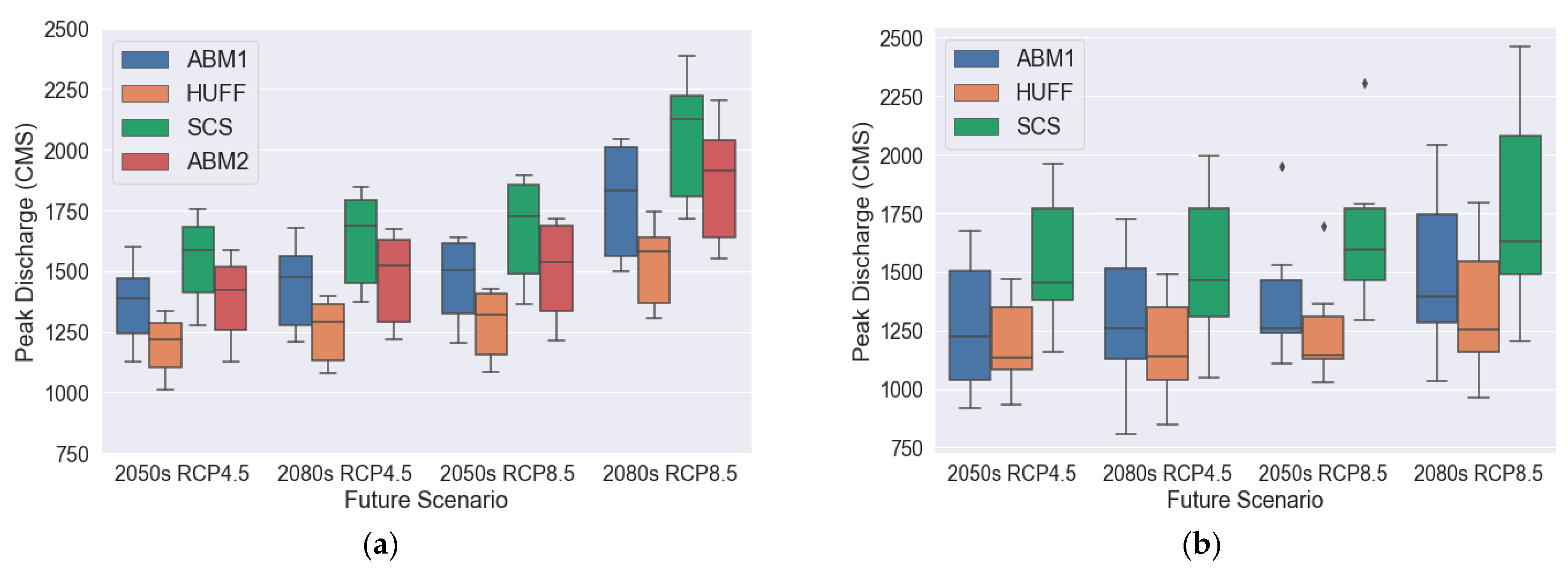
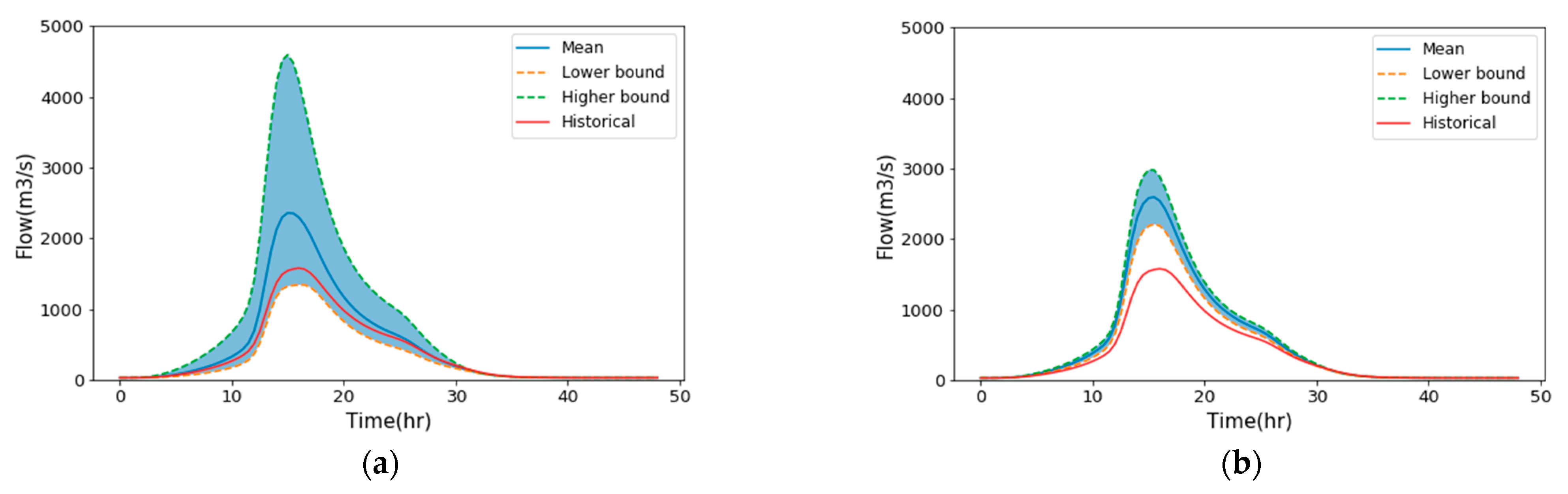
4.2.2. Uncertainties in Flow Hydrographs
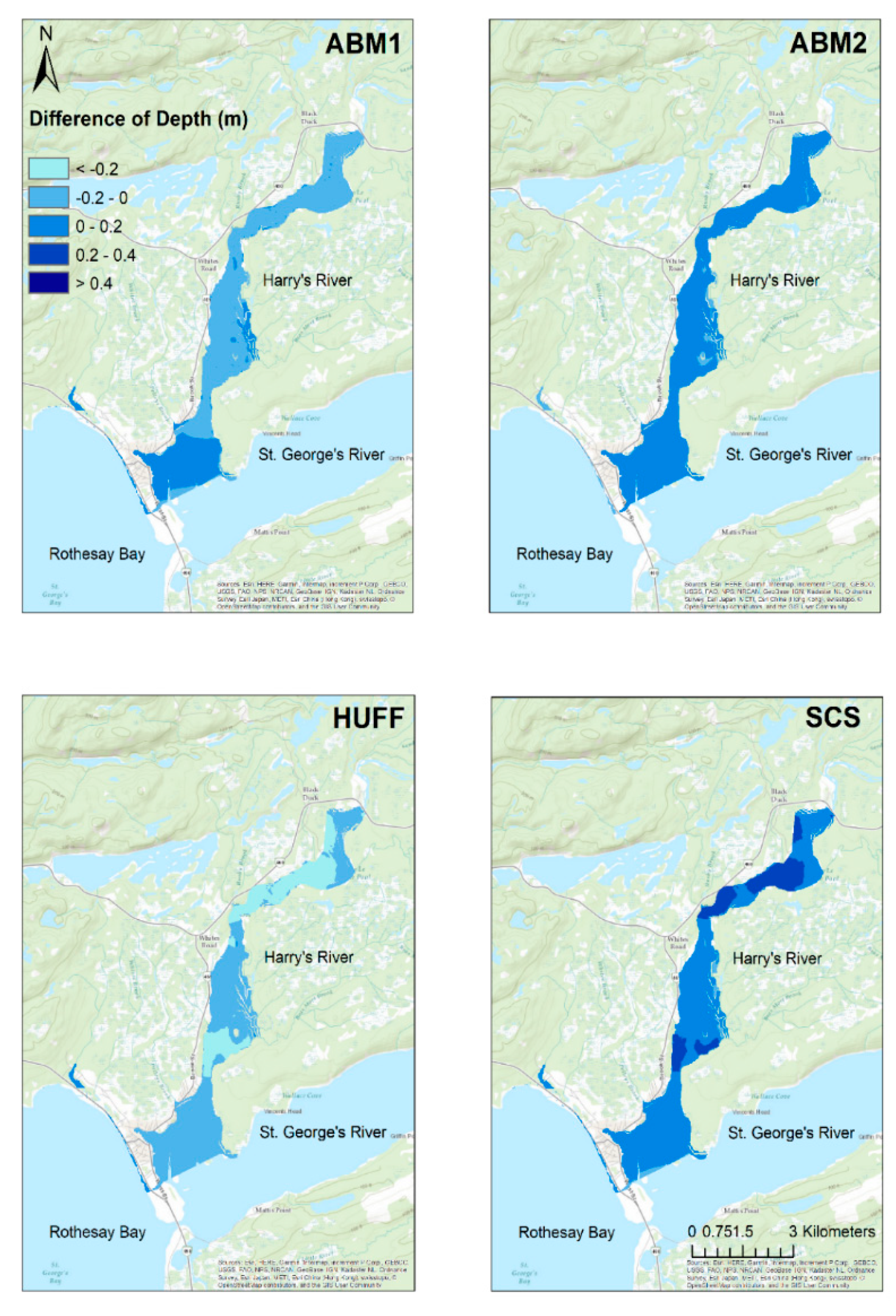
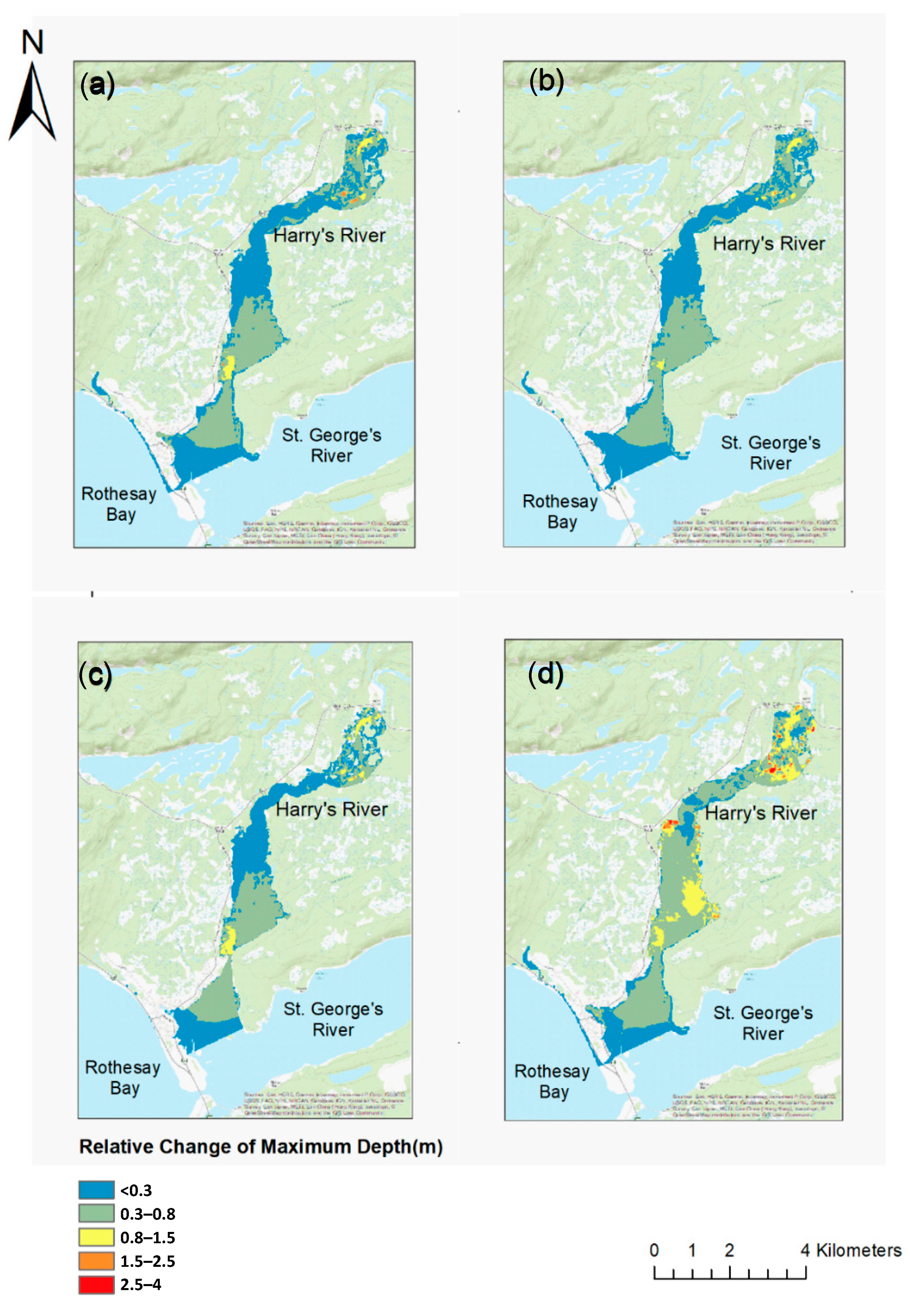
4.3. Projected Changes in Flood Characteristics and the Corresponding Uncertainties
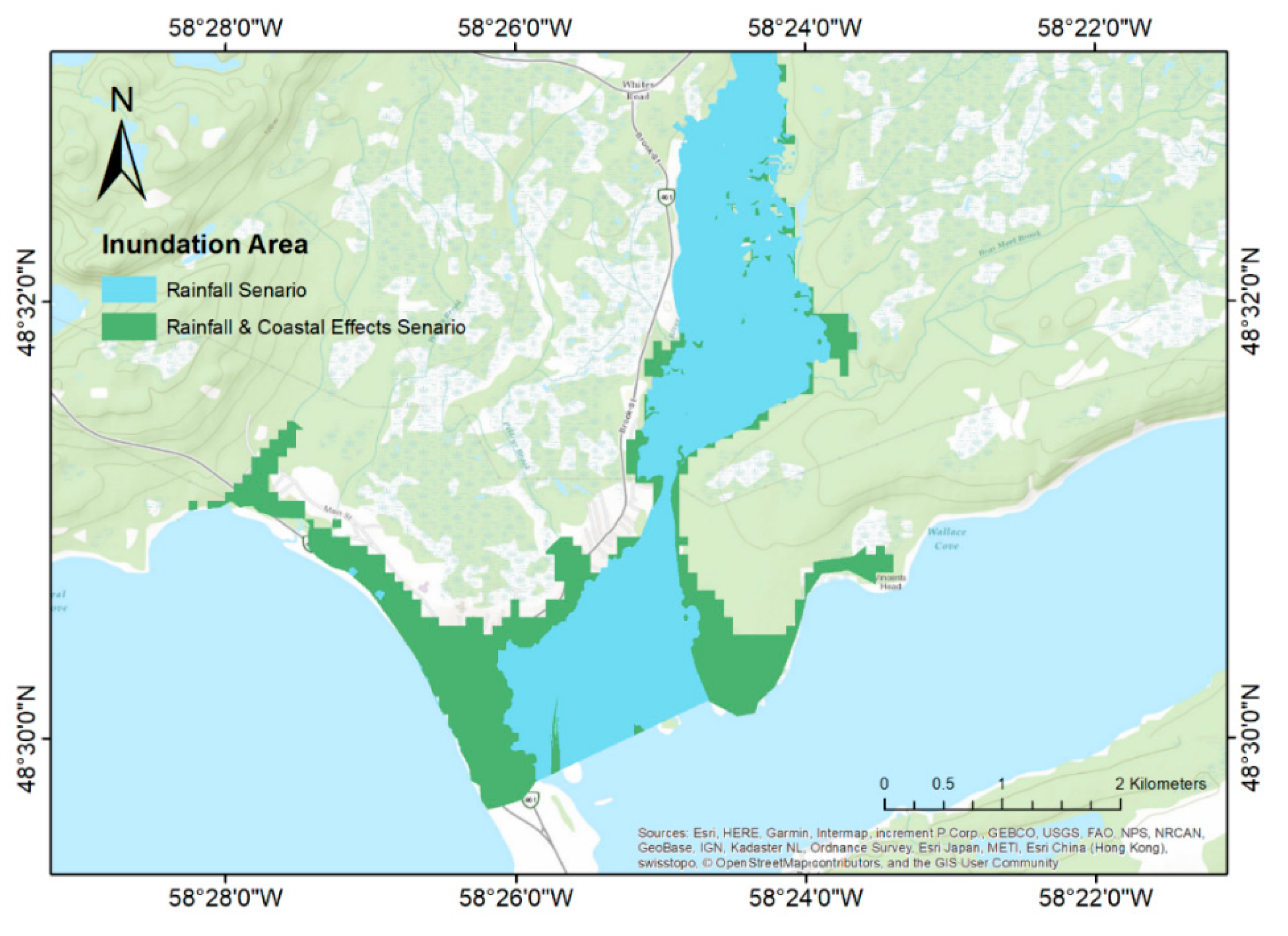
4.4. Compound Flood Assessment
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- United Nations Office for Disaster Risk Reduction; Centre for Research on the Epidemiology of Disaster. The Human Cost of Natural Disasters: A Global Perspective; UN Office for Disaster Risk Reduction: Geneva, Switzerland; Centre for Research on the Epidemiology of Disasters: Brussels, Belgium, 2015. [Google Scholar]
- Office of the Parliamentary Budget Officer. Estimate of the Average Annual Cost for Disaster Financial Assistance Arrangements Due to Weather Events; Office of the Parliamentary Budget Officer: Ottawa, ON, Canada, 2016. [Google Scholar]
- Atlantic Climate Adaption Solutions Association. Flood Risk and Vulnerability Analysis Project. 2012. Available online: https://atlanticadaptation.ca/en/islandora/object/acasa%253A446 (accessed on 26 June 2021).
- Zhou, Q.; Mikkelsen, P.S.; Halsnæs, K.; Arnbjerg-Nielsen, K. Framework for economic pluvial flood risk assessment considering climate change effects and adaptation benefits. J. Hydrol. 2012, 414, 539–549. [Google Scholar] [CrossRef]
- Kaspersen, P.S.; Ravn, N.H.; Arnbjerg-Nielsen, K.; Madsen, H.; Drews, M. Comparison of the impacts of urban devel-opment and climate change on exposing European cities to pluvial flooding. Hydrol. Earth Syst. Sci. 2017, 21, 4131–4147. [Google Scholar] [CrossRef] [Green Version]
- Pregnolato, M.; Ford, A.; Glenis, V.; Wilkinson, S.; Dawson, R. Impact of Climate Change on Disruption to Urban Transport Networks from Pluvial Flooding. J. Infrastruct. Syst. 2017, 23, 04017015. [Google Scholar] [CrossRef] [Green Version]
- Evans, B.; Chen, A.S.; Djordjević, S.; Webber, J.; Gómez, A.G.; Stevens, J. Investigating the Effects of Pluvial Flooding and Climate Change on Traffic Flows in Barcelona and Bristol. Sustainability 2020, 12, 2330. [Google Scholar] [CrossRef] [Green Version]
- Wilby, R.L.; Beven, K.J.; Reynard, N. Climate change and fluvial flood risk in the UK: More of the same? Hydrol. Process. 2008, 22, 2511–2523. [Google Scholar] [CrossRef]
- Van PD, T.; Popescu, I.; Van Griensven, A.; Solomatine, D.P.; Trung, N.H.; Green, A. A study of the climate change im-pacts on fluvial flood propagation in the Vietnamese Mekong Delta. Hydrol. Earth Syst. Sci. 2012, 16, 4637–4649. [Google Scholar] [CrossRef] [Green Version]
- Eccles, R.; Zhang, H.; Hamilton, D. A review of the effects of climate change on riverine flooding in subtropical and trop-ical regions. J. Water Clim. Chang. 2019, 10, 687–707. [Google Scholar] [CrossRef]
- Purvis, M.J.; Bates, P.D.; Hayes, C.M. A probabilistic methodology to estimate future coastal flood risk due to sea level rise. Coast. Eng. 2008, 55, 1062–1073. [Google Scholar] [CrossRef]
- Thompson, K.R.; Bernier, N.B.; Chan, P. Extreme sea levels, coastal flooding and climate change with a focus on Atlantic Canada. Nat. Hazards 2009, 51, 139–150. [Google Scholar] [CrossRef]
- Garner, A.J.; Mann, M.E.; Emanuel, K.A.; Kopp, R.E.; Lin, N.; Alley, R.B.; Horton, B.P.; DeConto, R.M.; Donnelly, J.P.; Pollard, D. Impact of climate change on New York City’s coastal flood hazard: Increasing flood heights from the preindustrial to 2300 CE. Proc. Natl. Acad. Sci. USA 2017, 114, 11861–11866. [Google Scholar] [CrossRef] [Green Version]
- Didier, D.; Baudry, J.; Bernatchez, P.; Dumont, D.; Sadegh, M.; Bismuth, E.; Bandet, M.; Dugas, S.; Sévigny, C. Multihazard simulation for coastal flood mapping: Bathtub versus numerical modelling in an open estuary, Eastern Canada. J. Flood Risk Manag. 2019, 12, 12505. [Google Scholar] [CrossRef]
- Zhang, X.; Flato, G.; Kirchmeier-Young, M.; Vincent, L.; Wan, H.; Wang, X.; Rong, R.; Fyfe, J.; Li, G.; Kharin, V.V. Changes in Temperature and Precipitation across Canada. In Canada’s Changing Climate Report; Bush, E., Lemmen, D.S., Eds.; Government of Canada: Ottawa, ON, USA, 2019; Chapter 4; pp. 112–193. [Google Scholar]
- Abbasian, M.S.; Abrishamchi, A.; Najafi, M.R.; Moghim, S. Multi-site statistical downscaling of precipitation using generalized hier-archical linear models: A case study of the imperilled Lake Urmia basin. Hydrol. Sci. J. 2020, 65, 2466–2481. [Google Scholar] [CrossRef]
- Abbasian, M.S.; Najafi, M.R.; Abrishamchi, A. Increasing risk of meteorological drought in the Lake Urmia basin under climate change: Introducing the precipitation–temperature deciles index. J. Hydrol. 2021, 592, 125586. [Google Scholar] [CrossRef]
- Kay, A.L.; Davies, H.N.; Bell, V.A.; Jones, R. Comparison of uncertainty sources for climate change impacts: Flood frequency in England. Clim. Chang. 2009, 92, 41–63. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H.; Jung, I.W. Assessing the uncertainties of hydrologic model selection in climate change impact studies. Hydrol. Process. 2011, 25, 2814–2826. [Google Scholar] [CrossRef]
- Najafi, M.R.; Zwiers, F.W.; Gillett, N.P. Attribution of Observed Streamflow Changes in Key British Columbia Drainage Basins. Geophys. Res. Lett. 2017, 44, 11–12. [Google Scholar] [CrossRef]
- Falconer, R.; Cobby, D.; Smyth, P.; Astle, G.; Dent, J.; Golding, B. Pluvial flooding: New approaches in flood warning, mapping and risk management. J. Flood Risk Manag. 2009, 2, 198–208. [Google Scholar] [CrossRef]
- Yin, J.; Yu, D.; Yin, Z.; Liu, M.; He, Q. Evaluating the impact and risk of pluvial flash flood on intra-urban road network: A case study in the city center of Shanghai, China. J. Hydrol. 2016, 537, 138–145. [Google Scholar] [CrossRef] [Green Version]
- Maksimović, Č.; Prodanović, D.; Boonya-Aroonnet, S.; Leitão, J.P.; Djordjević, S.; Allitt, R. Overland flow and pathway analysis for modelling of urban pluvial flooding. J. Hydraul. Res. 2009, 47, 512–523. [Google Scholar] [CrossRef]
- Yu, D.; Lane, S. Urban fluvial flood modelling using a two-dimensional diffusion-wave treatment, part 1: Mesh resolution effects. Hydrol. Process. 2004, 20, 1085–1092. [Google Scholar] [CrossRef]
- Xue, X.; Wang, N.; Ellingwood, B.R.; Zhang, K. The impact of climate change on resilience of communities vulnerable to riverine flooding. In Climate Change and Its Impacts; Springer: Cham, Switzerland, 2018; pp. 129–144. [Google Scholar]
- Bates, P.D.; Dawson, R.J.; Hall, J.W.; Horritt, M.S.; Nicholls, R.J.; Wicks, J.; Hassan, M.A.A.M. Simplified two-dimensional numerical modelling of coastal flooding and example applications. Coast. Eng. 2005, 52, 793–810. [Google Scholar] [CrossRef]
- Didier, D.; Bernatchez, P.; Boucher-Brossard, G.; Lambert, A.; Fraser, C.; Barnett, R.L.; Van-Wierts, S. Coastal flood as-sessment based on field debris measurements and wave runup empirical model. J. Mar. Sci. Eng. 2015, 3, 560–590. [Google Scholar] [CrossRef]
- Ganguli, P.; Merz, B. Extreme Coastal Water Levels Exacerbate Fluvial Flood Hazards in Northwestern Europe. Sci. Rep. 2019, 9, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Najafi, M.R.; Zhang, Y.; Martyn, N. A flood risk assessment framework for interdependent infrastructure systems in coastal envi-ronments. Sustain.Cities Soc. 2021, 64, 102516. [Google Scholar] [CrossRef]
- Serafin, K.A.; Ruggiero, P.; Parker, K.; Hill, D.F. What’s streamflow got to do with it? A probabilistic simulation of the competing oceanographic and fluvial processes driving extreme along-river water levels. Nat. Hazards Earth Syst. Sci. 2019, 19, 1415–1431. [Google Scholar] [CrossRef] [Green Version]
- Lian, J.; Xu, K.; Ma, C. Joint impact of rainfall and tidal level on flood risk in a coastal city with a complex river net-work: A case study of Fuzhou city, China. Hydrol. Earth Syst. Sci. 2013, 17, 679. [Google Scholar] [CrossRef] [Green Version]
- Zheng, F.; Westra, S.; Sisson, S.A. Quantifying the dependence between extreme rainfall and storm surge in the coastal zone. J. Hydrol. 2013, 505, 172–187. [Google Scholar] [CrossRef]
- Wahl, T.; Jain, S.; Bender, J.; Meyers, S.; Luther, M.E. Increasing risk of compound flooding from storm surge and rainfall for major US cities. Nat. Clim. Chang. 2015, 5, 1093–1097. [Google Scholar] [CrossRef]
- Zhang, Y.; Najafi, M.R. Probabilistic Numerical Modeling of Compound Flooding Caused by Tropical Storm Matthew Over a Da-ta-Scarce Coastal Environment. Water Resour. Res. 2020, 56, e2020WR028565. [Google Scholar] [CrossRef]
- Bevacqua, E.; Maraun, D.; Vousdoukas, M.I.; Voukouvalas, E.; Vrac, M.; Mentaschi, L.; Widmann, M. Higher probability of compound flooding from precipitation and storm surge in Europe under anthropogenic climate change. Sci. Adv. 2019, 5, eaaw5531. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Couasnon, A.; Eilander, D.; Muis, S.; Veldkamp, T.I.E.; Haigh, I.D.; Wahl, T.; Winsemius, H.C.; Ward, P.J. Measuring compound flood potential from river discharge and storm surge extremes at the global scale. Nat. Hazards Earth Syst. Sci. 2020, 20, 489–504. [Google Scholar] [CrossRef] [Green Version]
- Ikeuchi, H.; Hirabayashi, Y.; Yamazaki, D.; Muis, S.; Ward, P.J.; Winsemius, H.C.; Verlaan, M.; Kanae, S. Compound simulation of fluvial floods and storm surges in a global coupled river-coast flood model: Model development and its application to 2007 C yclone S idr in B angladesh. J. Adv. Modeling Earth Syst. 2017, 9, 1847–1862. [Google Scholar] [CrossRef]
- Jalili Pirani, F.; Najafi, M.R. Recent trends in individual and multivariate compound flood drivers in Canada’s coasts. Water Re-sour. Res. 2020, 56, e2020WR027785. [Google Scholar] [CrossRef]
- Kumbier, K.; Carvalho, R.C.; Vafeidis, A.T.; Woodroffe, C.D. Investigating Compound Flooding in an Estuary Using Hydrodynamic Modelling: A Case Study from the Shoalhaven River, Australia. Nat. Hazards Earth Syst. Sci. 2018, 18, 463–477. [Google Scholar] [CrossRef] [Green Version]
- Bunya, S.; Dietrich, J.C.; Westerink, J.J.; Ebersole, B.A.; Smith, J.M.; Atkinson, J.H.; Jensen, R.; Resio, D.T.; Luettich, R.A.; Dawson, C.; et al. A High-Resolution Coupled Riverine Flow, Tide, Wind, Wind Wave, and Storm Surge Model for Southern Louisiana and Mississippi. Part I: Model Development and Validation. Mon. Weather. Rev. 2010, 138, 345–377. [Google Scholar] [CrossRef] [Green Version]
- Ray, T.; Stepinski, E.; Sebastian, A.; Bedient, P.B. Dynamic Modeling of Storm Surge and Inland Flooding in a Texas Coastal Floodplain. J. Hydraul. Eng. 2011, 137, 1103–1110. [Google Scholar] [CrossRef]
- Bacopoulos, P.; Tang, Y.; Wang, D.; Hagen, S.C. Integrated Hydrologic-Hydrodynamic Modeling of Estuarine-Riverine Flooding: 2008 Tropical Storm Fay. J. Hydrol. Eng. 2017, 22, 04017022. [Google Scholar] [CrossRef]
- Bakhtyar, R.; Maitaria, K.; Velissariou, P.; Trimble, B.; Mashriqui, H.; Moghimi, S.; Abdolali, A.; van der Westhuysen, A.J.; Ma, Z.; Clark, E.P.; et al. A new 1D/2D coupled modeling approach for a riverine-estuarine system under storm events: Application to Delaware River Basin. J. Geophys. Res. Oceans 2020, 125, e2019JC015822. [Google Scholar] [CrossRef]
- Lee, C.; Hwang, S.; Do, K.; Son, S. Increasing flood risk due to river runoff in the estuarine area during a storm landfall. Estuar. Coast. Shelf Sci. 2019, 221, 104–118. [Google Scholar] [CrossRef]
- Pasquier, U.; He, Y.; Hooton, S.; Goulden, M.; Hiscock, K.M. An integrated 1D–2D hydraulic modelling approach to assess the sensitivity of a coastal region to compound flooding hazard under climate change. Nat. Hazards 2018, 98, 915–937. [Google Scholar] [CrossRef] [Green Version]
- Ganguli, P.; Paprotny, D.; Hasan, M.; Güntner, A.; Merz, B. Projected Changes in Compound Flood Hazard from Riverine and Coastal Floods in Northwestern Europe. Earth’s Future 2020, 8, e2020EF001752. [Google Scholar] [CrossRef]
- Garcia, E.S.; Loáiciga, H.A. Sea-level rise and flooding in coastal riverine flood plains. Hydrol. Sci. J. 2013, 59, 204–220. [Google Scholar] [CrossRef] [Green Version]
- Ghanbari, M.; Arabi, M.; Kao, S.; Obeysekera, J.; Sweet, W. Climate Change and Changes in Compound Coastal-Riverine Flooding Hazard Along the U.S. Coasts. Earth’s Future 2021, 9, e2021EF002055. [Google Scholar] [CrossRef]
- Moftakhari, H.R.; Salvadori, G.; AghaKouchak, A.; Sanders, B.; Matthew, R.A. Compounding effects of sea level rise and fluvial flooding. Proc. Natl. Acad. Sci. USA 2017, 114, 9785–9790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maraun, D.; Wetterhall, F.; Ireson, A.; Chandler, R.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48, RG3003. [Google Scholar] [CrossRef]
- Canada, S. 2016 Census of Canada: Technical Report; Statistics Canada: Ottawa, ON, Canada, 2016. [Google Scholar]
- Government of Newfoundland and Labrador. Hydrotechnical Study of Stephenville Crossing/Black Duck Siding; Water Resources Management Division, Department of Environment and Conservation: St. John’s, NL, Canada, 2012. [Google Scholar]
- Vitousek, S.; Barnard, P.L.; Fletcher, C.H.; Frazer, N.; Erikson, L.; Storlazzi, C.D. Doubling of coastal flooding frequency within decades due to sea-level rise. Sci. Rep. 2017, 7, 1399. [Google Scholar] [CrossRef] [PubMed]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill Interamericana: New York, NY, USA, 1959. [Google Scholar]
- Perez, J.; Menendez, M.; Mendez, F.J.; Losada, I.J. Evaluating the performance of cmip3 and cmip5 global climate models over the north-east Atlantic region. Climat. Dyn. 2014, 43, 2663–2680. [Google Scholar] [CrossRef]
- Mahmoudi, M.H.; Najafi, M.R.; Singh, H.; Schnorbus, M. Spatial and temporal changes in climate extremes over northwestern North America: The influence of internal climate variability and external forcing. Clim. Chang. 2021, 165, 1–19. [Google Scholar] [CrossRef]
- Singh, H.; Najafi, M.R.; Cannon, A.J. Characterizing non-stationary compound extreme events in a changing climate based on large-ensemble climate simulations. Clim. Dyn. 2021, 56, 1389–1405. [Google Scholar] [CrossRef]
- Simonovic, S.P.; Schardong, A.; Sandink, D.; Srivastav, R. A web-based tool for the development of Intensity Duration Frequency curves under changing climate. Environ. Model. Softw. 2016, 81, 136–153. [Google Scholar] [CrossRef]
- Rasmussen, K.L.; Prein, A.F.; Rasmussen, R.M.; Ikeda, K.; Liu, C. Changes in the convective population and thermodynamic environ-ments in convection-permitting regional climate simulations over the United States. Climat. Dyn. 2020, 55, 383–408. [Google Scholar] [CrossRef]
- Kimura, F.; Kitoh, A. Downscaling by Pseudo Global Warming Method; The Final Report of ICCAP; Research Institute for Humanity and Nature: Kyoto, Japan, 2007; pp. 43–46. [Google Scholar]
- Mugume, I.; Basalirwa, C.P.; Waiswa, D.; Ngailo, T. Spatial variation of WRF model rainfall prediction over Uganda. J. Environ. Chem. Ecol. Geol. Geophys. Eng. 2017, 11, 553–557. [Google Scholar]
- Innocenti, S.; Mailhot, A.; Frigon, A.; Cannon, A.J.; LeDuc, M. Observed and Simulated Precipitation over Northeastern North America: How Do Daily and Subdaily Extremes Scale in Space and Time? J. Clim. 2019, 32, 8563–8582. [Google Scholar] [CrossRef]
- Prein, A.F.; Rasmussen, R.M.; Ikeda, K.; Liu, C.; Clark, M.P.; Holland, A.F.P.R.M.R.K.I.C.L.M.P.C.G.J. The future intensification of hourly precipitation extremes. Nat. Clim. Chang. 2017, 7, 48–52. [Google Scholar] [CrossRef]
- Cannon, A.J.; Innocenti, S. Projected intensification of sub-daily and daily rainfall extremes in convection-permitting climate model simulations over North America: Implications for future intensity–duration–frequency curves. Nat. Hazards Earth Syst. Sci. 2019, 19, 421–440. [Google Scholar] [CrossRef] [Green Version]
- Pall, P.; Allen, M.R.; Stone, D.A. Testing the Clausius–Clapeyron constraint on changes in extreme precipitation under CO2 warming. Climat. Dyn. 2007, 28, 351–363. [Google Scholar] [CrossRef]
- Batterson, M.; Liverman, D. Past and Future Sea-Level Change in Newfoundland and Labrador: Guidelines for Policy and Planning: Current Research; Report 10–1; Newfoundland and Labrador Department of Natural Resources Geological Survey: St. John’s, NL, Canada, 2010. [Google Scholar]
- Tarasov, L.; Peltier, W. A geophysically constrained large ensemble analysis of the deglacial history of the North American ice-sheet complex. Quat. Sci. Rev. 2004, 23, 359–388. [Google Scholar] [CrossRef]
- Karim, M.; Mimura, N. Impacts of climate change and sea-level rise on cyclonic storm surge floods in Bangladesh. Glob. Environ. Chang. 2008, 18, 490–500. [Google Scholar] [CrossRef]
- Long, S.; E Fatoyinbo, T.; Policelli, F. Flood extent mapping for Namibia using change detection and thresholding with SAR. Environ. Res. Lett. 2014, 9, 035002. [Google Scholar] [CrossRef]
- Twele, A.; Cao, W.; Plank, S.; Martinis, S. Sentinel-1-based flood mapping: A fully automated processing chain. Int. J. Remote Sens. 2016, 37, 2990–3004. [Google Scholar] [CrossRef]
- Pasmurov, A.; Zinoviev, J. Radar Imaging and Holography; Bibliovault OAI Repository, the University of Chicago Press: Chicago, IL, USA, 2005. [Google Scholar] [CrossRef]
- Senthilnath, J.; Shenoy, H.V.; Rajendra, R.; Omkar, S.N.; Mani, V.; Diwakar, P.G. Integration of speckle de-noising and image segmentation using Synthetic Aperture Radar image for flood extent extraction. J. Earth Syst. Sci. 2013, 122, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Razi, M.; Ariffin, J.; Tahir, W.; Arish, N. Flood Estimation Studies using Hydrologic Modeling System (HEC-HMS) for Johor River, Malaysia. J. Appl. Sci. 2010, 10, 930–939. [Google Scholar] [CrossRef] [Green Version]
- Halwatura, D.; Najim, M. Application of the HEC-HMS model for runoff simulation in a tropical catchment. Environ. Model. Softw. 2013, 46, 155–162. [Google Scholar] [CrossRef]
- Tassew, B.G.; Belete, M.A.; Miegel, K. Application of HEC-HMS Model for Flow Simulation in the Lake Tana Basin: The Case of Gilgel Abay Catchment, Upper Blue Nile Basin, Ethiopia. Hydrology 2019, 6, 21. [Google Scholar] [CrossRef] [Green Version]
- Chow, V.T. Applied Hydrology: International Edition; MacGraw-Hill, Inc.: New York, NY, USA, 1988; p. 149. [Google Scholar]
- US Army Corps of Engineers. Hydrologic Modeling System (HEC-HMS) Application Guide; Version 3.1.0; Institute for Water Resources: Davis, CA, USA, 2008. [Google Scholar]
- Singh, H.; Najafi, M.R. Evaluation of gridded climate datasets over Canada using univariate and bivariate approaches: Implications for hydrological modelling. J. Hydrol. 2020, 584, 124673. [Google Scholar] [CrossRef]
- Singh, H.; Pirani, F.J.; Najafi, M.R. Characterizing the temperature and precipitation covariability over Canada. Theor. Appl. Clim. 2019, 139, 1543–1558. [Google Scholar] [CrossRef]
- Wu, W.; Westra, S.; Leonard, M. Estimating the probability of compound floods in estuarine regions. Hydrol. Earth Syst. Sci. 2021, 25, 2821–2841. [Google Scholar] [CrossRef]
- Zscheischler, J.; Westra, S.; Hurk, B.J.J.M.V.D.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T.; et al. Future climate risk from compound events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Lowe, J.A.; Gregory, J.M.; Flather, R.A. Changes in the occurrence of storm surges around the United Kingdom under a future climate scenario using a dynamic storm surge model driven by the Hadley Centre climate models. Clim. Dyn. 2001, 18, 179–188. [Google Scholar] [CrossRef]
- Rahmstorf, S. Rising hazard of storm-surge flooding. Proc. Natl. Acad. Sci. USA 2017, 114, 11806–11808. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.-A.; Kim, S.; Son, S.; Mori, N.; Mase, H. Correction to: Assessment of uncertainties in projecting future changes to extreme storm surge height depending on future SST and greenhouse gas concentration scenarios. Clim. Chang. 2020, 162, 425–442. [Google Scholar] [CrossRef]
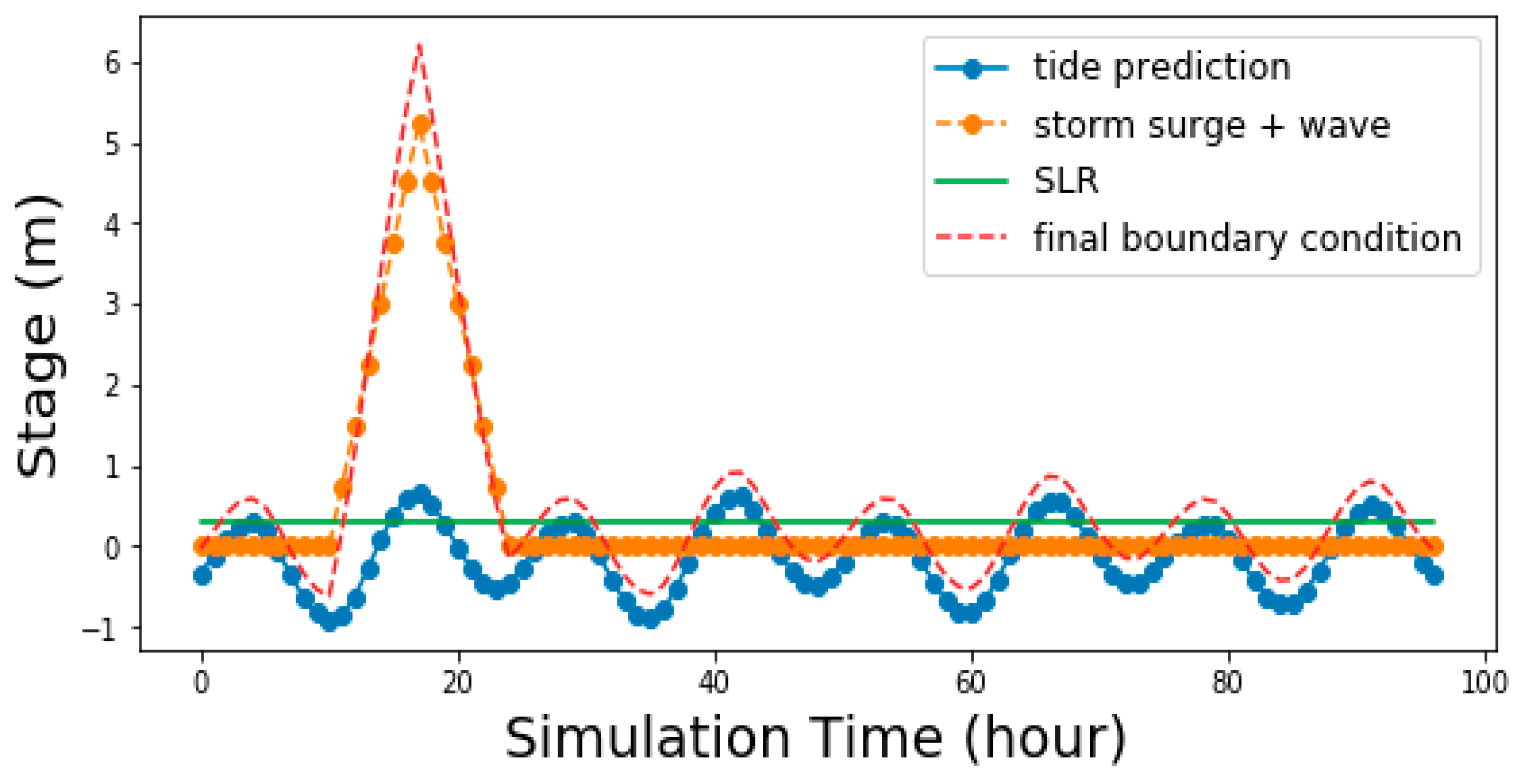





| Coastal Components | Scenarios | |
|---|---|---|
| Storm surge and wave (m) | 25-year event | 100-year event |
| 5.25 | 6.34 | |
| Sea-level rise (m) | 2050s period | 2080s period |
| 0.3 | 0.8 | |
| Return Period (Years) | Historical (mm) | Future (mm) | |||
|---|---|---|---|---|---|
| Period | RCP | The Multi-Model Ensemble Average of GCMs (Minimum and Maximum) | |||
| GCM-IDF | WRF-IDF | ||||
| 25 | 107.94 | 2050s | 4.5 | 131.44 (111.38, 152.31) | 137.17 (121.80, 147.35) |
| 8.5 | 135.75 (118.8, 169.00) | 143.03 (126.65, 154.14) | |||
| 2080s | 4.5 | 129.93 (105.00, 153.94) | 141.62 (127.04, 151.94) | ||
| 8.5 | 142.50 (113.86, 176.36) | 163.05 (145.5, 176.54) | |||
| 100 | 142.79 | 2050s | 4.5 | 184.82 (144.33, 233.31) | 169.73 (150.15, 182.70) |
| 8.5 | 185.32 (149.58, 241.31) | 177.20 (156.33, 191.35) | |||
| 2080s | 4.5 | 181.76 (124.37, 237.56) | 175.40 (156.83, 188.55) | ||
| 8.5 | 200.00 (133.85, 333.34) | 202.70 (180.34, 219.89) | |||
| Design Storm | 25-Year Event | Difference from Huff Method | 100-Year Event | Difference from Huff Method |
|---|---|---|---|---|
| ABM | 6.221 | 0.057 | 6.427 | 0.178 |
| SCS method | 6.21 | 0.046 | 6.431 | 0.182 |
| Huff method | 6.164 | 0 | 6.249 | 0 |
| Return Level | RCP | Future Period | Fluvial Flood Scenario | Compound Flood Scenario |
|---|---|---|---|---|
| Mean | Mean | |||
| 25-year event | 4.5 | 2050s | 6.16 | 6.66 |
| 2080s | 6.29 | 6.87 | ||
| 8.5 | 2050s | 6.28 | 6.75 | |
| 2080s | 6.78 | 7.3 | ||
| 100-year event | 4.5 | 2050s | 6.97 | 7.63 |
| 2080s | 7.88 | 8.7 | ||
| 8.5 | 2050s | 7.81 | 8.49 | |
| 2080s | 8.98 | 9.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Najafi, M.R.; Cannon, A.J.; Khan, A.A. Uncertainties in Riverine and Coastal Flood Impacts under Climate Change. Water 2021, 13, 1774. https://doi.org/10.3390/w13131774
Wang S, Najafi MR, Cannon AJ, Khan AA. Uncertainties in Riverine and Coastal Flood Impacts under Climate Change. Water. 2021; 13(13):1774. https://doi.org/10.3390/w13131774
Chicago/Turabian StyleWang, Shuyi, Mohammad Reza Najafi, Alex J. Cannon, and Amir Ali Khan. 2021. "Uncertainties in Riverine and Coastal Flood Impacts under Climate Change" Water 13, no. 13: 1774. https://doi.org/10.3390/w13131774
APA StyleWang, S., Najafi, M. R., Cannon, A. J., & Khan, A. A. (2021). Uncertainties in Riverine and Coastal Flood Impacts under Climate Change. Water, 13(13), 1774. https://doi.org/10.3390/w13131774







