Experimental Study on Hydraulic Conductivity and Resistance in Silty Sediments
Abstract
1. Introduction
2. Material and Methods
2.1. Experimental Setup
2.2. Test Materials
2.3. Test Procedure
- (1)
- In order to reduce the sidewall effect, i.e., to prevent seepage water from flowing through the gap between the soil and inner wall, a thin layer of Vaseline was applied uniformly on the wall of the cutting ring.
- (2)
- The test sample (with known void ratio) was placed in the permeameter.
- (3)
- The permeameter was then sealed hermetically and tightly, and the flow inlet, outlet, and piezometer tubes were connected.
- (4)
- The inlet valve was turned on to let water flow into the permeameter at a steady rate. The bubbles inside the permeameter and piezometer tubes were purged carefully, and the temperature and viscosity of the water were recorded.
- (5)
- When the water flow rate was steady, a certain amount of outflow water was collected, and the corresponding time interval was recorded. The water levels of the piezometer tubes were also observed and recorded.
- (6)
- Each test was performed three times to minimize the measurement error.
3. Results
3.1. Hydraulic Conductivity of Silty Sediments
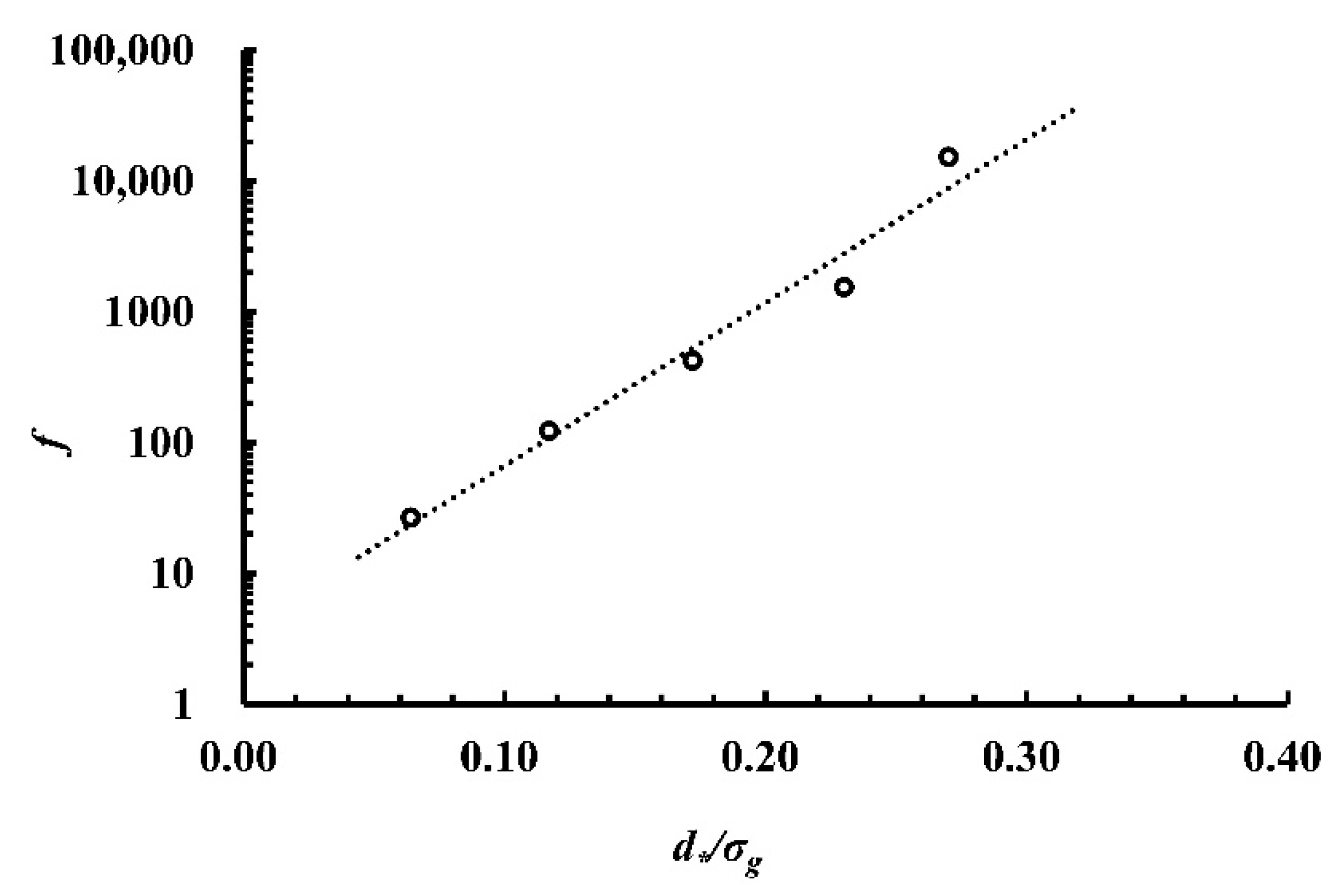
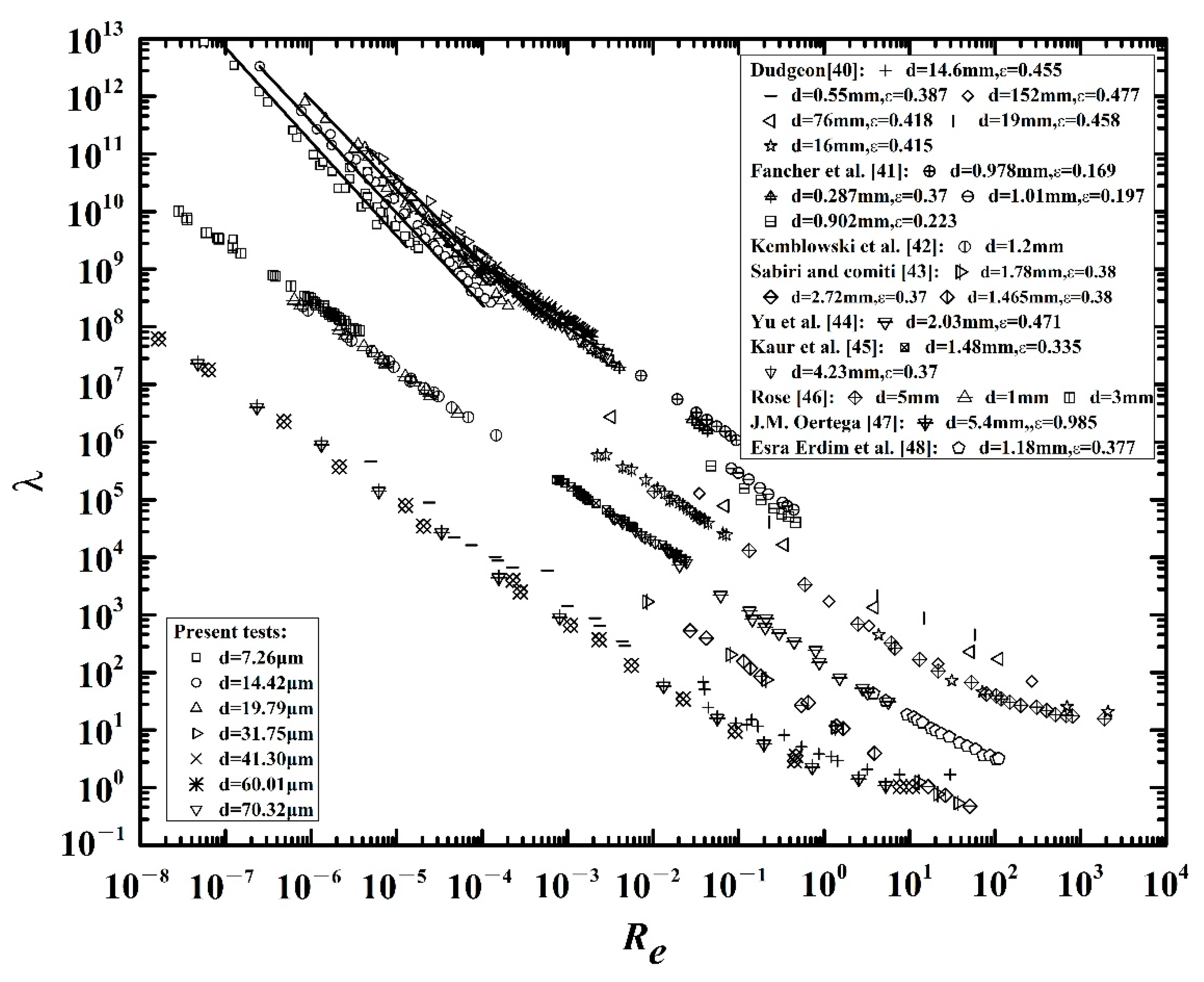
3.2. Seepage Resistance for Seepage Flow in Silty Sediments
4. Discussions
5. Conclusions
- (1)
- Hydraulic conductivity k is closely related to void ratio e and particle diameter d50 in silty sediments, and it was found that is a linear function of .
- (2)
- An empirical equation for the estimation of hydraulic conductivity was proposed, and was found applicable for particle grain size, d50 (3.1 μm < d50 < 87 μm) and sediment void ratio e (0.26 < e < 4).
- (3)
- The friction resistance to seepage flow in silty sediments exhibits distinct characteristics similar to seepage flow in coarse-grained sediments. The slopes of versus curves for seepage in silty sediments are variable and the value of the slope (log-log plot) decreases with increasing grain size, while the slope remains constant (−1) for flow in coarse-grained sediments.
- (4)
- The formulae for calculating the seepage friction factor in coarse-grained sediments are not applicable for silty sediments. A formula for calculating in silty sediments has been proposed. The value of in silty sediments is larger than that in coarse-grained sediments for the same Reynolds number .
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, M.; Zhu, X.; Yu, G.; Yan, J.; Wang, X.; Chen, M.; Wang, W. Permeability of muddy clay and settlement simulation. Ocean Eng. 2015, 104, 521–529. [Google Scholar] [CrossRef]
- Wu, D.Q.; Guo, L. Research progress of recycling Singapore solid wastes for land reclamation. Res. Environ. Sci. 2018, 31, 1174–1181. [Google Scholar]
- Vikolainen, V.; Bressers, H.; Lulofs, K. A shift toward building with nature in the dredging and port development industries: Managerial implications for projects in or near natural 2000 areas. Environ. Manag. 2014, 54, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Yan, J.; Yu, G. Vacuum preloading method for land reclamation using hydraulic filled slurry from the sea: A case study in coastal China. Ocean Eng. 2018, 152, 286–299. [Google Scholar] [CrossRef]
- Kaethigesu, T. Validity of Darcy’s Law for Low-Gradient Saturated flow through Bentonite and Sand Mixtures. Ph.D. Thesis, University of Manitoba, Winnipeg, MB, Canada, 1994. [Google Scholar]
- Sondergaard, M.; Jensen, J.P.; Jeppesen, E. Role of sediment and internal loading of phosphorus in shallow lakes. Hydrobiologia 2003, 506–509, 135–145. [Google Scholar] [CrossRef]
- Huang, X.; Liang, P.; Qian, Y. Excess sludge reduction induced by Tubifex tubifex in a recycled sludge reactor. J. Biotechnol. 2007, 127, 443–451. [Google Scholar] [CrossRef]
- Wang, L.; Yu, L.; Guo, Z. Seepage induced soil failure and its mitigation during suction caisson installation in silt. J. Offshore Mech. Arct. 2013, 136, 011103. [Google Scholar] [CrossRef]
- Steedman, R.S.; Sharp, M.K. Physical modelling analysis of the New Orleans levee breaches. Proc. Inst. Civil Eng. Geotech. Eng. 2011, 164, 353–372. [Google Scholar] [CrossRef]
- Olson, K.R.; Morton, L.W. The impacts of 2011 induced levee breaches on agricultural lands of Mississippi river valley. J. Soil Water Conserv. 2012, 67, 5–10. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, M.; Yu, G.; Petukhov, V.; Mymrin, V.; Gidarakos, E. Flow Resistance in Dredged Soil under a Vacuum Preloading System with Vertical Drainage Boards. J. Coastal Res. 2020, 36, 327–338. [Google Scholar] [CrossRef]
- Thiruvengadam, M.; Kumar, G.N.P.; Sivakumar, D.; Mohan, C. Non-dimensional equation of resistance coefficient with Reynolds number of porous media. Indian J. Sci. Technol. 2016, 9, 1–7. [Google Scholar] [CrossRef]
- Liu, H.; Li, L.; Birkholzer, J. Unsaturated properties for non-Darcian water flow in clay. J. Hydrol. 2012, 430–431, 173–178. [Google Scholar] [CrossRef]
- Chakraborty, D.; Chakraborty, A.; Santra, P.; Tomar, R.K.; Kalra, N. Prediction of hydraulic conductivity of soils from particle-size distribution. Curr. Sci. 2006, 90, 1526–1531. [Google Scholar]
- Roque, A.J.; Didier, G. Calculating hydraulic conductivity of fine-grained soils to leachates using linear expressions. Eng. Geol. 2006, 85, 147–157. [Google Scholar] [CrossRef]
- Chung, C.K.; Kim, J.H.; Kim, J.; Kim, T. Hydraulic conductivity variation of coarse-fine soil mixture upon mixing ratio. Adv. Civ. Eng. 2018, 2018, 6846584. [Google Scholar] [CrossRef]
- Taylor, D.W. Fundamentals of soil mechanics. Soil Sci. 1948, 66, 161. [Google Scholar] [CrossRef]
- Mesri, G.; Olson, R.E. Mechanisms controlling the permeability of clays. Clay. Clay Miner. 1971, 19, 151–158. [Google Scholar] [CrossRef]
- Samarasinghe, A.M.; Huang, Y.H.; Drnevich, V.P. Permeability and consolidation of normally consolidated soils. J. Geotech. Eng. Division 1982, 108, 835–850. [Google Scholar] [CrossRef]
- Ren, X.; Zhao, Y.; Deng, Q.; Li, D.; Wang, D. A relation of hydraulic conductivity–void ratio for soils based on Kozeny-Carman equation. Eng. Geol. 2016, 213, S0013795216302836. [Google Scholar] [CrossRef]
- Chapuis, R.P. Predicting the saturated hydraulic conductivity of soils: A review. Bull. Eng. Geol. Environ. 2012, 71, 401–434. [Google Scholar] [CrossRef]
- Ishaku, J.M.; Gadzama, E.W.; Kaigama, U. Evaluation of empirical formulae for the determination of hydraulic conductivity based on grain-size analysis. J. Geol. Min. Res. 2011, 3, 105–113. [Google Scholar]
- Beyer, W. Hydrogeologische untersuchungen bei der ablagerung von wasserschadstoffen. Z. Fuer Angew. Geol. 1966, 12, 599–606. (In German) [Google Scholar]
- Odong, J. Evaluation of empirical formula for determination of hydraulic conductivity based on grain size analysis. J. Am. Sci. 2007, 3, 54–60. [Google Scholar]
- Chen, C.Y.; Bullen, A.G.R.; Elnaggar, H.A. Permeability and Related Principles of Coal Refuse. Transp. Res. Rec. 1977, 640, 49–52. [Google Scholar]
- David, W.; Lii, C.; Asce, F. Goodbye, Hazen; Hello, KozenyCarman. J. Geotech. Geoenviron. Eng. 1962, 40, 260–261. [Google Scholar]
- Sanzeni, A.; Colleselli, F.; Grazioli, D. Specific surface and hydraulic conductivity of fine-grained soils. J. Geotech. Geoenviron. 2013, 139, 1828–1832. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Liakopoulos, A.; Sofos, F.; Karakasidis, T.E. Friction factor in nanochannel flows. Microfluid. Nanofluid. 2016, 20, 20–24. [Google Scholar] [CrossRef]
- Macdonald, I.F.; El-Sayed, M.S.; Mow, K.; Dullien, F.A.L. Flow through Porous Media—the Ergun Equation Revisited. Ind. Eng. Chem. Fundam. 1979, 18, 199–208. [Google Scholar] [CrossRef]
- Moutsopoulos, K.N.; Papaspyros, I.N.E.; Tsihrintzis, V.A. Experimental investigation of inertial flow processes in porous media. J. Hydrol. 2009, 374, 242–254. [Google Scholar] [CrossRef]
- Yang, W.; Yu, G.; Tan, S.K.; Wang, H. Rheological properties of dense natural cohesive sediments subject to shear loadings. Int. J. Sediment Res. 2014, 29, 454–470. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, G.; Rovere, A.L.; Ranzi, R. Erodibility of fluidized cohesive sediments in unidirectional open flows. Ocean Eng. 2017, 130, 523–530. [Google Scholar] [CrossRef]
- Zhang, M.; Yan, J.; Wang, X.; Chen, M.; Zhao, D.; Yu, G. Application of ultrasonic vibrator to sedimentation analysis m23sive sediment grain size. Water Resour. Hydropower Eng. 2014, 45, 100–103. (In Chinese) [Google Scholar]
- Yu, G.L.; Lim, S.Y. Modified manning formula for flow in alluvial channels with sand-beds. J. Hydraul. Res. 2003, 41, 597–608. [Google Scholar] [CrossRef]
- Dolinar, B. Predicting the hydraulic conductivity of saturated clays using plasticity–value correlations. Appl. Clay Sci. 2009, 45, 90–94. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through granular beds. Transp. Inst. Chem. Eng. 1997, 15, 32–48. [Google Scholar] [CrossRef]
- Yu, B.; Li, J. A geometry model for tortuosity of flow path in porous media. Chin. Phys. Lett. 2004, 21, 1569–1571. [Google Scholar]
- Zhang, M.; Yu, G. Critical conditions of incipient motion of cohesive sediments. Water Res. Res. 2017, 53, 7798–7815. [Google Scholar] [CrossRef]
- Dudgeon, C.R. An experimental study of the flow of water through coarse granular media. Houille Blanche 1966, 7, 785–801. [Google Scholar] [CrossRef]
- Fancher, G.H.; Lewis, J.A. Flow of simple fluids through porous materials. Ind. Eng. Chem. 1933, 25, 1139–1147. [Google Scholar] [CrossRef]
- Kemblowski, Z.; Michniewicz, M. A new look at the laminar flow of power law fluid through granular beds. Rheol. Acta 1979, 18, 730–739. [Google Scholar] [CrossRef]
- Sabiri, N.E.; Comiti, J. Experimental validation of a model allowing pressure gradient determination for non-Newtonian purely viscous fluid-flow through packed beds. Chem. Eng. Sci. 1997, 52, 3589–3592. [Google Scholar] [CrossRef]
- Yu, Y.H.; Wen, C.Y.; Bailie, R.C. Power-law fluids flow through multiparticle system. Can. J. Chem. Eng. 2010, 46, 149–154. [Google Scholar] [CrossRef]
- Kaur, N.; Singh, R.; Wanchoo, R.K. Flow of Newtonian and Non-Newtonian fluids through packed beds: An experimental study. Transp. Porous Med. 2011, 90, 655–671. [Google Scholar] [CrossRef]
- Rose, H.E. On the resistance coefficient–Reynolds number relationship for fluid flow through a bed of granular material. Proc. Inst. Mech. Eng. 1945, 153, 154–168. [Google Scholar] [CrossRef]
- Ortega, J.M. A porous media model for blood flow within reticulated foam. Chem. Eng. Sci. 2013, 99, 59–66. [Google Scholar] [CrossRef]
- Erdim, E.; Akgiray, O.; Demir, I. A revisit of pressure drop-flow rate correlations for packed beds of spheres. Powder Technol. 2015, 283, 488–504. [Google Scholar] [CrossRef]


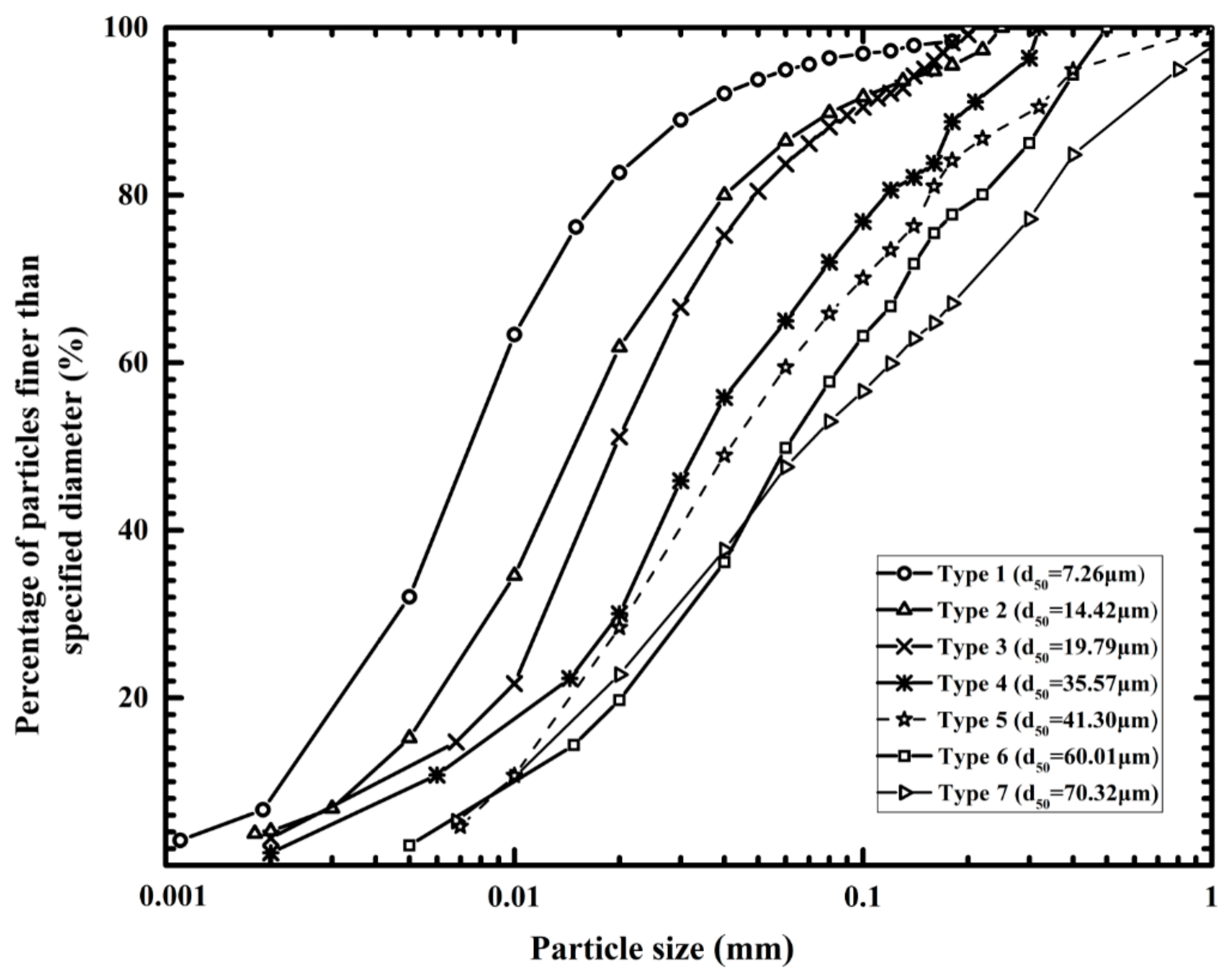
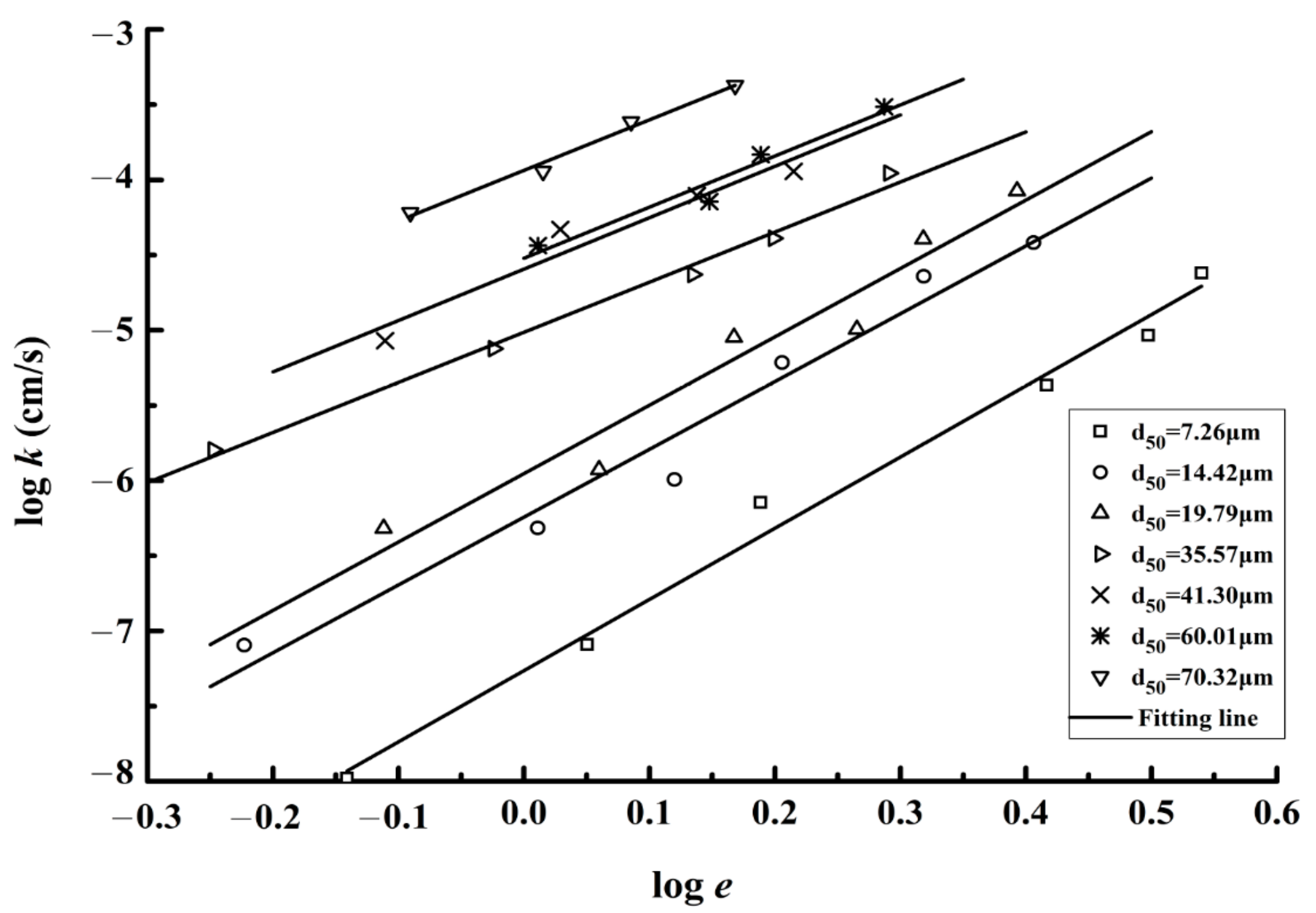
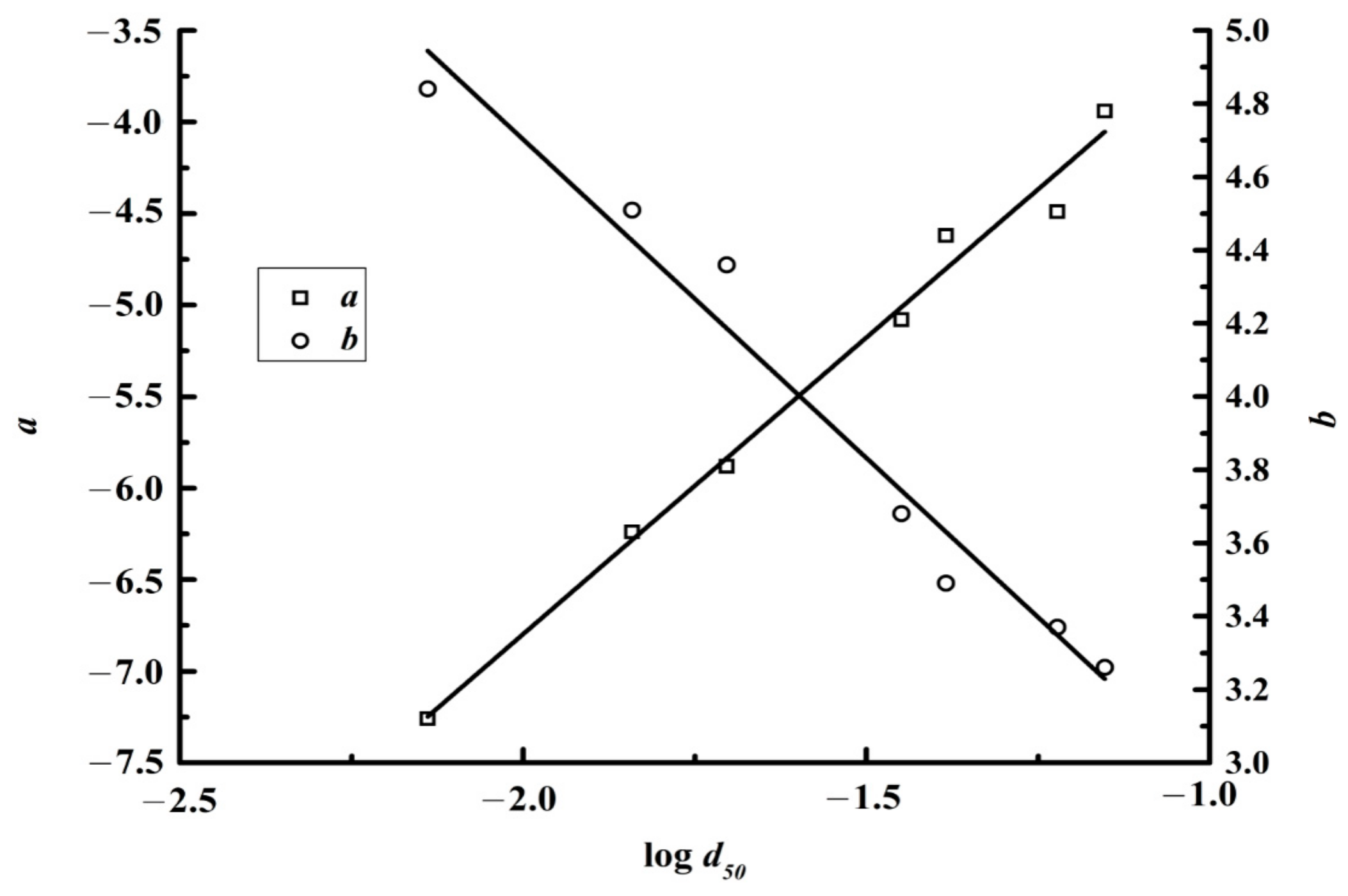

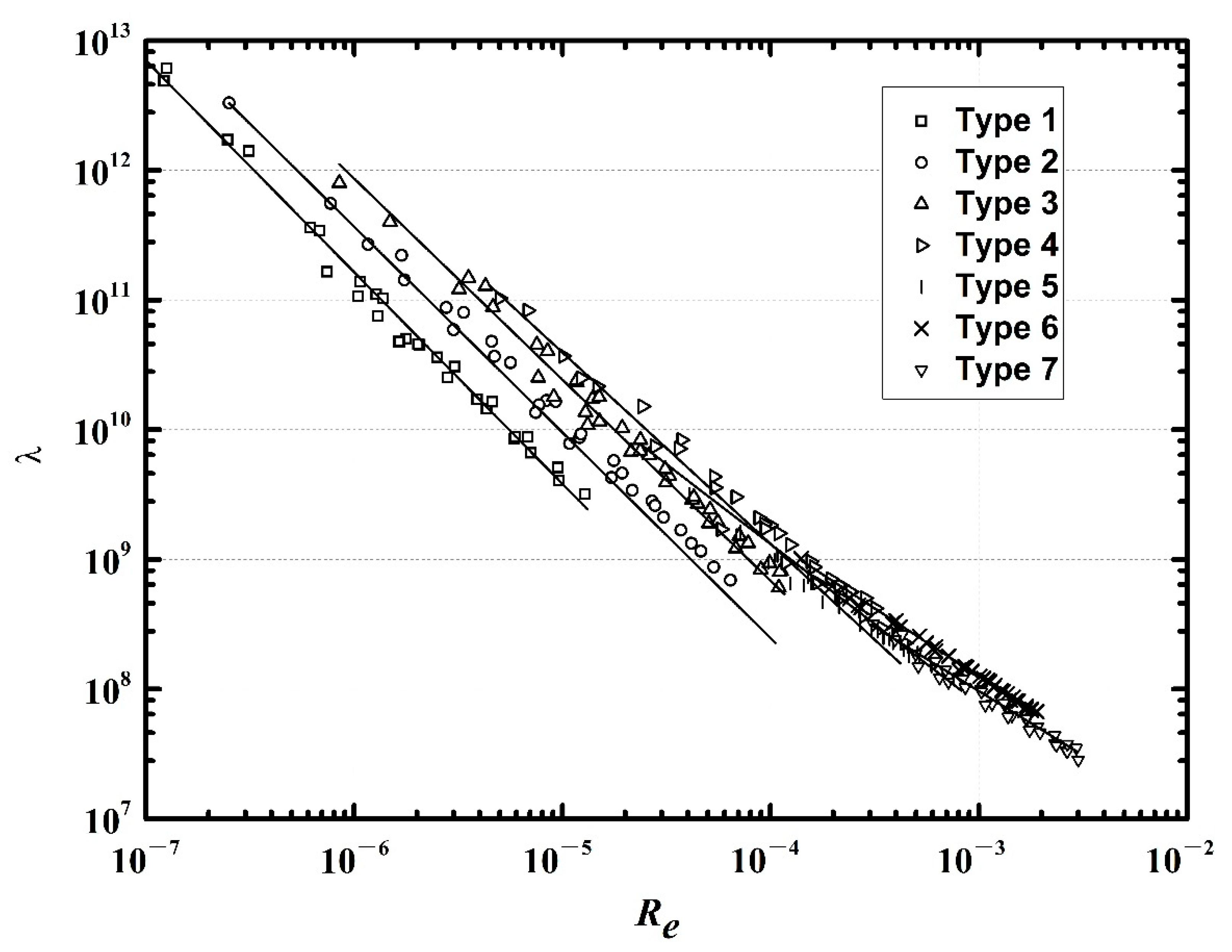

| Properties | Type 1 | Type 2 | Type 3 | Type 4 | Type 5 | Type 6 | Type 7 |
|---|---|---|---|---|---|---|---|
| Specific gravity Gs | 2.73 | 2.72 | 2.70 | 2.71 | 2.69 | 2.65 | 2.63 |
| Median grain size (μm) | 7.26 | 14.42 | 19.79 | 35.57 | 41.30 | 60.01 | 70.32 |
| Uniformity coefficient σg | 2.91 | 3.17 | 2.93 | 3.97 | 3.90 | 4.20 | 4.76 |
| Standard deviation of the grain size (μm) | 0.9 | 0.7 | 1.2 | 1.9 | 1.6 | 2.1 | 2.6 |
| Soil Types | Void Ratio e | |||||
|---|---|---|---|---|---|---|
| Type 1 | 0.723 | 1.123 | 1.544 | 2.610 | 3.144 | 3.467 |
| Type 2 | 0.599 | 1.026 | 1.318 | 1.606 | 2.083 | 2.548 |
| Type 3 | 0.773 | 1.148 | 1.470 | 1.842 | 2.081 | 2.471 |
| Type 4 | 0.566 | 0.946 | 1.363 | 1.581 | 1.953 | / |
| Type 5 | 0.775 | 1.069 | 1.374 | 1.641 | / | / |
| Type 6 | 1.026 | 1.405 | 1.544 | 1.937 | / | / |
| Type 7 | 0.812 | 1.036 | 1.217 | 1.474 | / | / |
| Sediment Type | f | ||||
|---|---|---|---|---|---|
| Type 1 | 7.26 | 0.187 | 0.064 | −1.607 | 26.75 |
| Type 2 | 14.42 | 0.370 | 0.117 | −1.521 | 123.22 |
| Type 3 | 19.79 | 0.505 | 0.172 | −1.490 | 425.22 |
| Type 4 | 35.57 | 0.910 | 0.230 | −1.363 | 1548.70 |
| Type 5 | 41.30 | 1.053 | 0.270 | −1.096 | 15367 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Zhang, M.; Sun, H.; Yu, G. Experimental Study on Hydraulic Conductivity and Resistance in Silty Sediments. Water 2021, 13, 75. https://doi.org/10.3390/w13010075
Zhu W, Zhang M, Sun H, Yu G. Experimental Study on Hydraulic Conductivity and Resistance in Silty Sediments. Water. 2021; 13(1):75. https://doi.org/10.3390/w13010075
Chicago/Turabian StyleZhu, Wenlong, Minxi Zhang, Hui Sun, and Guoliang Yu. 2021. "Experimental Study on Hydraulic Conductivity and Resistance in Silty Sediments" Water 13, no. 1: 75. https://doi.org/10.3390/w13010075
APA StyleZhu, W., Zhang, M., Sun, H., & Yu, G. (2021). Experimental Study on Hydraulic Conductivity and Resistance in Silty Sediments. Water, 13(1), 75. https://doi.org/10.3390/w13010075





