1. Introduction
Urban development causes profound changes in the hydrology of urbanizing areas (Burns et al., 2012) [
1]. Focusing on the quantitative effects, the water balance of urbanizing catchments is altered by the changes in catchment surface cover and of the corresponding hydrological abstractions, and by incorporation of new hydraulically efficient conveyance elements into the urban water system (Silanpää and Koivusalo 2015) [
2]. The resulting outcomes, in the form of reduced infiltration and evapotranspiration, and accelerated removal of surface runoff from the catchment, cause substantial increases in catchment runoff volumes and peak flows, and thereby contribute to the increased risk of water ponding or flooding (Konrad 2016) [
3].
In the early 1970s, the first step toward remediation of flooding within, and downstream of, urban areas was the implementation of flood management reservoirs, in the form of stormwater ponds storing urban runoff and, thereby, compensating for the loss of water storage in urbanized catchments. During the last two decades, a new approach to stormwater management in urban areas gained large following by emphasizing the need for restoration of the predevelopment catchment hydrology (Fletcher et al., 2015) [
4]. To gain quick acceptance of this approach, it was promoted under attractive terms, like Low Impact Development (LID), Water Sensitive Design (Fletcher et al., 2015) [
4], Sponge Cities (Zhang et al., 2018) [
5], and others.
Restorative measures for catchment hydrology emphasize the importance of infiltration and evapotranspiration abstractions, to reduce surface runoff from urban landscape, but this becomes challenging in localities with tight soils and low infiltration rates. Under such circumstances, the need for stormwater storage increases, with the objective of balancing and redistributing runoff flows. The role of storage in simulated runoff from an existing urban catchment, and three catchment scenarios with different LID measures, was elucidated by Khadka et al., (2019) [
6] who analyzed the respective simulations with a calibrated storm water management model (SWMM), applied with a 7-months rainfall record and three storm events with low frequencies of occurrence. Such analysis revealed that the catchment scenarios with high storage capacities displayed resilience against flooding and retained a more natural water cycle.
Stormwater storage in urban catchments can be created at various spatial scales (Marsalek and Schreier, 2009) [
7], starting with the lot scale (or property scale) measures (LSM), and moving toward the larger scales in the neighborhood, or the whole catchment. The complexity of storage structures increases with the scale, moving from a simple rain barrel or green roof on the lot, to e.g., a neighborhood bioretention cell, to a stormwater management pond at the catchment level. While the capacity of individual lot-level measures is small, they are used in high numbers and serve as “distributed” storage. In general, LSMs are the best management measures, of which performance is not prescribed or quantified, but they undoubtedly contribute to positive outcomes with respect to stormwater management. Furthermore, LSMs are recognized for their educational value leading to active participation of the public in stormwater management.
In search for new LSMs providing distributed storage of water in urban areas, Lundström et al., (2020) [
8] examined the feasibility of creating dynamic storage of rainwater or stormwater in sponge-like porous bodies (SPB) made of hydrogels. They proposed two types of such storage structures: (a) down-flow SPB storage (
Figure 1a), and (b) up-flow SPB storage (
Figure 1b,c), and demonstrated in numerical experiments that such bodies could fully absorb, in real time, Swedish design rainfalls of 1 h duration and a return period of 10 years. At the same time, they cautioned that this theoretical concept requires further development to advance its Technology Readiness Level and address some practical aspects.
When developing the governing inflow equations for computing the capacity and rates of filling of SPBs with incoming rainwater, Lundström et al., (2020) [
8] assumed that during the filling process, driven by diffusion only, SPBs would maintain the original shape. This assumption imposes a limit on the volume of water stored, setting it equal to the volumetric capacity of the original body. In this follow-up paper, the “no swelling” assumption was removed.
For an appropriately chosen material of the SPB, water may be transported by diffusion into the SPB, while such a body is swelling, but keeping the intercepted water in place. The objective of the present study is, therefore, to include the swelling mechanism in the analysis of SPBs. Focus is set on the first SPB storage variant, down-flow SPB storage (
Figure 1a), in which a relatively large area, such as sections of a roof, parking lot, playground, or football field, would be covered with material that absorbs the rainwater directly upon contact. The material then swells in the vertical direction, retaining the water.
4. Numerical Results
The case study parameters of the down-flow SPB storage under consideration are given in
Table 1. When compared to the results in [
6], smaller values of
B are considered. The reason for this is that smaller values of
B are more interesting when looking for greater amounts of absorption.
Before we consider the modification of the results from [
8], including the effect of swelling, we compare, for the purpose of verification of the numerical solution, the water content
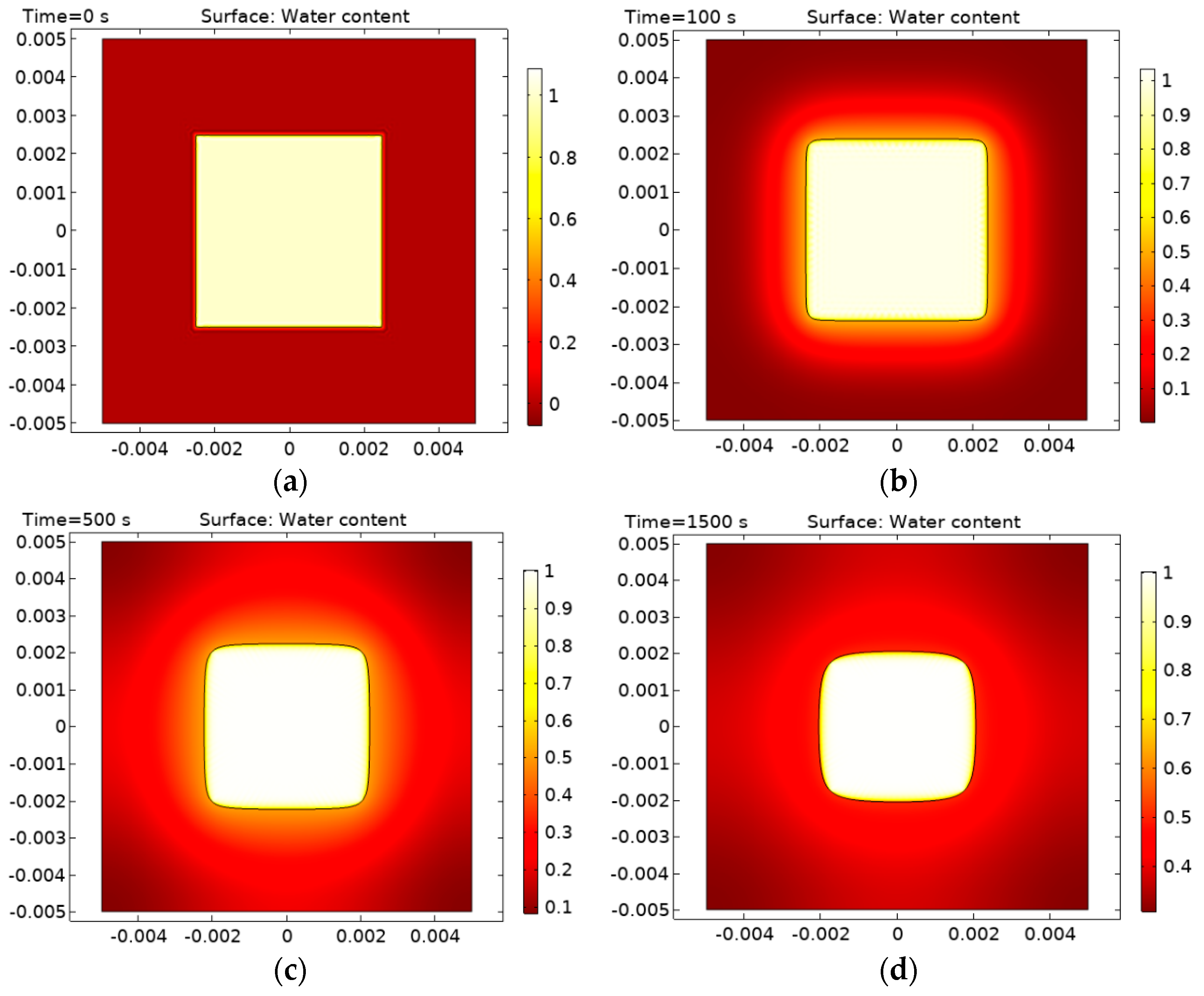
at short times for the case Down3 with the analytic solution in
Section 2. In
Figure 5 the numerical solution obtained in the region
is shown. Comparing with
Figure 4 it is seen that there is a qualitative agreement for short times, which is reasonable since the analytical solution in the application to the full SPB geometry is expected to be valid only in the region, where the boundary layer thickness
is much smaller than the characteristic dimensions of the SPB geometry, i.e.,
B, b, and
H.
The total water volume absorbed into each cell of the hydrogel is calculated from
where
is the domain of the hydrogel. Results are found for both 2D and 3D calculations. Considering the 3D case, some convergence problems are found when the deformation of the hydrogel becomes too large. The time-dependent solver in Comsol indicates that a singularity may have been reached. This is not a singularity in the physical model nor an instability in the time-stepping scheme since an implicit scheme is adopted, but probably due to an insufficiency in the mesh generated by the deformed geometry interface in Comsol.
However, considering the size of the unit cells, the greatest absorption is found for small cells with horizontal dimensions in the order of
B, which is much smaller than the vertical size of the cells,
H. A two-dimensional approximation should then be appropriate. So, in
Figure 6a comparison of the total absorbed water volume per unit square meter of the hydrogel domain is plotted for three different cases for 2D and 3D, as well as a comparison with the case with no swelling. It can be seen that the 2D approximation is quite good and theoretically it is expected that this approximation will improve with a declining magnitude of the ratio
. Therefore, only 2D results are considered from here on. In
Figure 6a, it can be noted that over a time period of 3600 s a difference between the not swelling and swelling cases is only seen for case Down3, being the most interesting case since it has the fastest growth toward the limit of the maximum volume of absorbed water. For case Down3, the maximum amount of water is 75 L per square meter without swelling, and about 87 L including the effect of swelling, which is an increase of about 14%. It can be shown that the maximum volume of absorbed water, without swelling, is given by
, which means that for the parameters chosen all cases Down1-3 reach 75 L without swelling. The cases Down1, -2, and -3 differ only by the times they need to reach this maximum. In
Figure 6b the cases Down2 and -3 are plotted for longer durations, which shows that, without swelling, Down2 and -3 both reach a maximum of 75 L. Reaching the same maximum seems to be also true for the same two cases when including the effect of swelling, with an increase in the maximum volume of about 14%. So, the conclusion regarding swelling is that the swelling simply increases the volume of the hydrogel so that a larger amount of water can be absorbed and that this increase is universal with a value of approximately 14%.
Of interest is also the form of the swelling hydrogel, so in
Figure 7 snapshots of the development of the swelling region are plotted for case Down3.
4.1. Verification of Numerical Results
Before performing a parameter sensitivity study, verification of the numerical results is considered. The absorbed volume can be calculated from the analytical results presented in
Section 2. This gives the following analytical result valid initially on a short time scale:
An approximate, simpler expression taking the asymptotic limit
is
This expression is valid only as long as the boundary layer thickness
is small compared to the geometrical dimensions of the variables
B, b, and
H. From (14) the numerical results are verified for short times, see
Figure 8. Initially the volume growth is then linear in
H,
b′, and
B and grows as
, the latter showing the typical dependence of diffusion processes on time, in general. The linear increase with
only applies on a short time scale, and as will be revealed in the numerical results, for longer times, the effect is the opposite.
4.2. Sensitivity Analysis of the Parameter b′
The dependence of absorbed volume on the parameter
b′ is presented in
Figure 9. Values around
b′ = 0.5 represent a good compromise between a fast initial absorption and the maximum volume captured, while still maintaining a sufficient volume of the absorbing material. As can be seen for short times, the volume captured initially increases with
b′ in agreement with the analytic solution (15). However, larger
b′ values result in decreasing maximum absorbed volumes, as can also be noted from the limit of maximum absorbed volume without swelling, which is
. A comparison of the volumes of water stored with and without swelling, displayed here, also shows a percentage increase of 14% in the former case.
4.3. Sensitivity Analysis of the Diffusion Coefficient
The dependence of the absorbed volume on the diffusion coefficient is presented in
Figure 10a,b for the case Down3. According to the analytic solution in (15), the growth of the volume captured scales initially as
, which seems to be the case also in the numerical solution. However, the maximum volume captured is the same and does not depend on the diffusion constant. For smaller diffusion coefficients it only takes longer times to reach the maximum, as seen in
Figure 10b.
4.4. Swelling in the Vertical Direction
Swelling in the vertical direction on the surface
shown in
Figure 3 is not included in the numerical analysis. An estimate of this swelling volume can be done using the analytic solution in
Section 2. The swelling front advances according to Equation (15),
. The swelling volume for a one-unit cell is then
For the parameters of Down3 this yields approximately 1.6 L, which is small in comparison to the numerical result (87 L) ignoring the swelling in the vertical direction. As long as H is sufficiently large, the swelling in the vertical direction provides a rather small contribution to the total absorbed volume.