Hydrological Image Building Using Curve Number and Prediction and Evaluation of Runoff through Convolution Neural Network
Abstract
1. Introduction
2. Materials and Methods
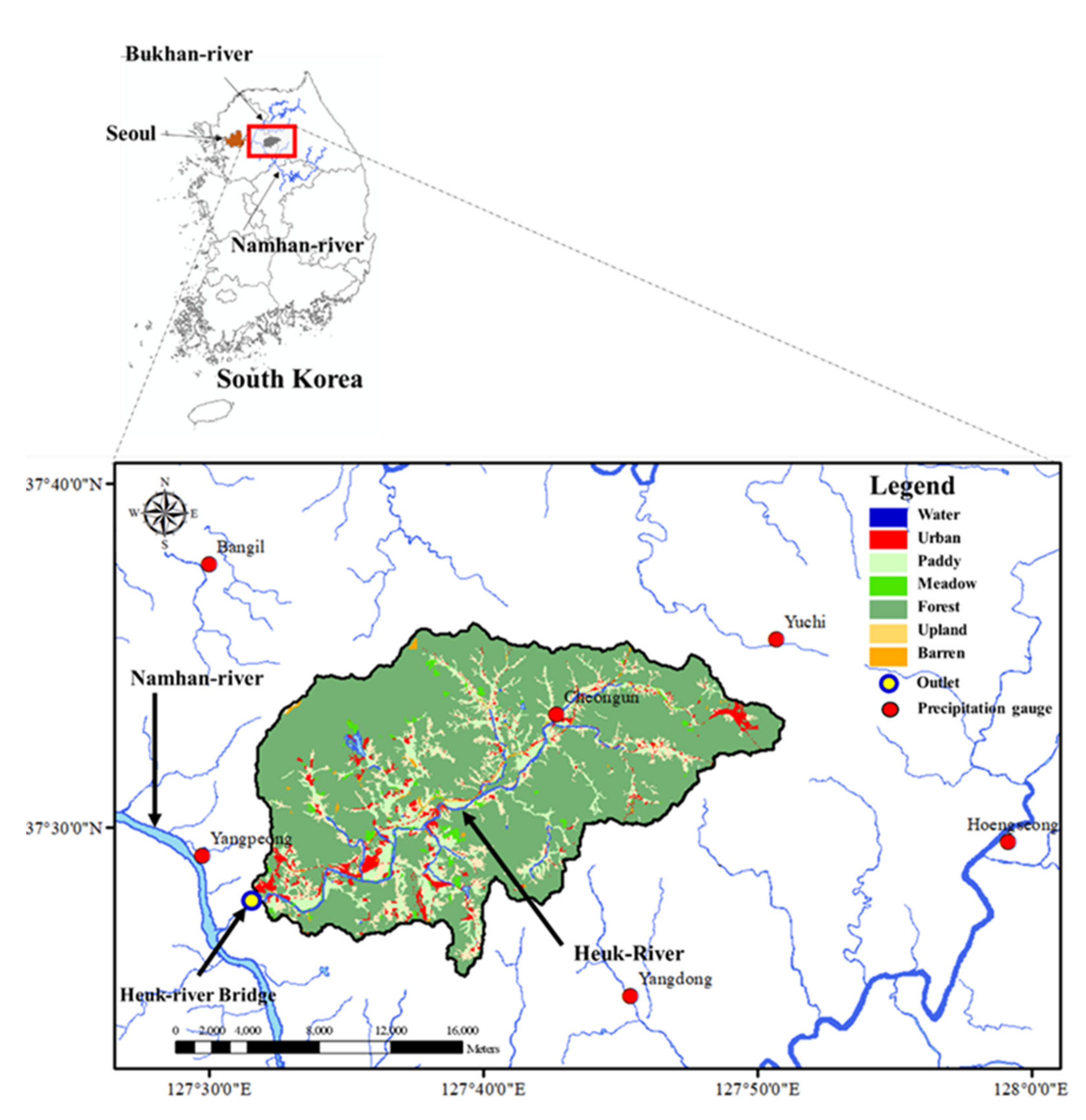
2.1. Study Area
2.2. Data Collection
2.3. Research Method
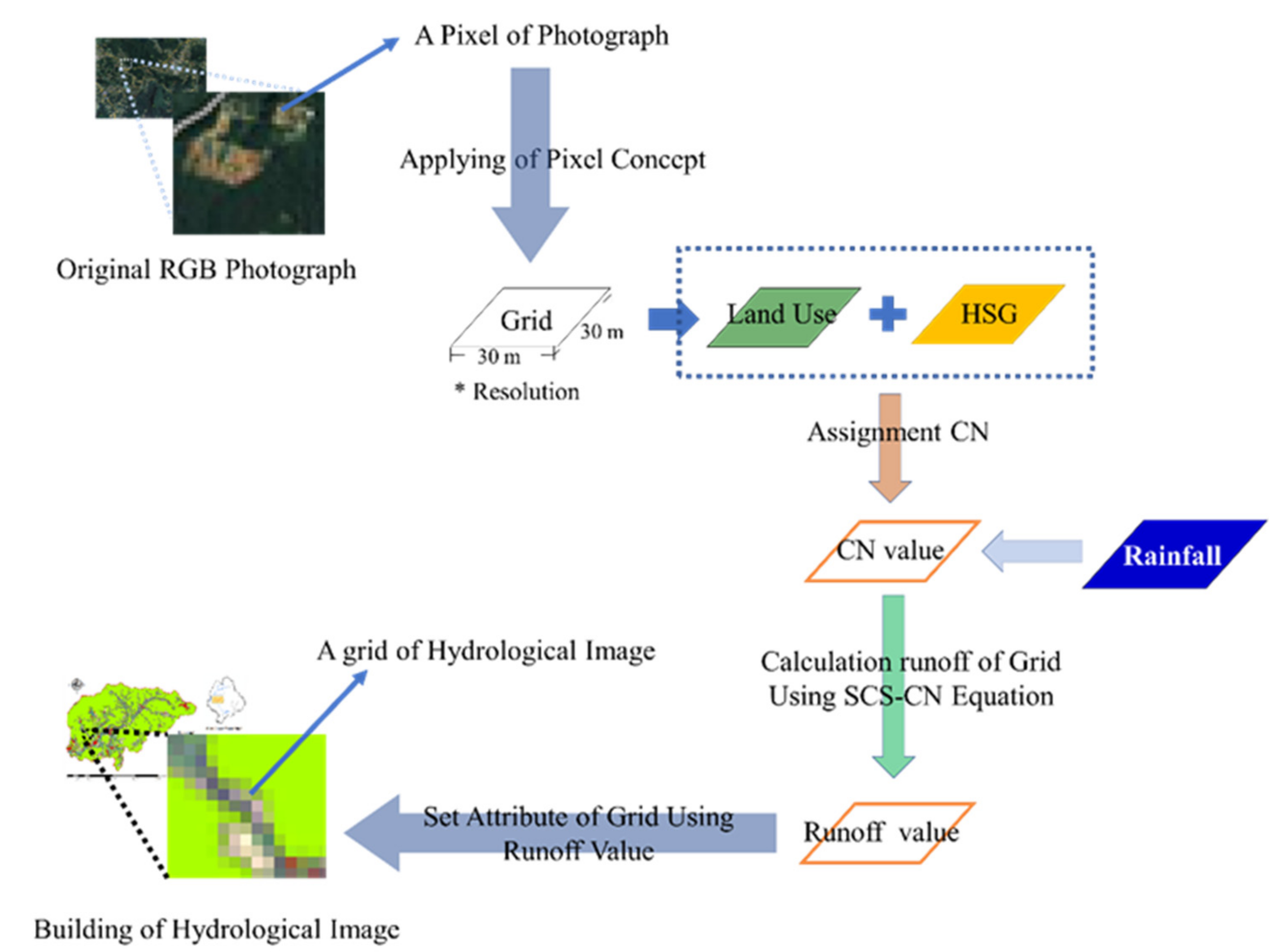
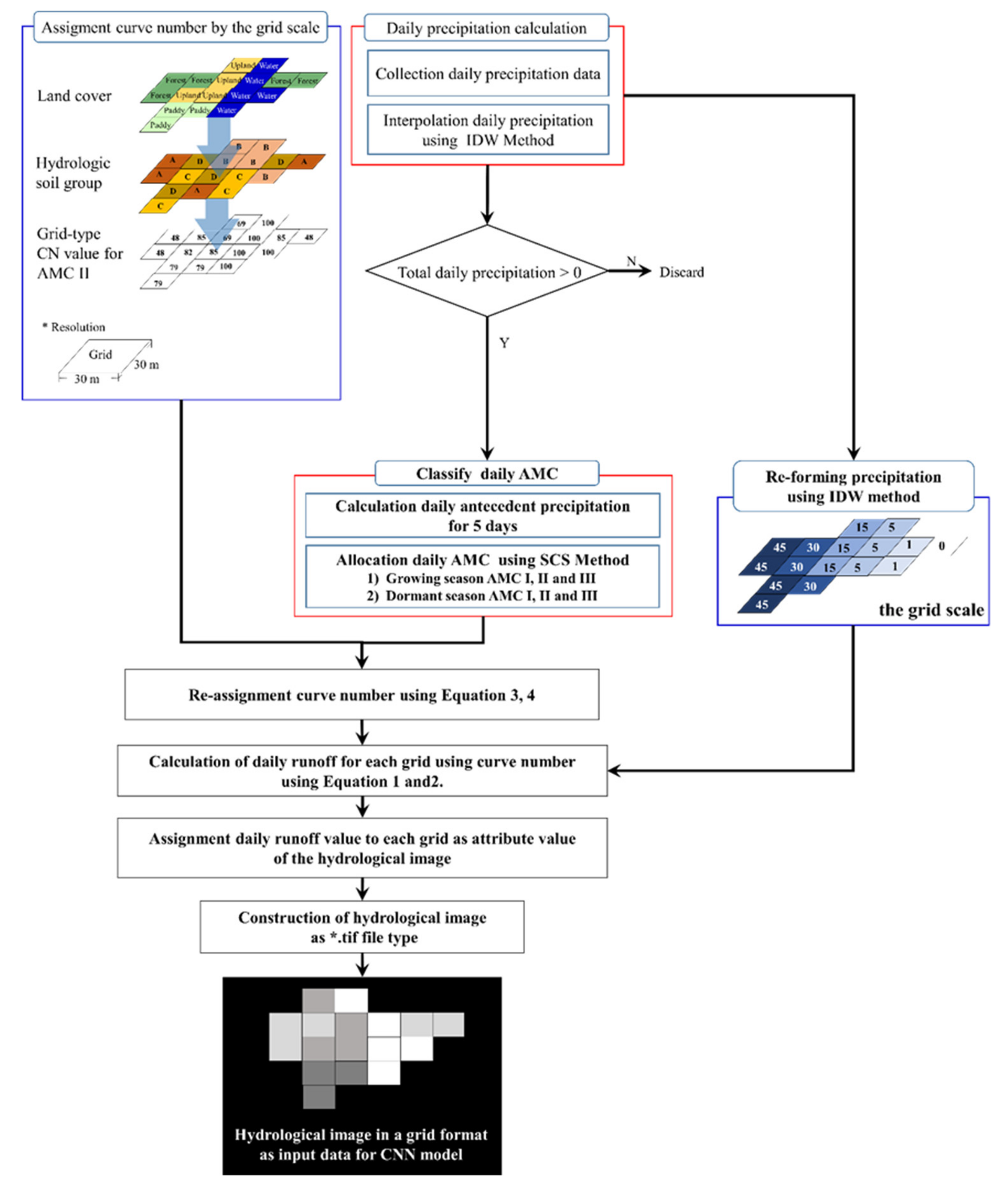
2.3.1. Hydrological Image Concept and Construction Method Using Curve Number
2.3.2. Target Data
2.3.3. CNN Model Architecture Configuration
2.3.4. Detailed CNN Model Settings
2.3.5. Model Evaluation Criteria
3. Results and Discussion
3.1. Building Results of the Hydrological Image Data and Target Data
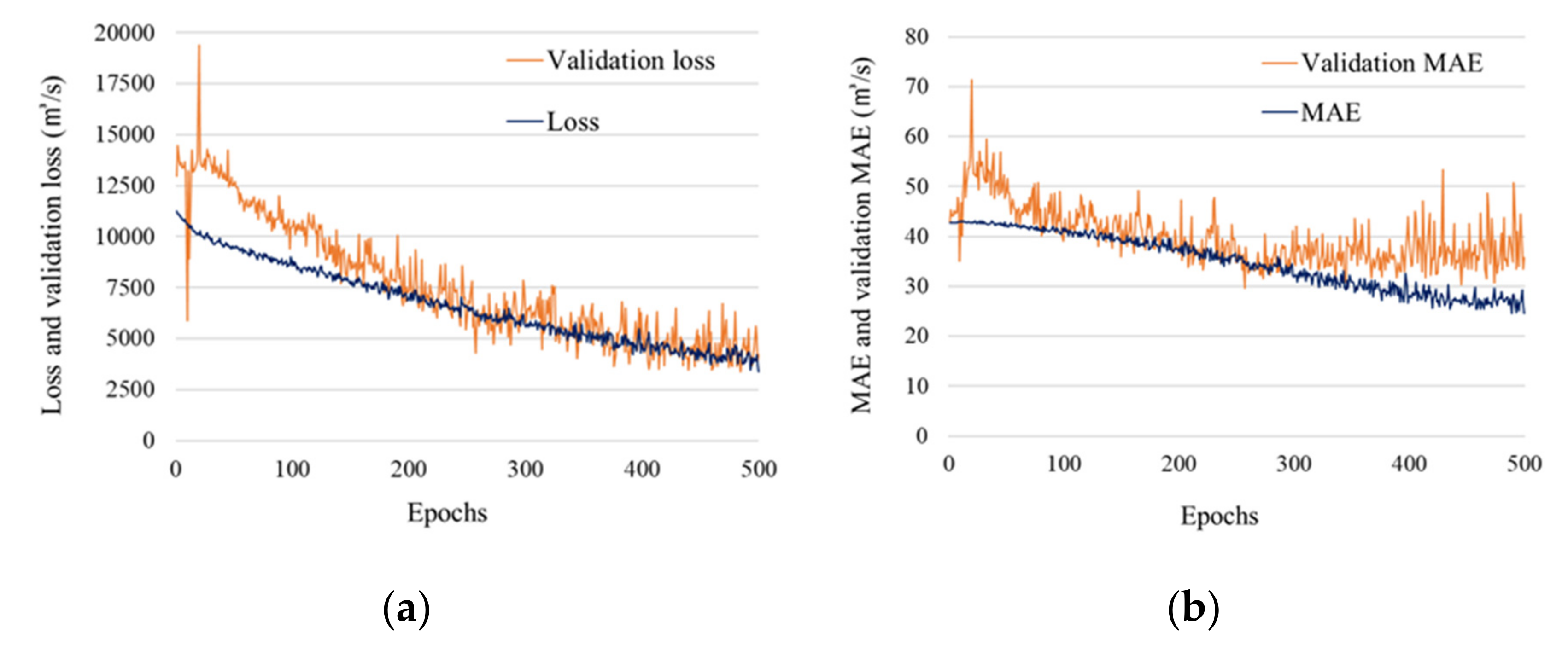
3.2. Model Training Results
3.3. Prediction Results and Model Evaluation
4. Conclusions
Funding
Conflicts of Interest
References
- Kimura, N.; Yoshinaga, I.; Sekijima, K.; Azechi, I.; Baba, D. Convolutional Neural Network Coupled with a Transfer-Learning Approach for Time-Series Flood Predictions. Water 2020, 12, 96. [Google Scholar] [CrossRef]
- Othman, F.; Naseri, M. Reservoir inflow forecasting using artificial neural network. Int. J. Phys. Sci. 2011, 6, 434–440. [Google Scholar] [CrossRef]
- Maier, H.; Jain, A.; Dandy, G.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Nourani, V.; Komasi, M.; Alami, M.T. Hybrid Wavelet—Genetic Programming Approach to Optimize ANN Modeling of Rainfall—Runoff Process. J. Hydrol. Eng. ASCE 2017, 17, 724–741. [Google Scholar] [CrossRef]
- Tokar, A.S.; Markus, M. Precipitation-runoff modeling using artificial neural networks and conceptual moldes. J. Hydrol. Eng. 2000, 5, 156–161. [Google Scholar] [CrossRef]
- Patel, B.; Joshi, G.S. Civil Modeling of Rainfall-Runoff Correlations Using Artificial Neural Network—A Case Study of Dharoi Watershed of a Sabarmati River Basin. CEJ 2017, 3, 78–87. [Google Scholar] [CrossRef]
- Salas, F.R.; Somos-Valenzuela, M.A.; Dugger, A.; Maidment, D.R.; Gochis, D.J.; David, C.H.; Yu, W.; Ding, D.; Clark, E.P.; Noman, N. Towards real-time continental scale streamflow simulation in continuous and discrete space. J. Am. Water Resour. Assoc. 2018, 54, 7–27. [Google Scholar] [CrossRef]
- Akhtar, M.K.; Corzo, G.A.; van Andel, S.J.; Jonoski, A. River flow forecasting with artificial neural networks using satellite observed precipitation pre-processed with flow length and travel time information: Case study of the Ganges river basin. Hydrol. Earth Syst. Sci. 2009, 13, 1607–1618. [Google Scholar] [CrossRef]
- Kalteh, A.M. Rainfall-runoff modelling using artificial neural networks (ANNs): Modelling and understanding. CJES 2008, 6, 53–58. [Google Scholar] [CrossRef]
- Mishra, P.K.; Karmakar, S. Performance of optimum neural network in rainfall-runoff modeling over a river basin. IJEST 2019, 16, 1289–1302. [Google Scholar] [CrossRef]
- Shoaib, M.; Shamseldin, A.Y.; Melville, B.W.; Khan, M.M. A comparison between wavelet based static and dynamic neural network approaches for runoff prediction. J. Hydrol. 2016, 535, 211–225. [Google Scholar] [CrossRef]
- Farias, C.A.; Santos, C.A.; Lourenço, A.M.; Carneiro, T.C. Kohonen neural networks for rainfall-runoff modeling: Case study of piancó river basin. JUEE 2013, 7, 176–182. [Google Scholar] [CrossRef]
- Zhang, B.; Govindaraju, R.S. Prediction of watershed runoff using Bayesian concepts and modular neural networks. Water Resour. Res. 2000, 36, 753–762. [Google Scholar] [CrossRef]
- Wilby, R.L.; Abrahart, R.J.; Dawson, C.W. Detection of conceptual model rainfall—Runoff processes inside an artificial neural network. Hydrol. Sci. J. 2003, 48, 163–181. [Google Scholar] [CrossRef]
- Jain, A.; Sudheer, K.P.; Srinivasulu, S. Identification of physical processes inherent in artificial neural network rainfall runoff models. Hydrol. Process. 2004, 18, 571–581. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Jain, A. Explaining the internal behaviour of artificial neural network river flow models. Hydrol. Process. 2004, 18, 833–844. [Google Scholar] [CrossRef]
- Taravat, A.; Del Frate, F.; Cornaro, C.; Vergari, S. Neural networks and support vector machine algorithms for automatic cloud classification of whole-sky ground-based images. IEEE Trans. Geosci. Remote Sens. 2015, 12, 666–670. [Google Scholar] [CrossRef]
- KMA: Korea Meteorological Administration. Available online: https://www.kma.go.kr (accessed on 3 January 2020).
- WAMIS: Water Management Information System, National Institute of Environmental Research. Available online: https://www.water.nier.go.kr (accessed on 1 March 2019).
- EGIS: Environmental Geographic Information Service. Available online: https://www.egis.me.go.kr (accessed on 9 January 2019).
- Li, C.; Liu, M.; Hu, Y.; Shi, T.; Zong, M.; Walter, M.T. Assessing the impact of urbanization on direct runoff using improved composite CN method in a large urban area. Int. J. Environ. Res. Public Health 2018, 15, 775. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y. Identifying key hydrological processes in highly urbanized watersheds for flood forecasting with a distributed hydrological model. Water 2019, 11, 1641. [Google Scholar] [CrossRef]
- Li, F.; Chen, J.; Liu, Y.; Xu, P.; Sun, H.; Engel, B.A.; Wang, S. Assessment of the impacts of land use/cover change and rainfall change on surface runoff in China. Sustainability 2019, 11, 3535. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Yin, Z.; Wen, X.; Si, J.; Li, C.; Deo, R. Identifying separate impacts of climate and land use/cover change on hydrological processes in upper stream of Heihe River, Northwest China. Hydrol. Process. 2017, 31, 1100–1112. [Google Scholar] [CrossRef]
- Soulis, K.X. Estimation of SCS Curve Number variation following forest fires. Hydrol. Sci. J. 2018, 63, 1332–1346. [Google Scholar] [CrossRef]
- Ling, L.; Yusop, Z.; Yap, W.-S.; Tan, W.L.; Chow, M.F.; Ling, J.L. A calibrated, watershed-specific SCS-CN method: Application to Wangjiaqiao Watershed in the Three Gorges Area, China. Water 2020, 12, 60. [Google Scholar] [CrossRef]
- Krajewski, A.; Sikorska-Senoner, A.E.; Hejduk, A.; Hejduk, L. Variability of the Initial Abstraction Ratio in an urban and an agroforested catchment. Water 2020, 12, 415. [Google Scholar] [CrossRef]
- Ajmal, M.; Waseem, M.; Kim, D.; Kim, T.-W. A Pragmatic Slope-Adjusted Curve Number Model to Reduce Uncertainty in Predicting Flood Runoff from Steep Watersheds. Water 2020, 12, 1469. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, Q.; Chen, X.; Chai, T. Improved Curve Number Estimation in SWAT by Reflecting the Effect of Rainfall Intensity on Runoff Generation. Water 2019, 11, 163. [Google Scholar] [CrossRef]
- Deshmukh, D.S.; Chaube, U.C.; Ekube, A.H.; Aberra, D.G.; Tegene, M.K. Estimation and comparison of curve number based on dynamic land use land cover change, observed rainfall-runoff data and land slope. J. Hydrol. 2013, 492, 89–101. [Google Scholar] [CrossRef]
- Pal, S.C.; Chakrabortty, R. Simulating the impact of climate change on soil erosion in sub-tropical monsoon dominated watershed based on RUSLE, SCS runoff and MIROC5 climatic model. Adv. Space Res. 2019, 64, 352–377. [Google Scholar] [CrossRef]
- Kim, N.W.; Lee, J.W. Temporally weighted average curve number method for daily runoff simulation. Hydrol. Process. 2008, 22, 4936–4948. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure and Transport, ref. of Korea. Design Flood Estimation Techniques; Ministry of Land Transport and Maritime Affairs: Seoul, Korea, 2012. (In Korean) [Google Scholar]
- Python. Available online: https://www.python.org (accessed on 4 January 2020).
- Medina, E.; Petraglia, M.R.; Gomes, J.G.R.; Petraglia, A. Comparison of CNN and MLP classifiers for algae detection in underwater pipelines. In Proceedings of the 2017 Seventh International Conference on Image Processing Theory, Tools and Applications (IPTA), Montreal, QC, Canada, 28 November–1 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Computer Vision-ECCV 2014, Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8689, pp. 818–833. [Google Scholar] [CrossRef]
- Tensorflow. Available online: https://www.tensorflow.org (accessed on 12 December 2019).
- Keras. Available online: https://keras.io (accessed on 12 December 2019).
- Ide, H.; Kurita, T. Improvement of learning for CNN with ReLU activation by sparse regularization. IJCNN 2017, 2684–2691. [Google Scholar] [CrossRef]
- Chen, Z.; Ho, P.H. Global-connected network with generalized ReLU activation. Pattern Recognit. 2019, 96, 106961. [Google Scholar] [CrossRef]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the COMPSTAT 2010 NEC Labs America, Princeton, NJ, USA, 22–27 August 2010; pp. 177–186. [Google Scholar] [CrossRef]
- Qian, N. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar] [CrossRef]
- Nesterov, Y. A method for unconstrained convex minimization problem with the rate of convergence. Dokl. ANSSSR 1983, 269, 543–547. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Dozat, T. Incorporating Nesterov Momentum into Adam; ICLR Workshop: San Juan, Puerto Rico, 2016. [Google Scholar]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701v1. [Google Scholar]
- Hinton, G.; Tieleman, T. RMSprop Gradient Optimization; Lecture 6e of his Coursera Class; 2014. Available online: https://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf (accessed on 10 February 2019).
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Alsumaiei, A.A. Utility of Artificial Neural Networks in Modeling Pan Evaporation in Hyper-Arid Climates. Water 2020, 12, 1508. [Google Scholar] [CrossRef]
- Lee, J.; Kim, C.-G.; Lee, J.E.; Kim, N.W.; Kim, H. Medium-Term Rainfall Forecasts Using Artificial Neural Networks with Monte-Carlo Cross-Validation and Aggregation for the Han River Basin, Korea. Water 2020, 12, 1743. [Google Scholar] [CrossRef]
- Mulualem, G.M.; Liou, Y.-A. Application of Artificial Neural Networks in Forecasting a Standardized Precipitation Evapotranspiration Index for the Upper Blue Nile Basin. Water 2020, 12, 643. [Google Scholar] [CrossRef]
- Abbasi, T.; Abbasi, T.; Luithui, C.; Abbasi, S.A. Modelling Methane and Nitrous Oxide Emissions from Rice Paddy Wetlands in India Using Artificial Neural Networks (ANNs). Water 2019, 11, 2169. [Google Scholar] [CrossRef]
- Chen, Z.; Ye, X.; Huang, P. Estimating Carbon Dioxide (CO2) Emissions from Reservoirs Using Artificial Neural Networks. Water 2018, 10, 26. [Google Scholar] [CrossRef]
- Pérez-Zárate, D.; Santoyo, E.; Acevedo-Anicasio, A.; Díaz-González, L.; García-López, C. Evaluation of artificial neural networks for the prediction of deep reservoir temperatures using the gas-phase composition of geothermal fluids. Comput. Geosci. 2019, 129, 49–68. [Google Scholar] [CrossRef]
- Lipiwattanakarn, S.; Saengsawang, S. Performance comparison of a conceptual hydrological model and a back-propagation neural network model in rainfall-runoff modeling. Eng. J. Res. Dev. 2005, 16, 35–42. [Google Scholar]
- Sundara Kumar, P.; Praveen, T.V.; Anjanaya Prasad, M. Artificial Neural Network Model for Rainfall-Runoff A Case Study. IJHIT 2016, 9, 263–272. [Google Scholar] [CrossRef]
- Kashani, M.H.; Ghorbani, M.A.; Dinpashoh, Y.; Shahmorad, S. Integration of Volterra model with artificial neural networks for rainfall-runoff simulation in forested catchment of northern Iran. J. Hydrol. 2016, 540, 340–354. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.S.; Cibin, R.; Sudheer, K.P.; Chaubey, I. Constructing prediction interval for artificial neural network rainfall runoff models based on ensemble simulations. J. Hydrol. 2013, 499, 275–288. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, J.; Song, L.; Zou, Q.; Zeng, X. Uncertainty assessment and optimization of hydrological model with the Shuffled Complex Evolution Metropolis algorithm: An application to artificial neural network rainfall-runoff model. Stoch. Environ. Res. Risk Assess. 2013, 27, 985–1004. [Google Scholar] [CrossRef]
- Maca, P.; Pech, P.; Pavlasek, J. Comparing the selected transfer functions and local optimization methods for neural network flood runoff forecast. Math. Probl. Eng. 2014, 782351. [Google Scholar] [CrossRef]
- Machado, F.; Mine, M.; Kaviski, E.; Fill, H. Monthly rainfall–runoff modelling using artificial neural networks. Hydrol. Sci. J. 2011, 56, 349–361. [Google Scholar] [CrossRef]




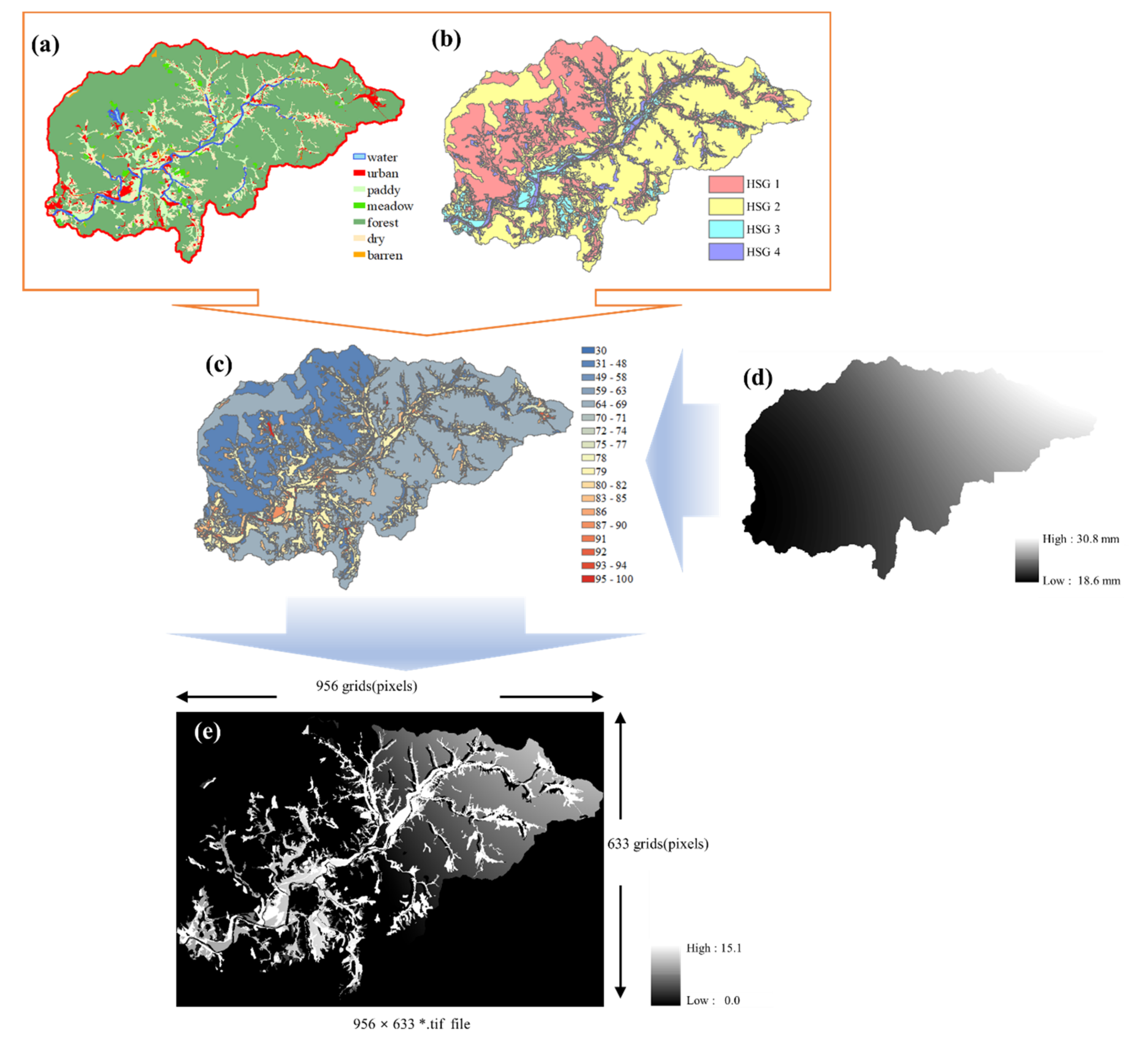

| Landcover | Water | Urban | Barren | Meadow | Forest | Paddy | Upland | Total |
|---|---|---|---|---|---|---|---|---|
| Area (km2) | 8.3 | 10.9 | 7.1 | 1.4 | 238.3 | 26.0 | 22.0 | 314.0 |
| Proportion (%) | 2.7 | 3.5 | 2.3 | 0.4 | 75.9 | 8.3 | 7.0 | 100.0 |
| Convolution Layer | Output Shape (Raw Size, Column Size, Image Channel) | Parameter (Weighted Value) | Activation Function |
| Conv2D_1 | 317, 478, 32 | 832 | ReLu |
| MaxPooling2_1 | 158, 239, 32 | 0 | |
| Conv2D_2 | 79, 120, 64 | 18,496 | ReLu |
| MaxPooling2_2 | 39, 60, 64 | 0 | |
| Conv2D_3 | 39, 60, 128 | 73,856 | ReLu |
| MaxPooling2_3 | 19, 30, 128 | 0 | |
| Conv2D_4 | 19, 30, 256 | 295,168 | ReLu |
| MaxPooling2_4 | 9, 15, 256 | 0 | |
| Conv2D_5 | 9, 15, 512 | 1,180,160 | ReLu |
| MaxPooling2_5 | 4, 7, 512 | 0 | |
| Fully Connected Layer | Output Shape (Number of Node) | Parameter (Weighted Value) | Activation Function |
| Flatten_1 | 14,336 | 0 | |
| Dense_1 | 256 | 3,670,272 | ReLu |
| Dense_2 | 128 | 32,896 | ReLu |
| BatchNormalization | 128 | 512 | |
| Dense_3 | 1 | 129 | Liner |
| Total Parameters: 5,272,321 | |||
| Trainable Parameters: 5,272,065 | |||
| Non-trainable Parameters: 256 | |||
| Optimizer Function: RMSprop (learning ratio = 1e − 4) Loss Function: MSE Metrics: MAE Epoch: 500 iterations | See Equation (5) See Equation (6) | ||
| Contents | NSE | RMSE (m3/s) | |
|---|---|---|---|
| Predict runoff | 0.87 | 0.60 | 16.20 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, C.M. Hydrological Image Building Using Curve Number and Prediction and Evaluation of Runoff through Convolution Neural Network. Water 2020, 12, 2292. https://doi.org/10.3390/w12082292
Song CM. Hydrological Image Building Using Curve Number and Prediction and Evaluation of Runoff through Convolution Neural Network. Water. 2020; 12(8):2292. https://doi.org/10.3390/w12082292
Chicago/Turabian StyleSong, Chul Min. 2020. "Hydrological Image Building Using Curve Number and Prediction and Evaluation of Runoff through Convolution Neural Network" Water 12, no. 8: 2292. https://doi.org/10.3390/w12082292
APA StyleSong, C. M. (2020). Hydrological Image Building Using Curve Number and Prediction and Evaluation of Runoff through Convolution Neural Network. Water, 12(8), 2292. https://doi.org/10.3390/w12082292





