Abstract
Continental-scale river forecasting platforms forecast streamflow at reaches that can be used as boundary conditions to drive a local-scale flood inundation model. Uncertainty accumulated during this process stems not only from any part of the forecasting chain but can also be caused by the daily variations in weather forcing that keeps evolving as the event advances. This work aims to examine the influence of the evolving forecast streamflow on predicting the maximum inundation for extreme floods. A diagnostic case study was made on the basis of a hindcast of Hurricane Matthew striking the eastern U.S. in 2016. The U.S. National Water Model was one-way coupled to a hydrodynamic inundation model through a developed automated workflow. Although the river forcing has significantly mismatched hydrographs versus observations, the simulated peak water surface elevations and maximum extents were validated to be comparable with the observations, which indicates that the inundation model may not be sensitive to the inherited uncertainty from the weather forcing. Moreover, the uncertainty of the forecast streamflow time series caused only one order of magnitude fewer variations in inundation prediction; this dampening effect may become clearer for extreme events with large areas inundated. In addition, the forecast total volume of stream discharge appears to be an important metric for assessing the performance of river forcing for inundation mapping, as a linear correlation between the total volume and the accuracy of the predicted peak water surface elevation and maximum extent was found, with the coefficients of determination all above 0.8. Extra best-practice experience of running similar operational tasks demonstrated the tradeoff between the cost and accuracy gain.
1. Introduction
Effective evacuation and damage reduction for extreme flooding events rely heavily on the accuracy of mapping the worst-case inundation, which provides pivotal information for consideration by civil protection authorities issuing early warnings to evacuate populations and secure infrastructures and properties. Mapping inundation in a timely and accurate manner for the consequential floods caused by major weather events is never easy and depends on a cascading chain of model structures with uncertainties accumulated at every node. A typical model chain usually takes an ensemble of numerical weather predictions (NWPs) as the boundary conditions to force a hydrologic model to simulate rainfall-runoff processes over the catchment and then adopts the simulated overland runoff as the successive boundary conditions to drive a hydraulic channel routing model to predict streamflow [1,2,3]. The chain of models coupled at various scales makes up the backbone of the current continental-scale and global-scale streamflow forecasting platforms, such as the European Flood Forecasting System (EFFS), the U.S. National Oceanic and Atmospheric Administration’s National Water Model (NWM), or the Global Flood Awareness System (GloFAS). The subsequent streamflow forecasts usually have a relatively coarse resolution to fulfill the task of guiding a local-scale flood prediction [4], whereas a hydrodynamic model and locally resolved grids are usually further needed for this purpose.
Uncertainties in the inundation prediction mainly arise from the unpredictability of streamflow forcing and from the incompleteness of the physical processes included in inundation models. The uncertainty in streamflow forecasting can stem from any parts of its forecasting chain such as the physical/statistical mechanisms, model structure, observation data flow, and parameterization. Selecting a range of the NWPs and parameters with textbook values usually leads to a wide envelope of uncertainty space. Bracketed by such wide extremes that can hardly be met, the uncertainty envelopes are more indicative of how inaccurate a forecast could be but are less insightful regarding the forecasting capacity that a model chain can achieve in a real situation. Given a cluster of predicted inundation scenarios with various probabilities, the local authorities would still need to make binary decisions such as whether or not to order an evacuation. Instead of simplifying and accelerating the decision-making process, an ensemble of forecasts implicitly transfers part of the obligation of predicting the flooding situations from scientists to administrators. To resolve this challenge, the decision-makers will then have to spend more time gaining the relevant expertise to fully understand each situation. Given that the forecast ensembles can come from other disciplines such as transportation and electricity networks, the ensembles of the multi-disciplinary ensembles can be even trickier to conclude. Moreover, even though the meteorological ensembles tend to increase the capability to issue flood warnings [5], the chance of false warnings would inevitably increase. Further, an ensemble approach does not compensate for errors among diverse models and does not eliminate the correlation between predictions [6,7]. Therefore, although the ensemble-based forecasts can create confidence intervals outlining the worst guesses of a future situation to strengthen our faith in them in general, deterministic forecasting can be at least an equally useful effort to help decision-makers. After all, error analysis of the latter’s products through hindcasts is the essential way to narrow down the uncertainty brackets for the ensemble of forecasts in the long run.
As the streamflow products from the continental-scale forecasting platforms become increasingly accessible, uncertainty propagation through the model chain of such systems has received greater attention [8,9]. A few pioneer studies have extended the diagnosis of inundation prediction by examining how the choices of the rating curves would affect the accuracy of the predicted inundation extent [6,10,11]. Even though the prediction of flood extents often appears to be constrained by the inadequacy and inconsistencies of rainfall forcing values [12], the impact of such uncertainties on the inundation mapping is not completely understood. Although the model configurations are usually set up before the event and hardly changed during an operational task, the weather forcing can be updated frequently as the event progresses, which results in a varying prediction of streamflow and inundation. For guiding the final decision-making process in response to every forecasting product, it becomes necessary for direct users to further distinguish the uncertainty caused by the selections of the parameters and the model structure from the uncertainty due to the pure variations in the driven data flows.
However, to the knowledge of the authors, the influence of the evolving forcing data, in terms of stream forecasts in this work, on the accuracy of inundation prediction is unclear and seldom studied. As current practices, the uncertainty in the driven data is usually neglected during the uncertainty analysis or bluntly counted towards other uncertainty sources. The real question is how much uncertainty in the data inputs will be translated into a data-driven flood mapping. Lacking such information, we would not completely comprehend the relative role of the uncertainty in parameters and model structures in affecting the inundation accuracy; their importance can be devalued if the driving data may pass far more uncertainty to the predicted inundation products.
Although the pioneer studies explored the uncertainty propagation through the model chain for some non-extreme fluvial floods [6,10,11], they did not often examine it for the extreme events such as hurricane events with high-flow floods, both fluvial and pluvial ingredients, and catastrophic consequences. It remains unknown if predicting extreme flood events may suffer more from uncertainty propagation. The knowledge gap is not only because of the lack of supporting evidence, but also because the relevant studies that have investigated extreme events or made such a comparison are overall scarce.
Predicting the hurricane-level extreme flood events requires a compromise between accuracy and efficiency. To accommodate the required lead time, the large-scale river forecasting systems usually adopt one-dimensional kinematic-wave or diffusive-wave equations to represent channel flows [13,14], which may or may not take account of adequate flow regimes on a local scale, especially when the two-way interactions between the channel flow and overland lateral inflow exist. For example, some non-physics-based simplified models could not be used for rapidly varying flow simulations [15]. Kinematic-wave equations can simulate gradually varying flow along steep channels, yet they miss the flow dynamics over time, as well as the backwater effect [14,16]. Diffusive-wave equations, commonly adopted by forecasting platforms, can simulate slowly to moderately rising flood waves and backflow conditions. However, neglecting the acceleration and advection terms in the momentum equation could be detrimental in determining the flood extent [17]. Moreover, the common forecasting systems often represent the channel flow in one dimension, which then neglect the lateral diffusion of flood waves and exhibit less reliable performance in estimating the distributed water depths [18]. Hurricane-level extreme events can come with floods and surges from the upstream and estuaries, causing high peaks and complicated flow and inundation regimes, which theoretically exceed the scope of the physical descriptions that simplified models are designed to incorporate. The hydrodynamic models, based on shallow-water-equations, are suitable for a wide range of flow problems, and are, therefore, the most widely used for inundation mapping [15]. Coupling the simplified momentum equations embed in streamflow forecast data with the hydrodynamic inundation models is currently the common practice for inundation forecasting. The soundness of coupling these models with various levels of physical details, however, has not been comprehensively evaluated but has been recently more frequently studied.
Corresponding to the above-mentioned knowledge gaps and research demands, the main objectives of this study were to examine the uncertainty in forecast streamflow caused by the evolving weather forcing during the operational forecasting tasks for hurricane-level extreme events and to evaluate the influence of such uncertainty on the accuracy of riverine inundation predictions. The forecast streamflow, as the main uncertainty source in this study, was used as the forcing to drive the inundation model. Other potential uncertainty sources such as the model structure, parameters, and geospatial auxiliary inputs (i.e., elevation and river network) were all fixed. The uncertainty in weather forcing was assumed as implicitly embedded in the forecast streamflow and was not discussed separately. A diagnostic case study was established on a hindcast of the major flooding events caused by Hurricane Matthew, which struck the eastern United States in 2016. The forecast streamflow including the lateral inflow from the bank was retrieved from the U.S. NWM. The inundation was simulated by a hydrodynamic model based on two-dimensional shallow-water-equations. An automated workflow via one-way coupling the NWM with the inundation model was developed. After the predicted peak flood elevations and maximum flooding extents were validated against the observations, the findings with regard to the error propagation were discussed accordingly. The best-practice experience of coupling the NWM with a hydrodynamic model was summarized at last.
2. Methodologies
2.1. River Forcing
This study used the streamflow and lateral inflow forecast by the U.S. National Water Model as the river forcing to drive a high-resolution flood inundation model. The National Water Model, as an implementation of the uncoupled Weather Research and Forecasting model-hydrological modeling system (WRF-Hydro), simulates the full hydrologic system over the continental United States (CONUS). Using the medium-resolution National Hydrography Dataset Plus Version 2 (NHDPlusV2) [19] dividing the national river network into streamline segments, the NWM simulates streamflow and lateral inflow at 2.7 million river reaches covering the entire CONUS. The hourly (short-range) and 3-hour (medium-range) time series of forecast streamflow are encapsulated in the Network Common Data Form (NetCDF) format. Each of the forecast points becomes the midpoint of the corresponding river reach, and, therefore, provides an ideal boundary condition to force a local-scale riverine flood mapping. However, to publish timely forecasts, the NWM is operationally configured to route channel flows by the Muskingum–Cunge method, which is based on the kinematic-wave approximation and cannot capture the backwater flows. Further, the channel spillage to the overland is currently not allowed, which requires further improvements to provide the riverine inundation. Therefore, this study also sought to explore how to use the NWM’s streamflow forecasts for guiding inundation mapping.
2.2. Flood Inundation Model
The flood inundation was simulated based on the Rapid Inundation Flood Tool (RIFT) which, as an implementation of the Nuflood model [20], solves the two-dimensional shallow water equations explicitly on a graphics processing unit (GPU) [21]. On the basis of the Kurganov–Petrova scheme [22,23], its governing equations can be represented as follows assuming incompressible fluid and neglecting Coriolis force, viscous forces, and wind stress:
where η is water surface elevation (m); h is water depth; u and v are the flow velocities (m/s) corresponding to x and y directions, respectively; g is the gravitational acceleration (9.81 m/s2); S0-x and S0−y are the bottom elevation slopes (unitless) in the x and y directions, respectively; n is the Manning’s roughness coefficient (0.035); Δx and Δy are the dimensions (m) of a grid cell; and Δt is the variable time step (s). The friction slope was calculated by Manning’s equation [24].
To be coupled with the NWM, RIFT was modified to include the former’s channel flow in the continuity and momentum equations:
where qin is the total streamflow (m3/s), and qin−x and qin−y are the proportions of the total streamflow (m3/s) in the x and y directions, respectively. The NWM’s forecast streamflow was loaded only at the head reaches of the channel network by being introduced into both the continuity equation and momentum equations as the upstream boundary conditions. For all the remaining downstream reaches in the network, the NWM’s forecast lateral inflow was loaded into the continuity equation only to conserve mass; the lateral inflow represents the rainfall-caused overland runoff and usually comes with a relatively much smaller velocity than the river flow, and thus the flow acceleration or deceleration due to the discharge of the lateral inflow was neglected in this study. The hydrologic forcing generated by the NWM was only “one-way” coupled to the inundation hydraulic model; in other words, the former was applied as the boundary condition to drive the latter, whereas the reverse direction was not simulated by this frame. The proportions of boundary inflow in the x and y directions were approximated by the tangent directions of the NHDPlusV2 streamlines, which the NWM adopts for building the stream network.
The computational domain was discretized by the “staggered” grid, where conserved unknowns are averaged at the cell center, bathymetric elevations are reconstructed at the cell vertices, and the derived fluxes are developed in the middle of the cell interfaces [22]. Every next-step solution (η, hu, hv) was developed by the first-order Euler integration scheme. The time step was constrained by a Courant–Friedrichs–Lewy (CFL) condition that guaranteed the fastest perturbation to pass through one-quarter of the grid cell [22].
2.3. Statistical Metrics
The accuracy of the model chain was validated by comparing the simulated peak water surface elevations and the maximum extents with the observations. The mean error (ME) and the 95% confidence intervals of the mean absolute error (ME95%) were used to compare the observed and modeled water levels:
where is the simulated peak water surface elevation at the ith location, ηmax,i is the observed water surface elevation at location i, z* is the corresponding standard score, is the standard deviation, is the forecast quantity, is the observed mean value, and N is the total number of pairs of comparisons. The ME can be positive or negative; the closer to zero the value is, the more accurate the model results are. The ME95% represents the variation of the model results. For extent mapping, the modeling performance was assessed by two binary measures: fit (F) [18,25] and Peirce’s skill score (PSS) [26]:
where is assigned a value of 1 for wet grid cells identified by both the observation and simulation, is assigned a value of 1 for wet grid cells identified by observation but not by the simulation, is assigned a value of 1 for wet grid cells identified by simulation only, and is assigned a value of 1 for dry grid cells identified both by the observation and the simulation. Both F indicator and PSS indicators vary between 0 and 1; the closer to 1, the more accurate the results are. The F indicator tends to be more sensitive to the wetted extent, whereas the PSS indicator also takes account of the dry cells (). The error of simulated water surface elevation was further assessed by the percent bias (PBIAS) and the Nash–Sutcliffe efficiency (NSE) representing their deviations from the observed values:
where is the observed quantity. The optimum value of PBIAS is zero, whereas the optimum value of NSE is one. Both PBIAS and NSE were also used to assess the deviations of the forecast streamflow from the observed streamflow.
2.4. Case Study
The case study was established on the basis of Hurricane Matthew, which occurred during 7–9 October 2016 and dumped 76–381 mm rainfall across the states of North Carolina and South Carolina, resulting in major flooding and over $1.9 billion damage to public properties and infrastructures, along with 33 fatalities [27]. To completely rebuild this historical event, the NWM short-range hourly stream forecasts (15 hours duration) and the medium-range 3-hour stream forecasts (10 days duration) published on 1–15 October 2016 (referred to as Forecast 1 Oct to 15 Oct afterward) were retrieved. The forecast streamflow was compared to the observed hydrographs at a total of six U.S. Geological Survey (USGS) stream gauges with available time series within the study areas (Table 1). To lessen the local effects of internal boundary conditions due to the structural elements such as bridges and culverts [10], the 30 m digital elevation model (DEM) collected from the USGS 3D Elevation Program was hydro-enforced on the basis of the HydroDEM data from the NHDPlusV2 to enforce channel connectivity.

Table 1.
Locations of the selected United States Geological Survey (USGS) stream gauges and their intersected National Water Model (NWM) reaches.
The highest elevation of the floodwater surface can be marked by the identified and recovered post-flood evidence, which is often named as high water mark (HWM) [28]. After Hurricane Matthew, a total of 106 riverine HWMs with the reported peak water elevation were retrieved from the USGS Short-Term Network (STN) Data Portal [29]. Coastal HWMs were excluded from this study to avoid tidal and surging influence. The HWMs were divided into 10 clusters representing 10 individual study sites. Although some HWMs could fall into multiple study areas, no HWMs were double counted through the comparisons.
A 10 km long (in both directions) rectangular bounding box centered on each cluster of HWMs was created as the forcing domain (Figure 1), within which the NWM river forcing corresponding to inbound stream reaches was loaded into the inundation model. Again, the NWM forecast streamflow and lateral inflow were applied to the head reaches (representing the river channels cut off by the domain boundary as well as the internal headwater sources without any upstream connections) and the following downstream reaches, respectively (Figure 2). The 5 km and 20 km wide forcing domains were further tested. Because the study regions have low-lying, flat terrains that affect the initial flow direction, the discharge loaded at head reaches near the boundary might tend to exit the forcing domain. To avoid such mass losses, we extended the forcing domain by up to 30 km longer in both directions as an extra buffer zone, which together made up the complete computational domain for each simulation. Because RIFT only registers the wet grid cells at each time step and excludes the dry cells from the computation, the extra buffer zone did not significantly elevate the cost. Each simulation began from a “wet” start when RIFT had been ramped up by iterating the initial river forcing until the steady-state was reached. Only after this “spin-up” was the run formally launched and RIFT started to pull the following time series of the corresponding river forcing and generate outputs.
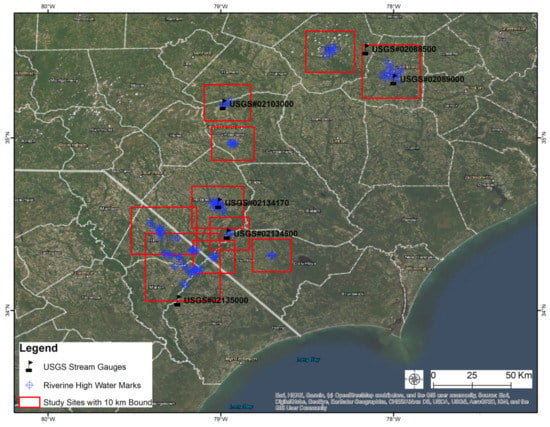
Figure 1.
Study sites with the 10 km long rectangular bound centered on the 10 clusters of riverine high water marks.
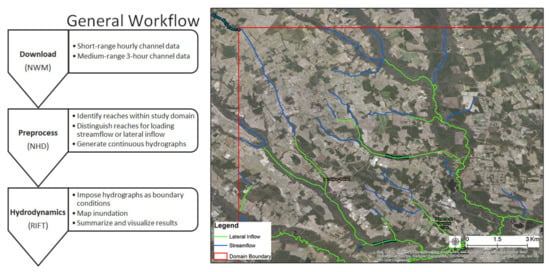
Figure 2.
General workflow and an example network of the river reaches to be loaded by lateral inflow and streamflow boundary conditions.
The simulated flooded areas were validated against the maximum inundation extent of Hurricane Matthew published by the U.S. Federal Emergency Management Agency (FEMA) Cloud GIS Infrastructure Production Site [30]. Because this dataset did not cover South Carolina, the study sites partly missed by this dataset were excluded from the extent validation. Additionally, the published flood extents did not necessarily cover our entire study sites. To make a fair comparison, the flood extents were only validated within a 1 km wide square bounding box, where simulated and observed extents co-exist.
2.5. Automated Coupling Workflow
The simulations were launched inside a Linux environment operated by Ubuntu 16.04.2 LTS equipped with the Intel Xeon CPU E5-2697 v4 (2.3 GHz) and NVIDIA Tesla K80 GPU (cores: 2496 × 2). On the basis of the developed Python and Bash scripts, this running process was automated by loosely coupling the NWM with the inundation model in terms of retrieving the NWM channel forecasts, preprocessing input data, running RIFT, and postprocessing results (Figure 2). During the preprocessing, the reaches within each study site were recorded in a list after being detected by clipping the NHDPlusV2 streamlines by the boundary of interest. The list of reaches was then used to extract the corresponding streamflow and lateral inflow time series out of the NWM forecast datasets, which were then written into an individual hydrograph file for each stream reach. The list of reaches and hydrograph files could then guide RIFT to load the discharge at the corresponding time and location. Each forecast dataset was developed by merging the 15 NWM short-range (hourly) channel flow with the 80 NWM medium-range (3-hour) channel flow published simultaneously. During the overlapped first 15 hours, the short-range forecasts were solely used due to their higher accuracy, yielding a total of 90 timestamps of discharge values for generated river forcing. Because each forecast dataset predicted the next 10 days’ situation, its time frame only covered a segment of the event. Each run lasted for 20 days, which included 10 days to load river forcing and the additional 10 days to allow the peak to flow out of the domain. In this manner, 15 days of NWM streamflow forecasts (1–15 October 2016) were analyzed separately to examine their temporally evolving pattern and its impacts on the inundation prediction.
3. Results and Discussion
3.1. Verification of Streamflow Forcing
The streamflow forecast by the NWM was verified against the observations at the six USGS stream gauges (Figure 3). The forecast baseflow before and after the peak was generally well captured for all days of forecasts, though the hydrographs appeared to be quite different during the peak periods. It turned out that the shape of all observed hydrographs was not well preserved in the river forcing, indicating that potential problems may have existed in the current model setups. Further, the river forcing released on various days also exhibited a great variance, which reflected the influence of the evolving weather forcing because the same model chain was used throughout the event. For the forecasts made in advance of the peak, the major flood pulse was mostly missed or significantly underestimated. Such underestimation was also found for other continental-scale streamflow forecasting systems [1,16]. This could be due to the limitations of the meteorological forcing used to drive the streamflow forecasting [12]. When approaching the days of the real peaks, the hydrographs were mostly forecast to have taller and thinner spikes with significantly overpredicted peak flow compared to the observations. In addition, those forecast hydrographs tended to have a higher rising limb before the crest, whereas their falling limbs generally dropped down quickly before the observed peaks arrived. To sum up, similar to the previous finding regarding the EFFS forecasts [31], the flood waves in this study were forecast to arrive earlier than the real fronts and took less time to pass through the channels. This may have been due to neglecting the convection terms in the kinematic-wave routing approximation adopted by the current NWM operational configuration, and also partly due to neglecting the overbank spillage, which together led to faster and more floodwater routed through the channel to the downstream.
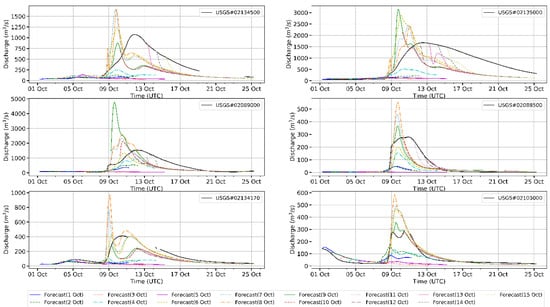
Figure 3.
Comparisons between the hydrographs observed from the United States Geological Survey (USGS) stream gauges and the hydrographs developed by the National Water Model streamflow forecasts.
Accordingly, the statistical test also shows that some of the forecast streamflow time series at the selected reaches did not have acceptable NSE coefficients (Figure 4). The exceptions include the forecasts made subsequent to the actual peaks at gauge 02103000 (9–11 October forecasts) and gauge 02088500 (11–13 October forecasts), which both matched well with the falling limbs of the observed hydrographs. Only the selected six stream gauges within the study sites recorded data during the event, and thus only the river reaches hosting those gauges were analyzed. However, considering that each study site had a total of 100–700 river reaches, they were expected to contribute a considerable amount of uncertainty in terms of volumes and dynamics to the inundation mapping. Between streamflow and lateral inflow, the latter may have relatively less contribution because it took up an average of 25% of the total incoming volume, utilizing the 8 October forecast as an example. However, this ratio varied in a wide range between 4% to 60% across different sites, and depended on factors such as the area of the domain, density of the river network, and the local stream orders.
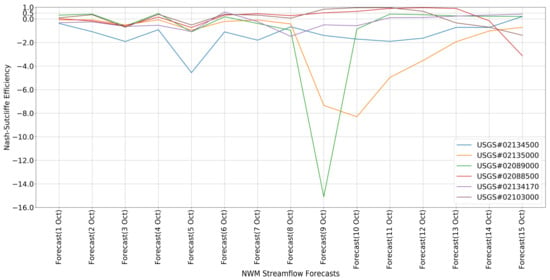
Figure 4.
Nash–Sutcliff efficiency coefficients for comparing the National Water Model (NWM) forecast streamflow with the United States Geological Survey (USGS) observed streamflow.
3.2. Inundation Validation
Driven by the streamflow and lateral inflow forecasts, the hydrodynamic model was run to map the corresponding riverine flood. The simulated inundation was validated against the HWMs and the published flood extents. On a point-to-point basis, the simulated peak water surface elevation of the corresponding grid cell covering each HWM was retrieved from the RIFT outputs via postprocessing. The comparison results were grouped by the days of streamflow forecasts to reflect the evolution of weather forcing along with the time (Figure 5). The errors were measured by ME and ME95%. Across all days of river forcing applied, the maximum water surface elevations were underestimated by less than 1 m on average. The forcing of 8 October 2016 achieved the best overall accuracy with an ME of −0.06 m. This corresponds with the previous observation that 8 October 2016 was one of a few river forcing datasets whose hydrographs had larger peaks than the observed ones (Figure 3).
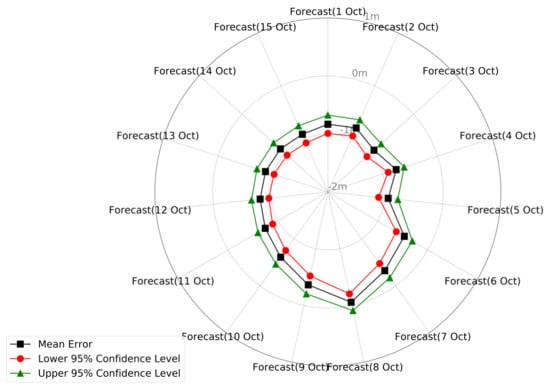
Figure 5.
The mean error and the 95% confidence levels of the errors of the simulated peak water surface elevations.
The simulated maximum flood extents generally fit with the published maps, as the F and PSS indicators were both around 0.6 (Figure 6). Consistent with the depth validation, the river forcing of 8 October 2016 best predicted the overall flood extents with the F indicator as 0.73 and the PSS indicator as 0.74. Before and after the actual peaks occurred, the forecast hydrographs either underpredicted or missed the real peaks (Figure 3), which may have caused relatively underestimated maximum flood elevations and extents observed here. In this perspective, the worst-case river forcing, though usually released as late as the actual peak, may usually be the most reliable one to use for predicting the peak inundation situation for the extreme events. However, despite the significantly mismatched forecast hydrographs, all river forcing ended up approximating the peak water elevations and flood extents very close to the observed conditions. This indicates that the inundation model may not be very sensitive to the uncertainty of the driving weather forcing.
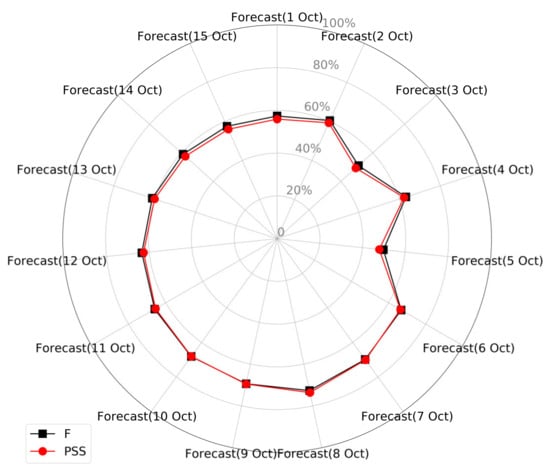
Figure 6.
The fit (F) and Peirce’s skill score (PSS) of the simulated inundated extents.
3.3. Error Propagation
As discussed previously, the evolving river forcing as the extreme event developed did not result in very different flood inundation predictions. The simulated peak water elevations, as well as the maximum extents, were not considerably different from the observations. Therefore, considering that the forecast hydrographs appear to be quite different from day to day, our findings can indicate that the uncertainty of the river forcing may have limited influence on the simulation of peak inundations. To further examine this hypothesis, the river forcing and the subsequent predicted peak water surface elevations and extents were compared to the corresponding observations again and summarized statistically. Specifically, the time series of the forecast streamflow were compared to observations with PBIAS and NSE computed. The forecast streamflow was confirmed as having a wide range of variations, with PBIAS varying from −0.89 to −0.15 and NSE varying from −0.64 to 0.53 (Table 2). In contrast, the simulated peak water surface elevations had one order of magnitude fewer variations, with PBIAS ranging from −0.03 to 0.00 and NSE ranging from 0.98 to 0.99 (Table 3); the simulated peak flood extents also had approximately one order of magnitude fewer variations, with the F indicator changing from 0.50 to 0.73 and the PSS indicator changing from 0.48 to 0.74. In other words, the errors of forecast streamflow time series did not cause an equal magnitude of errors in the peak inundation prediction. Therefore, the uncertainty in the weather and river forcing may not effectively accumulate and propagate into the inundation prediction for extreme events. This is consistent with multiple previous findings; for example, although the ensemble of forecast hydrographs mostly missed the observed peaks, 85% of the observed extents were predicted correctly [1]. Similarly, the uncertainty of inflow magnitudes did not show a notable influence on the downstream maximum water depths across different cross sections [32]. Our finding may also partially explain why only limited variations in the predicted inundation extents were attributed to the rainfall-runoff and inundation models [31]. In accordance with the previous study, the inundation model seems to be able to dampen the uncertainty originated from the ensemble of forecast precipitation [6]. Our study further shows that this effect may become more prominent in extreme events. When the affected areas are largely inundated, the errors caused by the uncertain meteorological forcing and flood models may thereby be concealed by the inundation-focused evaluating metrics.

Table 2.
Statistics of the forecast streamflow compared to the stream gauge observations.

Table 3.
Statistics of the simulated peak water elevations compared to the high water marks.
Another aspect of this finding may be more important. The highly uncertain weather and river forcing may not need to be extremely accurate to predict a reasonable inundation map for extreme events. This may help relieve the demand for using the ensemble of NWPs and reduce the required lead time. Compared to the peak water elevations, the maximum flood extents seemed to be relatively more affected by the uncertainty of river forcing. Consequently, improving the prediction of the overall inundation extent may be more cost-effective to invest than the prediction of the peak water surface elevations for certain hot spots.
3.4. Accuracy Measure of River Forcing
Although the errors of the peak inundation predictions did not increase with the errors of river forcing by the same order of magnitude, the mechanism controlling this uncertainty propagation is still unclear. The water elevations and extents were best predicted on the basis of the river forcing of 8 October 2016 (Figure 5, Figure 6, Table 3, Table 4), which, however, did not result in the single highest PBIAS and NSE statistics against other forecasts (Figure 4, Table 2). This discrepancy was caused by the restricted 10-day window of the river forcing. For example, even if the streamflow time series forecast on 15 October 2016 did not capture the peak event, it still fit well with the observed streamflow for the next 10 days, yielding the highest NSE value (Table 2). In this regard, fitting the time series of the forecast streamflow to the observation would not guarantee the accuracy of inundation mapping for extreme events. To look for a better metric, we computed the total of the volumetric discharge of six sampled stream gauges altogether through the entire event (1 October to 25 October 2016). Benchmarked by this observed volumetric total, the deviation of the total forecast streamflow volume of the six corresponding NWM reaches was also computed by each of the 15 river forcing datasets. Even though the 10-day forcing window was shorter than the observed data window (25 days), the point here was to quantify the deviation in total volume forecast by the streamflow forcing. The difference between the observed and forecast total flow volumes was statistically assessed by the percent bias again (denoted as PBIAS-V-NWM). The latter (PBIAS-V-NWM) was then compared to the NSE and PBIAS of the simulated peak water elevations (Figure 7), and to the F and PSS indicators of the simulated maximum flood extents (Figure 8). The comparisons present a clearly linear correlation between the discrepancy in the total volume forecast by the NWM river forcing and the accuracy of the peak inundation predictions, with the coefficients of determination all above 0.8. This indicates that the total volume is an important measure of the accuracy of river forcing for flood simulations. It explains why the forcing of 8 October 2016, with the highest PBIAS-V-NWM, best predicts the peak inundation conditions, as discussed previously. Therefore, for the purpose of predicting inundation for extreme events, forecasting the correct total volume of floodwater seems to matter more than having a forecast hydrograph well fit to observations within a limited time slice. This also helps explain why the lack of forecast total rainfall due to the deficient weather forcing led to an underpredicted inundation extent [31]. It is further consistent with the previous finding that the magnitude of inflow can be an important factor determining the maximum water level [11].

Table 4.
Statistics of the simulated peak flood extents compared to the published extents.
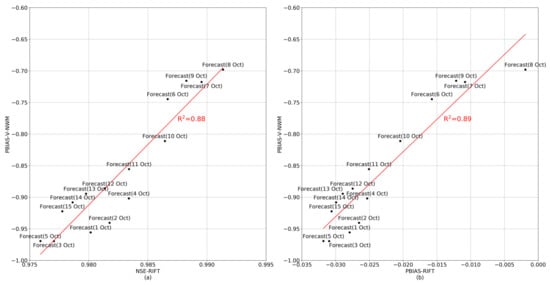
Figure 7.
The percent bias of the total volume of the National Water Model (NWM) streamflow forecasts was compared to the NSE (a) and PBIAS (b) of the simulated peak water elevations. The red line refers to the linear fit. Abbreviations: PBIAS-V-NWM, percent bias of the total volume of NWM forecast streamflow; NSE-RIFT, Nash–Sutcliffe efficiency of the peak water elevations simulated by Rapid Inundation Flood Tool; PBIAS-RIFT, percent bias of the peak water elevations simulated by Rapid Inundation Flood Tool; R2, coefficient of determination.
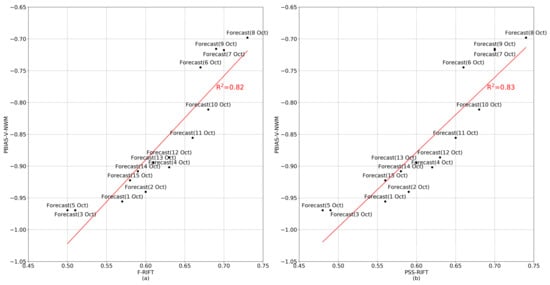
Figure 8.
The percent bias of the National Water Model (NWM) streamflow forecasts was compared to the F (a) and PSS (b) of the simulated maximum flood extents. The red line refers to the linear fit. Abbreviations: PBIAS-V-NWM, percent bias of the total volume of NWM forecast streamflow; F-RIFT, the measure of fit of the maximum flood extents simulated by Rapid Inundation Flood Tool; PSS-RIFT, Peirce’s skill score of the maximum flood extents simulated by Rapid Inundation Flood Tool; R2, coefficient of determination.
3.5. Tradeoff in Domain Size
The impact of the domain size on computational cost was examined in the hope of providing the extra best-practice experience for similar operational tasks. Additional domain sizes (5 km and 20 km) were tested on the basis of the forcing of 8 October 2016, which was proven to best predict the inundation. The peak water surface elevations were underpredicted for all domain sizes (Figure 9), which further reflects that the total volume of incoming discharge was underpredicted by the river forcing. As more river reaches were incorporated by using a larger forcing domain, the mean error became closer to zero. However, the improvement in ME slowed down when the domain size increased from 10 km to 20 km. Consistently, the maximum flood extents were better predicted as the domain size increased, but the improvement also became sluggish near the end. Considering that the computational cost did rise exponentially (Figure 9), the gain in accuracy would not keep pace with the rising cost as the domain enlarges. We found that the computational cost of our runs can depend on factors including the number of boundary conditions, the total volume of inflow, and the complexity of local topography. Out of our tests, a 10 km boundary seems to be a good starting size for predicting the riverine inundation, which seems to well balance the accuracy and the cost. Notably, we found that increasing the size of the forcing domain, that is, loading more river forcing in a larger area enclosing the area of interest, ended up with slightly lower F and PSS values for one of our sites (Figure 10). This might be because as more river reaches were incorporated in a larger domain, the overbank spillage from the minor tributaries and ditches may not have been well captured by the published flood extents (causing a larger ). This stresses the need to establish a well-accepted suite of verification and validation datasets for post-hurricane hindcasts.
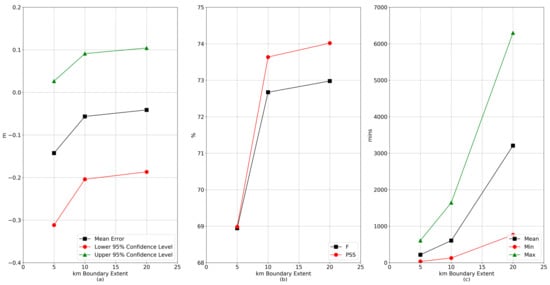
Figure 9.
The changes in the statistics of the simulated peak water surface elevations (a) and maximum extents (b) as well as the changes in the computational costs (c) along with the increase in the size of the forcing domain. The forecast streamflow of 8 October 2016 was used for all simulations. Abbreviations: F, the measure of fit; PSS, Peirce’s skill score.
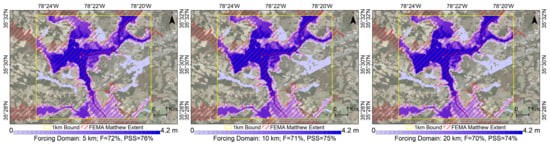
Figure 10.
The changes in simulated inundated areas along with the increase in the size of the forcing domain where forcing was loaded, compared to the flood extents published by the U.S. Federal Emergency Management Agency (FEMA).
4. Conclusions
Although several studies have traced the uncertainty propagation from the weather forcing to flood forecasting, the influence of the evolving weather states, as an extreme event advances, on the inundation prediction is seldom examined thoroughly. This study aimed to diagnose the uncertainty caused by such temporal evolution of forecast streamflow on inundation mapping for a real hurricane event. An automated workflow loosely coupling the NWM channel model with a high-resolution hydrodynamic inundation model was developed. The proposed workflow was validated by measured peak water surface elevations and maximum extents reported for Hurricane Matthew striking the eastern U.S. in 2016. A total of 15 forecasting datasets were examined at 10 study sites. The hydrographs forecast by the NWM river forcing on different days varied significantly as the event proceeded, and their shapes were also very different from the observed hydrographs, with NSE ranging from −15.09 to 0.96. The streamflow forecasts released before the actual peak period tended to miss or underpredict the observed peak flow. The forecast hydrographs released near the actual peak time did predict a spike, which, however, had a thinner and sharper shape with the overestimated extremes happening earlier than the real peak.
The river forcing with such significant uncertainty was then applied as the upstream and lateral inflow boundary conditions to drive the inundation model, which turned out to well predict the overall inundation conditions. The predicted peak water surface elevations and flood extents were all found to have one order of magnitude lower variations than the forecast river forcing when they were compared to their corresponding observations. The PBIAS and NSE of the predicted maximum water surface elevations both varied in narrow ranges from −0.03 to 0.00 and from 0.98 to 0.99, respectively. Consistently, the F and PSS indicators for the predicted maximum flood extent ranged from 0.50 to 0.73 and from 0.48 to 0.74, respectively. Considering the river forcing as the only uncertain contributor in this study, this demonstrated that the uncertainty of the forecast streamflow may not considerably cascade to the inundation mapping. Compared to the predicted peak water surface elevations, the predicted maximum flood extents seem to be slightly more subject to the variations in river forcing.
The total volume of discharge through the event was found as a better metric to assess the accuracy of weather/river forcing for inundation mapping, whereas the conventional metrics measuring the fitness between the forecast streamflow time series with the observations within the forecasting time window did not guarantee an accurate prediction of inundation. Both the PBIAS and NSE of the simulated peak water levels were shown to be highly correlated with the PBIAS of the total volume of forecast streamflow (PBIAS-V-NWM), with the coefficients of determination as 0.88 and 0.89, respectively. The F and PSS indicators of the simulated maximum extents also exhibited a linear correlation with the PBIAS of the total volumes of river forcing (PBIAS-V-NWM), with the coefficients of determination as 0.82 and 0.83, respectively.
This study argues that besides the temporal pattern as commonly emphasized by streamflow forecasting, the accuracy of the forecast total volume is another important ingredient for inundation predictions. In the studied extreme event, we offered new evidence that the forecast streamflow with imperfect temporal patterns did not cause the maximum inundation to be predicted far from the observations, as also shown by other models during different events [1,6,31,32]. This study further found that the flood extents and maximum water elevations tend to be better predicted when the volume of total incoming streamflow is more accurately forecast. It should not be interpreted that the temporal pattern of the forecast streamflow is unimportant for all cases, because the timing of the peak affects the decision of when to evacuate especially during flash floods. Although circumstances can be different case by case, we intend to stress that the community of streamflow forecasting should pay as much attention to matching the peak as to matching the total volume. In addition, considering that some recent hurricanes (such as Harvey and Florence) could be long-lived in the coastal zone leading to long-lasting inundation, the total consequences heavily depend on the largest affected area and the maximum depth of floodwater. Their predictions are proven by this study to be highly related to the accurate forecasting of the streamflow volume. This finding may also help explain why although the uncertainty of applying various rating curves for streamflow forecasting may affect the downstream inundation predictions [10], its influence was reported as not being dominant [11,32]. We infer that the accuracy of the forecast streamflow volume could be an additional important metric for diagnosing such inundation predictions. While we have demonstrated the significance of volumetric accuracy of streamflow forecasting on inundation prediction, we do not fully understand this effect for the events with significantly different sizes, topographies, and flow regimes such as compound floods. We need more follow-up studies on how the accuracy of the forecast streamflow volume in various cases affects the inundation prediction.
This work provides extra best-practice experience for similar operational tasks that need to predict a local-scale flood inundation driven by the streamflow forecast by large-scale river forecasting platforms. The gain in accuracy is not proportional to the increase in computational time. Modeling a larger forcing domain would require an exponential increase in cost. Our study shows that a 10 km boundary enclosing the area of interest seems to be a good starting point for loading the river forcing, which achieved an efficient compromise between the accuracy and the cost. Considering that study areas have low-lying terrains with a strong tendency of backwater flow near the boundary, a 10 km wide bounding box could, therefore, be recommended as the minimum forcing domain for most cases. An extra buffer zone may still be needed, depending on how a boundary is handled by the inundation model.
Author Contributions
Conceptualization, Y.F. and D.R.J.; methodology, Y.F. and D.R.J.; validation and analysis, Y.F.; writing, Y.F., D.R.J., and C.L.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank the National Atmospheric and Oceanic Administration’s Office of Water Prediction, especially Fernando Salas, for their kind help.
Conflicts of Interest
The authors declare no conflict of interest.
References
- De Roo, A.P.; Gouweleeuw, B.; Thielen, J.; Bartholmes, J.; Bongioannini-Cerlini, P.; Todini, E.; Bates, P.D.; Horritt, M.; Hunter, N.; Beven, K. Development of a European flood forecasting system. Int. J. River Basin Manag. 2003, 1, 49–59. [Google Scholar] [CrossRef]
- Judi, D.R.; Rakowski, C.L.; Waichler, S.R.; Feng, Y.; Wigmosta, M.S. Integrated Modeling Approach for the Development of Climate-Informed, Actionable Information. Water 2018, 10, 775. [Google Scholar] [CrossRef]
- Feng, Y.; Rakowski, C.L.; McPherson, T.N.; Judi, D.R. A partition of the combined impacts of socioeconomic development and climate variation on economic risks of riverine floods. J. Flood Risk Manag. 2019, 12, e12508. [Google Scholar] [CrossRef]
- Snow, A.D.; Christensen, S.D.; Swain, N.R.; Nelson, E.J.; Ames, D.P.; Jones, N.L.; Ding, D.; Noman, N.S.; David, C.H.; Pappenberger, F.; et al. A High-Resolution National-Scale Hydrologic Forecast System from a Global Ensemble Land Surface Model. Jawra J. Am. Water Resour. Assoc. 2016, 52, 950–964. [Google Scholar] [CrossRef]
- Cloke, H.L.; Pappenberger, F. Ensemble flood forecasting: A review. J. Hydrol. 2009, 375, 613–626. [Google Scholar] [CrossRef]
- He, Y.; Wetterhall, F.; Cloke, H.L.; Pappenberger, F.; Wilson, M.; Freer, J.; McGregor, G. Tracking the uncertainty in flood alerts driven by grand ensemble weather predictions. Meteorol. Appl. 2009, 16, 91–101. [Google Scholar] [CrossRef]
- Renner, M.; Werner, M.G.F.; Rademacher, S.; Sprokkereef, E. Verification of ensemble flow forecasts for the River Rhine. J. Hydrol. 2009, 376, 463–475. [Google Scholar] [CrossRef]
- Saleh, F.; Ramaswamy, V.; Georgas, N.; Blumberg, A.F.; Pullen, J. A retrospective streamflow ensemble forecast for an extreme hydrologic event: A case study of Hurricane Irene and on the Hudson River basin. Hydrol. Earth Syst. Sci. 2016, 20, 2649–2667. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Wang, H.; Qin, J.; Dong, L. Large-watershed flood forecasting with high-resolution distributed hydrological model. Hydrol. Earth Syst. Sci. 2017, 21, 735–749. [Google Scholar] [CrossRef]
- Pappenberger, F.; Matgen, P.; Beven, K.J.; Henry, J.-B.; Pfister, L.; Fraipont, P. Influence of uncertain boundary conditions and model structure on flood inundation predictions. Adv. Water Resour. 2006, 29, 1430–1449. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.J.; Ratto, M.; Matgen, P. Multi-method global sensitivity analysis of flood inundation models. Adv. Water Resour. 2008, 31, 1–14. [Google Scholar] [CrossRef]
- Young, P.C. Advances in real–time flood forecasting. Philos. Trans. R. Soc. Ser. A: Math. Phys. Eng. Sci. 2002, 360, 1433–1450. [Google Scholar] [CrossRef] [PubMed]
- Rajib, A.; Liu, Z.; Merwade, V.; Tavakoly, A.A.; Follum, M.L. Towards a large-scale locally relevant flood inundation modeling framework using SWAT and LISFLOOD-FP. J. Hydrol. 2020, 581, 124406. [Google Scholar] [CrossRef]
- Follum, M.L.; Tavakoly, A.A.; Niemann, J.D.; Snow, A.D. AutoRAPID: A Model for Prompt Streamflow Estimation and Flood Inundation Mapping over Regional to Continental Extents. Jawra J. Am. Water Resour. Assoc. 2017, 53, 280–299. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Buahin, C.A.; Sangwan, N.; Fagan, C.; Maidment, D.R.; Horsburgh, J.S.; Nelson, E.J.; Merwade, V.; Rae, C. Probabilistic Flood Inundation Forecasting Using Rating Curve Libraries. Jawra J. Am. Water Resour. Assoc. 2017, 53, 300–315. [Google Scholar] [CrossRef]
- Hunter, N.; Bates, P.; Neelz, S.; Pender, G.; Villanueva, I.; Wright, N.; Liang, D.; Falconer, R.A.; Lin, B.; Waller, S. Benchmarking 2D hydraulic models for urban flood simulations. Proceedings of the Institution of Civil Engineers: Water Management 2008, 161, 13–30. [Google Scholar] [CrossRef]
- Werner, M.; Blazkova, S.; Petr, J. Spatially distributed observations in constraining inundation modelling uncertainties. Hydrol. Process. 2005, 19, 3081–3096. [Google Scholar] [CrossRef]
- Horizon Systems Corporation. National Hydrography Dataset Plus Version 2 (NHDPlusV2). Available online: http://www.horizon-systems.com/NHDPlus/NHDPlusV2_home.php (accessed on 16 July 2019).
- Tasseff, B.; Judi, D. Nuflood, Version 1. x; Los Alamos National Lab: Los Alamos, NM, USA, 2016. [Google Scholar]
- Judi, D.R.; Burian, S.J.; McPherson, T.N. Two-dimensional fast-response flood modeling: Desktop parallel computing and domain tracking. J. Comput. Civ. Eng. 2010, 25, 184–191. [Google Scholar] [CrossRef]
- Brodtkorb, A.R.; Hagen, T.R.; Lie, K.-A.; Natvig, J.R. Simulation and visualization of the Saint-Venant system using GPUs. Comput. Vis. Sci. 2010, 13, 341–353. [Google Scholar] [CrossRef][Green Version]
- Kurganov, A.; Petrova, G. A second-order well-balanced positivity preserving central-upwind scheme for the Saint-Venant system. Commun. Math. Sci. 2007, 5, 133–160. [Google Scholar] [CrossRef]
- Chertock, A.; Cui, S.; Kurganov, A.; Wu, T. Well-balanced positivity preserving central-upwind scheme for the shallow water system with friction terms. Int. J. Numer. Methods Fluids 2015, 78, 355–383. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Effects of spatial resolution on a raster based model of flood flow. J. Hydrol. 2001, 253, 239–249. [Google Scholar] [CrossRef]
- Alfieri, L.; Burek, P.; Dutra, E.; Krzeminski, B.; Muraro, D.; Thielen, J.; Pappenberger, F. GloFAS-global ensemble streamflow forecasting and flood early warning. Hydrol. Earth Syst. Sci. 2013, 17, 1161. [Google Scholar] [CrossRef]
- Weaver, J.C.; Feaster, T.D.; Robbins, J.C. Preliminary Peak Stage and Streamflow Data at Selected Streamgaging Stations in North Carolina and South Carolina for Flooding Following Hurricane Matthew, October 2016; 2016-1205; U.S. Geological Survey: Reston, VA, USA, 2016; p. 38.
- Koenig, T.A.; Bruce, J.L.; O’Connor, J.; McGee, B.D.; Holmes, J.R.R.; Hollins, R.; Forbes, B.T.; Kohn, M.S.; Schellekens, M.; Martin, Z.W.; et al. Identifying and Preserving High-Water Mark Data; 3-A24; U.S. Geological Survey: Reston, VA, USA, 2016; p. 47.
- USGS. Short-Term Network (STN) Data Portal. Available online: https://stn.wim.usgs.gov/STNDataPortal/ (accessed on 16 July 2019).
- FEMA. Cloud GIS Infrastructure Production Site. Available online: https://data.femadata.com/ (accessed on 3 August 2017).
- Pappenberger, F.; Beven, K.J.; Hunter, N.; Bates, P.; Gouweleeuw, B.; Thielen, J.; De Roo, A. Cascading model uncertainty from medium range weather forecasts (10 days) through a rainfall-runoff model to flood inundation predictions within the European Flood Forecasting System (EFFS). Hydrol. Earth Syst. Sci. Discuss. 2005, 9, 381–393. [Google Scholar] [CrossRef]
- Hall, J.W.; Tarantola, S.; Bates, P.D.; Horritt, M.S. Distributed Sensitivity Analysis of Flood Inundation Model Calibration. J. Hydraul. Eng. 2005, 131, 117–126. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).