Uncertainty Quantification in Machine Learning Modeling for Multi-Step Time Series Forecasting: Example of Recurrent Neural Networks in Discharge Simulations

Abstract

As a revolutionary tool leading to substantial changes across many areas, Machine Learning (ML) techniques have obtained growing attention in the field of hydrology due to their potentials to forecast time series. Moreover, a subfield of ML, Deep Learning (DL) is more concerned with datasets, algorithms and layered structures. Despite numerous applications of novel ML/DL techniques in discharge simulation, the uncertainty involved in ML/DL modeling has not drawn much attention, although it is an important issue. In this study, a framework is proposed to quantify uncertainty contributions of the sample set, ML approach, ML architecture and their interactions to multi-step time-series forecasting based on the analysis of variance (ANOVA) theory. Then a discharge simulation, using Recurrent Neural Networks (RNNs), is taken as an example. Long Short-Term Memory (LSTM) network, a state-of-the-art DL approach, was selected due to its outstanding performance in time-series forecasting, and compared with simple RNN. Besides, novel discharge forecasting architecture is designed by combining the expertise of hydrology and stacked DL structure, and compared with conventional design. Taking hourly discharge simulations of Anhe (China) catchment as a case study, we constructed five sample sets, chose two RNN approaches and designed two ML architectures. The results indicate that none of the investigated uncertainty sources are negligible and the influence of uncertainty sources varies with lead-times and discharges. LSTM demonstrates its superiority in discharge simulations, and the ML architecture is as important as the ML approach. In addition, some of the uncertainty is attributable to interactions rather than individual modeling components. The proposed framework can both reveal uncertainty quantification in ML/DL modeling and provide references for ML approach evaluation and architecture design in discharge simulations. It indicates uncertainty quantification is an indispensable task for a successful application of ML/DL.

1. Introduction

Recently, Machine Learning (ML) techniques have obtained growing attention and Deep Learning (DL) techniques have led to substantial changes across many areas of study [1]. As a subfield of ML, DL is more concerned with datasets, algorithms and layered structures. Owing to the enhanced capability to characterize the system complexity and flexible structure, research and applications of ML/DL for time-series prediction are proliferating and promising. In hydrology, the advent of ML/DL techniques has encouraged novel applications or substantially improved old ones [2,3]. Though ML/DL approaches are also fundamentally black-box methods, they can be developed with minimal inputs and applied easily, without considering the redundant physical mechanism of the watershed system. ML approaches and their hybrid application have performed well or comparable when applied to predict hydrological time series, compared to physically based models [4]. The continuous improvement of ML/DL approaches and architectures demonstrates their suitability for discharge simulation. However, the application of ML/DL techniques depends heavily on datasets, algorithms and layered structures, so it is necessary to quantify uncertainty contributions of each component in ML/DL modeling.

In ML modeling, quantifying uncertainty is an indispensable task to improve the validity and predictability of ML model applications. Various uncertainty sources can be mainly divided into three types: sample set partitioning, ML approach selection and ML architectures design. Most of the previous studies only focused on the single source of uncertainty. Jha et al. [5] investigated the impact of dataset uncertainties on the performance of the ML model predictions. Rahmati et al. [6] quantified the predictive uncertainty of three ML approaches with quantile regression and uncertainty estimation based on local errors and clustering. Li et al. [7] demonstrated the uncertainty quantification analysis of neural network structure (the number of layers and nodes in each layer). Most studies of hydrological time-series forecasting have focused on the application of algorithms and rarely discussed the importance of model architectures’ design to simulation results [4]. Moreover, relatively few studies have been conducted to investigate the interaction among different uncertainty sources and their contributions to ML modeling, so it is necessary to establish a framework for quantifying uncertainty contributions of the sample set, ML approach, ML architectures and their interaction in ML modeling.

The choice of promising ML/DL approach is one of the most prominent activities for time-series forecasting. Among all ML approaches, Recurrent Neural Network (RNN) has established a reputation to deal with time series by its particular recurrent neural connections. Almost all exciting results based on RNNs have been achieved by Long Short-Term Memory (LSTM) network [8], so LSTM network has become the focus of DL. LSTM network was proposed by the German researchers Hochreiter and Schmidhuber as a solution to the long-term dependencies problem [9]. Due to the special network architecture, LSTM networks have great learning ability in dealing with time-series forecasting in many applications, such as speech recognition [10], stock price volatility [11], sentiment analysis [12], traffic forecast [13] and disease diagnosis [14]. Few attempts have been made to apply LSTM networks to hydrological problems [15]. In addition, most of the previous studies on evaluation of the LSTM network only focused on the comparison with other approaches, such as ANN [3], support vector regression [16] and RNNs [17]. However, there is no evaluation of the LSTM network based on the interactions between LSTM networks and other components of ML modeling.

To our knowledge, this idea serves as the first attempt to apply the analysis of variance (ANOVA) theory to the uncertainty quantification of ML modeling for multi-step time-series forecasting. The separate contributions and analysis to the total uncertainty budget can be estimated by ANOVA [18]. This paper focuses on comparing the uncertainty contributions ratio of components in ML modeling rather than evaluating the uncertainty of ML algorithms. The overall objectives of this paper are (1) to propose a framework to quantify uncertainty contributions of the sample set, ML approach, ML architecture and their interactions in ML modeling and evaluate multi-step time series forecasting models; and (2) to evaluate LSTM networks in discharge simulations under the proposed framework. In this paper, the standard LSTM cell is chosen because no variant can surpass the standard LSTM cell in all aspects [8].

To implement the proposed framework and evaluate LSTM networks, hourly flash-flood forecasting in small catchments is taken as a case study due to its more complex nonlinear relationship between rainfall and runoff in small temporal and spatial scales’ simulation. Five sample sets are constructed in the case study. Simple RNN is chosen as a comparison. To evaluate the interactions between LSTM networks and ML architecture, a novel ML architecture is designed by combining the expertise of hydrology and stacked DL structure, and compared with another conventional architecture. Then the simulated results of five sample sets, two RNN approaches and two ML architectures are evaluated and analyzed, respectively. Finally, we estimate the total ensemble uncertainty of the ML modeling and quantify the contributions of different uncertainty sources in discharge simulations.

2. Methodology

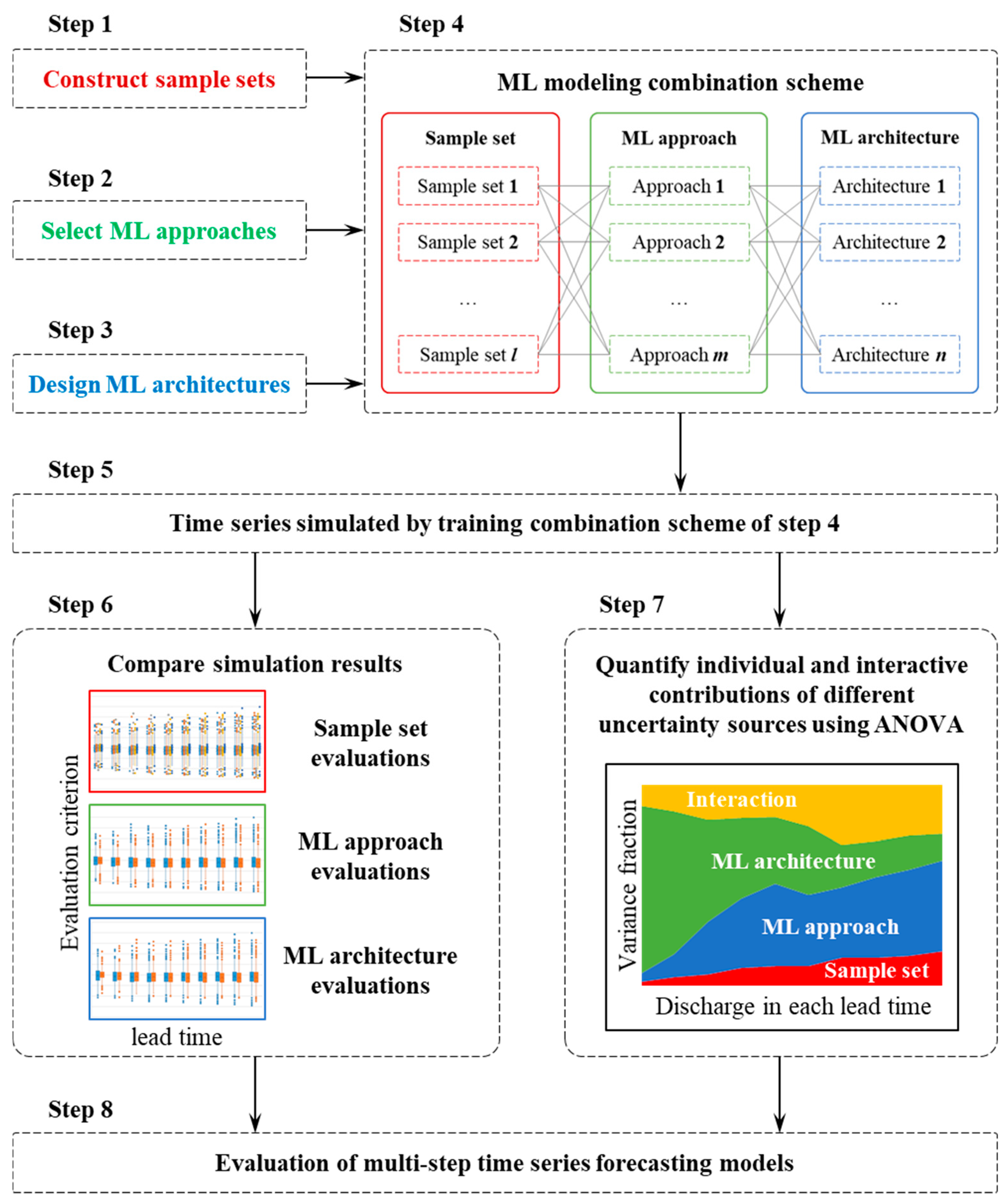
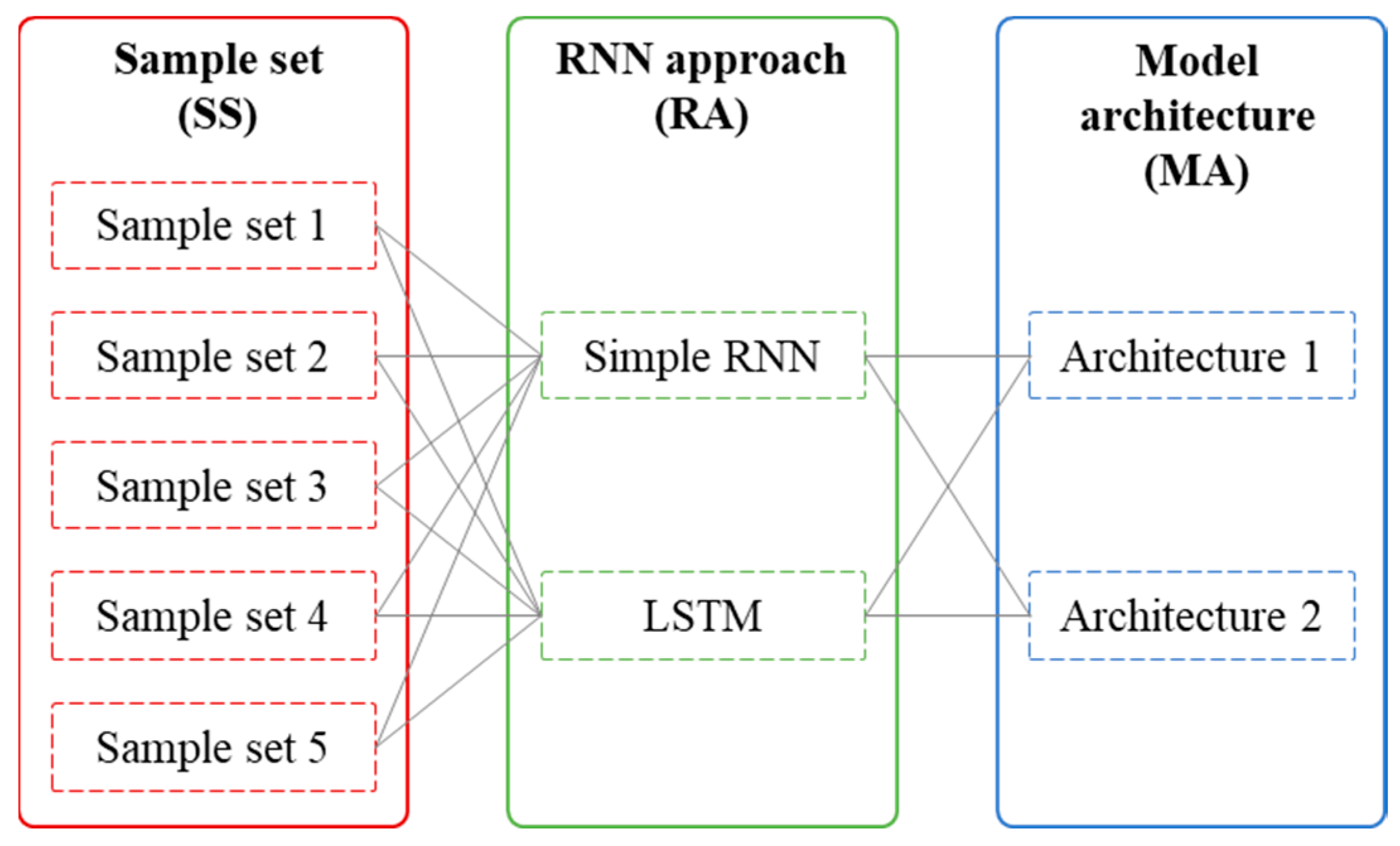
2.1. The Proposed Framework

Figure 1 shows the diagrammatic flowchart of the proposed framework for uncertainty quantification in ML modeling for multi-step time-series forecasting. This framework is composed of 8 steps: Steps 1–3 include three parts of ML modeling: partition sample sets, select ML approaches and design ML architectures. In Step 4, ML modeling combination scheme is established. Step 5 is to train all the combining schemes and simulate discharge. In Step 6, simulated results are compared to evaluate sample sets, ML approaches and ML architectures. The purpose of Step 7 is to quantify the individual and interactive contributions of different uncertainty sources, using ANOVA. Finally, Step 8 is to evaluate multi-step time-series forecasting models. In this paper, discharge simulations using by RNNs is taken as an example.

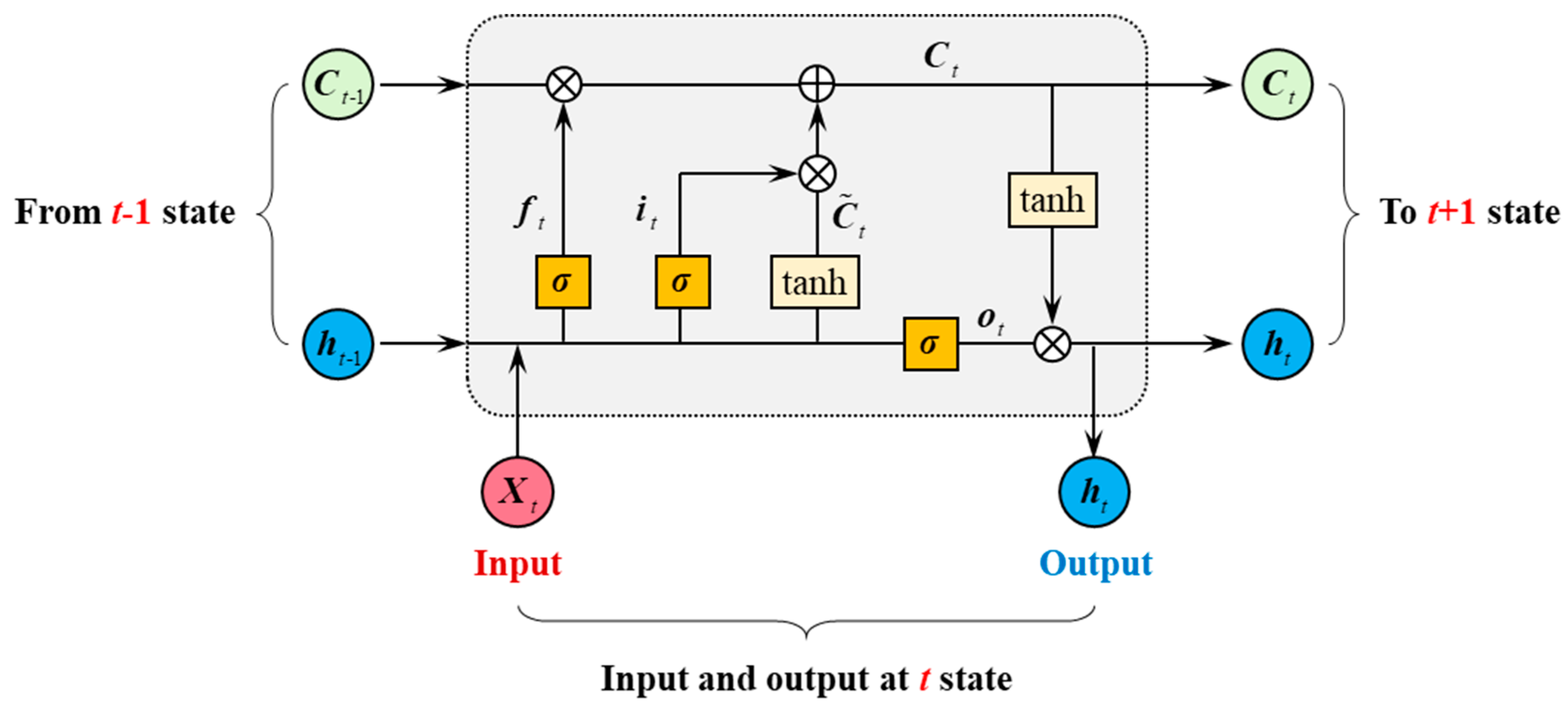
2.2. RNN Approaches

Two RNN approaches were selected for discharge simulations in this paper. Figure 2 and Figure 3 show the internals of a Simple RNN and LSTM memory cell, respectively.

2.2.1. Simple RNN

Simple RNN has the most basic structure in all RNNs [8]. In Figure 2, ${\mathit{X}}_t$ is the input at time-step t; ${\mathit{h}}_{t-1}$ is the hidden state and the output at time-step t−1; and ${\mathit{h}}_t$ is the hidden state and output of time-step t. Moreover, ${\mathit{h}}_t$ is calculated based on the previous hidden state ${\mathit{h}}_{t-1}$, the current input ${\mathit{X}}_t$ and activation function tanh().

2.2.2. LSTM Network

LSTM is an artificial RNN architecture which is suitable for processing and predicting the relatively long events in the time series [9]. Its particularity lies in that an LSTM memory cell is composed of four main elements: a forget gate, an input gate, a neuron with a self-recurrent connection and an output gate. In Figure 3, ${\mathit{X}}_t$ is the input to the memory cell at time-step t. ${\mathit{C}}_{t-1}, {\mathit{C}}_t$ and ${\mathit{h}}_{t-1}, {\mathit{h}}_t$ are the cell states and hidden states at time-step t−1, t. Moreover, ${\mathit{f}}_t, {\mathit{i}}_t, {\mathit{o}}_t$ are the states of forget gate, input gate and output gate; ${ \tilde{\mathit{C}}}_t$ is the candidate state of ${\mathit{C}}_t$; and $\sigma$ represents the activation function of sigmoid().

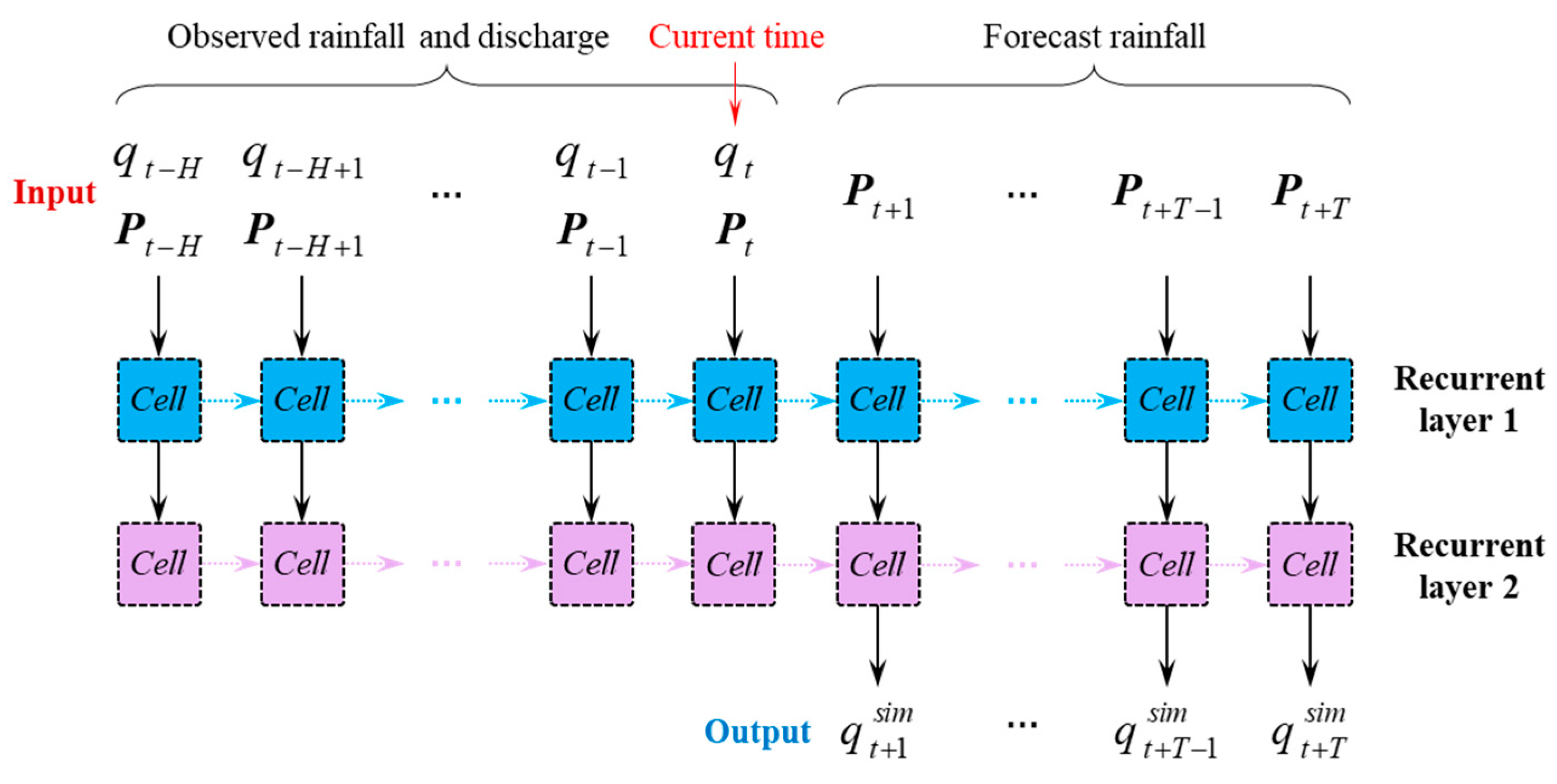
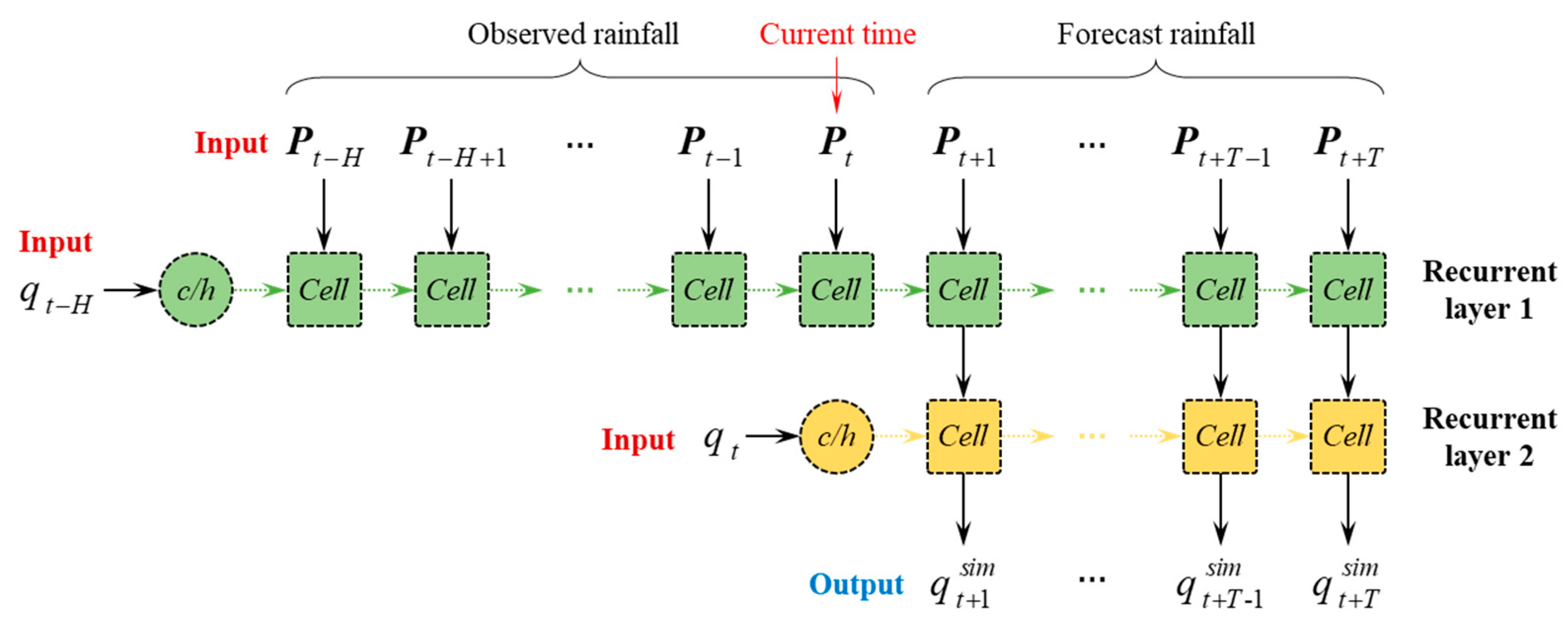
2.3. Model Architecture Design

Two model architectures are proposed based on a stacked DL structure for discharge simulations in this paper. Architecture 1 adopts the most common modeling strategy of time-series prediction, and architecture 2 is designed based on the expertise of hydrology. Figure 4 and Figure 5 show the data flow schematic diagram of model architectures. To make the data flow clearer, we only draw the Recurrent layers and omit other layers (i.e., Dense layers, TimeDistributed layers, Flatten layers and Concatenate layers). Recurrent layers are unrolled along the time dimension in Figure 4 and Figure 5. Additionally, the inputs of these two model architectures have not taken evaporation, infiltration and storage into account, since their variations give no relevant contribution to the river flow rate in the short period of heavy rain [19]. To achieve a longer discharge lead-time, potential future rainfall during lead-time periods is considered.

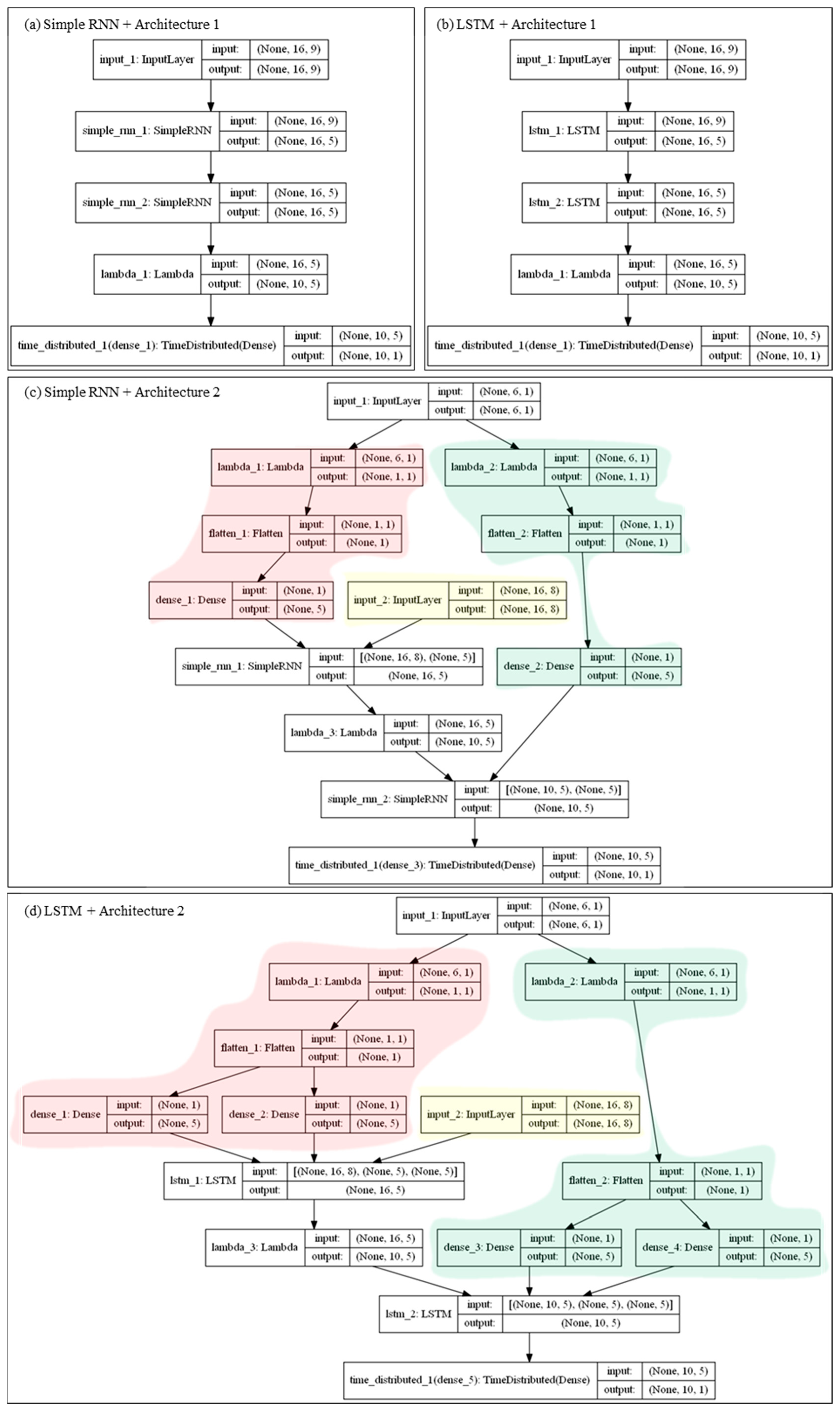
2.3.1. Model Architecture 1

As seen in Figure 4, two Recurrent layers are completely stacked. In layer 1, each time-step is a multivariate series comprised of discharge feature (q) and rainfall features (P). All features take the observed value during the observed period, and P take predicted value during the lead-time periods. Moreover, t represents the current time; H represents the maximum time lag in the basin; and T represents the maximum lead-time. The outputs $q_{t+1}^{sim}, \mathrm{\dots }, q_{t+T-1}^{sim}, q_{t+T}^{sim}$ are the forecasting discharges.

2.3.2. Model Architecture 2

As seen in Figure 5, two Recurrent layers are stacked in the lead-time periods; t, H, T and $q_{t+1}^{sim}, \mathrm{\dots }, q_{t+T-1}^{sim}, q_{t+T}^{sim}$ are the same as Figure 4. According to the expertise of hydrology, two crucial improvements are achieved in architecture 2. Firstly, rainfall and discharge features are no longer indiscriminately inputted into architecture 2. This is because the relationship between rainfall features, P, and output is totally different from the relationship between discharge feature q and output. These two different features play their respective roles in discharge simulation, so exploring different relationships by the ML model should not be restricted by the same input form. Secondly, the discharge feature is no longer inputted into the model at each time-step, and only discharge feature $q_{t-H}$ and $q_t$ are inputted to layer 1 and layer 2 as the initial cell state, c, and hidden state, h, respectively. As seen in Figure 4, the input form at each time-step of architecture 2 is the same as the rainfall input of hydrological models. In addition, architecture 2 weakens the effect of the observed discharges trend on forecasting discharges by discarding the input of $q_{t-H+1}, \mathrm{\dots }, q_{t-2}, q_{t-1}$. It emphasizes the direct driving effect of rainfall time series on forecasting discharges. In short, compared with architecture 1, architecture 2 is more in line with the hydrological model architecture.

In addition, we have tried a variety of architecture designs for discharge simulations, including different stacked architectures, different input modes and different numbers of Recurrent layers. The results of the case study indicate that architectures 1 and 2 are most representative, because (1) architecture 1 adopts the simplest design, in which both rainfall and discharge features are inputted at each time-step; (2) architecture 2 combines the expertise of hydrology and outperforms other architectures, in which discharge features are inputted as initial states. In other words, other architectures could be regarded as variants of architecture 1 or architecture 2, so architectures 1 and 2 are only chosen for variance decomposition in this study.

2.4. Criteria for Accuracy Assessment

Uncertainties of multi-step time-series forecasting models are evaluated based on discharge observations. The following evaluation criteria are used in discharge error assessment: Relative Peak-Discharge Error (RPE), Nash–Sutcliffe coefficient of efficiency (NSE), Mean Absolute Error (MAE) and Mean Square Error (MSE) [20]. In addition, NSE and RPE are suggested by the Chinese flood-forecasting guidelines and often used in flood-forecasting studies [21,22].

$$RPE = \frac{q_{peak}^{sim}-q_{peak}^{obs}}{q_{peak}^{obs}} \times 100\%$$

(1)

$$NSE= 1-\frac{{\displaystyle \sum _{t=1}^N{\left(q_t^{obs}-q_t^{sim}\right)}^2}}{{\displaystyle \sum _{t=1}^N{\left(q_t^{obs}-{\overline{q}}^{obs}\right)}^2}}$$

(2)

$$MAE= \frac{1}{N}\cdot {\displaystyle \sum _{t=1}^N\left|q_t^{obs}-q_t^{sim}\right|}$$

(3)

$$MSE= \frac{1}{N}\cdot {\displaystyle \sum _{t=1}^N{\left(q_t^{obs}-q_t^{sim}\right)}^2}$$

(4)

where $q_{peak}^{obs}$ and $q_{peak}^{sim}$ are the observed and simulated peak-discharge; $q_t^{obs}$ and $q_t^{sim}$ are the observed and simulated discharge; ${\overline{q}}^{obs}$ is the average value of the observed discharge; and N is the total number of observations.

2.5. Variance Decomposition

Figure 6 depicts the ML time-series forecasting modeling combination scheme employed in this study. It has three parts: sample set (SS), RNN approach (RA) and Model architecture (MA). In the variance decomposition, we aimed to decompose the total ensemble uncertainty into contributions from different elements of the ML modeling and interactions among them. The ML modeling ensemble consists of 10 combinations. For each of them, we estimated MAE, MSE, NSE and RPE. In the following, we describe these evaluation criteria as the general variable Y. To relate variable Y to the uncertainty sources, we use superscripts in $Y^{j, k, l}$, with j, k and l representing the different options of SS, RA and MA, respectively. The subsampling of the training sets and the ANOVA approach are explained in detail, as follows.

2.5.1. Subsampling Approach

The ANOVA approach could underestimate the variance in small sample sizes [23]. To diminish the effect of the sample size on the quantification of the variance contribution, Bosshard et al. [24] added the subsampling method to ANOVA approach. The purpose of the subsampling approach is to keep the same number of sample sizes for SS, RA and MA in each variance decomposition. In this paper, we subsample the five different SSs. In each subsampling iteration i, we select two SSs out of the five SSs, which results in a total of 10 possible SS pairs in Equation (5). To prevent confusion between the full set of five SSs and the subsampled SS pair, we replace the superscript j with g(h, i). As seen in Equation (5), the superscript g is a 2 × 10 matrix that contains the selected SSs for the particular subsampling iteration i ($i= 1, 2, \mathrm{\dots }, 10$). In each iteration i, there are two SSs ($h= 1, 2$).

$$\mathit{g}=\left(\begin{array}{cccccccccc}\mathrm{SS}1& \mathrm{SS}1& \mathrm{SS}1& \mathrm{SS}1& \mathrm{SS}2& \mathrm{SS}2& \mathrm{SS}2& \mathrm{SS}3& \mathrm{SS}3& \mathrm{SS}4\\ \mathrm{SS}2& \mathrm{SS}3& \mathrm{SS}4& \mathrm{SS}5& \mathrm{SS}3& \mathrm{SS}4& \mathrm{SS}5& \mathrm{SS}4& \mathrm{SS}5& \mathrm{SS}5\end{array}\right)$$

(5)

2.5.2. ANOVA Approach

In this study, we referred to an application of ANOVA in hydrological climate-impact projections [24]. According to the ANOVA theory, in each iteration i, the total sum of the squares ($SS{T}_i$) can be split into sums of squares due to the individual effects ($SS{A}_i$, $SS{B}_i$ and $SS{C}_i$) and their interactions ($SS{I}_i$) as follows:

$$SS{T}_i=SS{A}_i+SS{B}_i+SS{C}_i+SS{I}_i$$

(6)

where $SS{T}_i$ represents the total variance from two SSs, two RAs and two MAs in iteration i; $SS{A}_i$ represents the variance from two SSs in iteration i; $SS{B}_i$ represents the variance from two RAs in iteration i; $SS{C}_i$ represents the variance from two MAs in iteration i; $SS{I}_i$ represents the variance from the interaction among two SSs, two RAs and two MAs in iteration i. The terms in Equation (6) are estimated by the subsampling procedure, as follows:

$$SS{T}_i={\displaystyle \sum _{h=1}^H{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{l=1}^L{\left(Y^{g(h, i), k, l}-Y^{g(\circ , i), \circ , \circ }\right)}^2}}}$$

(7)

$$SS{A}_i=K\cdot L\cdot {\displaystyle \sum _{h=1}^H{\left(Y^{g(h, i), \circ , \circ }-Y^{g(\circ , i), \circ , \circ }\right)}^2}$$

(8)

$$SS{B}_i=H\cdot L\cdot {\displaystyle \sum _{k=1}^K{\left(Y^{g(\circ , i), k, \circ }-Y^{g(\circ , i), \circ , \circ }\right)}^2}$$

(9)

$$SS{C}_i=H\cdot K\cdot {\displaystyle \sum _{l=1}^L{\left(Y^{g(\circ , i), \circ , l}-Y^{g(\circ , i), \circ , \circ }\right)}^2}$$

(10)

$$SS{I}_i={\displaystyle \sum _{h=1}^H{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{l=1}^L{\left(Y^{g(h, i), k, l}-Y^{g(h, i), \circ , \circ }-Y^{g(\circ , i), k, \circ }-Y^{g(\circ , i), \circ , l}+2Y^{g(\circ , i), \circ , \circ }\right)}^2}}}$$

(11)

where variable Y represents evaluation criteria or simulated discharges; H, K and L represent the number of SS, RA and MA in iteration i. H, K and L are all equal to 2 in each iteration i. The symbol $\circ$ indicates averaging over the particular index. For example, in Equation (7), $Y^{g(\circ , i), \circ , \circ }$ equals to the average of $Y^{g(1, i), 1, 1}, Y^{g(1, i), 1, 2}, Y^{g(1, i), 2, 1}, Y^{g(1, i), 2, 2}, Y^{g(2, i), 1, 1}, Y^{g(2, i), 1, 2}, Y^{g(2, i), 2, 1}, Y^{g(2, i), 2, 2}$. Then, each variance fraction, ${\eta }^2$, is derived as follows:

$${\eta }_{SS}^2=\frac{1}{I}\cdot {\displaystyle \sum _{i=1}^I\frac{SS{A}_i}{SS{T}_i}}$$

(12)

$${\eta }_{RA}^2=\frac{1}{I}\cdot {\displaystyle \sum _{i=1}^I\frac{SS{B}_i}{SS{T}_i}}$$

(13)

$${\eta }_{MA}^2=\frac{1}{I}\cdot {\displaystyle \sum _{i=1}^I\frac{SS{C}_i}{SS{T}_i}}$$

(14)

$${\eta }_{Interactions}^2=\frac{1}{I}\cdot {\displaystyle \sum _{i=1}^I\frac{SS{I}_i}{SS{T}_i}}$$

(15)

where ${\eta }^2$ has a range of 0 to 1 and describes a 0–100% contribution to the total uncertainty of simulated discharges. According to the matrix (5), I is equal to 10 in this study. The sum of ${\eta }_{SS}^2, {\eta }_{RA}^2, {\eta }_{MA}^2, {\eta }_{Interactions}^2$ is equal to 1, and the larger the value of ${\eta }^2$ is, the relatively greater uncertainty contribution of corresponding compositions in ML modeling.

3. Case Study

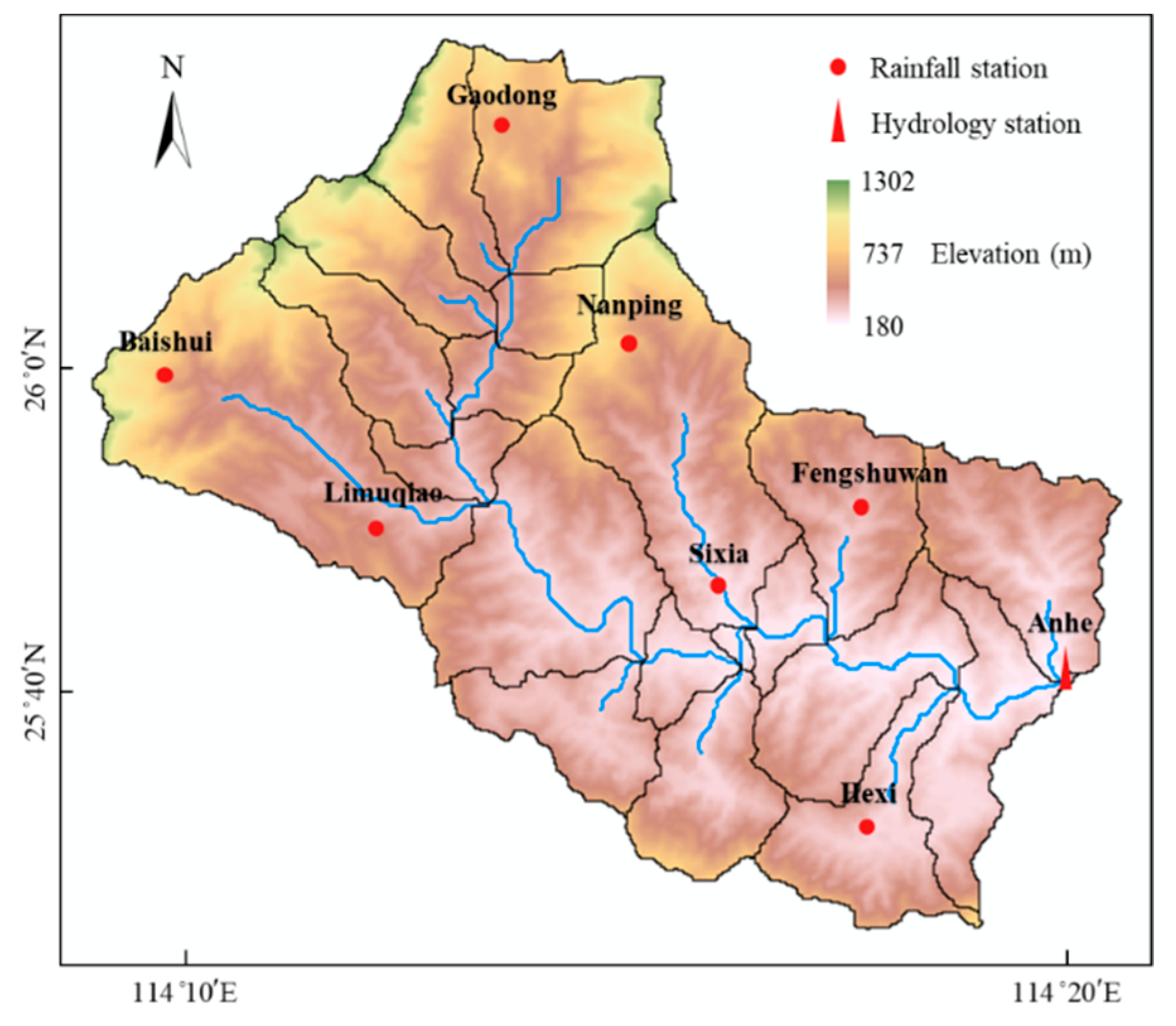
3.1. Study Area

Anhe catchment, located in the province of Jiangxi, in humid Southeastern China, with a drainage area of 251 km² and mean annual rainfall of 1426 mm, is taken as the case study. The rainfall data from eight rain stations and discharge data from one hydrology station were used in this study, as shown in Figure 7. According to statistical analysis, the maximum basin time lag of Anhe is 6 h. In this paper, observed rainfall measurements are taken as the perfect forecast for 1–10 h lead-time. Thus, we take H as 5 h and T as 10 h in the two model architectures (see Figure 4 and Figure 5).

The hourly time-series data for twenty-nine years (from 1984 to 2012; 75 flood events) are included in the modeling process. The beginning and the end of a flood event are taken as the rising point from base flow before the main rainfall and the recession point to base flow, respectively. In light of the time sequence of flood events and the representativeness of peak-discharge, 75 flood events are divided into five parts, and each part has 15 flood events (see Figure 8). Then, five sample sets are constructed, and each sample set is composed of a training set (four parts) and a validation set (one part). The training set is used to fit model parameters, and the validation set is used to tune the parameters for preventing overfitting or underfitting.

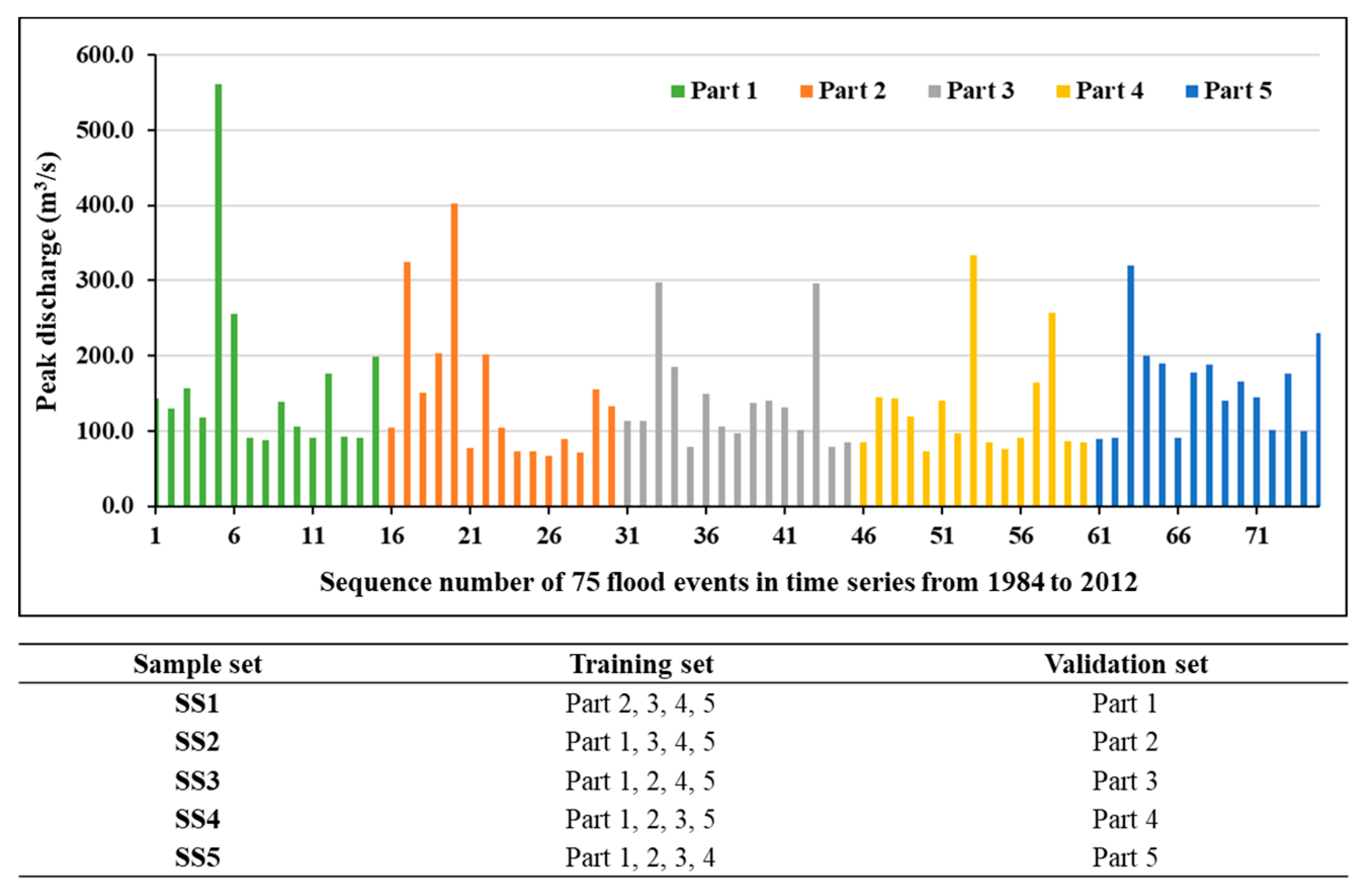
3.2. Model Training

(1) Data normalization: Observed rainfall, $p_{}^1, p_{}^2,\mathrm{\dots }, p_{}^8$, from eight rainfall stations, and observed discharge, $q$, from Anhe hydrology station are normalized in the range of 0 to 1, as Equation (16). $\widehat{x}$ is the normalized value; x is the observed value; $x_{\mathit{max}}$ and $x_{\mathit{min}}$ are the maximum and minimum observed value.

$$\widehat{x}=\frac{x-x_{\mathit{min}}}{x_{\mathit{max}}-x_{\mathit{min}}}$$

(16)

Rainfall and discharge data are normalized separately due to their different physical significance and dimensions.

(2) Establish a dataset: For each sample set, the training set (60 flood events) and validation set (15 flood events) are restructured to a supervised learning dataset by sliding window method [25]. In the supervised learning dataset, the sample size of the supervised learning training set is about 9000, and the sample size of the supervised learning validation set is about 2000. The sample size is slightly different in the supervised learning datasets for sample sets 1–5 because of different duration of 75 flood events.

As seen in Figure 4 and Figure 5, the time-step of each sample is 16 ($H= 5, T= 10$). In architecture 1, the input of each time-step, i, is composed of nine features: (a) $q_i^{}, p_i^1, p_i^2,\mathrm{\dots }, p_i^8$ before the current time, and (b) $0, p_i^1, p_i^2,\mathrm{\dots }, p_i^8$ after current time; in architecture 2, the input includes (a) $q_{t-5}, q_t$, and (b) eight features $p_i^1, p_i^2,\mathrm{\dots }, p_i^8$ for each time-step, i.

(3) Open-source software of the Deep-Learning framework TensorFlow and Keras in Python 3.6 was chosen in this study. Adaptive Moment Estimation was chosen as an optimization algorithm. MSE was determined as the loss function.

(4) The hyper-parameters in the ML models are determined through trial and error. The trial-and-error results are as follows: units in recurrent layer 1 and layer 2 are both 5; batch-size is 64; and the epoch of each ML model is different and determined by the learning curve. Figure 9 shows the visualization of tensor flow in four ML models by Keras. In Figure 9a,b, the numbers 16, 9, 10 and 5 represent the number of total time-steps, features, the forecasting time-steps and units, respectively. Moreover, 6, 8 and 1 represent the numbers of observed time-steps, rainfall features and discharge features in Figure 9c,d. In the red part, $q_{t-5}$ is inputted to simple_rnn_1 (or lstm_1) and turned into an initial hidden state (or both cell state and hidden state); in the green part, $q_t$ is inputted to simple_rnn_2 (or lstm_2) and turned into an initial hidden state (or both cell state and hidden state); the yellow part presents the inputs of eight rainfall features of 16 time-steps.

4. Results and Discussion

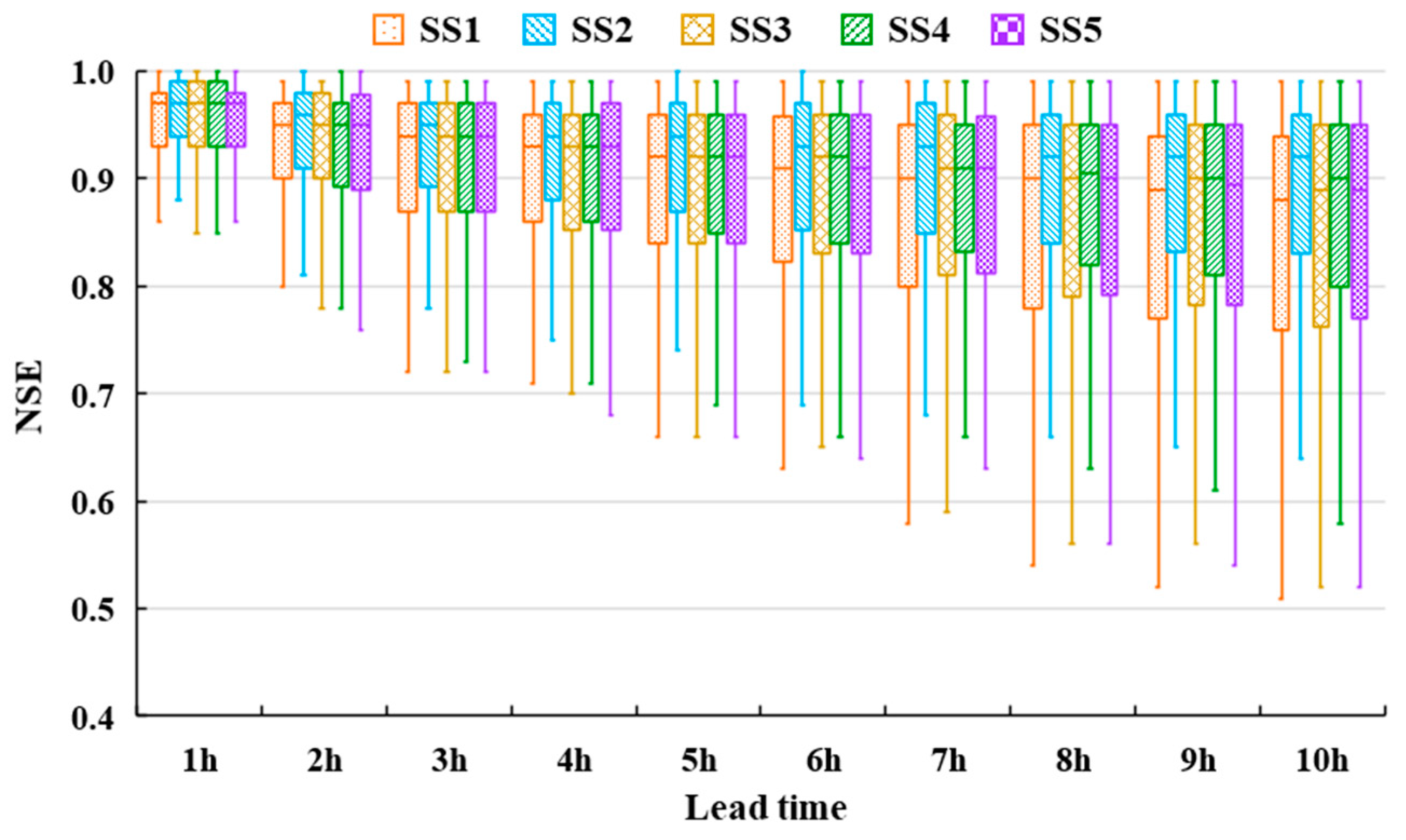
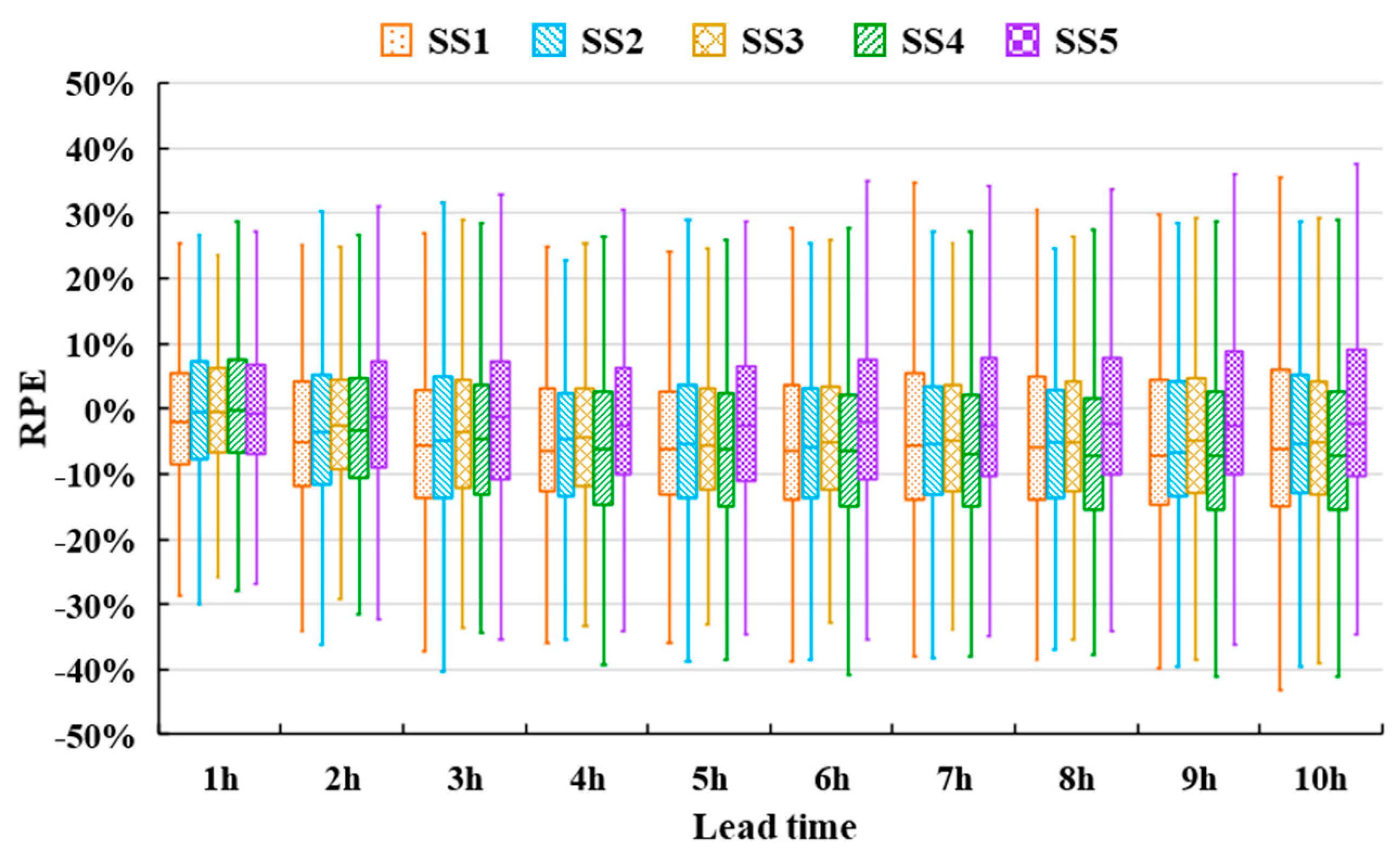
4.1. Sample Set Evaluations

The NSE and RPE for different sample sets at 1–10-h lead-time are summarized in box-and-whisker plots in Figure 10 and Figure 11, and each boxplot includes 300 simulated results from 75 flood events by four combination schemes, which consist of two RNN approaches and two model architectures. The minimum, maximum, 25th percentile (${\mathrm{Q}}_1$), 75th percentile (${\mathrm{Q}}_3$) and the median value (${\mathrm{Q}}_2$) are shown by the lower and upper whiskers, lower and upper bounds of the box, and the line within the box, respectively. The lower and upper whiskers indicate the values ${(\mathrm{Q}}_1-1.5\times \mathrm{IQR})$ and ${(\mathrm{Q}}_3+1.5\times \mathrm{IQR})$, where IQR is the Inter-Quartile Range ${(\mathrm{Q}}_3-{\mathrm{Q}}_1)$.

As shown in Figure 10, at least 75% of NSE is greater than 0.8 at 1–7-h lead-time. Different SSs have almost the same upper whisker, ${\mathrm{Q}}_2$ and ${\mathrm{Q}}_3$ at each lead-time. For ${\mathrm{Q}}_1$ and lower whisker, the differences between SSs are greater with the increase of lead-time. The NSE of SS2 is slightly better than others. Figure 11 indicates the RPE distributions of SS1–SS4 are almost the same. Compared with SS1–SS4, SS5 shows a slightly different distribution range of RPE. Figure 10 and Figure 11 illustrate that no SS outperforms others obviously in the statistic distribution of NSE and RPE, so it is feasible to divide the sample set by a time sequence of flood events and the representativeness of peak-discharge.

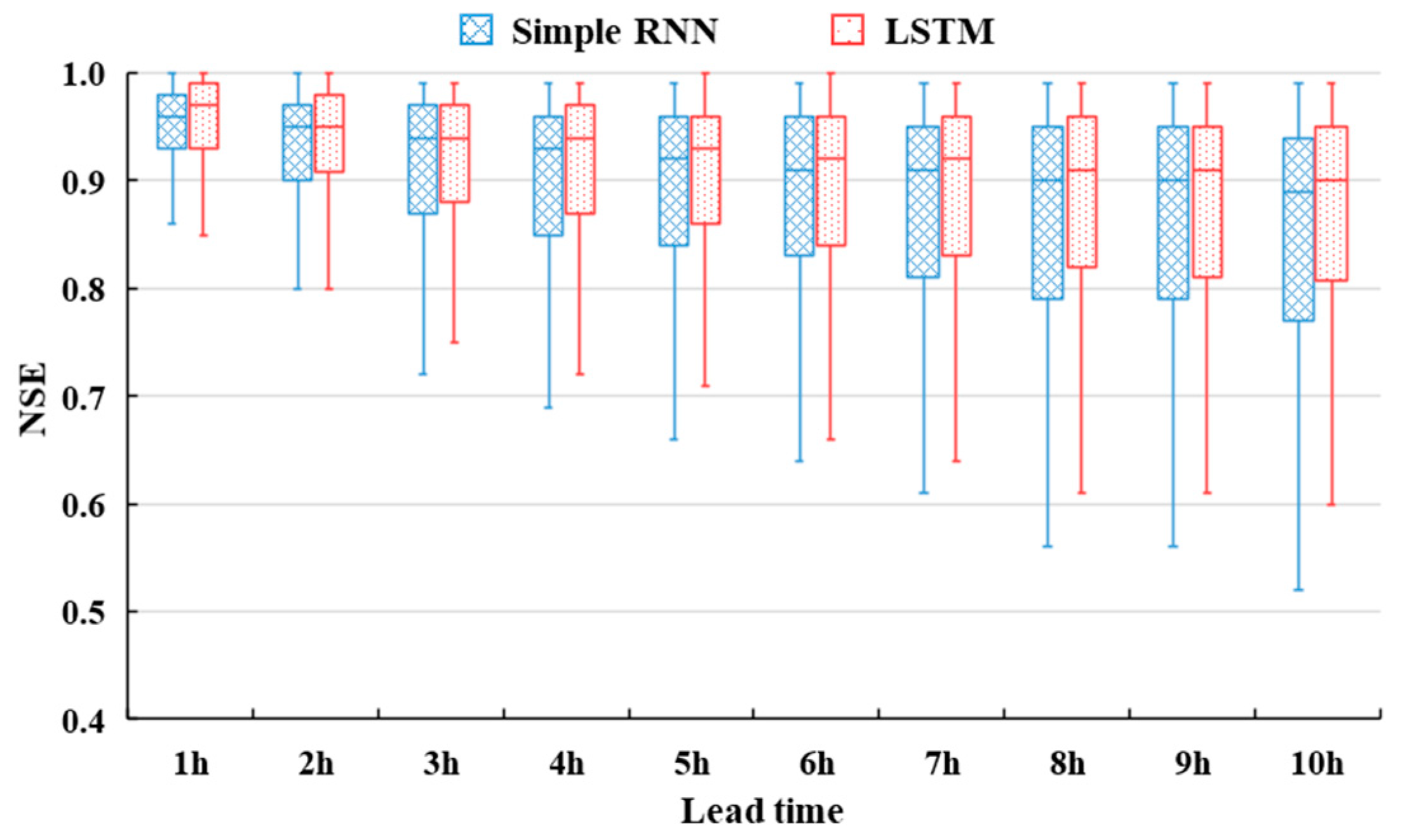
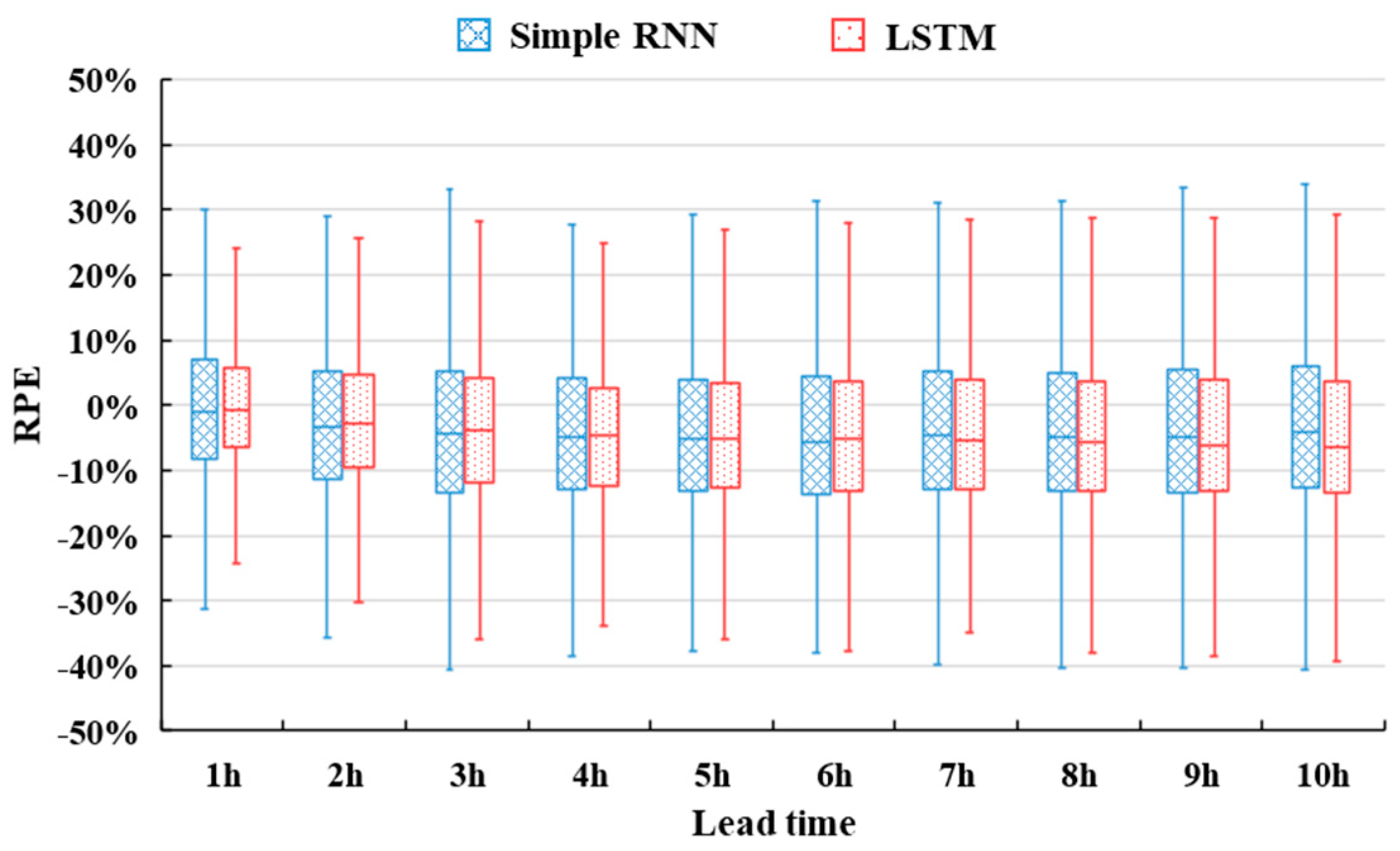
4.2. RNN Approach Evaluations

Figure 12 and Figure 13 show box-and-whisker plots of NSE and RPE for different RNN approaches at 1–10-h lead-time, and each boxplot includes 750 simulated results from 75 flood events by 10 combination schemes, which consist of five sample sets and two model architectures.

Figure 12 illustrates LSTM has higher Q₁, Q₂, Q₃ and whisker of NSE than that of Simple RNN. Except for 1, 2-h lead-time, LSTM shows a more compact NSE distribution (shorter distance between Q₁ and Q₃). It indicates LSTM takes obvious advantage with the increase of lead-time. Its advantage is mainly reflected in the flood events, which are simulated relatively well at short lead-times, and the flood events, which are simulated relatively poorly at long lead-times. Figure 13 illustrates the simulated peak discharges of LSTM have more compact RPE distribution at each lead-time. Both Figure 12 and Figure 13 indicate LSTM outperforms Simple RNN in discharge simulations, especially in the simulation of flood process at relatively long lead-times. LSTM indeed demonstrates its powerful ability for processing multi-step time-series discharge simulations due to its special gates structure.

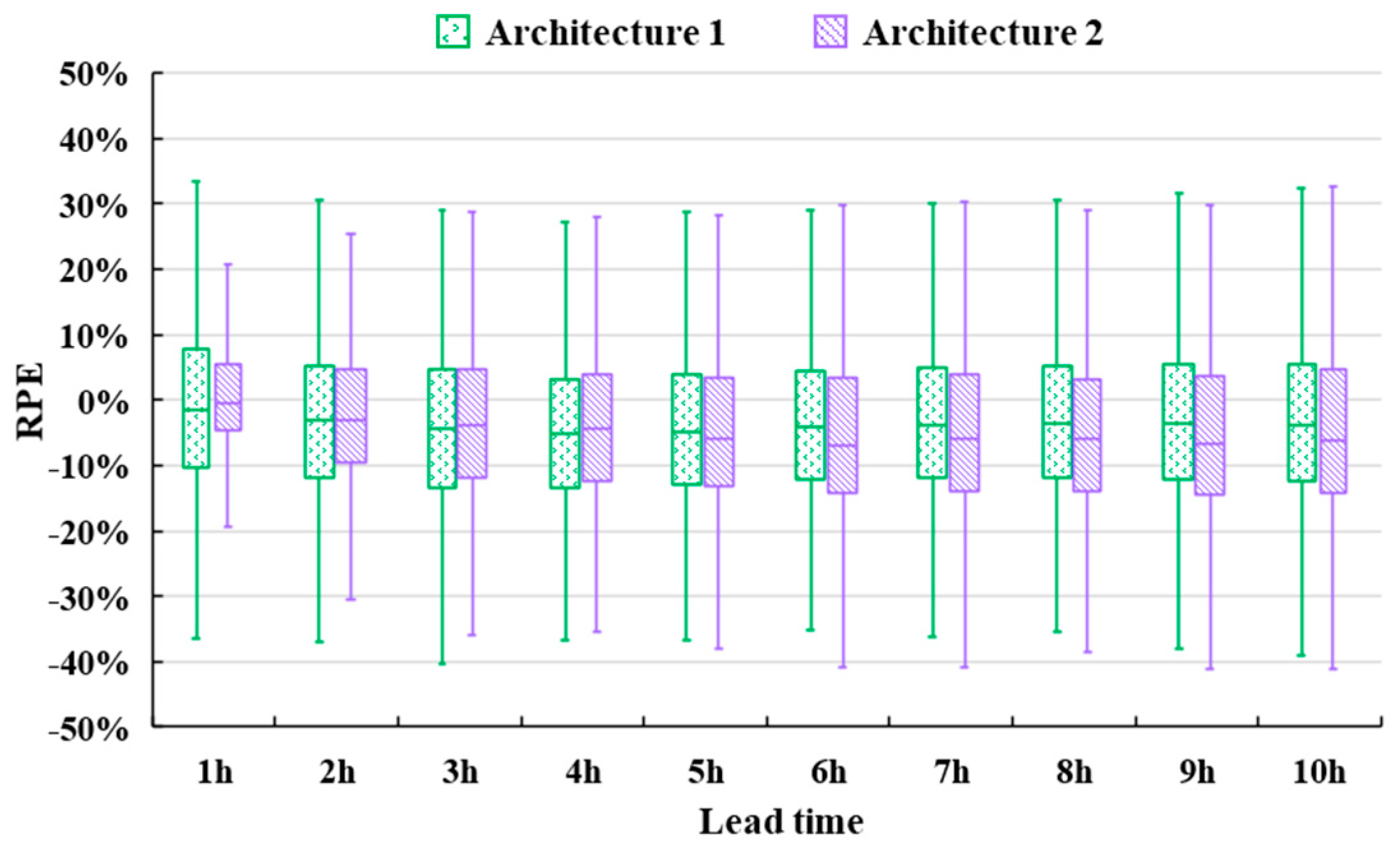
4.3. Model Architecture Evaluations

Figure 14 and Figure 15 compared box-and-whisker plots of NSE and RPE for different model architectures at 1–10-h lead-time, and each boxplot includes 750 simulated results from 75 flood events by 10 combination schemes, which consist of five sample sets and two RNN approaches.

Figure 14 illustrates that architecture 2 has higher Q₁, Q₂ and Q₃ and lower whisker of NSE than that of architecture 1. At 1–3-h lead-time, the advantages of architecture 2 are especially obvious. For RPE distribution in Figure 15, architecture 2 also has a distinct advantage at 1, 2-h lead-time. As the lead-time increases, the difference in RPE distribution between architecture 1 and 2 gets smaller. Both Figure 14 and Figure 15 indicate that Architecture 2 has absolute superiority in simulating peak discharge at 1-h lead-time and flood process at all lead-times, because a shorter distance between Q1 and Q3 means the quartile data are bunched together.

The results reveal that the strategy, $q_t$, is inputted as an initial cell state, c, and hidden state, h, to Recurrent layers and improves the simulation accuracy of both flood hydrograph and peak. As the lead-time increases, the difference of simulated discharges between two architectures decreases due to the similar architecture at long lead-time (see Figure 4 and Figure 5). In brief, the multi-step time-series forecasting models could obtain better performance by inputting the discharge feature and rainfall features separately. It suggests that the ML model might be improved by combining the expertise of hydrology.

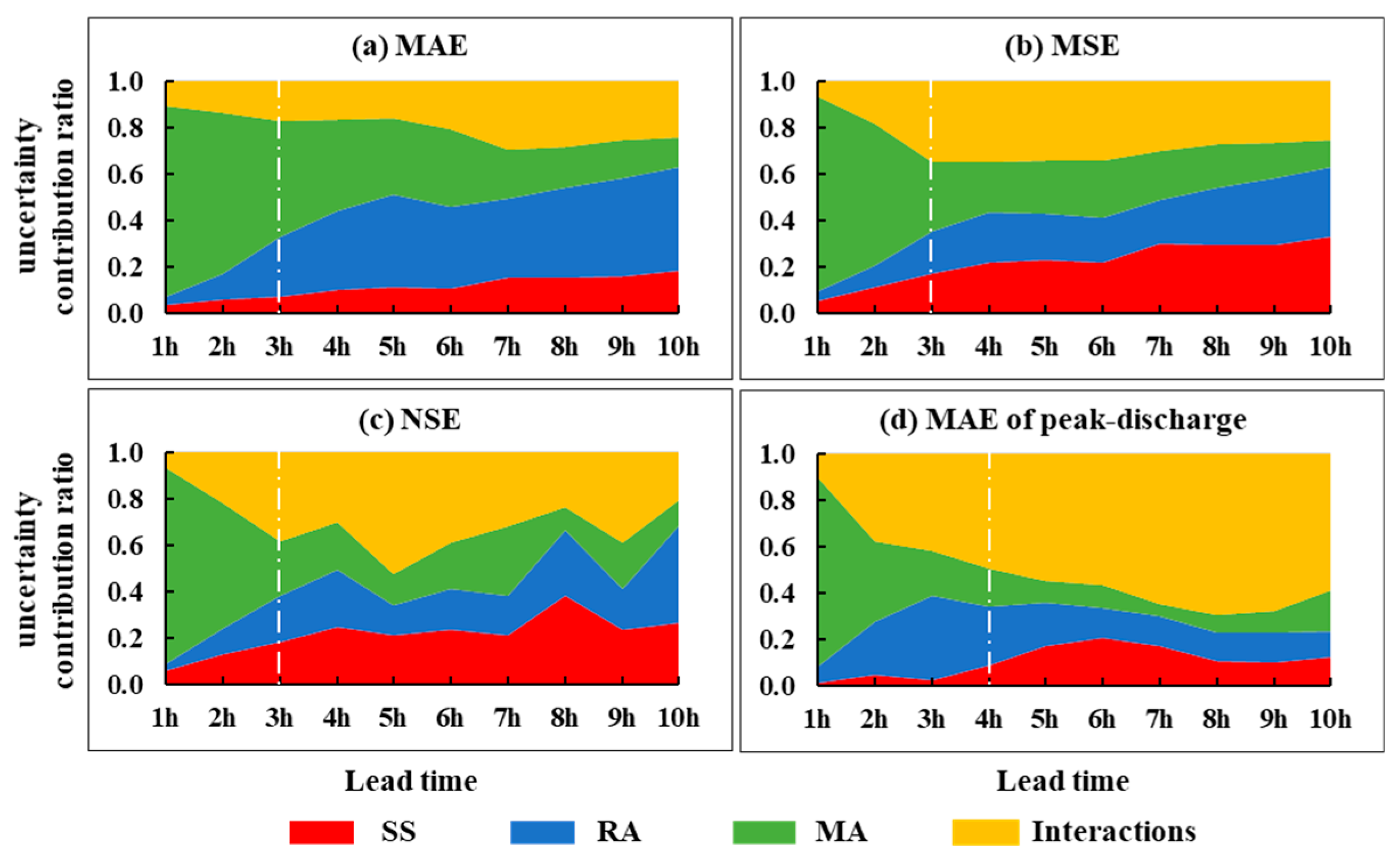
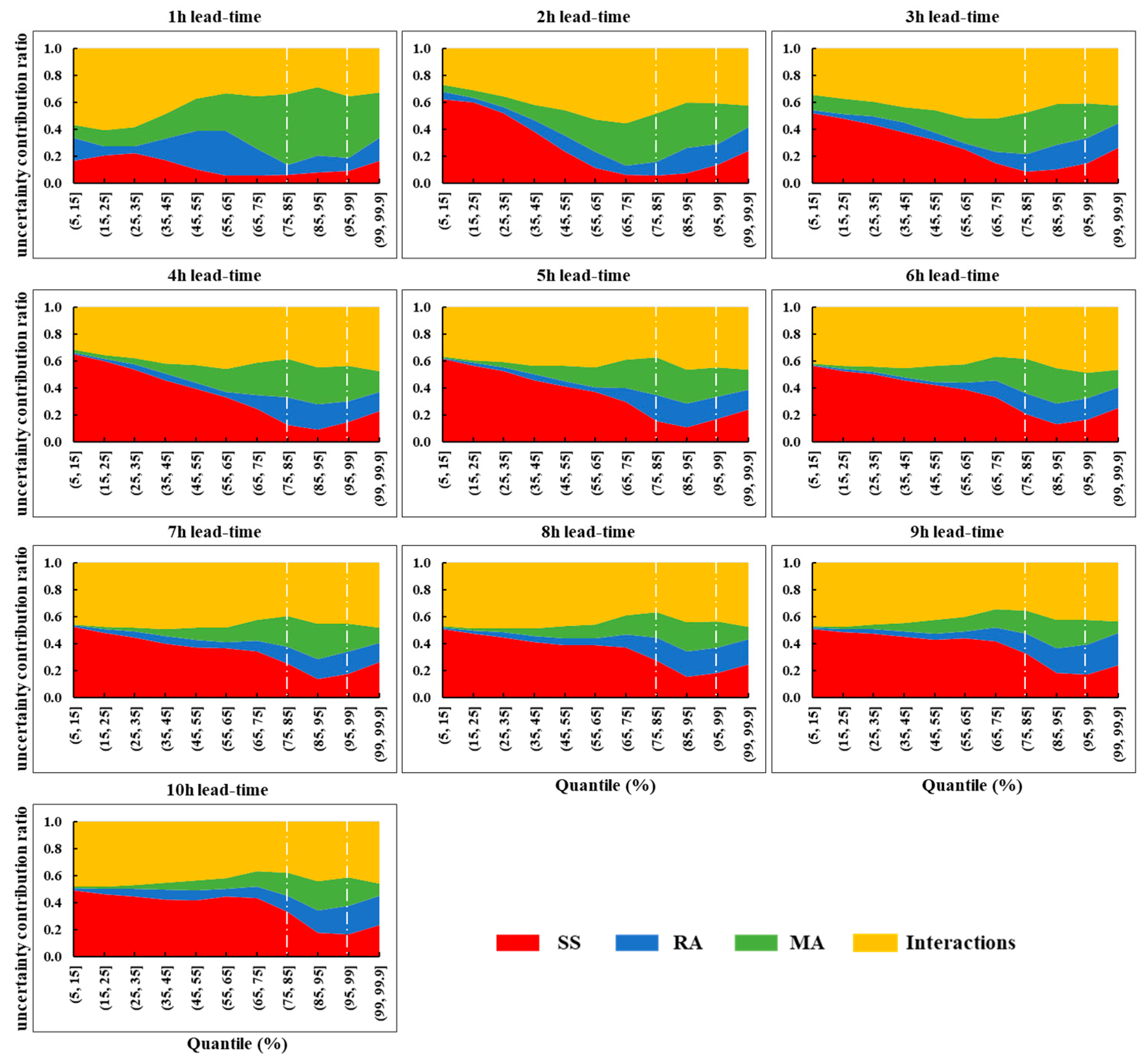
4.4. Uncertainty Source Quantification

As shown in Figure 16 and Figure 17, the stacked area chart is used to show the ratio of uncertainty contributions, which is calculated by Equations (12)–(15), at each lead-time or in the discharge quantile interval.

Figure 16a–c shows the ratio of the contribution of uncertainty sources to discharge simulations by MAE, MSE and NSE at 1–10-h lead-time. The MA is the dominant source at 1–3-h lead-time. The uncertainty contribution ratio of MA reaches 0.8 at 1-h lead-time. It is attributed to the strategy that $q_t$ is inputted as an initial state to Recurrent layers in architecture 2 because of the strong correlation between $q_t$ and $q_{t+1}$. Separately inputted discharge feature plays a major role at short lead-time, and the strong correlation between $q_t$ and $q_{t+1}, q_{t+2}, q_{t+3}$ weakens gradually with the increase of lead-time. At 4–10-h lead-time, the contributions of SS and RA gradually increase, while the contributions of MA gradually decrease. It indicates the conclusions of variance decomposition are consistent with the previous analysis of Section 4.2 and Section 4.3: (1) The outperformance of LSTM is manifested in the simulation of flood process at long lead-time, because LSTM could solve the problem that the Simple RNN would not learn long-term dependencies (see Figure 11); (2) the outperformance of architecture 2 is mainly manifested at short lead-time, because MAs have similar architecture at long lead-time (see Figure 4 and Figure 5).

By comparing Figure 16a and Figure 16b, we see the uncertainty contribution ratio of SS by MSE is greater than that of MAE. We concluded that the SS contributes more uncertainty in simulated outliers, because MAE has better robustness than MSE for outliers. On the contrary, the RA contributes less uncertainty in simulated outliers. Therefore, we suspect the simulated results of LSTM and Simple RNN might be similar for partial outliers, which are caused by the partition of SS.

Despite the contribution of uncertainty sources that fluctuate a little bit in Figure 16c, the overall trend is consistent with Figure 16a,b. Figure 16d shows the ratio of the contribution of uncertainty sources to peak-discharge simulations by MAE at 1–10-h lead-time.

Combining the previous analysis of Section 4.3, it indicates that (1) LSTM and architecture 2 shows their advantages of peak-discharge simulations mainly at 1–4-h lead-time; (2) the SS is the least important individual source of uncertainty for peak-discharge simulations at 1–4-h lead-time. Compared with Figure 15a–c, the uncertainty contribution of the interaction on peak-discharge simulations is much greater than other flood processes. It indicates that peak-discharge is more difficult to simulate, because the rainfall process with variable space–time distribution always occurs before the flood peak.

Figure 17 depicts the ratio of the contributions of uncertainty sources in different discharge quantiles. We take the mean of the variance decomposition for each quantile interval and divide the quantile bins into three parts: a low range (5–75%, 9.6–47.3 m³/s), an intermediate range (75–95%, 47.3–189.4 m³/s) and a high range (95–99.9%, 189.4–333.5 m³/s).

In the low quantile range, the SS is the dominant source of uncertainty at 2–10-h lead-time. It suggests that the different combinations of RA and MA make little difference for low discharge simulations. Small discharges mainly come from base flows or recession flows, which are relatively stable, barely affected by rainfall and much easier to simulate, whereas at 1-h lead-time, the MA and interactions contribute the majority of uncertainty sources due to the strong correlation between $q_t$ and $q_{t+1}$.

In the intermediate range, the contribution of the MA gradually decreases with the increase of lead-time, and the contribution of the SS and RA is relatively stable. Combined with the analysis of Figure 14 and Figure 15, it indicates that architecture 2 is more helpful to improve the discharge simulations in the intermediate and high quantile ranges. LSTM has more advantages in intermediate and high quantile ranges, in which the contribution ratio of RA is stable at 0.2. However, LSTM does not show any advantage compared to Simple RNN in the low quantile range.

Compared with the intermediate range, the contribution of the SS increases in the high range, because the division of training set and validation set is according to the value of peak-discharge. Moreover, the relatively small sample size in the 99–99.9% quantile also tends to increase the uncertainty contribution of the SS. The contribution of the interaction term to the total uncertainty varies throughout the different discharge quantiles between 0.4 and 0.5 and more stable at long lead-time.

The results of variance decomposition indicate that the contribution of individual uncertainty source quantification varies on different lead-time and different discharge quantiles. In addition, the contribution of interactions should not be ignored. Although the proposed framework cannot take all the uncertainties into account, or gives no further explanation of interactions, it is valuable to evaluate the multi-step time-series forecasting models. It suggests the combination of LSTM and model architecture 2 is superior to others in discharge simulations.

Finally, through the result analysis of model evaluation and uncertainty source quantification, several suggestions are put forward to the ML modeling for multi-step discharge simulations: (1) LSTM network demonstrates its superiority in discharge simulations, and ML architecture design is as important as ML approach selection; (2) it is essential to input discharge feature properly for short-term discharge forecasting; (3) for low discharge simulations, different combinations of RA and MA make little difference, and the sample set partitioning dominates the uncertainty in modeling.

5. Conclusions

A framework is proposed for uncertainty quantification of ML modeling and evaluation of multi-step time-series forecasting models. Discharge simulation using RNN networks and stacked DL structure in Anhe catchment of Southeastern China is taken as an example to quantify uncertainty contributions of each component (five different SSs, two RAs and two MAs). To evaluate the interactions between LSTM networks and ML architecture, a novel ML architecture is designed by combining the expertise of hydrology and stacked DL structure, and compared with another conventional architecture. We estimated the total ensemble uncertainty of the ML modeling and quantified the contributions of different uncertainty sources in discharge simulations. The proposed framework can reveal discharge-simulation uncertainties in ML multi-step time-series forecasting models based on ANOVA theory. Moreover, it also provides references for ML technology selection and architecture design. The results indicated that uncertainty quantification is an indispensable task that must be performed in multi-step time-series discharge simulations, for a successful application of ML. Conclusions from this study include the following:

(1) The results of variance decomposition indicate that the contribution of individual uncertainty source quantification varies at different lead-times and different discharge quantiles, and the contribution of interactions should not be ignored. With the increase of lead-time, the contributions of SS and RA gradually increase, while the contributions of MA gradually decrease. The SS is the dominant source of uncertainty in the low quantile range. In the intermediate and high quantile range, the contribution of the MA gradually decreases with the increase of lead-time, and the contribution of the SS and RA is relatively stable. Interactions contribute a lot to the total uncertainty in discharge simulations, and interactive impacts are influenced by discharge magnitude and lead-time. The evaluation results of the proposed framework demonstrate the model combining LSTM and architecture 2 is superior to others in the statistic distribution of NSE and RPE.

(2) As expected, the LSTM network outperforms Simple RNN in both flood processes and peak discharge. According to the analysis results of the proposed framework, the advantages of the LSTM network are mainly embodied in intermediate and high quantile ranges due to the dominant uncertainty contribution of SS in low quantile range. Comparing with ML architecture, the LSTM network shows limited advantage at short lead-time. In short, the LSTM network demonstrates its powerful ability for processing and predicting the relatively long events for multi-step time-series discharge simulations. It has more practical value to evaluate the LSTM network based on the interactions between LSTM networks and other components of ML modeling.

(3) ML architecture design is as necessary as ML approaches selection for multi-step time-series forecasting model. Architecture 2 has absolute superiority in simulating peak discharge at 1-h lead-time and flood process at all lead-times, especially in intermediate and high quantile ranges. It is mainly due to the strategy that incorporating hydrological expertise into stacking DL architecture.

(4) The SS is the dominant source of uncertainty in the low quantile range (except 1-h lead-time). In other words, different combinations of RA and MA make little difference for low discharge simulations. No one SS is better than the others in the statistic distribution of NSE and RPE. Therefore, it is feasible to divide the sample set by time sequence of flood events and the representativeness of peak-discharge.

Although this study only investigated a discharge simulation with two ML approaches and two ML architectures, the proposed framework is versatile and adjustable to research and applications of ML techniques in other areas of study. In addition, further research should also focus on the hydrological interpretation of ML models, such as the relationship between the dynamical changes of LSTM cell state and the soil moisture content.