A GPU-Accelerated Shallow-Water Scheme for Surface Runoff Simulations
Abstract
1. Introduction
2. Numerical Model
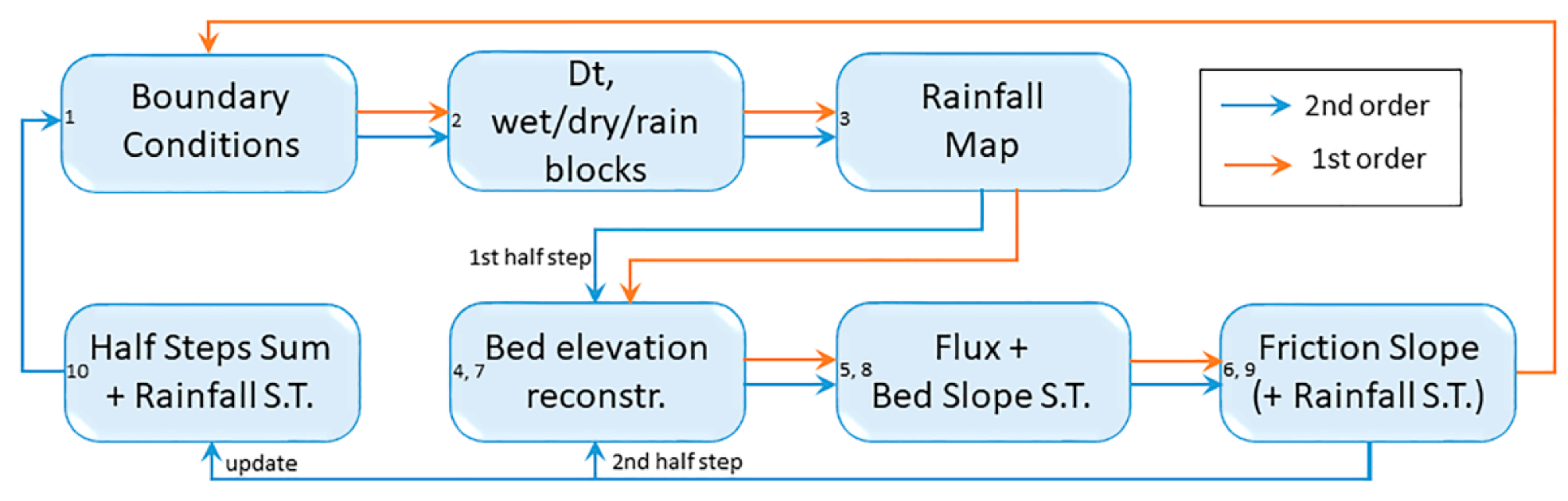
2.1. Numerical Scheme
2.2. Evaluation of Rainfall Excess
2.3. Graphics Processing Unit (GPU) Implementation of Shallow-Water Equation (SWE)
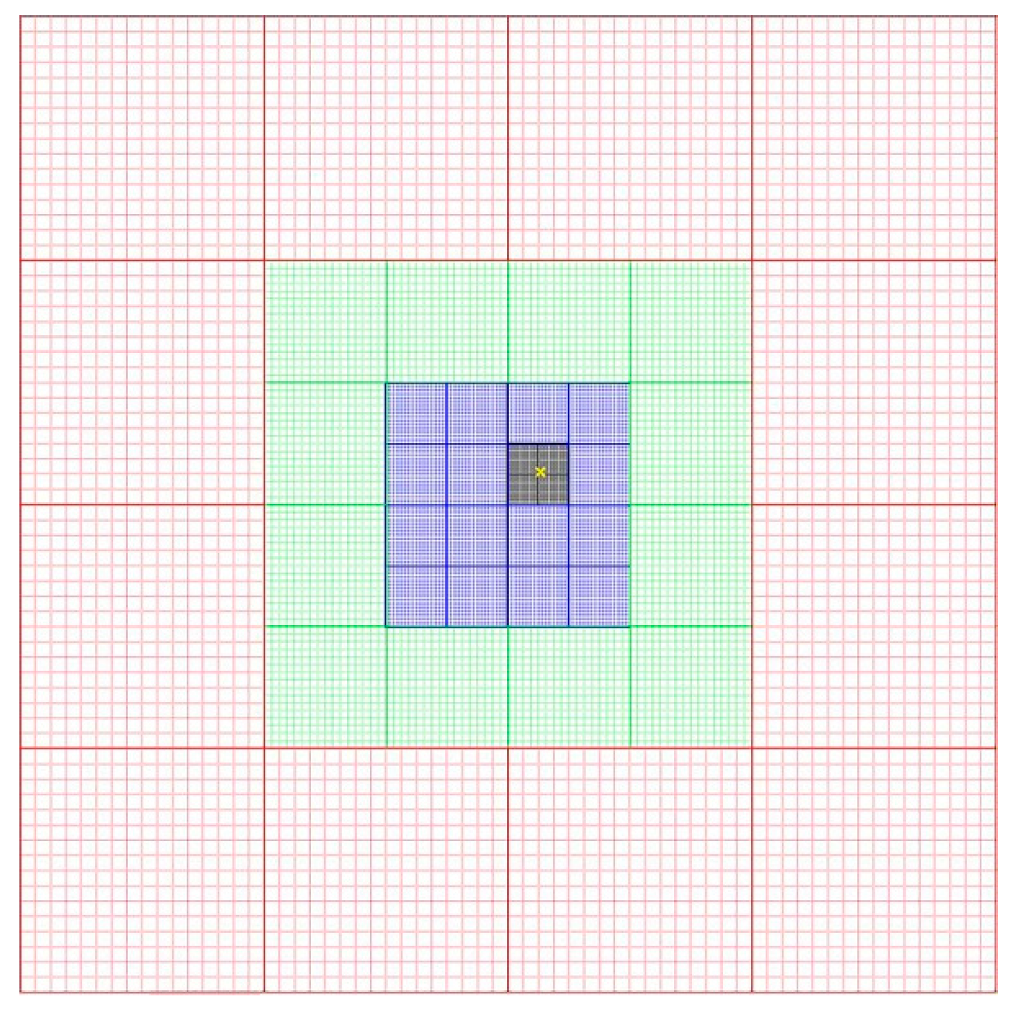
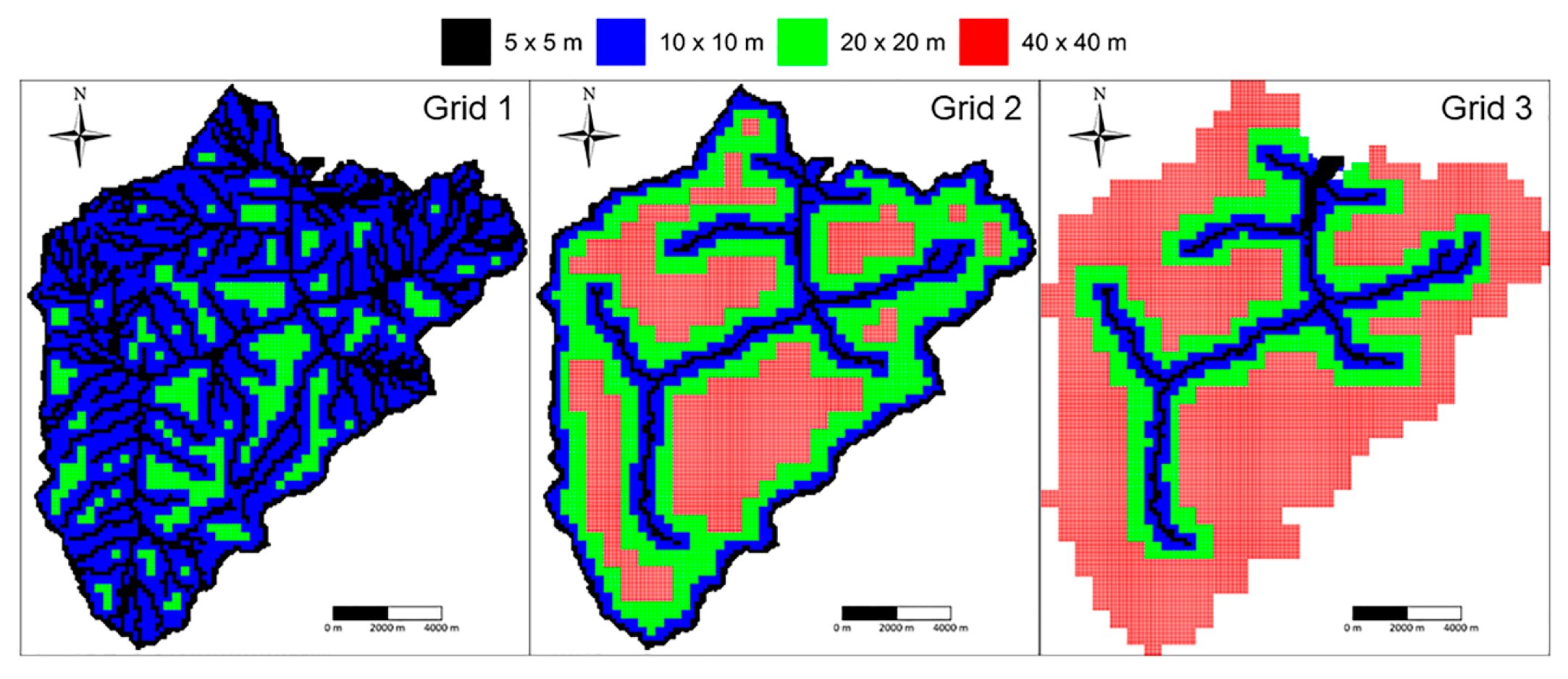
2.4. Block-Uniform Quadtree (BUQ) Grids
3. Experimental and Synthetic Rainfall-Runoff Tests
3.1. Test Case 1: One-Dimensional Three Planes Cascade Rainfall-Runoff Case
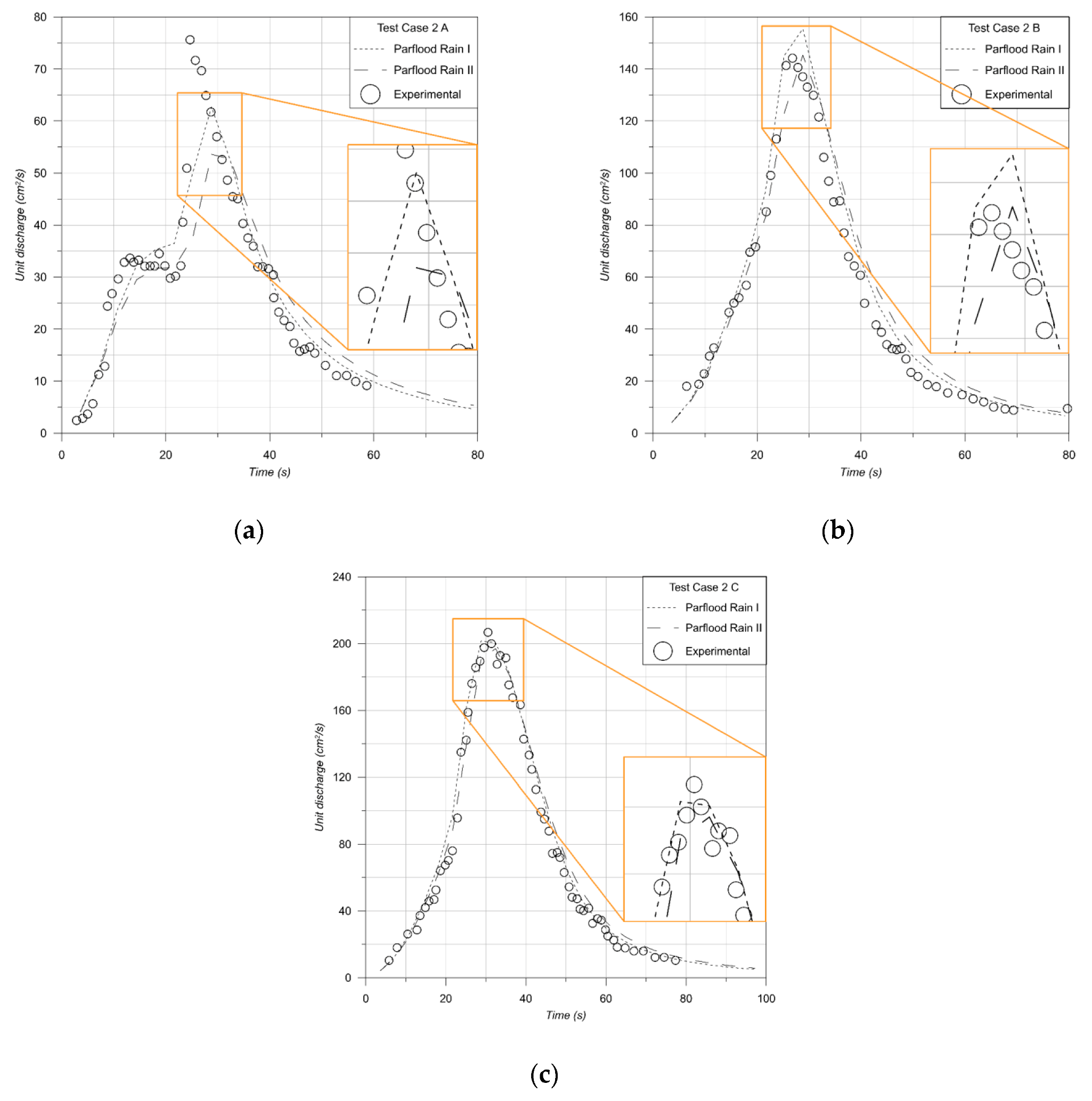
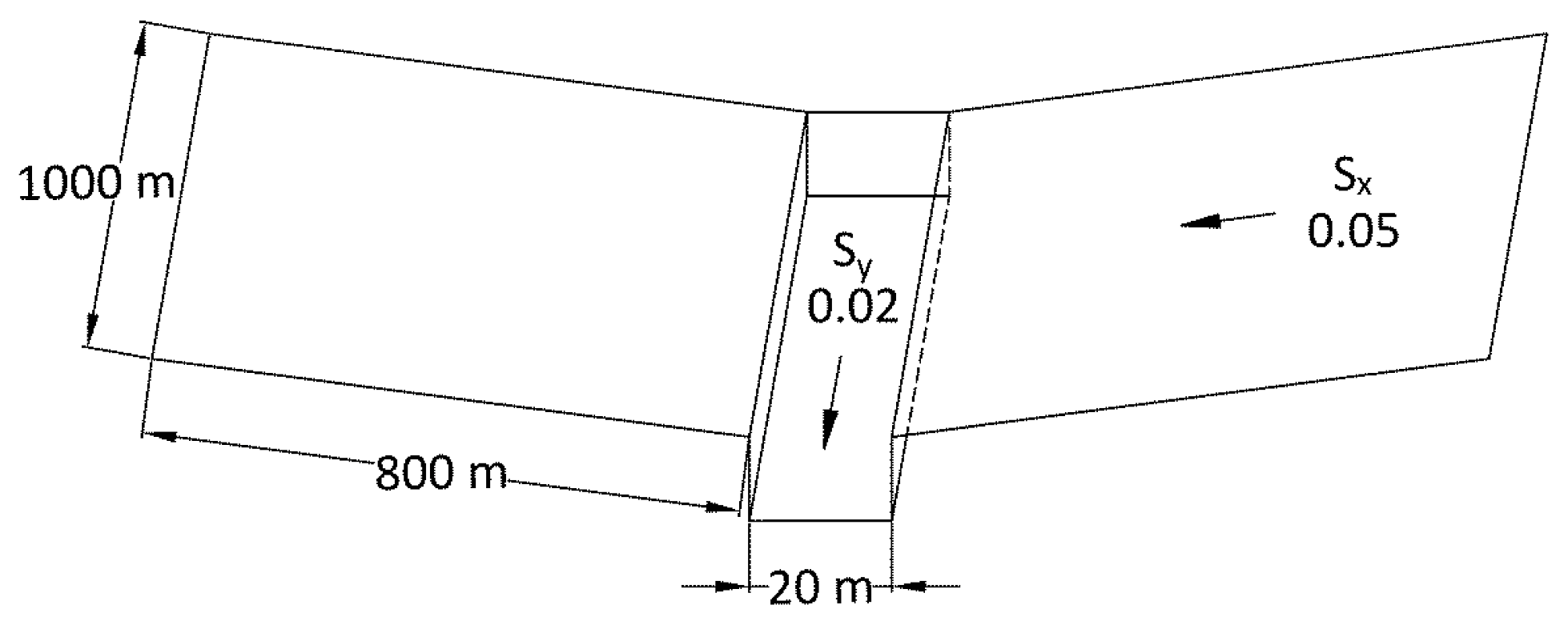
3.2. Test Case 2: Two-Dimensional V-Shaped Rainfall-Runoff Test Case
4. Nure Watershed Field Case
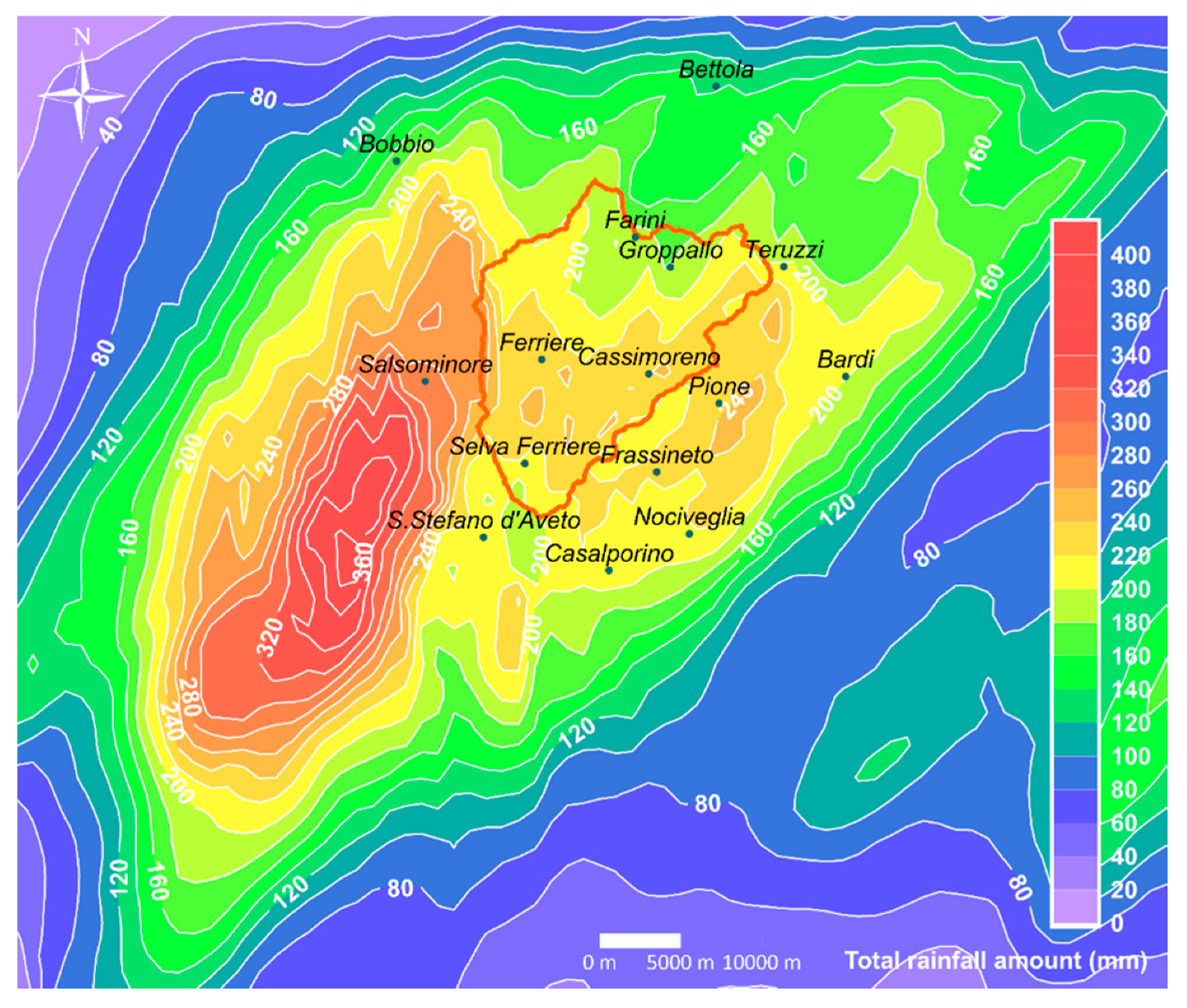
4.1. Event Description
4.2. Available Field Data
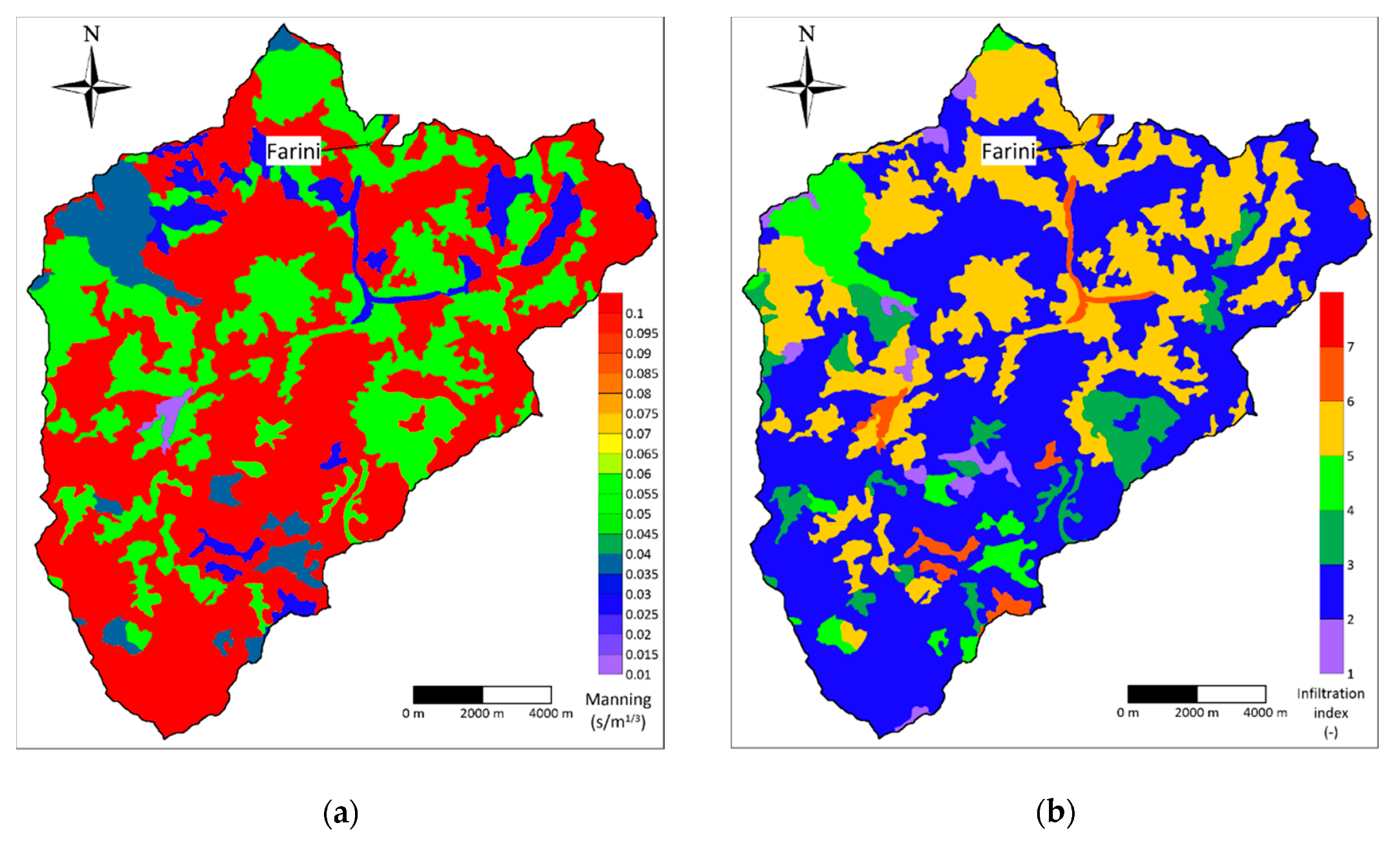
4.3. Bathymetry and Roughness
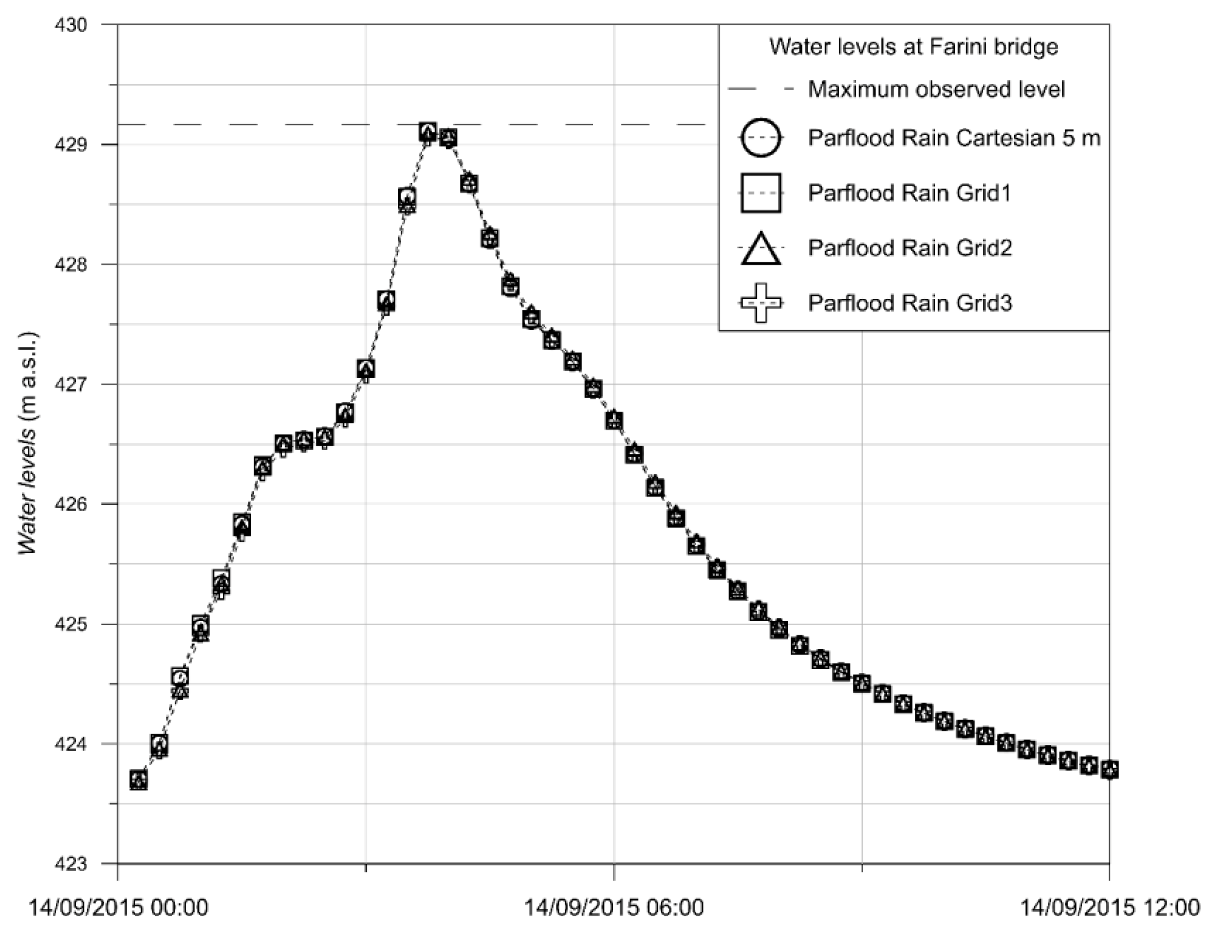
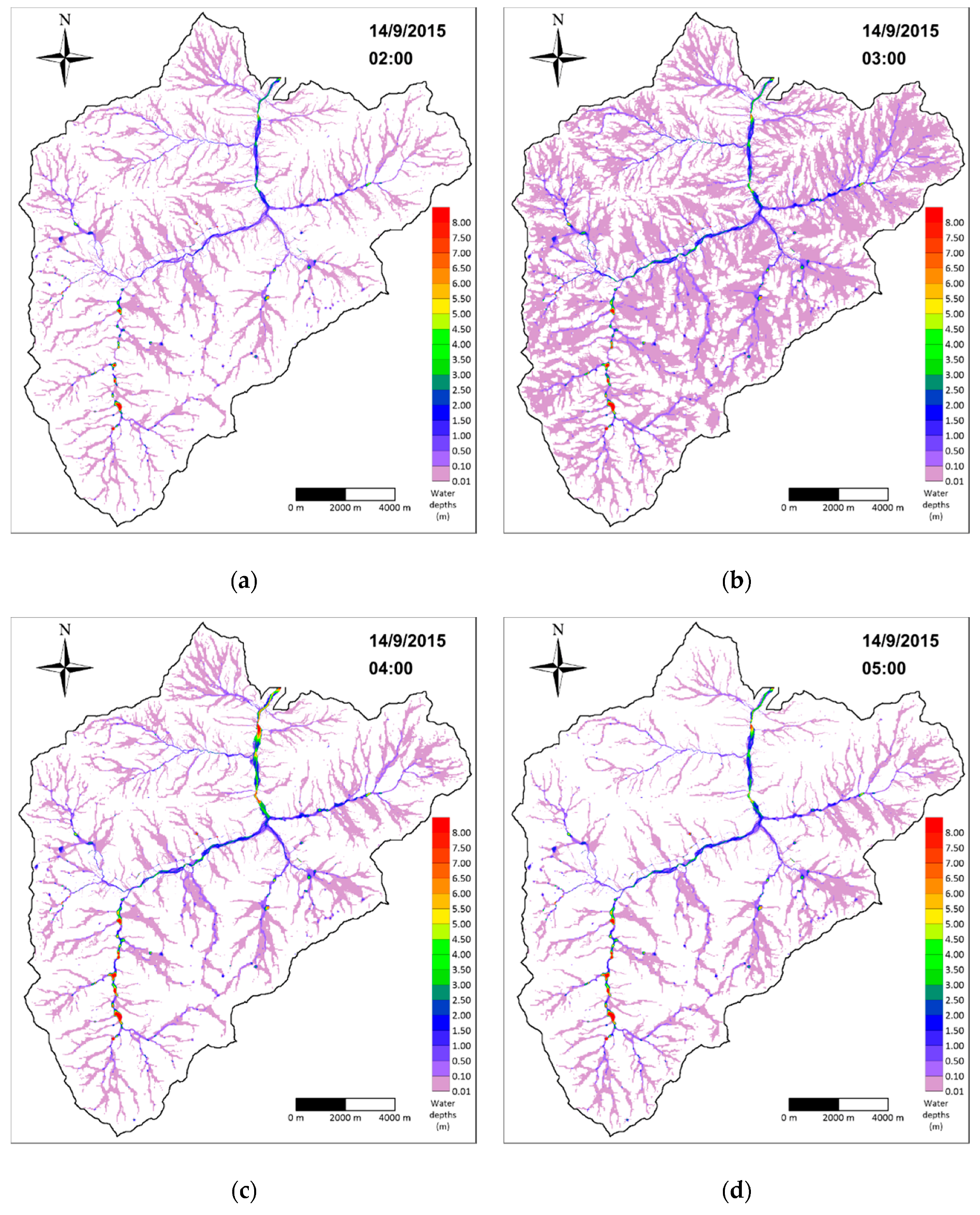
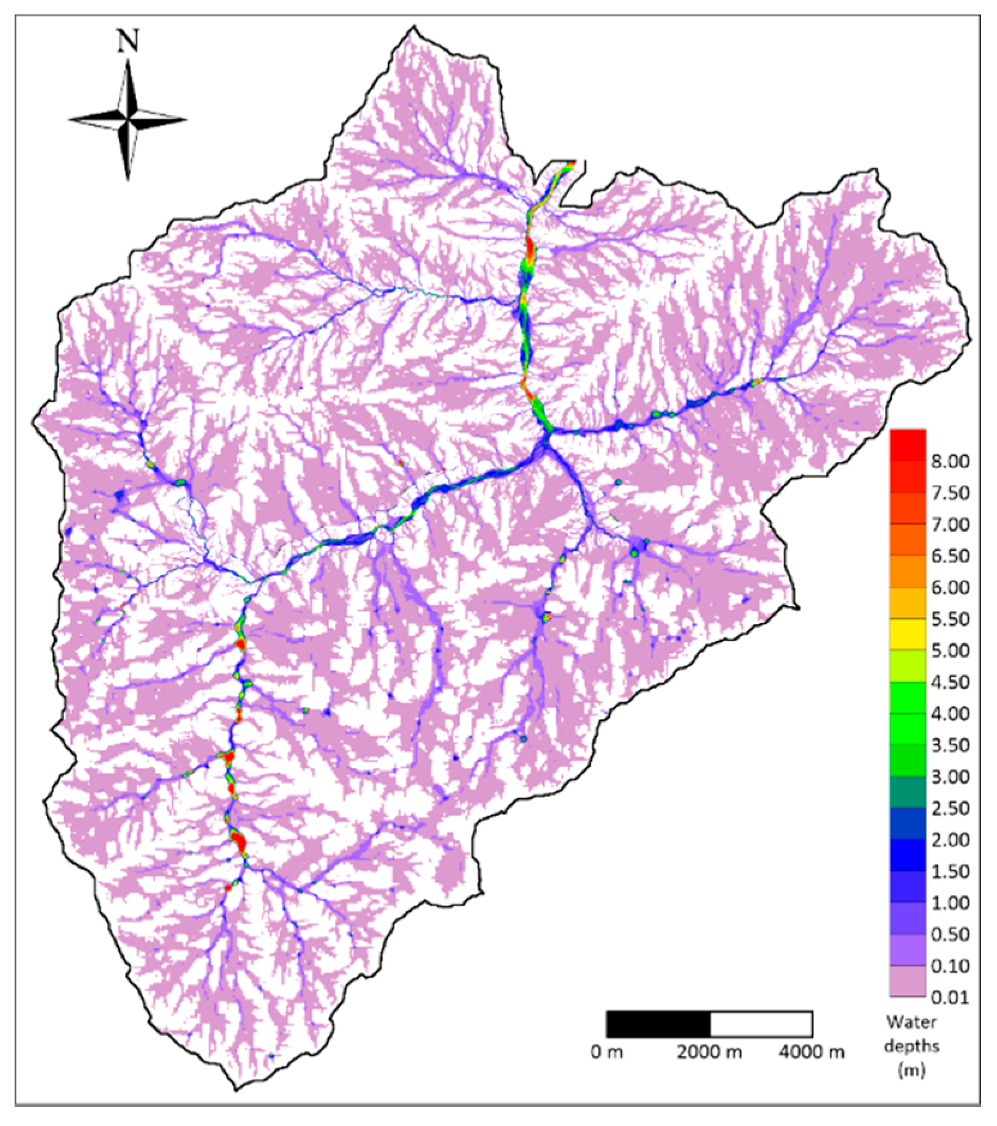
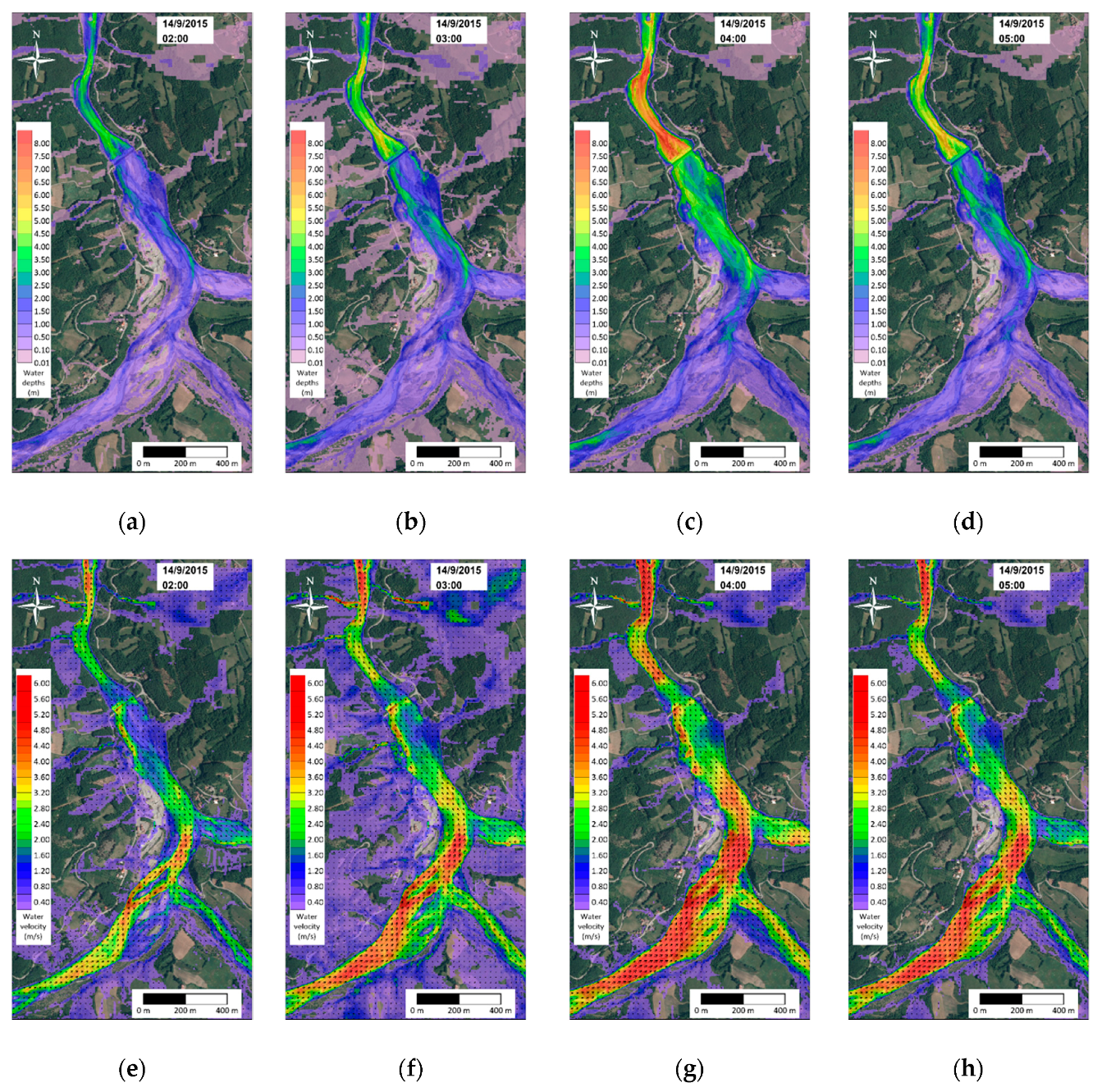
4.4. Results for the Nure Watershed Test Case
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
A.1. Bed Slope Source Term Treatment
A.2. Friction Source Term Treatment
A.3. Soil Conservation Service SCS Method
References
- Chow, V.T.; Ben-Zvi, A. Hydrodynamic modeling of two-dimensional watershed flow. J. Hydraul. Div. 1973, 99, 2023–2040. [Google Scholar]
- Kawahara, M.; Yokoyama, T. Finite element method for direct runoff flow. J. Hydraul. Div. 1980, 106, 519–534. [Google Scholar]
- Di Giammarco, P.; Todini, E.; Lamberti, P. A conservative finite elements approach to overland flow: The control volume finite element formulation. J. Hydrol. 1996, 175, 267–291. [Google Scholar] [CrossRef]
- Singh, J.; Altinakar, M.S.; Ding, Y. Numerical modeling of rainfall-generated overland flow using nonlinear shallow-water equations. J. Hydrol. Eng. 2015, 20. [Google Scholar] [CrossRef]
- Yu, C.; Duan, J. Two-dimensional hydrodynamic model for surface-flow routing. J. Hydraul. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Yu, C.; Duan, J. Simulation of surface runoff using hydrodynamic model. J. Hydrol. Eng. 2017, 22. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J.; Jácome, A.; Del Río, H.; Suárez, J. Overland flow computations in urban and industrial catchments from direct precipitation data using a two-dimensional shallow water model. Water Sci. Technol. 2010, 62, 1998–2008. [Google Scholar] [CrossRef]
- Cea, L.; Bladé, E. A simple and efficient unstructured finite volume scheme for solving the shallow water equations in overland flow applications. Water Resour. Res. 2015, 51, 5464–5486. [Google Scholar] [CrossRef]
- Liang, D.; Özgen, I.; Hinkelmann, R.; Xiao, Y.; Chen, J.M. Shallow water simulation of overland flows in idealised catchments. Environ. Earth Sci. 2015, 74, 7307–7318. [Google Scholar] [CrossRef]
- Xia, X.; Liang, Q.; Ming, X.; Hou, J. An efficient and stable hydrodynamic model with novel source term discretization schemes for overland flow and flood simulations. Water Resour. Res. 2017, 53, 3730–3759. [Google Scholar] [CrossRef]
- Zhang, L.; Nan, Z.; Liang, X.; Xu, Y.; Hernández, F.; Li, L. Application of the MacCormack scheme to overland flow routing for high-spatial resolution distributed hydrological model. J. Hydrol. 2018, 558, 421–431. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Macchione, F. A storm event watershed model for surface runoff based on 2D fully dynamic wave equations. Hydrol. Process. 2013, 27, 554–569. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Macchione, F. Performances and limitations of the diffusive approximation of the 2-d shallow water equations for flood simulation in urban and rural areas. Appl. Numer. Math. 2017, 116, 141–156. [Google Scholar] [CrossRef]
- European Environment Agency. Economic Losses from Climate-Related Extremes in Europe; European Environment Agency: Copenhagen, Denmark, 2019. [Google Scholar]
- Anselmo, V.; Galeati, G.; Palmieri, S.; Rossi, U.; Todini, E. Flood risk assessment using an integrated hydrological and hydraulic modelling approach: A case study. J. Hydrol. 1996, 175, 533–554. [Google Scholar] [CrossRef]
- Agnese, C.; Baiamonte, G.; Corrao, C. A simple model of hillslope response for overland flow generation. Hydrol. Process. 2001, 15, 3225–3238. [Google Scholar] [CrossRef]
- Wang, G.-T.; Chen, S.; Boll, J.; Stockle, C.O.; McCooL, D.K. Modelling overland flow based on Saint-Venant equations for a discretized hillslope system. Hydrol. Process. 2002, 16, 2409–2421. [Google Scholar] [CrossRef]
- Morbidelli, R.; Corradini, C.; Govindaraju, R.S. A simplified model for estimating field-scale surface runoff hydrographs. Hydrol. Process. 2007, 21, 1772–1779. [Google Scholar] [CrossRef]
- Jasper, K.; Gurtz, J.; Lang, H. Advanced flood forecasting in Alpine watersheds by coupling meteorological observations and forecasts with a distributed hydrological model. J. Hydrol. 2002, 267, 40–52. [Google Scholar] [CrossRef]
- Jaber, F.H.; Mohtar, R.H. Stability and accuracy of finite element schemes for the one-dimensional kinematic wave solution. Adv. Water Resour. 2002, 25, 427–438. [Google Scholar] [CrossRef]
- Jaber, F.H.; Mohtar, R.H. Stability and accuracy of two-dimensional kinematic wave overland flow modeling. Adv. Water Resour. 2003, 26, 1189–1198. [Google Scholar] [CrossRef]
- Lerat, J.; Perrin, C.; Andréassian, V.; Loumagne, C.; Ribstein, P. Towards robust methods to couple lumped rainfall-runoff models and hydraulic models: A sensitivity analysis on the Illinois River. J. Hydrol. 2012, 418–419, 123–135. [Google Scholar] [CrossRef]
- Nguyen, P.; Thorstensen, A.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Sanders, B.; Koren, V.; Cui, Z.; Smith, M. A high resolution coupled hydrologic–hydraulic model (HiResFlood-UCI) for flash flood modeling. J. Hydrol. 2016, 541, 401–420. [Google Scholar] [CrossRef]
- Kim, J.; Warnock, A.; Ivanov, V.Y.; Katopodes, N.D. Coupled modeling of hydrologic and hydrodynamic processes including overland and channel flow. Adv. Water Resour. 2012, 37, 104–126. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J. Experimental validation of two-dimensional depth-averaged models for forecasting rainfall–runoff from precipitation data in urban areas. J. Hydrol. 2010, 382, 88–102. [Google Scholar] [CrossRef]
- Jaber, F.H.; Mohtar, R.H. Dynamic time step for one-dimensional overland flow kinematic wave solution. J. Hydrol. Eng. 2002, 7, 3–11. [Google Scholar] [CrossRef]
- Warnock, A.; Kim, J.; Ivanov, V.; Katopodes, N.D. Self-adaptive kinematic-dynamic model for overland flow. J. Hydraul. Eng. 2014, 140, 169–181. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Macchione, F. Comparative analysis of overland flow models using finite volume schemes. J. Hydroinform. 2012, 14, 122–135. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; Fernández-Pato, J.; Hinz, C. Cellular automata and finite volume solvers converge for 2D shallow flow modelling for hydrological modelling. J. Hydrol. 2018, 563, 411–417. [Google Scholar] [CrossRef]
- Aricò, C.; Nasello, C. Comparative analyses between the zero-inertia and fully dynamic models of the shallow water equations for unsteady overland flow propagation. Water 2018, 10, 44. [Google Scholar] [CrossRef]
- Aricò, C.; Sinagra, M.; Begnudelli, L.; Tucciarelli, T. MAST-2D diffusive model for flood prediction on domains with triangular Delaunay unstructured meshes. Adv. Water Resour. 2011, 34, 1427–1449. [Google Scholar] [CrossRef]
- Bates, P.D. Remote sensing and flood inundation modelling. Hydrol. Process. 2004, 18, 2593–2597. [Google Scholar] [CrossRef]
- Jahanbazi, M.; Özgen, I.; Aleixo, R.; Hinkelmann, R. Development of a diffusive wave shallow water model with a novel stability condition and other new features. J. Hydroinform. 2017, 19, 405–425. [Google Scholar] [CrossRef]
- Savant, G.; Trahan, C.J.; Pettey, L.; McAlpin, T.O.; Bell, G.L.; McKnight, C.J. Urban and overland flow modeling with dynamic adaptive mesh and implicit diffusive wave equation solver. J. Hydrol. 2019, 573, 13–30. [Google Scholar] [CrossRef]
- Su, B.; Huang, H.; Zhu, W. An urban pluvial flood simulation model based on diffusive wave approximation of shallow water equations. Hydrol. Res. 2017, 50, 138–154. [Google Scholar] [CrossRef]
- Mignosa, P.; Vacondio, R.; Aureli, F.; Dazzi, S.; Ferrari, A.; Prost, F. High resolution 2D modelling of rapidly varying flows: Some case studies. Ital. J. Eng. Geol. Environ. 2018, 2018, 143–160. [Google Scholar]
- Dottori, F.; Todini, E. Testing a simple 2D hydraulic model in an urban flood experiment. Hydrol. Process. 2013, 27, 1301–1320. [Google Scholar] [CrossRef]
- Hou, J.; Wang, T.; Li, P.; Li, Z.; Zhang, X.; Zhao, J.; Hinkelmann, R. An implicit friction source term treatment for overland flow simulation using shallow water flow model. J. Hydrol. 2018, 564, 357–366. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; Fernández-Pato, J.; Hinz, C. Performance assessment of 2D Zero-Inertia and shallow water models for simulating rainfall-runoff processes. J. Hydrol. 2020. [Google Scholar] [CrossRef]
- Aureli, F.; Maranzoni, A.; Mignosa, P.; Ziveri, C. A weighted surface-depth gradient method for the numerical integration of the 2D shallow water equations with topography. Adv. Water Resour. 2008, 31, 962–974. [Google Scholar] [CrossRef]
- Brodtkorb, A.R.; Sætra, M.L.; Altinakar, M. Efficient shallow water simulations on GPUs: Implementation, visualization, verification, and validation. Comput. Fluids 2012, 55, 1–12. [Google Scholar] [CrossRef]
- Smith, L.S.; Liang, Q. Towards a generalised GPU/CPU shallow-flow modelling tool. Comput. Fluids 2013, 88, 334–343. [Google Scholar] [CrossRef]
- Lacasta, A.; Morales-Hernández, M.; Murillo, J.; García-Navarro, P. An optimized GPU implementation of a 2D free surface simulation model on unstructured meshes. Adv. Eng. Softw. 2014, 78, 1–15. [Google Scholar] [CrossRef]
- Liang, Q.; Xia, X.; Hou, J. Catchment-scale high-resolution flash flood simulation using the GPU-based technology. Procedia Eng. 2016, 154, 975–981. [Google Scholar] [CrossRef]
- Le, P.V.V.; Kumar, P.; Valocchi, A.J.; Dang, H.V. GPU-based high-performance computing for integrated surface-sub-surface flow modeling. Environ. Model. Softw. 2015, 73, 1–13. [Google Scholar] [CrossRef]
- Hu, X.; Song, L. Hydrodynamic modeling of flash flood in mountain watersheds based on high-performance GPU computing. Nat. Hazards 2018, 91, 567–586. [Google Scholar] [CrossRef]
- Xing, Y.; Liang, Q.; Wang, G.; Ming, X.; Xia, X. City-scale hydrodynamic modelling of urban flash floods: The issues of scale and resolution. Nat. Hazards 2019, 96, 473–496. [Google Scholar] [CrossRef]
- Vacondio, R.; Dal Palù, A.; Mignosa, P. GPU-enhanced finite volume shallow water solver for fast flood simulations. Environ. Model. Softw. 2014, 57, 60–75. [Google Scholar] [CrossRef]
- Lacasta, A.; Morales-Hernández, M.; Murillo, J.; García-Navarro, P. GPU implementation of the 2D shallow water equations for the simulation of rainfall/runoff events. Environ. Earth Sci. 2015, 74, 7295–7305. [Google Scholar] [CrossRef]
- Juez, C.; Lacasta, A.; Murillo, J.; García-Navarro, P. An efficient GPU implementation for a faster simulation of unsteady bed-load transport. J. Hydraul. Res. 2016, 54, 275–288. [Google Scholar] [CrossRef]
- Vacondio, R.; Dal Palù, A.; Ferrari, A.; Mignosa, P.; Aureli, F.; Dazzi, S. A non-uniform efficient grid type for GPU-parallel Shallow Water Equations models. Environ. Model. Softw. 2017, 88, 119–137. [Google Scholar] [CrossRef]
- García-Navarro, P.; Murillo, J.; Fernández-Pato, J.; Echeverribar, I.; Morales-Hernández, M. The shallow water equations and their application to realistic cases. Environ. Fluid Mech. 2019, 19, 1235–1252. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Mignosa, P. Internal boundary conditions for a GPU-accelerated 2D shallow water model: Implementation and applications. Adv. Water Resour. 2020, 137, 103525. [Google Scholar] [CrossRef]
- Ferrari, A.; Dazzi, S.; Vacondio, R.; Mignosa, P. Enhancing the resilience to flooding induced by levee breaches in lowland areas: A methodology based on numerical modelling. Nat. Hazards Earth Syst. Sci. 2020, 20, 59–72. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Dal Palù, A.; Mignosa, P. A local time stepping algorithm for GPU-accelerated 2D shallow water models. Adv. Water Resour. 2018, 111, 274–288. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Mignosa, P. Integration of a levee breach erosion model in a GPU-accelerated 2D shallow water equations code. Water Resour. Res. 2019, 55, 682–702. [Google Scholar] [CrossRef]
- Turchetto, M.; Dal Palu, A.; Vacondio, R. A general design for a scalable MPI-GPU multi-resolution 2D numerical solver. IEEE Trans. Parallel Distrib. Syst. 2019. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Liang, Q.; Borthwick, A.G.L. Adaptive quadtree simulation of shallow flows with wet–dry fronts over complex topography. Comput. Fluids 2009, 38, 221–234. [Google Scholar] [CrossRef]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Audusse, E.; Bouchut, F.; Bristeau, M.-O.; Klein, R.; Perthame, B. A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM J. Sci. Comput. 2004, 25, 2050–2065. [Google Scholar] [CrossRef]
- Liang, Q.; Marche, F. Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Resour. 2009, 32, 873–884. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- NVIDIA CUDA. Compute Unified Device Architecture Programming Guide. Available online: www.nvidia.com (accessed on 1 November 2019).
- Greaves, D.M.; Borthwick, A.G.L. Hierarchical tree-based finite element mesh generation. Int. J. Numer. Methods Eng. 1999, 45, 447–471. [Google Scholar] [CrossRef]
- Liang, Q. A structured but non-uniform Cartesian grid-based model for the shallow water equations. Int. J. Numer. Methods Fluids 2011, 66, 537–554. [Google Scholar] [CrossRef]
- Iwagaki, Y. Fundamental studies on the runoff by characteristics. 1955; 10, 1–25. [Google Scholar]
- Feng, K.; Molz, F.J. A 2-D, diffusion-based, wetland flow model. 1997; 196, 230–250. [Google Scholar]
- Busaman, A.; Mekchay, K.; Siripant, S. Dynamically adaptive tree grid modeling for simulation and visualization of rainwater overland flow. Int. J. Numer. Methods Fluids 2015, 79, 559–579. [Google Scholar] [CrossRef]
- West, D.W.; Kubatko, E.J.; Conroy, C.J.; Yaufman, M.; Wood, D. A multidimensional discontinuous Galerkin modeling framework for overland flow and channel routing. Adv. Water Resour. 2017, 102, 142–160. [Google Scholar] [CrossRef]
- Fiedler, F.R.; Ramirez, J.A. A numerical method for simulating discontinuous shallow flow over an infiltrating surface. Int. J. Numer. Methods Fluids 2000, 32, 219–240. [Google Scholar] [CrossRef]
- Simons, F.; Busse, T.; Hou, J.; Özgen, I.; Hinkelmann, R. A model for overland flow and associated processes within the Hydroinformatics Modelling System. J. Hydroinform. 2014, 16, 375–391. [Google Scholar] [CrossRef]
- Hou, J.; Guo, K.; Liu, F.; Han, H.; Liang, Q.; Tong, Y.; Li, P. Assessing slope forest effect on flood process caused by a short-duration storm in a small catchment. Water 2018, 10, 1256. [Google Scholar] [CrossRef]
- Xia, X.; Liang, Q. A new efficient implicit scheme for discretising the stiff friction terms in the shallow water equations. Adv. Water Resour. 2018, 117, 87–97. [Google Scholar] [CrossRef]
- Wooding, R.A. A hydraulic model for the catchment-stream problem. I. Kinematic-wave theory. J. Hydrol. 1965, 3, 254–267. [Google Scholar] [CrossRef]
- Wooding, R.A. A hydraulic model for the catchment-stream problem. II. Numerical solutions. J. Hydrol. 1965, 3, 268–282. [Google Scholar] [CrossRef]
- Overton, D.E.; Brakensiek, D.L. A kinematic model of surface runoff response. Hydrologie 1970, 1, 100–112. [Google Scholar]
- Overton, D.E. Estimation of surface water lag time from the kinematic wave equations. J. Am. Water Resour. Assoc. 1971, 7, 428–440. [Google Scholar] [CrossRef]
- Liggett, J.A.; Woolhiser, D.A. The use of the shallow water equations in runoff computation. In Proceedings of the Third annual American Water Resources Conference, San Francisco, CA, USA, 8–10 November 1967; pp. 117–126. [Google Scholar]
- Woolhiser, D.A.; Liggett, J.A. Unsteady, one-dimensional flow over a plane-The rising hydrograph. Water Resour. Res. 1967, 3, 753–771. [Google Scholar] [CrossRef]










| Grid | N (Millions) | T (Hours) | CR (–) | SU (–) |
|---|---|---|---|---|
| Cartesian 1 m × 1 m | 1.62 | 2.86 | – | – |
| Cartesian 10 m × 10 m | 0.016 | 0.042 | – | – |
| BUQ Grid | 0.29 | 0.46 | 5.59 | 6.21 |
| Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| CN | 57 | 61 | 72 | 75 | 84 | 86 | 90 |
| Grid | N (Millions) | T (Hours) | CR (–) | SU (–) |
|---|---|---|---|---|
| Cartesian 5 m × 5 m | 8.49 | 14.77 | – | – |
| BUQ Grid 1 | 4.12 | 7.66 | 2.06 | 1.93 |
| BUQ Grid 2 | 1.55 | 2.93 | 5.48 | 5.04 |
| BUQ Grid 3 | 0.88 | 1.88 | 9.65 | 7.86 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aureli, F.; Prost, F.; Vacondio, R.; Dazzi, S.; Ferrari, A. A GPU-Accelerated Shallow-Water Scheme for Surface Runoff Simulations. Water 2020, 12, 637. https://doi.org/10.3390/w12030637
Aureli F, Prost F, Vacondio R, Dazzi S, Ferrari A. A GPU-Accelerated Shallow-Water Scheme for Surface Runoff Simulations. Water. 2020; 12(3):637. https://doi.org/10.3390/w12030637
Chicago/Turabian StyleAureli, Francesca, Federico Prost, Renato Vacondio, Susanna Dazzi, and Alessia Ferrari. 2020. "A GPU-Accelerated Shallow-Water Scheme for Surface Runoff Simulations" Water 12, no. 3: 637. https://doi.org/10.3390/w12030637
APA StyleAureli, F., Prost, F., Vacondio, R., Dazzi, S., & Ferrari, A. (2020). A GPU-Accelerated Shallow-Water Scheme for Surface Runoff Simulations. Water, 12(3), 637. https://doi.org/10.3390/w12030637








