Application of Principal Component Analysis and Cluster Analysis in Regional Flood Frequency Analysis: A Case Study in New South Wales, Australia
Abstract
1. Introduction
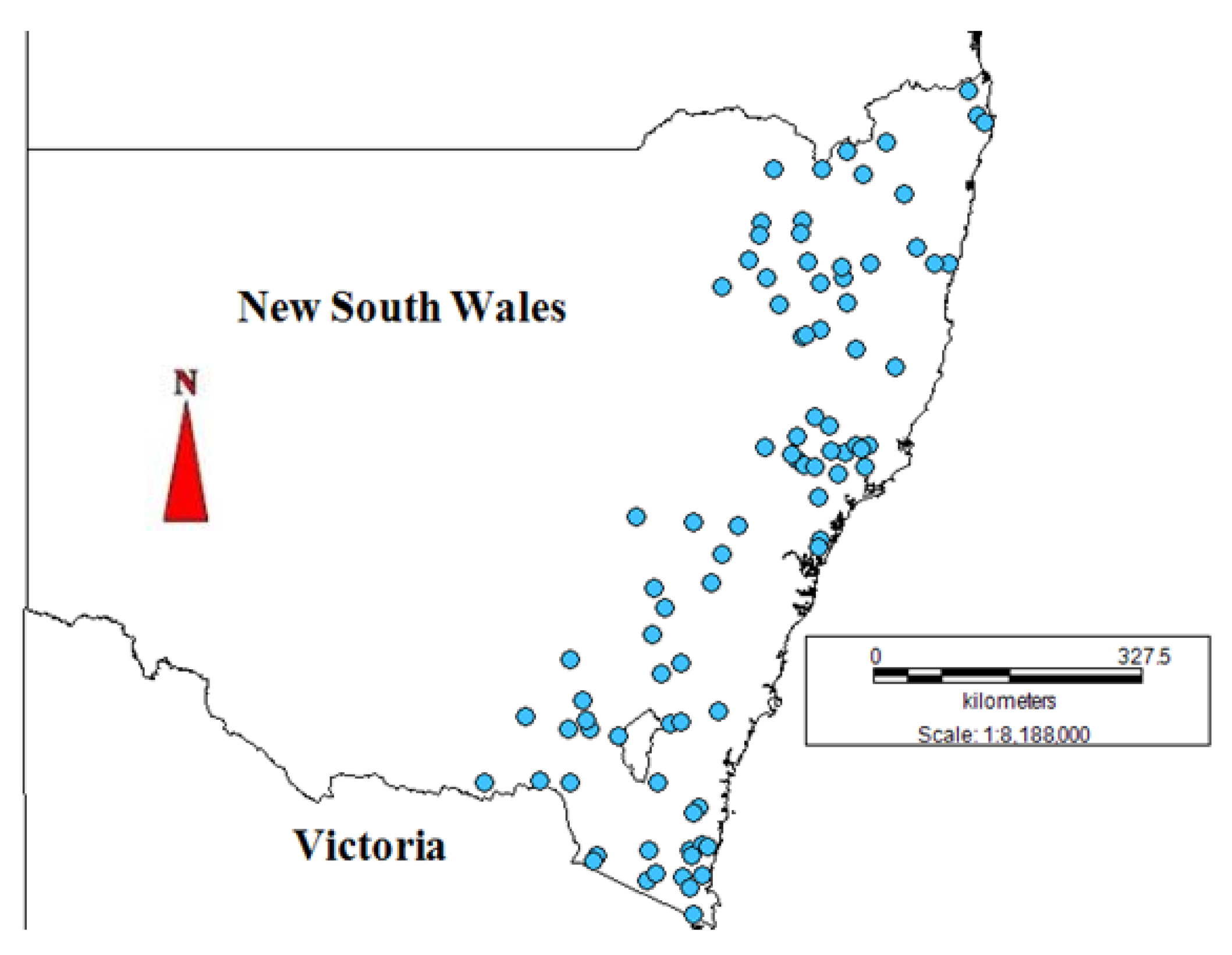
2. Study Area
3. Methods
3.1. Principal Component Analysis
3.2. Cluster Analysis
3.3. Region of Influence Approach
3.4. Homogeneity Assessment
3.5. Evaluation Statistics
4. Results and Discussion
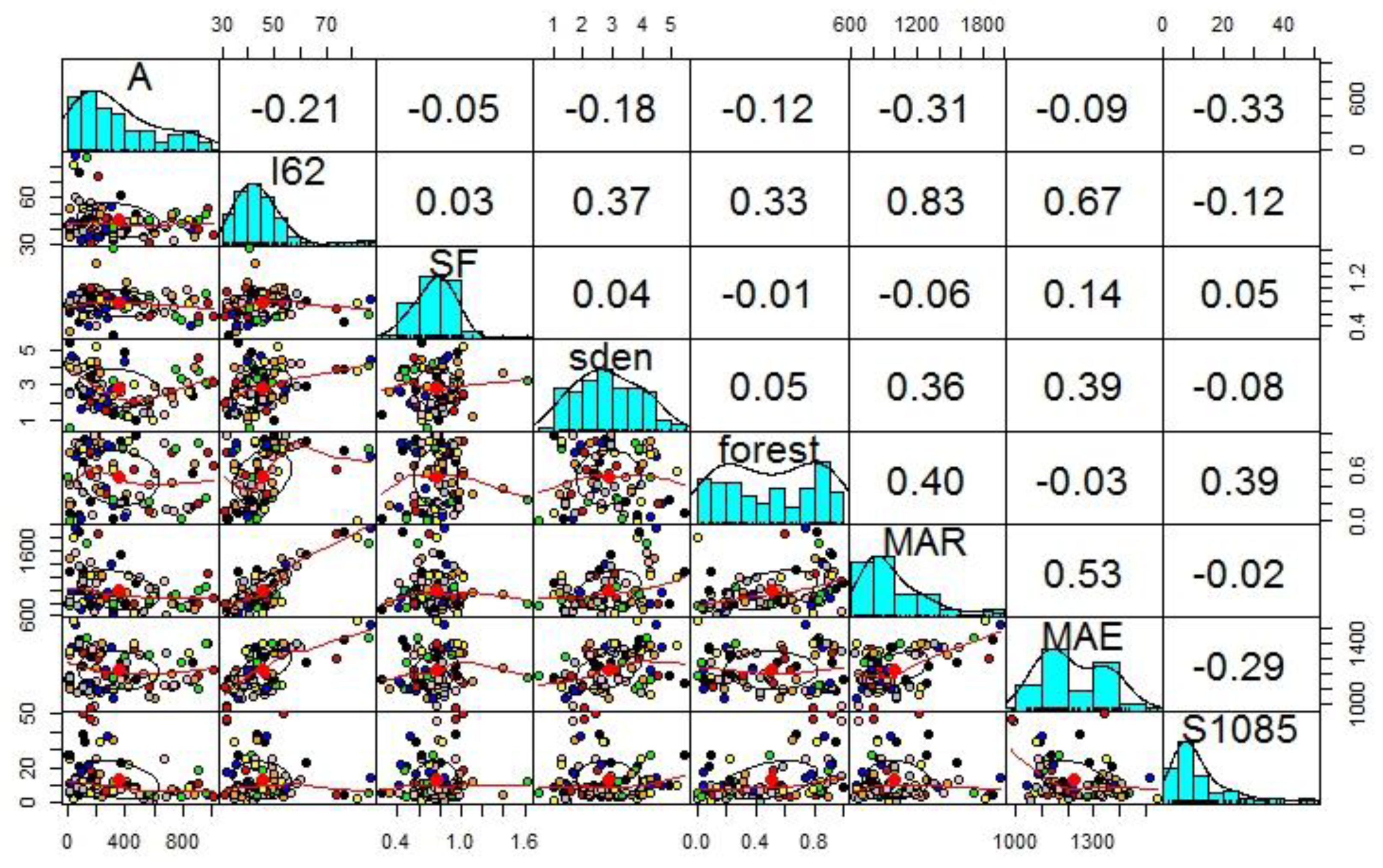
4.1. Principal Component Analysis
4.2. Development and Testing of Regression Equation in Fixed Region and ROI Framework
4.3. Application of Cluster Analysis
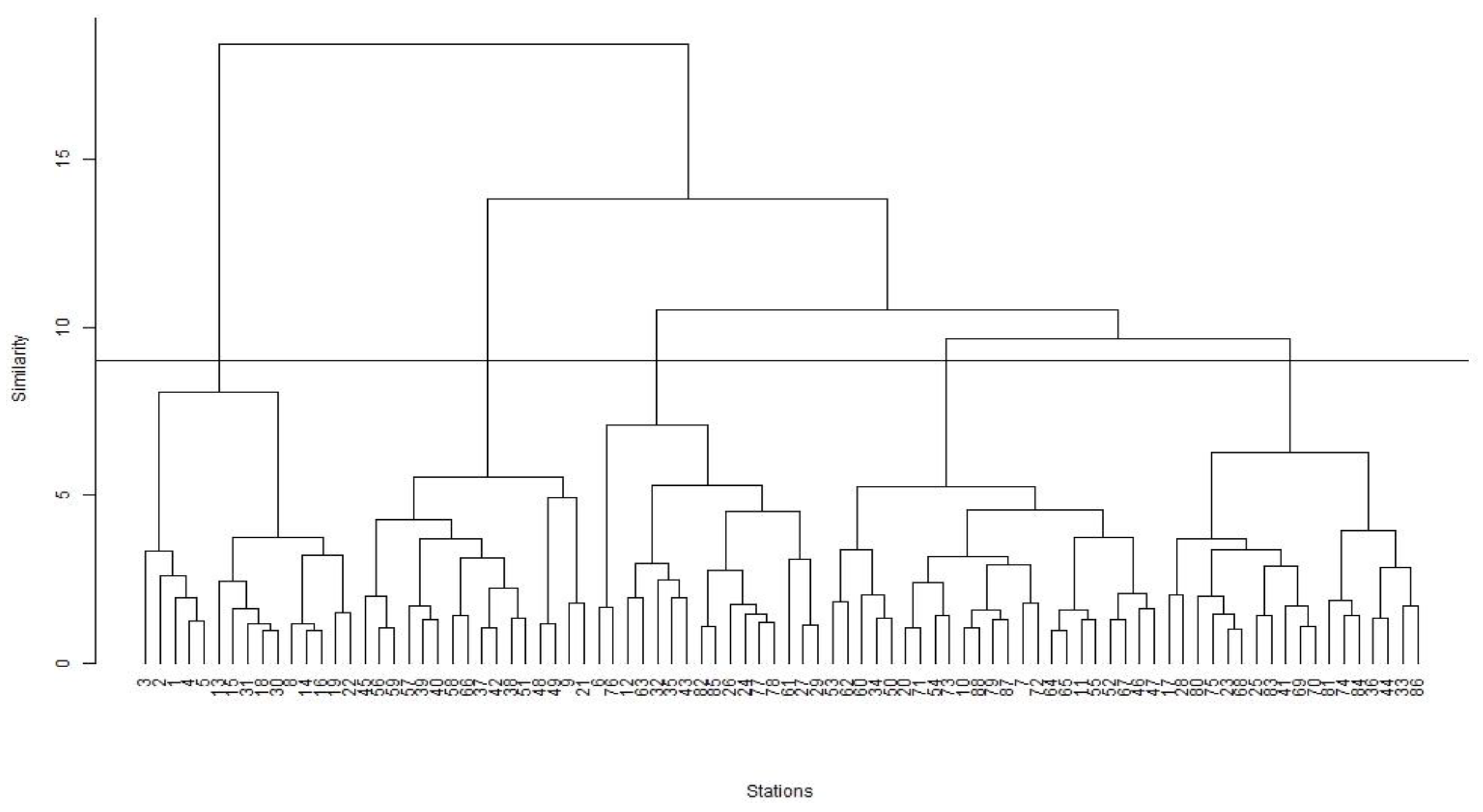
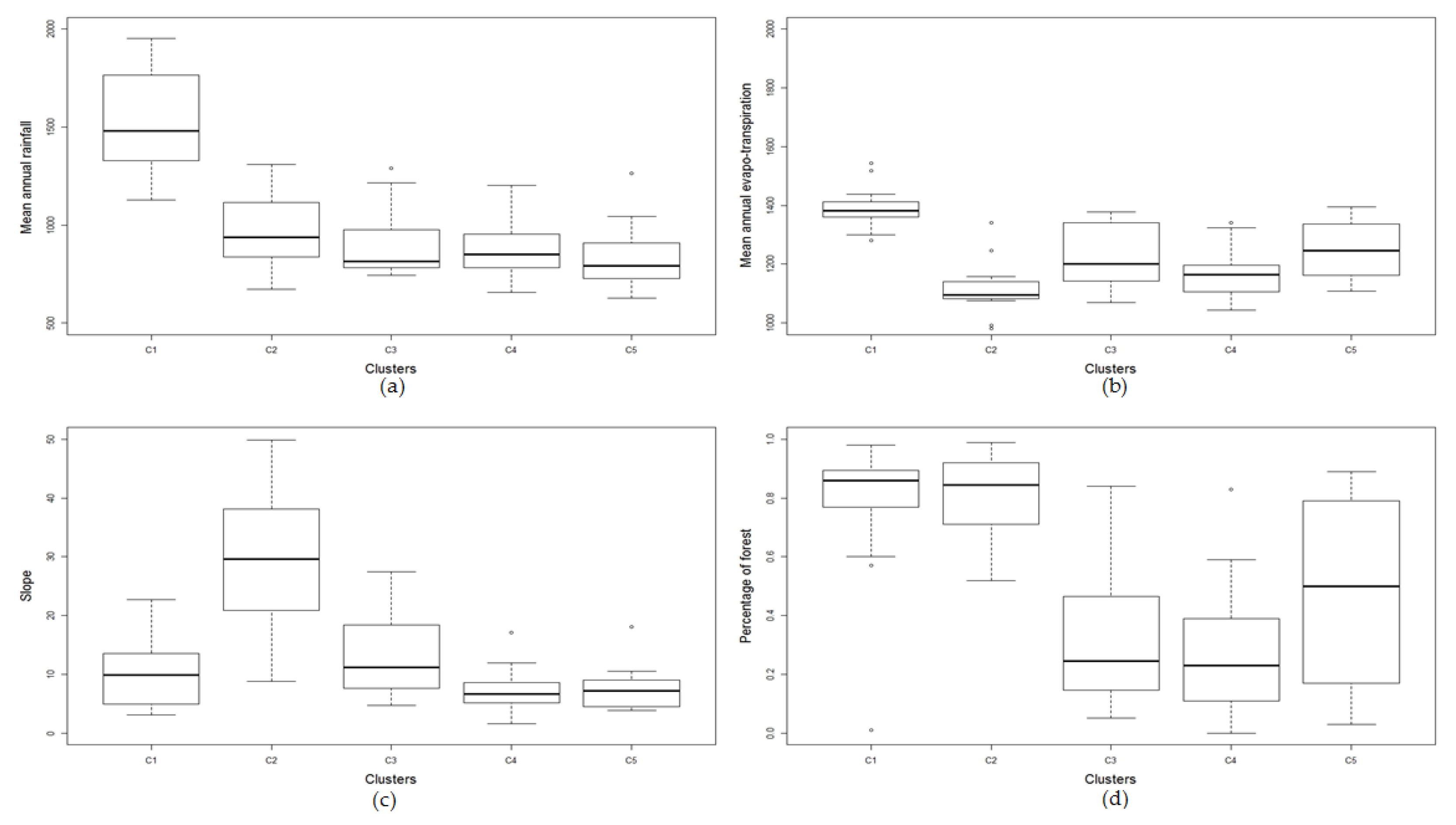
4.3.1. Cluster Formation
4.3.2. Homogeneity Analysis of the Clusters
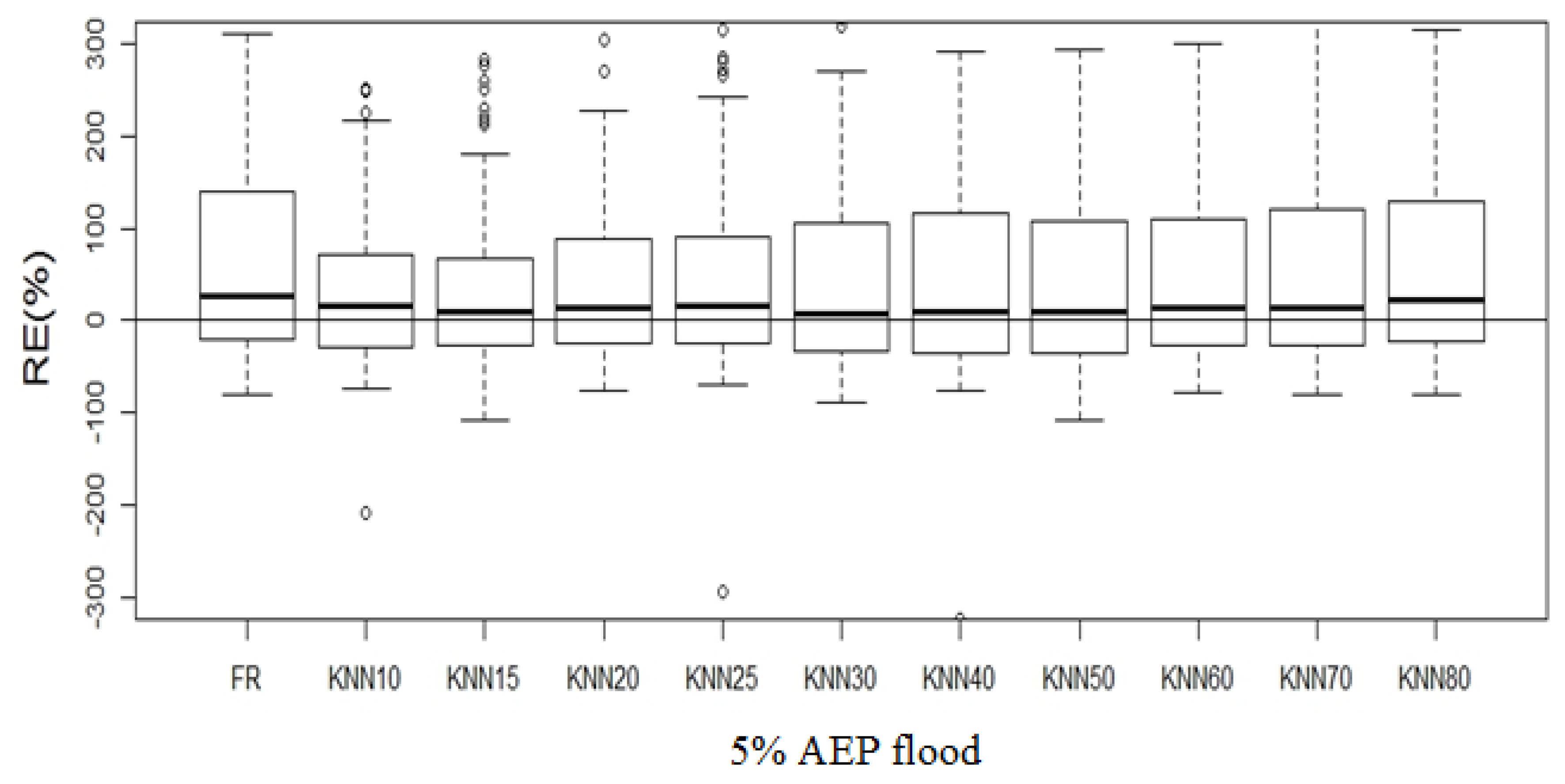
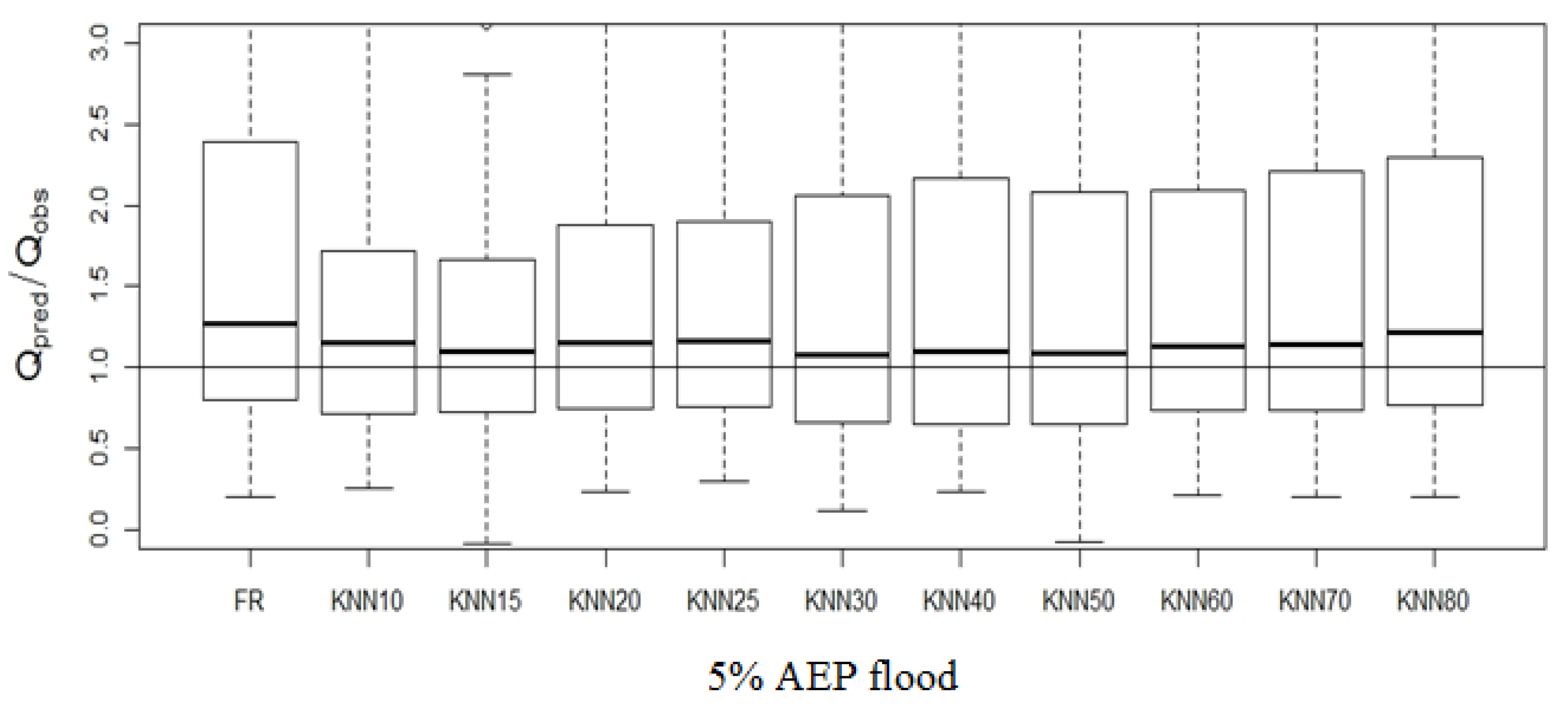
4.3.3. Development of Prediction Equation and Performance Testing
4.4. Comparison with ARR RFFA Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blöschl, G.; Sivapalan, M.; Wagener, T.; Savenije, H.; Viglione, A. (Eds.) Runoff prediction in Ungauged Basins: Synthesis across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ouarda, T.B.M.J.; St-Hilaire, A.; Bobée, B. A review of recent developments in regional frequency analysis of hydrological extremes. Revue des Sciences de l’eau 2008, 21, 219–232. [Google Scholar] [CrossRef][Green Version]
- Ouarda, T.B.M.J.; Bâ, K.M.; Diaz-Delgado, C.; Carsteanu, A.; Chokmani, K.; Gingras, H.; Quentin, E.; Trujillo, E.; Bobée, A.B. Intercomparison of regional flood frequency estimation methods at ungauged sites for a Mexican case study. J. Hydrol. 2008, 348, 40–58. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A.; Ling, F. Regional flood frequency analysis method for Tasmania, Australia: A case study on the comparison of fixed region and region-of-influence approaches. Hydrol. Sci. J. 2015, 60, 2086–2101. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J. Regional hydrological frequency analysis. In Encyclopedia of Environmetrics; El-Shaarawi, A.H., Piegorsch, W.W., Eds.; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Rahman, A.S.; Khan, Z.; Rahman, A. Application of Independent Component Analysis in Regional Flood Frequency Analysis: Comparison between Quantile Regression and Parameter Regression Techniques. J. Hydrol. 2019, 581, 124372. [Google Scholar] [CrossRef]
- Acreman, M.C. Regional Flood Frequency Analysis in the UK: Recent Research-New Ideas; Institute of Hydrology: Wallingford, UK, 1987. [Google Scholar]
- Acreman, M.C.; Sinclair, C.D. Classification of drainage basins according to their physical characteristics; an application for flood frequency analysis in Scotland. J. Hydrol. 1986, 84, 365–380. [Google Scholar] [CrossRef]
- Eng, K.; Tasker, G.D.; Milly, P.C.D. An analysis of region-of-influence methods for flood regionalisation in the-Gulf-Atlantic rolling plains. J. Am. Water Resour. Assoc. 2005, 41, 135–143. [Google Scholar] [CrossRef]
- Pilgrim, D.H. Australian Rainfall and Runoff; Institution of Engineers: Barton, Australia, 1987. [Google Scholar]
- Tasker, G.D.; Hodge, S.A.; Barks, C.S. Region of influence regression for estimating the 50 year flood at ungauged sites. J. Am. Water Resour. Assoc. 1996, 32, 163–170. [Google Scholar] [CrossRef]
- Burn, D.H. An appraisal of the “region of influence” approach to flood frequency analysis. Hydrol. Sci. J. 1990, 35, 149–165. [Google Scholar] [CrossRef]
- Burn, D.H. Evaluation of regional flood frequency analysis with a region of influence approach. Water Resour. Res. 1990, 26, 2257–2265. [Google Scholar] [CrossRef]
- Chebana, F.; Ouarda, T.B.M.J. Depth and homogeneity in regional flood frequency analysis. Water Resour. Res. 2008, 44, W11422. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Flood frequency regionalisation—Spatial proximity vs. catchment attributes. J. Hydrol. 2005, 302, 283–306. [Google Scholar] [CrossRef]
- Burn, D.H. Cluster analysis as applied to regional flood frequency. J. Water Res. Plan. Man. 1989, 115, 567–582. [Google Scholar] [CrossRef]
- Burn, D.H.; Boorman, D.B. Estimation of hydrological parameters at ungauged catchments. J. Hydrol. 1993, 143, 429–454. [Google Scholar] [CrossRef]
- Himeidan, Y.E.S.; Hamid, E.E.H. Rainfall variability in New Halfa agricultural scheme (Sudan). Univ. Khartoum J. Agric. Sci. 2019, 14, 383–391. [Google Scholar]
- Hughes, J.M.R.; James, B. A hydrological regionalization of streams in Victoria, Australia, with implications for stream ecology. Mar. Freshw. Res. 1989, 40, 303–326. [Google Scholar] [CrossRef]
- Mosley, M.P. Delimitation of New Zealand hydrologic regions. J. Hydrol. 1981, 49, 173–192. [Google Scholar] [CrossRef]
- Nathan, R.J.; McMahon, T.A. Identification of homogeneous regions for the purposes of regionalisation. J. Hydrol. 1990, 121, 217–238. [Google Scholar] [CrossRef]
- Rasheed, A.; Egodawatta, P.; Goonetilleke, A.; McGree, J. A Novel Approach for Delineation of Homogeneous Rainfall Regions for Water Sensitive Urban Design—A Case Study in Southeast Queensland. Water 2019, 11, 570. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Moura, R.; da Silva, R.M.; Costa, S.G.F. Cluster Analysis Applied to Spatiotemporal Variability of Monthly Precipitation over Paraíba State Using Tropical Rainfall Measuring Mission (TRMM) Data. Remote Sens. 2019, 11, 637. [Google Scholar] [CrossRef]
- Tasker, G.D. Comparing methods of hydrologic regionalisation. J. Am. Water Resour. Assoc. 1982, 18, 965–970. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach based on L-moments; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Eng, K.; Milly, P.C.; Tasker, G.D. Flood regionalisation: A hybrid geographic and predictor-variable region-of-influence regression method. J. Hydrol. Eng. 2007, 12, 585–591. [Google Scholar] [CrossRef]
- Eng, K.; Stedinger, J.R.; Gruber, A.M. Regionalisation of streamflow characteristics for the Gulf-Atlantic rolling plains using leverage-guided region-of-influence regression. In Proceedings of the World Environmental and Water Resources Congress 2007: Restoring Our Natural Habitat, Tampa, Florida, 15–19 May 2007; pp. 1–11. [Google Scholar]
- Gaál, L.; Kyselý, J.; Szolgay, J. Region-of-influence approach to a frequency analysis of heavy precipitation in Slovakia. Hydrol. Earth Sys. Sci. Discuss. 2008, 12, 825–839. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Regional flood frequency analysis in eastern Australia: Bayesian GLS regression-based methods within fixed region and ROI framework: Quantile regression vs. parameter regression technique. J. Hydrol. 2012, 430–431, 142–161. [Google Scholar] [CrossRef]
- Micevski, T.; Hackelbusch, A.; Haddad, K.; Kuczera, G.; Rahman, A. Regionalisation of the parameters of the log-Pearson 3 distribution: A case study for New South Wales, Australia. Hydrol. Process. 2015, 29, 250–260. [Google Scholar] [CrossRef]
- Rahman, A.; Haddad, K.; Kuczera, G.; Weinmann, P.E. Regional flood methods. Aust. Rainfall Runoff. 2019, 3, 105–146. [Google Scholar]
- Zrinji, Z.; Burn, D.H. Regional flood frequency with hierarchical region of influence. J. Water Res. Plan. Man. 1996, 122, 245–252. [Google Scholar] [CrossRef]
- Burn, D.H.; Goel, N.K. The formation of groups for regional flood frequency analysis. Hydrol. Sci. J. 2000, 45, 97–112. [Google Scholar] [CrossRef]
- Castellarin, A.; Burn, D.H.; Brath, A. Assessing the effectiveness of hydrological similarity measures for regional flood frequency analysis. J. Hydrol. 2001, 241, 270–285. [Google Scholar] [CrossRef]
- Burn, D.H. Catchment similarity for regional flood frequency analysis using seasonality measures. J. Hydrol. 1997, 202, 212–230. [Google Scholar] [CrossRef]
- Lim, Y.H.; Lye, L.M. Regional flood estimation for ungauged basins in Sarawak, Malaysia. Hydrol. Sci. J. 2003, 48, 79–94. [Google Scholar] [CrossRef]
- Zrinji, Z.; Burn, D.H. Flood frequency analysis for ungauged sites using a region of influence approach. J. Hydrol. 1994, 153, 1–21. [Google Scholar] [CrossRef]
- Bates, B.C.; Rahman, A.; Mein, R.G.; Weinmann, P.E. Climatic and physical factors that influence the homogeneity of regional floods in south-eastern Australia. Water Resour. Res. 1998, 34, 3369–3382. [Google Scholar] [CrossRef]
- Fill, H.D.; Stedinger, J.R. Using regional regression within IF procedures and an empirical Bayesian estimator. J. Hydrol. 1998, 210, 128–145. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A.; Stedinger, J.R. Regional flood frequency analysis using Bayesian generalized least squares: A comparison between quantile and parameter regression techniques. Hydrol. Process. 2012, 26, 1008–1021. [Google Scholar] [CrossRef]
- Griffis, V.W.; Stedinger, J.R. The use of GLS regression in regional hydrologic analyses. J. Hydrol. 2007, 344, 82–95. [Google Scholar] [CrossRef]
- Micevski, T.; Kuczera, G. Combining site and regional flood information using a Bayesian Monte Carlo approach. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Ouali, D.; Chebana, F.; Ouarda, T.B.M.J. Quantile regression in regional frequency analysis: A better exploitation of the available information. J. Hydrometeorol. 2016, 17, 1869–1883. [Google Scholar] [CrossRef]
- Rahman, A.; Charron, C.; Ouarda, T.B.M.J.; Chebana, F. Development of regional flood frequency analysis techniques using generalized additive models for Australia. Stoch. Environ. Res. Risk A 2018, 32, 123–139. [Google Scholar] [CrossRef]
- Rahman, A. A quantile regression technique to estimate design floods for ungauged catchments in south-east Australia. Australas. J. Water Resour. 2005, 9, 81–89. [Google Scholar] [CrossRef]
- Chebana, F.; Charron, C.; Ouarda, T.B.M.J.; Martel, B. Regional frequency analysis at ungauged sites with the generalized additive model. J. Hydrometeorol. 2014, 15, 2418–2428. [Google Scholar] [CrossRef]
- Burn, D.H. Delineation of groups for regional flood frequency analysis. J. Hydrol. 1988, 104, 345–361. [Google Scholar] [CrossRef]
- DeCoursey, D.G.; Deal, R.B. General Aspects of Multivariate Analysis with Applications. Misc. Publ. 1974, 1275, 47. [Google Scholar]
- Hawley, M.E.; McCuen, R.H. Water yield estimation in western United States. J. Irrig. Drain. Div. 1982, 108, 25–34. [Google Scholar]
- Kar, A.K.; Goel, N.K.; Lohani, A.K.; Roy, G.P. Application of clustering techniques using prioritized variables in regional flood frequency analysis—Case study of Mahanadi Basin. J. Hydrol. Eng. 2011, 17, 213–223. [Google Scholar] [CrossRef]
- Choi, T.H.; Kwon, O.E.; Koo, J.Y. Water demand forecasting by characteristics of city using principal component and cluster analyses. Environ. Eng. Res. 2010, 15, 135–140. [Google Scholar] [CrossRef][Green Version]
- Haque, M.M.; de Souza, A.; Rahman, A. Water demand modelling using independent component regression technique. Water Resour. Res. 2017, 31, 299–312. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, A.; Hagare, D.; Kibria, G. Principal component regression analysis in water demand forecasting: An application to the Blue Mountains, NSW, Australia. J. Hydrol. Environ. Res. 2013, 1, 49–59. [Google Scholar]
- Koo, J.Y.; Yu, M.J.; Kim, S.G.; Shim, M.H.; Koizumi, A. Estimating regional water demand in Seoul, South Korea, using principal component and cluster analysis. Water Sci. Tech. Water Supply 2005, 5, 1–7. [Google Scholar] [CrossRef]
- Ball, J.; Babister, M.; Nathan, R.; Weeks, W.; Weinmann, P.E.; Retallick, M.; Testoni, I. Australian Rainfall and Runoff-A Guide to Flood Estimation; Engineers Australia: Canberra, Australia, 2019. [Google Scholar]
- Rahman, A.; Haddad, K.; Haque, M.; Kuczera, G.; Weinmann, P.E. Australian Rainfall and Runoff Project 5: Regional Flood Methods: Stage 3 Report; (No. P5/S3, p. 025). technical report; Engineers Australia: Canberra, Australia, 2015. [Google Scholar]
- Çamdevýren, H.; Demýr, N.; Kanik, A.; Keskýn, S. Use of principal component scores in multiple linear regression models for prediction of Chlorophyll-a in reservoirs. Ecol. Model. 2005, 181, 581–589. [Google Scholar] [CrossRef]
- Olsen, R.L.; Chappell, R.W.; Loftis, J.C. Water quality sample collection, data treatment and results presentation for principal components analysis–literature review and Illinois River watershed case study. Water Res. 2012, 46, 3110–3122. [Google Scholar] [CrossRef] [PubMed]
- Pires, J.C.M.; Martins, F.G.; Sousa, S.I.V.; Alvim-Ferraz, M.C.M.; Pereira, M.C. Selection and validation of parameters in multiple linear and principal component regressions. Environ. Modell. Softw. 2008, 23, 50–55. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis; PrenticeHall International. Inc.: New Jersey, NJ, USA, 2007. [Google Scholar]
- Baeriswyl, P.A.; Rebetez, M. Regionalization of precipitation in Switzerland by means of principal component analysis. Theor. Appl. Climatol. 1997, 58, 31–41. [Google Scholar] [CrossRef]
- Bhaskar, N.R.; O’Connor, C.A. Comparison of method of residuals and cluster analysis for flood regionalization. J. Water Resour. Plan. Manag. 1989, 115, 793–808. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Fakheri-Fard, A.; Moghaddam, M.; Jahanbakhsh, S.; Mirnia, M. Selection of variables for the purpose of regionalization of Iran’s precipitation climate using multivariate methods. J. Hydrol. 2004, 297, 109–123. [Google Scholar] [CrossRef]
- Rao, A.R.; Srinivas, V.V. Regionalization of watersheds by hybrid-cluster analysis. J. Hydrol. 2006, 318, 37–56. [Google Scholar] [CrossRef]
- Kuczera, G. FLIKE HELP; Chapter 2 FLIKE Notes; University of Newcastle: Callaghan, Australia, 1999. [Google Scholar]
- Durocher, M.; Burn, D.H.; Zadeh, S.M. A nationwide regional flood frequency analysis at ungauged sites using ROI/GLS with copulas and super regions. J. Hydrol. 2018, 567, 191–202. [Google Scholar] [CrossRef]
- Chokmani, K.; Ouarda, T.B.M.J. Physiographical space-based kriging for regional flood frequency estimation at ungauged sites. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Shu, C.; Ouarda, T.B.M.J. Flood frequency analysis at ungauged sites using artificial neural networks in canonical correlation analysis physiographic space. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]


| Variables | Range | Median | Mean | Standard Deviation |
|---|---|---|---|---|
| Catchment area (A) in km2 | 8–1010 | 260 | 351.9 | 281.4 |
| Rainfall intensity (I62) in mm/h | 31.3–87.3 | 43.1 | 45.4 | 11.3 |
| Shape factor (SF) | 0.3–1.6 | 0.8 | 0.8 | 0.2 |
| Stream density (sden) in /km | 0.5–5.5 | 2.8 | 2.7 | 1.1 |
| Mean annual rainfall (MAR) in mm | 626.2–1953.2 | 1000.3 | 909.9 | 304.5 |
| Mean annual evapo-transpiration (MAE) in mm/y | 980.4–1543.3 | 1223.7 | 1185.6 | 126.3 |
| Fraction forest (forest) | 0–1 | 0.5 | 0.5 | 0.3 |
| Mainstream slope (S1085) in m/km | 1.5–49.8 | 12.9 | 9.1 | 10.8 |
| A | I62 | SF | sden | forest | MAR | MAE | |
|---|---|---|---|---|---|---|---|
| I62 | −0.208 | ||||||
| 0.052 | |||||||
| SF | −0.054 | 0.035 | |||||
| 0.619 | 0.746 | ||||||
| sden | −0.175 | 0.367 | 0.037 | ||||
| 0.102 | 0 | 0.733 | |||||
| forest | −0.116 | 0.33 | −0.007 | 0.046 | |||
| 0.283 | 0.002 | 0.951 | 0.667 | ||||
| MAR | −0.314 | 0.83 | −0.058 | 0.361 | 0.405 | ||
| 0.003 | 0 | 0.592 | 0.001 | 0 | |||
| MAE | −0.094 | 0.671 | 0.136 | 0.392 | −0.031 | 0.533 | |
| 0.381 | 0 | 0.206 | 0 | 0.771 | 0 | ||
| S1085 | −0.331 | −0.121 | 0.051 | −0.081 | 0.387 | −0.021 | −0.286 |
| 0.002 | 0.262 | 0.637 | 0.451 | 0 | 0.844 | 0.007 |
| Name | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| Eigenvalue | 2.822 | 1.641 | 1.070 | 0.915 | 0.702 | 0.432 | 0.278 | 0.141 |
| Proportion | 0.353 | 0.205 | 0.134 | 0.114 | 0.088 | 0.054 | 0.035 | 0.018 |
| Cumulative | 0.353 | 0.558 | 0.692 | 0.806 | 0.894 | 0.948 | 0.982 | 1 |
| 5% AEP | KNN10 | KNN15 | KNN20 | KNN25 | KNN30 | KNN40 | KNN50 | KNN60 | KNN70 | KNN80 | FR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MSE | 443296.69 | 228884.66 | 183799.06 | 187180.23 | 179135.55 | 181519.00 | 170279.10 | 166945.45 | 163644.38 | 163850.83 | 163447.17 |
| RMSE | 665.81 | 478.42 | 428.72 | 432.64 | 423.24 | 426.05 | 412.65 | 408.59 | 404.53 | 404.78 | 404.29 |
| BIAS | −65.51 | 1.20 | −11.94 | −13.12 | −0.82 | −20.07 | −14.73 | −21.27 | −18.68 | −6.20 | −0.29 |
| RBIAS | 22.24 | −0.44 | 55.31 | 63.94 | 54.40 | 61.69 | 65.54 | 56.98 | 54.34 | 69.90 | 65.48 |
| RRMSE | 0.11 | 0.00 | 0.02 | 0.02 | 0.00 | 0.03 | 0.03 | 0.04 | 0.03 | 0.01 | 0.00 |
| RMSNE | 5.40 | 3.15 | 3.28 | 3.03 | 2.38 | 2.77 | 2.28 | 2.05 | 2.05 | 2.69 | 2.43 |
| med_Rr | 59.03 | 53.41 | 54.46 | 52.61 | 55.12 | 51.48 | 49.01 | 50.74 | 47.15 | 46.59 | 48.08 |
| med_Qpred/Qobs | 1.03 | 1.01 | 1.16 | 1.07 | 1.14 | 1.19 | 1.20 | 1.16 | 1.16 | 1.18 | 1.17 |
| RE | FR | KNN10 | KNN15 | KNN20 | KNN25 | KNN30 | KNN40 | KNN50 | KNN60 | KNN70 | KNN80 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean_abs | 139.75 | 229.93 | 114.81 | 152.82 | 123.56 | 133.99 | 122.83 | 122.97 | 127.89 | 131.03 | 133.88 | |
| 50% | Median_abs | 51.76 | 63.84 | 42.70 | 45.76 | 42.70 | 48.91 | 42.19 | 44.84 | 46.70 | 49.10 | 50.12 |
| Std Dev_abs | 356.39 | 623.98 | 156.38 | 310.14 | 204.57 | 238.60 | 218.48 | 247.15 | 227.90 | 266.56 | 323.67 | |
| Mean_abs | 122.18 | 206.85 | 117.88 | 134.93 | 132.02 | 126.40 | 117.35 | 112.29 | 111.24 | 113.35 | 125.28 | |
| 20% | Median_abs | 48.32 | 51.22 | 51.25 | 54.02 | 43.64 | 50.44 | 46.03 | 50.88 | 50.09 | 46.27 | 45.36 |
| Std Dev_abs | 276.38 | 530.31 | 164.84 | 242.12 | 211.61 | 243.99 | 264.68 | 230.54 | 244.19 | 246.78 | 286.58 | |
| Mean_abs | 118.13 | 208.47 | 130.45 | 140.34 | 135.02 | 127.57 | 125.56 | 115.12 | 105.84 | 107.25 | 122.45 | |
| 10% | Median_abs | 48.62 | 55.19 | 55.39 | 54.23 | 48.77 | 50.32 | 49.57 | 51.92 | 53.24 | 47.21 | 41.70 |
| Std Dev_abs | 223.95 | 504.74 | 182.24 | 260.47 | 236.11 | 225.52 | 247.62 | 200.09 | 197.48 | 200.13 | 247.30 | |
| Mean_abs | 118.95 | 213.73 | 153.93 | 143.57 | 135.83 | 127.49 | 132.75 | 121.48 | 111.44 | 108.40 | 124.36 | |
| 5% | Median_abs | 48.09 | 59.03 | 53.41 | 54.46 | 52.62 | 55.13 | 51.48 | 49.02 | 50.74 | 47.15 | 46.59 |
| Std Dev_abs | 213.32 | 498.85 | 276.47 | 297.00 | 272.61 | 201.63 | 244.73 | 193.92 | 172.80 | 174.95 | 239.47 | |
| Mean_abs | 130.02 | 225.32 | 197.48 | 154.64 | 144.06 | 140.61 | 150.67 | 137.73 | 126.73 | 118.43 | 134.54 | |
| 2% | Median_abs | 52.16 | 66.95 | 58.87 | 56.14 | 58.25 | 60.52 | 54.35 | 52.14 | 50.76 | 53.10 | 53.28 |
| Std Dev_abs | 258.97 | 516.14 | 542.05 | 374.04 | 359.08 | 251.26 | 308.61 | 256.72 | 218.79 | 194.39 | 279.09 | |
| Mean_abs | 143.45 | 239.70 | 248.66 | 174.50 | 164.45 | 163.20 | 170.96 | 156.71 | 144.20 | 130.90 | 147.16 | |
| 1% | Median_abs | 53.56 | 71.95 | 68.67 | 61.21 | 59.66 | 59.80 | 52.97 | 50.99 | 49.75 | 47.46 | 51.92 |
| Std Dev_abs | 322.07 | 548.06 | 848.84 | 458.31 | 459.05 | 351.10 | 400.20 | 341.21 | 294.90 | 239.05 | 335.53 | |
| Overall mean | 128.75 | 220.67 | 160.53 | 150.13 | 139.16 | 136.54 | 136.69 | 149.15 | 121.22 | 131.30 | 133.48 | |
| Overall median | 49.77 | 61.39 | 54.90 | 54.42 | 51.31 | 55.06 | 50.63 | 47.42 | 50.17 | 45.15 | 45.95 | |
| Overall Std Dev | 278.68 | 536.23 | 443.19 | 330.54 | 303.33 | 255.48 | 286.29 | 350.60 | 228.51 | 255.40 | 264.04 | |
| Ratio | FR | KNN10 | KNN15 | KNN20 | KNN25 | KNN30 | KNN40 | KNN50 | KNN60 | KNN70 | KNN80 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean_abs | 2.00 | 2.72 | 1.67 | 2.09 | 1.84 | 1.96 | 1.81 | 1.84 | 1.86 | 1.87 | 1.94 | |
| 50% | Median_abs | 1.16 | 1.09 | 1.10 | 1.12 | 1.15 | 1.12 | 1.10 | 1.12 | 1.17 | 1.16 | 1.14 |
| Std Dev_abs | 3.44 | 6.20 | 1.60 | 2.95 | 2.02 | 2.39 | 2.10 | 2.33 | 2.12 | 2.56 | 3.12 | |
| Mean_abs | 1.85 | 2.53 | 1.69 | 1.90 | 1.90 | 1.85 | 1.79 | 1.77 | 1.71 | 1.73 | 1.89 | |
| 20% | Median_abs | 1.14 | 1.14 | 1.09 | 1.19 | 1.20 | 1.23 | 1.09 | 1.18 | 1.09 | 1.11 | 1.16 |
| Std Dev_abs | 2.68 | 5.23 | 1.60 | 2.38 | 2.08 | 2.36 | 2.57 | 2.20 | 2.36 | 2.40 | 2.80 | |
| Mean_abs | 1.83 | 2.53 | 1.81 | 1.93 | 1.92 | 1.87 | 1.88 | 1.81 | 1.72 | 1.73 | 1.89 | |
| 10% | Median_abs | 1.15 | 1.17 | 1.24 | 1.19 | 1.13 | 1.33 | 1.12 | 1.22 | 1.17 | 1.14 | 1.13 |
| Std Dev_abs | 2.23 | 4.98 | 1.70 | 2.62 | 2.38 | 2.22 | 2.44 | 1.97 | 1.94 | 1.98 | 2.46 | |
| Mean_abs | 1.88 | 2.58 | 2.04 | 1.97 | 1.94 | 1.87 | 1.98 | 1.90 | 1.80 | 1.76 | 1.93 | |
| 5% | Median_abs | 1.19 | 1.26 | 1.19 | 1.24 | 1.12 | 1.21 | 1.22 | 1.22 | 1.21 | 1.18 | 1.20 |
| Std Dev_abs | 2.18 | 4.93 | 2.61 | 3.02 | 2.79 | 2.07 | 2.47 | 1.99 | 1.77 | 1.79 | 2.44 | |
| Mean_abs | 2.00 | 2.67 | 2.45 | 2.08 | 2.07 | 2.04 | 2.16 | 2.07 | 1.96 | 1.86 | 2.04 | |
| 2% | Median_abs | 1.17 | 1.28 | 1.20 | 1.13 | 1.21 | 1.23 | 1.22 | 1.21 | 1.26 | 1.21 | 1.21 |
| Std Dev_abs | 2.70 | 5.12 | 5.29 | 3.83 | 3.68 | 2.61 | 3.16 | 2.68 | 2.30 | 2.07 | 2.89 | |
| Mean_abs | 2.15 | 2.77 | 2.95 | 2.29 | 2.27 | 2.27 | 2.37 | 2.25 | 2.14 | 1.99 | 2.17 | |
| 1% | Median_abs | 1.27 | 1.22 | 1.29 | 1.22 | 1.33 | 1.33 | 1.17 | 1.20 | 1.26 | 1.23 | 1.26 |
| Std Dev_abs | 3.33 | 5.47 | 8.36 | 4.68 | 4.69 | 3.62 | 4.09 | 3.54 | 3.08 | 2.54 | 3.47 | |
| Overall mean | 1.95 | 2.63 | 2.10 | 2.04 | 1.99 | 1.98 | 2.00 | 1.94 | 1.87 | 1.82 | 1.98 | |
| Overall median | 1.17 | 1.18 | 1.14 | 1.17 | 1.19 | 1.19 | 1.16 | 1.18 | 1.18 | 1.17 | 1.20 | |
| Overall Std Dev | 2.79 | 5.31 | 4.34 | 3.32 | 3.08 | 2.59 | 2.87 | 2.50 | 2.29 | 2.23 | 2.87 | |
| Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | |
|---|---|---|---|---|---|
| No. of stations | 15 | 16 | 16 | 23 | 18 |
| Period of records (median) | 29–80 (36) | 26–71 (40) | 30–82 (36) | 25–70 (37) | 32–56 (37.5) |
| Area (km2) (median) | 20–363 (156) | 103–673 (194.5) | 8–391 (161) | 14–740 (365) | 454–1010 (835.5) |
| I62 (mm) (median) | 50–88 (58.4) | 31–54 (43.1) | 76–133 (41.3) | 31–48 (38.4) | 34–54 (44.9) |
| SF (median) | 0.4–1.02 (0.8) | 0.4–1.02 (0.8) | 0.4–1.7 (0.8) | 0.2–1.2 (0.7) | 0.4–1 (0.8) |
| sden (median) | 2.2–5.2 (3.9) | 1–3 (1.9) | 3.2–5.5 (3.9) | 0.5–3.1 (1.7) | 2–5 (3.1) |
| MAR (mm) (median) | 1128–1954 (1480.2) | 672–1310 (937.5) | 744–1289 (815.2) | 656–1204 (851.2) | 626–1265 (791.9) |
| MAE (mm) (median) | 1280–1544 (1382.7) | 980–1341 (1094.6) | 1069–1378 (1200.5) | 1044–1342 (1165.2) | 1107–1396 (1245.9) |
| S1085 (median) | 3–23 (9.9) | 8–50 (29.6) | 4–28 (11.2) | 1–18 (6.7) | 3–19 (7.2) |
| forest (median) | −1 (0.9) | 0.5–1 (0.9) | 0.05–1 (0.3) | 0–0.83 (0.2) | 0.03–1 (0.5) |
| Number of Stations | H1 | H2 | H3 | |
|---|---|---|---|---|
| Cluster 1 | 15 | 5.11 | 4.93 | 3.71 |
| Cluster 2 | 16 | 7.38 | 2.92 | −0.05 |
| Cluster 3 | 16 | 7.59 | 6.13 | 3.62 |
| 15 | 7.55 | 5.26 | 2.74 | |
| Cluster 4 | 23 | 1.93 | 1.16 | 0.64 |
| Cluster 5 | 18 | 5.54 | 4.06 | 2.70 |
| Cluster | β0 | β1 | β2 | β3 | β4 | β5 | β6 | β7 | β8 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.29 | 0.94 | 1.53 | 0 | 0.75 | 0 | −2.14 | −0.15 | 0 |
| 2 | −9.84 | 0.29 | 7.26 | −1.80 | −0.52 | −3.93 | 3.75 | −0.80 | 0 |
| 3 | −4.62 | 0.81 | 3.19 | −1.21 | 0 | 0 | 0 | 0 | 0 |
| 4 | −0.94 | 0.72 | 0.96 | 0 | 0.52 | 0 | 0 | 0 | 0 |
| 5 | 4.10 | 0.49 | 4.42 | −0.34 | 0.74 | −0.62 | −2.65 | 0 | −0.22 |
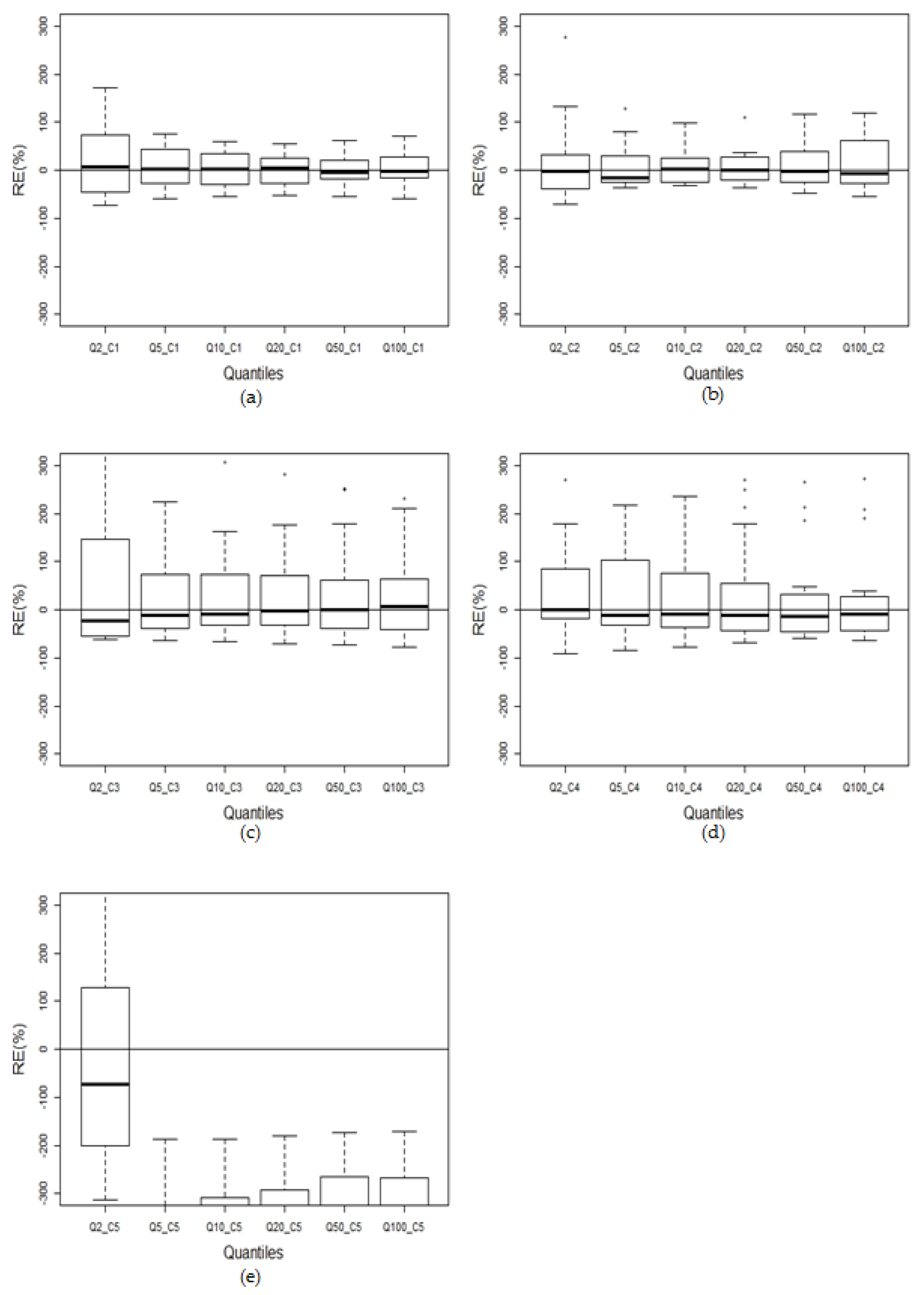
| RE | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | |
|---|---|---|---|---|---|---|
| 50% | Mean_abs | 76.25 | 56.02 | 104.51 | 64.69 | 471.67 |
| Median_abs | 48.41 | 36.56 | 54.86 | 33.76 | 183.76 | |
| Std Dev_abs | 89.91 | 70.76 | 108.34 | 76.86 | 580.00 | |
| 20% | Mean_abs | 89.88 | 36.57 | 71.11 | 82.74 | 542.75 |
| Median_abs | 43.06 | 25.92 | 42.39 | 39.87 | 424.41 | |
| Std Dev_abs | 210.38 | 29.72 | 89.01 | 113.28 | 317.63 | |
| 10% | Mean_abs | 173.56 | 27.91 | 66.26 | 90.36 | 503.40 |
| Median_abs | 31.84 | 24.90 | 35.48 | 45.83 | 422.76 | |
| Std Dev_abs | 558.54 | 25.44 | 79.88 | 130.68 | 254.32 | |
| 5% | Mean_abs | 412.96 | 27.82 | 66.62 | 94.14 | 453.41 |
| Median_abs | 28.01 | 22.86 | 32.80 | 46.33 | 403.45 | |
| Std Dev_abs | 1500.24 | 24.66 | 76.09 | 140.28 | 208.10 | |
| 2% | Mean_abs | 1427.02 | 34.25 | 71.15 | 96.05 | 403.47 |
| Median_abs | 21.34 | 26.55 | 46.46 | 47.05 | 380.24 | |
| Std Dev_abs | 5427.65 | 30.44 | 82.16 | 145.37 | 170.96 | |
| 1% | Mean_abs | 3637.99 | 44.37 | 78.85 | 96.41 | 376.95 |
| Median_abs | 21.17 | 30.53 | 42.31 | 40.13 | 342.35 | |
| Std Dev_abs | 13984.54 | 35.89 | 94.50 | 146.08 | 154.74 | |
| Overall mean | 969.61 | 37.82 | 76.42 | 87.40 | 458.61 | |
| Overall median | 33.56 | 26.16 | 42.92 | 43.07 | 387.51 | |
| Overall Std Dev | 6121.12 | 39.71 | 87.63 | 125.93 | 313.49 | |
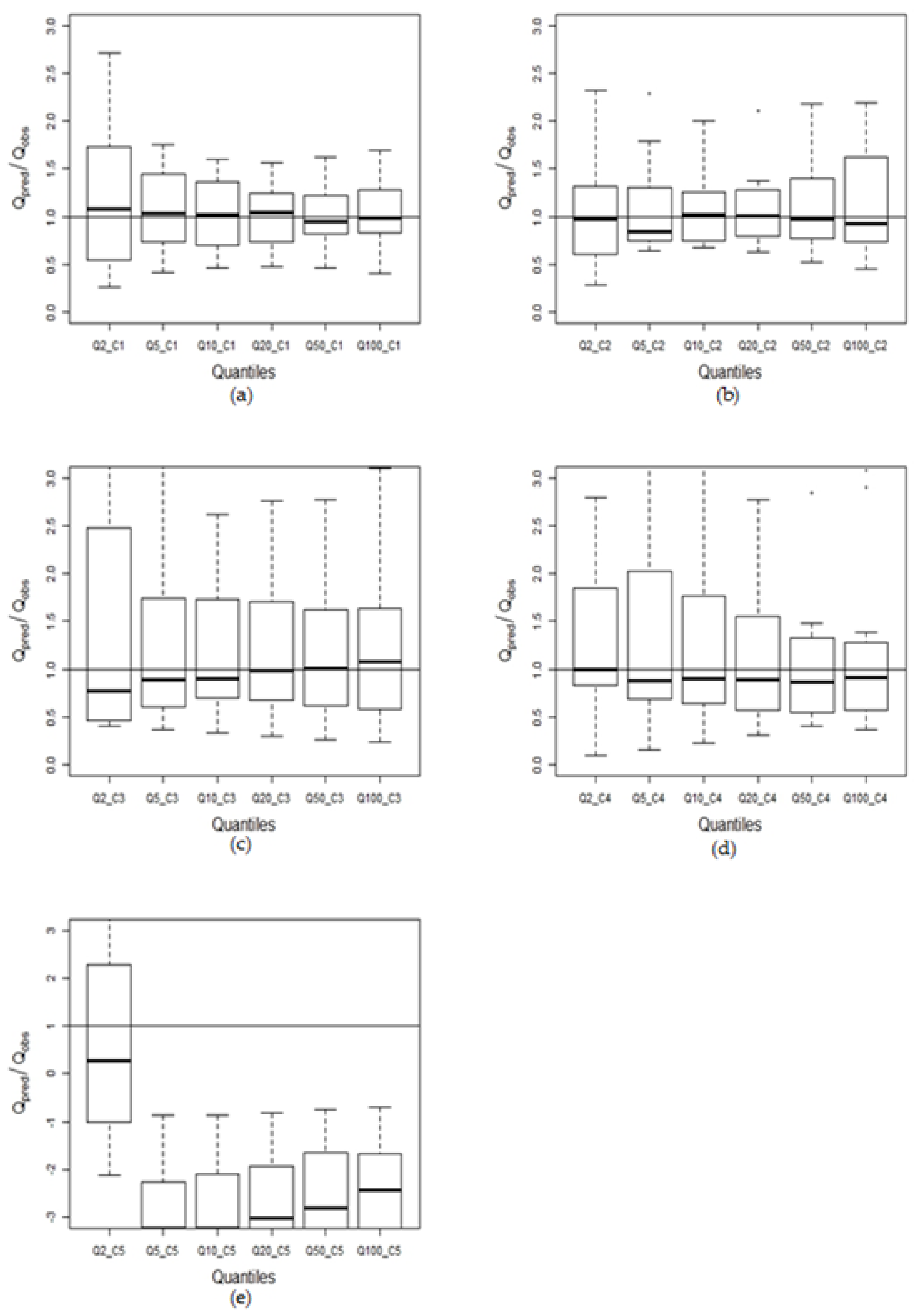
| Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | ||
|---|---|---|---|---|---|---|
| 50% | Mean_abs | 1.38 | 1.21 | 1.52 | 1.35 | 4.68 |
| Median_abs | 1.08 | 0.97 | 0.78 | 1.00 | 1.85 | |
| Std Dev_abs | 1.13 | 0.89 | 1.43 | 0.95 | 6.10 | |
| 20% | Mean_abs | 1.60 | 1.09 | 1.33 | 1.44 | 4.43 |
| Median_abs | 1.03 | 0.85 | 0.89 | 0.88 | 3.24 | |
| Std Dev_abs | 2.21 | 0.47 | 1.11 | 1.34 | 3.18 | |
| 10% | Mean_abs | 2.47 | 1.07 | 1.30 | 1.49 | 4.03 |
| Median_abs | 1.02 | 1.02 | 0.91 | 0.90 | 3.23 | |
| Std Dev_abs | 5.66 | 0.38 | 1.00 | 1.52 | 2.54 | |
| 5% | Mean_abs | 4.88 | 1.07 | 1.31 | 1.52 | 3.53 |
| Median_abs | 1.04 | 1.01 | 0.98 | 0.89 | 3.03 | |
| Std Dev_abs | 15.07 | 0.37 | 0.98 | 1.62 | 2.08 | |
| 2% | Mean_abs | 15.02 | 1.10 | 1.36 | 1.54 | 3.03 |
| Median_abs | 0.95 | 0.98 | 1.01 | 0.87 | 2.80 | |
| Std Dev_abs | 54.35 | 0.45 | 1.04 | 1.67 | 1.71 | |
| 1% | Mean_abs | 37.11 | 1.15 | 1.42 | 1.54 | 2.77 |
| Median_abs | 0.99 | 0.93 | 1.08 | 0.91 | 2.42 | |
| Std Dev_abs | 139.92 | 0.56 | 1.17 | 1.67 | 1.55 | |
| Overall mean | 10.41 | 1.12 | 1.37 | 1.48 | 3.75 | |
| Overall median | 1.00 | 0.96 | 0.96 | 0.94 | 2.88 | |
| Overall Std Dev | 61.26 | 0.54 | 1.10 | 1.46 | 3.25 | |
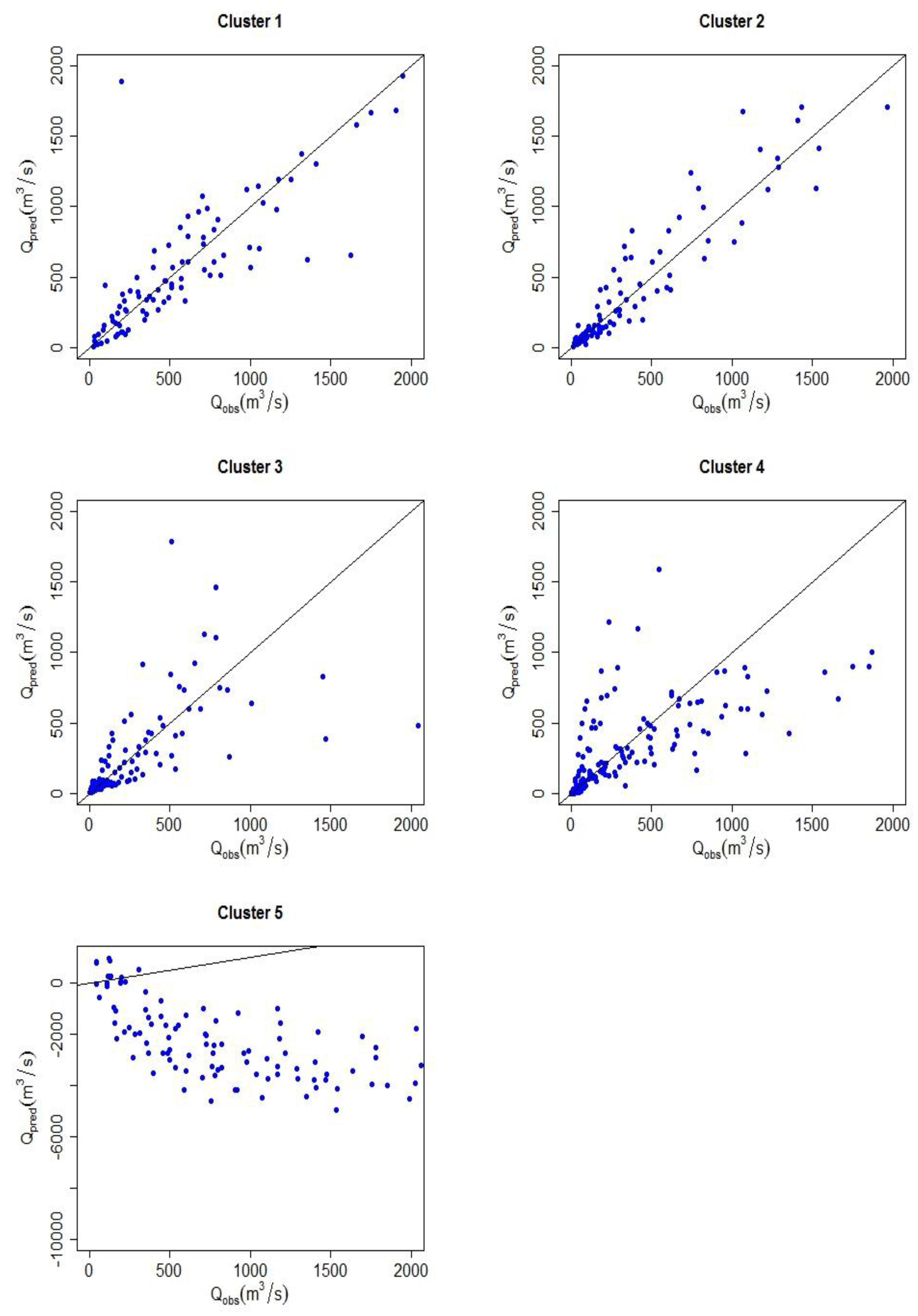
| MSE | RMSE | BIAS | RBIAS | RRMSE | RMSNE | REr | med_Qpred/Qobs | |
|---|---|---|---|---|---|---|---|---|
| Cluster 1 | 34034166.24 | 5833.88 | 1480.61 | 388.4 | 2.34 | 15.07 | 28.01 | 1.04 |
| Cluster 2 | 25309.52 | 159.09 | 5.54 | 7.30 | 0.01 | 0.37 | 22.86 | 1.01 |
| Cluster 3 | 58766.74 | 242.42 | 11.39 | 30.91 | 0.04 | 0.99 | 32.79 | 0.98 |
| Cluster 4 | 91284.23 | 302.13 | −47.02 | 51.92 | 0.12 | 1.66 | 45.54 | 0.89 |
| Cluster 5 | 17065693.55 | 4131.06 | −4056.77 | −453.41 | 3.61 | 4.96 | 403.44 | −3.03 |
| AEPs | ARR RFFA Model Absolute RE (%) | PCR_KNN15 Absolute RE (%) | PCR_KNN25 Absolute RE (%) | Cluster 2 Absolute RE (%) |
|---|---|---|---|---|
| 50% | 63.07 | 42.7 | 42.70 | 36.56 |
| 20% | 57.25 | 51.25 | 43.64 | 25.92 |
| 10% | 57.48 | 55.39 | 48.77 | 24.9 |
| 5% | 58.85 | 53.41 | 52.62 | 22.86 |
| 2% | 60.39 | 58.87 | 58.25 | 26.55 |
| 1% | 64.06 | 68.67 | 59.66 | 30.53 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, A.S.; Rahman, A. Application of Principal Component Analysis and Cluster Analysis in Regional Flood Frequency Analysis: A Case Study in New South Wales, Australia. Water 2020, 12, 781. https://doi.org/10.3390/w12030781
Rahman AS, Rahman A. Application of Principal Component Analysis and Cluster Analysis in Regional Flood Frequency Analysis: A Case Study in New South Wales, Australia. Water. 2020; 12(3):781. https://doi.org/10.3390/w12030781
Chicago/Turabian StyleRahman, Ayesha S, and Ataur Rahman. 2020. "Application of Principal Component Analysis and Cluster Analysis in Regional Flood Frequency Analysis: A Case Study in New South Wales, Australia" Water 12, no. 3: 781. https://doi.org/10.3390/w12030781
APA StyleRahman, A. S., & Rahman, A. (2020). Application of Principal Component Analysis and Cluster Analysis in Regional Flood Frequency Analysis: A Case Study in New South Wales, Australia. Water, 12(3), 781. https://doi.org/10.3390/w12030781





