Forecasting of Landslides Using Rainfall Severity and Soil Wetness: A Probabilistic Approach for Darjeeling Himalayas
Abstract
1. Introduction
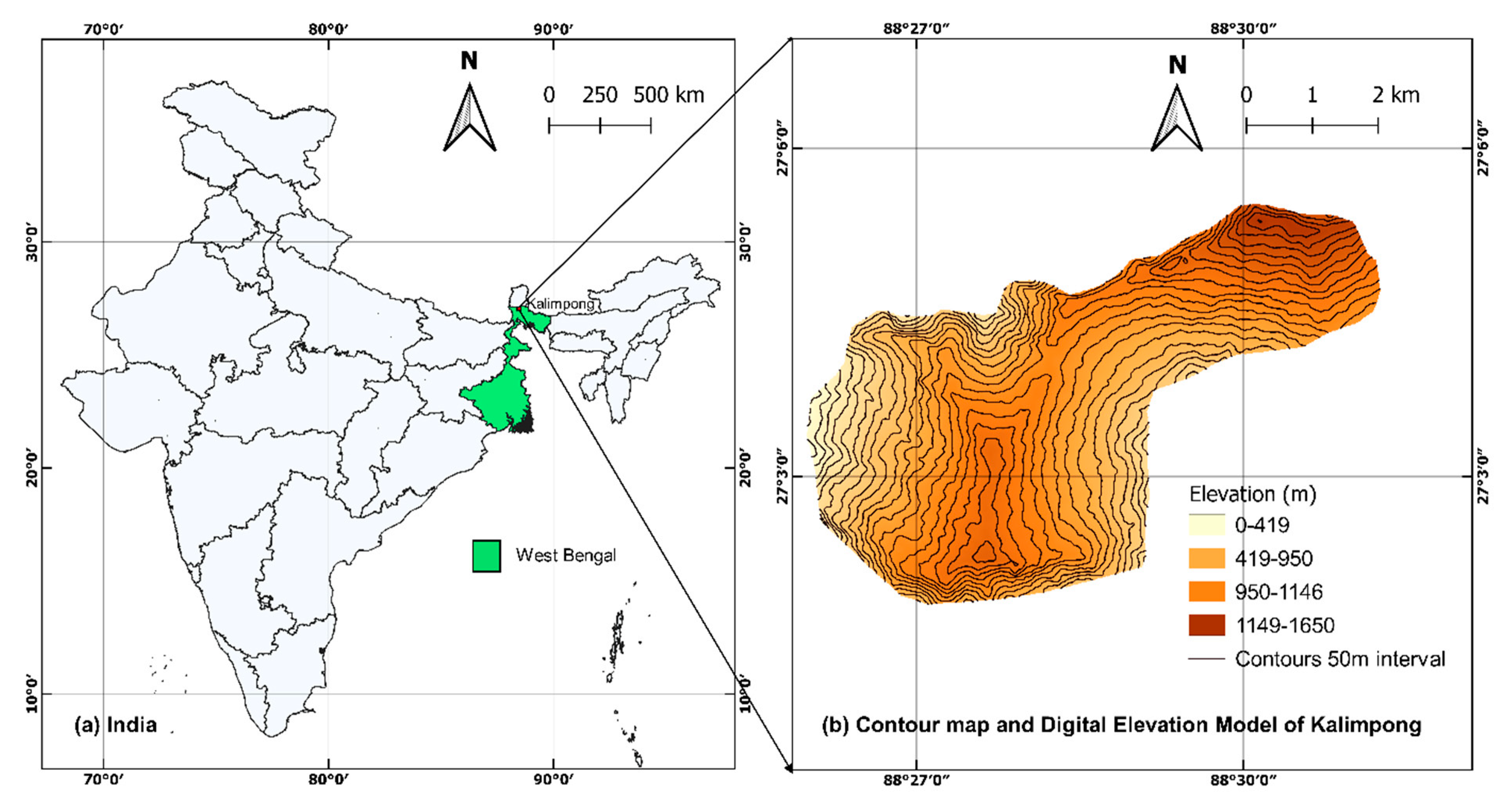
2. Study Area
2.1. Geology
2.2. Geohydrology
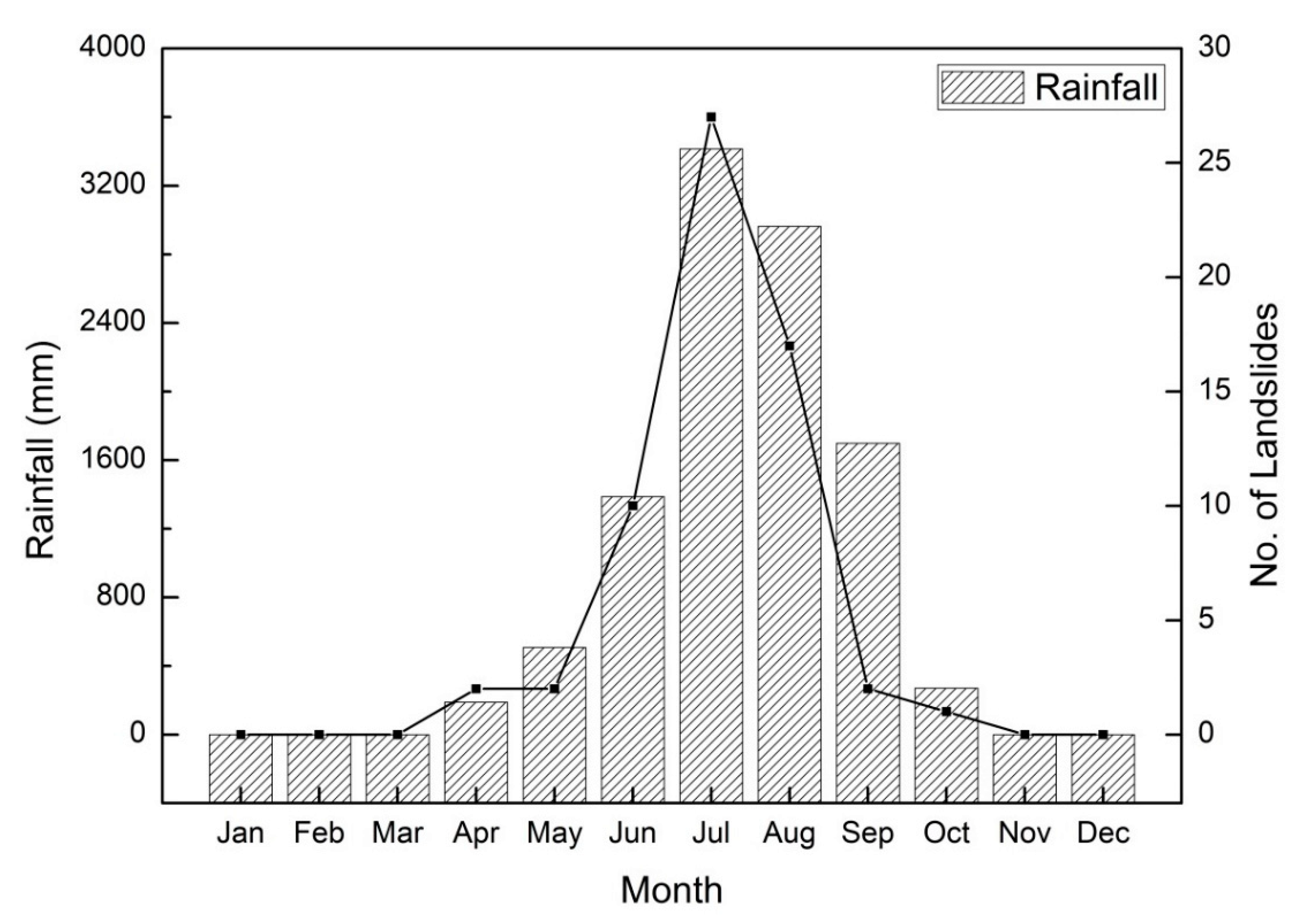
3. Landslides in Kalimpong
3.1. Rainfall
3.2. Drainage System
3.3. Data for the Hydrological Simulation
4. Methodology of Study
4.1. Simulation of Soil Moisture
- (a)
- Penman–Monteith equation [57] for evapotranspiration;
- (b)
- Saint–Venant equations, two dimensional diffusion wave approximation [57] for overland flow;
- (c)
- Saint–Venant equations, one dimensional diffusion wave approximation [57] for channel flow;
- (d)
- Rutter equation [57] for canopy drip and interception;
- (e)
- Variably saturated flow equation (3D) [58] for subsurface flow;
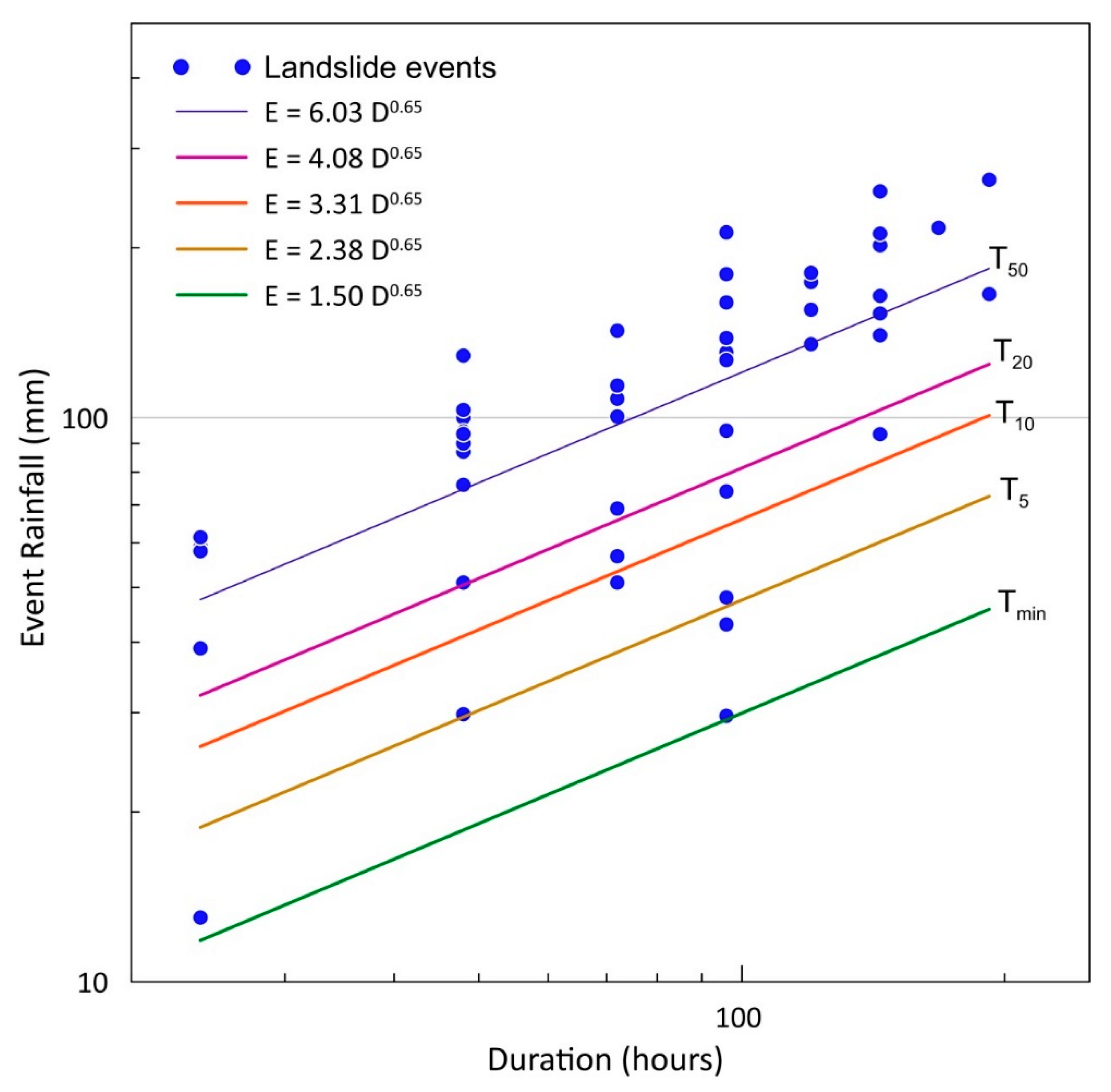
4.2. Rainfall Events and Empirical Thresholds
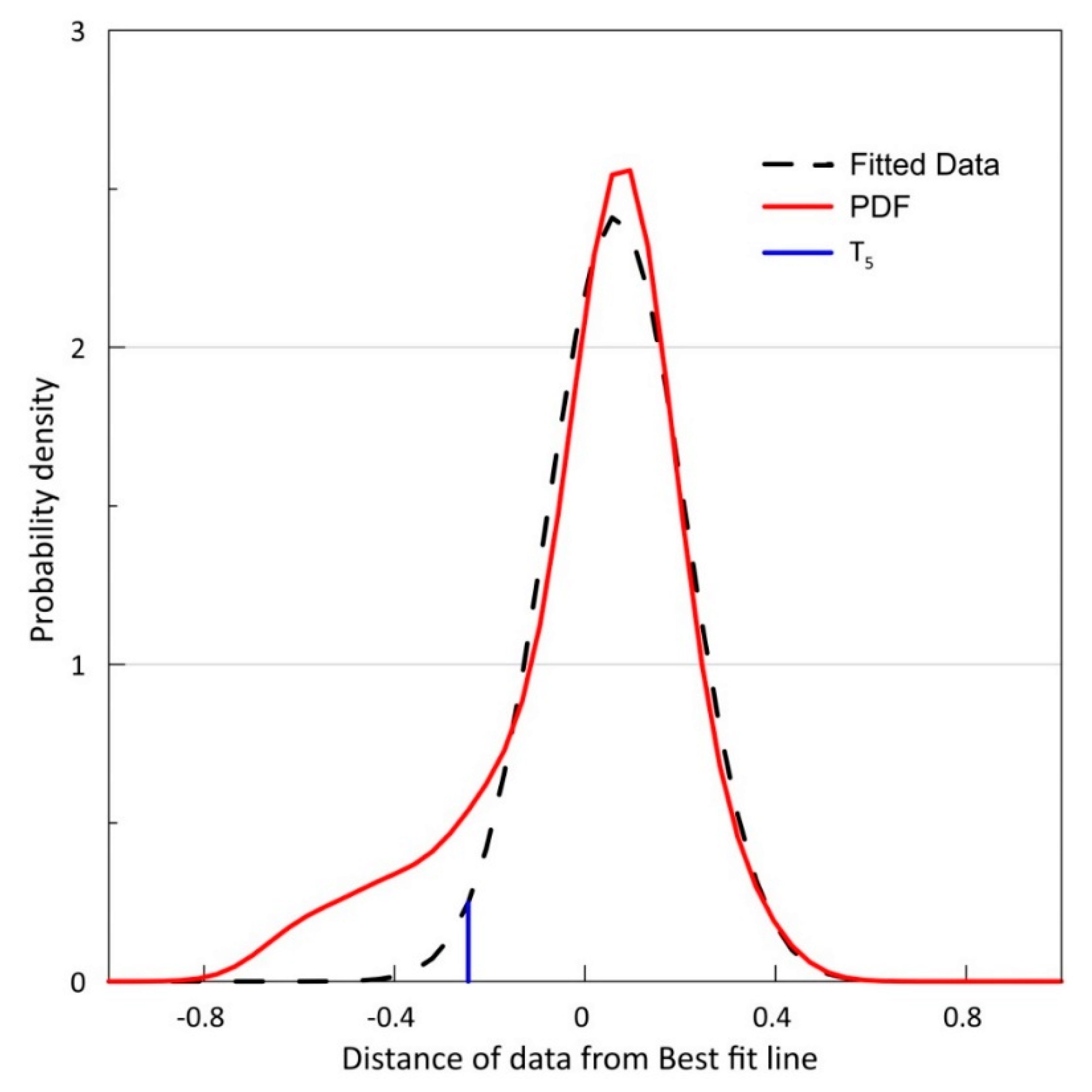
4.3. Bayes’ Theorem
- NA = The total number of landslide events (If n number of landslides occur on the same day, it is considered as one landslide event)
- NR = The total number of rainfall events during the study period
- NB,C = The number of events in each cell condition
- N(B,C|A) = The number of rainfall events that resulted in landslides while satisfying a cell condition
5. Results and Discussion
5.1. Soil Moisture Estimation
5.2. Rainfall Thresholds
5.3. Probabilistic Thresholds
- (a)
- the severity of a rainfall event exceeds 50% and the soil wetness is between 0.4 and 0.6
- (b)
- the severity of a rainfall event between 20% and 50% and the soil wetness is between 0.6 and 0.8
- (c)
- the severity of a rainfall event between 5% and 10% and the soil wetness is between 0.6 and 0.8.
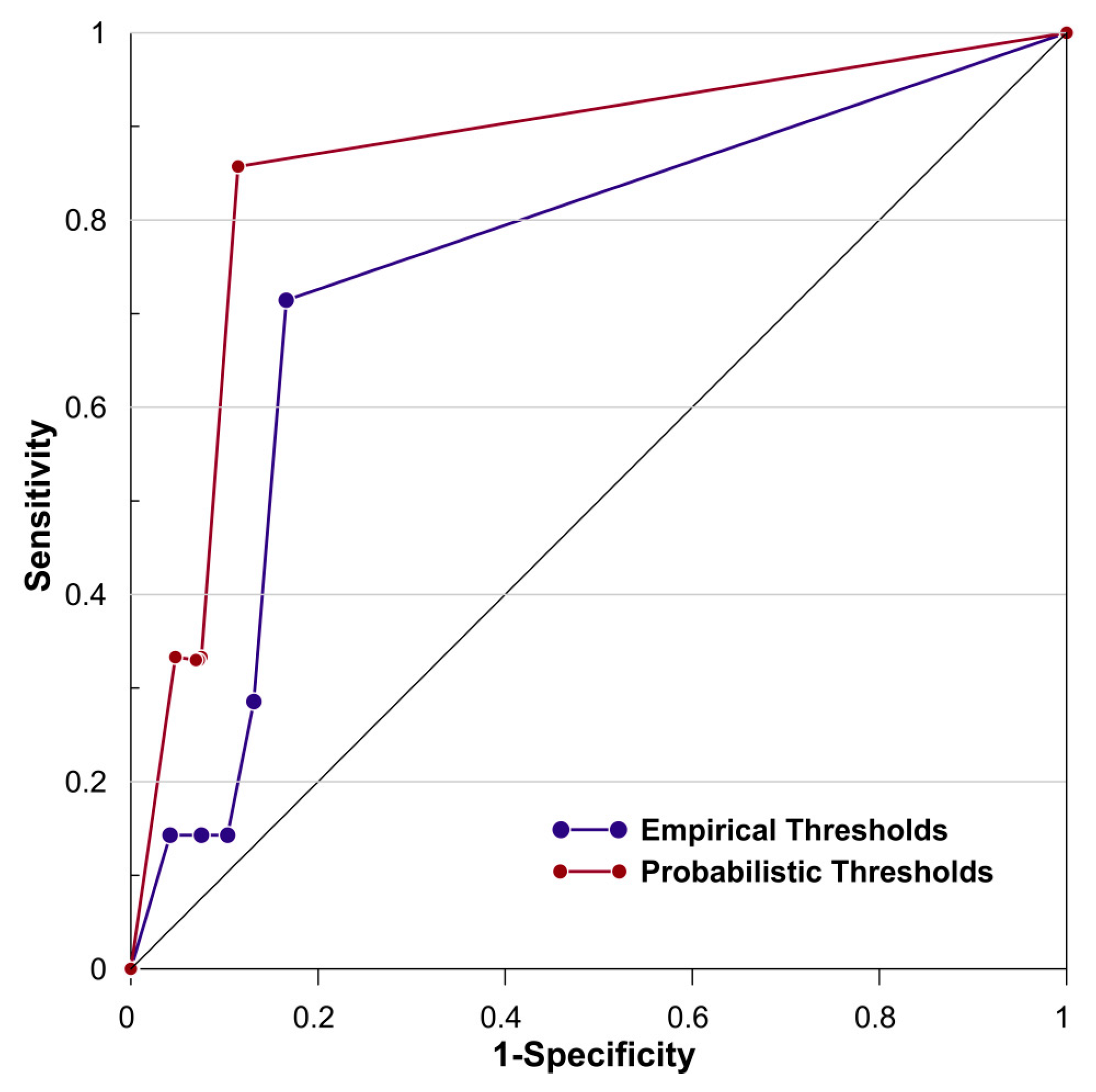
6. Validation
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Panagoulia, D.; Zarris, D.; Maggina, K. An Assessment of the Interaction Between Storm Events and Sediment Transport. In Proceedings of the 5th International Synposium on Ecohydraulics, Aguatic Habitats: Analysis & Restoration, Madrid, Spain, 12–17 September 2004. [Google Scholar]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Crozier, M.J. Deciphering the effect of climate change on landslide activity: A review. Geomorphology 2010, 124, 260–267. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, Y. Spatial and temporal analysis of a fatal landslide inventory in China from 1950 to 2016. Landslides 2018, 15, 2357–2372. [Google Scholar] [CrossRef]
- Kirschbaum, D.; Stanley, T.; Zhou, Y. Spatial and temporal analysis of a global landslide catalog. Geomorphology 2015, 249, 4–15. [Google Scholar] [CrossRef]
- Bordoni, M.; Corradini, B.; Lucchelli, L.; Valentino, R.; Bittelli, M.; Vivaldi, V.; Meisina, C. Empirical and physically based thresholds for the occurrence of shallow landslides in a prone area of northern italian apennines. Water 2019, 11, 2653. [Google Scholar] [CrossRef]
- Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Geogr. Ann. Ser. A Phys. Geogr. 1980, 62, 23–27. [Google Scholar]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Guzzetti, F. An Algorithm for the objective reconstruction of rainfall events responsible for landslides. Landslide 2014, 12, 311–320. [Google Scholar] [CrossRef]
- Abraham, M.T.; Pothuraju, D.; Satyam, N. Rainfall Thresholds for Prediction of Landslides in Idukki, India: An Empirical Approach. Water 2019, 11, 2113. [Google Scholar] [CrossRef]
- Fusco, F.; De Vita, P.; Mirus, B.B.; Baum, R.L.; Allocca, V.; Tufano, R.; Clemente, E.D.; Calcaterra, D. Physically based estimation of rainfall thresholds triggering shallow landslides in volcanic slopes of Southern Italy. Water 2019, 11, 1915. [Google Scholar] [CrossRef]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS—A Fortran Program for Transient Rainfall Infiltration and Grid-Based Regional Slope Stability Analysis, Version 2.0; Open File Report 2008–1159; US Geological Survey: Reston, VA, USA, 2008; 75p.
- Dikshit, A.; Satyam, N.; Pradhan, B. Estimation of rainfall—induced landslides using the trigrs model. Earth Syst. Environ. 2019, 3, 575–584. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, D.N. Estimation of rainfall thresholds for landslide occurrences in Kalimpong, India. Innov. Infrastruct. Solut. 2018, 3, 24. [Google Scholar] [CrossRef]
- Innes, J.L. Debris flows. Prog. Phys. Geog. 1983, 7, 469–501. [Google Scholar] [CrossRef]
- Aleotti, P. A warning system for rainfall-induced shallow failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Lagomarsino, D.; Segoni, S.; Rosi, A.; Rossi, G.; Battistini, A.; Catani, F.; Casagli, N. Quantitative comparison between two different methodologies to define rainfall thresholds for landslide forecasting. Nat. Hazards Earth Syst. Sci. 2015, 15, 2413–2423. [Google Scholar] [CrossRef]
- Campbell, R.H. Debris flows originating from soil slips during rainstorms in Southern California. Q. J. Eng. Geol. 1974, 7, 339–349. [Google Scholar] [CrossRef]
- Crosta, G.B.; Frattini, P. Rainfall thresholds for soil slip and debris flow triggering. In Proceedings of the 2nd EGS Plinius Conference on Mediterranean Storms, Siena, Italy, 16–18 October 2000; pp. 463–487. [Google Scholar]
- Song, S.; Wang, W. Impacts of antecedent soil moisture on the rainfall-runoff transformation process based on high-resolution observations in soil tank experiments. Water 2019, 11, 296. [Google Scholar] [CrossRef]
- Glade, T.; Crozier, M.; Smith, P. Applying probability determination to refine landslide-triggering rainfall thresholds using an empirical Antecedent Daily Rainfall Model. Pure Appl. Geophys. 2000, 157, 1059–1079. [Google Scholar] [CrossRef]
- Ponziani, F.; Pandolfo, C.; Stelluti, M.; Berni, N.; Brocca, L.; Moramarco, T. Assessment of rainfall thresholds and soil moisture modeling for operational hydrogeological risk prevention in the Umbria region (central Italy). Landslides 2012, 9, 229–237. [Google Scholar] [CrossRef]
- Zhao, B.; Dai, Q.; Han, D.; Dai, H.; Mao, J.; Zhuo, L.; Rong, G. Estimation of soil moisture using modified antecedent precipitation index with application in landslide predictions. Landslides 2019, 16, 2381–2393. [Google Scholar] [CrossRef]
- Segoni, S.; Rosi, A.; Lagomarsino, D.; Fanti, R.; Casagli, N. Brief communication: Using averaged soil moisture estimates to improve the performances of a regional-scale landslide early warning system. Nat. Hazards Earth Syst. Sci. 2018, 18, 807–812. [Google Scholar] [CrossRef]
- Segoni, S.; Rosi, A.; Fanti, R.; Gallucci, A.; Monni, A.; Casagli, N. A regional-scale landslide warning system based on 20 years of operational experience. Water 2018, 10, 1297. [Google Scholar] [CrossRef]
- Zhao, B.; Dai, Q.; Han, D.; Dai, H.; Mao, J.; Zhuo, L. Probabilistic thresholds for landslides warning by integrating soil moisture conditions with rainfall thresholds. J. Hydrol. 2019, 574, 276–287. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, D.N.; Towhata, I. Early warning system using tilt sensors in Chibo, Kalimpong, Darjeeling Himalayas, India. Nat. Hazards 2018, 94, 727–741. [Google Scholar] [CrossRef]
- Raffelli, G.; Previati, M.; Canone, D.; Gisolo, D.; Bevilacqua, I.; Capello, G.; Biddoccu, M.; Cavallo, E.; Deiana, R.; Cassiani, G.; et al. Local-and plot-scale measurements of soil moisture: Time and spatially resolved field techniques in plain, hill and mountain sites. Water 2017, 9, 706. [Google Scholar] [CrossRef]
- Panagoulia, D.; Dimou, G. Sensitivities of groundwater-streamflow interaction to global climate change. Hydrol. Sci. J. 1996, 41, 781–796. [Google Scholar] [CrossRef]
- Parkin, G. SHETRAN Water Flow Component, Equations and Algorithms. Ph.D. Thesis, Newcastle University, Newcastle upon Tyne, UK, 1995. [Google Scholar]
- Birkinshaw, S.J.; Ewen, J. Nitrogen transformation component for SHETRAN catchment nitrate transport modelling. J. Hydrol. 2000, 230, 1–17. [Google Scholar] [CrossRef]
- Bathurst, J.C.; Moretti, G.; Burton, A.; Bathurst, J.C.; Moretti, G.; Scenario, A.B. Scenario modelling of basin-scale, shallow landslide sediment yield, Valsassina, Italian Southern Alps. Nat. Hazards Earth Syst. Sci. 2005, 5, 189–202. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- De Hipt, F.O.; Diekkrüger, B.; Steup, G.; Yira, Y.; Hoffmann, T.; Rode, M. Applying SHETRAN in a tropical west African catchment (Dano, Burkina Faso)-calibration, validation, uncertainty assessment. Water 2017, 9, 101. [Google Scholar] [CrossRef]
- Teja, T.S.; Dikshit, A.; Satyam, N. Determination of Rainfall Thresholds for Landslide Prediction Using an Algorithm-Based Approach: Case Study in the Darjeeling Himalayas, India. Geosciences 2019, 9, 302. [Google Scholar] [CrossRef]
- Dikshit, A.; Sarkar, R.; Satyam, N. Probabilistic approach toward Darjeeling Himalayas landslides-A case study. Cogent Eng. 2018, 5, 1–11. [Google Scholar] [CrossRef]
- Kalimpong District Webpage. Available online: https://kalimpongdistrict.in/ (accessed on 3 December 2019).
- Chatterjee, R. Landslide Hazard Zonation Mapping of Kalimpong; VDM Verlag Dr. Müller: Saarbrücken, Germany, 2010. [Google Scholar]
- Chakraborty, I.; Ghosh, S.; Bhattacharya, D.; Bora, A. Earthquake Induced Landslides in the Sikkim-Darjeeling Himalayas—An Aftermath of the 18th September 2011 Sikkim Earthquake. Available online: http://www.sikenvis.nic.in/Database/Sikkimearthquake_4089.aspx (accessed on 28 July 2019).
- Mukherjee, A.; Mitra, A. Geotechnical Study of Mass Movements Along the Kalimpong Approach Road in the Eastern Himalayas. Indian J. Geol. 2001, 73, 271–279. [Google Scholar]
- Save The Hills Blog. Available online: http://savethehills.blogspot.com/ (accessed on 3 December 2019).
- CartoDEM. Available online: https://bhuvan-app3.nrsc.gov.in/data/download/index.php (accessed on 20 August 2019).
- Dikshit, A.; Satyam, N. Rainfall Thresholds for the prediction of Landslides using Empirical Methods in Kalimpong, Darjeeling, India. In Proceedings of the JTC1 Workshop on Advances in Landslide Understanding, Barcelona, Spain, 24–26 May 2017. [Google Scholar]
- McGeary, D.; Charles, C.P.; Diane, H.C. Physical Geology: Earth Revealed; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Kim, S.W.; Chun, K.W.; Otsuki, K.; Shinohara, Y.; Kim, M.I.l.; Kim, M.S.; Lee, D.K.; Seo, J.I.l.; Choi, B.K. Heavy rain types for triggering shallow landslides in South Korea. J. Fac. Agric. Kyushu Univ. 2015, 60, 243–249. [Google Scholar]
- Zhang, R.; Santos, C.A.G.; Moreira, M.; Freire, P.K.M.M.; Corte-Real, J. Automatic calibration of the SHETRAN hydrological modelling system using MSCE. Water Resour. Manag. 2013, 27, 4053–4068. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, S.; Bao, H.; Zhao, X. Characteristics and influencing factors of rainfall-induced landslide and debris flow hazards in Shaanxi Province, China. Nat. Hazards Earth Syst. Sci. 2019, 19, 93–105. [Google Scholar] [CrossRef]
- Marc, O.; Stumpf, A.; Malet, J.P.; Gosset, M.; Uchida, T.; Chiang, S.H. Initial insights from a global database of rainfall-induced landslide inventories: The weak influence of slope and strong influence of total storm rainfall. Earth Surf. Dyn. 2018, 6, 903–922. [Google Scholar] [CrossRef]
- De Vita, P.; Reichenbach, P.; Bathurst, J.C.; Borga, M.; Crozier, G.M.; Glade, T.; Guzzetti, F.; Hansen, A.; Wasowski, J. Rainfall-triggered landslides: A reference list. Environ. Geol. 1998, 35, 219–233. [Google Scholar] [CrossRef]
- Lazzari, M.; Piccarreta, M. Landslide disasters triggered by extreme rainfall events: The case of montescaglioso (Basilicata, Southern Italy). Geosciences 2018, 8, 377. [Google Scholar] [CrossRef]
- CartoDEM: A National Digital Elevation Model from Cartosat-1 Stereo Data. Available online: https://www.nrsc.gov.in/ (accessed on 7 January 2020).
- Copernicus Climate Change Service. Available online: https://cds.climate.copernicus.eu/ (accessed on 30 December 2019).
- MERRA Date. Available online: http://www.cgd.ucar.edu/cas/catalog/reanalysis/merra/index.html (accessed on 30 December 2019).
- Birkinshaw, S.J. Physically-based modelling of double-peak discharge responses at Slapton Wood catchment. Hydrol. Process. 2008, 22, 1419–1430. [Google Scholar] [CrossRef]
- Norouzi Banis, Y.; Bathurst, J.C.; Walling, D.E. Use of caesium-137 data to evaluate SHETRAN simulated long-term erosion patterns in arable lands. Hydrol. Process. 2004, 18, 1795–1809. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System—Systeme Hydrologique Europeen “SHE”, 2: Structure of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Parkin, G. A Three-Dimensional Variably-Saturated Subsurface Modelling System for River Basins. Ph.D. Thesis, Newcastle University, Newcastle upon Tyne, UK, 1996. [Google Scholar]
- Nash, J.E.; Sutcliffe, I. V River Flow Forecasting Through Conceptual Models Part I—A Discussion of Priciples. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Garambois, P.A.; Roux, H.; Larnier, K.; Labat, D.; Dartus, D. Caractérisation de comportements de bassins versants et sélection de pluies pour la calibration de modèles hydrologiques dans le cas de crues éclair: Bassins de l’est des Pyrénées. Hydrol. Sci. J. 2015, 60, 424–447. [Google Scholar] [CrossRef]
- Berti, M.; Martina, M.L.V.; Franceschini, S.; Pignone, S.; Simoni, A.; Pizziolo, M. Probabilistic rainfall thresholds for landslide occurrence using a Bayesian approach. J. Geophys. Res. Earth Surf. 2012, 117, 1–20. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Luciani, S.; Vennari, C.; Guzzetti, F. Lithological and seasonal control on rainfall thresholds for the possible initiation of landslides in central Italy. Geomorphology 2012, 139–140, 79–90. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Luciani, S.; Valigi, D.; Guzzetti, F. Rainfall thresholds for the possible occurrence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 447–458. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Lyons, L. Bayes and Frequentism: A particle physicist’s perspective. Contemp. Phys. 2013, 54, 1–16. [Google Scholar] [CrossRef][Green Version]
- Ippisch, O.; Vogel, H.J.; Bastian, P. Validity limits for the van Genuchten-Mualem model and implications for parameter estimation and numerical simulation. Adv. Water Resour. 2006, 29, 1780–1789. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; Genuchten, M.T. Van ROSETTA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Jensen, D.; Hargreaves, G.; Temesgen, B.; Allen, R. Com-putation of ETo under nonideal conditions. J. Irrig. Drain. Eng. 1997, 123, 394–400. [Google Scholar] [CrossRef]
- Ho-Hagemann, H.T.M.; Hagemann, S.; Rockel, B. On the role of soil moisture in the generation of heavy rainfall during the Oder flood event in July 1997. Tellus Ser. A Dyn. Meteorol. Oceanogr. 2015, 6, 28611. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, N. Probabilistic rainfall thresholds in Chibo, India: Estimation and validation using monitoring system. J. Mt. Sci. 2019, 16, 870–883. [Google Scholar] [CrossRef]


| Month | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
| June | 316.8 | 337.0 | 354.9 | 248.0 | 396.4 | 568.0 | 327.2 | 153.7 |
| July | 665.4 | 678.0 | 433.1 | 424.6 | 371.2 | 534.4 | 869.8 | 811.5 |
| August | 425.3 | 525.6 | 250.8 | 401.0 | 571.8 | 242.3 | 262.6 | 432.1 |
| September | 268.2 | 384.1 | 467.9 | 113.0 | 265.4 | 331.2 | 366.8 | 287.6 |
| Parameters | Calibrated Value |
|---|---|
| Canopy storage | 5 mm |
| AE/PE at field capacity | 1 |
| Maximum Rooting Depth | 1.6 m |
| Saturated water content | 0.40 |
| Strickler overland flow coefficient | 0.50 m1/3s−1 |
| Saturated hydraulic conductivity | 1.14 m/day |
| Leaf Area Index | 1 |
| Residual water content | 0.08 |
| vanGenuchten-n | 1.17 |
| vanGenuchten-alpha | 0.03 cm−1 |
| Exceedance Probability (%) | α | γ |
|---|---|---|
| 50 | 6.03 | 0.65 |
| 20 | 4.08 | 0.65 |
| 10 | 3.31 | 0.65 |
| 5 | 2.38 | 0.65 |
| min | 1.50 | 0.65 |
| Statistical Attributes | TP | FP | FN | TN | Sensitivity = TP/(TP + FN) | Specificity = TN/(FP + TN) | False Positive Rate = FP/(FP + TN) | Likelihood Ratio = Sensitivity/(1 − Specificity) | |
|---|---|---|---|---|---|---|---|---|---|
| Empirical Thresholds | Tmin | 5 | 67 | 2 | 291 | 0.7143 | 0.8128 | 0.1872 | 3.8166 |
| T5 | 2 | 47 | 5 | 311 | 0.2857 | 0.8687 | 0.1313 | 2.1763 | |
| T10 | 1 | 37 | 6 | 321 | 0.1429 | 0.8966 | 0.1034 | 1.3822 | |
| T20 | 1 | 27 | 6 | 331 | 0.1429 | 0.9246 | 0.0754 | 1.8942 | |
| T50 | 1 | 15 | 6 | 343 | 0.1429 | 0.9581 | 0.0419 | 3.4095 | |
| Probabilistic Thresholds | P > 0.1 | 6 | 41 | 1 | 317 | 0.8571 | 0.8855 | 0.1145 | 7.4843 |
| P > 0.2 | 2 | 27 | 5 | 331 | 0.2857 | 0.9246 | 0.0754 | 3.7884 | |
| P > 0.4 | 2 | 26 | 5 | 332 | 0.2857 | 0.9274 | 0.0726 | 3.9341 | |
| P > 0.6 | 2 | 25 | 5 | 333 | 0.2857 | 0.9302 | 0.0698 | 4.0914 | |
| P > 0.8 | 2 | 17 | 5 | 341 | 0.2857 | 0.9525 | 0.0475 | 6.0168 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abraham, M.T.; Satyam, N.; Pradhan, B.; Alamri, A.M. Forecasting of Landslides Using Rainfall Severity and Soil Wetness: A Probabilistic Approach for Darjeeling Himalayas. Water 2020, 12, 804. https://doi.org/10.3390/w12030804
Abraham MT, Satyam N, Pradhan B, Alamri AM. Forecasting of Landslides Using Rainfall Severity and Soil Wetness: A Probabilistic Approach for Darjeeling Himalayas. Water. 2020; 12(3):804. https://doi.org/10.3390/w12030804
Chicago/Turabian StyleAbraham, Minu Treesa, Neelima Satyam, Biswajeet Pradhan, and Abdullah M. Alamri. 2020. "Forecasting of Landslides Using Rainfall Severity and Soil Wetness: A Probabilistic Approach for Darjeeling Himalayas" Water 12, no. 3: 804. https://doi.org/10.3390/w12030804
APA StyleAbraham, M. T., Satyam, N., Pradhan, B., & Alamri, A. M. (2020). Forecasting of Landslides Using Rainfall Severity and Soil Wetness: A Probabilistic Approach for Darjeeling Himalayas. Water, 12(3), 804. https://doi.org/10.3390/w12030804






