Hydrodynamic-Based Numerical Assessment of Flood Risk of Tamuín City, Mexico, by Tampaón River: A Forecast Considering Climate Change
Abstract
1. Introduction
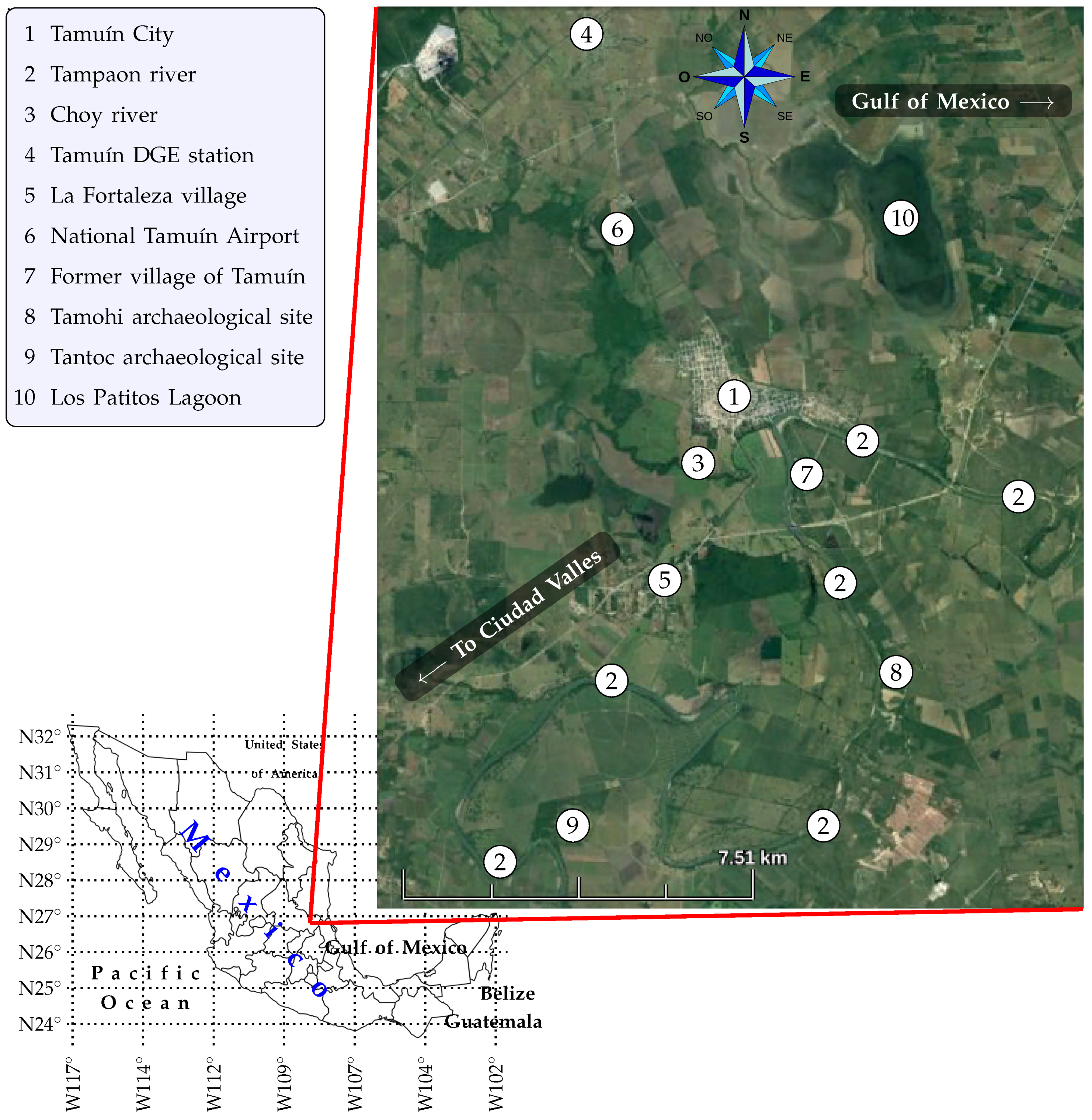
2. Region Under Study
2.1. Location
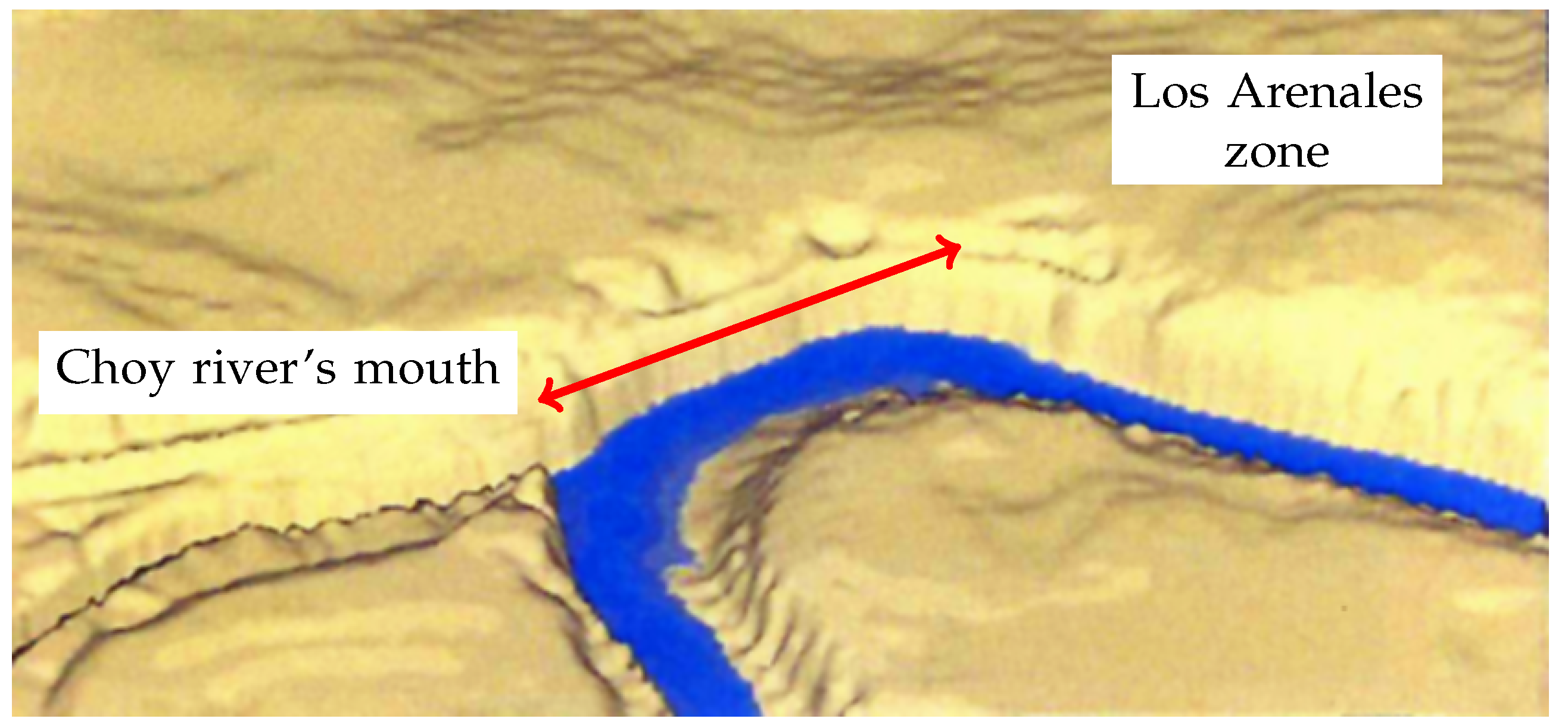
2.2. Evolution of the Region
2.3. Hydrodynamics
2.4. Climate
3. Methodology
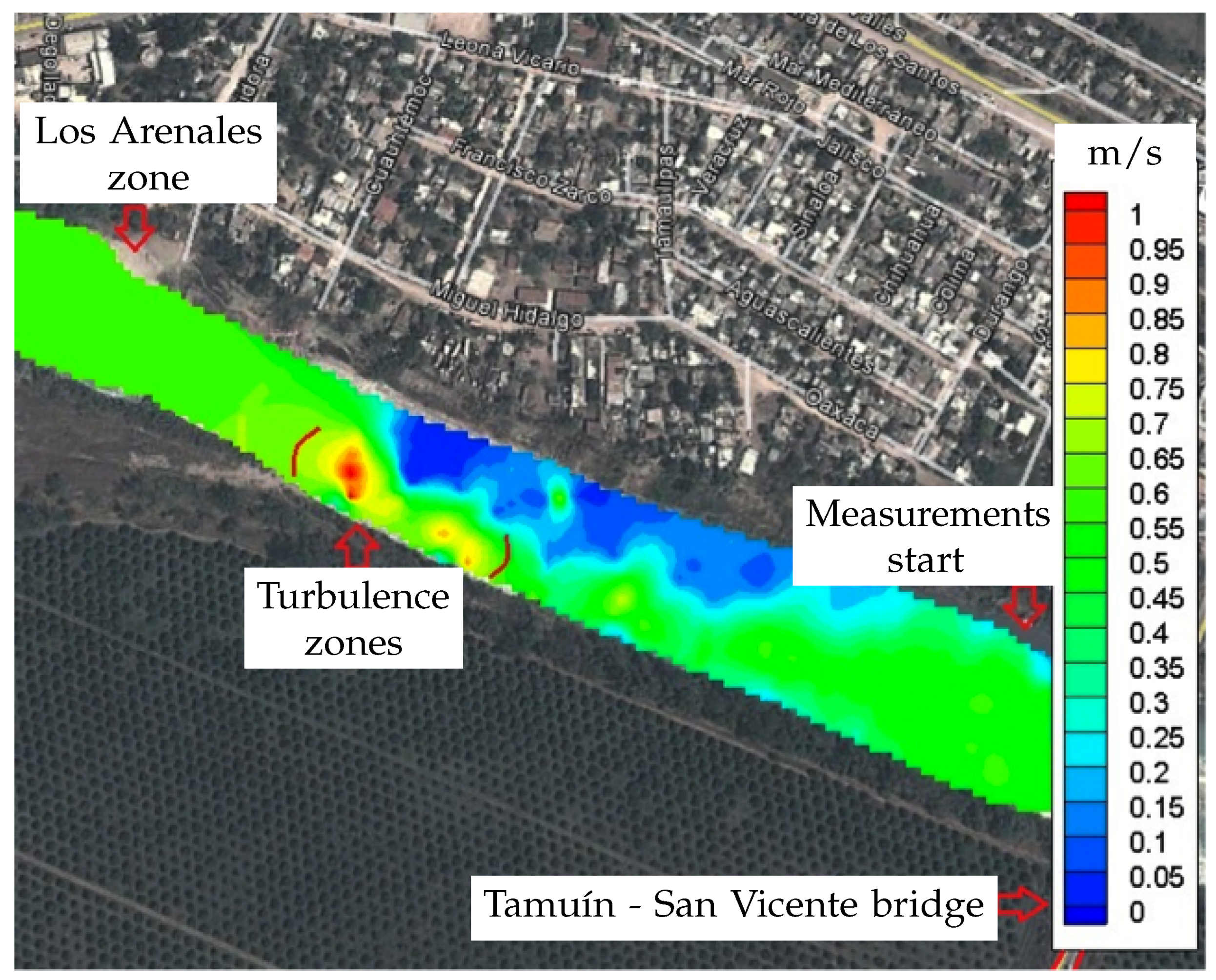
3.1. Field Measurement Investigation
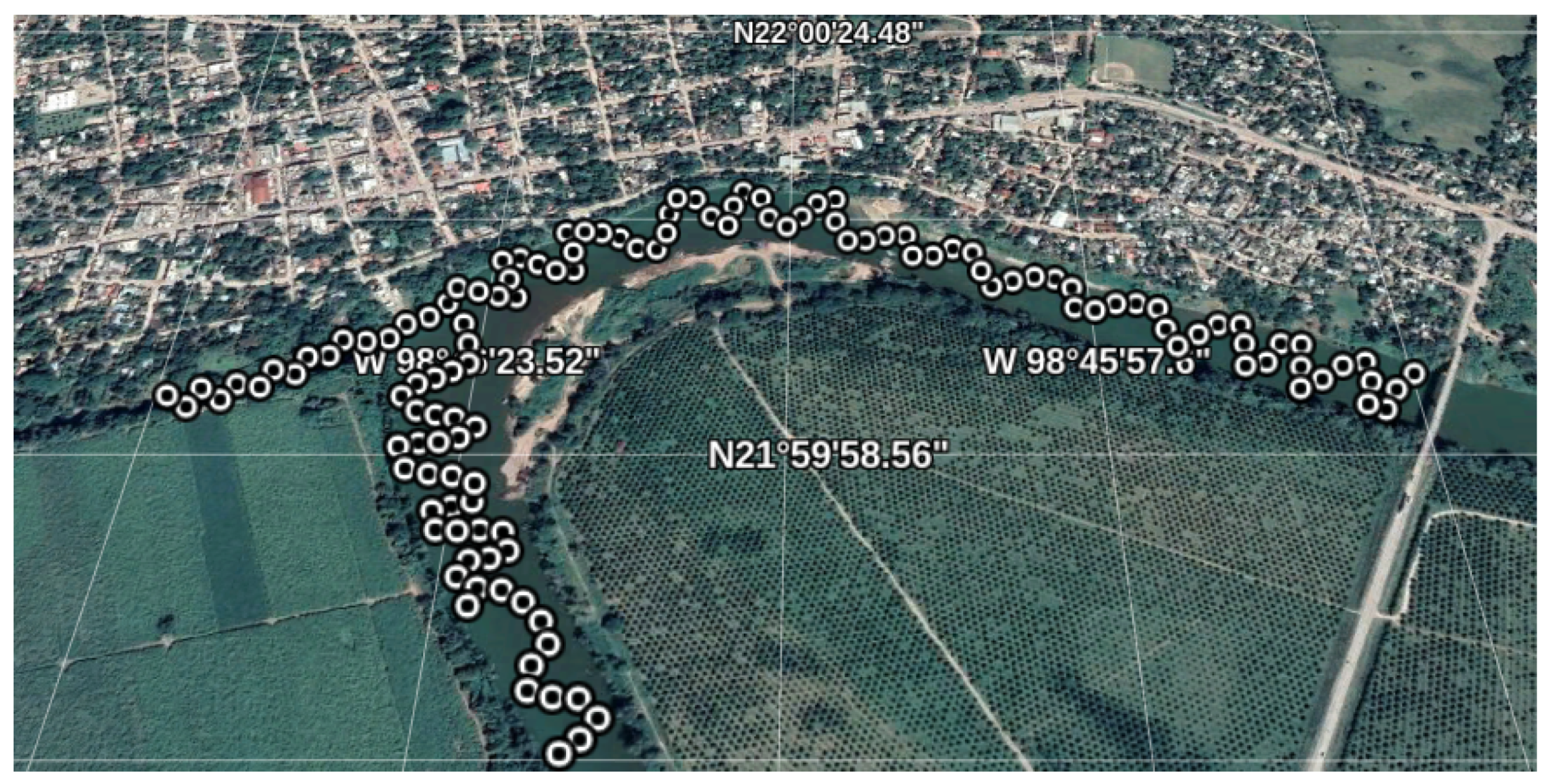
3.1.1. Transects
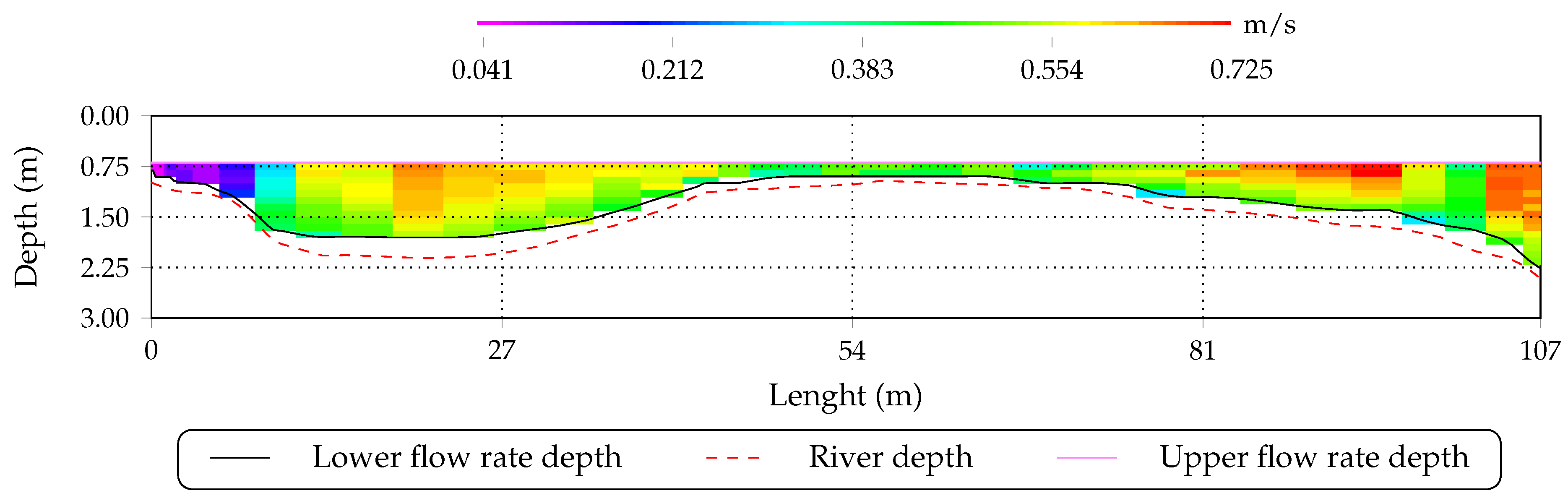
3.1.2. Bathymetry
3.1.3. Flow Velocity
3.1.4. Flow Rates
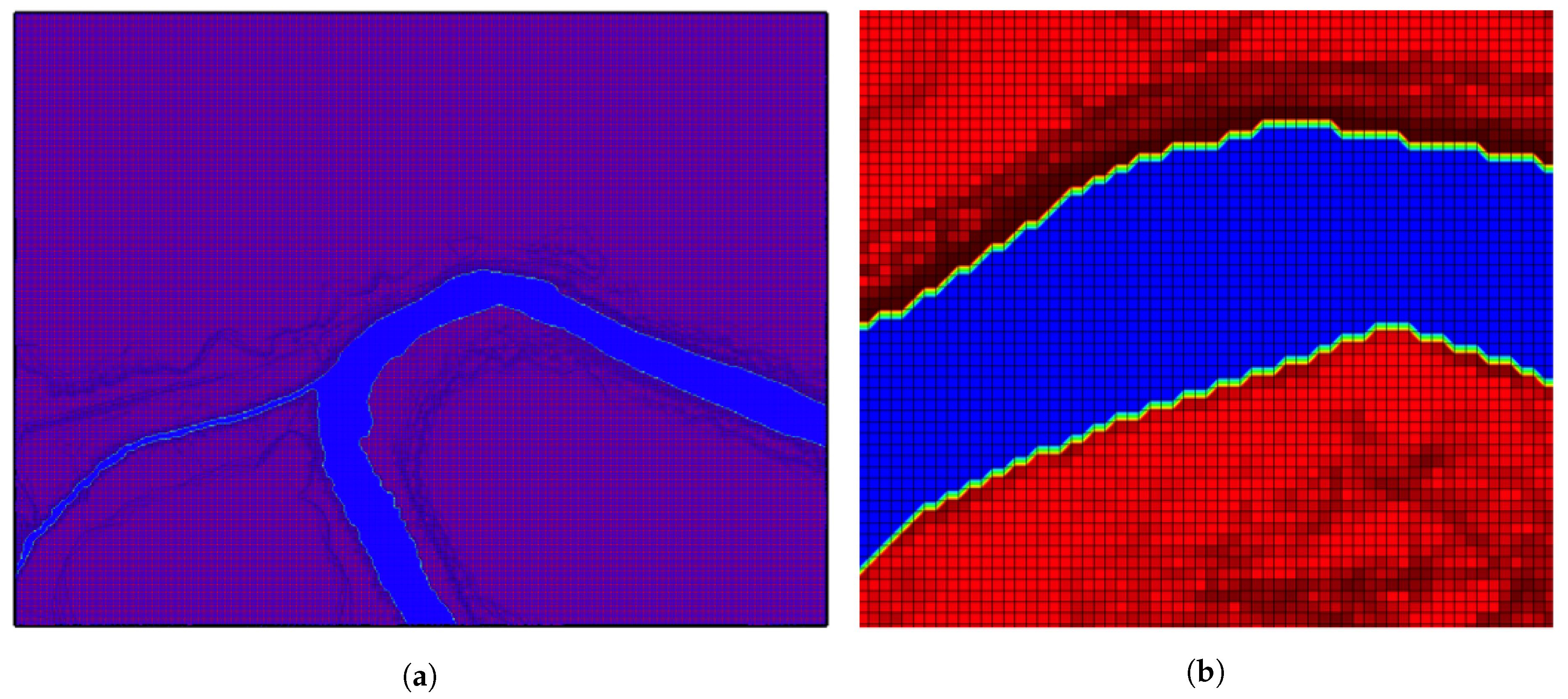
3.2. Boundary Conditions
3.3. Calibration Approach
3.4. Future Precipitations in the Zone Under Study
3.5. Numerical Experiments
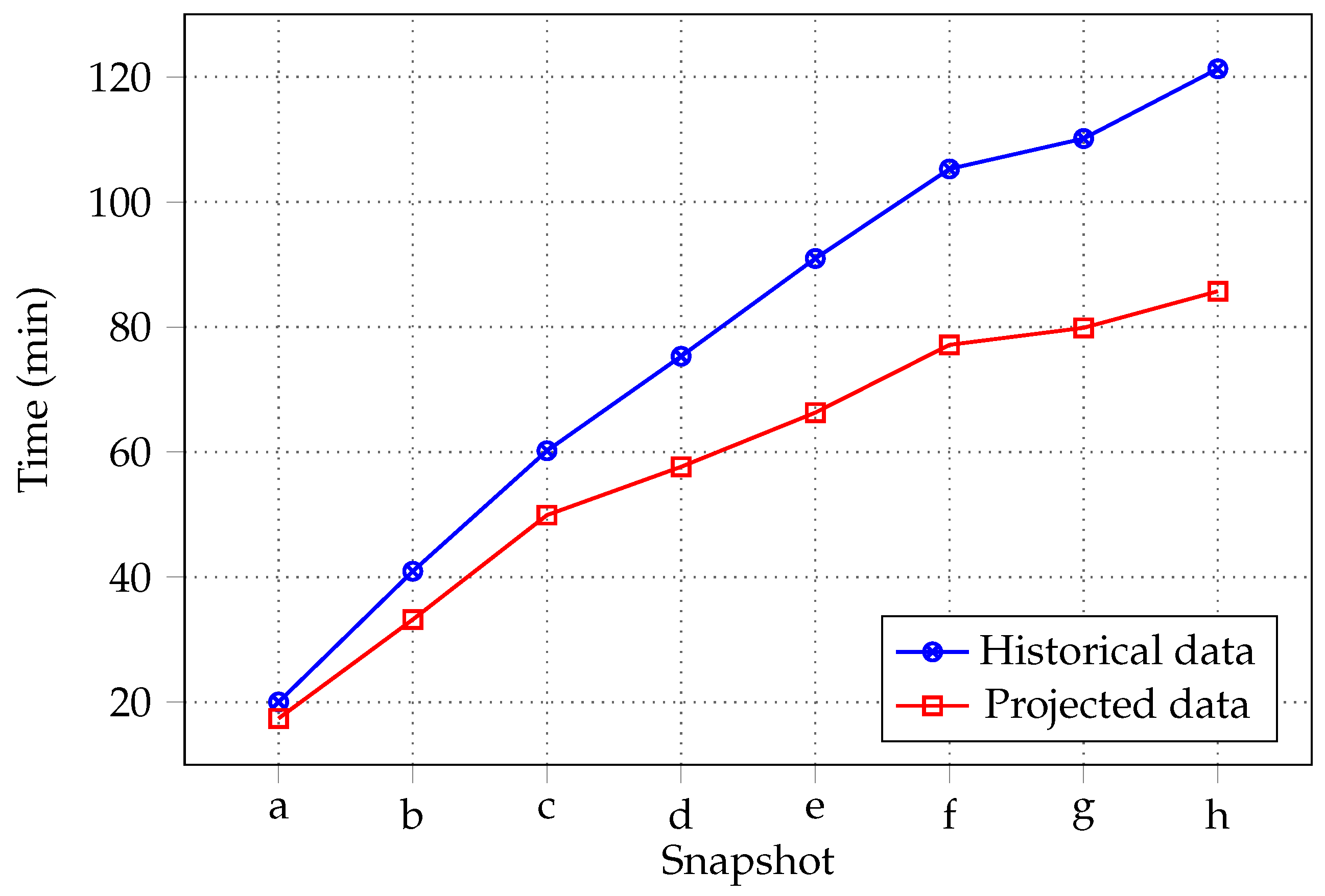
- A first simulation was set up with historical data with a 20-year return value.
- The time at which the cross section of Tamuín city settled in the lower part of topography (Figure 5) was fully flooded was recorded.
- A second simulation was set up with the projected streamflows under CC.
- The time at which the second simulation achieved the flood level of the first experiment was recorded.
- Comparison between flooding times was performed.
4. Results
5. Discussion
6. Conclusions
Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
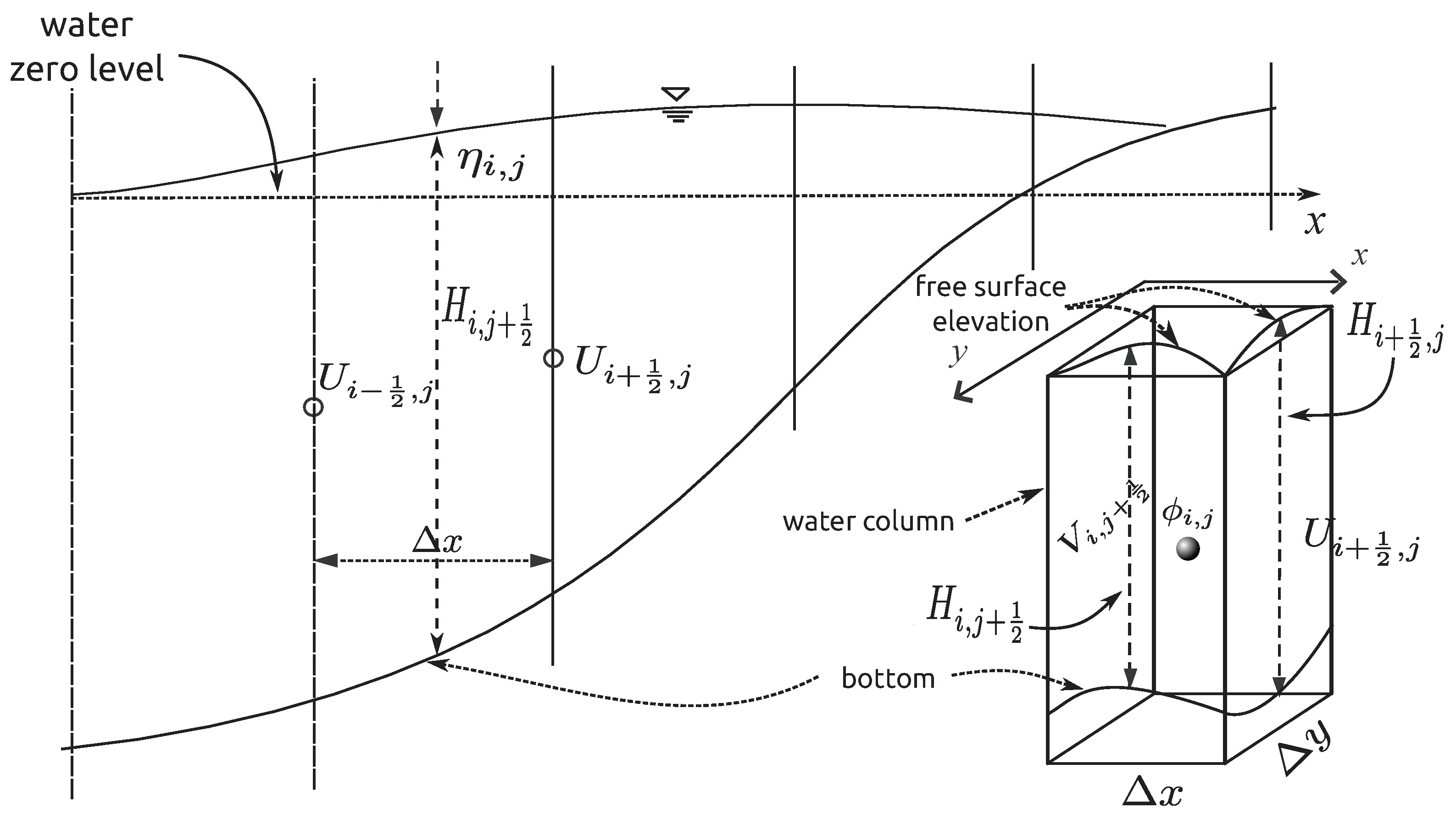
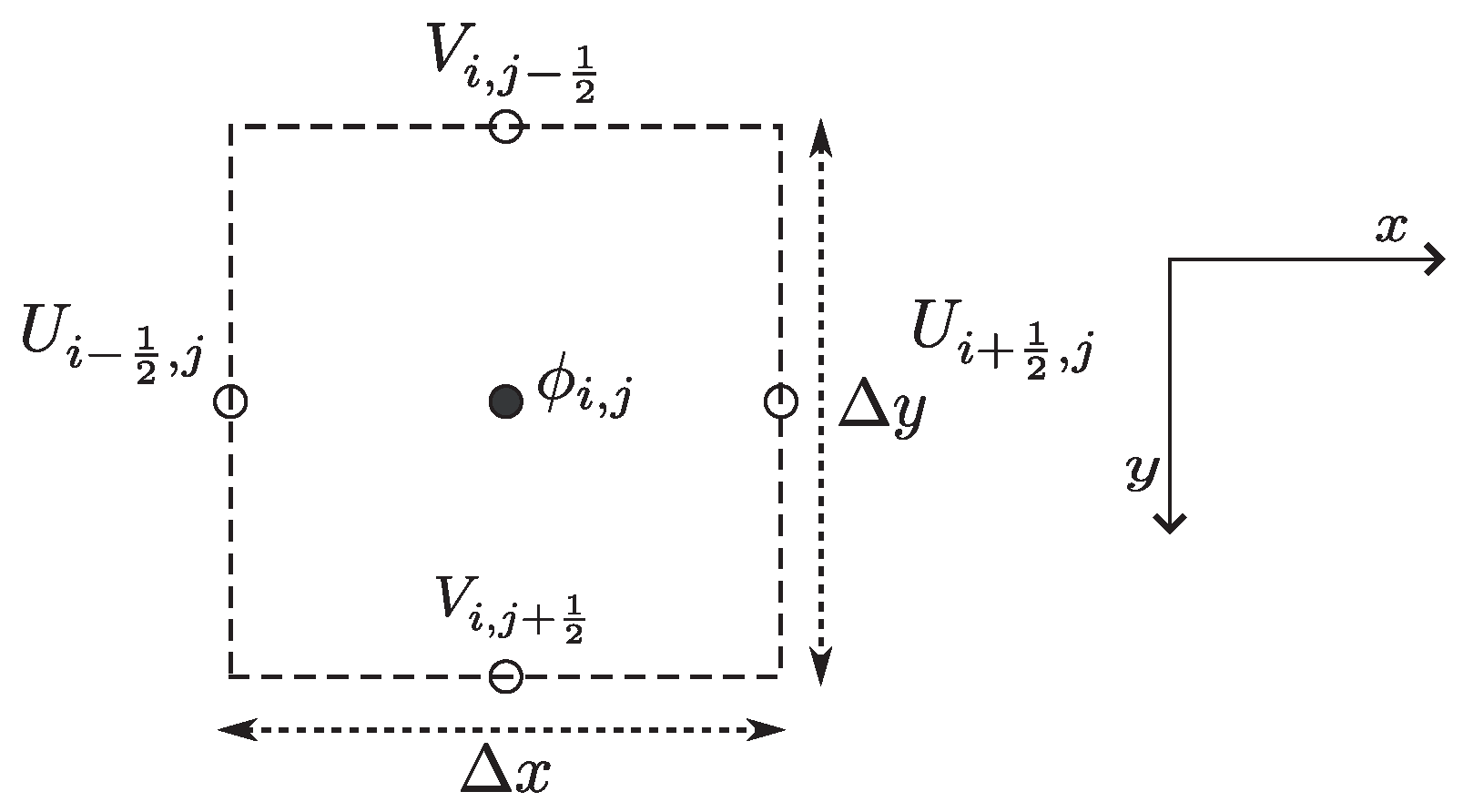
Appendix A. Hydrodynamics
Appendix A.1. Hydrodynamic Equations
Appendix B. Numerical Solution Strategy
Software
References
- Interngubernamental Panel on Climate Change. IPCC: Working Group I Contribution to the IPCC Fifth Assessment Report, Climate Change 2013: The Physical Science Basis. IPCC. AR5; Interngubernamental Panel on Climate Change: Paris, France, 2014. [Google Scholar]
- Suarez Gallareta, E.; Hernández Gómez, J.J.; Cetzal Balam, G.; Orozco del Castillo, M.; Moreno Sabido, M.; Silva Aguilera, R.A. Sistema Híbrido Basado en Redes Neuronales Artificiales y Descomposición Modal Empírica para la Evaluación de la Interrelación entre la Irradiancia Solar Total y el Calentamiento Global. Res. Comput. Sci. 2018, 147, 319–332. [Google Scholar]
- Dong, B.; Sutton, R.T.; Shaffrey, L.; Klingaman, N.P. Attribution of forced decadal climate change in coupled and uncoupled ocean—Atmosphere model experiments. J. Clim. 2017, 30, 6203–6223. [Google Scholar] [CrossRef]
- Kay, J.E.; Wall, C.; Yettella, V.; Medeiros, B.; Hannay, C.; Caldwell, P.; Bitz, C. Global climate impacts of fixing the Southern Ocean shortwave radiation bias in the Community Earth System Model (CESM). J. Clim. 2016, 29, 4617–4636. [Google Scholar] [CrossRef]
- Saba, V.S.; Griffies, S.M.; Anderson, W.G.; Winton, M.; Alexander, M.A.; Delworth, T.L.; Hare, J.A.; Harrison, M.J.; Rosati, A.; Vecchi, G.A.; et al. Enhanced warming of the Northwest Atlantic Ocean under climate change. J. Geophys. Res. Ocean. 2016, 121, 118–132. [Google Scholar] [CrossRef]
- Tang, Q.; Oki, T. Terrestrial Water Cycle and Climate Change: Natural and Human-Induced Impacts; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Tian, H.; Yang, Q.; Najjar, R.G.; Ren, W.; Friedrichs, M.A.; Hopkinson, C.S.; Pan, S. Anthropogenic and climatic influences on carbon fluxes from eastern North America to the Atlantic Ocean: A process-based modeling study. J. Geophys. Res. Biogeosci. 2015, 120, 757–772. [Google Scholar] [CrossRef]
- Xia, X.; Wu, Q.; Mou, X.; Lai, Y. Potential impacts of climate change on the water quality of different water bodies. J. Environ. Inform. 2015, 25, 85–98. [Google Scholar] [CrossRef]
- Schwefel, R.; Gaudard, A.; Wüest, A.; Bouffard, D. Effects of climate change on deepwater oxygen and winter mixing in a deep lake (Lake Geneva): Comparing observational findings and modeling. Water Resour. Res. 2016, 52, 8811–8826. [Google Scholar] [CrossRef]
- Hetherington, A.L.; Schneider, R.L.; Rudstam, L.G.; Gal, G.; DeGaetano, A.T.; Walter, M.T. Modeling climate change impacts on the thermal dynamics of polymictic Oneida Lake, New York, United States. Ecol. Model. 2015, 300, 1–11. [Google Scholar] [CrossRef]
- Butcher, J.B.; Nover, D.; Johnson, T.E.; Clark, C.M. Sensitivity of lake thermal and mixing dynamics to climate change. Clim. Chang. 2015, 129, 295–305. [Google Scholar] [CrossRef]
- Cousino, L.K.; Becker, R.H.; Zmijewski, K.A. Modeling the effects of climate change on water, sediment, and nutrient yields from the Maumee River watershed. J. Hydrol. Reg. Stud. 2015, 4, 762–775. [Google Scholar] [CrossRef]
- Mohammed, I.N.; Bomblies, A.; Wemple, B.C. The use of CMIP5 data to simulate climate change impacts on flow regime within the Lake Champlain Basin. J. Hydrol. Reg. Stud. 2015, 3, 160–186. [Google Scholar] [CrossRef]
- Stefanova, A.; Krysanova, V.; Hesse, C.; Lillebø, A.I. Climate change impact assessment on water inflow to a coastal lagoon: the Ria de Aveiro watershed, Portugal. Hydrol. Sci. J. 2015, 60, 929–948. [Google Scholar] [CrossRef]
- Hesse, C.; Krysanova, V.; Stefanova, A.; Bielecka, M.; Domnin, D.A. Assessment of climate change impacts on water quantity and quality of the multi-river Vistula Lagoon catchment. Hydrol. Sci. J. 2015, 60, 890–911. [Google Scholar] [CrossRef]
- Robins, P.E.; Skov, M.W.; Lewis, M.J.; Gimenez, L.; Davies, A.G.; Malham, S.K.; Neill, S.P.; McDonald, J.E.; Whitton, T.A.; Jackson, S.E.; et al. Impact of climate change on UK estuaries: A review of past trends and potential projections. Estuar. Coast. Shelf Sci. 2016, 169, 119–135. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, T.; Voisin, N.; Copping, A. Estuarine response to river flow and sea-level rise under future climate change and human development. Estuar. Coast. Shelf Sci. 2015, 156, 19–30. [Google Scholar] [CrossRef]
- Sohma, A.; Shibuki, H.; Nakajima, F.; Kubo, A.; Kuwae, T. Modeling a coastal ecosystem to estimate climate change mitigation and a model demonstration in Tokyo Bay. Ecol. Model. 2018, 384, 261–289. [Google Scholar] [CrossRef]
- Miller, N. California climate change, hydrologic response, and flood forecasting. In Urban Flood Management; CRC Press: Boca Raton, FL, USA, 2018; pp. 143–156. [Google Scholar]
- Alamdari, N. Modeling Climate Change Impacts on the Effectiveness of Stormwater Control Measures in Urban Watersheds. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2018. [Google Scholar]
- Moor, H.; Hylander, K.; Norberg, J. Predicting climate change effects on wetland ecosystem services using species distribution modeling and plant functional traits. Ambio 2015, 44, 113–126. [Google Scholar] [CrossRef]
- Lee, S.Y.; Ryan, M.E.; Hamlet, A.F.; Palen, W.J.; Lawler, J.J.; Halabisky, M. Projecting the hydrologic impacts of climate change on montane wetlands. PLoS ONE 2015, 10, e0136385. [Google Scholar] [CrossRef] [PubMed]
- Havril, T.; Tóth, Á.; Molson, J.W.; Galsa, A.; Mádl-Szőnyi, J. Impacts of predicted climate change on groundwater flow systems: Can wetlands disappear due to recharge reduction? J. Hydrol. 2018, 563, 1169–1180. [Google Scholar] [CrossRef]
- Huang, L.; Zeng, G.; Liang, J.; Hua, S.; Yuan, Y.; Li, X.; Dong, H.; Liu, J.; Nie, S.; Liu, J. Combined impacts of land use and climate change in the modeling of future groundwater vulnerability. J. Hydrol. Eng. 2017, 22, 05017007. [Google Scholar] [CrossRef]
- Gemitzi, A.; Ajami, H.; Richnow, H.H. Developing empirical monthly groundwater recharge equations based on modeling and remote sensing data–Modeling future groundwater recharge to predict potential climate change impacts. J. Hydrol. 2017, 546, 1–13. [Google Scholar] [CrossRef]
- Aslam, R.A.; Shrestha, S.; Pandey, V.P. Groundwater vulnerability to climate change: a review of the assessment methodology. Sci. Total. Environ. 2018, 612, 853–875. [Google Scholar] [CrossRef] [PubMed]
- Kumar, C. Impact of climate change on groundwater resources. In Handbook of Research on Climate Change Impact on Health and Environmental Sustainability; IGI Global: Hershey, PA, USA, 2016; pp. 196–221. [Google Scholar]
- Meixner, T.; Manning, A.H.; Stonestrom, D.A.; Allen, D.M.; Ajami, H.; Blasch, K.W.; Brookfield, A.E.; Castro, C.L.; Clark, J.F.; Gochis, D.J.; et al. Implications of projected climate change for groundwater recharge in the western United States. J. Hydrol. 2016, 534, 124–138. [Google Scholar] [CrossRef]
- Bekele, D.; Alamirew, T.; Kebede, A.; Zeleke, G.; Melesse, A.M. Modeling climate change impact on the Hydrology of Keleta watershed in the Awash River basin, Ethiopia. Environ. Model. Assess. 2019, 24, 95–107. [Google Scholar] [CrossRef]
- Kim, J.; Ryu, J.H. Modeling Hydrological and Environmental Consequences of Climate Change and Urbanization in the Boise River Watershed, Idaho. J. Am. Water Resour. Assoc. 2019, 55, 133–153. [Google Scholar] [CrossRef]
- Givati, A.; Thirel, G.; Rosenfeld, D.; Paz, D. Climate change impacts on streamflow at the upper Jordan River based on an ensemble of regional climate models. J. Hydrol. Reg. Stud. 2019, 21, 92–109. [Google Scholar] [CrossRef]
- Jin, L.; Whitehead, P.G.; Addo, K.A.; Amisigo, B.; Macadam, I.; Janes, T.; Crossman, J.; Nicholls, R.J.; McCartney, M.; Rodda, H.J. Modeling future flows of the Volta River system: Impacts of climate change and socio-economic changes. Sci. Total. Environ. 2018, 637, 1069–1080. [Google Scholar] [CrossRef] [PubMed]
- Raimonet, M.; Thieu, V.; Silvestre, M.; Oudin, L.; Rabouille, C.; Vautard, R.; Garnier, J. Landward perspective of coastal eutrophication potential under future climate change: the Seine River case (France). Front. Mar. Sci. 2018, 5, 136. [Google Scholar] [CrossRef]
- Su, B.; Huang, J.; Zeng, X.; Gao, C.; Jiang, T. Impacts of climate change on streamflow in the upper Yangtze River basin. Clim. Chang. 2017, 141, 533–546. [Google Scholar] [CrossRef]
- Dlamini, N.S.; Kamal, M.R.; Soom, M.A.B.M.; Mohd, M.S.F.b.; Abdullah, A.F.B.; Hin, L.S. Modeling potential impacts of climate change on streamflow using projections of the 5th assessment report for the Bernam River Basin, Malaysia. Water 2017, 9, 226. [Google Scholar] [CrossRef]
- Gelfan, A.; Gustafsson, D.; Motovilov, Y.; Arheimer, B.; Kalugin, A.; Krylenko, I.; Lavrenov, A. Climate change impact on the water regime of two great Arctic rivers: modeling and uncertainty issues. Clim. Chang. 2017, 141, 499–515. [Google Scholar] [CrossRef]
- Mekonnen, B.A.; Mazurek, K.A.; Putz, G. Modeling of nutrient export and effects of management practices in a cold-climate prairie watershed: Assiniboine River watershed, Canada. Agric. Water Manag. 2017, 180, 235–251. [Google Scholar] [CrossRef]
- Vaighan, A.A.; Talebbeydokhti, N.; Bavani, A.M.; Whitehead, P. Modeling impacts of climate and land use change on streamflow, nitrate, and ammonium in the Kor River, southwest of Iran. J. Water Clim. Chang. 2018. [Google Scholar] [CrossRef]
- Sorribas, M.V.; Paiva, R.C.; Melack, J.M.; Bravo, J.M.; Jones, C.; Carvalho, L.; Beighley, E.; Forsberg, B.; Costa, M.H. Projections of climate change effects on discharge and inundation in the Amazon basin. Clim. Chang. 2016, 136, 555–570. [Google Scholar] [CrossRef]
- Patrick, L.; Solecki, W.; Jacob, K.; Kunreuther, H.; Nordenson, G. New york city panel on climate change 2015 report chapter 3: Static coastal flood mapping. Ann. New York Acad. Sci. 2015, 1336, 45–55. [Google Scholar] [CrossRef] [PubMed]
- Arnell, N.W.; Gosling, S.N. The impacts of climate change on river flood risk at the global scale. Clim. Chang. 2016, 134, 387–401. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Aerts, J.C.; van Beek, L.P.; Bierkens, M.F.; Bouwman, A.; Jongman, B.; Kwadijk, J.C.; Ligtvoet, W.; Lucas, P.L.; Van Vuuren, D.P.; et al. Global drivers of future river flood risk. Nat. Clim. Chang. 2016, 6, 381. [Google Scholar] [CrossRef]
- Francesch-Huidobro, M.; Dabrowski, M.; Tai, Y.; Chan, F.; Stead, D. Governance challenges of flood-prone delta cities: Integrating flood risk management and climate change in spatial planning. Prog. Plan. 2017, 114, 1–27. [Google Scholar] [CrossRef]
- Alfieri, L.; Feyen, L.; Di Baldassarre, G. Increasing flood risk under climate change: A pan-European assessment of the benefits of four adaptation strategies. Clim. Chang. 2016, 136, 507–521. [Google Scholar] [CrossRef]
- Birhanu, D.; Kim, H.; Jang, C.; Park, S. Flood Risk and Vulnerability of Addis Ababa City Due to Climate Change and Urbanization. Procedia Eng. 2016, 154, 696–702. [Google Scholar] [CrossRef]
- Yamashita, S.; Matsuda, S.; Watanabe, R.; Shimatani, Y.; Moriyama, T.; Hayashi, H.; Iyooka, H.; Hamada, T.; Yamashita, T.; Kakudo, K.; et al. A registration system for preventing/mitigating urban flood disasters as one way to smartly adapt to climate change in Japanese cities. Int. Rev. Spat. Plan. Sustain. Dev. 2016, 4, 18–29. [Google Scholar] [CrossRef][Green Version]
- Balica, S.; Wright, N.; van der Meulen, F. A flood vulnerability index for coastal cities and its use in assessing climate change impacts. Nat. Hazards 2012, 64, 73–105. [Google Scholar] [CrossRef]
- Jeffers, J. The Cork City flood of November 2009: Lessons for flood risk management and climate change adaptation at the urban scale. Irish Geogr. 2011, 44, 61–80. [Google Scholar] [CrossRef]
- Bleck, M.; Krebs, H.; Scholz, A.; Spekker, H. Flood protection in the Federal State and the city of Bremen by adjustment of climate changes [Hochwasserschutz im Land Bremen Anpassung an Prognostizierte Klimaveränderungen]. Bautechnik 2009, 86, 470–479. [Google Scholar] [CrossRef]
- Miller, J.D.; Hutchins, M. The impacts of urbanisation and climate change on urban flooding and urban water quality: A review of the evidence concerning the United Kingdom. J. Hydrol. Reg. Stud. 2017, 12, 345–362. [Google Scholar] [CrossRef]
- Ek, K.; Goytia, S.; Pettersson, M.; Spegel, E. Analysing and Evaluating Flood Risk Governance in Sweden: Adaptation to Climate Change? STAR-FLOOD Consortium: Oxfordshire, UK, 2016. [Google Scholar]
- Álvarez, B.; Santacruz De León, G.; Ramos Leal, J.; Morán Ramírez, A. Water poverty index in subtropical Zones: The case of Huasteca Potosina, Mexico. Rev. Int. Contam. Ambient. 2015, 31, 173–184. [Google Scholar]
- Morán-Ramírez, J.; Ramos-Leal, J.; López-Álvarez, B.; Lozada, S.; León, G.D. Hydrogeochemical behavior of underground flow in fractured karstic aquifers, using inverse modeling: The Huasteca Potosina case [Comportamiento hidrogeoquímico de flujos subterráneos en acuíferos cársticos fracturados, aplicando modelación inversa: Caso huasteca potosina]. Bol. Soc. Geol. Mex. 2013, 65, 71–82. [Google Scholar]
- Valenzuela, R.; Raymundo, T.; Cifuentes, J.; Castillo, G.; Amalfi, M.; Decock, C. Two undescribed species of Phylloporia from Mexico based on morphological and phylogenetic evidence. Mycol. Prog. 2011, 10, 341–349. [Google Scholar] [CrossRef]
- González Soriano, E.; Noguera, F.; Oñate Ocaña, L. A biodiversity hotspot for odonates in mexico: The huasteca potosina, san luis potosí. Odonatologica 2011, 40, 179–190. [Google Scholar]
- Carmona Jimenez, J.; Montejano Zurita, C. Phycological characterization of springs in the lower Panuco Basin, Mexico [Caracterizacion ficologica en manantiales de la cuenca baja del sistema hidrologico del Panuco, Mexico]. Bol. Soc. Bot. Mex. 1993, 53, 21–41. [Google Scholar]
- Josabad Alonso-Castro, A.; Jose Maldonado-Miranda, J.; Zarate-Martinez, A.; Jacobo-Salcedo, M.; Fernández-Galicia, C.; Alejandro Figueroa-Zuñiga, L.; Abel Rios-Reyes, N.; Angel De León-Rubio, M.; Andrés Medellín-Castillo, N.; Reyes-Munguia, A.; et al. Medicinal plants used in the Huasteca Potosina, México. J. Ethnopharmacol. 2012, 143, 292–298. [Google Scholar] [CrossRef] [PubMed]
- Elliott, W. Cave Biodiversity and Ecology of the Sierra de El Abra Region; Academic Press: San Diego, CA, USA, 2015; pp. 59–76. [Google Scholar]
- Santiago-Figueroa, I.; Lara-Bueno, A.; González-Garduño, R.; López-Arellano, M.; de la Rosa-Arana, J.; Maldonado-Simán, E. Anthelmintic resistance in hair sheep farms in a sub-humid tropical climate, in the Huasteca Potosina, Mexico. Vet. Parasitol. Reg. Stud. Rep. 2019, 17. [Google Scholar] [CrossRef] [PubMed]
- Vieyra-Alberto, R.; Domínguez-Vara, I.; Olmos-Oropeza, G.; Martínez-Montoya, J.; Borquez-Gastelum, J.; Palacio-Nuñez, J.; de la Fuente, J.; Morales-Almaráz, E. Mineral profile and interrelationship in water, forage and blood serum of beef cattle during two seasons in the Huasteca Potosina, México [Perfil e interrelación mineral en Agua, forraje y suero sanguíneo de bovinos durante dos Épocas en la huasteca potosina, México]. Agrociencia 2013, 47, 121–133. [Google Scholar]
- Hernández, H.; Robledo, M.; Rivera, J.; Vázquez, I. Land cover and land use change in the Pujal-Coy project area, San Luis Potosí, Mexico, 1973–2000 [Cambios en la cubierta vegetal y uso del suelo en el área del proyecto Pujal-Coy, San Luis Potosí, México, 1973–2000]. Investig. Geogr. 2006, 59, 26–42. [Google Scholar]
- Hernández, H.; Robledo, M.; Rivera, J.; Martínez, J. Spatial configuration of land-use/land-cover in the Pujal-Coy project area, Huasteca Potosina Region, Mexico. Ambio 2008, 37, 381–389. [Google Scholar] [CrossRef] [PubMed]
- Tiedje, K. Gender and ethnic identity in rural grassroots development: An outlook from the Huasteca Potosina, Mexico. Urban Anthropol. 2002, 31, 261–316. [Google Scholar]
- Granados-Ramírez, R.; Galindo-Mendoza, M.; Contreras-Servin, C.; Hernández-Cerda, M.; Valdez-Madero, G. Monitoring land cover and land use using NOAA-AVHRR data in the Husteca Potosina, Mexico. Geocarto Int. 2008, 23, 273–285. [Google Scholar] [CrossRef]
- Hudson, P.; Colditz, R. Flood delineation in a large and complex alluvial valley, lower Pánuco basin, Mexico. J. Hydrol. 2003, 280, 229–245. [Google Scholar] [CrossRef]
- León, H.; Piña, H.; Cuevas, C.; Castañeda, C. Baroclinic mathematical modeling of fresh water plumes in the interaction river-sea. Int. J. Numer. Anal. Model. 2005, 2, 1–14. [Google Scholar]
- Ramírez-León, H.; Couder-Castañeda, C.; Herrera-Díaz, I.; Barrios-Piña, H. Numerical modeling of the thermal discharge of the Laguna Verde power station [Modelación numérica de la descarga térmica de la Central Nucleoeléctrica Laguna Verde]. Rev. Int. Metod. Numer. Para Calc. Diseno Ing. 2013, 29, 114–121. [Google Scholar]
- Barrios-Piña, H.; Ramírez-León, H.; Rodríguez-Cuevas, C.; Couder-Castañeda, C. Multilayer numerical modeling of flows through vegetation using a mixing-length turbulence model. Water 2014, 6, 2084–2103. [Google Scholar] [CrossRef]
- Torres-Bejarano, F.; Couder-Castañeda, C.; Ramírez-León, H.; Hernández-Gómez, J.; Rodríguez-Cuevas, C.; Herrera-Díaz, I.; Barrios-Piña, H. Numerical Modelling of Heavy Metal Dynamics in a River-Lagoon System. Math. Probl. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Rodriguez-Cuevas, C.; Couder-Castañeda, C.; Flores-Mendez, E.; Herrera-Díaz, I.; Cisneros-Almazan, R. Modelling shallow water wakes using a hybrid turbulence model. J. Appl. Math. 2014, 2014, 714031. [Google Scholar] [CrossRef]
- Horritt, M. Parameterisation, validation and uncertainty analysis of CFD models of fluvial and flood hydraulics in the natural environment. In Computational Fluid Dynamics: Applications in Environmental Hydraulics; John Wiley and Sons: Hoboken, NJ, USA, 2005; pp. 193–213. [Google Scholar]
- Kharin, V.V.; Zwiers, F.; Zhang, X.; Wehner, M. Changes in temperature and precipitation extremes in the CMIP5 ensemble. Clim. Chang. 2013, 119, 345–357. [Google Scholar] [CrossRef]
- Thomson, A.M.; Calvin, K.V.; Smith, S.J.; Kyle, G.P.; Volke, A.; Patel, P.; Delgado-Arias, S.; Bond-Lamberty, B.; Wise, M.A.; Clarke, L.E.; et al. RCP4.5: A pathway for stabilization of radiative forcing by 2100. Clim. Chang. 2011, 109, 77. [Google Scholar] [CrossRef]
- Romero-Lankao, P.; Smith, J.; Davidson, D.; Diffenbaugh, N.; Kinney, P.; Kirshen, P.; Kovacs, P.; Ruiz, L.V. North America. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Barros, V., Field, C., Dokken, D., Mastrandrea, M., Mach, K., Bilir, T., Chatterjee, M., Ebi, K., Estrada, Y., Genova, R., et al., Eds.; Cambridge University Press: Cambridge, UK, 2004; Chapter 26; pp. 1439–1498. [Google Scholar]
- Comisión Nacional del Agua. Plan Nacional Hídrico 2007–2012. Available online: http://www.conagua.gob.mx/CONAGUA07/Contenido/Documentos/PNH_05-08.pdf (accessed on 15 April 2019).
- Hudson, P. Event sequence and sediment exhaustion in the lower Panuco Basin, Mexico. Catena 2003, 52, 57–76. [Google Scholar] [CrossRef]
- Melgar, E.; Solís, R.; Ruvalcaba, J. Technological and material characterization of lapidary artifacts from Tamtoc Archaeological Site, Mexico. Mater. Res. Soc. Symp. Proc. 2012, 1374, 103–114. [Google Scholar] [CrossRef]
- Zaragoza Ocaña, D. La arquitectura de Tamohi. Arqueología 2007, 2007, 71–92. [Google Scholar]
- Zaragoza Ocaña, D. Tamohi, su Pintura Mural; Serie Museo de la Cultura Huasteca; Gobierno del Estado de Tamaulipas, Secretaría de Educación, Cultura y Deporte, Instituto Tamaulipeco para la Cultura y las Artes, Gobierno Municipal; CONACULTA/Instituto Nacional de Antropología e Historia: Mexico City, Mexico, 2003.
- INEGI. Instituto Nacional de Estadística y Geografía; INEGI: Mexico City, Mexico, 2010. [Google Scholar]
- Comisión Estatal de Derechos Humanos, San Luis Potosí. Informe CEDH-INEGI Economía: Tamuín, San Luis Potosí. Available online: http://www.cedhslp.org.mx/Docs_old/Informe_CEDH/TAMUIN/inegi.pdf (accessed on 13 January 2019).
- Bedient, P.; Huber, W.; Vieux, B. Hydrology and Floodplain Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 2008. [Google Scholar]
- US Bureau of Reclamation. Design of Small Dams; U.S. Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1987.
- Velázquez, J.; Troin, M.; Caya, D. Hydrological modeling of the Tampaón River in the context of climate change. Tecnol. Cienc. Agua 2015, 6, 17–30. [Google Scholar]
- Moreno-Mata, A.; Villasís-Keever, R.; Morató, J. Climatic Change, Management of Water Rain and Flood Risk in the Metropolitan Area of San Luis Potosí, México. In Urban Resilience for Risk and Adaptation Governance: Theory and Practice; Brunetta, G., Caldarice, O., Tollin, N., Rosas-Casals, M., Morató, J., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 175–206. [Google Scholar]
- Teledyne Rd Instruments. WinRiver II User’s Guide; Teledyne Rd Instruments: Poway, CA, USA, 2007. [Google Scholar]
- Le, T.; Devisch, O.; Trinh, T. Flood-resilient urban parks: Toward a framework. Area 2019. [Google Scholar] [CrossRef]
- Alvarez, J.; Lira, M. Flood control in the plain rivers. Proc. IAHR Int. Symp. River Mech. 1973, 2, 303–314. [Google Scholar]
- Garrote, J.; Bernal, N.; Díez-Herrero, A.; Martins, L.; Bodoque, J. Civil engineering works versus self-protection measures for the mitigation of floods economic risk. A case study from a new classification criterion for cost-benefit analysis. Int. J. Disaster Risk Reduct. 2019, 37. [Google Scholar] [CrossRef]
- Ishak, E.; Rahman, A. Examination of Changes in Flood Data in Australia. Water 2019, 11, 1734. [Google Scholar] [CrossRef]
- Ishak, E.H.; Rahman, A.; Westra, S.; Sharma, A.; Kuczera, G. Evaluating the non-stationarity of Australian annual maximum flood. J. Hydrol. 2013, 494, 134–145. [Google Scholar] [CrossRef]
- Casulli, V.; Cheng, R.T. Semi-implicit finite difference methods for three dimentional shallow water flow. Int. J. Numer. Methods Fluids. 1992, 15, 629–648. [Google Scholar] [CrossRef]
- León, H.R.; Cuevas, C.R.; Díaz, E.H. Multilayer hydrodynamic models and their application to sediment transport in estuaries. In Current Trends in High Performance Computing and Its Applications; Springer: Berlin/Heidelbergpp, Germany, 2005; pp. 59–70. [Google Scholar]
- Booij, M.J. Impact of climate change on river flooding assessed with different spatial model resolutions. J. Hydrol. 2005, 303, 176–198. [Google Scholar] [CrossRef]






| (Years) | Flow Rate (m/s) |
|---|---|
| 2 | 762.71 |
| 5 | 1525.43 |
| 10 | 3813.57 |
| 20 | 4066.10 |
| 25 | 4194.92 |
| 50 | 4461.87 |
| 100 | 4652.55 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Cuevas, C.; Rocha-Escalante, H.; Couder-Castañeda, C.; Medina, I.; Hernández-Gómez, J.J. Hydrodynamic-Based Numerical Assessment of Flood Risk of Tamuín City, Mexico, by Tampaón River: A Forecast Considering Climate Change. Water 2019, 11, 1867. https://doi.org/10.3390/w11091867
Rodríguez-Cuevas C, Rocha-Escalante H, Couder-Castañeda C, Medina I, Hernández-Gómez JJ. Hydrodynamic-Based Numerical Assessment of Flood Risk of Tamuín City, Mexico, by Tampaón River: A Forecast Considering Climate Change. Water. 2019; 11(9):1867. https://doi.org/10.3390/w11091867
Chicago/Turabian StyleRodríguez-Cuevas, Clemente, Hermann Rocha-Escalante, Carlos Couder-Castañeda, Isaac Medina, and Jorge J. Hernández-Gómez. 2019. "Hydrodynamic-Based Numerical Assessment of Flood Risk of Tamuín City, Mexico, by Tampaón River: A Forecast Considering Climate Change" Water 11, no. 9: 1867. https://doi.org/10.3390/w11091867
APA StyleRodríguez-Cuevas, C., Rocha-Escalante, H., Couder-Castañeda, C., Medina, I., & Hernández-Gómez, J. J. (2019). Hydrodynamic-Based Numerical Assessment of Flood Risk of Tamuín City, Mexico, by Tampaón River: A Forecast Considering Climate Change. Water, 11(9), 1867. https://doi.org/10.3390/w11091867






