Temporal Effects of Groundwater on Physical and Biotic Components of a Karst Stream
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. Data Collection and Preparation
2.3. Statistical Analysis
3. Results
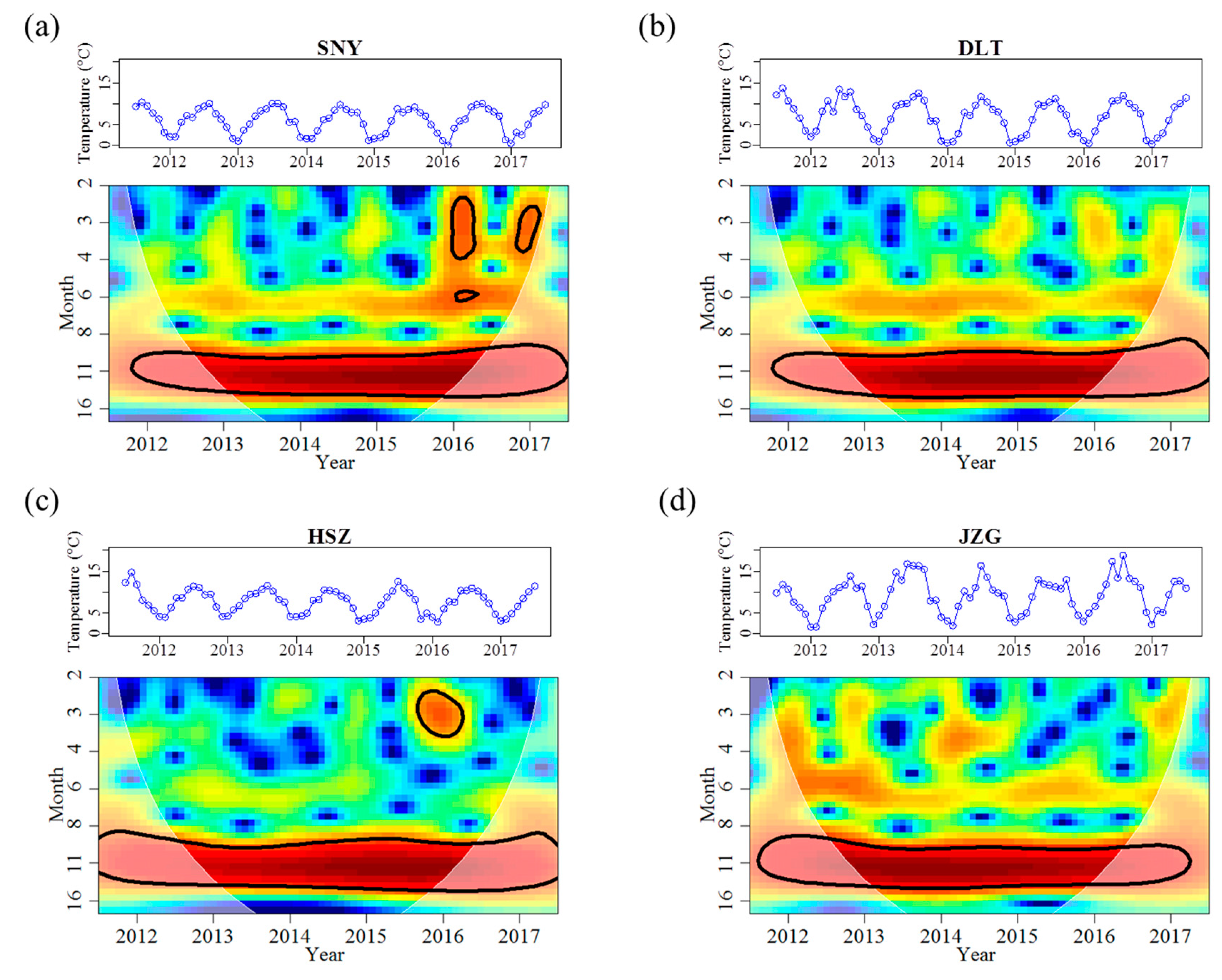
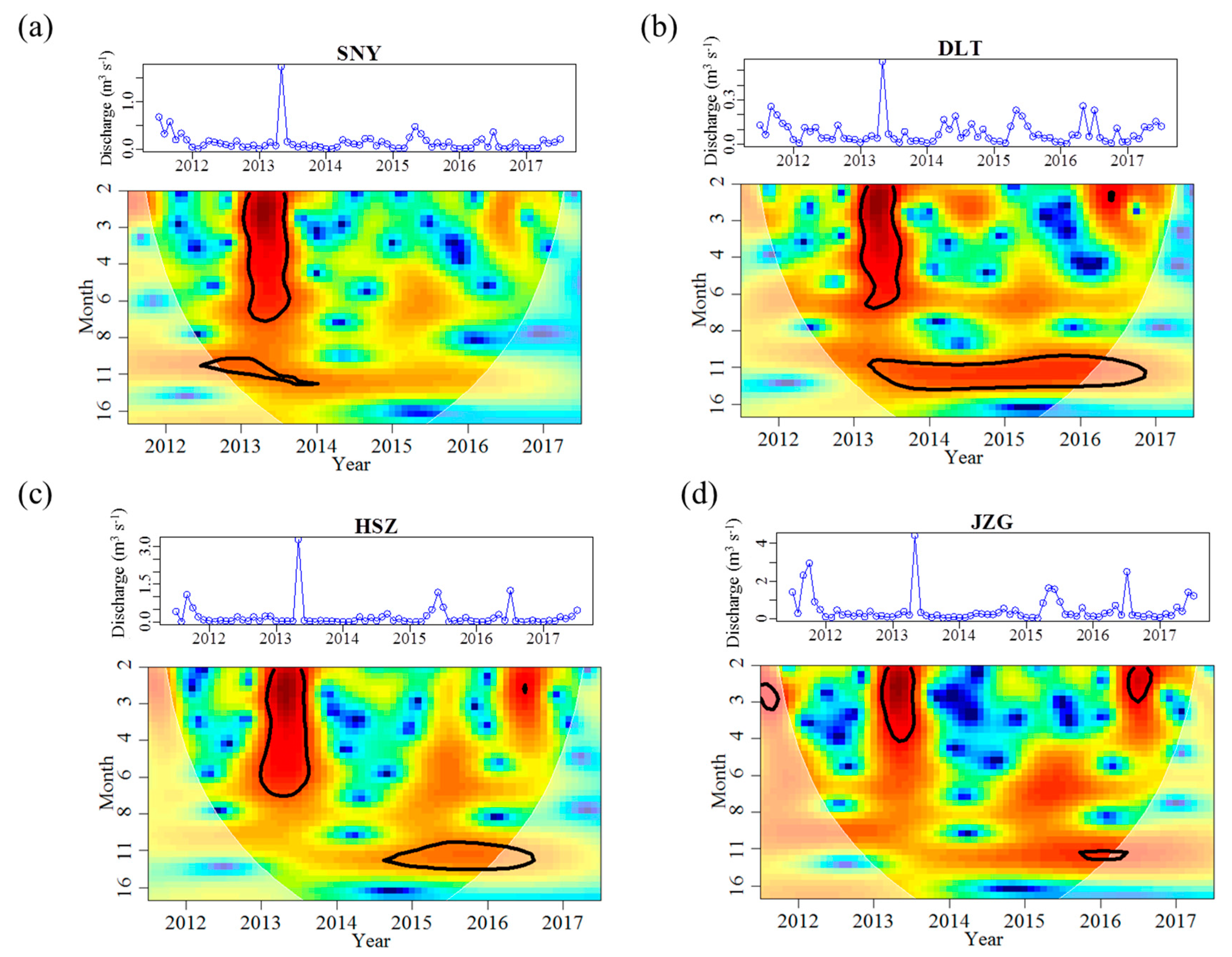
3.1. Effects of Groundwater on Stream Water Temperature and Discharge Regimes
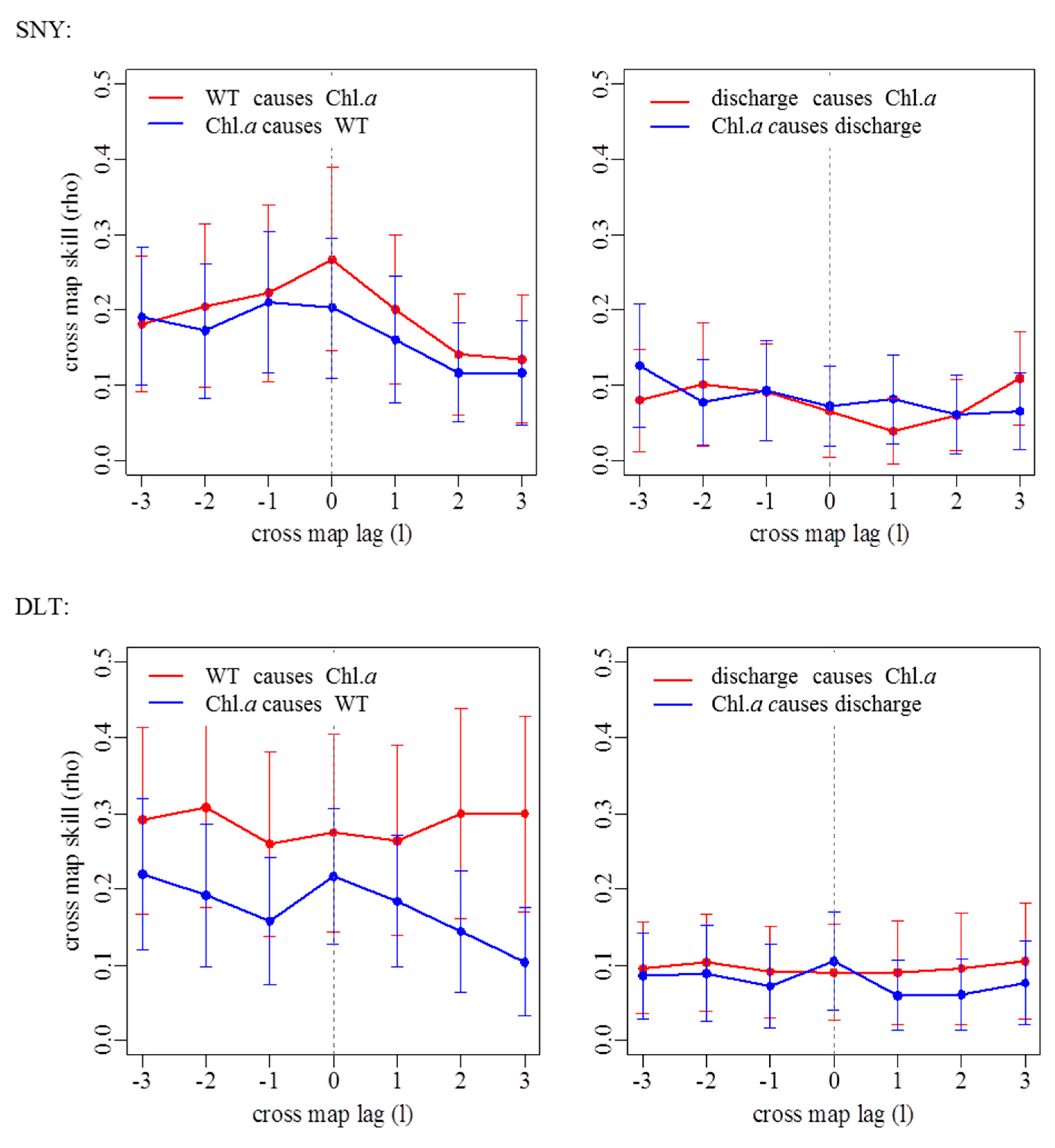
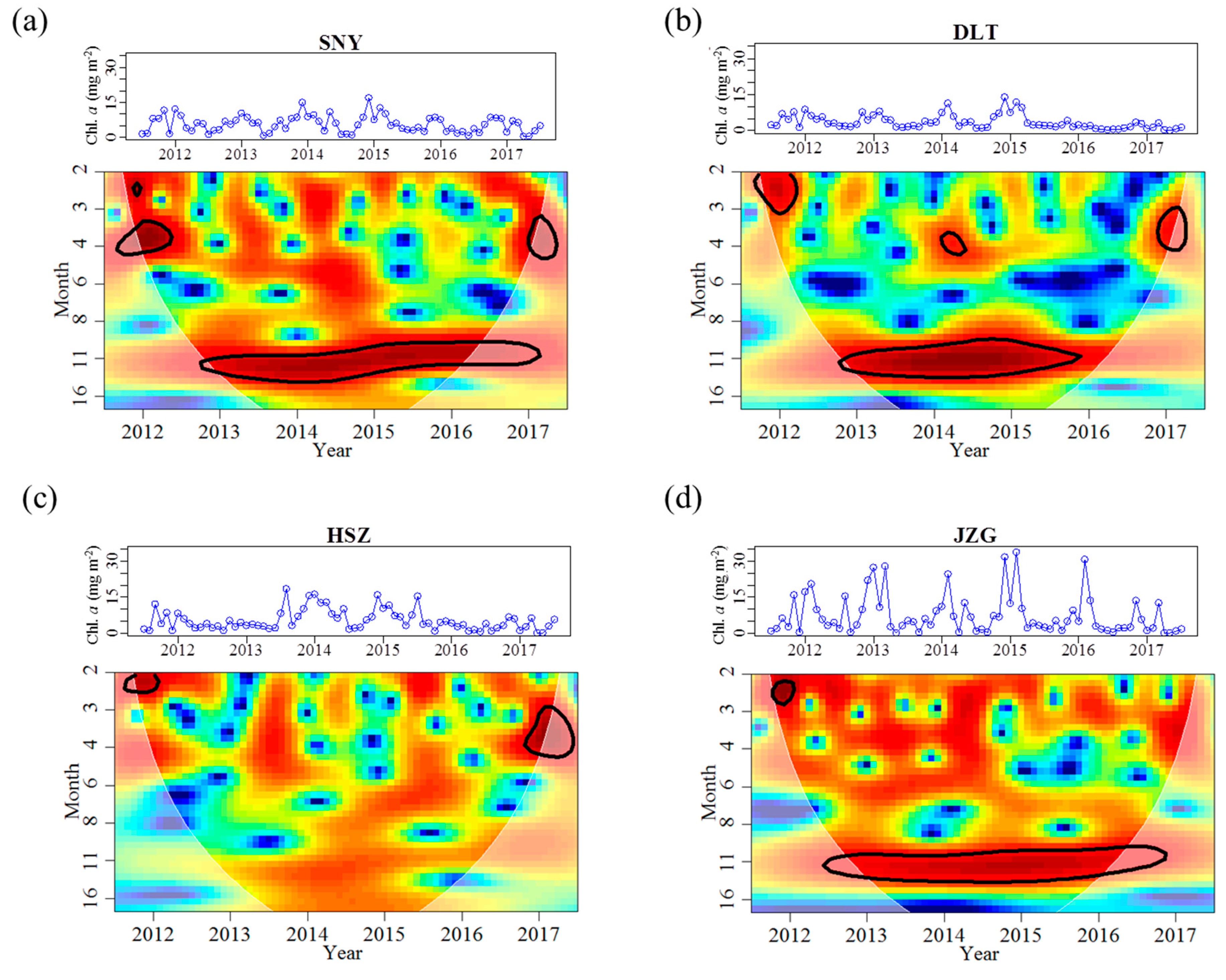
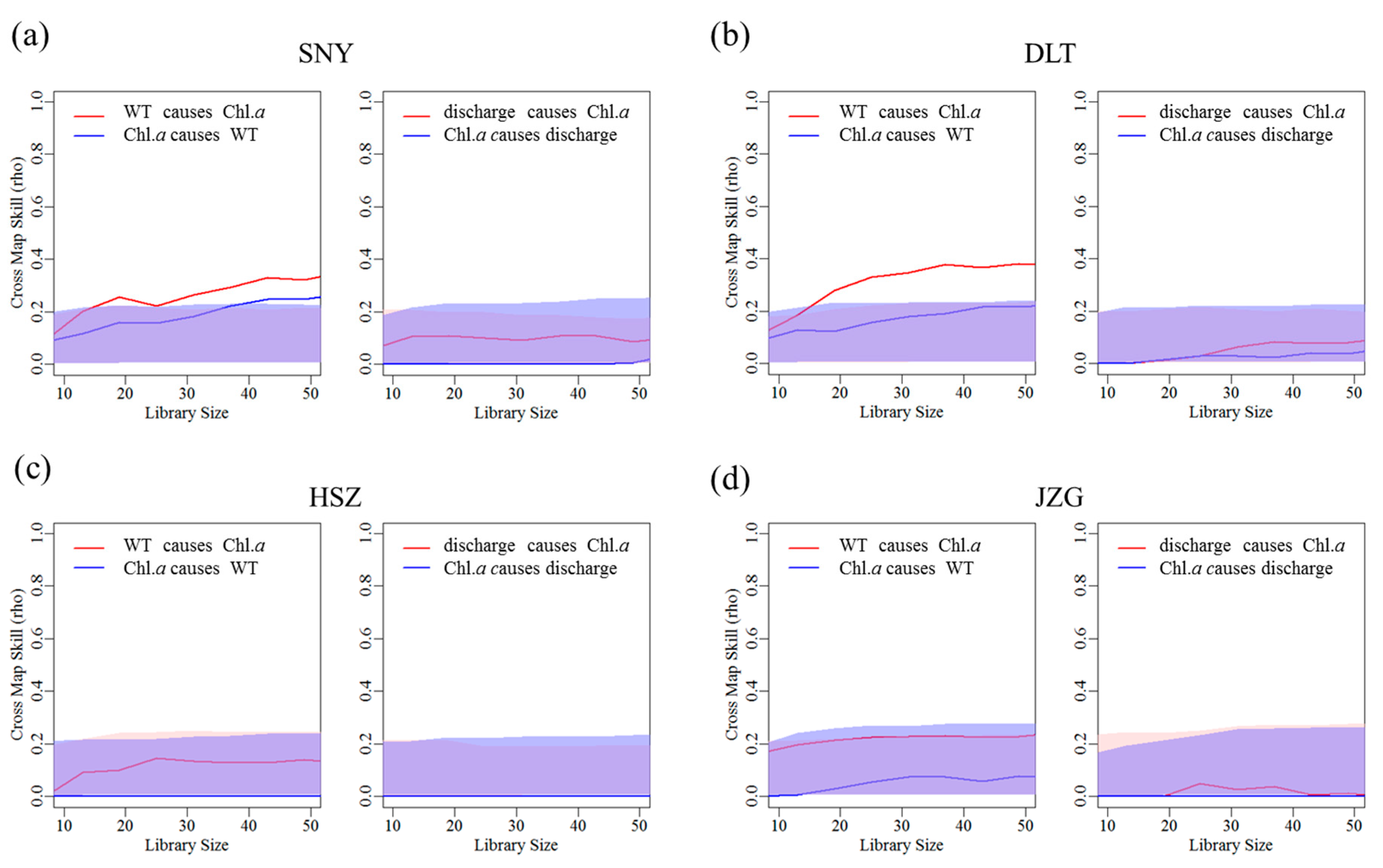
3.2. Effects of Groundwater on Associations between Chl. a Dynamics, Water Temperature, and Discharge
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Stream Reach | WT Causing Chl. a | Discharge Causing Chl. a | ||
|---|---|---|---|---|
| ρ | Time Lag (Month) | ρ | Time Lag (Month) | |
| SNY | 0.267 | 0 | 0.101 | 2 |
| DLT | 0.309 | 2 | 0.103 | 2 |
| HSZ | 0.135 | 0 | - | |
| JZG | 0.230 | 0 | 0.089 | 2 |


References
- Hayashi, M.; Rosenberry, D.O. Effects of ground water exchange on the hydrology and ecology of surface water. Groundwater 2002, 40, 309–316. [Google Scholar] [CrossRef]
- Wondzell, S.M. Groundwater–surface-water interactions: Perspectives on the development of the science over the last 20 years. Freshw. Sci. 2015, 34, 368–376. [Google Scholar] [CrossRef]
- Boulton, A.J.; Hancock, P.J. Rivers as groundwater-dependent ecosystems: A review of degrees of dependency, riverine processes and management implications. Aust. J. Bot. 2006, 54, 133–144. [Google Scholar] [CrossRef]
- Pipan, T. Epikarst—A Promising Habitat: Copepod Fauna, Its Diversity and Ecology: A Case Study From Slovenia (Europe); ZRC Publishing: Postojna–Ljubljana, Slovenia, 2005. [Google Scholar]
- Boulton, A.J.; Findlay, S.; Marmonier, P.; Stanley, E.H.; Valett, H.M. The functional significance of the hyporheic zone in streams and rivers. Annu. Rev. Ecol. Syst. 1998, 29, 59–81. [Google Scholar] [CrossRef]
- Burrows, R.M.; Rutlidge, H.; Valdez, D.G.; Venarsky, M.; Bond, N.R.; Andersen, M.S.; Fry, B.; Eberhard, S.M.; Kennard, M.J. Groundwater supports intermittent-stream food webs. Freshw. Sci. 2018, 37, 42–53. [Google Scholar] [CrossRef]
- Robinson, C.T.; Doering, M. Spatial patterns in macroinvertebrate assemblages in surface-flowing waters of a glacially-influenced floodplain. Aquat. Sci. 2013, 75, 373–384. [Google Scholar] [CrossRef]
- Malard, F.; Tockner, K.; Dole-Olivier, M.J.; Ward, J. A landscape perspective of surface-subsurface hydrological exchanges in river corridors. Freshw. Biol. 2002, 47, 621–640. [Google Scholar] [CrossRef]
- Findlay, S. Importance of surface-subsurface exchange in stream ecosystems: The hyporheic zone. Limnol. Oceanogr. 1995, 40, 159–164. [Google Scholar] [CrossRef]
- Robertson, A.; Wood, P. Ecology of the hyporheic zone: Origins, current knowledge and future directions. Fund. Appl. Limnol. 2010, 176, 279–289. [Google Scholar] [CrossRef]
- Boulton, A.J.; Datry, T.; Kasahara, T.; Mutz, M.; Stanford, J.A. Ecology and management of the hyporheic zone: Stream-groundwater interactions of running waters and their floodplains. J. N. Am. Benthol. Soc. 2010, 29, 26–40. [Google Scholar] [CrossRef]
- Mathers, K.L.; Hill, M.J.; Wood, P.J. Benthic and hyporheic macroinvertebrate distribution within the heads and tails of riffles during baseflow conditions. Hydrobiologia 2017, 794, 17–30. [Google Scholar] [CrossRef]
- Dole-Olivier, M.-J. The hyporheic refuge hypothesis reconsidered: A review of hydrological aspects. Mar. Freshw. Res. 2011, 62, 1281–1302. [Google Scholar] [CrossRef]
- Kawanishi, R.; Inoue, M.; Dohi, R.; Fujii, A.; Miyake, Y. The role of the hyporheic zone for a benthic fish in an intermittent river: A refuge, not a graveyard. Aquat. Sci. 2013, 75, 425–431. [Google Scholar] [CrossRef]
- Mejia, F.H.; Baxter, C.V.; Berntsen, E.K.; Fremier, A.K. Linking groundwater-surface water exchange to food production and salmonid growth. Can. J. Fish. Aquat. Sci. 2016, 73, 1650–1660. [Google Scholar] [CrossRef]
- Olsen, D.A.; Young, R.G. Significance of river-aquifer interactions for reach-scale thermal patterns and trout growth potential in the Motueka River, New Zealand. Hydrogeol. J. 2009, 17, 175–183. [Google Scholar] [CrossRef]
- Torgersen, C.E.; Price, D.M.; Li, H.W.; McIntosh, B.A. Multiscale thermal refugia and stream habitat associations of chinook salmon in northeastern Oregon. Ecol. Appl. 1999, 9, 301–319. [Google Scholar] [CrossRef]
- Pepin, D.M.; Hauer, F.R. Benthic responses to groundwater–surface water exchange in 2 alluvial rivers in northwestern Montana. J. N. Am. Benthol. Soc. 2002, 21, 370–383. [Google Scholar] [CrossRef]
- Wright, K.K.; Baxter, C.V.; Li, J.L. Restricted hyporheic exchange in an alluvial river system: Implications for theory and management. J. N. Am. Benthol. Soc. 2005, 24, 447–460. [Google Scholar] [CrossRef]
- Arrigoni, A.S.; Poole, G.C.; Mertes, L.A.K.; O’Daniel, S.J.; Woessner, W.W.; Thomas, S.A. Buffered, lagged, or cooled? Disentangling hyporheic influences on temperature cycles in stream channels. Water Resour. Res. 2008, 44, W09418. [Google Scholar] [CrossRef]
- Kath, J.; Harrison, E.; Kefford, B.J.; Moore, L.; Wood, P.J.; Schäfer, R.B.; Dyer, F. Looking beneath the surface: Using hydrogeology and traits to explain flow variability effects on stream macroinvertebrates. Ecohydrology 2016, 9, 1480–1495. [Google Scholar] [CrossRef]
- Stubbington, R. The hyporheic zone as an invertebrate refuge: A review of variability in space, time, taxa and behaviour. Mar. Freshw. Res. 2012, 63, 293–311. [Google Scholar] [CrossRef]
- Kløve, B.; Ala-aho, P.; Bertrand, G.; Boukalova, Z.; Ertürk, A.; Goldscheider, N.; Ilmonen, J.; Karakaya, N.; Kupfersberger, H.; Kvœrner, J.; et al. Groundwater dependent ecosystems. Part I: Hydroecological status and trends. Environ. Sci. Policy 2011, 14, 770–781. [Google Scholar] [CrossRef]
- Coulter, A.A.; Galarowicz, T.L. Fish assemblage and environmental differences upstream and downstream of a cave: A potential reset mechanism. Environ. Biol. Fishes 2015, 98, 1223–1231. [Google Scholar] [CrossRef]
- Stubbington, R.; Wood, P.J.; Reid, I.; Gunn, J. Benthic and hyporheic invertebrate community responses to seasonal flow recession in a groundwater-dominated stream. Ecohydrology 2011, 4, 500–511. [Google Scholar] [CrossRef]
- Arismendi, I.; Johnson, S.L.; Dunham, J.B.; Haggerty, R. Descriptors of natural thermal regimes in streams and their responsiveness to change in the Pacific Northwest of North America. Freshw. Biol. 2013, 58, 880–894. [Google Scholar] [CrossRef]
- Olden, J.D.; Naiman, R.J. Incorporating thermal regimes into environmental flows assessments: Modifying dam operations to restore freshwater ecosystem integrity. Freshw. Biol. 2010, 55, 86–107. [Google Scholar] [CrossRef]
- Caissie, D. The thermal regime of rivers: A review. Freshw. Biol. 2006, 51, 1389–1406. [Google Scholar] [CrossRef]
- Woodward, G.; Bonada, N.; Brown, L.E.; Death, R.G.; Durance, I.; Gray, C.; Hladyz, S.; Ledger, M.E.; Milner, A.M.; Ormerod, S.J. The effects of climatic fluctuations and extreme events on running water ecosystems. Philos. Trans. R. Soc. B 2016, 371, 20150274. [Google Scholar] [CrossRef]
- Lau, D.C.P.; Goedkoop, W.; Vrede, T. Cross-ecosystem differences in lipid composition and growth limitation of a benthic generalist consumer. Limnol. Oceanogr. 2013, 58, 1149–1164. [Google Scholar] [CrossRef]
- Brett, M.T.; Bunn, S.E.; Chandra, S.; Galloway, A.W.E.; Guo, F.; Kainz, M.J.; Kankaala, P.; Lau, D.C.P.; Moulton, T.P.; Power, M.E.; et al. How important are terrestrial organic carbon inputs for secondary production in freshwater ecosystems? Freshw. Biol. 2017, 62, 833–853. [Google Scholar] [CrossRef]
- DeNicola, D. Periphyton responses to temperature at different ecological levels. In Algal Ecology: Freshwater Benthic Ecosystems; Stevenson, R.J., Bothwell, M.L., Lowe, R.L., Thorp, J.H., Eds.; Academic Press: San Diego, CA, USA, 1996; pp. 149–181. ISBN 0-12-668450-2. [Google Scholar]
- Biggs, B.J.F.; Nikora, V.I.; Snelder, T.H. Linking scales of flow variability to lotic ecosystem structure and function. River Res. Appl. 2005, 21, 283–298. [Google Scholar] [CrossRef]
- Zhu, Z.; Song, C. Scientific Survey of Shennongjia Nature Reserve; China Forestry Publishing House: Beijing, China, 1999; ISBN 7-5038-2335-8. (In Chinese) [Google Scholar]
- Sweeting, M.M. Karst in China: Its Geomorphology and Environment; Springer-Verlag: Berlin/Heidelberg, Germany, 1995; 265p, ISBN 3642795226. [Google Scholar]
- Gore, J.A.; Banning, J. Chapter 3—Discharge measurements and streamflow analysis. In Methods in Stream Ecology, 3rd ed.; Hauer, F.R., Lamberti, G.A., Eds.; Academic Press: Boston, MA, USA, 2017; Volume 1, pp. 49–70. [Google Scholar]
- Tang, T.; Jia, X.; Jiang, W.; Cai, Q. Multi-scale temporal dynamics of epilithic algal assemblages: Evidence from a Chinese subtropical mountain river network. Hydrobiologia 2016, 770, 289–299. [Google Scholar] [CrossRef]
- Bureau, C.E.P. Standard Methods for Examination of Water and Wastewater, 4th ed.; Chinese Environmental Science Press: Beijing, China, 2004; ISBN 7-80163-400-4. (In Chinese) [Google Scholar]
- O’Driscoll, M.A.; DeWalle, D.R. Stream-air temperature relations to classify stream-ground water interactions in a karst setting, central Pennsylvania, USA. J. Hydrol. 2006, 329, 140–153. [Google Scholar] [CrossRef]
- Harig, A.L.; Fausch, K.D. Minimum habitat requirements for establishing translocated cutthroat trout populations. Ecol. Appl. 2002, 12, 535–551. [Google Scholar] [CrossRef]
- Rodman, A.R.; Scott, J.T. Comparing two periphyton collection methods commonly used for stream bioassessment and the development of numeric nutrient standards. Environ. Monit. Assess. 2017, 189, 360. [Google Scholar] [CrossRef]
- Winder, M.; Cloern, J.E. The annual cycles of phytoplankton biomass. Philos. Trans. R. Soc. B 2010, 365, 3215–3226. [Google Scholar] [CrossRef] [PubMed]
- Cazelles, B.; Chavez, M.; Berteaux, D.; Ménard, F.; Vik, J.O.; Jenouvrier, S.; Stenseth, N.C. Wavelet analysis of ecological time series. Oecologia 2008, 156, 287–304. [Google Scholar] [CrossRef]
- Keitt, T.H.; Fischer, J. Detection of scale-specific community dynamics using wavelets. Ecology 2006, 87, 2895–2904. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Vasseur, D.A.; Yodzis, P. The color of environmental noise. Ecology 2004, 85, 1146–1152. [Google Scholar] [CrossRef]
- Cloern, J.E.; Jassby, A.D. Patterns and scales of phytoplankton variability in estuarine–coastal ecosystems. Estuaries coasts 2010, 33, 230–241. [Google Scholar] [CrossRef]
- Chang, C.-W.; Ushio, M.; Hsieh, C. Empirical dynamic modeling for beginners. Ecol. Res. 2017, 32, 785–796. [Google Scholar] [CrossRef]
- Deyle, E.R.; Fogarty, M.; Hsieh, C.; Kaufman, L.; MacCall, A.D.; Munch, S.B.; Perretti, C.T.; Ye, H.; Sugihara, G. Predicting climate effects on Pacific sardine. Proc. Natl. Acad. Sci. USA 2013, 110, 6430–6435. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.; Deyle, E.; Fogarty, M.; Munch, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Ye, H.; Sugihara, G. Information leverage in interconnected ecosystems: Overcoming the curse of dimensionality. Science 2016, 353, 922–925. [Google Scholar] [CrossRef] [PubMed]
- Van Nes, E.H.; Scheffer, M.; Brovkin, V.; Lenton, T.M.; Ye, H.; Deyle, E.; Sugihara, G. Causal feedbacks in climate change. Nat. Clim. Chang. 2015, 5, 445–448. [Google Scholar] [CrossRef]
- Ye, H.; Deyle, E.R.; Gilarranz, L.J.; Sugihara, G. Distinguishing time-delayed causal interactions using convergent cross mapping. Sci. Rep. 2015, 5, 14750. [Google Scholar] [CrossRef]
- Burkholder, B.K.; Grant, G.E.; Haggerty, R.; Khangaonkar, T.; Wampler, P.J. Influence of hyporheic flow and geomorphology on temperature of a large, gravel-bed river, Clackamas River, Oregon, USA. Hydrol. Process. 2008, 22, 941–953. [Google Scholar] [CrossRef]
- Hannah, D.M.; Malcolm, I.A.; Bradley, C. Seasonal hyporheic temperature dynamics over riffle bedforms. Hydrol. Process. 2009, 23, 2178–2194. [Google Scholar] [CrossRef]
- Story, A.; Moore, R.; Macdonald, J. Stream temperatures in two shaded reaches below cutblocks and logging roads: Downstream cooling linked to subsurface hydrology. Can. J. For. Res. 2003, 33, 1383–1396. [Google Scholar] [CrossRef]
- Ford, D.; Williams, P.D. Karst Hydrogeology and Geomorphology; John Wiley & Sons Ltd.: Chichester, UK, 2007; ISBN 978-0-470-84996-5. [Google Scholar]
- Wyatt, K.H.; Hauer, F.R.; Pessoney, G.F. Benthic algal response to hyporheic-surface water exchange in an alluvial river. Hydrobiologia 2008, 607, 151–161. [Google Scholar] [CrossRef]
- Álvarez, M.; Pardo, I. Factors controlling epilithon biomass in a temporary, karstic stream: The interaction between substratum and grazing. J. N. Am. Benthol. Soc. 2007, 26, 207–220. [Google Scholar] [CrossRef]
- Godwin, C.M.; Carrick, H.J. Spatio-temporal variation of periphyton biomass and accumulation in a temperate spring-fed stream. Aquat. Ecol. 2008, 42, 583–595. [Google Scholar] [CrossRef]
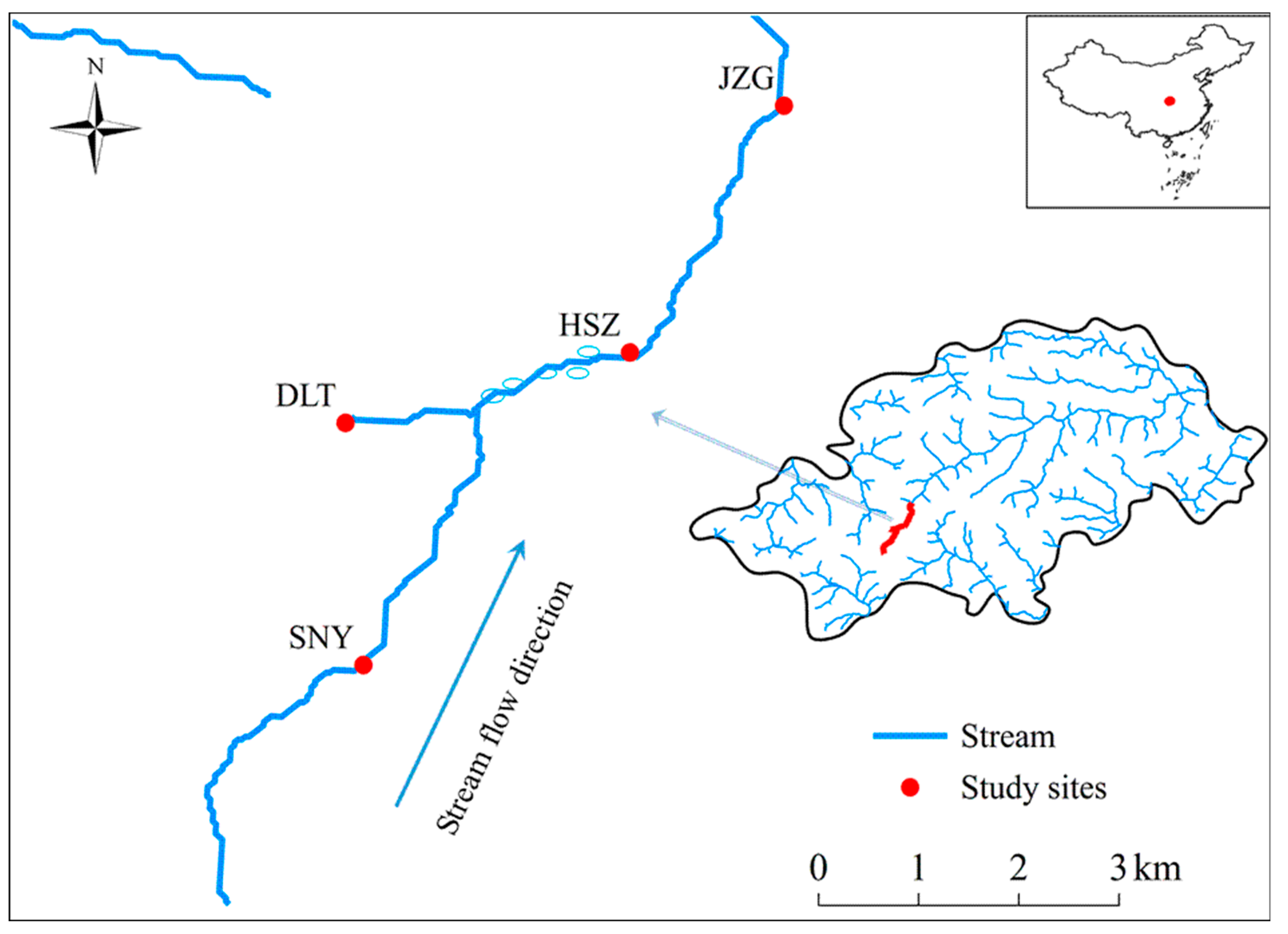
| Sheng Nong Yuan | Da Long Tan | Hong Shi Zi | Ji Zi Gou | |
|---|---|---|---|---|
| Abbreviation | SNY | DLT | HSZ | JZG |
| Latitude (°N) | 31.4722 | 31.4935 | 31.4997 | 31.5215 |
| Longitude (°E) | 110.2983 | 110.2967 | 110.3222 | 110.3361 |
| Elevation (m a.s.l.) | 2320 | 2220 | 1950 | 1820 |
| Stream order | 1 | 1 | 2 | 2 |
| Wetted width (m, mean ± SD) | 3.03 ± 2.34 | 2.81 ± 0.87 | 5.82 ± 3.63 | 6.05 ± 3.07 |
| Water depth (cm, mean± SD) | 16.5 ± 7.4 | 11.5 ± 3.8 | 18.1 ± 7.8 | 20.5 ± 5.0 |
| Stream Reach | Regression Coefficient | R2adj | |
|---|---|---|---|
| Y Intercept | Slope | ||
| SNY | 2.296 | 0.373 | 0.807 |
| DLT | 1.834 | 0.453 | 0.830 |
| HSZ | 4.162 | 0.352 | 0.861 |
| JZG | 3.327 | 0.476 | 0.850 |
| Regime | Descriptors | Metrics | Stream Reach | |||
|---|---|---|---|---|---|---|
| SNY | DLT | HSZ | JZG | |||
| Water temperature | Magnitude | Mean (°C) | 5.9 | 6.7 | 7.6 | 9.1 |
| Mean_max (°C) | 9.6 | 12.0 | 11.4 | 14.7 | ||
| Mean_min (°C) | 1.2 | 0.9 | 3.7 | 2.7 | ||
| Variability | Range (°C) | 10.3 | 13.4 | 11.9 | 17.3 | |
| CV (%) | 52.4 | 59.5 | 37.9 | 48.6 | ||
| Frequency | Months < 3 °C | 19 | 19 | 2 | 8 | |
| Months > 10 °C | 1 | 17 | 19 | 33 | ||
| Timing | M_mean_max | Aug | Aug | Aug | Aug | |
| M_mean_min | Jan | Jan | Jan | Jan | ||
| Discharge | Magnitude | Mean (m3 s−1) | 0.145 | 0.080 | 0.196 | 0.482 |
| Mean_max (m3 s−1) | 0.527 | 0.227 | 0.700 | 1.274 | ||
| Mean_min (m3 s−1) | 0.012 | 0.016 | 0.013 | 0.096 | ||
| Variability | Range (m3 s−1) | 1.717 | 0.553 | 3.251 | 4.329 | |
| CV (%) | 163.3 | 108.0 | 234.4 | 155.8 | ||
| Frequency | Months < 0.02 m3 s−1 | 15 | 14 | 19 | 0 | |
| Months > 0.20 m3 s−1 | 12 | 5 | 14 | 38 | ||
| Timing | M_mean_max | May | May | May | May | |
| Mmean_min | Feb | Jan | Jan | Jan | ||
| Chl. a | Magnitude | Mean (mg m−2) | 5.60 | 3.56 | 5.28 | 7.58 |
| Mean_max (mg m−2) | 9.46 | 6.70 | 7.98 | 20.42 | ||
| Mean_min (mg m−2) | 2.68 | 1.44 | 2.43 | 2.24 | ||
| Variability | Range (mg m−2) | 16.83 | 13.81 | 18.38 | 33.82 | |
| CV (%) | 66.0 | 83.8 | 82.7 | 112.4 | ||
| Frequency | Months < 5 mg m−2 | 32 | 54 | 43 | 38 | |
| Months > 10 mg m−2 | 8 | 3 | 11 | 19 | ||
| Timing | M_mean_max | Dec | Feb | Dec | Feb | |
| M_mean_min | July | July | May | Apr | ||
| SNY | DLT | HSZ | JZG | |
|---|---|---|---|---|
| WT | 10–14 (12) | 10–14 (12) | 10–14 (12) | 10–14 (12) |
| Discharge | 12 | 11–13 (12) | 12 | 12 |
| Chl. a | 10–13 (12) | 11–13 (12) | - | 10–13 (12) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, T.; Guo, S.; Tan, L.; Li, T.; Burrows, R.M.; Cai, Q. Temporal Effects of Groundwater on Physical and Biotic Components of a Karst Stream. Water 2019, 11, 1299. https://doi.org/10.3390/w11061299
Tang T, Guo S, Tan L, Li T, Burrows RM, Cai Q. Temporal Effects of Groundwater on Physical and Biotic Components of a Karst Stream. Water. 2019; 11(6):1299. https://doi.org/10.3390/w11061299
Chicago/Turabian StyleTang, Tao, Shuhan Guo, Lu Tan, Tao Li, Ryan M. Burrows, and Qinghua Cai. 2019. "Temporal Effects of Groundwater on Physical and Biotic Components of a Karst Stream" Water 11, no. 6: 1299. https://doi.org/10.3390/w11061299
APA StyleTang, T., Guo, S., Tan, L., Li, T., Burrows, R. M., & Cai, Q. (2019). Temporal Effects of Groundwater on Physical and Biotic Components of a Karst Stream. Water, 11(6), 1299. https://doi.org/10.3390/w11061299






