The Effect of Stream Discharge on Hyporheic Exchange
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Field Measurement
2.3. Field Data Analysis
2.4. Modeling Framework
3. Results
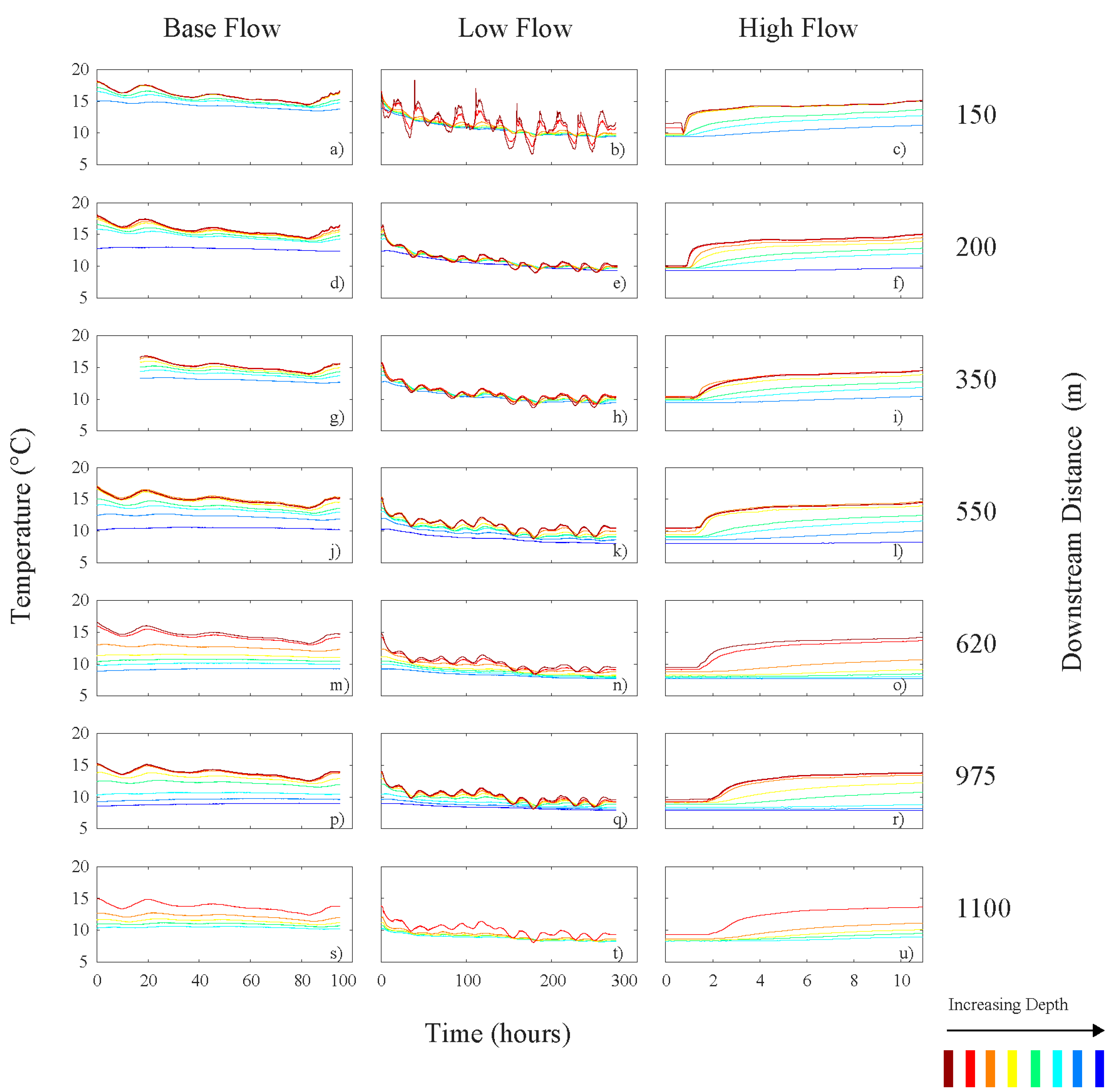
3.1. Water Temperature
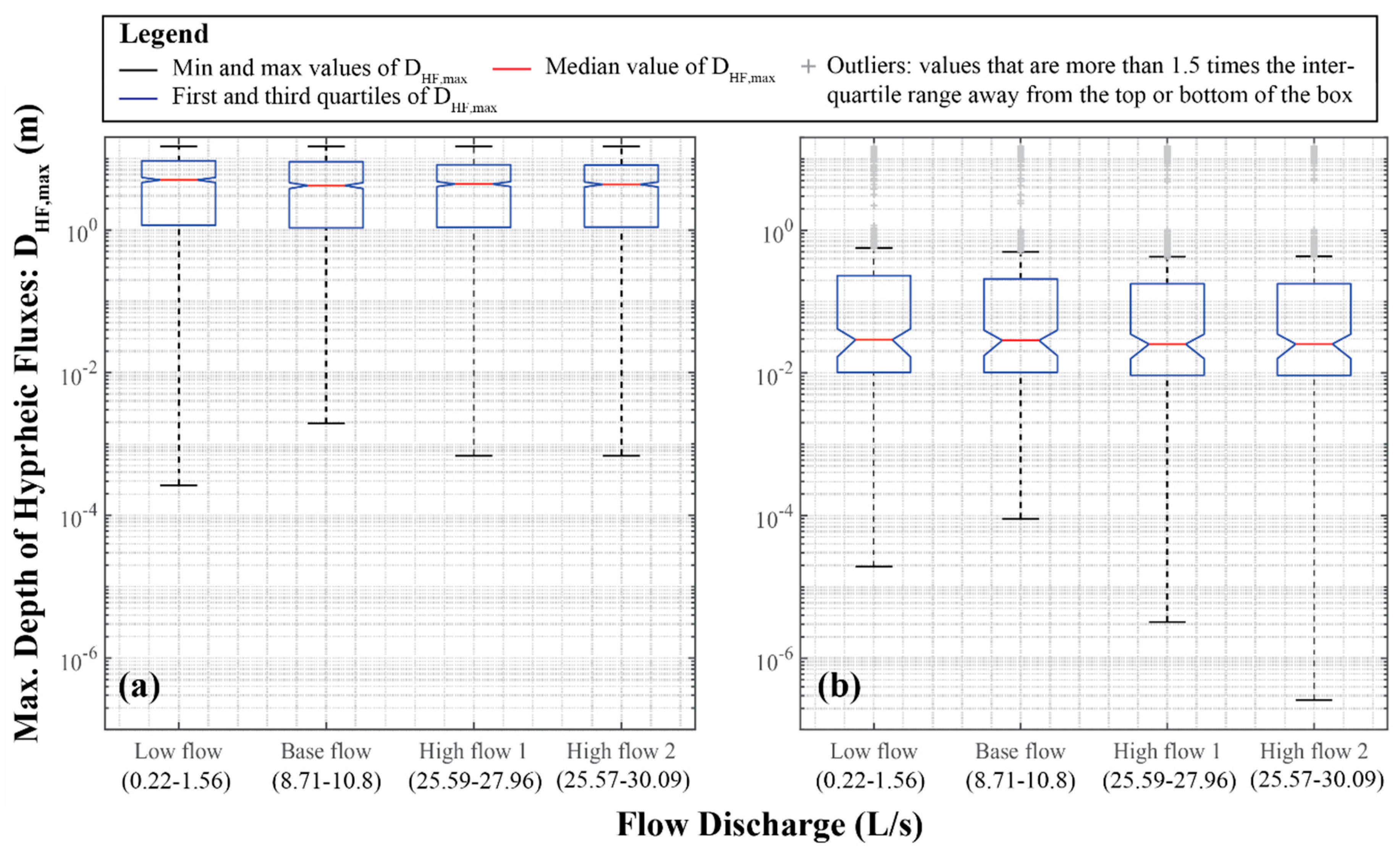
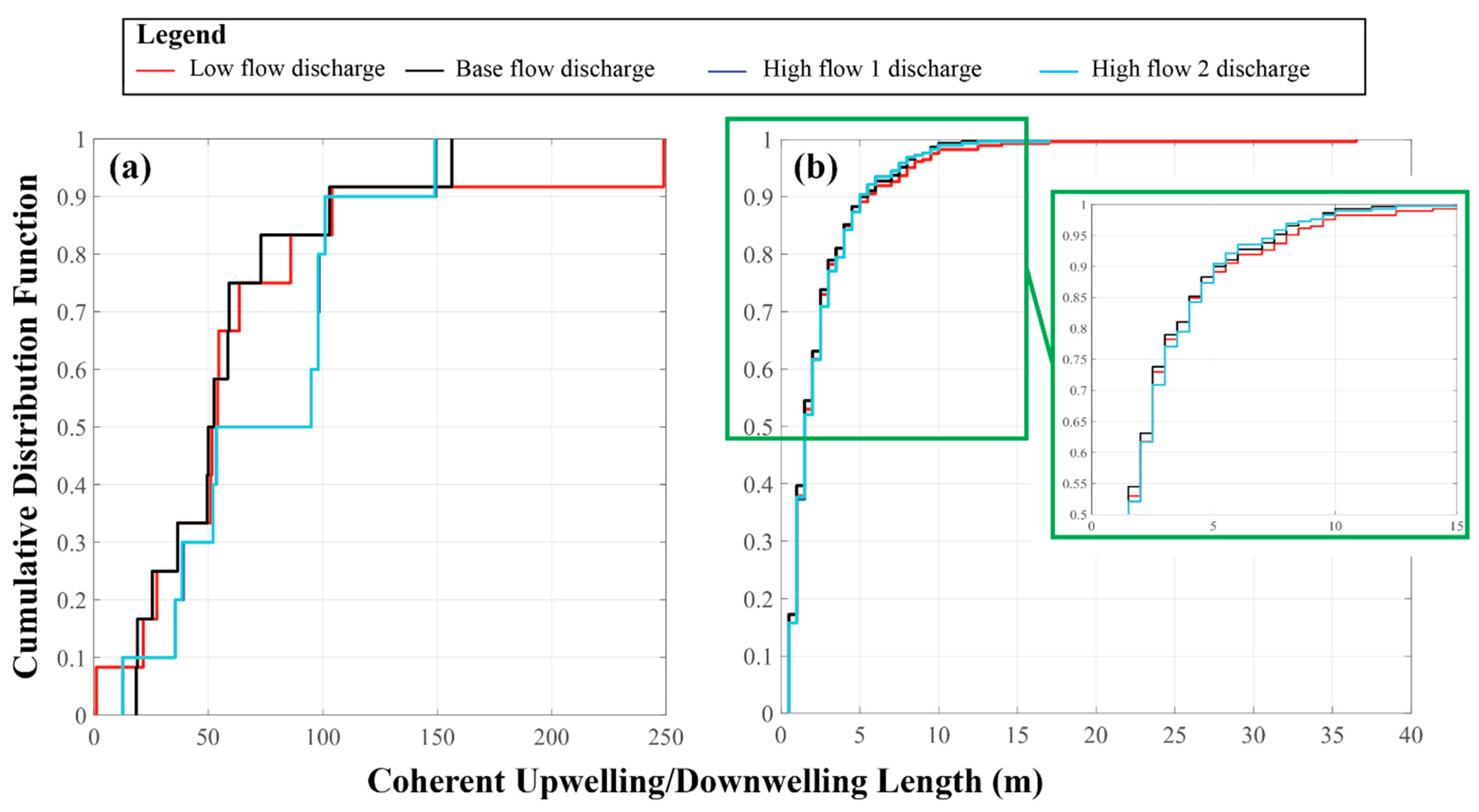
3.2. Modeling Results
4. Discussion
4.1. Temperature Variation in the Streambed Sediment
4.2. The Role of the Heterogeneity of Sediment Permeability in Hyporheic Exchange
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cardenas, M.B. Hyporheic zone hydrologic science: A historical account of its emergence and a prospectus. Water Resour. Res. 2015, 51, 3601–3616. [Google Scholar] [CrossRef]
- Tonina, D.; Buffington, J.M. Effects of stream discharge, alluvial depth and bar amplitude on hyporheic flow in pool-riffle channels. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Stanford, J.A.; Ward, J.V. The hyporheic habitat of river ecosystems. Nature 1988, 335, 64–66. [Google Scholar] [CrossRef]
- Sawyer, A.H.; Bayani Cardenas, M.; Buttles, J. Hyporheic temperature 165 dynamics and heat exchange near channel-spanning logs. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Harvey, J.W.; Böhlke, J.K.; Voytek, M.A.; Scott, D.; Tobias, C.R. Hyporheic zone denitrification: Controls on effective reaction depth and contribution to whole stream mass balance. Water Resour. Res. 2013, 49, 6298–6316. [Google Scholar] [CrossRef]
- Boano, F.; Camporeale, C.; Revelli, R.; Ridolfi, L. Sinuosity-driven hyporheic exchange in meandering rivers. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Elliott, A.H.; Brooks, N.H. Transfer of nonsorbing solutes to a streambed with bed forms: Theory. Water Resour. Res. 1997, 33, 123–136. [Google Scholar] [CrossRef]
- Gomez-Velez, J.D.; Krause, S.; Wilson, J.L. Effect of low-permeability layers on spatial patterns of hyporheic exchange and groundwater upwelling. Water Resour. Res. 2014, 50, 5196–5215. [Google Scholar] [CrossRef]
- Stonedahl, S.H.; Harvey, J.W.; Packman, A.I. Interactions between hyporheic flow produced by stream meanders, bars, and dunes. Water Resour. Res. 2013, 49, 5450–5461. [Google Scholar] [CrossRef]
- Sawyer, A.H.; Cardenas, M.B.; Bomar, A.; Mackey, M. Impact of dam operations on hyporheic exchange in the riparian zone of a regulated river. Hydrol. Process. 2009, 23, 2129–2137. [Google Scholar] [CrossRef]
- McGlynn, B.L.; McDonnell, J.J.; Shanley, J.B.; Kendall, C. Riparian zone flowpath dynamics during snowmelt in a small headwater catchment. J. Hydrol. 1999, 222, 75–92. [Google Scholar] [CrossRef]
- Malcolm, I.A.; Soulsby, C.; Youngson, A.F.; Petry, J. Heterogeneity in ground water–surface water interactions in the hyporheic zone of a salmonid spawning stream. Hydrol. Process. 2003, 17, 601–617. [Google Scholar] [CrossRef]
- Schmidt, C.; Bayer-Raich, M.; Schirmer, M. Characterization of spatial heterogeneity of groundwater-stream water interactions using multiple depth streambed temperature measurements at the reach scale. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 1419–1446. [Google Scholar] [CrossRef]
- Boano, F.; Revelli, R.; Ridolfi, L. Reduction of the hyporheic zone volume due to the stream-aquifer interaction. Geophys. Res. Lett. 2008, 35, L09401. [Google Scholar] [CrossRef]
- Mojarrad, B.B.; Riml, J.; Wörman, A.; Laudon, H. Fragmentation of the hyporheic zone due to regional groundwater circulation. Water Resour. Res. 2019, 55, 1242–1262. [Google Scholar] [CrossRef]
- Saar, M.O.; Manga, M. Depth dependence of permeability in the Oregon Cascades inferred from hydrogeologic, thermal, seismic, and magmatic modeling constraints. J. Geophys. Res. 2004, 109, B04204. [Google Scholar] [CrossRef]
- Marklund, L.; Wörman, A. The use of spectral analysis-based exact solutions to characterize topography-controlled groundwater flow. Hydrogeol. J. 2011, 19, 1531–1543. [Google Scholar] [CrossRef]
- Morén, I.; Wörman, A.; Riml, J. Design of remediation actions for nutrient mitigation in the hyporheic zone. Water Resour. Res. 2017, 53, 8872–8899. [Google Scholar] [CrossRef]
- Brunke, M.; Gonser, T. The ecological significance of exchange processes between rivers and groundwater. Freshwater Biol. 1997, 37, 1–33. [Google Scholar] [CrossRef]
- Conant, B.; Cherry, J.; Gillham, R. A PCE groundwater plume discharging to a river: Influence of the streambed and near-river zone on contaminant distributions. J. Contam. Hydrol. 2004, 73, 249–279. [Google Scholar] [CrossRef]
- Kalbus, E.; Schmidt, C.; Bayer-Raich, M.; Leschik, S.; Reinstorf, F.; Balcke, G.; Schirmer, M. New methodology to investigate potential contaminant mass fluxes at the stream-aquifer interface by combining integral pumping tests and streambed temperatures. Environ. Pollut. 2007, 148, 808–816. [Google Scholar] [CrossRef] [PubMed]
- Chapman, S.W.; Parker, B.L.; Cherry, J.A.; Aravena, R.; Hunkeler, D. Groundwater-surface water interaction and its role on TCE groundwater plume attenuation. J. Contam. Hydrol. 2007, 91, 203–232. [Google Scholar] [CrossRef] [PubMed]
- Kalbus, E.; Reinstorf, F.; Schirmer, M. Measuring methods for groundwater? Surface water interactions: A review. Hydrol. Earth Syst. Sci. 2006, 10, 873–887. [Google Scholar] [CrossRef]
- Anderson, M.P. Heat as a ground water tracer. Groundwater 2005, 43, 951–968. [Google Scholar] [CrossRef] [PubMed]
- Conant, B. Delineating and quantifying ground water discharge zones using streambed temperatures. Groundwater 2004, 42, 243–257. [Google Scholar] [CrossRef]
- Constantz, J. Heat as a tracer to determine streambed water exchanges. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Rau, G.C.; Andersen, M.S.; McCallum, A.M.; Acworth, R.I. Analytical methods that use natural heat as a tracer to quantify surface water–groundwater exchange, evaluated using field temperature records. Hydrogeol. J. 2010, 18, 1093–1110. [Google Scholar] [CrossRef]
- Krause, S.; Blume, T. Impact of seasonal variability and monitoring mode on the adequacy of fiber-optic distributed temperature sensing at aquifer-river interfaces. Water Resour. Res. 2013, 49, 2408–2423. [Google Scholar] [CrossRef]
- Selker, J.; van de Giesen, N.; Westhoff, M.; Luxemburg, W.; Parlange, M.B. Fiber optics opens window on stream dynamics. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Selker, J.S.; Thévenaz, L.; Huwald, H.; Mallet, A.; Luxemburg, W.; Van De Giesen, N.; Stejskal, M.; Zeman, J.; Westhoff, M.; Parlange, M.B. Distributed fiber-optic temperature sensing for hydrologic systems. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Krause, S.; Hannah, D.M.; Fleckenstein, J.H.; Heppell, C.M.; Kaeser, D.; Pickup, R.; Pinay, G.; Robertson, A.L.; Wood, P.J. Inter-disciplinary perspectives on processes in the hyporheic zone. Ecohydrology 2011, 4, 481–499. [Google Scholar] [CrossRef]
- Boano, F.; Revelli, R.; Ridolfi, L. Modeling hyporheic exchange with unsteady stream discharge and bedform dynamics. Water Resour. Res. 2013, 49, 4089–4099. [Google Scholar] [CrossRef]
- Gomez-Velez, J.D.; Wilson, J.L.; Cardenas, M.B.; Harvey, J.W. Flow and residence times of dynamic river bank storage and sinuosity-driven hyporheic exchange. Water Resour. Res. 2017, 53, 8572–8595. [Google Scholar] [CrossRef]
- Malzone, J.M.; Anseeuw, S.K.; Lowry, C.S.; Allen-King, R. Temporal hyporheic zone response to water table fluctuations. Groundwater 2016, 54, 274–285. [Google Scholar] [CrossRef] [PubMed]
- Malzone, J.M.; Lowry, C.S.; Ward, A.S. Response of the hyporheic zone to transient groundwater fluctuations on the annual and storm event time scales. Water Resour. Res. 2016, 52, 5301–5321. [Google Scholar] [CrossRef]
- Schmadel, N.M.; Ward, A.S.; Lowry, C.S.; Malzone, J.M. Hyporheic exchange controlled by dynamic hydrologic boundary conditions. Geophys. Res. Lett. 2016, 43, 4408–4417. [Google Scholar] [CrossRef]
- Trauth, N.; Fleckenstein, J.H. Single discharge events increase reactive efficiency of the hyporheic zone. Water Resour. Res. 2017, 53, 779–798. [Google Scholar] [CrossRef]
- Singh, T.; Wu, L.; Gomez-Velez, J.D.; Lewandowski, J.; Hannah, D.M.; Krause, S. Dynamic Hyporheic Zones: Exploring the Role of Peak Flow Events on Bedform-Induced Hyporheic Exchange. Water Resour. Res. 2019, 55, 218–235. [Google Scholar] [CrossRef]
- McCallum, J.L.; Shanafield, M. Residence times of stream-groundwater exchanges due to transient stream stage fluctuations. Water Resour. Res. 2016, 52, 2059–2073. [Google Scholar] [CrossRef]
- Sickbert, T.; Peterson, E.W. The effects of surface water velocity on hyporheic interchange. J. Water Resour. Prot. 2014, 6, 327–336. [Google Scholar] [CrossRef]
- Wroblicky, G.; Campana, M.; Valett, H.; Dahm, C. Seasonal variation in surface-subsurface water exchange and lateral hyporheic area of two stream-aquifer systems. Water Resour. Res. 1998, 34, 317–328. [Google Scholar] [CrossRef]
- Laudon, H.; Taberman, I.; Agren, A.; Futter, M.; Ottosson-Löfvenius, M.; Bishop, K. The Krycklan Catchment Study: A flagship infrastructure for hydrology, biogeochemistry, and climate research in the boreal landscape. Water Resour. Res. 2013, 49, 7154–7158. [Google Scholar] [CrossRef]
- Karlsen, R.H.; Grabs, T.; Bishop, K.; Buffam, I.; Laudon, H.; Seibert, J. Landscape controls on spatiotemporal discharge variability in a boreal catchment. Water Resour. Res. 2016, 52, 6541–6556. [Google Scholar] [CrossRef]
- Leach, J.A.; Lidberg, W.; Kuglerová, L.; Peralta-Tapia, A.; Ågren, A.; Laudon, H. Evaluating topography-based predictions of shallow lateral groundwater discharge zones for a boreal lake-stream system. Water Resour. Res. 2017, 53, 5420–5437. [Google Scholar] [CrossRef]
- Laudon, H.; Ottosson-Löfvenius, M. Adding snow to the picture: Providing complementary winter precipitation data to the Krycklan catchment study database. Hydrol. Process. 2016, 30, 2413–2416. [Google Scholar] [CrossRef]
- Lupon, A.; Denfeld, B.A.; Laudon, H.; Leach, J.; Karlsson, J.; Sponseller, R.A. Groundwater inflows control patterns and sources of greenhouse gas emissions from streams. Limnol. Oceanogr. 2019, 64. [Google Scholar] [CrossRef]
- Munz, M.; Oswald, S.E.; Schmidt, C. Sand box experiments to evaluate the influence of subsurface temperature probe design on temperature based water flux calculation. Hydrol. Earth Syst. Sci. 2011, 15, 3495–3510. [Google Scholar] [CrossRef]
- Sterte, E.J.; Johansson, E.; Sjöberg, Y.; Karlsen, R.H.; Laudon, H. Groundwater-surface water interactions across scales in a boreal landscape investigated using a numerical modelling approach. J. Hydrol. 2018, 560, 184–201. [Google Scholar] [CrossRef]
- Briggs, M.A.; Lautz, L.K.; Buckley, S.F.; Lane, J.W. Practical limitations on the use of diurnal temperature signals to quantify groundwater upwelling. J. Hydrol. 2014, 519, 1739–1751. [Google Scholar] [CrossRef]
- Shanafield, M.; Hatch, C.; Pohll, G. Uncertainty in thermal time series analysis estimates of streambed water flux. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Taniguchi, M. Evaluation of vertical groundwater fluxes and thermal properties of aquifers based on transient temperature-depth profiles. Water Resour. Res. 1993, 29, 2021–2026. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Wilson, J.L.; Zlotnik, V.A. Impact of heterogeneity, bed forms, and stream curvature on subchannel hyporheic exchange. Water Resour. Res. 2004, 40, W08307. [Google Scholar] [CrossRef]
- Salehin, M.; Packman, A.I.; Paradis, M. Hyporheic exchange with heterogeneous streambeds: Laboratory experiments and modeling. Water Resour. Res. 2004, 40, W11504. [Google Scholar] [CrossRef]
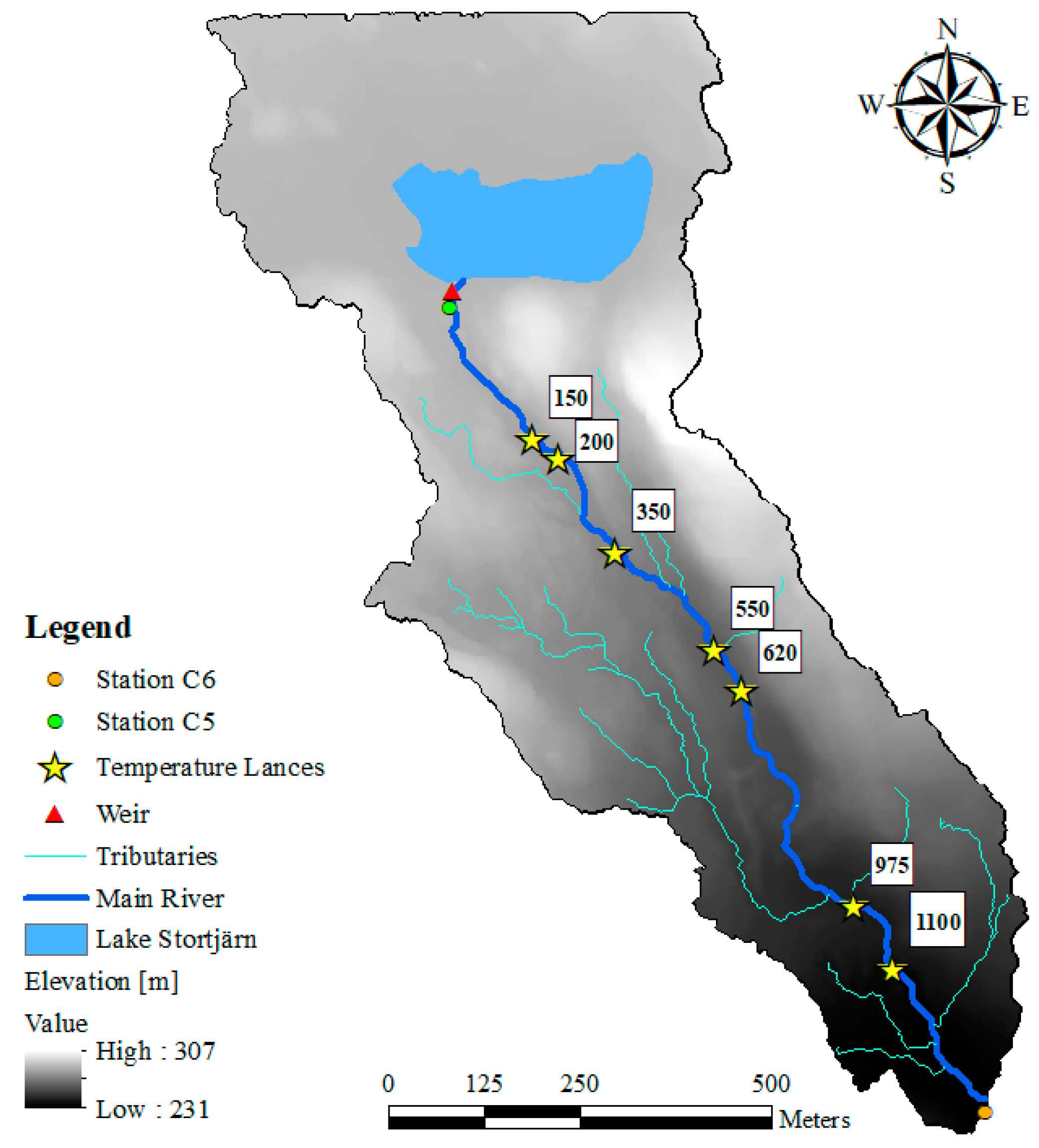



| Distance from Upstream Station [m] | Drainage Area [m2] | Snow Melt Flow (22 May 2017) | Summer Base Flow (27 June 2017) | Low Flow (18 August 2017) | High Flow (19 August 2017) | Autumn Base Flow (30 August 2017) | |||||
| Q [L/s] | d [cm] | Q [L/s] | d [cm] | Q [L/s] | d [cm] | Q [L/s] | d [cm] | Q [L/s] | d [cm] | ||
| 0 | 234,446 | 54.48 | 31 | 2.63 | 11 | 0.19 | 3 | 25.58 | 17 | 7.36 | 9 |
| 50 | 236,031 | 54.54 | 31 | 2.65 | 11 | 0.19 | 3 | 25.59 | 17 | 7.42 | 9 |
| 100 | 243,262 | 54.81 | 31 | 2.76 | 11 | 0.21 | 2 | 25.63 | 11 | 7.48 | 7 |
| 150 | 250,838 | 55.09 | 32 | 2.86 | 15 | 0.23 | 18 | 25.67 | 24 | 7.55 | 26 |
| 200 | 258,334 | 55.37 | 28 | 2.97 | 17 | 0.26 | 21 | 25.71 | 35 | 7.61 | 25 |
| 250 | 262,731 | 55.53 | 32 | 3.03 | 9 | 0.27 | 8 | 25.74 | 26 | 7.67 | 14 |
| 300 | 265,497 | 55.63 | 33 | 3.07 | 19 | 0.27 | 7 | 25.76 | 16 | 7.73 | 13 |
| 350 | 267,926 | 55.72 | 27 | 3.11 | 7 | 0.28 | 6 | 25.77 | 8 | 7.79 | 10 |
| 400 | 291,324 | 56.59 | 27 | 3.44 | 11 | 0.35 | 9 | 25.90 | 12 | 7.86 | 6 |
| 450 | 293,516 | 56.67 | 29 | 3.47 | 0.35 | 7 | 25.91 | 19 | 7.92 | 14 | |
| 500 | 296,214 | 56.77 | 21 | 3.51 | 0.36 | 5 | 25.93 | 16 | 7.98 | 10 | |
| 550 | 337,040 | 58.29 | 20 | 4.09 | 0.47 | 26 | 26.16 | 34 | 8.04 | 22 | |
| 600 | 343,055 | 58.51 | 42 | 4.17 | 0.49 | 15 | 26.19 | 24 | 8.11 | 16 | |
| 650 | 357,882 | 59.07 | 32 | 4.39 | 0.53 | 8 | 26.28 | 19 | 8.17 | 13 | |
| 700 | 373439 | 59.64 | 29 | 4.61 | 0.57 | 19 | 26.37 | 33 | 8.23 | 27 | |
| 750 | 375,921 | 59.74 | 27 | 4.64 | 0.58 | 14 | 26.38 | 20 | 8.29 | 11 | |
| 800 | 379,197 | 59.86 | 35 | 4.69 | 0.58 | 5 | 26.40 | 15 | 8.35 | 5 | |
| 850 | 396,899 | 60.52 | 22 | 4.94 | 0.63 | 5 | 26.50 | 16 | 8.42 | 17 | |
| 900 | 405,145 | 60.82 | 15 | 5.06 | 0.66 | 9 | 26.54 | 16 | 8.48 | 12 | |
| 950 | 411,322 | 61.05 | 26 | 5.14 | 0.67 | 4 | 26.58 | 19 | 8.54 | 14 | |
| 1000 | 413,347 | 61.13 | 29 | 5.17 | 0.68 | 24 | 26.59 | 29 | 8.60 | 29 | |
| 1050 | 535,591 | 65.67 | 31 | 6.91 | 1.01 | 6 | 27.28 | 17 | 8.66 | 10 | |
| 1100 | 558,355 | 66.51 | 21 | 7.24 | 1.07 | 4 | 27.41 | 9 | 8.73 | 8 | |
| 1150 | 567,113 | 66.84 | 14 | 7.36 | 1.10 | 2 | 27.46 | 9 | 8.79 | 5 | |
| 1200 | 568,492 | 66.89 | 28 | 7.38 | 1.10 | 2 | 27.47 | 20 | 8.85 | 4 | |
| 1250 | 573,211 | 67.07 | 30 | 7.45 | 1.11 | 14 | 27.49 | 23 | 8.91 | 20 | |
| 1300 | 578,673 | 67.27 | 35 | 7.52 | 1.13 | 19 | 27.52 | 32 | 8.98 | 26 | |
| 1437 | 648,703 | 69.87 | 35 | 8.52 | 1.32 | 19 | 27.92 | 32 | 9.19 | 26 | |
| Flow Discharge | Time Period | Mean Upstream Discharge [L/s] | Mean Downstream Discharge [L/s] |
|---|---|---|---|
| Base flow | 03–07August | 8.71 | 10.8 |
| Low flow | 07–19 August | 0.22 | 1.56 |
| High flow 1 | 19 August | 25.59 | 27.96 |
| High flow 2 | 21 August | 25.57 | 30.09 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mojarrad, B.B.; Betterle, A.; Singh, T.; Olid, C.; Wörman, A. The Effect of Stream Discharge on Hyporheic Exchange. Water 2019, 11, 1436. https://doi.org/10.3390/w11071436
Mojarrad BB, Betterle A, Singh T, Olid C, Wörman A. The Effect of Stream Discharge on Hyporheic Exchange. Water. 2019; 11(7):1436. https://doi.org/10.3390/w11071436
Chicago/Turabian StyleMojarrad, Brian Babak, Andrea Betterle, Tanu Singh, Carolina Olid, and Anders Wörman. 2019. "The Effect of Stream Discharge on Hyporheic Exchange" Water 11, no. 7: 1436. https://doi.org/10.3390/w11071436
APA StyleMojarrad, B. B., Betterle, A., Singh, T., Olid, C., & Wörman, A. (2019). The Effect of Stream Discharge on Hyporheic Exchange. Water, 11(7), 1436. https://doi.org/10.3390/w11071436





