Assessment of Climate Change Impacts in the North Adriatic Coastal Area. Part II: Consequences for Coastal Erosion Impacts at the Regional Scale
Abstract
1. Introduction
2. Study Area
3. Methods
- (1)
- Input data collection: vulnerability and hazard matrices;
- (2)
- Hazard scenario assessment;
- (3)
- Exposure assessment;
- (4)
- Susceptibility assessment;
- (5)
- Risk assessment;
- (6)
- Damage assessment.
3.1. Input Data: Hazard and Vulnerability Matrices
3.2. Hazard Scenario Assessment
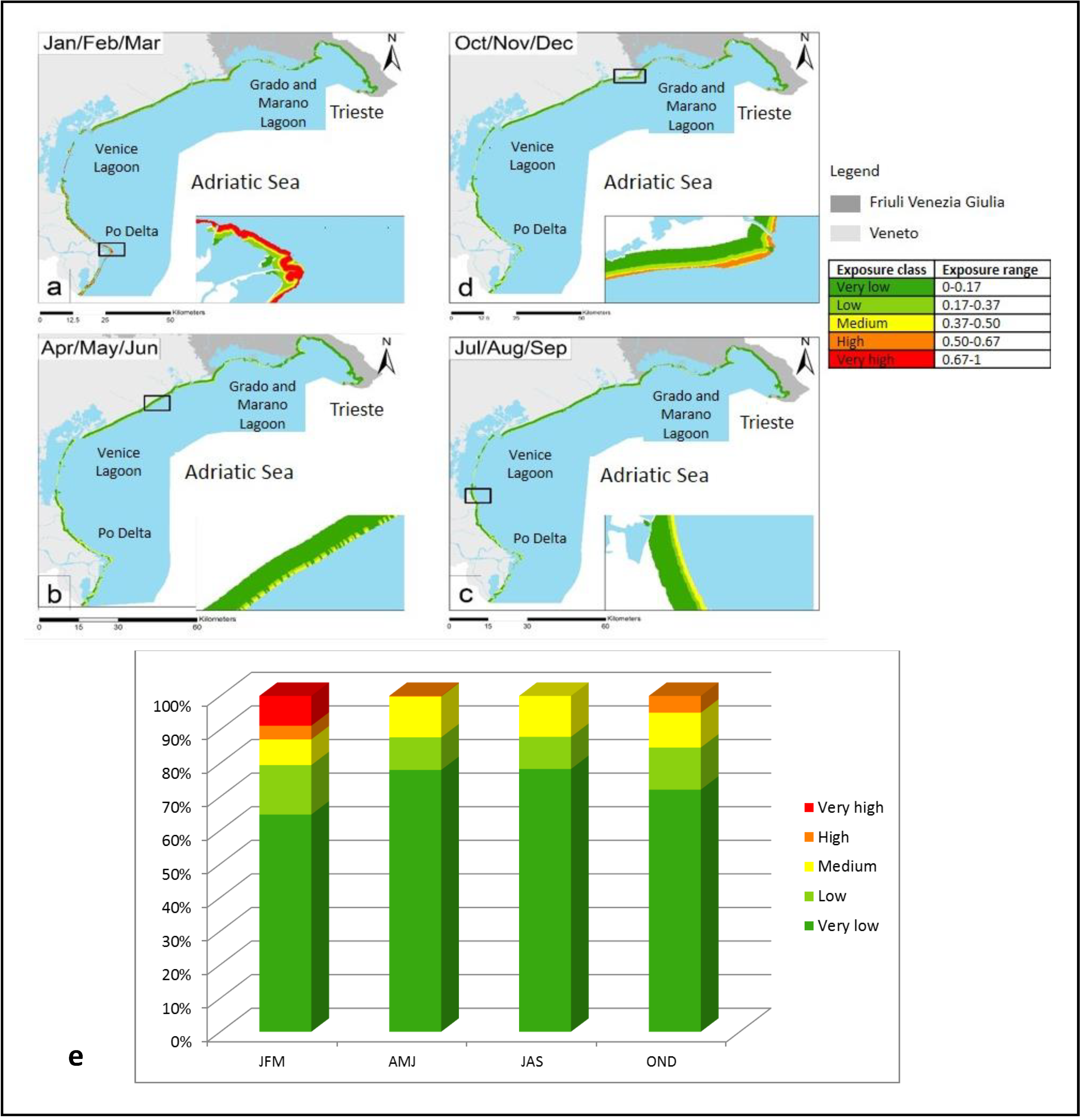
3.3. Exposure Assessment
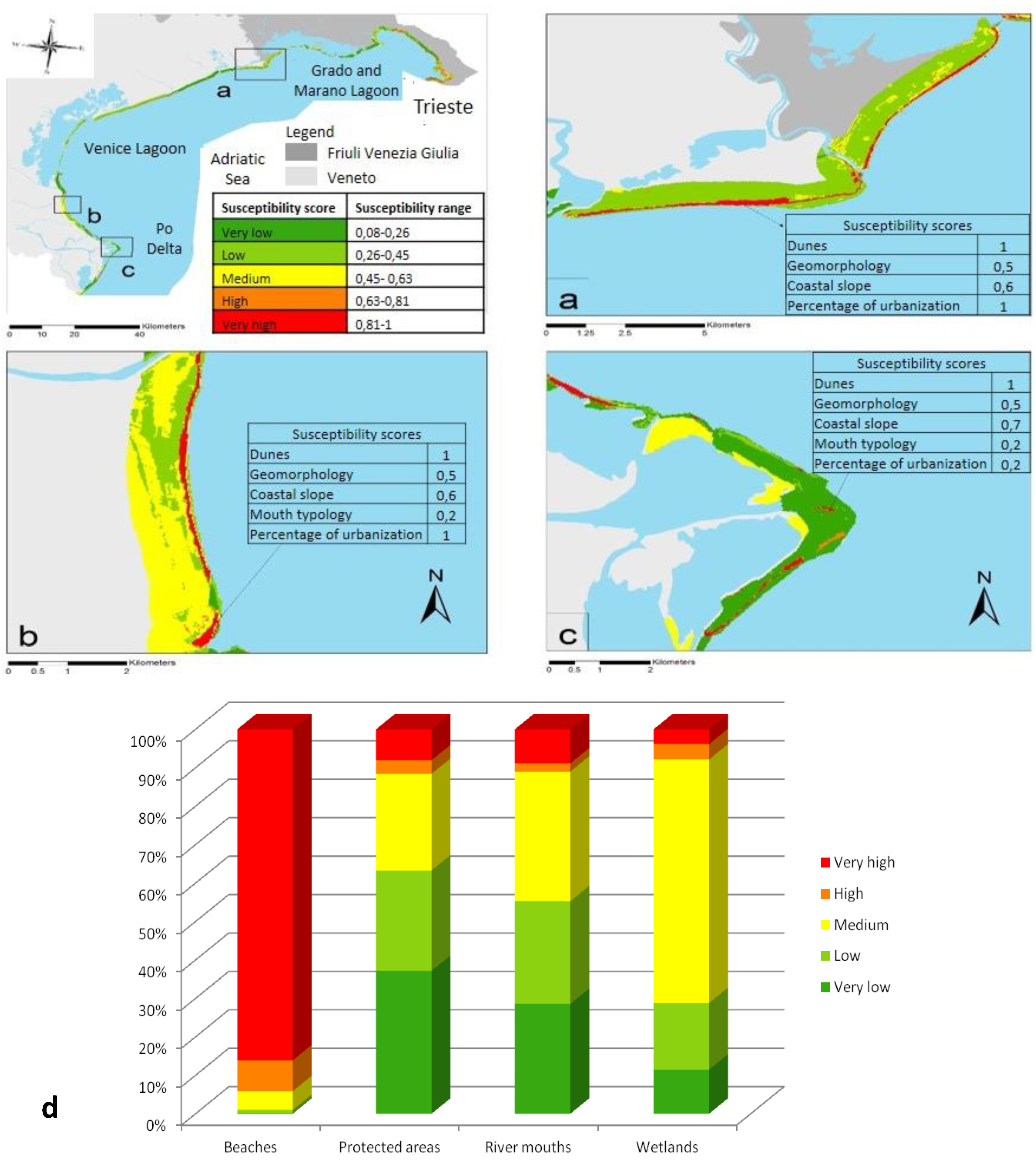
3.4. Susceptibility Assessment
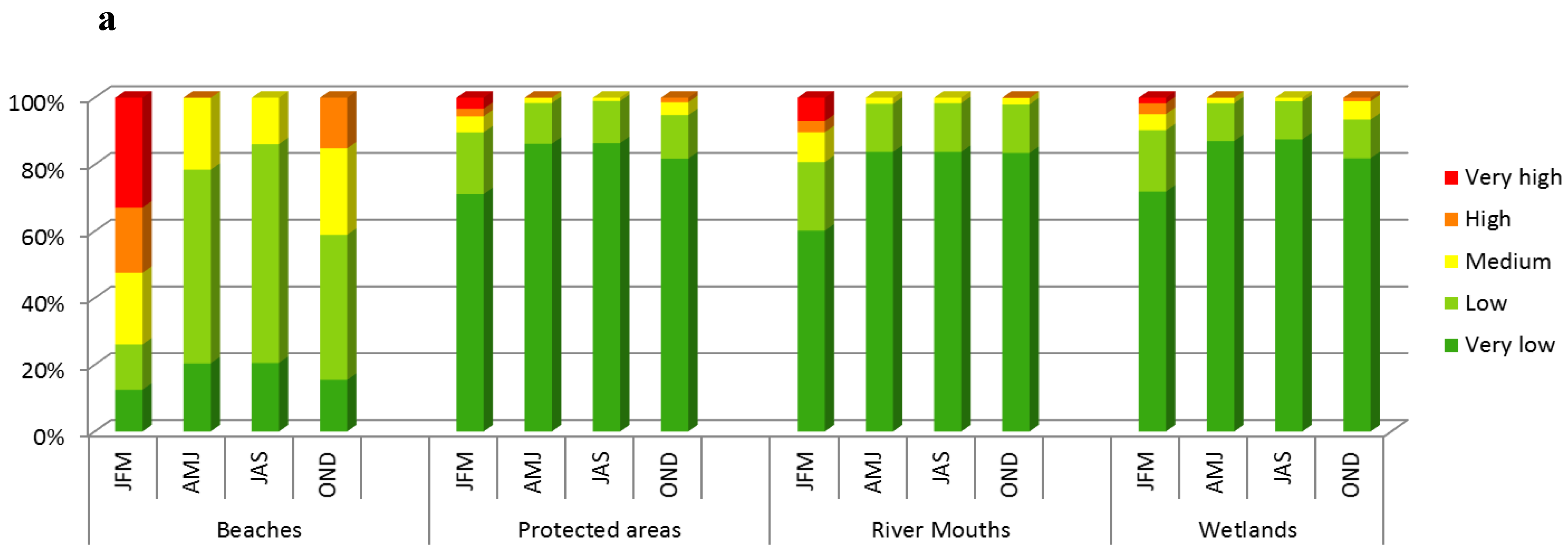
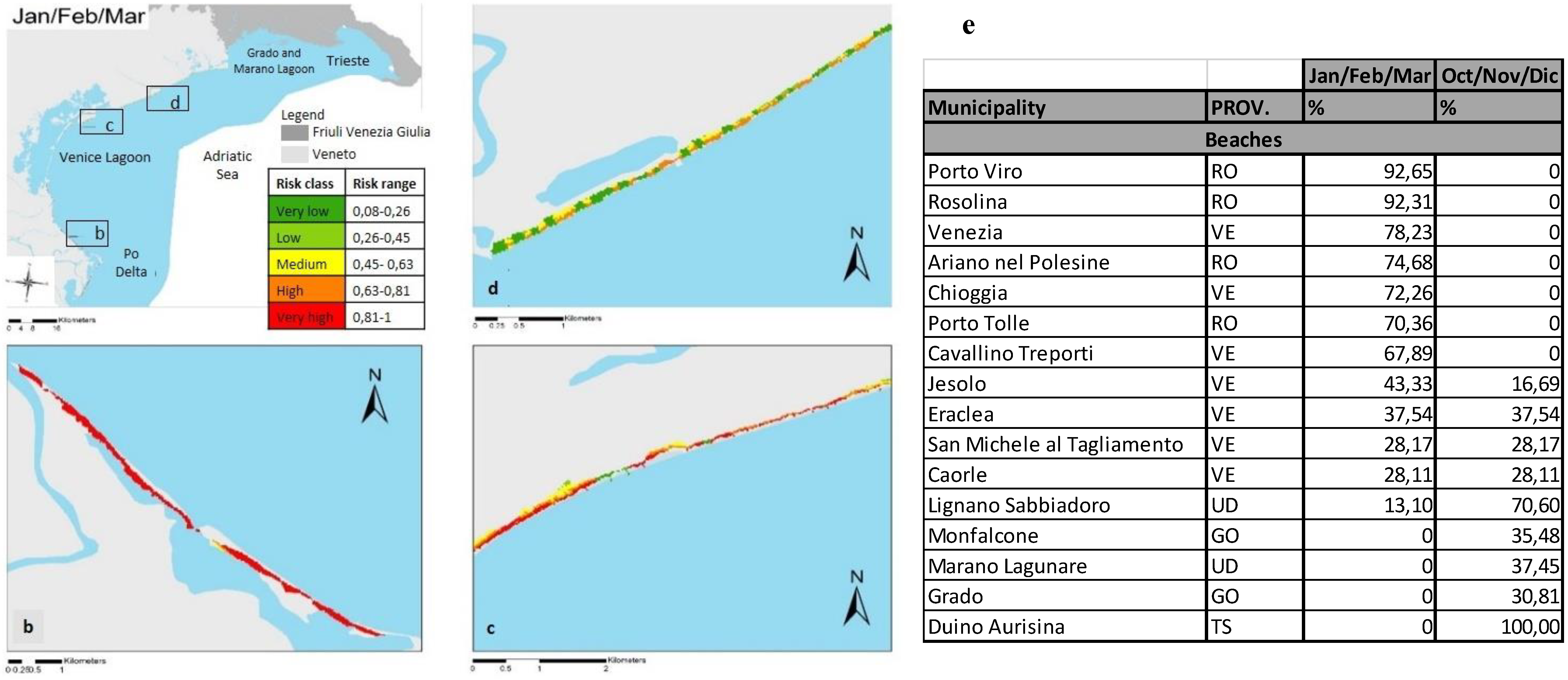
3.5. Risk Assessment
3.6. Damage Assessment
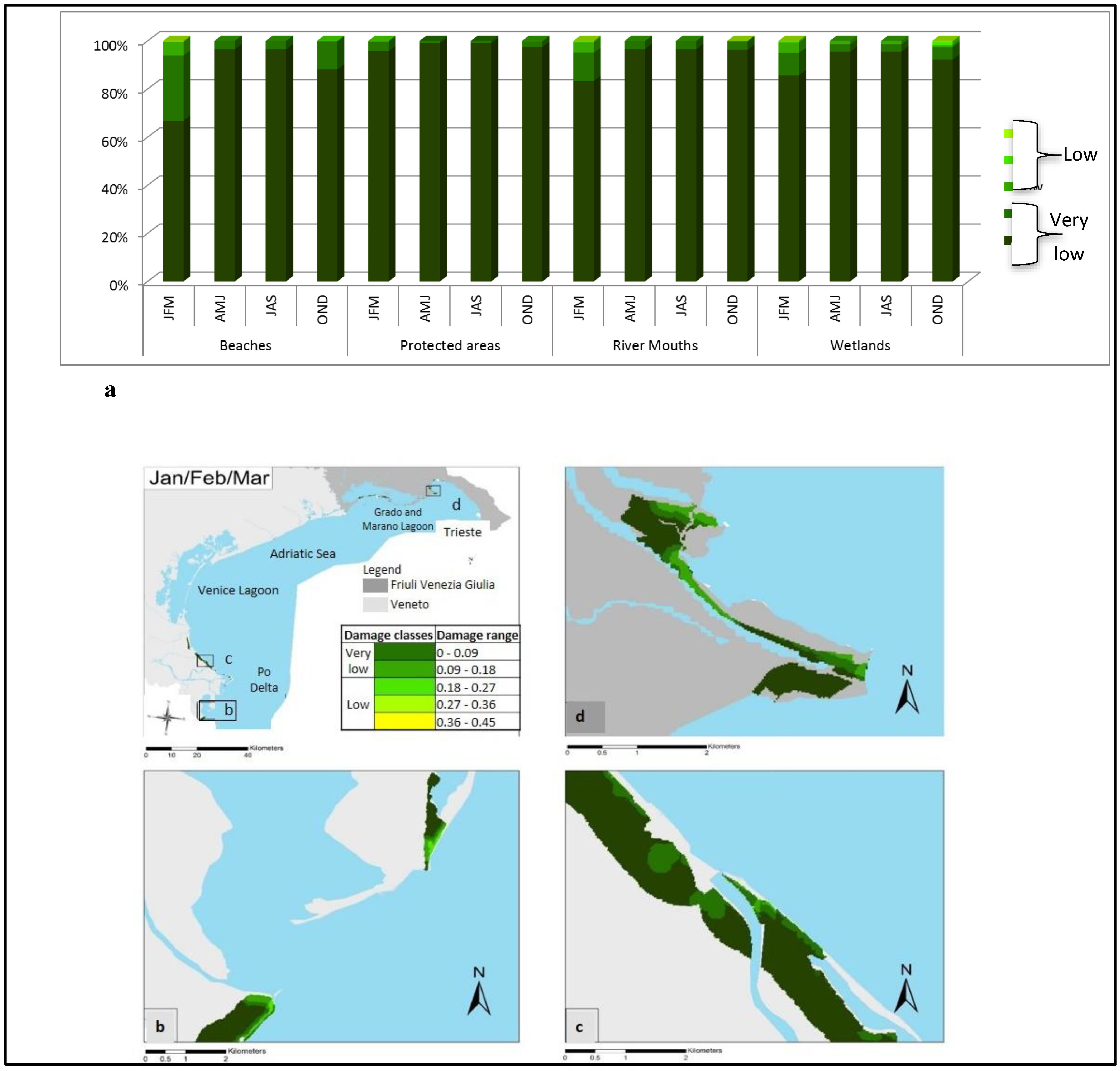
4. Results and Discussion
4.1. Exposure Maps
4.2. Susceptibility Maps
4.3. Risk Maps
4.4. Damage Maps
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Summary for policymakers. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1–32. [Google Scholar]
- EEA. Report No. 1/2017. Climate Change, Impacts and Vulnerability in Europe 2016. An Indicator-Based Report; EEA: Copenhagen, Denmark, 2017; ISSN 1977-8449. [Google Scholar]
- IPCC. Climate Change 2013: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
- Gualdi, S.; Somot, S.; Li, L.; Artale, V.; Adani, M. The CIRCE simulations: A new set of regional climate change projections performed with a realistic representation of the Mediterranean Sea. Bull. Am. Meteorol. Soc. 2013, 94, 65–81. [Google Scholar] [CrossRef]
- Lovato, T.; Vichi, M.; Oddo, P. High resolution simulations of Mediterranean Sea physical oceanography under current and scenario climate conditions: Model description, assessment and scenario analysis. CMCC Res. Pap. 2013, 1–26. [Google Scholar] [CrossRef]
- Colin, R.T.; Evans, E.P.; Penning-Rowsell, E.C. Future Flooding and Coastal Erosion Risks; Thomas Telford Publishing, Thomas Telford Ltd.: London, UK, 2007; p. 256. ISBN 978-0-7277-3449-5. [Google Scholar]
- IPCC. Summary for Policymakers. In Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2007. [Google Scholar]
- Australian Government. Climate Change Risks to Australia’s Coast. A First Pass National Assessment; Australian Government: Canberra, Australia, 2009; ISBN 978-1-921298-71-4.
- EC. Living with Coastal Erosion in Europe: Sediment and Space for Sustainability; Part I—Major Findings and Policy Recommendations of the EUROSION Project; EUCC: Leiden, The Netherlands, 2004. [Google Scholar]
- Vafeidis, A.T.; Nicholls, R.J.; McFadden, L.; Tol, R.S.J.; Hinkel, J.; Spencer, T.; Grashoff, P.S.; Boot, G.; Klein, R.J.T. A New Global Coastal Database for Impact and Vulnerability Analysis to Sea-Level Rise. J. Coast. Res. 2008. [Google Scholar] [CrossRef]
- Bruun, P. Sea-level rise as a cause of shore erosion: Proceedings of the American Society of Civil Engineers. J. Waterw. Harb. Div. 1962, 88, 117–130. [Google Scholar]
- CEAC. Final Technical Report Development of Coastal Erosion Hazard Maps San Pedro, Belize; CEAC: Kingston, Jamaica, 2006.
- Harvey, N.; Woodroffe, C.D. Australian approaches to coastal vulnerability assessment. Sustain. Sci. 2008, 3, 67–87. [Google Scholar] [CrossRef]
- Sharples, C. Indicative Mapping of Tasmanian Coastal Vulnerability to Climate Change and Sealevel Rise: Explanatory Report, 2nd ed.; Department of Primary Industries, Water & Environment: Hobart, Australia, 2006; 112p.
- Abuodha, P.A.O.; Woodroffe, C.D. Assessing Vulnerability of Coast to Climate Change: A Review of Approaches and Their Application to the Australian Coast; University of Wollongong, Faculty of Science Papers: Wollongong, Australia, 2006. [Google Scholar]
- Gornitz, V.M.; Daniels, R.C.; White, T.W.; Birdwell, K.R. The Development of a Coastal Risk Assessment Database: Vulnerability to Sea-Level Rise in the U.S. Southeast; U.S. Government Report DE-AC05-84OR21400; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1993.
- Ramieri, E.; Hartley, A.; Barbanti, A.; Duarte Santos, F.; Gomes, A.; Hilden, M.; Laihonen, P.; Marinova, N.; Santini, M. Methods for Assessing Coastal Vulnerability to Climate Change; European Topic Centre on Climate Change Impacts, Vulnerability and Adaptation (ETC CCA) Technical Paper; European Environment Agency: Bologna, Italy, 2011; p. 93. [Google Scholar]
- Torresan, S.; Critto, A.; Dalla Valle, M.; Harvey, N.; Marcomini, A. Assessing coastal vulnerability to climate change: Comparing segmentation at global and regional scales. Sustain. Sci. 2008, 3, 45–65. [Google Scholar] [CrossRef]
- Idier, D.; Castelle, B.; Poumadere, M.; Balouin, Y.; Bertoldo, R.B.; Bouchette, F.; Boulahya, F.; Brivois, O.; Calvete, D.; Capo, S.; et al. Vulnerability of sandy coasts to climate variability. Clim. Res. 2013, 57, 19–44. [Google Scholar] [CrossRef]
- Di Paola, G.; Aucelli, P.P.; Benassai, G.; Rodríguez, G. Coastal vulnerability to wave storms of Sele littoral plain (southern Italy). Nat. Hazards 2014, 71, 1795–1819. [Google Scholar] [CrossRef]
- Hereher, M.E. Coastal vulnerability assessment for Egypt’s Mediterranean coast. Geomat. Nat. Hazards Risk 2015, 6, 342–355. [Google Scholar] [CrossRef]
- Satta, A.; Snoussi, M.; Puddu, M.; Flayou, L.; Hout, R. An index-based method to assess risks of climate-related hazards in coastal zones: The case of Tetouan. Estuar. Coast. Shelf Sci. 2016. [Google Scholar] [CrossRef]
- Pantusa, D.; D’Alessandro, F.; Riefolo, L.; Principato, F.; Tomasicchio, G.R. Application of a coastal vulnerability index. A case study along the Apulian Coastline, Italy. Water 2018, 10, 1218. [Google Scholar] [CrossRef]
- Landis, W.G. Regional Scale Ecological Risk Assessment. Using the Relative Risk Model; Landis, W.G., Ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Zanuttigh, B.; Simcic, D.; Bagli, S.; Bozzeda, F.; Pietrantoni, L.; Zagonari, F.; Hoggart, S.; Nicholls, R.J. THESEUS decision support system for coastal risk management. Coast. Eng. 2014, 87, 218–239. [Google Scholar] [CrossRef]
- Hagenlocher, M.; Renaud, F.G.; Haas, S.; Sebesvari, Z. Vulnerability and risk of deltaic social-ecological systems exposed to multiple hazards. Sci. Total Environ. 2018, 631–632, 71–80. [Google Scholar] [CrossRef] [PubMed]
- Sperotto, A.; Torresan, S.; Gallina, V.; Coppola, E.; Critto, A.; Marcomini, A. A multi-disciplinary approach to evaluate pluvial floods risk under changing climate: The case study of the municipality of Venice (Italy). Sci. Total Environ. 2016, 562, 1031–1043. [Google Scholar] [CrossRef]
- Ronco, P.; Zennaro, F.; Torresan, S.; Critto, A.; Santini, M.; Trabucco, A.; Zollo, A.L.; Galluccio, G.; Marcomini, A. A risk assessment framework for irrigated agriculture under climate change. Adv. Water Resour. 2017, 110, 562–578. [Google Scholar] [CrossRef]
- Sanuy, M.; Duo, E.; Jäger, W.S.; Ciavola, P.; Jiménez, J.A. Linking source with consequences of coastal storm impacts for climate change and risk reduction scenarios for Mediterranean sandy beaches. Nat. Hazards Earth Syst. Sci. 2018. [Google Scholar] [CrossRef]
- Torresan, S.; Gallina, V.; Gualdi, S.; Bellafiore, D.; Umgiesser, G.; Carniel, S.; Sclavo, M.; Benetazzo, A.; Giubilato, E.; Critto, A. Assessment of climate change impacts in the North Adriatic coastal area. Part I: A multi-model chain for the definition of climate change hazard scenarios. Water 2019, 11, 1157. [Google Scholar] [CrossRef]
- Torresan, S.; Critto, A.; Rizzi, J.; Zabeo, A.; Furlan, E.; Marcomini, A. DESYCO: A decision support system for the regional risk assessment of climate change impacts in coastal zones. Ocean Coast. Manag. 2016, 120, 49–63. [Google Scholar] [CrossRef]
- Antonioli, F.; Anzidei, M.; Amorosi, A.; Lo Presti, V.; Mastronuzzi, G.; Deiana, G.; De Falco, G.; Fontana, A.; Fontolan, G.; Lisco, S.; et al. Sea-level rise and potential drowning of the Italian coastal plains: Flooding risk scenarios for 2100. Quat. Sci. Rev. 2017. [Google Scholar] [CrossRef]
- Marsico, A.; Lisco, S.; Lo Presti, V.; Antonioli, F.; Amorosi, A.; Anzidei, M.; Deiana, G.; De Falco, G.; Fontana, A.; Fontolan, G.; et al. Flooding scenario for four italian coastal plains using three relative sea level rise models. J. Maps 2017. [Google Scholar] [CrossRef]
- Carbognin, L.; Teatini, P.; Tomasin, A.; Tosi, L. Global change and relative sea level rise at Venice: What impact in term of flooding. Clim. Dyn. 2009, 35, 1039–1047. [Google Scholar] [CrossRef]
- Tomasin, A.; Pirazzoli, P.A. Extreme Sea Levels on the Adriatic Coasts: A Comparison of Estimation Methods; Atti dell’Istituto Veneto di Scienze, Lettere ed Arti Tomo CLXVII (2008–2009); Istituto Veneto di Scienze, Lettere ed Arti: Venice, Italy, 2008; pp. 53–82. [Google Scholar]
- Umgiesser, G.; Anderson, J.B.; Artale, V.; Breil, M.; Gualdi, S.; Lionello, P.; Marinova, N.; Orlić, M.; Pirazzoli, P.; Rahmstorf, S.; et al. From Global to regional: Local Sea Level Rise Scenarios. Focus on the Mediterranean Sea and the Adriatic Sea; Workshop Report n.1; United Nations Educational Scientific and Cultural Organization (UNESCO): Paris, France, 2011; p. 25. [Google Scholar]
- Rizzi, J.; Torresan, S.; Zabeo, A.; Critto, A.; Tosoni, A.; Tomasin, A.; Marcomini, A. Assessing storm surge risk under future sea-level rise scenarios: A case study in the North Adriatic coast. J. Coast. Conserv. 2016. [Google Scholar] [CrossRef]
- Ferretti, O.; Delbono, I.; Furia, S.; Barsanti, M. Elementi di Gestione Costiera Parte Prima Tipi Morfo-Sedimentologici dei Litorali Italiani; RT/2003/42/CLIM; ENEA: Rome, Italy, 2003; ISSN 0393-3016. [Google Scholar]
- Cecconi, G. The VeniceLagoon mobile barriers. Sea level rise and impact of barrier closures. In Proceedings of the Italian Days of Coastal Engineering, International Debate-PIC 97, Venice, Italy, 16 May 1997. [Google Scholar]
- Cecconi, G.; Ardone, V. La protezione dei litorali con ripascimento delle spiagge. L’esperienza dei litorali di Cavallino e Pellestrina. In Proceedings of the La progettazione ambientale nei sistemi costieri, a cura di M. Pietrobelli, Atti del X Seminario, Roma, Italy, 10 July 1998; International Association for Environmental Design (IAED, Quaderno 12); pp. 11–31. [Google Scholar]
- CVN. La fonte di Approvvigionamento della Sabbia nel Ripascimento dei Litorali Veneti; Cecconi, G., Ardone, V., Eds.; Consorzio Venezia Nuova: Venezia, Italy, 2000. [Google Scholar]
- Cecconi, G.; Ardone, V. La fonte di Approvvigionamento della Sabbia nel Ripascimento dei Litorali Veneti, Intervento alla Presentazione della Costa Ligure; Regione Liguria: Genova, Italy, 2–4 February 2000. [Google Scholar]
- Visintini Romanin, M.; Rismondo, A.; Scarton, F.; Leita, L. Interventi per il recupero morfologico della laguna di Venezia. La barena Fossei Est in laguna Sud. Quad. Trimest. 2000, 3–4, 3–35. [Google Scholar]
- Regione, F.V.G. Piano di gestione del SIC IT3320037 Laguna di Grado e Marano. Carta delle aree di Tutela e di Intervento scala 1:50,000; Agriconsulting: Friuli Venezia Giulia Region, Italy, 2008. [Google Scholar]
- Fagherazzi, S.; Wiberg, P.L. Importance of wind conditions, fetch, and water levels on wave-generated shear stresses in shallow intertidal basins. J. Geophys. Res. 2009, 114, F03022. [Google Scholar] [CrossRef]
- Özyurt, G. Vulnerability of Coastal Areas to Sea Level Rise: Case Study on Goksu Delta. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2007. [Google Scholar]
- Carniel, S.; Sclavo, M.; Archetti, R. Towards validating a last generation, integrated wave-current-sediment numerical model in coastal regions using video measurements. Oceanol. Hydrobiol. Stud. 2011, 40, 11–20. [Google Scholar] [CrossRef]
- Benetazzo, A.; Carniel, S.; Sclavo, M.; Bucchignani, E.; Ricchi, A. Wave climate of the Adriatic Sea: A future scenario simulation. Nat. Hazards Earth Syst. Sci. 2012, 12, 2065–2076. [Google Scholar] [CrossRef]
- Torresan, S.; Critto, A.; Rizzi, J.; Marcomini, A. Assessment of coastal vulnerability to climate change hazards at the regional scale: The case study of the North Adriatic Sea. Nat. Hazards Earth Syst. Sci. 2012, 12, 2347–2368. [Google Scholar] [CrossRef]
- VE Region. Map of National and Regional Established Parks, Environmental Planning and Parks Unit. 2006. Available online: http://idt.regione.veneto.it/app/metacatalog/ (accessed on 16 June 2019). (In Italian).
- FVG Region. Digital Elevation Model (DEM) for the Friuli Venezia Giulia Region, Geographic Information System and Cartography Unit. 2006. Available online: http://irdat.regione.fvg.it/consultatore-dati-ambientali-territoriali/ (accessed on 16 June 2019). (In Italian).
- FVG Region. Monitoring Land Use/Cover Dynamics (MOLAND) Map for the Friuli Venezia Giulia Region, Geographic Information System and Cartography Unit. 2000. Available online: http://irdat.regione.fvg.it/consultatore-dati-ambientali-territoriali/ (accessed on 16 June 2019). (In Italian).
- VE Region. Regional Land cover Map based on Corine Land Cover legend, Geographic Information System and Cartography Unit. 2009. Available online: http://idt.regione.veneto.it/app/metacatalog/ (accessed on 16 June 2019). (In Italian).
- Nakićenovićet, N.; Alcamo, J.; Davis, G.; de Vries, H.J.M.; Fenhann, J.; Gaffin, S.; Gregory, K.; Grubler, A.; Jung, T.Y.; Kram, T.; et al. Special Report on Emissions Scenarios. Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions Part I Model description and validation. J. Geoph. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Bergamasco, A.; Carniel, S.; Pastres, R.; Pecenik, G. A unified approach to the modelling of the Venice Lagoon–Adriatic Sea ecosystem. Estuar. Coast. Shelf Sci. 1998, 46, 483–492. [Google Scholar] [CrossRef]
- McLaughlin, S.; Cooper, J.A.G. A multi-scale coastal vulnerability index: A tool for coastal managers? Environ. Hazards 2010, 9, 233–248. [Google Scholar] [CrossRef]
- Zald, A.E.; Shelly, S.; Wade, T. A to Z GIS: An Illustrated Dictionary of Geographic Information Systems; ESRI Press: Beijing, China, 2006. [Google Scholar]
- Crozier, M.; Glade, T. Landslide hazard and risk: Issues, concepts and approach. In Landslide Hazard and Risk; Glade, T., Anderson, M., Crozier, M., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2005; pp. 1–40. [Google Scholar]
- Kalbfleisch, J.G. Probability and Statistical Inference: Volume 1: Probability; Springer Science & Business Media: Berlin, Germany, 1985. [Google Scholar]
- Preston, B.L.; Smith, T.F.; Brooke, C.; Gorddard, R.; Measham, T.G.; Withycombe, G.; Mcinnes, K.; Abbs, D.; Beveridge, B.; Morrison, C. Mapping Climate Change Vulnerability in the Sydney Coastal Councils Group; Sydney Coastal Councils Group: Manly, Australia, 2008. [Google Scholar]
- ARC. Coastal Erosion Management Manual Technical Publication No. 130; ARC: Canberra, Australia, 2000. [Google Scholar]
- Eurosion. Living with Coastal Erosion in Europe: Sediment and Space for Sustainability. PART III—Methodology for Assessing Regional Indicators. 20 May 2004. Available online: http://www.eurosion.org/reportsonline/part3.pdf (accessed on 19 June 2015).
- Greiving, S.; Fleischhauer, M.; Lückenkötter, M. A Methodology for an Integrated Risk Assessment of Spatially Relevant Hazards. J. Environ. Plan. Manag. 2006, 49, 1–19. [Google Scholar] [CrossRef]
- EC. ARMONIA Project. Applied Multi-Risk Mapping of Natural Hazards for Impact Assessment; Deliverable 4.1.2. Report: Technical Glossary of a Multi Hazard Related Vulnerability and Risk Assessment Language—Final Version; EC: Brussels, Belgium, 2007. [Google Scholar]
- Bonaldo, D.; Benetazzo, A.; Sclavo, M.; Carniel, S. Modelling wave-driven sediment transport in a changing climate: A case study for northern Adriatic Sea (Italy). Reg. Environ. Chang. 2014. [Google Scholar] [CrossRef]
- Bosco, C.; de Rigo, D.; Dewitte, O.; Poesen, J.; Panagos, P. Modelling soil erosion at European scale: Towards harmonization and reproducibility. Nat. Hazards Earth Syst. Sci. 2015, 15, 225–245. [Google Scholar] [CrossRef]
- Klein, R.J.T.; Midgley, G.F.; Preston, B.L.; Alam, M.; Berkhout, F.G.; Dow, K.; Li, Y.E.; Mateescu, E.; Shaw, M.R.; Botzen, W.; et al. Adaptation opportunities, constraints, and limits. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, MA, USA; New York, NY, USA, 2014; pp. 899–943. [Google Scholar]

| Hazard Matrix | ||
|---|---|---|
| Stressors | Climate change impact | |
| Bottom stress | wave | |
| Bottom stress | Height | Coastal erosion |
| Receptors | Beaches | River Mouths | Wetlands | Protected Areas | |
|---|---|---|---|---|---|
| Impact | |||||
| Coastal erosion | - Distance from coastline | - Distance from coastline | - Distance from coastline | - Distance from coastline | |
| - Artificial protections | - Artificial protections | - Artificial protections | - Artificial protections | ||
| - Vegetation cover | - Vegetation cover | - Vegetation cover | - Vegetation cover | ||
| - Coastal slope | - Geomorphology | - Geomorphology | - Geomorphology | ||
| - Geomorphology | - Sediment budget | - Sediment budget | - Sediment budget | ||
| - Sediment budget | - Mouth typology | - Wetland extension | - % of urbanization | ||
| - Dunes | - Protection level | - % of urbanization | - Protection level | ||
| - % of urbanization | - Population density | - Protection level | - Population density | ||
| - Protection level | - Urban typology | - Population density | - Urban typology | ||
| - Population density | - Agricultural typology | - Wetland extension | - Agricultural typology | ||
| Legend | |||||
| Vulnerability Factors | Definition | ||||
| Pathway factors (pf) | Physical characteristics of the receptors (i.e., distance from coastline) which determine the possibility that coastal erosion reach receptors. | ||||
| Attenuation factors (af) | Elements that could attenuate the intensity of the coastal erosion (i.e., artificial protections). | ||||
| Susceptibility factors (sf) | Geo-physical or ecological factors used to determine the susceptibility of a receptor to coastal erosion (e.g., vegetation cover, coastal slope, geomorphology, dunes, sediment budget). | ||||
| Value factors (vf) | Relevant environmental and socio-economic values of the receptors that need to be preserved for the interest of the community (e.g., protection level, population density). | ||||
| Vulnerability Factor | Definition | Dataset (Source) |
|---|---|---|
| Pathway factor | ||
| Distance from coastline | The distance of a location (e.g., a pixel of the map) from the coastline (km). | 25 m Digital Elevation Model (DEM) [50,51] |
| Attenuation factor | ||
| Artificial protection | Artificial protections (e.g., dikes) for the defence of the coastline from storm surge and coastal erosion impacts. | Corine Land Cover, 1:100,000 [52,53] |
| Susceptibility factors | ||
| Vegetation cover | The typology of vegetation that cover an area (i.e., natural grassland and meadow, shrub, forest). | Corine Land Cover, 1:100,000, Land use, 1:25,000 [52,53] |
| Coastal slope | Average topographic slope (in degrees) along the coastline. | 25 m Digital Elevation Model (DEM) [50,51] |
| Geomorphology | Geomorphologic structure of the coastal zone. It refers to muddy (non consolidated), sandy or rocky coast typology. | Geologic and Geomorphological Map of the Po river delta, 1:50,000 (Veneto Po Delta Regional Park Authority, https://www.parcodeltapo.org/index.php/it/) |
| Dunes | It refers to the presence or absence of natural dunes. | Corine Land Cover, 1:100,000 [52,53] |
| Sediment budget | It refers to the morphological variations of coastlines (i.e., eroding advancing or stable shores). | Geographic Coastal Information System (SIGC) (ISPRA, www.mais.sinanet.apat.it/cartanetms/coste/) |
| Mouth typology | It refers to the type of river mouths (i.e., estuary, delta). | Hydrologic basins: rivers and channels 1:25,000. [52] (ISPRA, www.mais.sinanet.apat.it/cartanetms/) |
| Wetland extension | The extent of wetlands in square kilometres (km2). | Corine Land Cover, 1:100,000 [52,53] |
| % of urbanization | The percentage of urbanized areas within each municipality. | Corine Land Cover, 1:100,000, Land use, 1:25,000 [52,53] |
| Value factors | ||
| Protection level | It refers to the type of protected areas within the considered receptor (i.e., national area, regional area, nature 2000 area). | Protected Areas and ARIA zones, 1:150,000 [52] |
| Population density (inhabitants/km2) | The average number of people who live on each square kilometre of land for each municipality. | Census data [52,53] |
| Urban typology | The typology of buildings (e.g., residential, commercial, infrastructures). | Corine Land Cover, 1:100,000, Land use, 1:25,000 [52,53] |
| Agricultural typology | The typology of farming in an area (e.g., permanent culture, stable meadow, arable). | Corine Land Cover, 1:100,000, Land use, 1:25,000 [52,53] |
| Equation | Description |
|---|---|
| (1) | Exposure function is aimed at the relative ranking of areas potentially exposed to changes in coastal erosion stressors. It integrates information about the hazard metrics influenced by climate change (i.e., wave height and bottom stress, Paragraph 3.2), the presence of artificial protections and the distance from the sea. |
| where: Ece,s = exposure score related to coastal erosion (ce) scenario s; pf1 = pathway factor represented by the distance of the center of the cell from the sea (always ≥ 1 m); s1 = threshold given by decision maker representing the distance of the coastline from the sea beyond which the erosion has no influence (m); ⊗ = “probabilistic or” function [60] (see Table S2); h′ce,1,…,n,s = hazard metrics from 1 to n related to the coastal erosion impact classified and weighted in (0,1) through h′k,s = si,kwi,k where h′k,s = weighted hazard metric; si,k = score of the i-th hazard metric for the impact k; wi,k = weight of the i-th hazard metric for the impact k. Atce = attenuation related to the presence of artificial protections (see Table S2); d1 = distance from the shoreline calculated through a hyperbolic function (see Table S2). | |
| (2) | Susceptibility function is aimed at the aggregation of the major physical and environmental factors that may influence the response of the receptors to the hazard scenarios. |
| where: Sce = susceptibility score of the cell to the coastal erosion ce; ⊗ = “probabilistic or” function (see Table S2); sf’i,ce = ith susceptibility factor score related to the coastal erosion ce; and sf’i,ce = si,ce wi,ce, where sf’i,e = weighted susceptibility factor score; si,ce = score of the i-th susceptibility factor for the coastal erosion ce; wi,ce = weigh of the i-th susceptibility factor for the coastal erosion ce. | |
| (3) | Risk function is aimed at the integration of exposure and susceptibility information. |
| where: Rce,s = risk score related to coastal erosion ce and scenario s; Ece,s = exposure score related with the coastal erosion ce in scenario s, according to Equation (1); Sce= susceptibility score to the impact ce, according to Equation (2). | |
| (4) | Value function is aimed at the identification and ranking of receptors with relevant environmental and socio-economic values that need to be preserved for the interest of the community (e.g., land use, agricultural areas). |
| where: Vj = value score of the receptor j; vf’i,j = i-th value factor score related to the receptor j; and vf’ = si,j wi,j, where vf’ = weighted value factor score; si,j = score of the i-th factor for the receptor j; wi,j = weigh of the i-th factor for the receptor j; n = number of value factors. | |
| (5) | Damage function is aimed at the integration of risk and value information. |
| where: Dj,ce,s = damage score related to coastal erosion ce and a receptor j in the scenario s; Rce,s = risk score related to coastal erosion ce in scenario s, according to Equation (3); Vj = value score of receptor j, according to Equation (4). |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallina, V.; Torresan, S.; Zabeo, A.; Rizzi, J.; Carniel, S.; Sclavo, M.; Pizzol, L.; Marcomini, A.; Critto, A. Assessment of Climate Change Impacts in the North Adriatic Coastal Area. Part II: Consequences for Coastal Erosion Impacts at the Regional Scale. Water 2019, 11, 1300. https://doi.org/10.3390/w11061300
Gallina V, Torresan S, Zabeo A, Rizzi J, Carniel S, Sclavo M, Pizzol L, Marcomini A, Critto A. Assessment of Climate Change Impacts in the North Adriatic Coastal Area. Part II: Consequences for Coastal Erosion Impacts at the Regional Scale. Water. 2019; 11(6):1300. https://doi.org/10.3390/w11061300
Chicago/Turabian StyleGallina, Valentina, Silvia Torresan, Alex Zabeo, Jonathan Rizzi, Sandro Carniel, Mauro Sclavo, Lisa Pizzol, Antonio Marcomini, and Andrea Critto. 2019. "Assessment of Climate Change Impacts in the North Adriatic Coastal Area. Part II: Consequences for Coastal Erosion Impacts at the Regional Scale" Water 11, no. 6: 1300. https://doi.org/10.3390/w11061300
APA StyleGallina, V., Torresan, S., Zabeo, A., Rizzi, J., Carniel, S., Sclavo, M., Pizzol, L., Marcomini, A., & Critto, A. (2019). Assessment of Climate Change Impacts in the North Adriatic Coastal Area. Part II: Consequences for Coastal Erosion Impacts at the Regional Scale. Water, 11(6), 1300. https://doi.org/10.3390/w11061300







