Probabilistic Assessment of Correlations of Water Levels in Polish Coastal Lakes with Sea Water Level with the Application of Archimedean Copulas
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Study Area
2.2. Methods
2.2.1. Mann–Kendall Test
2.2.2. Correlation
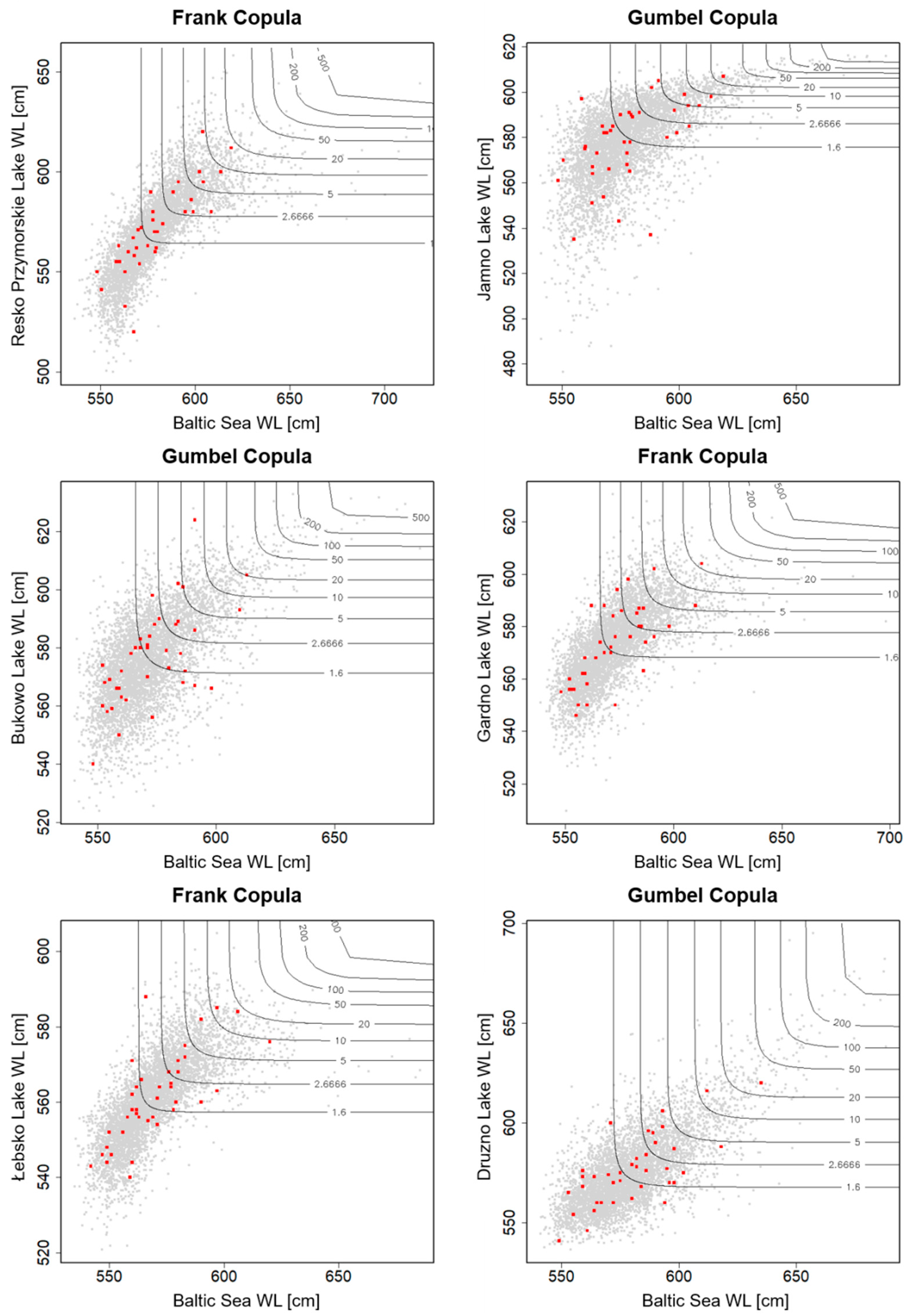
2.2.3. Application of the Copula Theory
- Sector 1: LHWLS–LHWLL (X ≤ S62.5%, Y ≤ L62.5%);
- Sector 5: MHWLS–MHWLL (S62.5%< X ≤ S37.5%, L62.5% < Y ≤ L37.5%);
- Sector 9: HHWLS–HHWLL (X > S37.5%, Y > L37.5%);
- Sector 2: LHWLS–MHWLL (X ≤ S62.5%, L62.5% < Y ≤ L37.5%);
- Sector 3: LHWLS–HHWLL (X ≤ S62.5%, Y > L37.5%);
- Sector 4: MHWLS–LHWLL (S62.5%< X ≤ S37.5%, Y ≤ L62.5%);
- Sector 6: MHWLS–HHWLL (S62.5%< X ≤ S37.5%, Y > L37.5%);
- Sector 7: HHWLS–LHWLL (X > S37.5%, Y ≤ L62.5%);
- Sector 8: HHWLS–MHWLL (X > S37.5%, L62.5% < Y ≤ L37.5%);
- Probable maximum water levels with a probability of occurrence of <62.5% were designated as LHWL;
- Probable maximum water levels with a probability of occurrence in a range >62.5% and <37.5% were designated as MHWL; and
- Probable maximum water levels with a probability of occurrence >37.5% were designated as HHWL.
3. Results
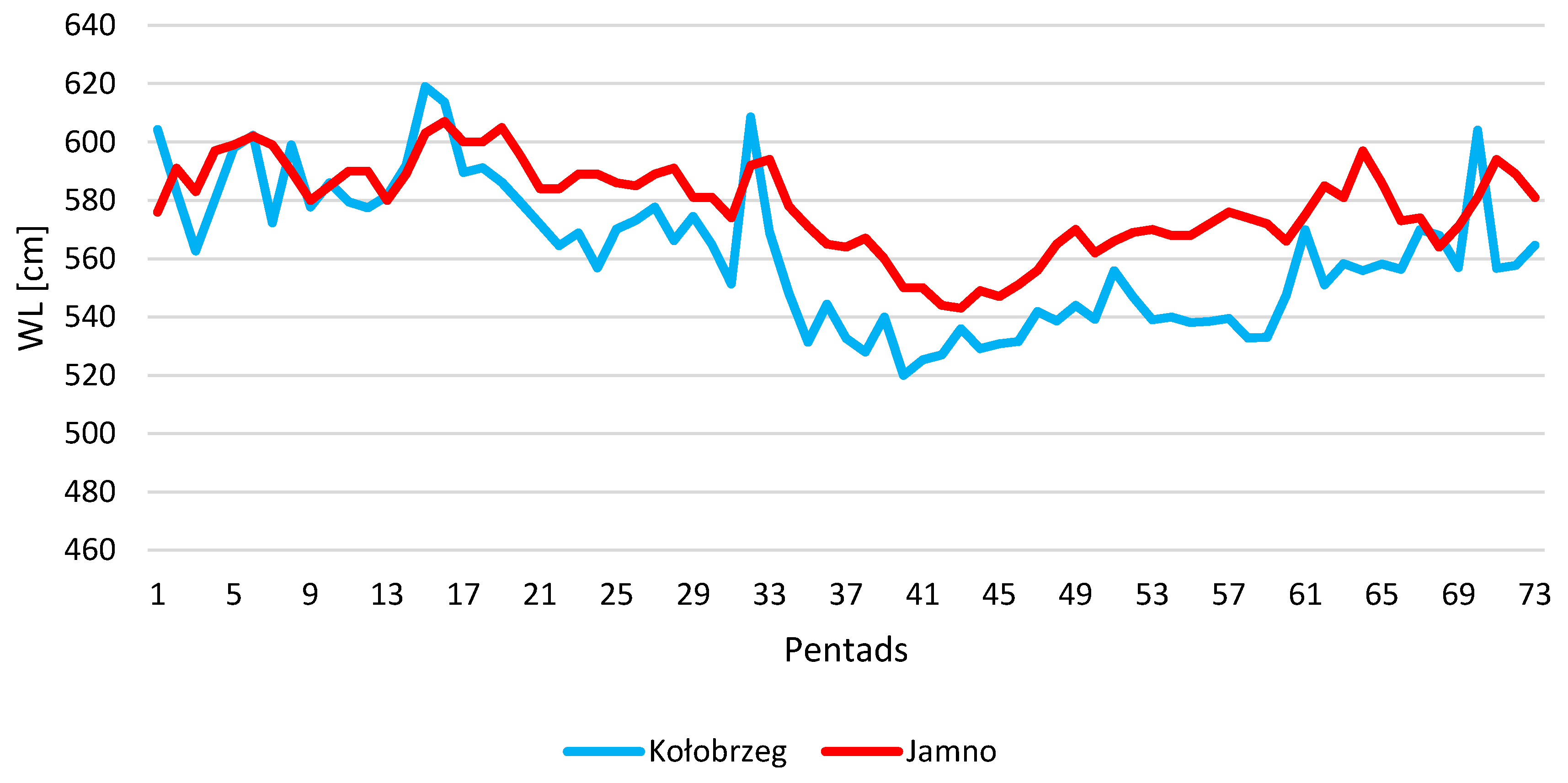
3.1. Mann–Kendall Test
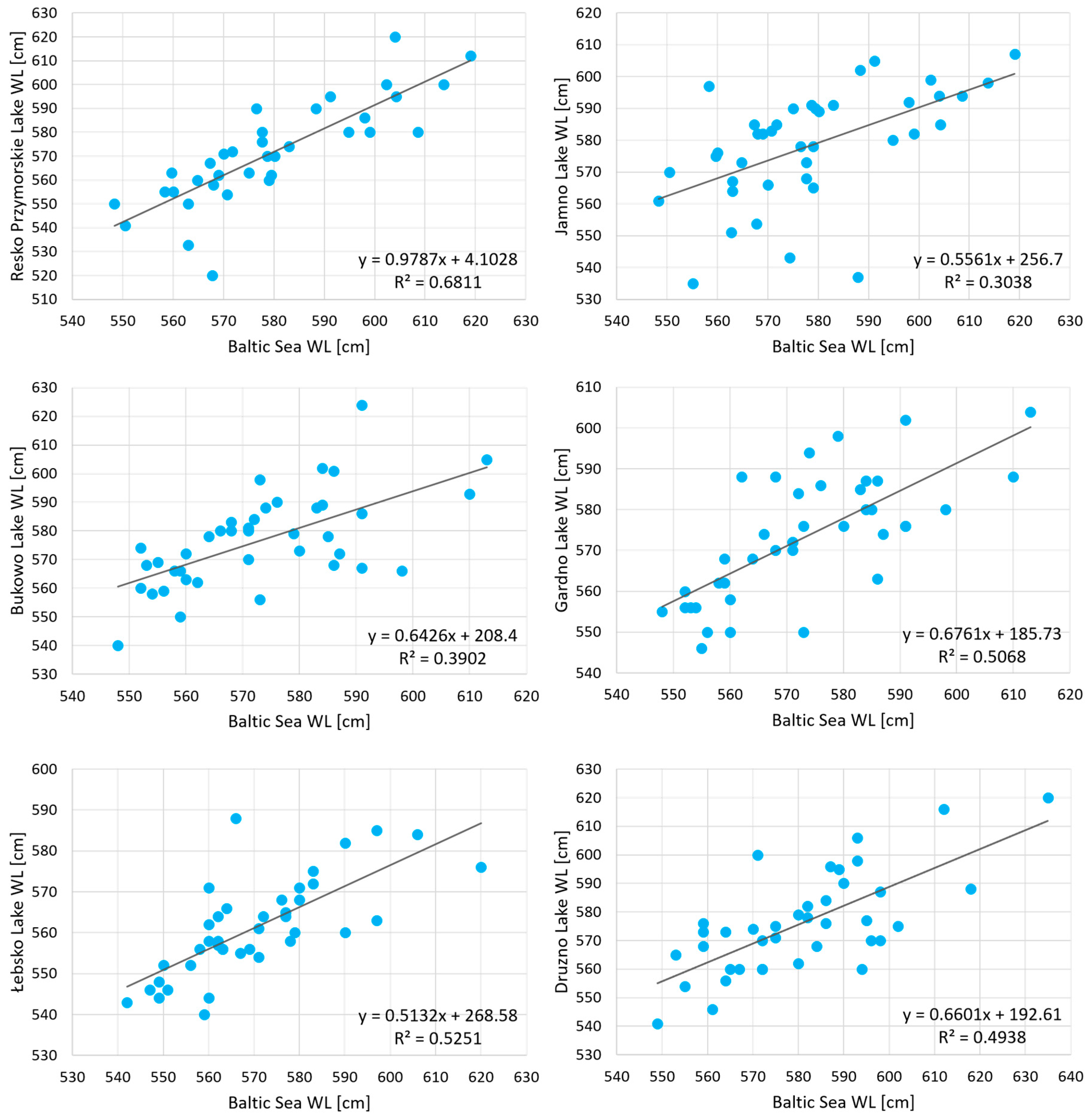
3.2. Correlation
3.2.1. Maximum Annual Water Levels
3.2.2. Maximum Monthly Water Levels
3.3. Synchronous–Asynchronous Encounter Probability
3.3.1. Maximum Annual Water Levels
3.3.2. Maximum Monthly Water Levels
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Choiński, A. Limnologia Fizyczna Polski; Wydawnictwo Naukowe UAM: Poznań, Poland, 2007. [Google Scholar]
- Mikulski, Z.; Bojanowicz, M. Bilans wodny jeziora znajdującego się pod wpływem morza (na przykładzie jeziora Druzno). Przegląd Geofiz. 1967, 12, 3–4. [Google Scholar]
- Cieśliński, R. Zróżnicowanie typologiczne i funkcjonalne jezior w polskiej strefie brzegowej południowego Bałtyku. Probl. Ekol. Kraj. 2010, 26, 135–144. [Google Scholar]
- Cieśliński, R.; Drwal, J.; Chlost, I. Sea water intrusions to the Lake Gardno. Balt. Coast. Zone 2009, 13 Pt I, 85–98. [Google Scholar]
- Rotnicki, K. (Ed.) Przemiany Środowiska Geograficznego Nizin Nadmorskich Południowego Bałtyku w Vistulianie i Holocenie; Bogucki Wydawnictwo Naukowe UAM: Poznań, Poland, 2001. [Google Scholar]
- Wolski, T.; Wiśniewski, B. Changes of maximum sea levels at selected gauge stations on the Polish and Swedish Baltic coast. Stud. Prac. WNEIZ 2012, 29, 209–227. [Google Scholar]
- Schallenberg, M.; Larned, S.T.; Hayward, S.; Arbuckle, C. Contrasting effects of managed opening regimes on water quality in two intermittently closed and open coastal lakes. Estuar. Coast. Shelf Sci. 2010, 86, 587–597. [Google Scholar] [CrossRef]
- Dye, A.; Barros, F. Spatial patterns of macrofaunal assemblages in intermittently closed/open coastal lakes in New South Wales, Australia. Estuar. Coast. Shelf Sci. 2005, 64, 357–371. [Google Scholar] [CrossRef]
- Trojanowski, J.; Antonowicz, J. Heavy metals in surface microlayer in water of Lake Gardno. Arch. Environ. Prot. 2011, 37, 75–88. [Google Scholar]
- Jarosiewicz, A. Seasonal changes of nutrients concentration in two shallow estuarine lakes Gardno and Lebsko; Comparison. Balt. Coast. Zone J. Ecol. Prot. Coastline 2009, 13, 121–133. [Google Scholar]
- Mudryk, Z.J. Antibiotic Resistance among Bacteria Inhabiting Surface and Subsurface Water Layers in the Estuarine Lake Gardno. Pol. J. Environ. Stud. 2002, 11, 401–406. [Google Scholar]
- Cieśliński, R. Zmiany zasolenia i poziomu wody jeziora Jamno wynikające z budowy wrót przeciwsztormowych. Inżynieria I Ochr. Środowiska 2016, 19, 517–539. [Google Scholar] [CrossRef]
- Sheela, A.M.; Letha, J.; Sabu, J.; Ramachandran, K.K.; Justus, J. Detection of extent of sea level rise in a coastal lake system using IRS Satellite Imagery. Water Resour. Manag. 2013, 27, 2657–2670. [Google Scholar] [CrossRef]
- Wunsam, S.; Schmidt, R.; Müller, J. Holocene lake development of two Dalmatian lagoons (Malo and Veliko Jezero, Isle of Mljet) in respect to changes in Adriatic sea level and climate. Palaeogeogr. Palaeoclimatol. Palaeoecol. 1999, 146, 251–281. [Google Scholar] [CrossRef]
- García-Rodríguez, F.; Sprechmann, P.; Metzeltin, D.; Scafati, L.; Melendi, D.L.; Volkheimer, W.; Mazzeo, N.; Hiller, A.; von Tümpling, W.; Scasso, F. Holocene trophic state changes in relation to sea level variation in Lake Blanca, SE Uruguay. J. Paleolimnol. 2004, 31, 99–115. [Google Scholar] [CrossRef]
- Timms, B.V. A limnological survey of the freshwater coastal lakes of east Gippsland, Victoria. Mar. Freshw. Res. 1973, 24, 1–20. [Google Scholar] [CrossRef]
- Paturej, E. Zooplankton Przymorskich Jezior Pobrzeża Bałtyckiego; Wydawnictwo Uniwersytetu Warmińsko-Mazurskiego: Olsztyn, Poland, 2005. [Google Scholar]
- Paturej, E.; Goździejewska, A. Zooplankton-based assessment of the trophic state of three coastal lakes–Łebsko, Gardno, and Jamno. Bull. Sea Fish. Inst. 2005, 3, 7–25. [Google Scholar]
- Paturej, E. Assessment of the trophic state of the coastal Lake Gardno based on community structure and zooplankton-related indices. Electron. J. Pol. Agric. Univ. 2006, 9, 17. [Google Scholar]
- Morozińska-Gogol, J.; Bachowska, A. Parasites of roach Rutilus rutilus (L.) from the Lake Lebsko. Balt. Coast. Zone 2002, 7, 75–80. [Google Scholar]
- Drwal, J.; Cieśliński, R. Coastal lakes and marine intrusions on the southern Baltic coast. Oceanol. Hydrobiol. Stud. 2007, 36, 61–75. [Google Scholar] [CrossRef]
- Grudzinska, I.; Vassiljev, J.; Saarse, L.; Reitalu, T.; Veski, S. Past environmental change and seawater intrusion into coastal Lake Lilaste, Latvia. J. Paleolimnol. 2017, 57, s10917–s10933. [Google Scholar] [CrossRef]
- Girjatowicz, J. Charakterystyki zlodzenia polskich jezior przybrzeżnych. Inżynieria Morska I Geotech. 2001, 2, 73–76. [Google Scholar]
- Li, X.-Y.; Xu, H.-Y.; Sun, Y.-L.; Zhang, D.-S.; Yang, Z.-P. Lake-level change and water balance analysis at lake Qinghai, West China during recent decades. Water Resour. Manag. 2007, 21, 1505–1516. [Google Scholar] [CrossRef]
- Duo, B.; Bianbaciren; Li, L.; Wang, W.; Zhaxiyangzong. The response of lake change to climate fluctuation in north Qinghai-Tibet Plateau in last 30 years. J. Geogr. Sci. 2009, 19, 131–142. [Google Scholar] [CrossRef]
- Singh, C.R.; Thompson, J.R.; French, J.R.; Kingston, D.G.; MacKay, A.W. Modelling the impact of prescribed global warming on runoff from headwater catchments of the Irrawaddy River and their implications for the water level regime of Loktak Lake, northeast India. Hydrol. Earth Syst. Sci. 2010, 14, 1745–1765. [Google Scholar] [CrossRef]
- Konatowska, M.; Rutkowski, P. The changes of the area and of the water-level of Kamińsko Lake (Zielonka Experimental Forestry Division) in the period of recent 150 years. Studia I Mater. Cent. Edukac. Przyr. Leśnej 2008, 10, 205–217. [Google Scholar]
- Zhuang, C.; Ouyang, Z.; Xu, W.; Bai, Y.; Zhou, W.; Zheng, H.; Wang, X. Impacts of human activities on the hydrology of Baiyangdian Lake, China. Environ. Earth Sci. 2011, 62, 1343–1350. [Google Scholar] [CrossRef]
- Wrzesiński, D.; Ptak, M. Water level changes in Polish lakes during 1976–2010. J. Geogr. Sci. 2016, 26, 83–101. [Google Scholar] [CrossRef]
- Chlost, I.; Cieśliński, R. Change of level of waters Lake Łebsko. Limnol. Rev. 2005, 5, 17–26. [Google Scholar]
- Girjatowicz, J.P. Związek między poziomem wody w jeziorach przybrzeżnych i wodami morskimi polskiego wybrzeża Morza Bałtyckiego. Przegląd Geofiz. 2008, 2, 141–153. [Google Scholar]
- Girjatowicz, J.P. Miesięczne i sezonowe charakterystyki poziomów wody wybranych polskich jezior przybrzeżnych. Inżynieria Morska Geotech. 2008, 1, 27–32. [Google Scholar]
- Girjatowicz, J.P. Wpływ Morza Bałtyckiego na poziomy wód polskich jezior przybrzeżnych. Inżynieria Morska Geotech. 2011, 1, 18–22. [Google Scholar]
- Fac-Beneda, J. Charakterystyka hydrologiczna jeziora Druzno. In Monografia Jeziora Druzno, Monografia Przyrodnicza; Nitecki, C., Ed.; Wyd. Mantis: Olsztyn, Poland, 2013. [Google Scholar]
- Choiński, A. Zarys Limnologii Fizycznej Polski; Wydawnictwo Naukowe UAM: Poznań, Poland, 1975. [Google Scholar]
- Borowiak, D. Reżimy Wodne i Funkcje Hydrologiczne Jezior Niżu Polskiego; Katedra Limnologii Uniwersytetu Gdańskiego: Gdańsk, Poland, 2000. [Google Scholar]
- Plewa, K. Typy przebiegu pentadowych współczynników stanu wody jezior Niżu Polskiego. Bad. Fizjogr. Ser. A – Geogr. Fiz. 2018, A69, 161–177. [Google Scholar]
- Gurgul, P.; Syrek, R. Zastosowanie mieszanki kopul do modelowania współzależności pomiędzy wybranymi sektorami gospodarki. Ekon. Menedżerska 2009, 6, 129–139. [Google Scholar]
- Zhang, D.; Chen, P.; Zhang, Q.; Li, X. Copula-based probability of concurrent hydrological drought in the Poyang lake-catchment-river system (China) from 1960 to 2013. J. Hydrol. 2017, 553, 773–784. [Google Scholar] [CrossRef]
- Assani, A.A.; Landry, R.; Biron, S.; Frenette, J.-J. Analysis of the interannual variability of annual daily extreme water levels in the St Lawrence River and Lake Ontario from 1918 to 2010. Hydrol. Process. 2014, 28, 4011–4022. [Google Scholar] [CrossRef]
- Assani, A.A. Analysis of the Impacts of Man-Made Features on the Stationarity and Dependence of Monthly Mean Maximum and Minimum Water Levels in the Great Lakes and St. Lawrence River of North America. Water 2016, 8, 485. [Google Scholar] [CrossRef]
- Kim, K.; Lee, S.; Jin, Y. Forecasting quarterly inflow to reservoirs combining a copula-based bayesian network method with drought forecasting. Water 2018, 10, 233. [Google Scholar] [CrossRef]
- Zhou, N.-Q.; Zhao, L.; Shen, X.-P. Copula-based Probability Evaluation of Rich-Poor Runoff and Sediment Encounter in Dongting Lake Basin. Sci. Geogr. Sin. 2014, 34, 242–248. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, Z.; You, J. The joint probability distribution of runoff and sediment and its change characteristics with multi-time scales. J. Hydrol. Hydromech. 2014, 62, 218–225. [Google Scholar] [CrossRef]
- You, Q.; Jiang, H.; Liu, Y.; Liu, Z.; Guan, Z. Probability Analysis and Control of River Runoff–sediment Characteristics based on Pair-Copula Functions: The Case of the Weihe River and Jinghe River. Water 2019, 11, 510. [Google Scholar] [CrossRef]
- Gu, H.; Yu, Z.; Li, G.; Ju, Q. Nonstationary Multivariate Hydrological Frequency Analysis in the Upper Zhanghe River Basin, China. Water 2018, 10, 772. [Google Scholar] [CrossRef]
- Chen, J.; Shixiang, G.; Zhang, T. Synchronous-Asynchronous Encounter Probability Analysis of High-Low Runoff for Jinsha River, China, using Copulas. Matec Web Conf. 2018, 246, 01094. [Google Scholar] [CrossRef]
- Burandt, P.; Kobus, S.; Sidoruk, M.; Glińska-Lewczuk, K. Hydrographic and hydrological characteristics Part I: Liwia Łuża, Resko Przymorskie, Jamno, Kopań and Wicko. In Hydroecological Determinants of Fuctioning of Southern Baltic Coastal Lakes; Obolewski, K., Ed.; Polish Scientific Publishers PWN: Warszawa, Poland, 2017. [Google Scholar]
- Choiński, A. Katalog Jezior Polski; Wydawnictwo Naukowe Uniwersytetu im. Adama Mickiewicza: Poznań, Poland, 2006. [Google Scholar]
- Salmi, T.; Määttä, A.; Anttila, P.; Ruoho-Airola, T.; Amnell, T. Detecting Trends of Annual Values of Atmospheric Pollutants by the Mann-Kendall Test and Sen’s Slope Estimates—The Excel Template Application Makesens; Publications on Air Quality 31; Finnish Meteorological Institute: Helsinki, Finland, 2002; p. 35.
- Sklar, M. Fonctions de répartition à n dimensions et leurs marges. Publ. L’inst. Stat. L’université De Paris 1959, 8, 229–231. [Google Scholar]
- Karmakar, S.; Simonovic, S.P. Water resources research report. In Flood Frequency Analysis Using Copula with Mixed Marginal Distributions; The University of Western Ontario Department of Civil and Environmental Engineering: London, ON, Canada, 2007. [Google Scholar]
- Koutsoyiannis, D. Probability and Statistics for Geophysical Processes; National Technical University of Athens: Athens, Greece, 2008. [Google Scholar]
- Zhao, L.; Xia, J.; Sobkowiak, L.; Wang, Z.; Guo, F. Spatial Pattern Characterization and Multivariate Hydrological Frequency Analysis of Extreme Precipitation in the Pearl River Basin, China. Water Resour. Manag. 2012, 26, 3619–3637. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–722. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 1999. [Google Scholar]
- Zhang, L.; Singh, V.P. Bivariate flood frequency analysis using the copula method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar] [CrossRef]
- Grimaldi, S.; Serinaldi, F. Asymmetric copula in multivariate flood frequency analysis. Adv. Water Resour. 2006, 29, 1115–1167. [Google Scholar] [CrossRef]
- Genest, C.; Rivest, L.-P. Statistical inference procedure for bivariate Archimedean copulas. J. Am. Stat. Assoc. 1993, 88, 1034–1043. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.-C. Everything you always wanted to know about copula Modeling but were afraid to ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Cyberski, J.; Jędrasik, J. Wymiana i cyrkulacja wód w jeziorze Gardno. In Zlewnia Przymorskiej Rzeki Łupawy i jej Jeziora; Korzeniewski, K., Ed.; WSP: Słupsk, Poland, 1992. [Google Scholar]
- Rokiciński, K. Geograficzna i hydrometeorologiczna charakterystyka Morza Bałtyckiego jako obszaru prowadzenia działań asymetrycznych. Zesz. Nauk. Akad. Mar. Wojennej 2007, 48, 65–82. [Google Scholar]
- Mikosch, T. Copulas: Tales and facts. Extremes 2006, 9, 3–20. [Google Scholar] [CrossRef]
- Mikosch, T. Copulas: Tales and facts—Rejoinder. Extremes 2006, 9, 55–62. [Google Scholar] [CrossRef]
- Plewa, K.; Wrzesiński, D.; Baczyńska, A. Przestrzenne i czasowe zróżnicowanie amplitud stanów wody jezior w Polsce w latach 1981-2015. Bad. Fizjogr. Ser. A Geogr. Fiz. 2017, A68, 115–126. [Google Scholar] [CrossRef]
- Cieśliński, R. Hydrochemiczna ocena porównawcza wód jeziora Jamno i Bukowo. Przegląd Geol. 2005, 53, 1066–1067. [Google Scholar]



| No. | Lake | Area (ha) | Volume (thousand m3) | Average Depth (m) | Max Depth (m) |
|---|---|---|---|---|---|
| 1 | Resko Przymorskie (P.) | 559.0 | 7703.4 | 1.3 | 2.5 |
| 2 | Jamno | 2231.5 | 31,528.0 | 1.4 | 3.9 |
| 3 | Bukowo | 1644.0 | 32,071.7 | 1.8 | 2.8 |
| 4 | Gardno | 2337.5 | 30,950.5 | 1.3 | 2.6 |
| 5 | Łebsko | 7020.0 | 117,521.0 | 1.6 | 6.3 |
| 6 | Druzno | 1147.5 | 17,352.0 | 1.2 | 2.5 |
| Lake/Gauge Station | Water Level (m) | Amplitudes of Water Level (m) | Coefficient of Variation (Cv) | ||||
|---|---|---|---|---|---|---|---|
| Annual Mean | Max | Min | Annual Max | Annual Mean | Extreme Multiyear | ||
| Lakes | |||||||
| Resko P. | 502 | 571 | 460 | 175 | 111 | 200 | 0.043 |
| Jamno | 533 | 578 | 506 | 104 | 73 | 131 | 0.039 |
| Bukowo | 529 | 577 | 494 | 126 | 82 | 158 | 0.044 |
| Gardno | 520 | 573 | 485 | 122 | 88 | 134 | 0.040 |
| Łebsko | 509 | 561 | 475 | 120 | 86 | 127 | 0.036 |
| Druzno | 520 | 576 | 479 | 138 | 97 | 176 | 0.041 |
| Baltic Sea | |||||||
| Kołobrzeg | 503 | 579 | 436 | 181 | 132 | 220 | 0.041 |
| Ustka | 505 | 573 | 443 | 161 | 119 | 188 | 0.041 |
| Łeba | 505 | 570 | 446 | 151 | 114 | 196 | 0.041 |
| Tolkmicko | 509 | 581 | 456 | 168 | 124 | 201 | 0.041 |
| Copula Family | Generator | Parameter | Kendall’s | (5) | |
| Clayton | |||||
| Gumbel–Hougaard | |||||
| Frank |
| Lake/Gauges | Period | Year | Nov | Dec | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lakes | ||||||||||||||
| Resko P. | 1981–2015 | 0.612 | −0.724 | −0.227 | 1.053 | 0.697 | 1.151 | −0.442 | 1.010 | 1.096 | 0.355 | −0.270 | 0.712 | 0.555 |
| Jamno | 1976–2015 | 3.032 | 2.937 | 2.005 | 2.342 | 3.207 | 3.183 | 2.682 | ||||||
| Bukowo | 1976–2015 | −0.944 | −0.723 | −1.516 | 0.175 | 2.006 | 2.729 | 2.030 | 1.144 | 2.381 | 0.070 | 1.202 | 0.443 | −0.816 |
| Gardno | 1976–2015 | −0.642 | −0.234 | −1.353 | −0.175 | 0.373 | 0.759 | 0.607 | 0.339 | 2.662 | −0.233 | −0.467 | −1.295 | −0.455 |
| Łebsko | 1976–2015 | −0.082 | 0.233 | −0.466 | 0.175 | 1.049 | 1.621 | 0.665 | 2.217 | 0.958 | 0.969 | −0.058 | 0.793 | |
| Druzno | 1976–2014 | 1.006 | 1.017 | −0.218 | 1.065 | 2.325 | 2.470 | 1.273 | 2.967 | 1.977 | 2.315 | 0.654 | 0.921 | |
| Baltic Sea | ||||||||||||||
| Kołobrzeg | 1981–2015 | 0.483 | −0.639 | 0.241 | −0.810 | −0.142 | 1.364 | −0.114 | 1.094 | 2.003 | 1.122 | 0.000 | 0.170 | −0.156 |
| Kołobrzeg | 1976–2015 | 0.874 | −0.350 | 0.606 | −0.070 | 1.503 | 1.433 | 0.000 | 2.424 | 2.307 | 1.258 | 0.804 | −0.023 | 0.466 |
| Ustka | 1976–2015 | 0.513 | −0.152 | 0.396 | 0.128 | 1.213 | 1.271 | 0.338 | 2.450 | 1.995 | 1.450 | 0.945 | −0.058 | 0.023 |
| Łeba | 1976–2015 | 0.000 | −0.268 | 0.012 | −0.035 | 0.875 | 1.270 | 0.385 | 1.902 | 1.890 | 0.058 | 0.187 | −0.665 | 0.000 |
| Tolkmicko | 1976–2014 | 1.393 | −0.061 | 0.048 | 0.436 | 1.634 | 1.659 | −0.145 | 1.805 | 1.116 | 1.962 | 0.157 | 0.242 | |
| No. | Gauge stations (Sea–Lake) | Period | Annual Max Water Level | ||
|---|---|---|---|---|---|
| Correlation Coefficient | Synchronicity (%) | Asynchronicity (%) | |||
| 1 | Kołobrzeg–Resko P. | 1981–2015 | 75.18 | 24.82 | |
| 2 | Kołobrzeg–Jamno | 1976–2015 | 58.20 | 41.80 | |
| 3 | Ustka–Bukowo | 1976–2015 | 56.82 | 43.18 | |
| 4 | Ustka–Gardno | 1976–2015 | 65.92 | 34.08 | |
| 5 | Łeba–Łebsko | 1976–2015 | 69.82 | 30.18 | |
| 6 | Tolkmicko–Druzno | 1976–2014 | 60.42 | 39.58 | |
| Sector | Kołobrzeg–Jamno | Ustka–Bukowo | Ustka–Gardno | Łeba–Łebsko | Tolkmicko–Druzno | Kołobrzeg–Resko |
|---|---|---|---|---|---|---|
| 1 | 24.56 | 23.80 | 26.78 | 29.48 | 25.86 | 30.64 |
| 5 | 8.54 | 8.30 | 10.14 | 10.42 | 8.46 | 13.12 |
| 9 | 25.10 | 24.72 | 29.00 | 29.92 | 26.10 | 31.42 |
| 2 | 8.92 | 9.88 | 8.06 | 6.62 | 8.46 | 6.48 |
| 4 | 8.88 | 9.34 | 6.90 | 7.20 | 8.76 | 6.14 |
| 8 | 7.68 | 6.92 | 8.04 | 7.22 | 6.92 | 5.52 |
| 6 | 7.26 | 7.62 | 6.94 | 6.66 | 7.08 | 5.32 |
| 9 | 4.52 | 4.68 | 1.74 | 1.30 | 4.32 | 0.78 |
| 7 | 4.54 | 4.74 | 2.40 | 1.18 | 4.04 | 0.58 |
| Syn. | 58.20 | 56.82 | 65.92 | 69.82 | 60.42 | 75.18 |
| Asyn. | 41.80 | 43.18 | 34.08 | 30.18 | 39.58 | 24.82 |
| Sector | Nov | Dec | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jamno–Kołobrzeg | ||||||||||||
| 1 | 24.30 | 26.64 | 25.16 | 24.84 | 25.70 | 17.26 | 24.76 | 25.42 | 25.10 | 23.12 | 23.06 | 22.72 |
| 5 | 8.64 | 9.06 | 9.06 | 10.06 | 9.22 | 7.40 | 7.64 | 7.68 | 7.94 | 7.54 | 6.64 | 7.12 |
| 9 | 25.60 | 27.00 | 28.04 | 27.86 | 26.28 | 18.12 | 22.00 | 22.06 | 22.06 | 19.22 | 22.36 | 20.00 |
| 2 | 8.32 | 7.78 | 8.32 | 8.36 | 8.34 | 9.78 | 9.52 | 7.18 | 6.30 | 7.96 | 8.50 | 7.80 |
| 4 | 8.94 | 7.72 | 8.76 | 8.70 | 9.00 | 9.28 | 8.56 | 6.90 | 7.58 | 7.66 | 8.66 | 7.08 |
| 8 | 7.16 | 7.42 | 7.14 | 6.96 | 6.80 | 8.86 | 8.96 | 10.36 | 9.18 | 9.50 | 8.38 | 10.22 |
| 6 | 7.08 | 8.02 | 7.50 | 6.76 | 7.66 | 8.86 | 8.58 | 9.54 | 10.28 | 9.98 | 8.78 | 11.12 |
| 9 | 5.50 | 3.00 | 3.08 | 3.02 | 3.54 | 11.08 | 4.84 | 5.38 | 5.92 | 7.50 | 6.72 | 6.72 |
| 7 | 4.46 | 3.36 | 2.94 | 3.44 | 3.46 | 9.36 | 5.14 | 5.48 | 5.64 | 7.52 | 6.90 | 7.22 |
| Syn. | 58.54 | 62.70 | 62.26 | 62.76 | 61.20 | 42.78 | 54.40 | 55.16 | 55.10 | 49.88 | 52.06 | 49.84 |
| Asyn. | 41.46 | 37.30 | 37.74 | 37.24 | 38.80 | 57.22 | 45.60 | 44.84 | 44.90 | 50.12 | 47.94 | 50.16 |
| Gardno–Ustka | ||||||||||||
| 1 | 32.66 | 31.64 | 31.42 | 32.82 | 31.38 | 25.8 | 30.42 | 28.64 | 29.46 | 30.26 | 28.72 | 32.94 |
| 5 | 17.28 | 10.74 | 15.48 | 16.22 | 13.04 | 9.62 | 11.20 | 11.06 | 12.54 | 9.16 | 9.30 | 14.34 |
| 9 | 33.92 | 27.52 | 32.90 | 32.74 | 30.82 | 26.58 | 26.06 | 30.68 | 30.42 | 26.30 | 25.74 | 28.90 |
| 2 | 3.82 | 5.36 | 5.36 | 4.68 | 6.32 | 8.78 | 5.12 | 6.92 | 6.74 | 6.10 | 6.14 | 4.32 |
| 4 | 4.26 | 4.92 | 5.62 | 4.64 | 6.06 | 8.66 | 5.36 | 7.42 | 6.20 | 5.76 | 6.54 | 4.46 |
| 8 | 4.02 | 8.08 | 3.94 | 4.60 | 5.14 | 6.90 | 9.18 | 5.86 | 6.34 | 8.96 | 8.78 | 7.38 |
| 6 | 3.82 | 9.00 | 4.60 | 4.12 | 5.76 | 7.30 | 8.72 | 6.12 | 6.44 | 8.98 | 9.70 | 6.90 |
| 9 | 0.10 | 1.22 | 0.36 | 0.04 | 0.88 | 3.04 | 2.12 | 1.54 | 0.96 | 2.26 | 2.38 | 0.46 |
| 7 | 0.12 | 1.52 | 0.32 | 0.14 | 0.60 | 3.32 | 1.82 | 1.76 | 0.90 | 2.22 | 2.70 | 0.30 |
| Syn. | 83.86 | 69.90 | 79.80 | 81.78 | 75.24 | 62.00 | 67.68 | 70.38 | 72.42 | 65.72 | 63.76 | 76.18 |
| Asyn. | 16.14 | 30.10 | 20.20 | 18.22 | 24.76 | 38.00 | 32.32 | 29.62 | 27.58 | 34.28 | 36.24 | 23.82 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plewa, K.; Perz, A.; Wrzesiński, D.; Sobkowiak, L. Probabilistic Assessment of Correlations of Water Levels in Polish Coastal Lakes with Sea Water Level with the Application of Archimedean Copulas. Water 2019, 11, 1292. https://doi.org/10.3390/w11061292
Plewa K, Perz A, Wrzesiński D, Sobkowiak L. Probabilistic Assessment of Correlations of Water Levels in Polish Coastal Lakes with Sea Water Level with the Application of Archimedean Copulas. Water. 2019; 11(6):1292. https://doi.org/10.3390/w11061292
Chicago/Turabian StylePlewa, Katarzyna, Adam Perz, Dariusz Wrzesiński, and Leszek Sobkowiak. 2019. "Probabilistic Assessment of Correlations of Water Levels in Polish Coastal Lakes with Sea Water Level with the Application of Archimedean Copulas" Water 11, no. 6: 1292. https://doi.org/10.3390/w11061292
APA StylePlewa, K., Perz, A., Wrzesiński, D., & Sobkowiak, L. (2019). Probabilistic Assessment of Correlations of Water Levels in Polish Coastal Lakes with Sea Water Level with the Application of Archimedean Copulas. Water, 11(6), 1292. https://doi.org/10.3390/w11061292





