Soil Water Content Estimation Using High-Frequency Ground Penetrating Radar
Abstract
1. Introduction
2. Materials and Methods
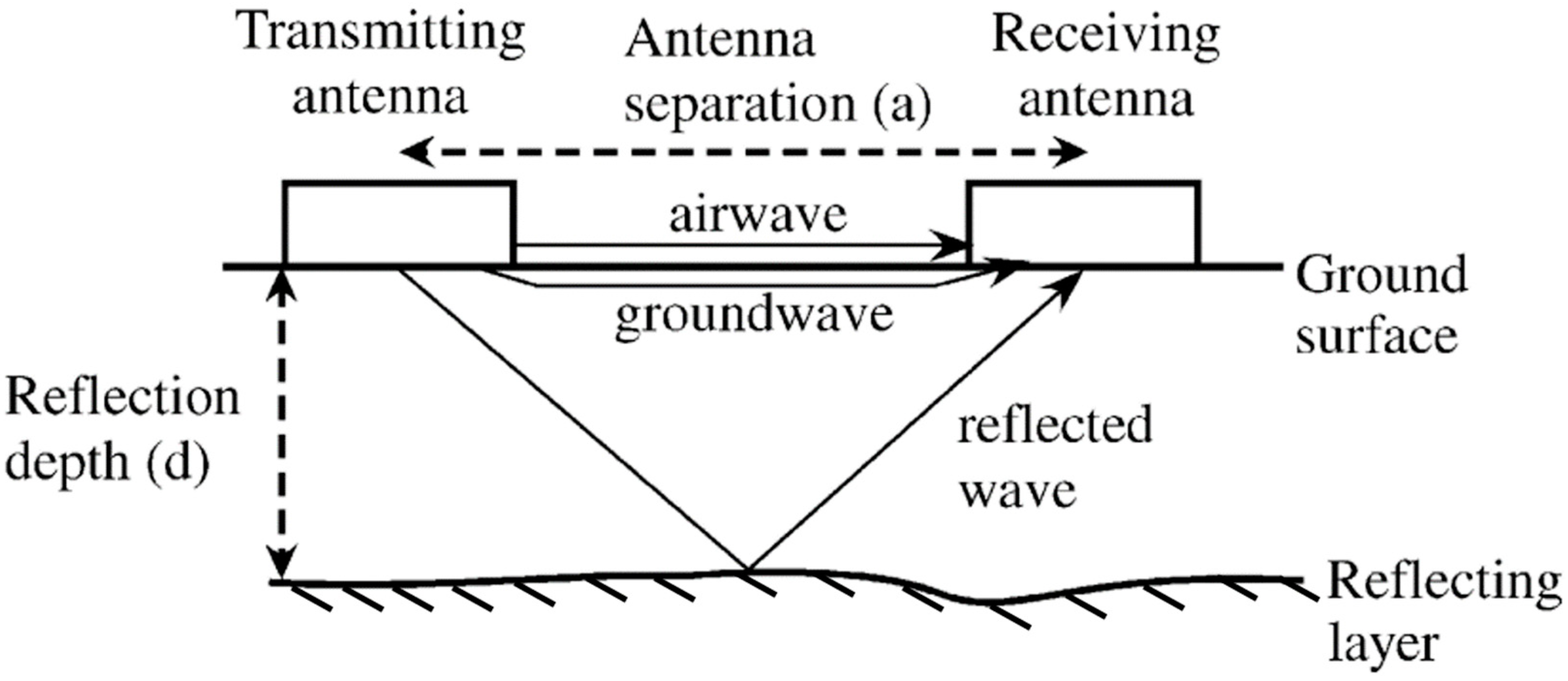
2.1. GPR Background
2.2. Experimental Materials
2.3. Experimental Design
2.4. GPR Key Parameter Acquisition
3. Results
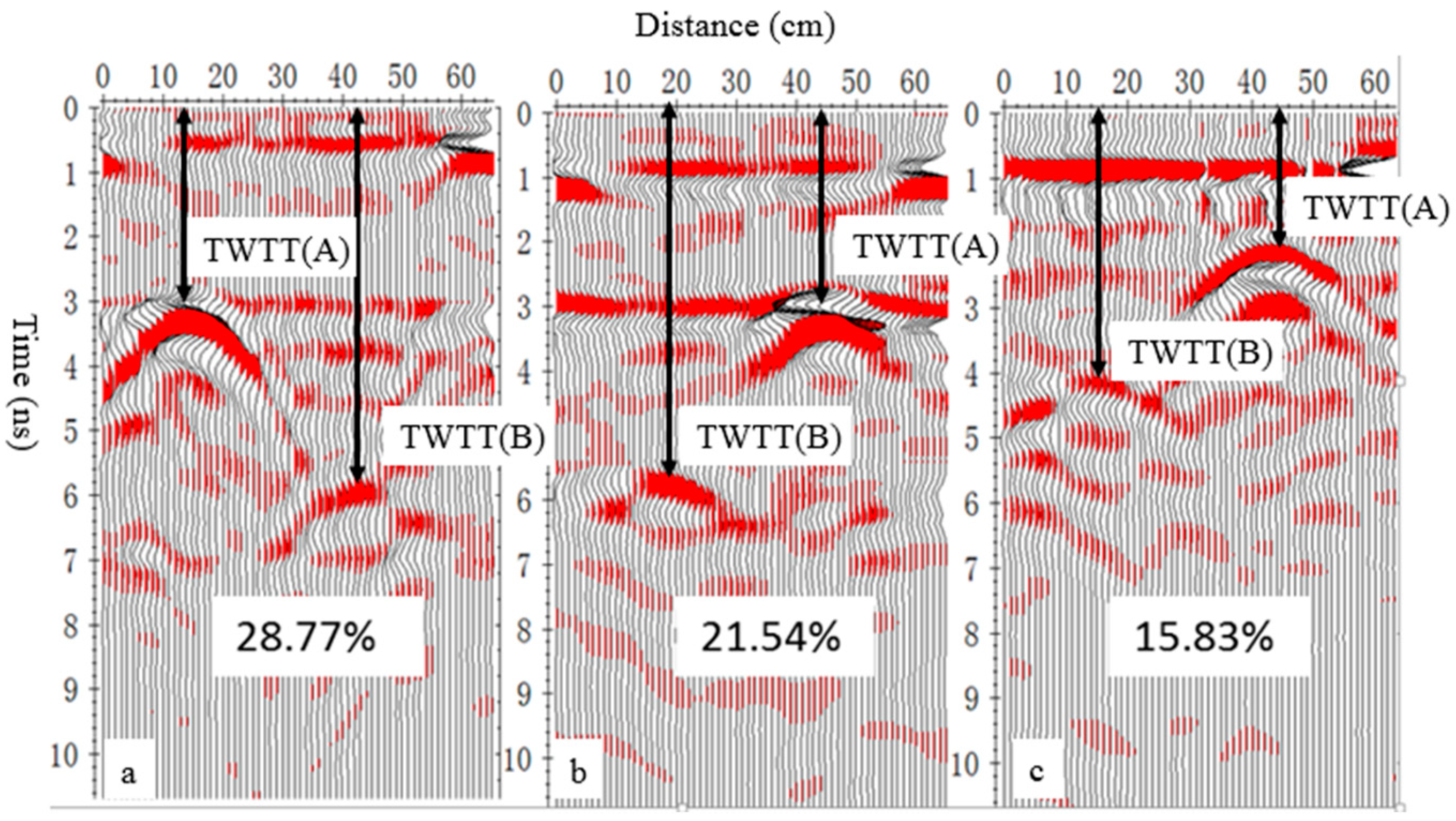
3.1. GPR Reflected Wave Image Features
3.2. Effect of SWC on GPR Electromagnetic Properties
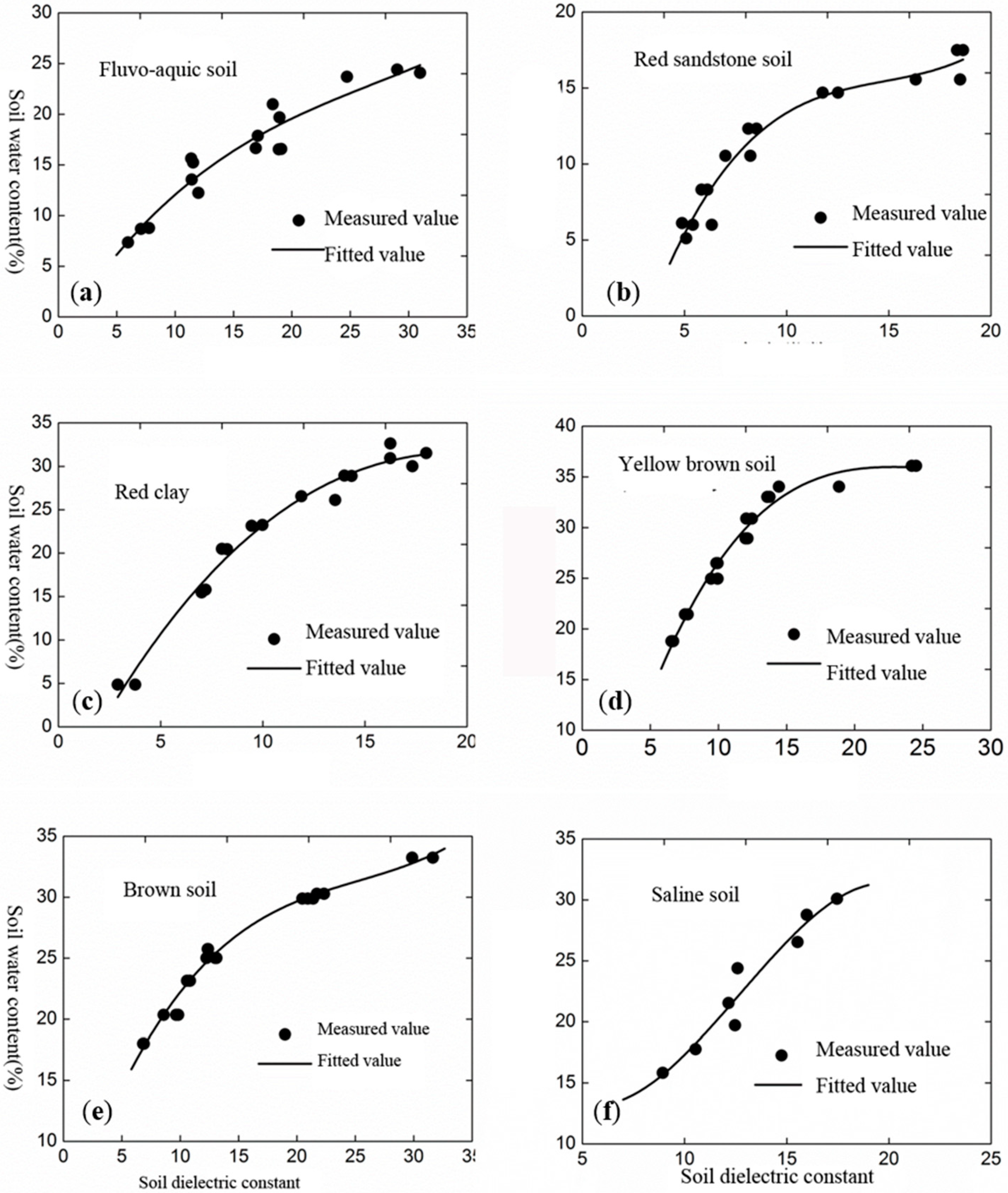
3.3. Retrieving SWC from the Soil Dielectric Permittivities
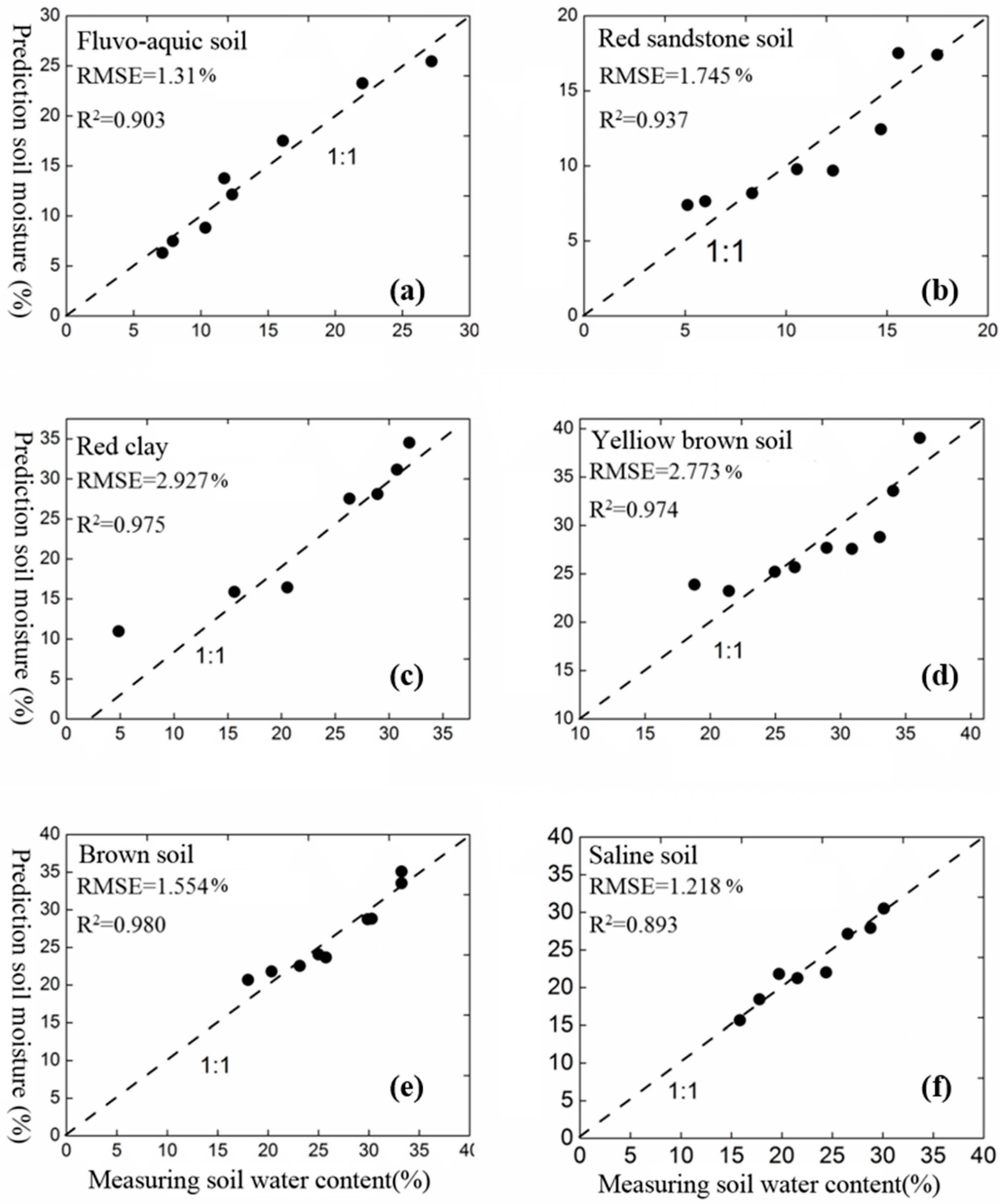
3.4. GPR-Derived SWC Validation
4. Discussion
4.1. Approach Based on Signal Velocity Analysis
4.2. Effects of Soil Properties on the Soil Dielectric Permittivity
4.3. Impact of Soil Parameters on SWC Prediction
4.4. Comparative Analysis of SWC Predicted by GPRs with Different Frequencies
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moghadas, D.; Jadoon, K.Z.; Lambot, S.; Vanderborght, J.; Vereecken, H. Monitoring near surface soil moisture profiles during evaporation using off-ground zero-offset ground-penetrating radar. EGU Gen. Assem. 2012, 14, 11988. [Google Scholar]
- Klotzsche, A.; Jonard, F.; Looms, M.C.; van der Kruk, J.; Huisman, J.A. Measuring Soil Water Content with Ground Penetrating Radar: A Decade of Progress. Vadose Zone J. 2018, 17, 1–9. [Google Scholar] [CrossRef]
- Vereecken, H.; Schnepf, A.; Hopmans, J.W.; Javaux, M.; Or, D.; Roose, T.; Vanderborght, J.; Young, M.H.; Amelung, W.; Aitkenhead, M. Modeling Soil Processes: Review, Key Challenges, and New Perspectives. Vadose Zone J. 2016, 15, 1–57. [Google Scholar] [CrossRef]
- Huisman, J.A. Measuring soil water content with ground penetrating radar: A review. Vadose Zone J. 2003, 2, 476–491. [Google Scholar] [CrossRef]
- Algeo, J.; Dam, R.L.V.; Slater, L. Early-Time, GPR: A Method to Monitor Spatial Variations in Soil Water Content during Irrigation in Clay Soils. Vadose Zone J. 2016, 15, 1–9. [Google Scholar] [CrossRef]
- Benedetto, A.; Tosti, F.; Ortuani, B.; Giudici, M.; Mele, M. Mapping the spatial variation of soil moisture at the large scale using GPR for pavement applications. Near Surf. Geophys. 2015, 13, 269–278. [Google Scholar] [CrossRef]
- Luo, T.X.H.; Lai, W.W.L.; Chang, R.K.W.; Goodman, D. GPR imaging criteria. J. Appl. Geophys. 2019, 165, 37–48. [Google Scholar] [CrossRef]
- Shamir, O.; Goldshleger, N.; Basson, U.; Reshef, M. Laboratory Measurements of Subsurface Spatial Moisture Content by Ground-Penetrating Radar (GPR) Diffraction and Reflection Imaging of Agricultural Soils. Remote Sens. 2018, 10, 1667. [Google Scholar] [CrossRef]
- Ercoli, M.; Di Matteo, L.; Pauselli, C.; Mancinelli, P.; Frapiccini, S.; Talegalli, L.; Cannata, A. Integrated GPR and laboratory water content measures of sandy soils: From laboratory to field scale. Constr. Build. Mater. 2018, 159, 734–744. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Weitz, A.M.; Grauel, W.T.; Keller, M.; Veldkamp, E. Calibration of time domain reflectometry technique using undisturbed soil samples from humid tropical soils of volcanic origin. Water Resour. Res. 1997, 33, 1241–1249. [Google Scholar] [CrossRef]
- Dam, R.L.V. Calibration Functions for Estimating Soil Moisture from GPR Dielectric Constant Measurements. Commun. Soil Sci. Plant Anal. 2014, 45, 392–413. [Google Scholar]
- Huisman, J.A.; Sperl, C.; Bouten, W.; Verstraten, J.M. Soil water content measurements at different scales: Accuracy of time domain reflectometry and ground-penetrating radar. J. Hydrol. 2001, 245, 48–58. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. Satellite remote sensing applications for surface soil moisture monitoring: A review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Bauer-Marschallinger, B.; Freeman, V.; Cao, S.; Paulik, C.; Schaufler, S.; Stachl, T.; Modanesi, S.; Massari, C.; Ciabatta, L.; Brocca, L.; et al. Toward Global Soil Moisture Monitoring With Sentinel-1: Harnessing Assets and Overcoming Obstacles. IEEE Trans. Geosci. Remote Sens. 2019, 57, 520–539. [Google Scholar] [CrossRef]
- Zeng, X.; Shan, W.; Zhang, Y.; Wang, C. Soil water content retrieval based on Sentinel-1A and Landsat 8 image for Bei’an-Heihe Expressway. Chin. J. Eco-Agric. 2017, 25, 118–126. (In Chinese) [Google Scholar]
- Chanzy, A.; Tarussov, A.; Judge, A.; Bonn, F. Soil Water Content Determination Using a Digital Ground-Penetrating Radar. Soil Sci. Soc. Am. J. 1996, 60, 1318–1326. [Google Scholar] [CrossRef]
- Jackson, T.J.; Schmugge, J.; Engman, E.T. Remote sensing applications to hydrology: Soil moisture. Int. Assoc. Sci. Hydrol. Bull. 1996, 41, 517–530. [Google Scholar] [CrossRef]
- Zreda, M.; Desilets, D.; Ferre, T.P.A.; Scott, R.L. Measuring soil moisture content non-invasively at intermediate spatial scale using cosmic-ray neutrons. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Jiao, Q.; Liu, S.; Jin, R.; Du, F. Research and Application of Cosmic-ray Fast Neutron Method to Measure Soil Moisture in the Field. Adv. Earth Sci. 2013, 28, 1136–1143. [Google Scholar]
- Strati, V.; Albéri, M.; Anconelli, S.; Baldoncini, M.; Bittelli, M.; Bottardi, C.; Chiarelli, E.; Fabbri, B.; Guidi, V.; Raptis, K.; et al. Modelling Soil Water Content in a Tomato Field: Proximal Gamma Ray Spectroscopy and Soil–Crop System Models. Agriculture 2018, 8, 60. [Google Scholar] [CrossRef]
- Baldoncini, M.; Albéri, M.; Bottardi, C.; Chiarelli, E.; Raptis, K.G.C.; Strati, V.; Mantovani, F. Biomass water content effect on soil moisture assessment via proximal gamma-ray spectroscopy. Geoderma 2019, 335, 69–77. [Google Scholar] [CrossRef]
- Yochim, A.; Zytner, R.G.; Mcbean, E.A.; Endres, A.L. Estimating water content in an active landfill with the aid of GPR. Waste Manag. 2013, 33, 2015–2028. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Hu, Z.; Zhao, Y.; Li, X. Experimental study of soil compaction effects on GPR signals. J. Appl. Geophys. 2016, 126, 128–137. [Google Scholar] [CrossRef]
- Zhou, L.G.; Yu, D.S.; Wang, X.Y.; Wang, X.H.; Zhang, H.D. Determination of top soil water content based on high-frequency ground penetrating radar. Acta Pedol. Sin. 2016, 53, 621–626. (In Chinese) [Google Scholar]
- Lu, Y.; Song, W.; Lu, J.; Wang, X.; Tan, Y. An Examination of Soil Moisture Estimation Using Ground Penetrating Radar in Desert Steppe. Water 2017, 9, 521. [Google Scholar] [CrossRef]
- Zajícová, K.; Chuman, T. Application of ground penetrating radar methods in soil studies: A review. Geoderma 2019, 343, 116–129. [Google Scholar] [CrossRef]
- Overmeeren, R.A.V.; Sariowan, S.V.; Gehrels, J.C. Ground penetrating radar for determining volumetric soil water content; results of comparative measurements at two test sites. J. Hydrol. 1997, 197, 316–338. [Google Scholar] [CrossRef]
- Rogers, M.; Leon, J.F.; Fisher, K.D.; Manning, S.W.; Sewell, D. Comparing Similar Ground-penetrating Radar Surveys Under Different Moisture Conditions at Kalavasos-Ayios Dhimitrios, Cyprus. Archaeol. Prospect. 2012, 19, 297–305. [Google Scholar] [CrossRef]
- Reynolds, J.M. An Introduction to Applied and Environmental Geophysics; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Daniels, D. Ground Penetrating Radar, 2nd ed.; Wiley Interscience: London, UK, 2004. [Google Scholar]
- Ardekani, M.R.M. Off-and on-ground GPR techniques for field-scale soil moisture mapping. Geoderma 2013, 200, 55–66. [Google Scholar] [CrossRef]
- Lunt, I.A.; Hubbard, S.S.; Rubin, Y. Soil moisture content estimation using ground-penetrating radar reflection data. J. Hydrol. 2005, 307, 254–269. [Google Scholar] [CrossRef]
- Mohamed, A.-M.O.; Paleologos, E.K. Chapter 16—Dielectric Permittivity and Moisture Content. In Fundamentals of Geoenvironmental Engineering; Mohamed, A.-M.O., Paleologos, E.K., Eds.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 581–637. [Google Scholar]
- Scudiero, E.; Berti, A.; Teatini, P.; Morari, F. Simultaneous Monitoring of Soil Water Content and Salinity with a Low-Cost Capacitance-Resistance Probe. Sensors 2012, 12, 17588–17607. [Google Scholar] [CrossRef]
- Leandro, C.G.; Barboza, E.G.; Caron, F.; de Jesus, F.A.N. GPR trace analysis for coastal depositional environments of southern Brazil. J. Appl. Geophys. 2019, 162, 1–12. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, W.; Wang, K.; Pan, F.; Yang, S.; Shu, S. Factors controlling accumulation of soil organic carbon along vegetation succession in a typical karst region in Southwest China. Sci. Total Environ. 2015, 521–522, 52–58. [Google Scholar] [CrossRef]
- Chiara, F.D.; Fontul, S.; Fortunato, E. GPR Laboratory Tests For Railways Materials Dielectric Properties Assessment. Remote Sens. 2014, 6, 9712–9728. [Google Scholar] [CrossRef]
- Salat, C.; Junge, A. Dielectric permittivity of fine-grained fractions of soil samples from eastern Spain at 200 MHz. Geophysics 2010, 75, J1–J9. [Google Scholar] [CrossRef]
- Mohamed, A.-M.O.; Paleologos, E.K. Chapter 14—Electrical Properties of Soils. In Fundamentals of Geoenvironmental Engineering; Mohamed, A.-M.O., Paleologos, E.K., Eds.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 497–533. [Google Scholar]
- Lal, H.B.; Dar, N.; Kumar, A. Electrical and magnetic properties of Er2(WO4)3. J. Phys. C Solid State Phys. 1975, 8, 2745–2748. [Google Scholar] [CrossRef]
- Cassidy, N.J. Chapter 2—Electrical and Magnetic Properties of Rocks, Soils and Fluids. In Ground Penetrating Radar Theory and Applications; Jol, H.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 41–72. [Google Scholar]
- Sevostianova, E.; Deb, S.; Serena, M.; VanLeeuwen, D.; Leinauer, B. Accuracy of two electromagnetic soil water content sensors in saline soils. Soil Sci. Soc. Am. J. 2015, 79, 1752–1759. [Google Scholar] [CrossRef]
- Wu, Y.; Cui, F.; Wang, L.; Chen, J.; Li, Y. Detecting moisture content of soil by transmission-type ground penetrating radar. Trans. Chin. Soc. Agric. Eng. 2014, 30, 125–131. (In Chinese) [Google Scholar]
- Ji, L.Q.; Zhu, A.N.; Zhang, J.B.; Xin, X.L.; Li, X.P. Determining Soil Water Content by Using Low-frequency Ground-penetrating Radar Ground Wave Techniques. Soils 2011, 43, 123–129. (In Chinese) [Google Scholar]



| Test Item | Soil Types | |||||
|---|---|---|---|---|---|---|
| Saline Soil | Fluvo-Aquic Soil | Yellow Brown Soil | Brown Soil | Red Clay | Red Sandstone Soil | |
| pH | 7.26 ± 0.21 | 6.69 ± 0.19 | 5.46 ± 0.31 | 7.62 ± 0.22 | 5.40 ± 0.24 | 5.70 ± 0.34 |
| Organic matter (g kg−1) | 7.98 ± 0.32 | 14.52 ± 0.17 | 8.78 ± 0.26 | 17.59 ± 0.18 | 20.16 ± 0.25 | 9.80 ± 0.23 |
| Soil bulk density (g cm−3) | 1.25 ± 0.031 | 1.19 ± 0.040 | 1.39 ± 0.052 | 1.14 ± 0.044 | 1.13 ± 0.063 | 1.32 ± 0.064 |
| Salt content (%) | 0.03 ± 0.0021 | 0.006 ± 0.0023 | 0.008 ± 0.0012 | 0.01 ± 0.0020 | 0.20 ± 0.021 | 0.10 ± 0.030 |
| Sand (2~0.05 mm) (%) | 14.8 ± 0.71 | 15.9 ± 1.00 | 17.7 ± 0.90 | 26.20 ± 1.72 | 29.2 ± 1.63 | 81.60 ± 2.12 |
| Silt (0.05~0.002 mm) (%) | 79.50 ± 1.22 | 68.50 ± 2.31 | 55.80 ± 1.17 | 66.40 ± 2.14 | 29.00 ± 1.23 | 11.20 ± 0.48 |
| Clay (<0.002 mm) (%) | 5.70 ± 0.51 | 15.6 ± 1.23 | 26.50 ± 0.36 | 7.40 ± 0.37 | 41.80 ± 2.11 | 7.20 ± 0.37 |
| Antenna Frequency | Material Type | Interval (m) | Time Window (ns) | Stacking Fold | Depth (m) |
|---|---|---|---|---|---|
| 2 GHz | Soil | 0.005 | 13 | 8 | 0.4 |
| Soil Type | SWC (%) | TWTT(A) ns | TWTT(B) ns | Velocity (108 m s−1) | Soil Dielectric Permittivity (ε) | ||
|---|---|---|---|---|---|---|---|
| Fluvo-aquic soil | 24.00 | 2.78 | 4.41 | 0.07 | 0.09 | 0.08 ± 0.003 | 17.39 ± 1.45 |
| 16.65 | 2.19 | 4.23 | 0.09 | 0.09 | 0.09 ± 0.004 | 10.79 ± 0.86 | |
| 8.35 | 2.02 | 3.92 | 0.10 | 0.10 | 0.10 ± 0.002 | 9.18 ± 0.81 | |
| Red sandstone soil | 17.49 | 2.44 | 5.12 | 0.08 | 0.08 | 0.08 ± 0.003 | 13.40 ± 1.14 |
| 10.03 | 2.31 | 4.31 | 0.09 | 0.09 | 0.09 ± 0.003 | 12.01 ± 1.08 | |
| 6.12 | 2.12 | 3.83 | 0.09 | 0.10 | 0.10 ± 0.004 | 10.11 ± 1.02 | |
| Red clay soil | 30.74 | 2.64 | 4.85 | 0.08 | 0.08 | 0.08 ± 0.002 | 15.68 ± 1.23 |
| 15.48 | 2.51 | 4.53 | 0.08 | 0.09 | 0.08 ± 0.002 | 14.18 ± 1.27 | |
| 4.85 | 1.45 | 3.01 | 0.14 | 0.13 | 0.14 ± 0.004 | 4.73 ± 0.57 | |
| Yellow brown soil | 36.00 | 3.12 | 6.43 | 0.06 | 0.06 | 0.06 ± 0.001 | 21.90 ± 1.89 |
| 28.00 | 2.80 | 5.26 | 0.07 | 0.08 | 0.07 ± 0.002 | 17.64 ± 1.72 | |
| 21.00 | 2.21 | 4.62 | 0.09 | 0.09 | 0.09 ± 0.003 | 10.99 ± 0.89 | |
| Brown soil | 25.74 | 2.81 | 5.82 | 0.07 | 0.07 | 0.07 ± 0.002 | 17.77 ± 1.49 |
| 20.34 | 2.08 | 4.12 | 0.10 | 0.10 | 0.10 ± 0.000 | 9.73 ± 0.79 | |
| 18.01 | 1.42 | 3.01 | 0.14 | 0.13 | 0.14 ± 0.004 | 4.54 ± 0.37 | |
| Saline soil | 28.77 | 3.08 | 6.02 | 0.06 | 0.07 | 0.07 ± 0.002 | 21.34 ± 1.68 |
| 21.54 | 2.68 | 3.58 | 0.07 | 0.11 | 0.09 ± 0.003 | 16.16 ± 1.27 | |
| 15.83 | 2.00 | 4.08 | 0.10 | 0.10 | 0.10 ± 0.003 | 9.00 ± 0.71 | |
| Soil Types | Soil Texture | Curve Fitting | R2 |
|---|---|---|---|
| Fluvo-aquic soil | Silty loam | 0.90 | |
| Red sandstone soil | Loamy sand | 0.93 | |
| Red clay | Clay | 0.97 | |
| Yellow brown soil | Silty loam | 0.97 | |
| Brown soil | Silty loam | 0.98 | |
| Saline soil | Silty loam | 0.89 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Yu, D.; Wang, Z.; Wang, X. Soil Water Content Estimation Using High-Frequency Ground Penetrating Radar. Water 2019, 11, 1036. https://doi.org/10.3390/w11051036
Zhou L, Yu D, Wang Z, Wang X. Soil Water Content Estimation Using High-Frequency Ground Penetrating Radar. Water. 2019; 11(5):1036. https://doi.org/10.3390/w11051036
Chicago/Turabian StyleZhou, Ligang, Dongsheng Yu, Zhaoyan Wang, and Xiangdong Wang. 2019. "Soil Water Content Estimation Using High-Frequency Ground Penetrating Radar" Water 11, no. 5: 1036. https://doi.org/10.3390/w11051036
APA StyleZhou, L., Yu, D., Wang, Z., & Wang, X. (2019). Soil Water Content Estimation Using High-Frequency Ground Penetrating Radar. Water, 11(5), 1036. https://doi.org/10.3390/w11051036





