Dynamics of the Flow Exchanges between Matrix and Conduits in Karstified Watersheds at Multiple Temporal Scales
Abstract
1. Introduction
2. Material and Methods
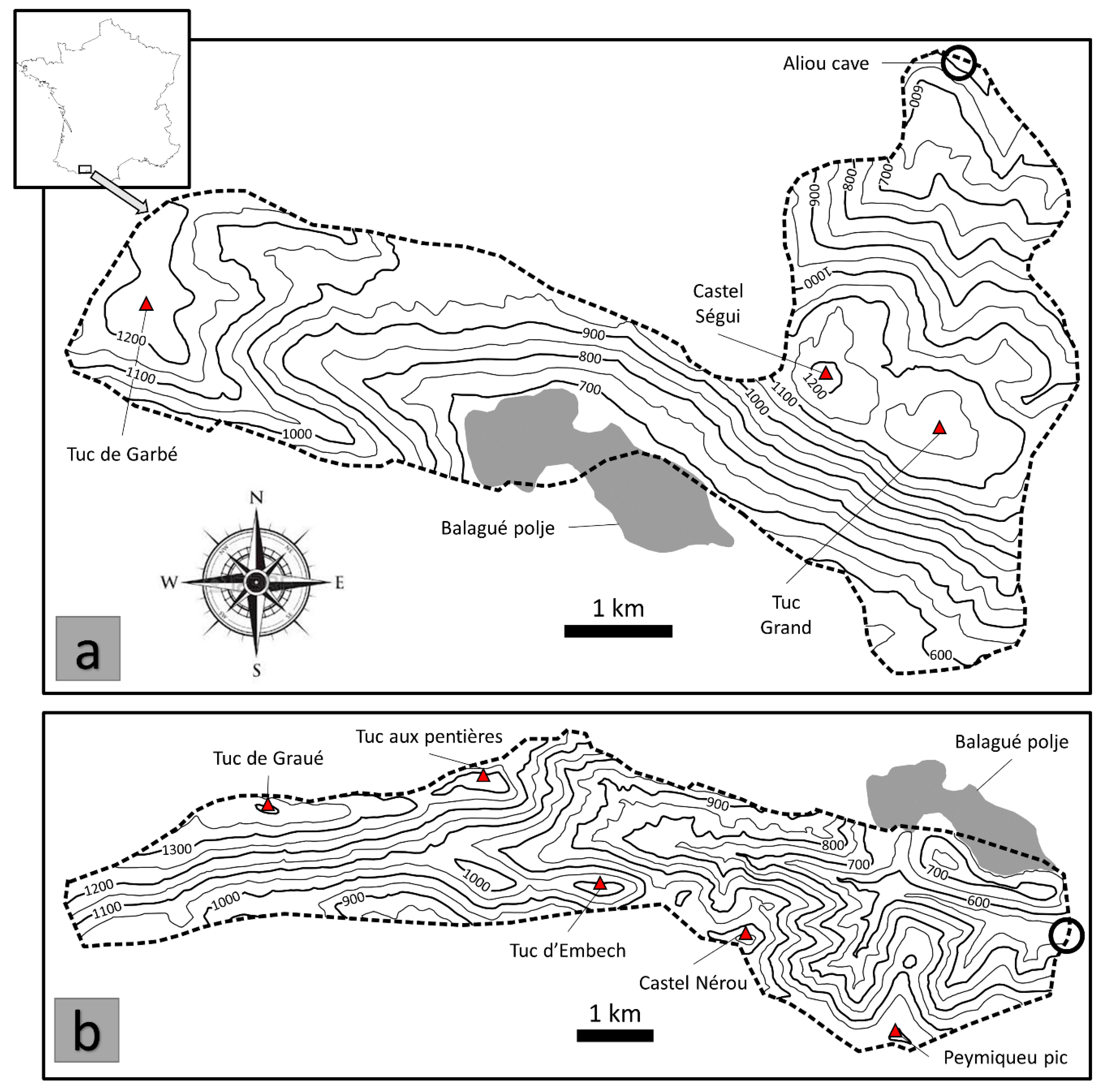
2.1. Study Sites
2.2. Modeling Approach
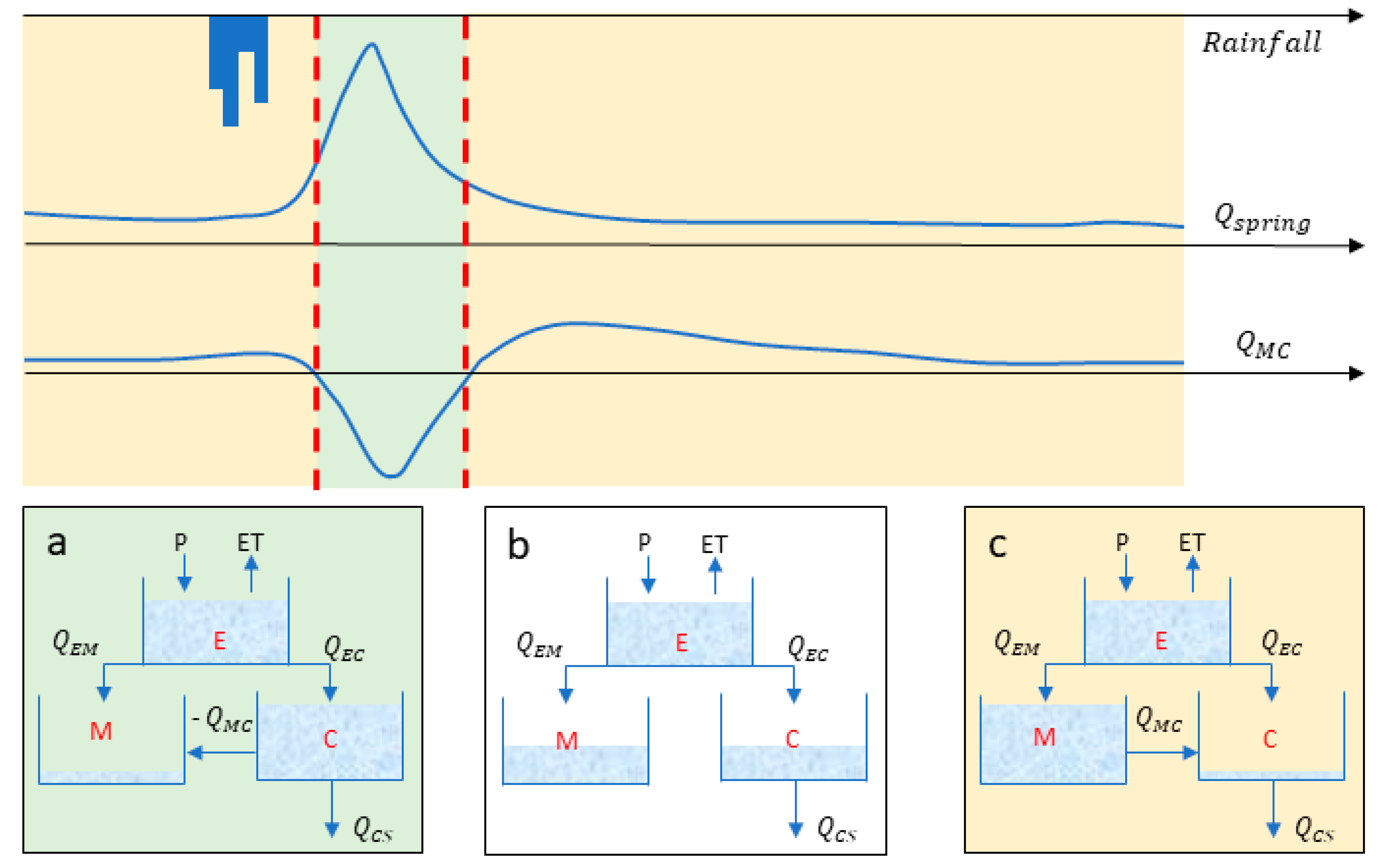
2.2.1. Conceptual Reservoir Modeling
2.2.2. Model Calibration
2.2.3. Scale Effects
3. Results and Discussion
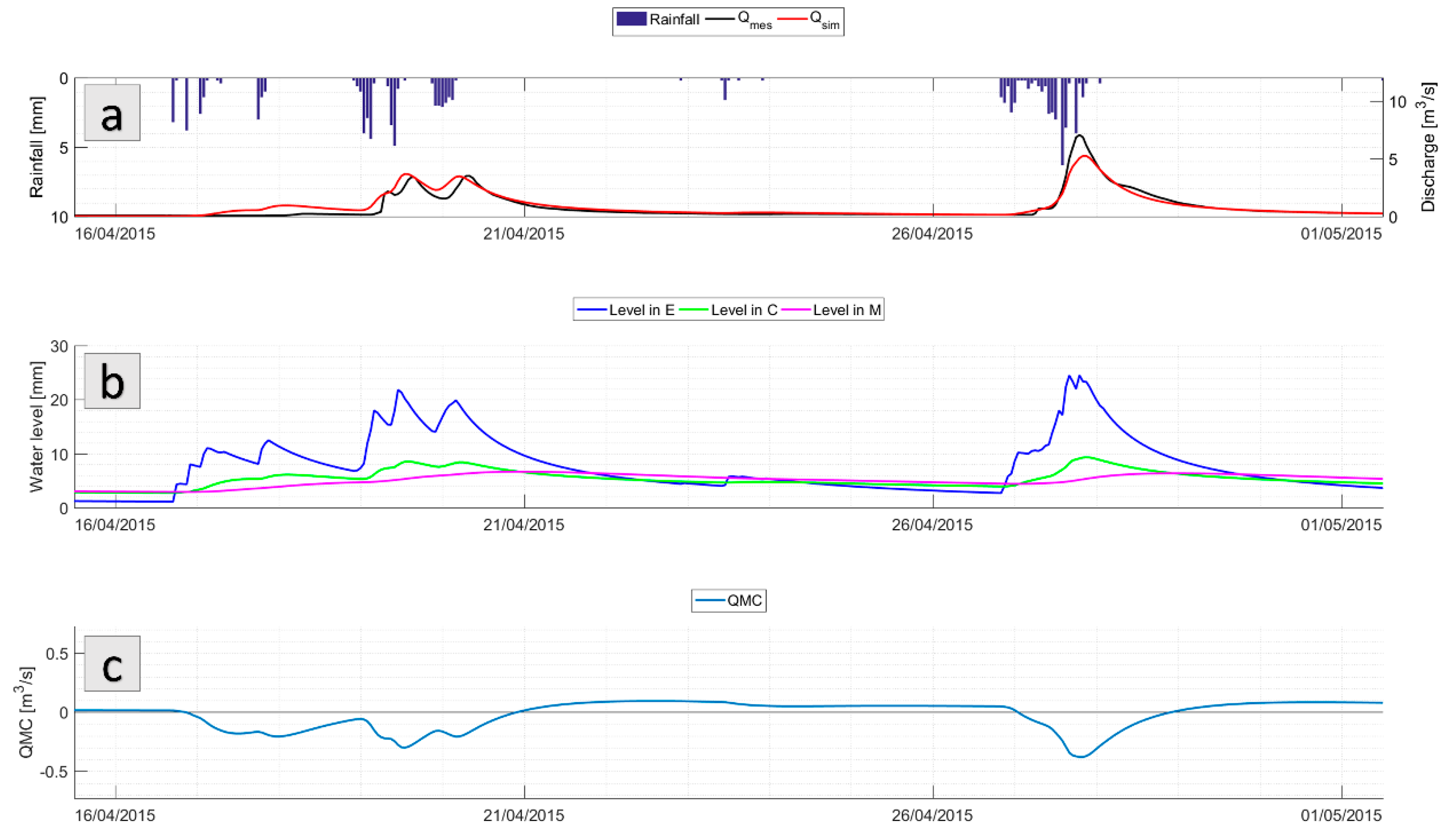
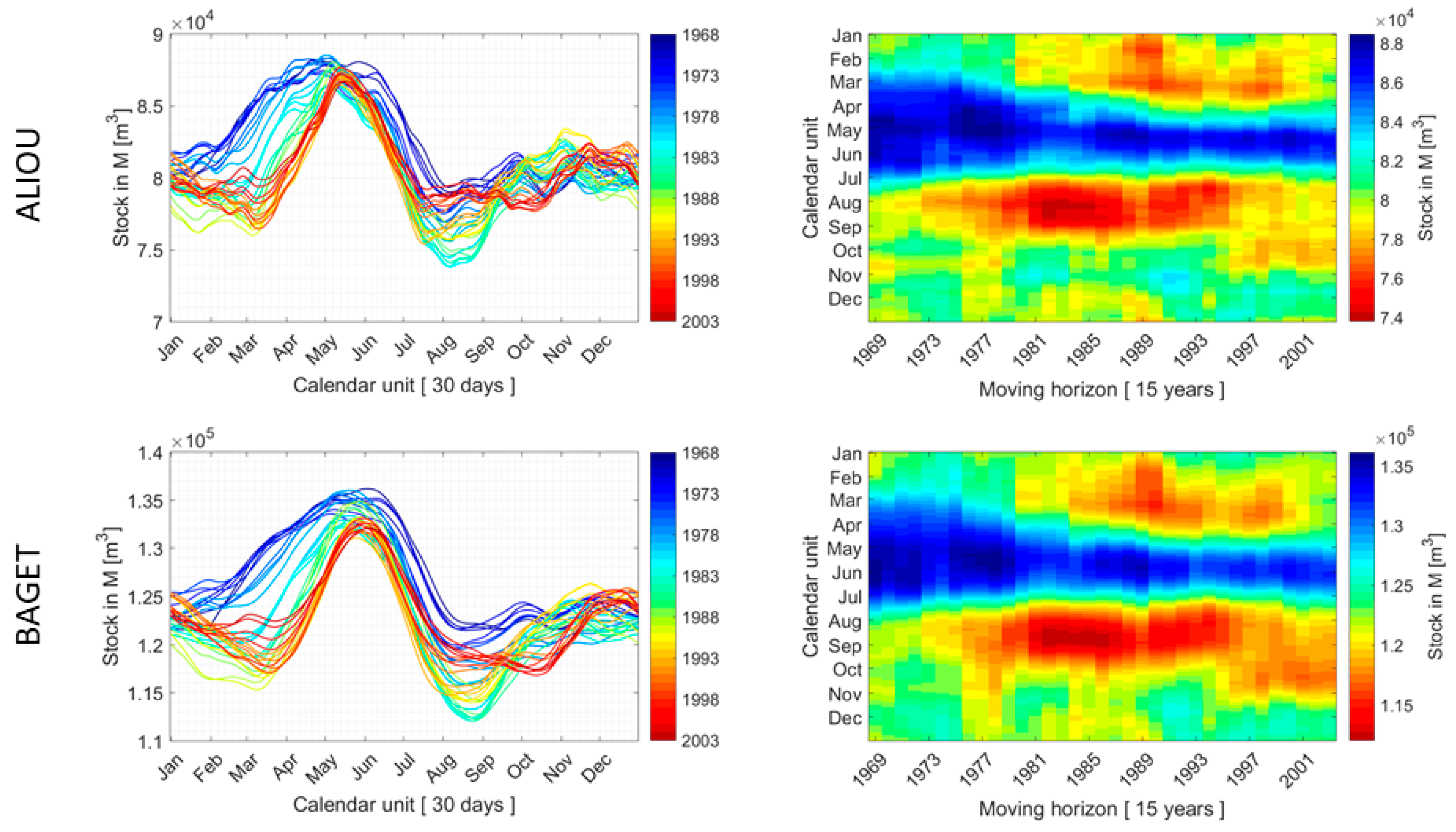
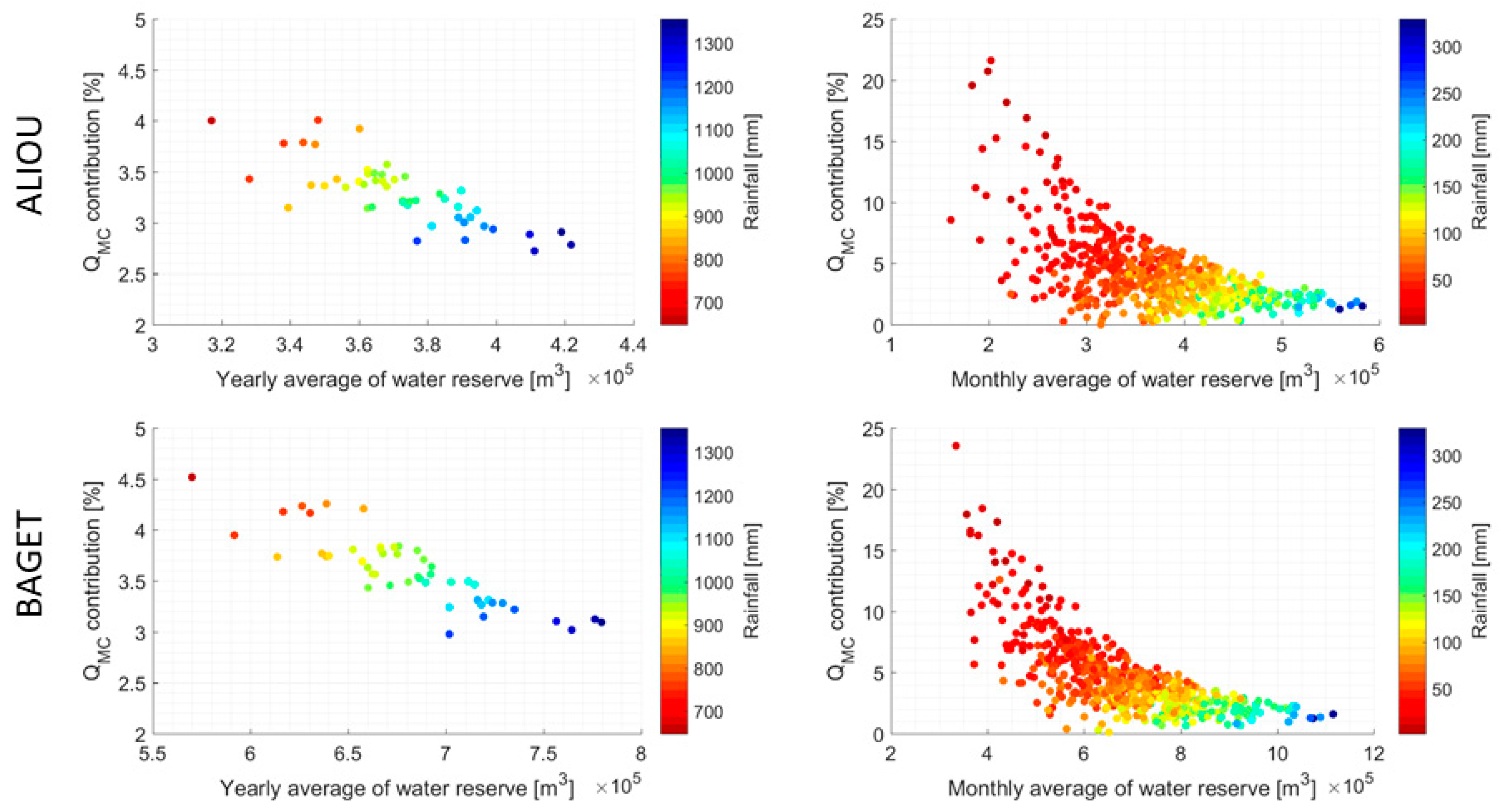
3.1. Short-term Varibility of Internal Fluxes
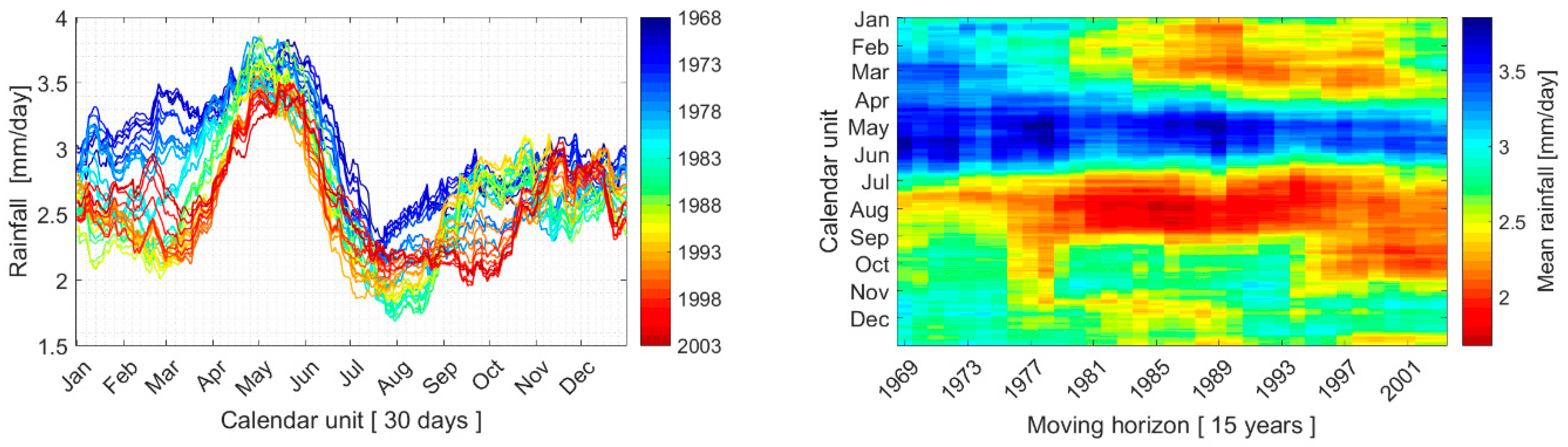
3.2. Long-Term Variability of Internal Dynamics
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Quinif, Y. Karst et évolution des rivières: Le cas de l’Ardenne. Geodin. Acta 1999, 12, 267–277. [Google Scholar] [CrossRef]
- Ford, D.; Williams, P.D. Karst Hydrogeology and Geomorphology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; ISBN 978-0-470-84996-5. [Google Scholar]
- Kiraly, L. Karstification and groundwater flow. Speleogenesis Evol. Karst Aquifers 2003, 1, 26. [Google Scholar]
- Mangin, A. Contribution à l’étude Hydrodynamique des Aquifères Karstiques. Ph.D. Thesis, Université de Bourgogne, Dijon, France, 1975. [Google Scholar]
- Marsaud, B. Structure et Fonctionnement de la Zone Noyée des Karsts à Partir des Résultats Expérimentaux. Ph.D. Thesis, Université de Paris XI Orsay, Paris, France, 1997. [Google Scholar]
- Klimchouk, A. Karst morphogenesis in the epikarstic zone. Cave Karst Sci. 1995, 21, 45–50. [Google Scholar]
- Batiot, C.; Emblanch, C.; Blavoux, B. Total Organic Carbon (TOC) and magnesium (Mg2+): Two complementary tracers of residence time in karstic systems. Comptes Rendus Geosci. 2003, 335, 205–214. [Google Scholar] [CrossRef]
- Emblanch, C.; Zuppi, G.; Mudry, J.; Blavoux, B.; Batiot, C. Carbon 13 of TDIC to quantify the role of the unsaturated zone: The example of the Vaucluse karst systems (Southeastern France). J. Hydrol. 2003, 279, 262–274. [Google Scholar] [CrossRef]
- Garry, B. Etude des Processus d’écoulements de la Zone non Saturée Pour la Modélisation des Aquifères Karstiques: Expérimentation Hydrodynamique et Hydrochimique sur les Sites du Laboratoire Souterrain à Bas Bruit (LSBB) de Rustrel et de Fontaine de Vauclusee. Ph.D. Thesis, Université d’Avignon et des pays de Vaucluse, Avignon, France, 2007. [Google Scholar]
- Lastennet, R. Rôle de la Zone non Saturée Dans le Fonctionnement des Aquifères Karstiques. Approche par l’étude Physico-Chimique et Isotopique du Signal D’entrée et des Exutoires du Massif du Ventoux (Vaucluse). Ph.D. Thesis, Université d’Avignon et des pays de Vaucluse, Avignon, France, 1994. [Google Scholar]
- Puig, J.-M. Le système Karstique de la Fontaine de Vaucluse. Ph.D. Thesis, Université d’Avignon et des pays de Vaucluse, Avignon, France, 1987. [Google Scholar]
- Labat, D.; Hoang, C.T.; Masbou, J.; Mangin, A.; Tchiguirinskaia, I.; Lovejoy, S.; Schertzer, D. Multifractal behavior of long-term karstic discharge fluctuations. Hydrol. Process. 2013, 27, 3708–3717. [Google Scholar] [CrossRef]
- Labat, D.; Ababou, R.; Mangin, A. Analyse multirésolution croisée de pluies et débits de sources karstiques. Comptes Rendus Géosc. 2002, 334, 551–556. [Google Scholar] [CrossRef]
- Labat, D.; Mangin, A.; Ababou, R. Rainfall–runoff relations for karstic springs: Multifractal analyses. J. Hydrol. 2002, 256, 176–195. [Google Scholar] [CrossRef]
- Labat, D.; Ababou, R.; Mangin, A. Introduction of wavelet analyses to rainfall/runoffs relationship for karstic basin: The case of Licq-Atherey karstic system (France). Ground Water 2001, 39, 605–615. [Google Scholar] [CrossRef]
- Ficchi, A. An adaptative Hydrological Model for Multiple Time-Steps: Diagnostics and Improvements Based on Fluxes Consistency. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2017. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survay Modular Ground-Water Model-the Ground-Water Flow Process; U.S. Geological Survey Techniques and Methods 6-A16; U.S. Geological Survey: Reston, VA, USA, 2005.
- Hartmann, A.; Goldscheider, N.; Wagener, T.; Lange, J.; Weiler, M. Karst water resources in a changing world: Review of hydrological modeling approaches. Rev. Geophys. 2014, 52, 218–242. [Google Scholar] [CrossRef]
- Chen, Z.; Goldscheider, N. Modeling spatially and temporally varied hydraulic behavior of a folded karst system with dominant conduit drainage at catchment scale, Hochifen–Gottesacker, Alps. J. Hydrol. 2014, 514, 41–52. [Google Scholar] [CrossRef]
- Denić-Jukić, V.; Jukić, D. Composite transfer functions for karst aquifers. J. Hydrol. 2003, 274, 80–94. [Google Scholar] [CrossRef]
- Weiler, M.; McGlynn, B.L.; McGuire, K.J.; McDonnell, J.J. How does rainfall become runoff? A combined tracer and runoff transfer function approach. Water Resour. Res. 2003, 39, 1315. [Google Scholar] [CrossRef]
- Cormary, Y.; Guilbot, A. Ajustement et réglage des modèles déterministes méthode de calage des paramètres. La Houille Blanche 1971, 2, 131–140. [Google Scholar] [CrossRef]
- Bezes, C. Contribution à la Modélisation des Systèmes Aquifères Karstiques: Établissement du Modèle Bemer, Son Application à Quatre Systèmes Karstiques du Midi de la France; CERGA: Montpellier, France, 1976. [Google Scholar]
- Thiéry, D. Logiciel GARDIENA Version 8.2: Guide d’utilisation; BRGM: Orléans, France, 2016; p. 126, 65 fig., 2ann; Available online: https://www.brgm.fr/sites/default/brgm/logiciels/gardenia/GARDENIA_v8_2_RP-62797-FR_Notice.pdf (accessed on 18 March 2019).
- Fleury, P.; Plagnes, V.; Bakalowicz, M. Modelling of the functioning of karst aquifers with a reservoir model: Application to Fontaine de Vaucluse (South of France). J. Hydrol. 2007, 345, 38–49. [Google Scholar] [CrossRef]
- Tritz, S.; Guinot, V.; Jourde, H. Modelling the behavior of a karst system catchment using non-linear hysteretic conceptual model. J. Hydrol. 2011, 397, 250–262. [Google Scholar] [CrossRef]
- Jourde, H.; Mazzilli, N.; Lecoq, N.; Arfib, B.; Bertin, D. KarstMod: A Generic Modular Reservoir Model Dedicated to Spring Discharge Modeling and Hydrodynamic Analysis in Karst. In Hydrogeological and Environmental Investigations in Karst Systems; Environmental Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2015; pp. 339–344. ISBN 978-3-642-17434-6. [Google Scholar]
- Mazzilli, N.; Guinot, V.; Jourde, H.; Lecoq, N.; Labat, D.; Arfib, B.; Baudement, C.; Danquigny, C.; Dal Soglio, L.; Bertin, D. KarstMod: A modelling platform for rainfall—Discharge analysis and modelling dedicated to karst systems. Environ. Model. Softw. 2017. [Google Scholar] [CrossRef]
- Bittner, D.; Narany, T.S.; Kohl, B.; Disse, M.; Chiogna, G. Modeling the hydrological impact of land use change in a dolomite-dominated karst system. J. Hydrol. 2018, 567, 267–279. [Google Scholar] [CrossRef]
- Labat, D.; Masbou, J.; Beaulieu, E.; Mangin, A. Scaling behavior of the fluctuations in stream flow at the outlet of karstic watersheds, France. J. Hydrol. 2011, 410, 162–168. [Google Scholar] [CrossRef]
- Mangin, A. Pour une meilleure connaissance des systèmes hydrologiques à partir des analyses corrélatoire et spectrale. J. Hydrol. 1984, 67, 25–43. [Google Scholar] [CrossRef]
- Jourde, H.; Massei, N.; Mazzilli, N.; Binet, S.; Batiot-Guilhe, C.; Labat, D.; Steinmann, M.; Bailly-Comte, V.; Seidel, J.L.; Arfib, B.; et al. SNO KARST: A French Network of Observatories for the Multidisciplinary Study of Critical Zone Processes in Karst Watersheds and Aquifers. Vadose Zone J. 2018, 17. [Google Scholar] [CrossRef]
- Duran, L. Approche Physique, Conceptuelle et Statistique du Fonctionnement Hydrologique d’un Karst sous Couverture. Ph.D. Thesis, Université de Rouen, Rouen, France, 2015. [Google Scholar]
- Baudement, C.; Mazzilli, N.; Jouves, J.; Guglielmi, Y. Groundwater Management of a Highly Dynamic Karst by Assessing Baseflow and Quickflow with a Rainfall-Discharge Model (Dardennes Springs, SE France). Bull. Soc. Géol. Fr. 2017, 188, 40. [Google Scholar] [CrossRef]
- Kazakis, N.; Chalikakis, K.; Mazzilli, N.; Ollivier, C.; Manakos, A.; Voudouris, K. Management and research strategies of karst aquifers in Greece: Literature overview and exemplification based on hydrodynamic modelling and vulnerability assessment of a strategic karst aquifer. Sci. Total Environ. 2018, 643, 592–609. [Google Scholar] [CrossRef] [PubMed]
- Poulain, A.; Watlet, A.; Kaufmann, O.; Camp, M.V.; Jourde, H.; Mazzilli, N.; Rochez, G.; Deleu, R.; Quinif, Y.; Hallet, V. Assessment of groundwater recharge processes through karst vadose zone by cave percolation monitoring. Hydrol. Process. 2018, 32, 2069–2083. [Google Scholar] [CrossRef]
- Bauer, S.; Liedl, R.; Sauter, M. Modeling of karst aquifer genesis: Influence of exchange flow. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Labat, D.; Ababou, R.; Mangin, A. Rainfall–runoff relations for karstic springs. Part I: Convolution and spectral analyses. J. Hydrol. 2000, 238, 123–148. [Google Scholar] [CrossRef]
- Labat, D.; Ababou, R.; Mangin, A. Rainfall–runoff relations for karstic springs. Part II: Continuous wavelet and discrete orthogonal multiresolution analyses. J. Hydrol. 2000, 238, 149–178. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Does a large number of parameters enhance model performance? Comparative assessment of common catchment model structures on 429 catchments. J. Hydrol. 2001, 242, 275–301. [Google Scholar] [CrossRef]
- Charlier, J.-B.; Bertrand, C.; Mudry, J. Conceptual hydrogeological model of flow and transport of dissolved organic carbon in a small Jura karst system. J. Hydrol. 2012, 460–461, 52–64. [Google Scholar] [CrossRef]
- Hartmann, A.; Barberá, J.A.; Lange, J.; Andreo, B.; Weiler, M. Progress in the hydrologic simulation of time variant recharge areas of karst systems—Exemplified at a karst spring in Southern Spain. Adv. Water Resour. 2013, 54, 149–160. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Ficchì, A.; Perrin, C.; Andréassian, V. Impact of temporal resolution of inputs on hydrological model performance: An analysis based on 2400 flood events. J. Hydrol. 2016, 538, 454–470. [Google Scholar] [CrossRef]
- Wang, Y.; He, B.; Takase, K. Effects of temporal resolution on hydrological model parameters and its impact on prediction of river discharge/Effets de la résolution temporelle sur les paramètres d’un modèle hydrologique et impact sur la prévision de l’écoulement en rivière. Hydrol. Sci. J. 2009, 54, 886–898. [Google Scholar] [CrossRef]
- Jothityangkoon, C.; Sivapalan, M. Temporal scales of rainfall-runoff processes and spatial scaling of flood peaks: Space-time connection through catchment water balance. Adv. Water Resour. 2001, 24, 1015–1036. [Google Scholar] [CrossRef]
- Robinson, J.S.; Sivapalan, M. An investigation into the physical causes of scaling and heterogeneity of regional flood frequency. Water Resour. Res. 1997, 33, 1045–1059. [Google Scholar] [CrossRef]
- Cholet, C. Fonctionnement Hydrogéologique et Processus de Transport dans les Aquifères Karstiques du Massif du Jura. Ph.D. Thesis, Université de Bourgogne Franche-Comté, Besançon, France, 2017. [Google Scholar]
- Goldscheider, N. A new quantitative interpretation of the long-tail and plateau-like breakthrough curves from tracer tests in the artesian karst aquifer of Stuttgart, Germany. Hydrogeol. J. 2008, 16, 1311–1317. [Google Scholar] [CrossRef]
- Li, G.; Loper, D.E.; Kung, R. Contaminant sequestration in karstic aquifers: Experiments and quantification. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Mohammadi, Z.; Gharaat, M.J.; Field, M. The Effect of Hydraulic Gradient and Pattern of Conduit Systems on Tracing Tests: Bench-Scale Modeling. Groundwater 2018. [Google Scholar] [CrossRef]
- Worthington, S.R.H.; Soley, R.W.N. Identifying turbulent flow in carbonate aquifers. J. Hydrol. 2017, 552, 70–80. [Google Scholar] [CrossRef]
- Ender, A.; Goeppert, N.; Goldscheider, N. Spatial resolution of transport parameters in a subtropical karst conduit system during dry and wet seasons. Hydrogeol. J. 2018. [Google Scholar] [CrossRef]
- Dewaide, L.; Bonniver, I.; Rochez, G.; Hallet, V. Solute transport in heterogeneous karst systems: Dimensioning and estimation of the transport parameters via multi-sampling tracer-tests modelling using the OTIS (One-dimensional Transport with Inflow and Storage) program. J. Hydrol. 2016, 534, 567–578. [Google Scholar] [CrossRef]
- Cholet, C.; Charlier, J.-B.; Moussa, R.; Steinmann, M.; Denimal, S. Assessing lateral flows and solute transport during floods in a conduit-flow-dominated karst system using the inverse problem for the advection–diffusion equation. Hydrol. Earth Syst. Sci. 2017, 21, 3635–3653. [Google Scholar] [CrossRef]
- Charlier, J.-B.; Moussa, R.; Bailly-Comte, V.; Danneville, L.; Desprats, J.-F.; Ladouche, B.; Marchandise, A. Use of a flood-routing model to assess lateral flows in a karstic stream: Implications to the hydrogeological functioning of the Grands Causses area (Tarn River, Southern France). Environ. Earth Sci. 2015, 74, 7605–7616. [Google Scholar] [CrossRef]
- Bailly-Comte, V.; Martin, J.B.; Jourde, H.; Screaton, E.J.; Pistre, S.; Langston, A. Water exchange and pressure transfer between conduits and matrix and their influence on hydrodynamics of two karst aquifers with sinking streams. J. Hydrol. 2010, 386, 55–66. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, X.; Soulsby, C. Catchment-scale conceptual modelling of water and solute transport in the dual flow system of the karst critical zone. Hydrol. Process. 2017, 31, 3421–3436. [Google Scholar] [CrossRef]
- Anghileri, D.; Pianosi, F.; Soncini-Sessa, R. Trend detection in seasonal data: From hydrology to water resources. J. Hydrol. 2014, 511, 171–179. [Google Scholar] [CrossRef]
- De Stefano, L.; Duncan, J.; Dinar, S.; Stahl, K.; Strzepek, K.M.; Wolf, A.T. Climate change and the institutional resilience of international river basins. J. Peace Res. 2012, 49, 193–209. [Google Scholar] [CrossRef]
- Wagener, T.; Sivapalan, M.; Troch, P.A.; McGlynn, B.L.; Harman, C.J.; Gupta, H.V.; Kumar, P.; Rao, P.S.C.; Basu, N.B.; Wilson, J.S. The future of hydrology: An evolving science for a changing world. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Sarrazin, F.; Hartmann, A.; Pianosi, F.; Wagener, T. V2Karst V1.0: A parsimonious large-scale integrated vegetation-recharge model to simulate the impact of climate and land cover change in karst regions. Geosci. Model Dev. Discuss. 2018, 11, 4933–4964. [Google Scholar] [CrossRef]
| [24 h] | [1 h] | |||||
|---|---|---|---|---|---|---|
| Period | Warm-Up | Calibration | Validation | Warm-Up | Calibration | Validation |
| from | 1 January 1968 | 1 October1970 | 1 October 1980 | 1 October 2009 | 1 October 2010 | 1 October 2012 |
| to | 30 September 1970 | 30 September 1980 | 31 December 2016 | 30 September 2010 | 30 September 2012 | 31 May 2017 |
| Parameter | Calibration [24 h] | Calibration [1 h] | ||
|---|---|---|---|---|
| Aliou | RA | Recharge area | 14.8 km2 | 14.2 km2 |
| kEM | Recession coefficient from E to M | 6.10 × 10−3 mm/day | 1.11 × 10−4 mm/h | |
| kEC | Recession coefficient from E to C | 9.83 × 10−3 mm/day | 2.69 × 10−3 mm/h | |
| kCS | Recession coefficient from C to S | 2.36 × 10−3 mm/day | 1.80 × 10−4 mm/h | |
| kMC | Recession coefficient from M to C | 3.17 × 10−1 mm/day | 2.41 × 10−2 mm/h | |
| Baget | RA | Recharge area | 15.8 km2 | 13.1 km2 |
| kEM | Recession coefficient from E to M | 3.36 × 10−3 mm/day | 2.09 × 10−4 mm/h | |
| kEC | Recession coefficient from E to C | 2.71 × 10−3 mm/day | 4.35 × 10−4 mm/h | |
| kCS | Recession coefficient from C to S | 1.21 × 10−3 mm/day | 7.21 × 10−4 mm/h | |
| kMC | Recession coefficient from M to C | 7.03 × 10−2 mm/day | 1.25 × 10−1 mm/h |
| [24 h] | [1 h] | ||||
|---|---|---|---|---|---|
| Periods | Calibration | Validation | Calibration | Validation | |
| (1970–1980) | (1980–2016) | (2010–2012) | (2012–2017) | ||
| Aliou | NSE | 0.53 | 0.51 | 0.63 | 0.5 |
| BE | 0.88 | 0.97 | 0.99 | 0.91 | |
| KGE | 0.58 | 0.51 | 0.67 | 0.54 | |
| Baget | NSE | 0.59 | 0.52 | 0.56 | 0.47 |
| BE | 0.94 | 0.89 | 0.98 | 0.77 | |
| KGE | 0.61 | 0.52 | 0.64 | 0.44 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sivelle, V.; Labat, D.; Mazzilli, N.; Massei, N.; Jourde, H. Dynamics of the Flow Exchanges between Matrix and Conduits in Karstified Watersheds at Multiple Temporal Scales. Water 2019, 11, 569. https://doi.org/10.3390/w11030569
Sivelle V, Labat D, Mazzilli N, Massei N, Jourde H. Dynamics of the Flow Exchanges between Matrix and Conduits in Karstified Watersheds at Multiple Temporal Scales. Water. 2019; 11(3):569. https://doi.org/10.3390/w11030569
Chicago/Turabian StyleSivelle, Vianney, David Labat, Naomi Mazzilli, Nicolas Massei, and Hervé Jourde. 2019. "Dynamics of the Flow Exchanges between Matrix and Conduits in Karstified Watersheds at Multiple Temporal Scales" Water 11, no. 3: 569. https://doi.org/10.3390/w11030569
APA StyleSivelle, V., Labat, D., Mazzilli, N., Massei, N., & Jourde, H. (2019). Dynamics of the Flow Exchanges between Matrix and Conduits in Karstified Watersheds at Multiple Temporal Scales. Water, 11(3), 569. https://doi.org/10.3390/w11030569







