A Novel Approach for Delineation of Homogeneous Rainfall Regions for Water Sensitive Urban Design—A Case Study in Southeast Queensland
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Event Seperation
- An event was considered independent only if the consecutive event was separated by at least 3 h antecedent duration. Otherwise, those events were treated as a single event. There is no guideline or literature available to suggest an accurate value for minimum antecedent dry period to consider two consecutive events as independent events. Therefore, 3 h was selected as a reasonable value based on previous experience and expert advice.
- An event that constituted less than 1 mm total rainfall for a period greater than 1 h was not considered as a storm event and not considered for the analysis.
- The maximum rainfall intensity (in mm/h) of the events was estimated by calculating the moving total of 1 h rainfall throughout the rainfall duration.
- Any event having data entries of false quality based on quality classifications of BoM was discarded from the study.
2.3. Cluster Analysis
2.3.1. k-Means Clustering
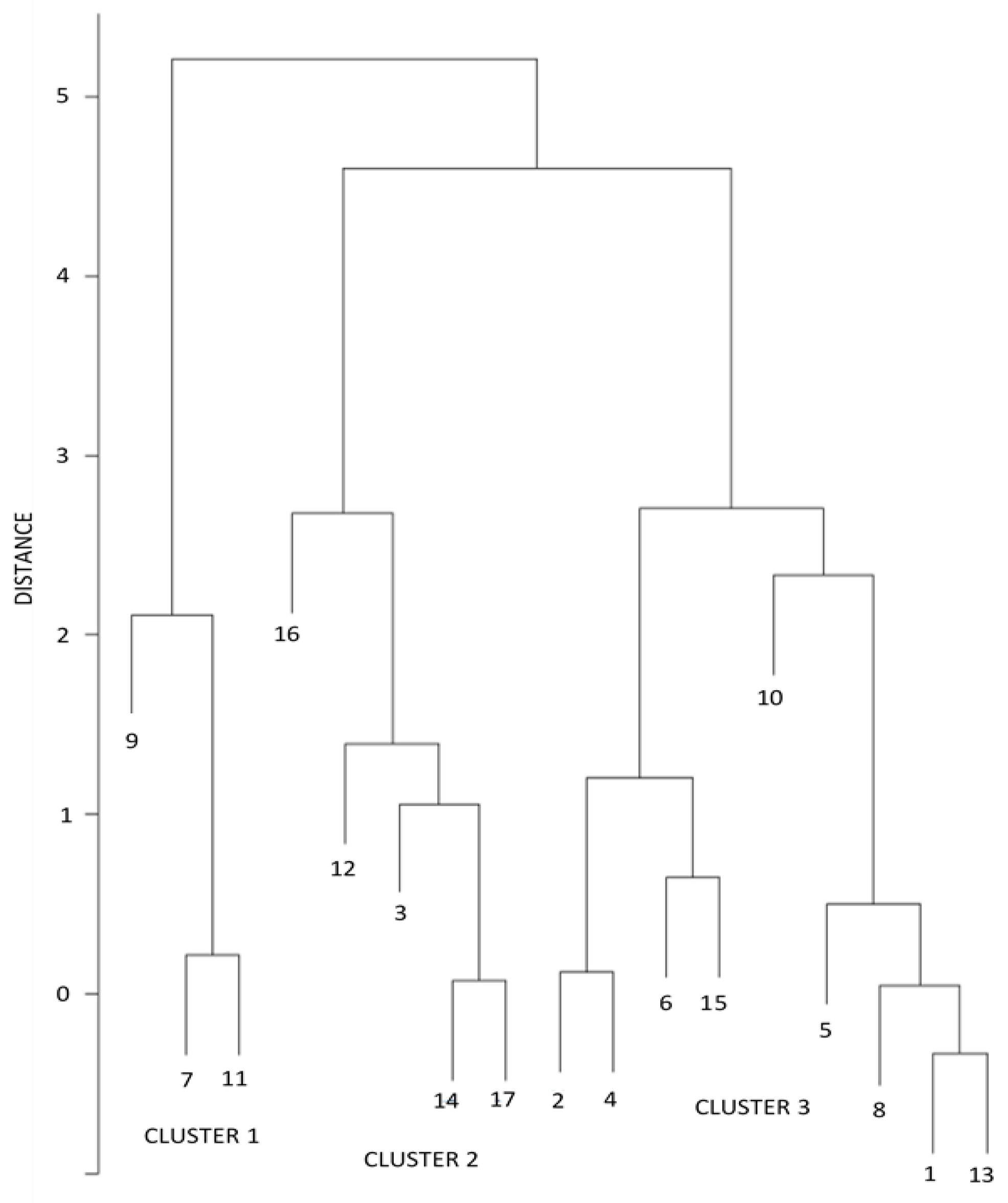
2.3.2. Hierarchical Clustering
2.4. Hosking–Wallis Heterogeneity Test
3. Results and Discussion
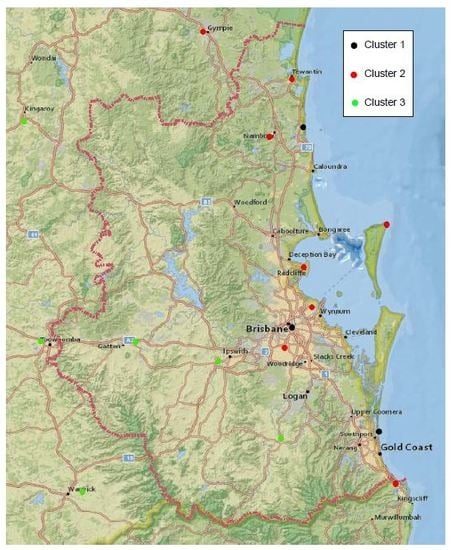
3.1. Conventional Approach
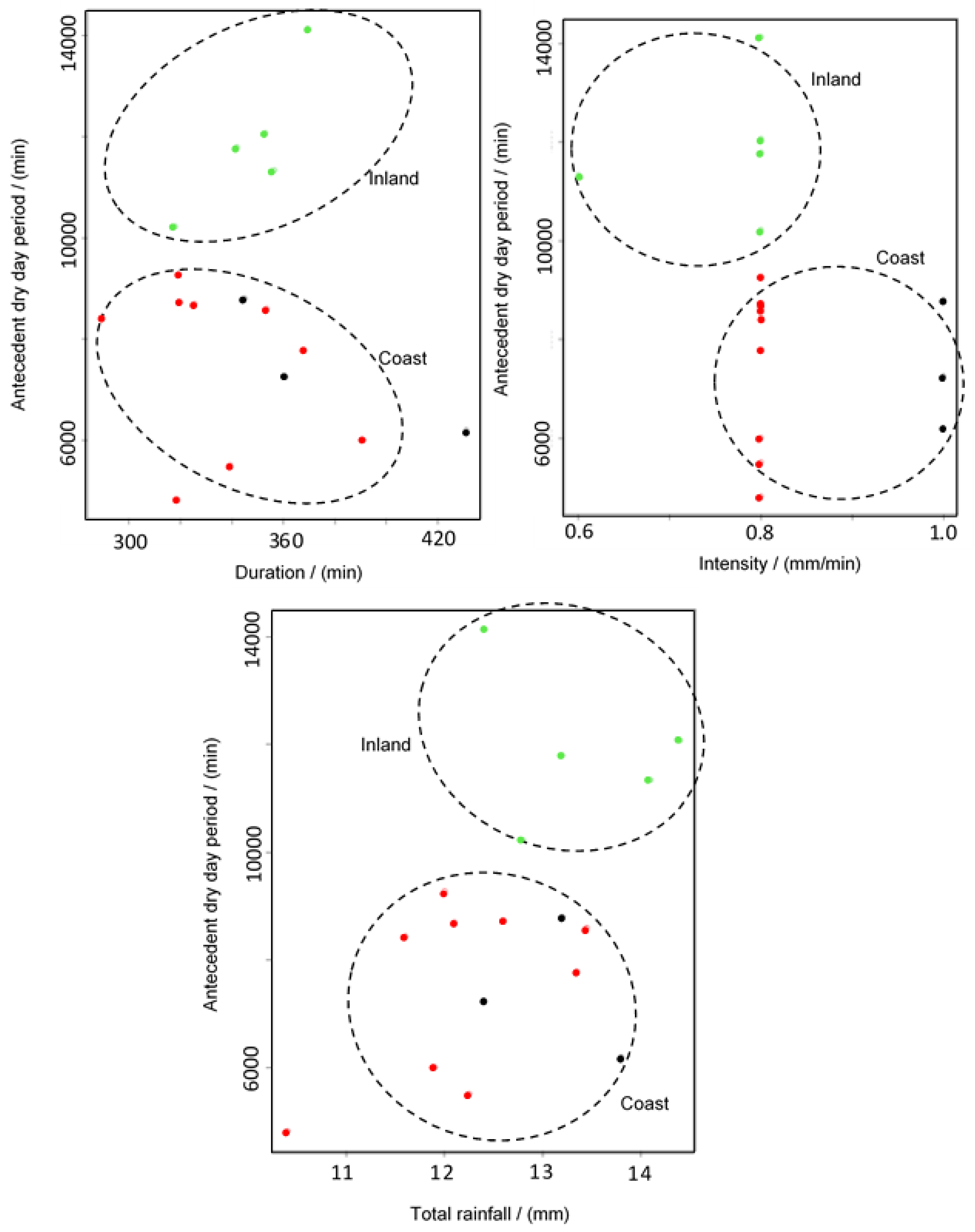
3.2. Modified Approach
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| > install.packages (“homtest”) |
| > library (homtest) |
| > HW.tests (rf, sd, Nsim = 500) |
| # Arguments |
| # rf—vector representing data from many samples defined with sd |
| # sd—array that defines the data subdivision among sites |
| # Nsim—number of simulations |
References
- Hosking, J.; Wallis, J. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Schaefer, M.G. Regional analyses of precipitation annual maxima in Washington State. Water Resour. Res. 1990, 26, 119–131. [Google Scholar] [CrossRef]
- Pearson, C.P. New Zealand regional flood frequency analysis using L-moments. J. Hydrol. 1991, 30, 53–64. [Google Scholar]
- Lin, G.F.; Chen, L.H. Identification of homogeneous regions for regional frequency analysis using the self-organizing map. J. Hydrol. 2006, 324, 1–9. [Google Scholar] [CrossRef]
- Ngongondo, C.S.; Xu, C.Y.; Tallaksen, L.M.; Alemaw, B.; Chirwa, T. Regional frequency analysis of rainfall extremes in Southern Malawi using the index rainfall and L-moments approaches. Stoch. Environ. Res. Risk Assess. 2011, 25, 939–955. [Google Scholar] [CrossRef]
- Munoz-Diaz, D.; Rodrigo, F.S. Spatio-temporal patterns of seasonal rainfall in Spain (1912–2000) using cluster and principal component analysis: comparison. Ann. Geophys. 2004, 22, 1435–1448. [Google Scholar] [CrossRef]
- Unal, Y.; Kindap, T.; Karaca, M. Redefining Climate Zones for Turkey Using Cluster Analysis. J. Hydrol. 2003, 23, 1045–1055. [Google Scholar] [CrossRef]
- Dyer, T.G. The assignment of Rainfall stations into homogeneous groups: An application of principal component analysis. Q. J. R. Meteorol. Soc. 1975, 101, 1005–1013. [Google Scholar] [CrossRef]
- BCC MBW. Water Sensitive Urban Design Technical Design Guidelines for South East Queensland; South East Queensland Healthy Waterways Partnership and Brisbane City Council: Brisbane, Australia, 2006; Volume 1.
- NDTPI. Water Sensitive Urban Design Planing Guide—Final; Northern Territory Department of Planning and Infrastructure: Darwin Australia, 2009.
- Liu, A. Influence of Rainfall and Catchment Characteristics on Urban Stormwater Quality. Ph.D. Thesis, Faculty of Built Environment and Engineering, Queensland University of Technology, Brisbane, Australia, 2011. [Google Scholar]
- Ma, Y. Human Health Risk of Toxic Chemical Pollutants Generated from Traffic and Land Use Activities. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, 2016. [Google Scholar]
- Egodawatta, P. Translation of Small Plot Pollution Mobilisation and Transport Measurement from Impermeable Urban Surface to Urban Catchment Scale. Ph.D. Thesis, Faculty of Built Environment and Engineering, Queensland University of Technology, Brisbane, Australia, 2007. [Google Scholar]
- Luo, P.; Mu, D.; Xue, H.; Ngo-Duc, T.; Dang-Dinh, K.; Takara, K.; Nover, D.; Schladow, G. Flood inundation assessment for the Hanoi Central Area, Vietnam under historical and extreme rainfall conditions. Sci. Rep. 2018, 8, 12623. [Google Scholar] [CrossRef]
- Luo, P.; He, B.; Duan, W.; Takara, K.; Nover, D. Impact assessment of rainfall scenarios and land-use change on hydrologic response using synthetic Area IDF curves. J. Flood Risk Manag. 2018, 11, S84–S97. [Google Scholar] [CrossRef]
- Luo, P.; He, B.; Takara, K.; Xiong, Y.E.; Nover, D.; Duan, W.; Fukushi, K. Historical Assessment of Chinese and Japanese Flood Management Policies and Implications for Managing Future Floods. Environ. Sci. Policy 2015, 48, 265–277. [Google Scholar] [CrossRef]
- Zoppou, C. Review of urban storm water models. Environ. Model. Softw. 2001, 16, 195–231. [Google Scholar] [CrossRef]
- Sartor, J.D.; Boyd, G.B.; Agardy, F.J. Water Pollution Aspects of Street Surface Contaminants. J. Water Pollut. Control Fed. 1974, 46, 458–467. [Google Scholar] [PubMed]
- Ball, J.E.; Jenks, R.; Aubourg, D. An assessment of the availability of pollutant constituents on road surfaces. Sci. Total Environ. 1998, 209, 243–254. [Google Scholar] [CrossRef]
- Wang, W.P.; Zhang, P.P.; Ye, X.Q. Study on Rainfall and Roof Rainwater Quality Changes Oriented to Stormwater Recycling. In Proceedings of the 2010 4th International Conference on Bioinformatics and Biomedical Engineering, Chengdu, China, 10–12 June 2010. [Google Scholar]
- Lee, J.H.; Bang, K.W. Characterization of urban stormwater runoff. Water Res. 2000, 34, 1773–1780. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; McMahon, T.A. Modelling runoff and diffuse pollution loads in urban areas. Water Sci. Technol. 1999, 39, 241–248. [Google Scholar] [CrossRef]
- Terassi, P.; Galvani, E. Identification of Homogeneous Rainfall Regions in the Eastern Watersheds of the State of Paraná, Brazil. Climate 2017, 5, 53. [Google Scholar] [CrossRef]
- Lyra, G.B.; Oliveira-Júnior, J.F.; Zeri, M. Cluster analysis applied to the spatial and temporal variability of monthly rainfall in Alagoas state, Northeast of Brazil. Int. J. Climatol. 2014, 34, 3546–3558. [Google Scholar] [CrossRef]
- Goyal, M.K.; Gupta, V. Identification of Homogeneous Rainfall Regimes in Northeast Region of India using Fuzzy Cluster Analysis. Water Res. Manag. 2014, 28, 4491–4511. [Google Scholar] [CrossRef]
- de Oliveira-Júnior, J.F.; Xavier, F.M.G.; Teodoro, P.E.; de Gois, G.; Delgado, R.C. Cluster analysis identified rainfall homogeneous regions in Tocantins state, Brazil. Biosci. J. 2017, 33. [Google Scholar] [CrossRef]
- Tan, P.N.; Steinbach, M.; Kumar, V. Cluster Analysis: Basic Concepts and Algorithms. Introd. Data Min. 2006, 8, 487–568. [Google Scholar]
- Fowler, H.J.; Kilsby, C.G. A regional frequency analysis of United Kingdom extreme rainfall from 1961 to 2000. Int. J. Climatol. 2003, 23, 1313–1334. [Google Scholar] [CrossRef]
- Trefry, C.M.; Watkins, D.W., Jr.; Johnson, D. Regional Rainfall Frequency Analysis for the State of Michigan. J. Hydrol. Eng. 2005, 10, 437–449. [Google Scholar] [CrossRef]
- Raes, D. Frequency analysis of rainfall data. In KU Leuven and Inter-University Programme in Water Resources Engineering (IUPWARE); KU Leuven: Leuven, Belgium, 2004. [Google Scholar]
- Kumar Mishra, B.; Herath, S. Assessment of Future Floods in the Bagmati River Basin of Nepal Using Bias-Corrected Daily GCM Precipitation Data. J. Hydrol. Eng. 2015, 20, 05014027. [Google Scholar] [CrossRef]
- Viglione, A. homtest: Homogeneity Tests for Regional Frequency Analysis; R Foundation for Statistical Computing: Vienna, Austria, 2012. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Green, J.; Xuereb, K.; Johnson, F.; Moore, G. The Revised Intensity-Frequency-Duration (IFD) Design Rainfall Estimates for Australia—An Overview; Engineers Australia: Barton, Australia, 2012. [Google Scholar]
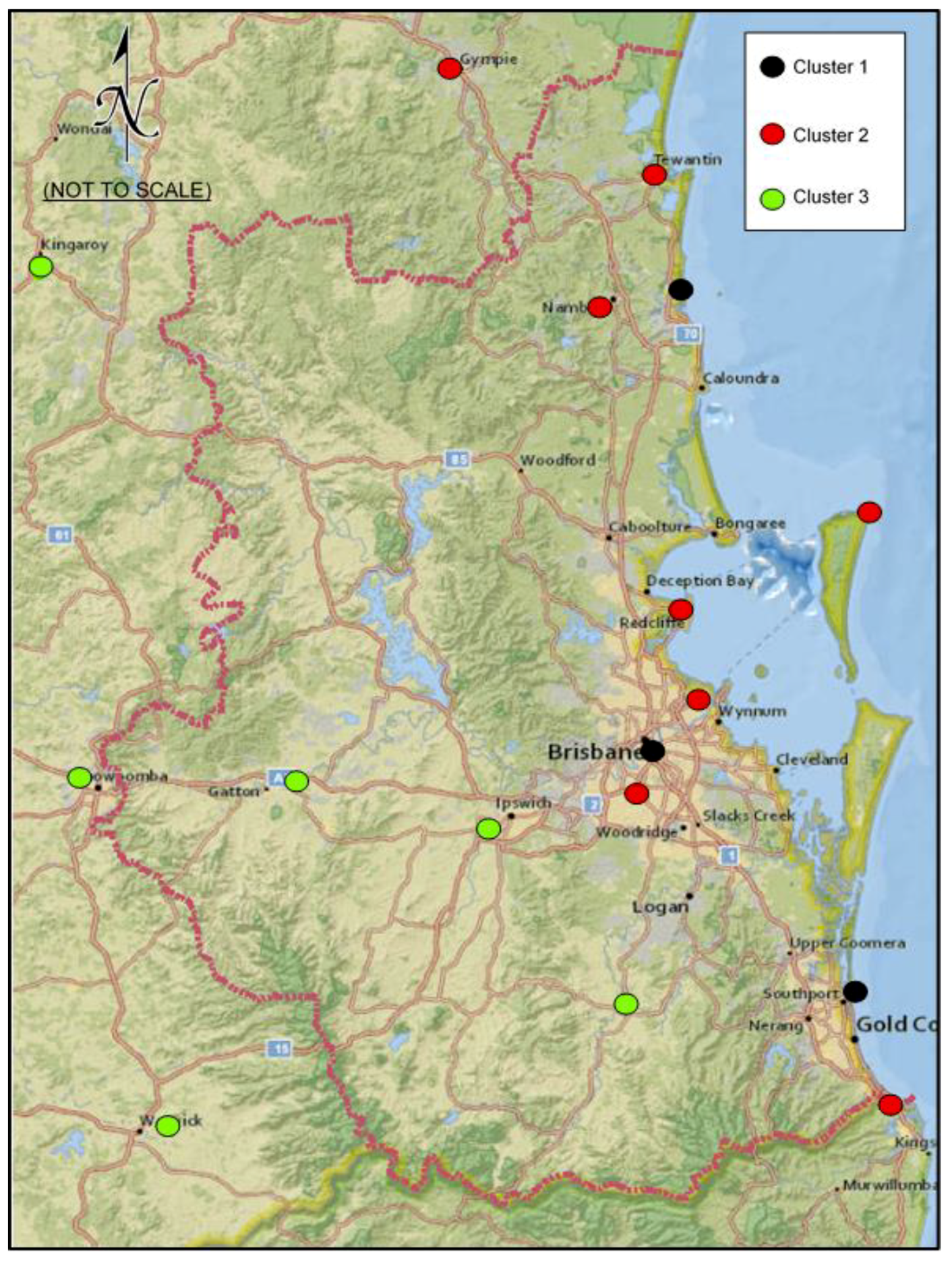
| Serial No. | Station No. | Station | Latitude | Longitude | No. of Events (2011–2015) |
|---|---|---|---|---|---|
| 1 | 40004 | Amberley AMO | −27.6297 | 152.7111 | 265 |
| 2 | 40043 | Cape Moreton Lighthouse | −27.0314 | 153.4661 | 350 |
| 3 | 40082 | University of Queensland | −27.5436 | 152.3375 | 274 |
| 4 | 40093 | Gympie | −26.1831 | 152.6414 | 379 |
| 5 | 40211 | Archerfield Airport | −27.5717 | 153.0078 | 358 |
| 6 | 40717 | Coolangatta | −28.1681 | 153.5053 | 501 |
| 7 | 40764 | Gold Coast Seaway | −27.939 | 153.4283 | 455 |
| 8 | 40842 | Brisbane Aero | −27.3917 | 153.1292 | 377 |
| 9 | 40861 | Sunshine Coast Airport | −26.6006 | 153.0903 | 471 |
| 10 | 40908 | Tewantin RSL Park | −26.3911 | 153.0403 | 426 |
| 11 | 40913 | Brisbane | −27.4808 | 153.0389 | 380 |
| 12 | 40922 | Kingaroy Airport | −26.5737 | 151.8398 | 249 |
| c | 40958 | Redcliffe | −27.2169 | 153.0922 | 385 |
| 14 | 40983 | Beaudesert Drumley St | −27.9707 | 152.9898 | 297 |
| 15 | 40988 | Nambour Daff—Hillside | −26.6442 | 152.9383 | 506 |
| 16 | 41525 | Warwick | −28.2061 | 152.1003 | 213 |
| 17 | 41529 | Toowoomba Airport | −27.5425 | 151.9134 | 275 |
| Event Characteristics | Remarks | ||
|---|---|---|---|
| Antecedent dry days | 3.37 | 1.16 | Heterogeneous |
| Maximum rainfall intensity | 1.95 | 0.59 | Possibly heterogeneous |
| Total rainfall | 0.81 | 0.32 | Homogeneous |
| Duration | 0.25 | 0.10 | Homogeneous |
| Serial No. | Station No. | 3rd Quartile Values—Q3 | |||
|---|---|---|---|---|---|
| Antecedent Dry Day/(days) | Maximum Intensity/(mm/h) | Total Rainfall/(mm) | Duration (h) | ||
| 1 | 40004 | 6.4 | 7.1 | 12.0 | 5.3 |
| 2 | 40043 | 5.4 | 6.7 | 13.4 | 6.1 |
| 3 | 40082 | 8.4 | 7.6 | 14.4 | 5.9 |
| 4 | 40093 | 6.0 | 6.0 | 13.5 | 5.9 |
| 5 | 40211 | 5.9 | 6.8 | 11.6 | 4.8 |
| 6 | 40717 | 3.8 | 6.4 | 12.3 | 5.7 |
| 7 | 40764 | 5.0 | 7.0 | 12.4 | 6.0 |
| 8 | 40842 | 6.0 | 6.6 | 12.1 | 5.4 |
| 9 | 40861 | 4.3 | 8.2 | 13.8 | 7.2 |
| 10 | 40908 | 3.3 | 5.9 | 10.4 | 5.3 |
| 11 | 40913 | 6.1 | 7.4 | 13.2 | 5.8 |
| 12 | 40922 | 9.8 | 8.2 | 12.4 | 6.2 |
| 13 | 40958 | 6.1 | 7.3 | 12.6 | 5.3 |
| 14 | 40983 | 7.1 | 7.6 | 12.8 | 5.3 |
| 15 | 40988 | 4.2 | 6.2 | 11.9 | 6.5 |
| 16 | 41525 | 7.9 | 6.6 | 14.1 | 5.9 |
| 17 | 41529 | 8.2 | 7.8 | 13.2 | 5.7 |
| Event Characteristics | Coastal-SEQ | Inland-SEQ | ||
|---|---|---|---|---|
| H1 | H2 | H1 | H2 | |
| Antecedent dry day periods | −0.20 | 1.18 | −0.35 | 0.06 |
| Maximum rainfall intensity | 0.78 | 0.97 | −0.61 | −0.65 |
| Total rainfall | −0.55 | 0.65 | −0.54 | −0.10 |
| Duration | 0.26 | 0.32 | −1.29 | −1.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasheed, A.; Egodawatta, P.; Goonetilleke, A.; McGree, J. A Novel Approach for Delineation of Homogeneous Rainfall Regions for Water Sensitive Urban Design—A Case Study in Southeast Queensland. Water 2019, 11, 570. https://doi.org/10.3390/w11030570
Rasheed A, Egodawatta P, Goonetilleke A, McGree J. A Novel Approach for Delineation of Homogeneous Rainfall Regions for Water Sensitive Urban Design—A Case Study in Southeast Queensland. Water. 2019; 11(3):570. https://doi.org/10.3390/w11030570
Chicago/Turabian StyleRasheed, Ashiq, Prasanna Egodawatta, Ashantha Goonetilleke, and James McGree. 2019. "A Novel Approach for Delineation of Homogeneous Rainfall Regions for Water Sensitive Urban Design—A Case Study in Southeast Queensland" Water 11, no. 3: 570. https://doi.org/10.3390/w11030570
APA StyleRasheed, A., Egodawatta, P., Goonetilleke, A., & McGree, J. (2019). A Novel Approach for Delineation of Homogeneous Rainfall Regions for Water Sensitive Urban Design—A Case Study in Southeast Queensland. Water, 11(3), 570. https://doi.org/10.3390/w11030570