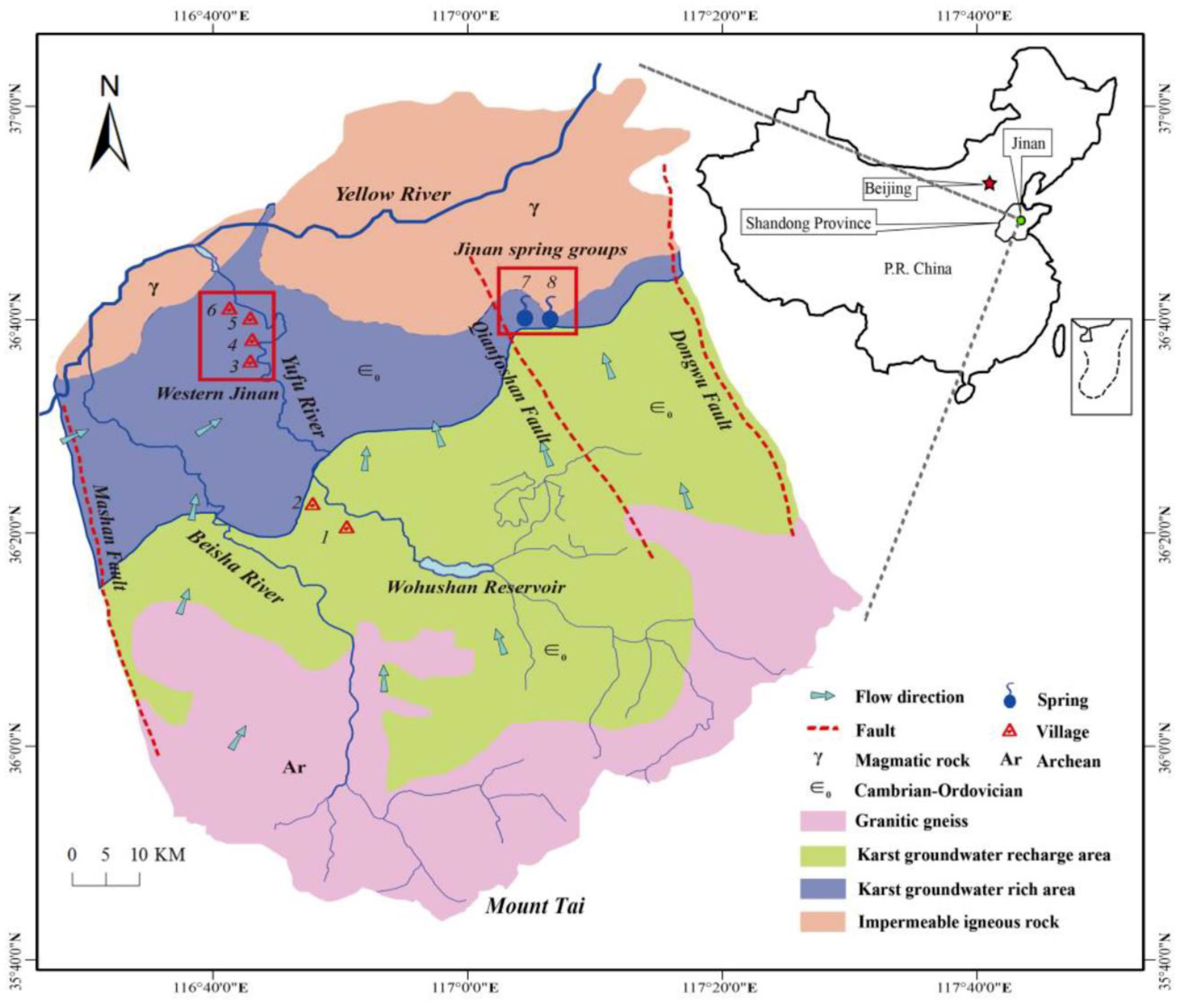
1. Introduction
Jinan is well-known for its springs and is known as “Spring City”, and therefore attracts many tourists. The natural spring water resources have historically contributed to the socioeconomic development of Jinan. In recent years, the rapid urbanization process and the sharply increased urban population has resulted in huge pressure on the urban water supply and an increasingly prominent contradiction between supply and demand. This situation will raise the over-extraction of karst groundwater, which causes the karst groundwater table and the outflow of springs to be reduced considerably in Jinan spring groups. The drying-up phenomenon in springs has occurred many times, and the regional groundwater ecosystem has undergone a series of negative impacts. Moreover, considering the poor water infrastructure and the few sources of urban water supply in Jinan, the government urgently requires measures to ensure abundant and sustainable water resources for spring water protection and urban daily use. Therefore, the surface water of the South–North Water Diversion Project and Yellow River has been gradually used by Jinan as urban water supply sources. Although these measures can relieve the pressure of urban water supply and reduce the exploitation of karst groundwater to a certain extent, they do not fundamentally repair the regional groundwater funnel caused by over-exploitation of groundwater. Hence, launching an effective groundwater recharge project to recover groundwater resources and maintain perennial outflow of the springs is necessary. However, the geological structure of Jinan is rather complex; blindly conducting the recharge project not only has a heavy workload but also causes a huge consumption of labor, material resources, finance, and water resources. Thus, selecting preferential sites to optimize the layout of recharge and exploitation following the hydraulic connectivity is a critical link in executing the projects for urban water supply and spring protection.
Traditional studies on the hydraulic connectivity of karst aquifers have been conducted by measurement of hydraulic head (pumping test), hydrochemistry ion and environmental isotope tracer tests, and numerical simulation [
1,
2,
3,
4]. These studies provide additional insights for exploring hydraulic connectivity and play an important role in environmental and hydraulic engineering. Other examples of studies that have adopted hydrochemistry ion and environmental isotope methods to explore long-term hydrogeological patterns and hydraulic connectivity were described in references [
5,
6,
7,
8,
9]. Kattan [
10] recently investigated the aquifer interaction and the origin of groundwater salinization using hydrochemical and environmental isotope methods based on the karst groundwater quality of wells in Syria. The author described the hydraulic connectivity in the Hongdunzi coal mining region in Northwest China by employing hydrochemical and environmental isotope methods [
11]. The appeal of numerical simulation for exploring the hydraulic connectivity of karst aquifer systems is that it combines water flow models with computer science, thereby facilitating visualization of simulation results [
12,
13,
14,
15]. The effects of the aquifer connectivity and geological structure on groundwater flow were described by using FEFLOW software to build the 3D geological model [
16]. Raiber [
17] developed a multilayer 3D hydrogeology model that introduced long-term monitoring data to describe the hydraulic connection of the aquifer in Wairau Plain, New Zealand. The hydrogeological parameters over the past 35 years in the study area were carefully surveyed, and on this basis, the hydraulic connectivity in the unconfined aquifer was investigated by Visual MODFLOW software [
18].
The multiple methods have been combined with one another, to try to draw on the advantages of different methods to investigate the connectivity and feature of a complex aquifer system [
19,
20,
21,
22,
23]. Environmental isotope tracers and hydrochemistry ions, which flow with the karst groundwater, are highly efficient in exploring the aquifer system within a specific area and are helpful if combined with other research methods of hydraulic connectivity [
24,
25,
26,
27,
28,
29]. The valuable perspectives and methods for the exploration of hydraulic connectivity have been obtained by adopting cumbersome mathematical derivation and detailed hydrogeological parameters following the methods described by references [
30,
31,
32,
33,
34,
35,
36,
37,
38].
The aforementioned methods, which investigate the complex and uncertain hydraulic connectivity, have achieved promising results and have vital practical significance. However, the general quantitative methods of hydraulic connectivity measurements, such as conventional experiments, often have some limitations. These mainly include the long work cycle, the high cost and requirements of adequate data, detailed understanding for hydrogeological parameters, and negative impact on the environment. Meanwhile, most conventional research methods need large-scale and continuous execution. If the conventional experiments are carried out blindly, this will not only enlarge the negative effect of the above shortcomings, but also cause a huge waste of resources. Therefore, the choice of experiment sites is crucial. We should consider whether we can use some methods to select the sites of conventional experiments, which can preliminarily locate the preferential sites of recharge and exploitation. Ultimately, conventional experiments that rely on these preferential sites are implemented. This approach can selectively narrow the scope of experiment sites to optimize the layouts of recharge and exploitation, thereby decreasing the experimental expenditure and adverse impact on the ecological environment. However, current studies rarely consider a pre-selected issue for experiment sites prior to implementing conventional experiments. Fortunately, even if the relationships between factors are uncertain and the sample size is small, the grey relation analysis method can be utilized. Thus, considered applying this method to reveal the hydraulic connectivity of a complicated karst aquifer system. In light of this, we attempt to present a pre-study method (an improved grey amplitude relation model) to select preliminarily the preferential sites of conventional experiments, which can acquire a series of data to describe hydraulic connectivity quantitatively.
Grey systems theory is one of the widely adopted methods at present, which successfully investigates uncertain problems with limited available information. This method has obvious advantages for handling small sample size and inadequate information [
39], and it is not limited by strict requirements for distribution and length of a data sequence and can effectively simplify the calculation process of complex problems [
40]. The grey relation degree models are an important part of grey systems theory, and the degree of inter-sequence relations is assessed by measuring the similarity or proximity of the sequences [
41]. This model was initially developed in system engineering [
42], and since then, different types of grey relation degree models have been widely applied by researchers. The grey absolute relation degree model was first adopted in environmental science to evaluate the relationships of environment and economics [
43], and the correlation between pollutants in lake water was investigated utilizing Deng’s relation degree [
44]. As research progresses, the types of grey relation degree models are further expanded. Dang [
45] presented a grey slope incidence model, which was sourced from the slope of a straight line. This model was successfully applied to study the relationship of water tables between different regions [
46]. The grey close incidence model was developed in reference [
47] to study the influence of human activity on ecological thresholds. The relationship between China’s marine–land economy and different sectors were analyzed by using the improved grey periodic relation method [
48].
To date, the grey relation degree models were constructed mainly relying on the angle, distance, slope, and change rate of the data sequence; however, they cannot reflect positive and negative correlations. Although the sequence data in real life are usually affected by the dual disturbance of vertical and horizontal coordinates (amplitude and period), the existing research remains less concerned about these two aspects [
49]. The grey amplitude relation model was developed by references [
50,
51,
52] to avoid the aforementioned problems. This model is only affected by the amplitude factors; it can reflect positive and negative correlations and is appropriate for sequence values that have obvious fluctuation trends.
In this paper, the grey amplitude relation model is improved to investigate the groundwater table sequence with an obvious fluctuation trend. To precisely reflect the features of the research object, the data are preprocessed in this study before modeling and the specific calculation period is divided based on the influence factors of groundwater table fluctuation. Accordingly, we present a new quantized index, water table fluctuation relation degree (WTFRD), to preliminarily discuss the hydraulic connectivity of a complex aquifer system. In conclusion, the quantized index WTFRD offers a new insight for the preliminary exploration of hydraulic connectivity. Meanwhile, the improved grey amplitude relation method serves as a viable pre-study method for selecting the preferential sites of conventional experiments. Ultimately, specific experiments are conducted in the preferential sites (with the highest and lowest WTFRD) to verify the hydraulic connectivity. Then, the layouts of recharge and exploration are optimized based on the hydraulic connectivity.
5. Discussion
To protect springs and supply water, Jinan urgently needs to determine as soon as possible the hydraulic connectivity between Jinan spring groups and other regions. The karst groundwater recharge project can be conducted in the regions with the high hydraulic connectivity to restore the karst groundwater resources in Jinan spring groups effectively. Meanwhile, the karst groundwater will be exploited in the regions with the low hydraulic connectivity (the minimum influence on Jinan spring groups’ aquifer) for urban water supply. To study the hydraulic connectivity, many conventional experiments are implemented blindly and subjectively; these experiments have a long work cycle, a high cost, and some negative effects on the environment and human health. In this context, we attempt to apply the improved grey amplitude relation method that is a pre-study of conventional experiments to explore initially the hydraulic connectivity of the aquifer system, and the preferential sites are further selected to implement conventional experiments. This method has the features of simple calculation and convenient operation. It also has the following advantages: (i) It only considers the fluctuation amplitudes between two sequences and eliminates the interference of other factors, such as the fluctuation period, which is suited for dealing with the water table sequence with an obvious fluctuation trend; (ii) the method provides a quantitative study for hydraulic connectivity of a complex aquifer system; (iii) it does not need many hydrogeological parameters in the calculation process, while it only needs the karst groundwater table data of existing observation wells; (iv) this method does not consume massive labor, physical resources, and finances; (v) it does not use any hydrochemistry ions and environmental isotope tracers, so it will not produce any negative effect on the ecological environment and aquifer systems as well as on the daily life of neighboring residents. Ultimately, the scope of conventional experimental sites is effectively reduced, and the adverse effect in large-scale and continuous conventional experiments can be decreased as much as possible. Furthermore, this method provides a quantitative study of hydraulic connectivity, which is highly suited to investigate the karst groundwater table sequence with an obvious fluctuation trend.
Possible future research based on this study include the following: (i) The average karst groundwater table is calculated in a 15-day cycle in this study because of the limitations of the data itself. Future studies can attempt to calculate the average karst groundwater table in different cycles based on the feature of research objects and of data itself. (ii) The research objects (Western Jinan and Jinan spring groups) in this study are only a typical case to introduce the quantized evaluation index WTFRD; future studies can increase the number of observation wells and enlarge the range of research area. (iii) The improved grey amplitude relation can be as a pre-study method before conducting the conventional experiments, and this combined method can achieve their full potential in future. (iv) The karst groundwater table is used to calculate the WTFRD in this study, and further research can use water quality indicators such as electrical conductivity to calculate the WTFRD. (v) The grey amplitude relation model can be used to study the hysteretic nature between two variables, and it has been successfully applied in China’s economic field [
66]. This approach provides an idea to investigate the hysteretic time of karst groundwater movement, which deserves further study by the authors.