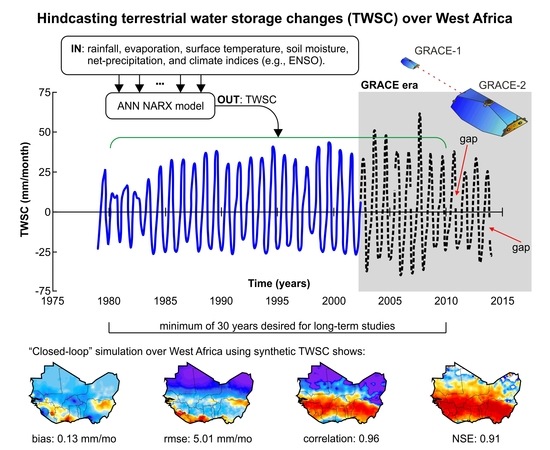
A Multi-Sourced Data Retrodiction of Remotely Sensed Terrestrial Water Storage Changes for West Africa
Abstract
1. Introduction
2. Materials and Methods
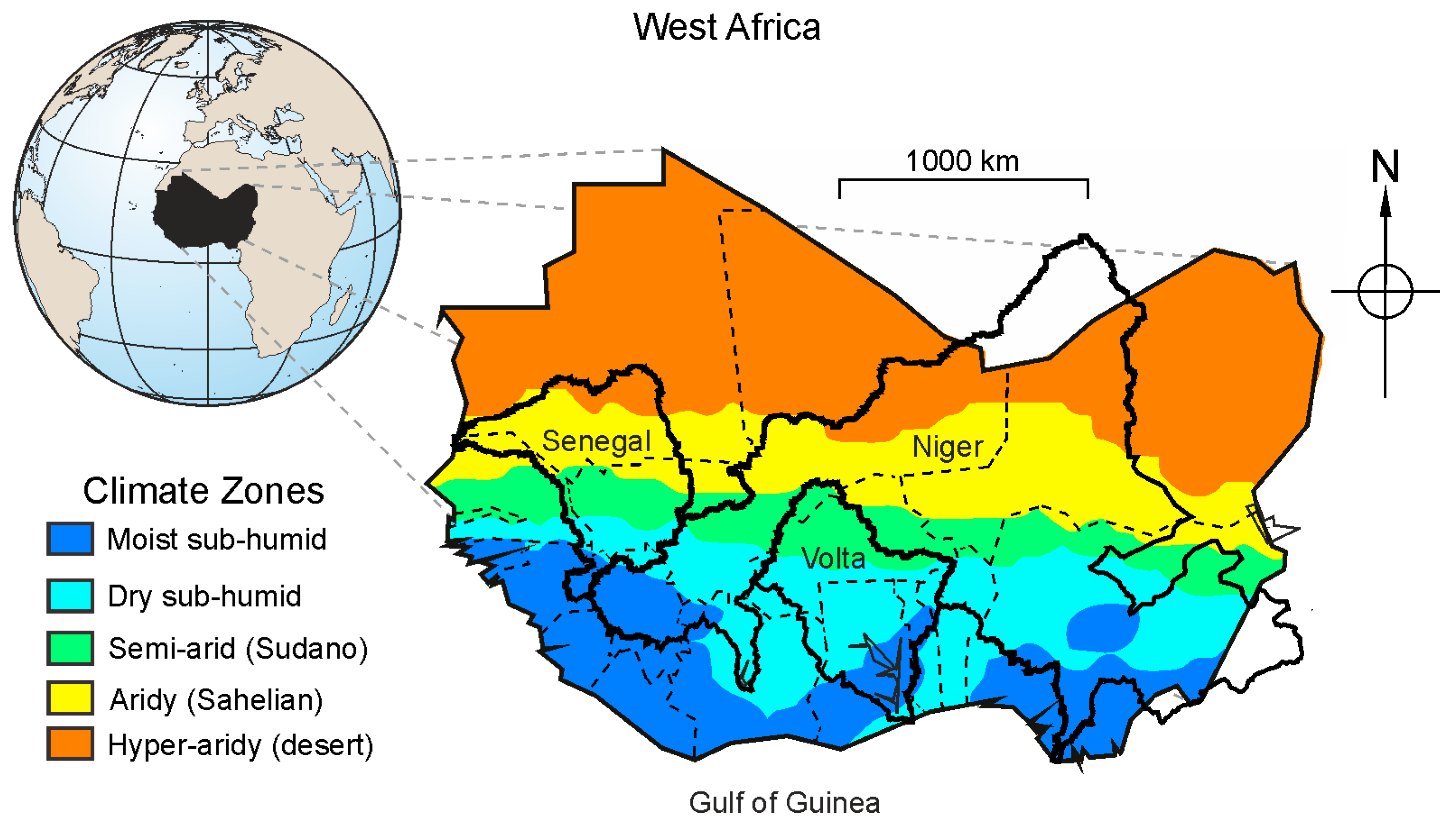
2.1. Study Area
2.2. Datasets
2.2.1. ARCv2 Rainfall
2.2.2. ERA-Interim Data System
2.2.3. GLDAS-Noah Version 2
2.2.4. Climate Indices
2.2.5. GRACE Fields
2.3. Methods
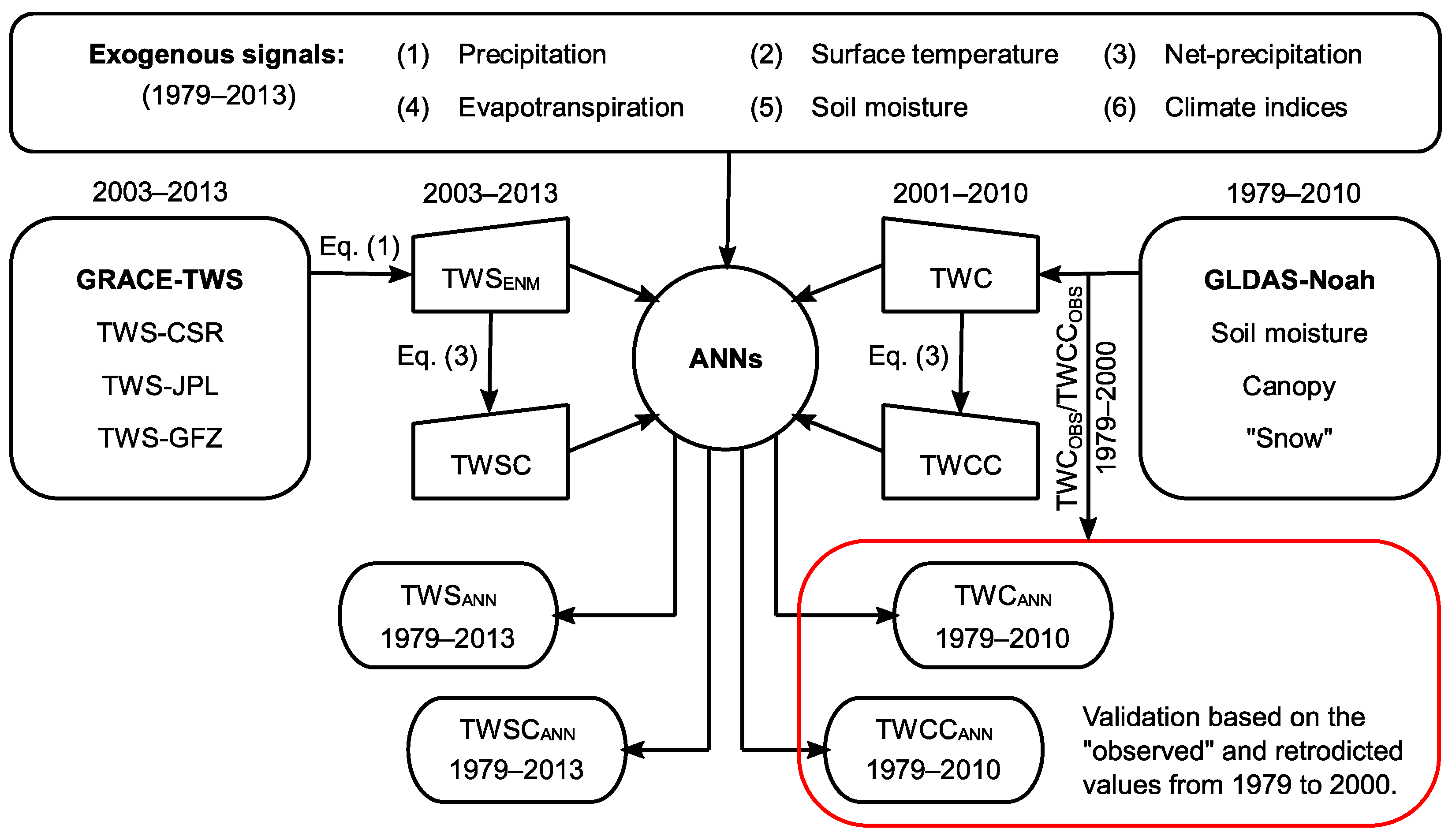
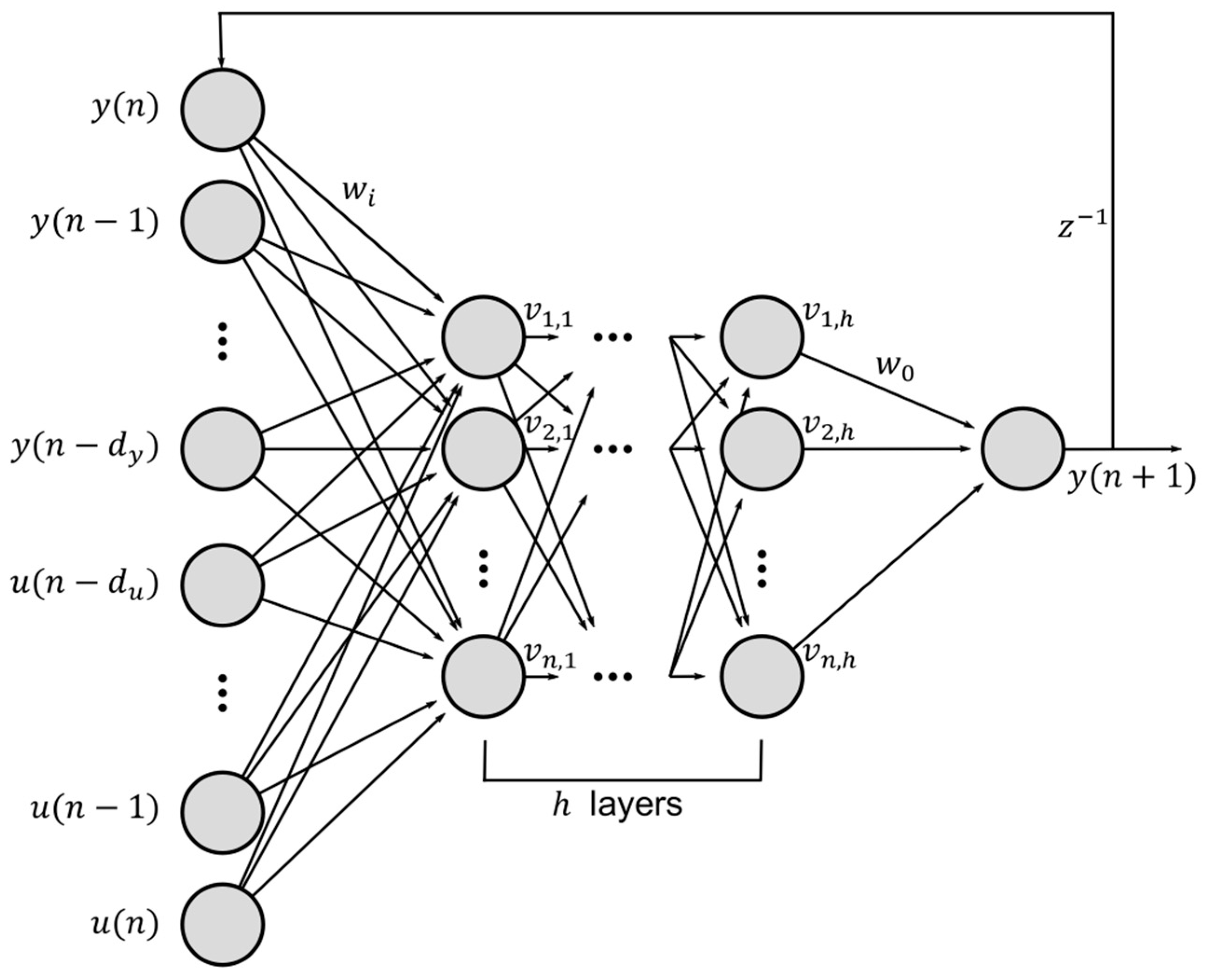
2.3.1. Reconstruction of GRACE-Derived TWS/TWSC
2.3.2. Validation Metrics
3. Results
3.1. The Ensemble GRACE-TWS Fields
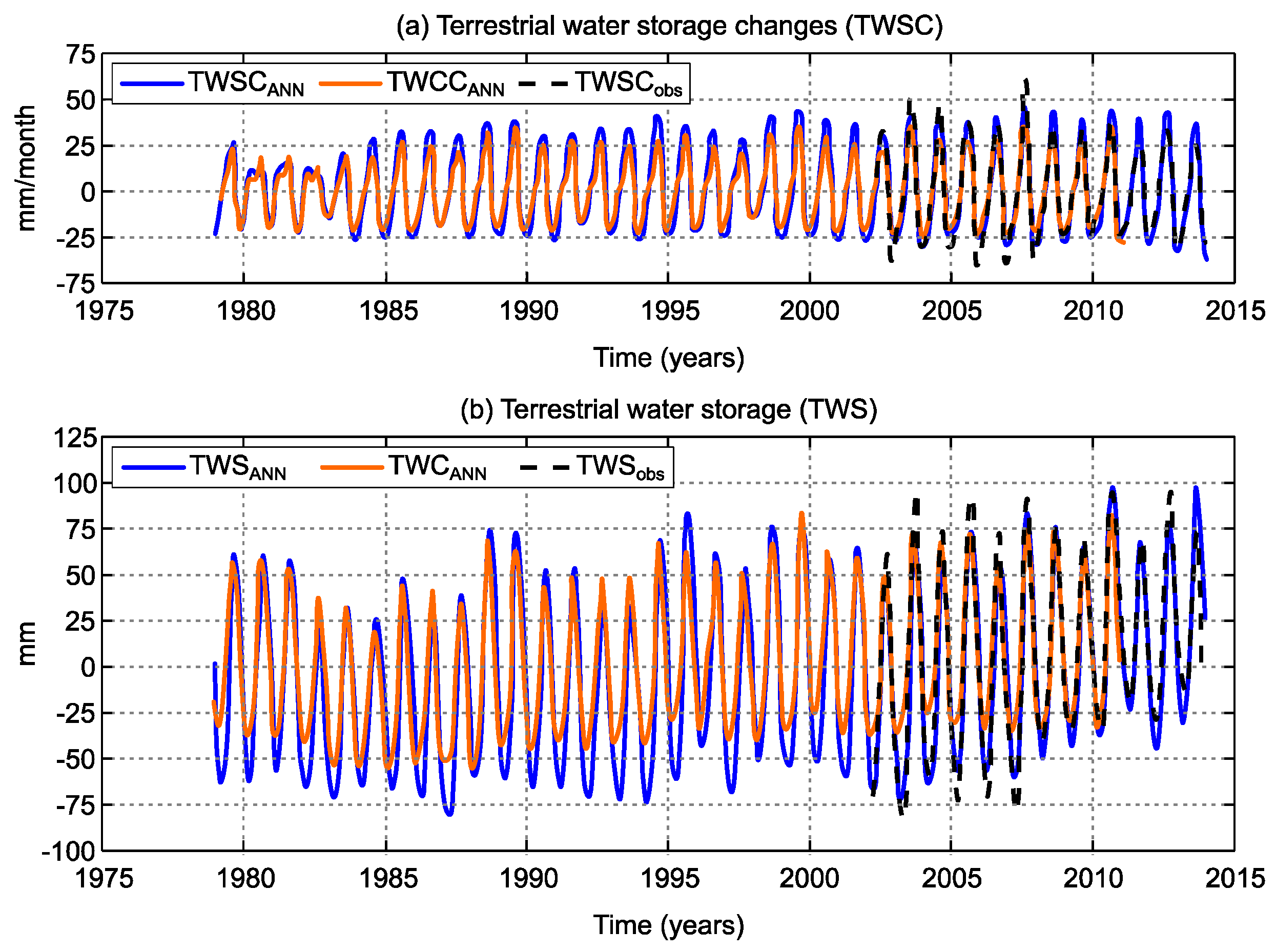
3.2. Confirmatory Study Based on Noah-Derived TWCC Prediction
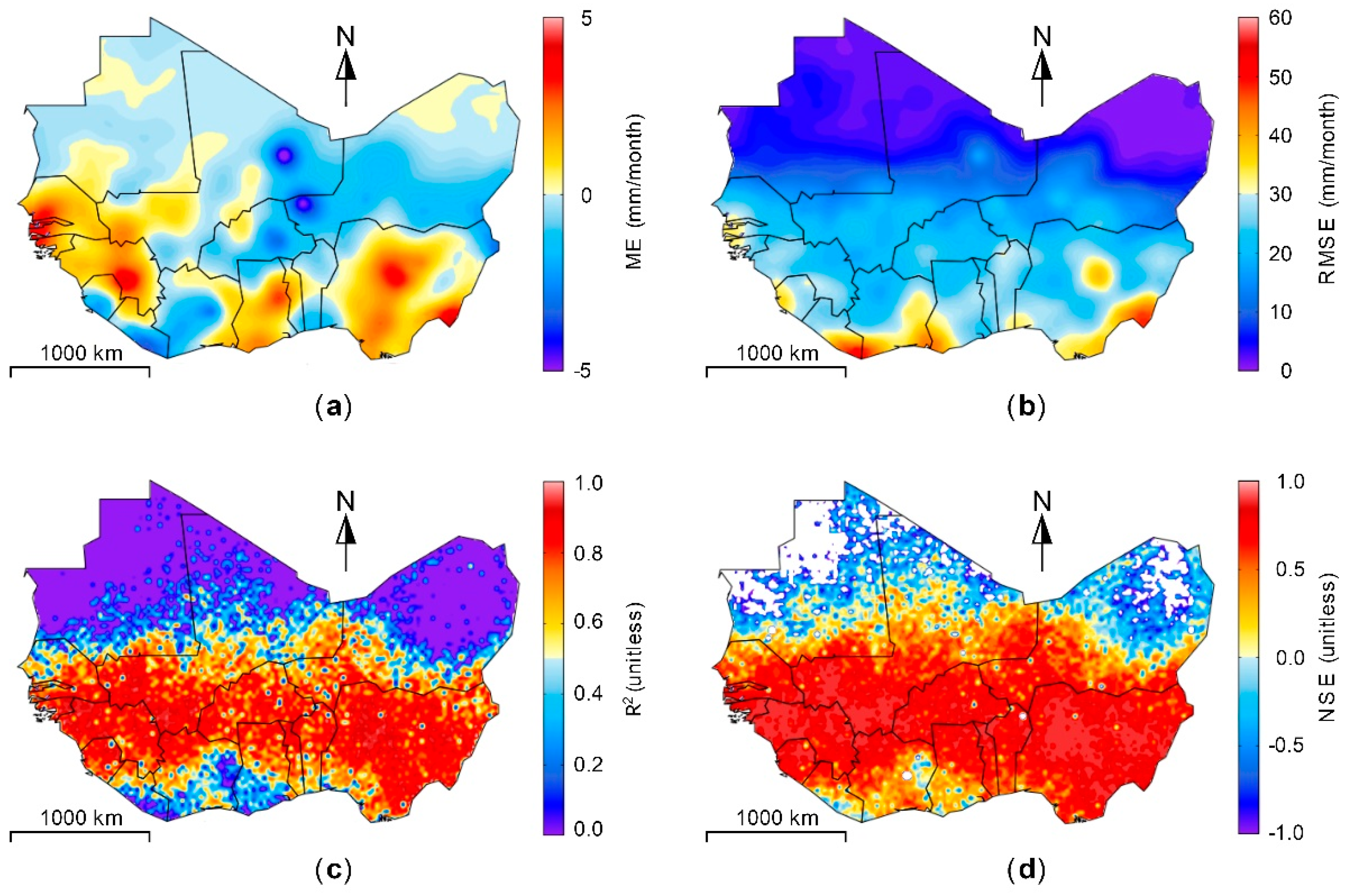
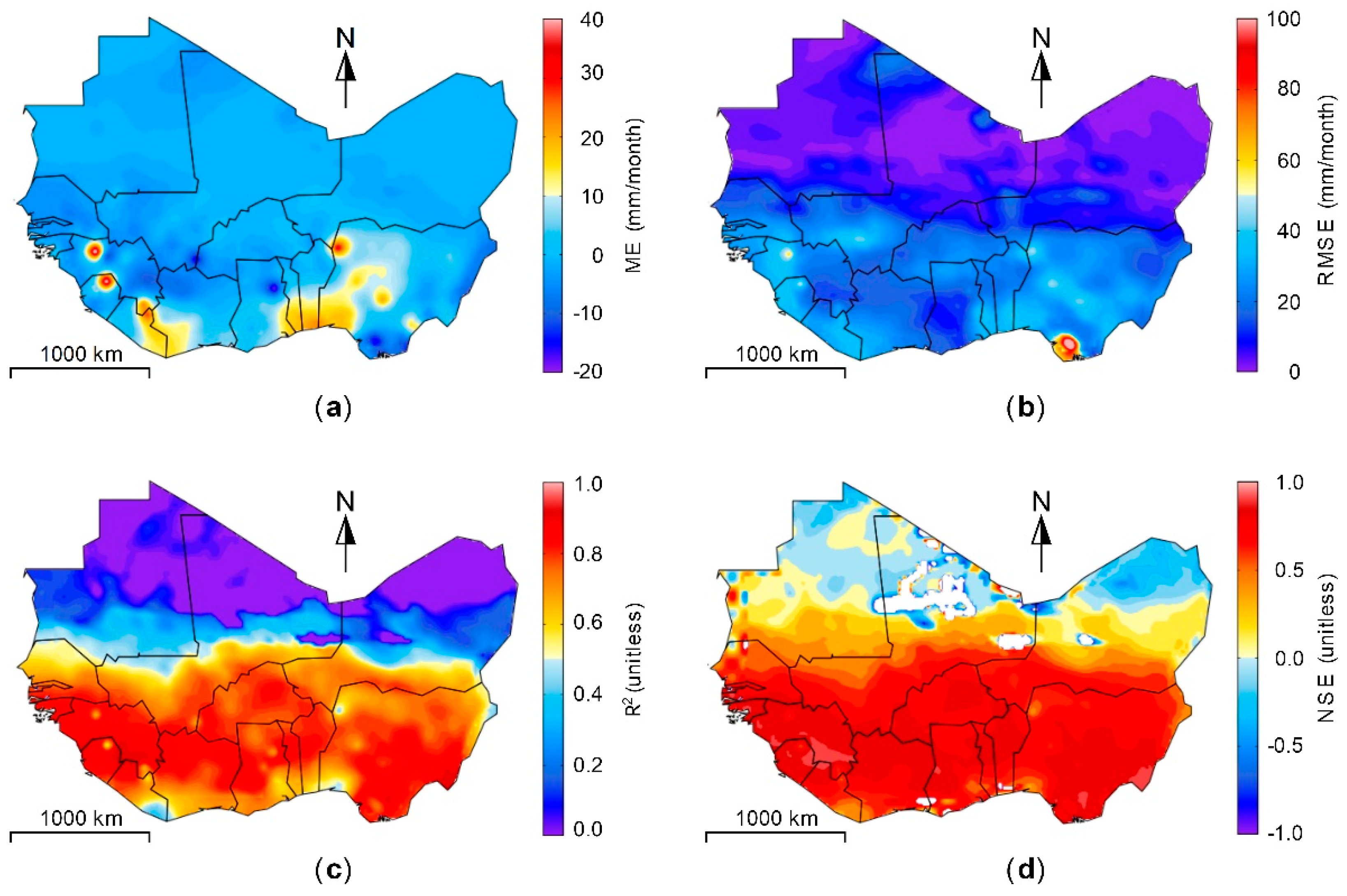
3.3. Evaluation of Backcasted GRACE-Derived TWSC
4. Discussion
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Region | ME (mm/month) | RMSE (mm/month) | NSE | R2 | |
|---|---|---|---|---|---|
| Basin | Niger | 2.76 | 13.10 | 0.90 | 0.92 |
| Senegal | 1.56 | 16.50 | 0.82 | 0.83 | |
| Volta | 5.36 | 23.01 | 0.83 | 0.84 | |
| Climate zones | Humid | −2.64 | 30.90 | 0.82 | 0.88 |
| Dry sub-humid | 4.65 | 20.66 | 0.90 | 0.92 | |
| Sudanian | 4.81 | 18.47 | 0.89 | 0.83 | |
| Sahelian | 3.76 | 13.90 | 0.76 | 0.84 | |
| Sahara | 1.13 | 4.92 | 0.26 | 0.92 | |
| WA | 2.21 | 11.00 | 0.89 | 0.92 | |
References
- Xie, H.; Longuevergne, L.; Ringler, C.; Scanlon, B. Calibration and evaluation of a semi-distributed watershed model of sub-Saharan Africa using GRACE data. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 2071–2120. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K.C. Calibration and uncertainty issues of a hydrological model (SWAT) applied to West Africa. Adv. Geosci. 2006, 2, 137–143. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.-H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef] [PubMed]
- Forootan, E.; Kusche, J.; Loth, I.; Schuh, W.-D.; Eicker, A.; Awange, J.; Longuevergne, L.; Diekkrüger, B.; Schmidt, M.; Shum, C.K. Multivariate Prediction of Total Water Storage Changes Over West Africa from Multi-Satellite Data. Surv. Geophys. 2014, 35, 913–940. [Google Scholar] [CrossRef]
- Becker, M.; Meyssignac, B.; Xavier, L.; Cazenave, A.; Alkama, R.; Decharme, B. Past terrestrial water storage (1980-2008) in the Amazon Basin reconstructed from GRACE and in situ river gauging data. Hydrol. Earth Syst. Sci. 2011, 15, 533–546. [Google Scholar] [CrossRef]
- de Linage, C.; Famiglietti, J.S.; Randerson, J.T. Statistical prediction of terrestrial water storage changes in the Amazon Basin using tropical Pacific and North Atlantic sea surface temperature anomalies. Hydrol. Earth Syst. Sci. 2014, 18, 2089–2102. [Google Scholar] [CrossRef]
- Yin, W.; Hu, L.; Han, S.; Zhang, M.; Teng, Y. Reconstructing Terrestrial Water Storage Variations from 1980 to 2015 in the Beishan Area of China. Geofluids 2019, 2019, 3874742. [Google Scholar] [CrossRef]
- Wilby, R.L.; Abrahart, R.J.; Dawson, C.W. Detection of conceptual model rainfall—Runoff processes inside an artificial neural network. Hydrol. Sci. J. 2003, 48, 163–181. [Google Scholar] [CrossRef]
- Mukhopadhyay, A. Application of visual, statistical and artificial neural network methods in the differentiation of water from the exploited aquifers in Kuwait. Hydrogeol. J. 2003, 11, 343–356. [Google Scholar] [CrossRef]
- Feng, L.; Hong, W. On hydrologic calculation using artificial neural networks. Appl. Math. Lett. 2008, 21, 453–458. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN System Satellite–Based Estimates of Tropical Rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Gebremichael, M. Using self-organizing maps and wavelet transforms for space–time pre-processing of satellite precipitation and runoff data in neural network based rainfall–runoff modeling. J. Hydrol. 2013, 476, 228–243. [Google Scholar] [CrossRef]
- Goyal, M.K. Monthly rainfall prediction using wavelet regression and neural network: An analysis of 1901–2002 data, Assam, India. Theor. Appl. Climatol. 2014, 118, 25–34. [Google Scholar] [CrossRef]
- Haykin, S.O. Neural Networks and Learning Machines, 3rd ed.; Pearson: London, UK, 2008; ISBN 9780131471405. [Google Scholar]
- Yirdaw-Zeleke, S. Implications of GRACE Satellite Gravity Measurements for Diverse Hydrological Applications. Ph.D. Thesis, University of Manitoba, Winnipeg, MB, Canada, 2010. [Google Scholar]
- Miro, M.E.; Famiglietti, J.S. Downscaling GRACE remote sensing datasets to high-resolution groundwater storage change maps of California’s Central Valley. Remote Sens. 2018, 10, 143. [Google Scholar] [CrossRef]
- Sun, A.Y. Predicting groundwater level changes using GRACE data. Water Resour. Res. 2013, 49, 5900–5912. [Google Scholar] [CrossRef]
- Yang, Y.; Long, D.; Guan, H.; Scanlon, B.R.; Simmons, C.T.; Jiang, L.; Xu, X. GRACE satellite observed hydrological controls on interannual and seasonal variability in surface greenness over mainland Australia. J. Geophys. Res. Biogeosci. 2014, 119, 2245–2260. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Q.; Werner, A.D.; Liu, X. GRACE-Based Hydrological Drought Evaluation of the Yangtze River Basin, China. J. Hydrometeorol. 2016, 17, 811–828. [Google Scholar] [CrossRef]
- Mukherjee, A.; Ramachandran, P. Prediction of GWL with the help of GRACE TWS for unevenly spaced time series data in India: Analysis of comparative performances of SVR, ANN and LRM. J. Hydrol. 2018, 558, 647–658. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, J.; Li, H. Drought and flood monitoring of the Liao River Basin in Northeast China using extended GRACE data. Remote Sens. 2018, 10, 1168. [Google Scholar] [CrossRef]
- Andam-Akorful, S.A.; Ferreira, V.G.; Ndehedehe, C.E.; Quaye-Ballard, J.A. An investigation into the freshwater variability in West Africa during 1979-2010. Int. J. Climatol. 2017, 37, 333–349. [Google Scholar] [CrossRef]
- Nicholson, S.E. The Spatial Coherence of African Rainfall Anomalies: Interhemispheric Teleconnections. J. Clim. Appl. Meteorol. 1986, 25, 1365–1381. [Google Scholar] [CrossRef]
- Novella, N.S.; Thiaw, W.M. African Rainfall Climatology Version 2 for Famine Early Warning Systems. J. Appl. Meteorol. Climatol. 2013, 52, 588–606. [Google Scholar] [CrossRef]
- Africa Rainfall Climatology (ARC). ARC Version 2 (ARC2). Available online: ftp://ftp.cpc.ncep.noaa.gov/fews/fewsdata/africa/arc2/bin/ (accessed on 15 March 2015).
- Awange, J.L.; Ferreira, V.G.; Forootan, E.; Khandu; Andam-Akorful, S.A.; Agutu, N.O.; He, X.F. Uncertainties in remotely sensed precipitation data over Africa. Int. J. Climatol. 2016, 36, 303–323. [Google Scholar] [CrossRef]
- Ahn, J.; Hong, S.; Cho, J.; Lee, Y.-W.; Lee, H. Statistical Modeling of Sea Ice Concentration Using Satellite Imagery and Climate Reanalysis Data in the Barents and Kara Seas, 1979–2012. Remote Sens. 2014, 6, 5520–5540. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts (ECMWF). Interim Reanalysis Data (ERA). Available online: https://apps.ecmwf.int/datasets/data/interim-full-moda/levtype=sfc/ (accessed on 26 April 2015).
- Forootan, E.; Didova, O.; Schumacher, M.; Kusche, J.; Elsaka, B. Comparisons of atmospheric mass variations derived from ECMWF reanalysis and operational fields, over 2003–2011. J. Geod. 2014, 88, 503–514. [Google Scholar] [CrossRef]
- Global Land Data Assimilation System (GLDAS). GLDAS Noah Land Surface Model L4 3 hourly 0.25 x 0.25 degree, V2.0. Available online: https://disc.gsfc.nasa.gov/ (accessed on 10 February 2018).
- Smith, C.A.; Sardeshmukh, P.D. The effect of ENSO on the intraseasonal variance of surface temperatures in winter. Int. J. Climatol. 2000, 20, 1543–1557. [Google Scholar] [CrossRef]
- Lutz, K.; Rathmann, J.; Jacobeit, J. Classification of warm and cold water events in the eastern tropical Atlantic Ocean. Atmos. Sci. Lett. 2013, 14, 102–106. [Google Scholar] [CrossRef]
- Nicholson, S.E. The West African Sahel: A Review of Recent Studies on the Rainfall Regime and Its Interannual Variability. ISRN Meteorol. 2013, 2013, 1–32. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, W04531. [Google Scholar] [CrossRef]
- Bruinsma, S.; Lemoine, J.-M.; Biancale, R.; Valès, N. CNES/GRGS 10-day gravity field models (release 2) and their evaluation. Adv. Space Res. 2010, 45, 587–601. [Google Scholar] [CrossRef]
- Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Montecino, H.D.C.; Yakubu, C.I.; Heck, B. Uncertainties of the Gravity Recovery and Climate Experiment time-variable gravity-field solutions based on three-cornered hat method. J. Appl. Remote Sens. 2016, 10, 015015. [Google Scholar] [CrossRef]
- Ardalani-Farsa, M.; Zolfaghari, S. Chaotic time series prediction with residual analysis method using hybrid Elman–NARX neural networks. Neurocomputing 2010, 73, 2540–2553. [Google Scholar] [CrossRef]
- Garcia, D. Robust smoothing of gridded data in one and higher dimensions with missing values. Comput. Stat. Data Anal. 2010, 54, 1167–1178. [Google Scholar] [CrossRef] [PubMed]
- Mathworks. Deep Learning Toolbox, MATLAB. 2018. Available online: https://www.mathworks.com/products/deep-learning.html (accessed on 15 December 2018).
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Day, R.W.; Quinn, G.P. Comparisons of Treatments After an Analysis of Variance in Ecology. Ecol. Monogr. 1989, 59, 433–463. [Google Scholar] [CrossRef]
- Rafter, J.A.; Abell, M.L.; Braselton, J.P. Multiple Comparison Methods for Means. SIAM Rev. 2002, 44, 259–278. [Google Scholar] [CrossRef]
- Ndehedehe, C.E.; Agutu, N.O.; Okwuashi, O.; Ferreira, V.G. Spatio-temporal variability of droughts and terrestrial water storage over Lake Chad Basin using independent component analysis. J. Hydrol. 2016, 540, 106–128. [Google Scholar] [CrossRef]
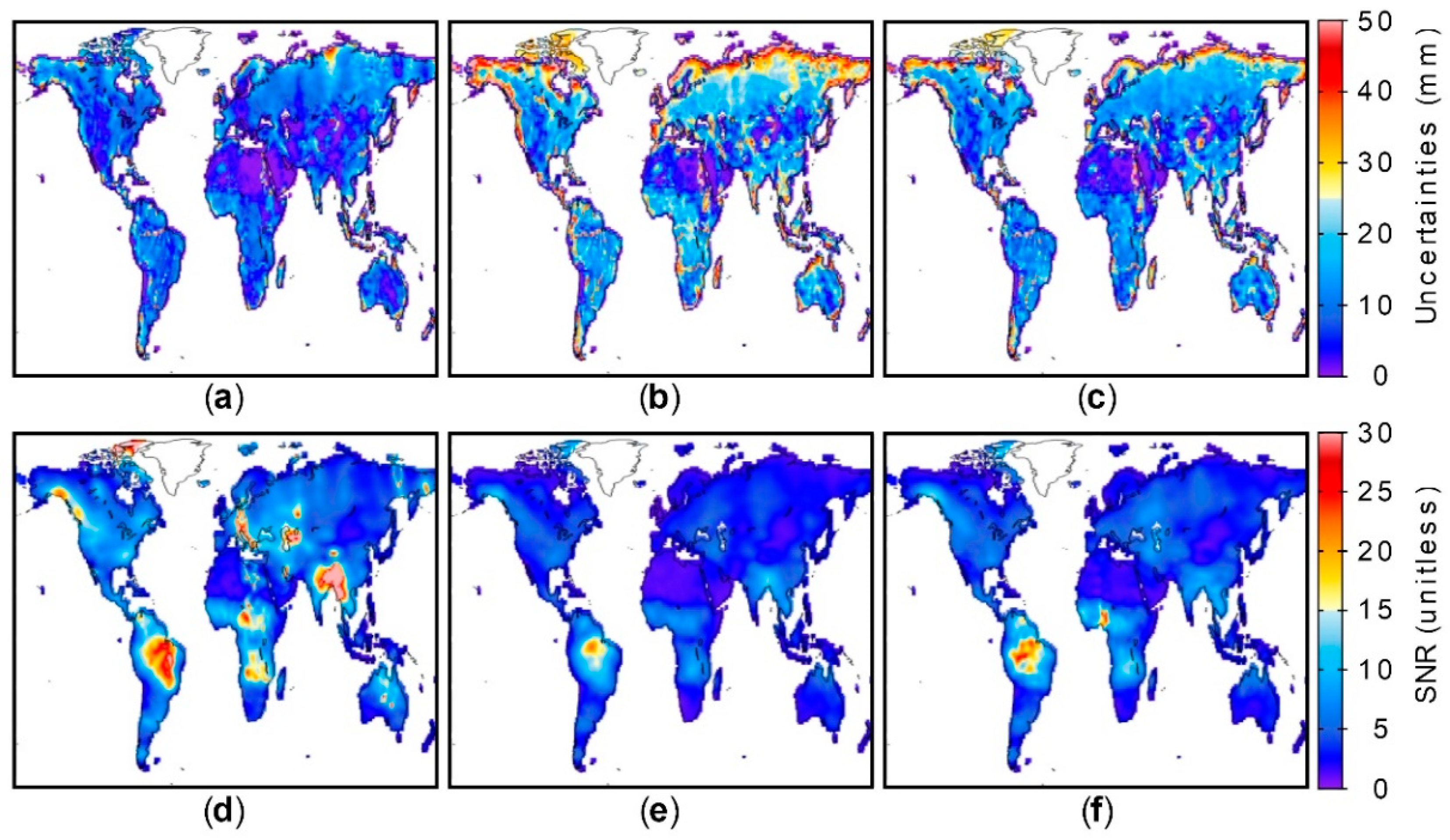
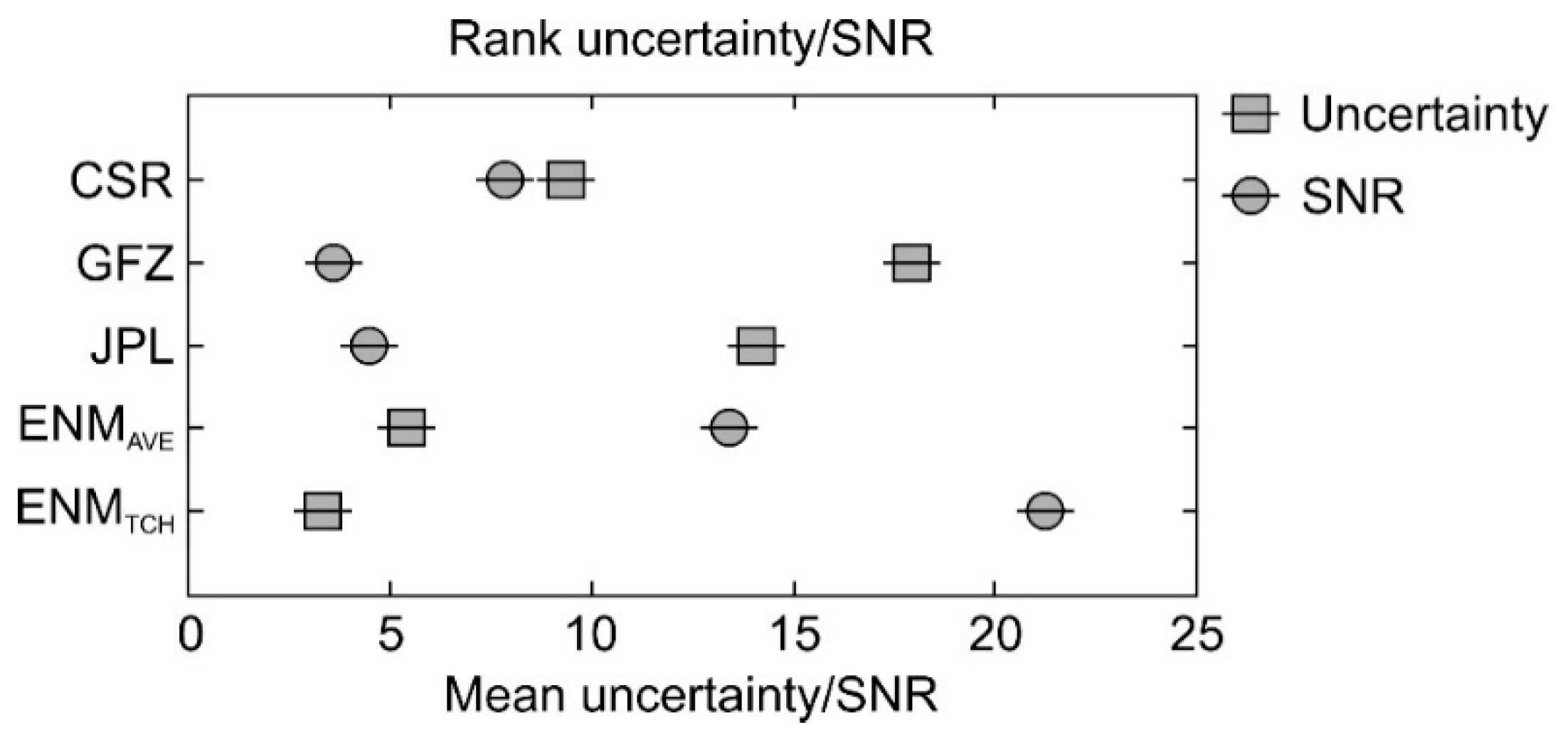
| Product | Uncertainties Intervals (mm) | |||||
| 0–20 | 20–40 | 40–60 | 60–80 | 80–100 | 100–120 | |
| CSR | 91.5% | 7.4% | 0.8% | 0.2% | 0.1% | 0.0% |
| GFZ | 63.6% | 29.7% | 4.9% | 1.3% | 0.4% | 0.1% |
| JPL | 77.9% | 18.7% | 2.6% | 0.6% | 0.1% | 0.1% |
| Product | SNR Intervals (Unitless) | |||||
| 0–20 | 20–40 | 40–60 | 60–80 | 80–100 | 100–120 | |
| CSR | 95.5% | 3.7% | 0.5% | 0.2% | 0.1% | 0.0% |
| GFZ | 99.9% | 0.1% | 0.0% | 0.0% | 0.0% | 0.0% |
| JPL | 99.5% | 0.5% | 0.0% | 0.0% | 0.0% | 0.0% |
| Product | Uncertainties Intervals (mm) | |||||
| 0–10 | 10–20 | 20–30 | 30–40 | 50–60 | 60–70 | |
| ENMAVE | 87.1% | 11.2% | 1.2% | 0.3% | 0.1% | 0.1% |
| ENMTCH | 97.1% | 2.6% | 0.2% | 0.1% | 0.0% | 0.0% |
| Product | SNR Intervals (Unitless) | |||||
| 0–20 | 20–40 | 40–60 | 60–80 | 80–100 | 100–120 | |
| ENMAVE | 85.7% | 11.1% | 1.6% | 0.9% | 0.3% | 0.1% |
| ENMTCH | 64.1% | 27.4% | 5.3% | 1.8% | 0.9% | 0.5% |
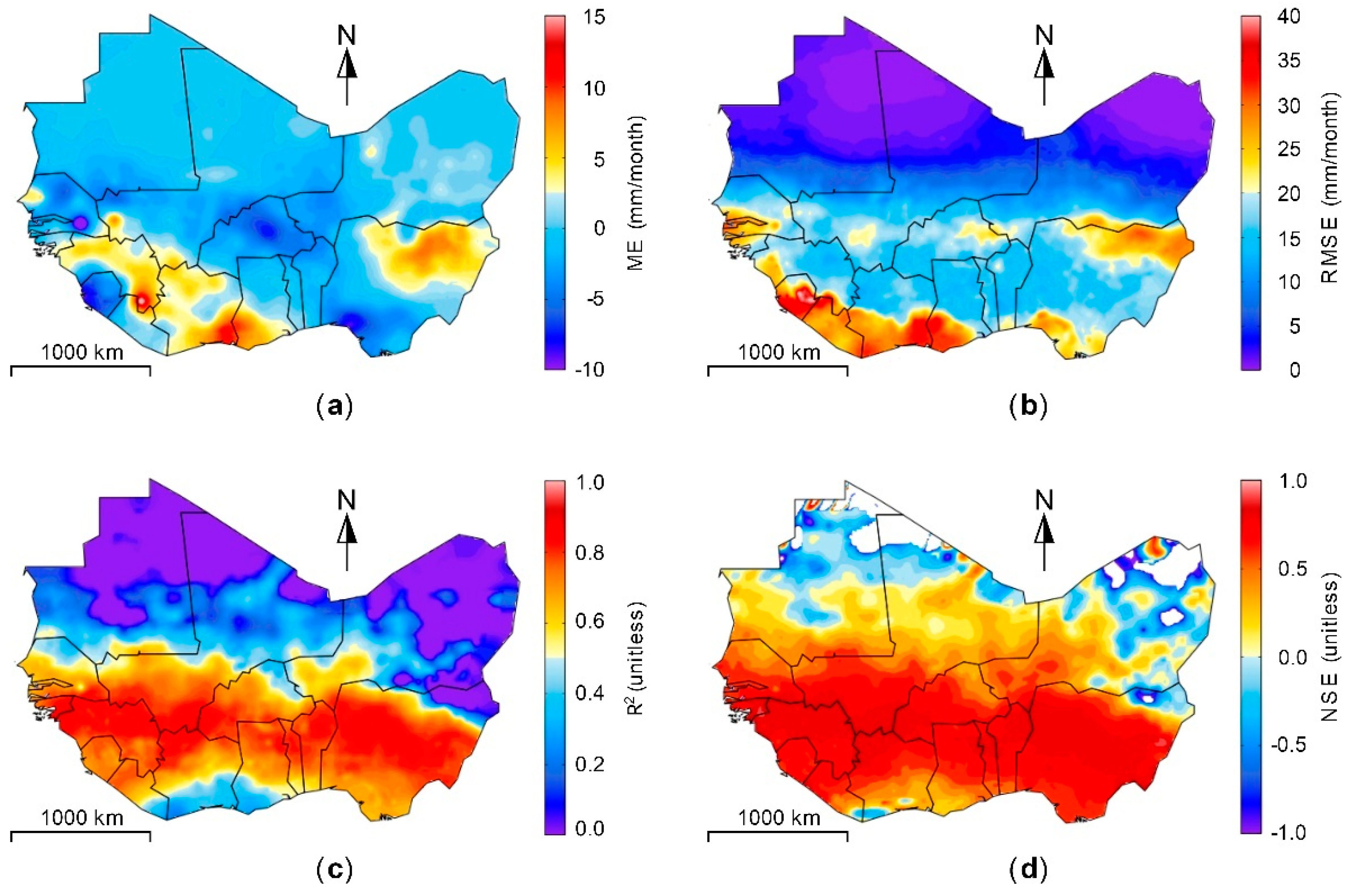
| Region | ME (mm/month) | RMSE (mm/month) | NSE | R2 | |
|---|---|---|---|---|---|
| Basin | Niger | 0.15 | 6.21 | 0.90 | 0.92 |
| Senegal | −0.96 | 7.70 | 0.83 | 0.83 | |
| Volta | −1.58 | 10.40 | 0.88 | 0.90 | |
| Climate zones | Humid | 1.24 | 10.90 | 0.89 | 0.92 |
| Dry sub-humid | 1.18 | 8.42 | 0.93 | 0.94 | |
| Sudanian | −1.04 | 12.46 | 0.84 | 0.86 | |
| Sahelian | −0.95 | 6.78 | 0.74 | 0.76 | |
| Sahara | 0.06 | 1.09 | 0.51 | 0.57 | |
| WA | 0.13 | 5.01 | 0.91 | 0.93 | |
| Region | ME (mm/month) | RMSE (mm/month) | NSE | R2 | |
|---|---|---|---|---|---|
| Basin | Niger | 0.08 | 8.26 | 0.91 | 0.91 |
| Senegal | −0.50 | 10.68 | 0.78 | 0.78 | |
| Volta | −0.01 | 13.23 | 0.89 | 0.89 | |
| Climate zones | Humid | 2.40 | 14.83 | 0.93 | 0.84 |
| Dry sub-humid | 0.47 | 14.17 | 0.91 | 0.91 | |
| Sudanian | −0.22 | 13.00 | 0.86 | 0.78 | |
| Sahelian | −0.67 | 5.16 | 0.81 | 0.89 | |
| Sahara | −0.66 | 1.93 | 0.26 | 0.91 | |
| WA | 0.05 | 6.98 | 0.91 | 0.91 | |
| Product | Span | Linear Trend (mm/year) | p-Value |
|---|---|---|---|
| TWSobs | 2002–2013 | 3.64 ± 1.20 | 3.8 × 10−3 |
| TWSANN | 2002–2013 | 3.44 ± 1.06 | 1.4 × 10−3 |
| TWSANN | 1979–2013 | 1.04 ± 0.21 | 6.5 × 10−7 |
| TWCNoah | 1979–2010 | 0.76 ± 0.19 | 7.5 × 10−7 |
| TWSANN | 1979–2006 | 0.67 ± 0.28 | 1.8 × 10−2 |
| TWSANN | 2007–2013 | 4.36 ± 2.38 | 7.1 × 10−2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, V.G.; Andam-Akorful, S.A.; Dannouf, R.; Adu-Afari, E. A Multi-Sourced Data Retrodiction of Remotely Sensed Terrestrial Water Storage Changes for West Africa. Water 2019, 11, 401. https://doi.org/10.3390/w11020401
Ferreira VG, Andam-Akorful SA, Dannouf R, Adu-Afari E. A Multi-Sourced Data Retrodiction of Remotely Sensed Terrestrial Water Storage Changes for West Africa. Water. 2019; 11(2):401. https://doi.org/10.3390/w11020401
Chicago/Turabian StyleFerreira, Vagner G., Samuel A. Andam-Akorful, Ramia Dannouf, and Emmanuel Adu-Afari. 2019. "A Multi-Sourced Data Retrodiction of Remotely Sensed Terrestrial Water Storage Changes for West Africa" Water 11, no. 2: 401. https://doi.org/10.3390/w11020401
APA StyleFerreira, V. G., Andam-Akorful, S. A., Dannouf, R., & Adu-Afari, E. (2019). A Multi-Sourced Data Retrodiction of Remotely Sensed Terrestrial Water Storage Changes for West Africa. Water, 11(2), 401. https://doi.org/10.3390/w11020401