Abstract
The SWOT (Surface Water and Ocean Topography) mission, to be launched in 2021, will provide water surface elevations, slopes, and river width measurements for rivers wider than 100 m. In this study, synthetic SWOT data are assimilated in a regional hydrometeorological model in order to improve the dynamics of continental waters over the Garonne catchment, one of the major French catchments. The aim of this paper is to demonstrate that the sequential assimilation of SWOT-like river depths allows the correction of river bed roughness coefficients and thus simulated river depths. An extended Kalman filter is implemented and the data assimilation strategy was applied to four experiments of gradually increasing complexity regarding observation and model error over the 1995–2000 period. With respect to a “true” river state, assimilating river depths allows the proper retrieval of constant and spatially distributed roughness coefficients with a root mean square error of 1 m1/3 s−1, and the estimation of associated river depths. It was also shown that river depth differences can be assimilated, resulting in a higher root mean square error for roughness coefficients with respect to the true river state. Finally, the last experiment shows how one can take into account more realistic sources of SWOT error measurements, in particular the importance of the estimation of the tropospheric water content in the process.
1. Introduction
Surface water storage and fluxes in rivers, lakes, reservoirs, and wetlands are currently poorly observed at global and regional scales, even though they represent major components of the water cycle and impact human societies deeply [1], both in terms of water resources and catastrophic events, such as floods. In situ networks are heterogeneously distributed in space, and many river basins and most lakes–especially in the developing world and in sparsely populated regions–remain unmonitored [2]. The continental water cycle can be formulated in a simple mass balance equation, linking the total water storage variation in time (ΔS) with different water fluxes between the continental surface, the atmosphere, and the underground domain: These are precipitation (P), evapotranspiration (E), the infiltration in the subsurface (I), and the overland flow (Q). The mass balance equation simply assumes that the total water storage variation, ΔS, is equal to the precipitation, P, from which are subtracted the terms, E, Q, and I. Altimetry products from remote sensing are increasingly used for the monitoring of these hydrological cycle components [3,4,5]. Several altimetric satellites have been launched in the past to measure water surface elevations, among which ERS-1 (1991–2000), TOPEX/Poseidon (1992–2006), ERS-2 (1995–2003), Jason-1 (2001–2013), Envisat (2002–2012), Cryosat-2 (2010–now), SARAL (2013–now), Sentinel-3 (2016–now), and Jason-3 (2016–now). They provide repetitive water elevation measurements on a global scale, something which is particularly important for ungauged basins. They do, however, have many limitations, such as a longer revisit time (between 10 and 35 days [6]), and coarse spatial resolution. The instruments’ footprints are several square km and they are only observed from their nadir (from the vertical of the satellite). Among them, the CryoSat-2 mission, launched in 2010, offers a very dense spatial sampling pattern with an across-track distance of only 7.5 km, but with a drifting ground track and a full repeat cycle of 369 days [7]. To overcome these limitations, a new satellite mission based on SAR (synthetic aperture radar) interferometry was proposed: This was called WATER (Water and Terrestrial Elevation Recovery), providing water elevation maps for two 50 km swaths [8]. In 2007, the National Research Council recommended this new satellite mission to NASA (The National Aeronautics and Space Administration), under the name SWOT (Surface and Ocean Topography), to measure both the ocean and land water surface topography. This new mission, conjointly developed by NASA, CNES (Centre National d’Etudes Spatiales), CSA/ASC (Canadian Space Agency/Agence Spatiale Canadienne), and UKSA (United-Kindom Space Agency), is planned for launch in 2021 and will observe the whole continental water-estuaries-ocean continuum. SWOT is designed to observe a large fraction of rivers and lakes globally and will provide observations of their seasonal cycles. SWOT will be the first altimetry mission to provide a quasi-global coverage of continental surfaces between 78° S and 78° N. Especially, it is designed to observe big and intermediate (or regional)-scale basins (i.e., 50,000–200,000 km2 drainage area) in 21 days, the duration of a full orbital cycle [9]. Water level measurement errors are expected to be 10 cm aggregating pixels over a 1 km2 water area (e.g., a 10-km reach length for a 100-m-wide river) [10]. This offers a new opportunity for the linking of open water surface elevations, land surface processes, and meteorology more closely on this scale. The SWOT mission will provide relevant information on the temporal evolution of the surface water storage. This information will allow a better understanding of the term, Q, both spatially and temporally, playing an important role in the mass balance equation.
DA (data assimilation) techniques are increasingly used by hydrologists to improve the performance of numerical models. The DA techniques are used to correct either the model parameters and/or the model state. The merits of remotely sensed DA have been shown in various studies. GRACE (Gravity Recovery And Climate Experiment) data were used on total water storage over the Mississipi river to improve the soil water content and different water fluxes in the basin [11]. In the field of wide swath altimetry, synthetic SWOT data were assimilated in the Arctic Ob River in Siberia to improve water elevation and discharge [12]: The combination of hydrologic and hydraulic models with the SWOT data allowed better description of temporal variations of open water surface elevations. At a large scale catchment, synthetic SWOT data were assimilated in the Niger basin to correct the roughness coefficient of the river bed, in order to better represent river discharge and flood plain dynamics [13]. These examples demonstrate the strong capability of spatialized satellite information to improve our knowledge of the continental hydrological cycle. Wide swath altimetry measurements made by the SWOT satellite mission will provide the potential for high-resolution characterization of open water surface elevations and will contribute to a fundamental understanding of the global water cycle by providing global measurements of terrestrial surface water storage changes and discharge.
In the specific context of SWOT pre-launch studies, most studies focused on big river basins to investigate the benefits of SWOT for hydrology modeling (e.g., [12,13]). The present paper aims to focus on a regional scale. The time evolution of physical processes is faster, and it is important to analyze whether or not the information given by SWOT will be able to improve our understanding of the hydrological cycle on this spatial and temporal scale. The ability of a regional hydrometeorological model to simulate river depths comparable with the future SWOT open surface water elevation observations was assessed [14]; the same model is used in the current study. The river depth is equal to the vertical distance between the river bed and the open surface water elevation of the river. The distributed ISBA/MODCOU (Interaction Soil Biosphere Atmosphere/MODèle COUplé) model was used over the Garonne catchment, taking into account a variable flow velocity in the river channel. This kinematic wave formulation is used in the present study in the form of the Manning-Strickler equations, derived from the full Saint-Venant equation system. It takes into consideration that there is no diffusion of the flood wave from upstream to downstream in the river. In the present study, synthetic SWOT-like data are assimilated into a regional scale hydrological model over the Garonne catchment in the South-West of France. The study is based on the previous numerical developments for the implementation of data assimilation achieved on the Niger basin (2,118,000 km2) [13], but focuses on a smaller basin (Garonne, 56,000 km2) located in another climatic region. The present study uses a different hydrological model, which has a much higher spatial resolution and a much more ramified river network than other studies (e.g., [13]).
This work is carried out in the framework of OSSE (observing system simulation experiment) with the ISBA/MODCOU hydrometeorological model to prepare future exploitation of the SWOT data. The paper is divided into five sections. Section 2 presents the Garonne catchment and the ISBA/MODCOU model that simulated river depths. The DA strategy is developed in Section 3: A short description of the SWOT mission is given, the OSSE framework is explained, and the filtering data assimilation algorithm is presented along with its implementation. Results are presented in Section 4 on four different experimental settings. Conclusions and perspectives concerning the DA strategy and link with the SWOT mission are finally given in Section 5.
2. Catchment and Hydrological Model Description
2.1. The Garonne River Catchment
The study is carried out over the Garonne River catchment (Figure 1). The Garonne catchment is one of the major catchments in France (56,000 km²) with a river width ranging from 150 m in Toulouse to 300 m near Bordeaux. It is located in southwestern France and drains the northern slopes of the Pyrenees chain (along the French border with Spain). The Pyrenees and the Massif Central mountains border the basin to the south and the east, respectively. The main tributaries of the Garonne river are the Tarn and Lot rivers. The climate over the basin is under the influence of oceanic conditions over the western part of the domain, characterized by heavy rainfall events during winter and relatively warm weather during summer. There is a significant precipitation gradient from west to east, ranging from approximately 1200 mm year −1 over the Atlantic coastal region to about 600 mm year−1 in the eastern part of the catchment. The upper Garonne and the Ariège rivers regime are characterized by spring snow melt in the Pyrenees [15], while summer flows are very low due to relatively dry summers.
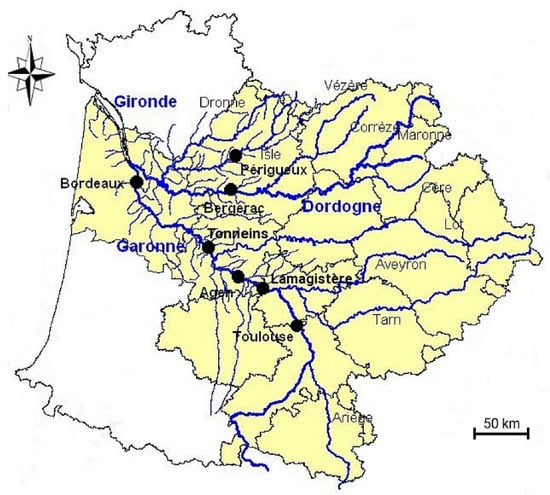
Figure 1.
The Garonne catchment with the names of main rivers (blue) and tributaries (black), and the names of main cities (dark black).
2.2. The ISBA/MODCOU Hydrological Model
The ISBA land surface model [16] within the SURFEX (SURFface EXternalisée) platform is used to simulate the physical variables every 3 h in the upper soil, soil surface, and vegetation and to simulate water and energy exchanges within the soil–surface–atmosphere continuum [17]. Its parameters are derived from the ECOCLIMAP-II ecosystems and surface parameters database [18] at a 1-km resolution. ISBA is forced every 3 h by the SAFRAN (Système d’Analyse Fournissant des Renseignements Adaptés à la Nivologie) meteorological analysis [19]. ISBA uses a multilayer approach to solve the one-dimensional Fourier law and the mixed form of the Richards equation explicitly in order to calculate the time evolution of the soil energy and water budgets [20,21]. In terms of hydrology, the soil water balance accounts for infiltration, land surface evapotranspiration, and total runoff. The infiltration rate is provided by the difference between the through fall rate and the surface runoff. The throughfall rate is the sum of the rainfall not intercepted by the canopy, the dripping from the interception reservoir, and the snowmelt from the snowpack [22]. The total runoff is composed of the surface runoff, a lateral subsurface flow in the topsoil, and a free drainage condition at the bottom of the hydrological soil column.
The hydrological and hydrogeological model platform, MODCOU, routes the continental surface water into the river. The surface runoff simulated by ISBA is transferred to the river by the ISO (ISOchrone transfer module) [23]. Water is then routed within the river by the parallel-computing-based RAPID module [24,25], with a spatial resolution of 1 or 2 km. MODCOU is the name given to the full platform with its two components, ISO and RAPID. The kinematic wave method is used for the river transfer routing RAPID, with the implementation of the Manning-Strickler equations. The equation linking the river depth and the roughness coefficient is the following (Equation (1)):
where h is the river depth (m), Kstr is the Strickler coefficient (m3 s−1), Q is the discharge (m3 s−1), W is the width (m), and So is the bed slope (-). The formulation is derived from the full Saint-Venant equation system, and supposes that the bed slope, So, of the river bed is entirely compensated by the friction slope, Sf. Thus, So = Sf means that there is no diffusion, but a simple translation in the time of the flood wave along the river channel. The Kstr coefficients are supposed to be constant over time and are spatially distributed for each grid cell of the model. The bed slopes, So, are calculated from the Digital Elevation Model SRTM 90 m [26] in the full river network of the Garonne catchment. The discharge regime is permanent and uniform in each grid cell of the model, where the values of the water storage, the discharge, and the river depth simulation are solved with a «Runge-Kutta order 4» method to prevent numerical bias caused by the nonlinearity of the Manning-Strickler formula [27]. This routing method is used in global hydrological models (e.g., in the TRIP model [27,28,29]) or in the regional ISBA/MODCOU model [14]. In the present paper, a time step of 300 s is chosen for the river routing. The geometry of the river channel is assumed to be rectangular. This approximation is based on the assumption that using rectangular or trapezoidal river channel cross-sections leads to close results in term of water depth [14]: in the Garonne river at Tonneins, by imposing discharge values ranging from 0 to 1500 m3 s−1 and considering a low angle (30°) between the river banks and the vertical plane, the river depth difference between the rectangular and trapezoidal channel does not exceed 3 cm for high discharge values. By using a high angle (60°), the river depth difference is about 8 cm for a high discharge regime. This means that simulated river depths in RAPID are slightly overestimated for large flows in comparison with a high angle trapezoidal geometry.
3. Assimilation of Synthetic SWOT Data in ISBA/MODCOU: Experimental Design
3.1. The SWOT Mission
The observation of water elevations from space provides important information for many physical processes in hydrology. In the continental domain, the open water surface elevations of lakes and rivers can be observed by altimetry satellites. The SWOT mission (the launch of which is expected in 2021) is a wide swath altimetry mission able to measure the spatial and temporal evolution of the open water surface elevation of oceans, lakes and reservoirs, and rivers on the continental surface between 78° S and 78° N [1]. The nominal SWOT mission lifetime is 3 years. The principal SWOT payload is the SAR (Synthetic Aperture Radar) KaRIN (Ka-band Radar INterferometer), developed at the JPL (Jet Propulsion Laboratory). The instrument has two antennas separated by a baseline distance of 10 m (Figure 2a): By observing the same area from two different positions, the estimation of the elevation and the position of the target can be deducted. Each swath, from either side of the nadir area, is 50 km wide and they are separated by a distance of 20 km.
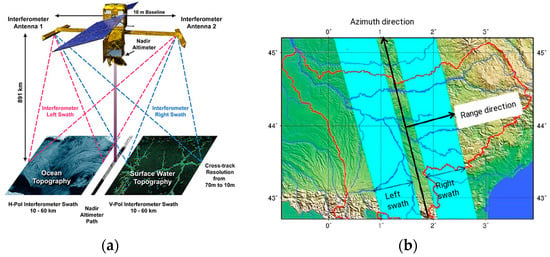
Figure 2.
(a) Illustration of SWOT (© NASA-http://swot.jpl.nasa.gov/): The widths of the two rectangles represent two swaths of 50 km wide, observed by the two antennas of the satellite. They can observe either ocean or continental open water surfaces. (b) Illustration of the left and right swaths of SWOT, with the range direction perpendicular to the satellite track (which is the azimuth direction).
The SWOT’s orbit will be at an 891-km altitude, have a 77.6° inclination, and function with a 21-day repeat period (the satellite flies over the same track every 21 days). Only 3.6% of the continental surfaces between 78° S and 78° N will be never observed by SWOT [1]. The observed variables over continents will be open water surface elevations maps, the surface slope, and the width of the river. The satellite will be designed to observe rivers wider than 100 m (requirement), with the goal being to observe rivers wider than 50 m [10]. In this study, water elevations correspond to the distance between the top of the surface water body and a reference surface, such as a geoid or an ellipsoid. The spatial resolution of the SWOT radar image in the range direction is 60 m for the near range of the swath and 10 m for the far range of the swath (Figure 2a). It is around 5 m in the azimuth direction: The range direction is perpendicular to the propagation axis of the satellite, and the azimuth direction is parallel to the propagation axis of the satellite (Figure 2b). At this resolution, however, the vertical accuracy of the instrument could be several meters. This accuracy tends to increase when water pixels are averaged together. The requirement for the measurement is to acquire a 10 cm vertical precision on water elevation, having averaged over 1 km² of the water area [10]. Measurement errors can be systematic or unsystematic. Unsystematic errors correspond to random errors (this, for example, is the case of errors induced by the instrument thermal noise). Systematic errors correspond to other sources of errors (such as errors induced by the atmosphere on the propagation of the signal emitted by SWOT). For many catchments in the world, only a few locations are sampled by in situ gauges. SWOT data will thus allow us to better understand the spatial and temporal evolution of open surface water elevations. SWOT will be the first wide-swath altimetry mission specifically designed to observe continental surfaces, providing maps of water elevations over regional-scale basins. SWOT will observe most areas between two and eight times during each 21-day repeat period, with the number of observations primarily depending on the distance from the equator [9]. The Garonne catchment will be observed from zero to four times per cycle, thanks to the satellite swaths, allowing several observations per cycle in most regions of the basin. However, due to these swaths overlapping, for locations with more than one observation per cycle, the temporal sampling between these observations will not be constant within a cycle. The number of observations inside one DA cycle, however, will be always the same: The distribution of the river reach observations in the catchment during one cycle will be shown in Section 3.4.1.
3.2. Data Assimilation Algorithm and SWOT Observing System Simulation Experiment
The EKF (Extended Kalman Filter) was successfully employed in previous SWOT-related work over the Niger basin using ISBA/TRIP (Total Runoff Integrated Pathway) for model parameter correction, specifically friction coefficients [13]. This algorithm is well adapted for a weakly non-linear relation between the model outputs (noted y) and the DA control parameters to be corrected. EKF is used here over the Garonne basin to assimilate synthetic SWOT river depth observations in the RAPID module of the hydrological model, ISBA/MODCOU, to correct Strickler coefficients, Kstr (noted x). Based on initial values of x, known as the background vector, xb, the analyzed parameters, xa, are calculated from Equation (2) [30]. We call “increment” the difference in value between the background, xb, and the analysis, xa.
where B and R are, respectively, the model error matrix and the observation model error matrix, yo represents the observation vector (river depth or river depth difference as a function of the experiment, see results). H is the observation operator that maps the control vector onto the observation space, it is the composition of the hydrometeorological model integration and the extraction of output values at observation time and space. H is the Jacobian matrix of H, calculated by using a finite difference scheme. It is a linear approximation of the observation operator, H [30].
xa = xb + (B−1 + HR−1HT)−1 × HTR−1 × (yo − H(xb))
The EKF method assumes that the system is linear. The following approximation (Equation (3)) should therefore be valid:
To keep the system in the domain of the linearity, the term, Δx, should remain reasonably low, so that the value of the term, H(x + Δx), is near the value of the term, H(x) + . The higher the Δx value, the higher the difference between the left and right term of the equation. The value of Δx should be similar to the maximal difference between xa and xb that we decided to impose on the model, and that we call the «limitation of increment».
By replacing the terms, H and x, in Equation (3) to the river depth, h, and its argument, Kstr, we obtained the following equation (Equation (4)):
Δh should be equal to 0 in the case of a perfect linear model. In practice, it should remain sufficiently small to ensure good accuracy of the DA system.
OSSE are widely used to validate DA algorithms and strategies before working with real-data. They offer a convenient framework for the testing of various hypotheses on observation errors, observation spatial and temporal resolution, model error, the choice of DA algorithm, or the cycling of the analysis. Knowing a SWOT’s orbit and pass plan over a 21-day cycle allows the extraction of SWOT-like data from a reference simulation output of ISBA/MODCOU over the Garonne catchment. The settings of the reference simulation (noted SIM_TRUE, blue box on the top, Figure 3) features unperturbed forcing and parameters resulting from the calibration of a RAPID model with a 1 or 2 km resolution [14]. An error of 10 cm standard deviation is added to the SIM_TRUE outputs to get some virtual SWOT-like observations averaged over a 1 km2 area (blue box on the bottom, Figure 3). This simple hypothesis will be further investigated in Section 4.4. A perturbed set of forcing and parameters, xb, is then used to run the background integration (noted SIM_PERT, red box, Figure 3) in which synthetic SWOT data are assimilated to retrieve the unperturbed forcing and parameters. The analysis branch (noted SIM_ANA, green box, Figure 3) for the control vector, xa, allows then the calculation of the corrected parameters to provide corrected river depths and discharge. The DA analysis is carried out over a sliding time window covering several observation times beyond which a forecast can be issued. The tool used to set up our DA scheme is the Open-PALM (Parallel Assimilation with a Lot of Modularity) software [31,32] developed at CERFACS (Centre Européen de Recherche et Formation Avancée en Calcul Scientifique) and ONERA (Office National d’Etudes et de Recherches Aérospatiales). This software allows the coupling of codes of calculation between them, and in this way, allows the exchange of variables, such as vector or matrix, between these codes. OpenPALM provides a parallel environment based on high performance implementation of the Message Passing Interface standard: This interface is able to perform both data parallelism and task parallelism [33].
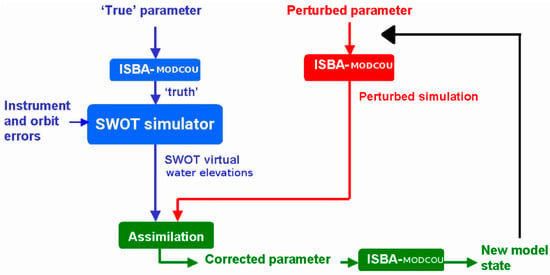
Figure 3.
Schematic illustration of the twin experiment. The red boxes describe the perturbed parameters of the model (SIM_PERT). The blue boxes represent the truth SIM_TRUE (reference simulation) to which white noise is added to generate SWOT-like measurement error. The green boxes represent the corrected parameters of the model after a DA window: We obtained corrected parameters of the model (SIM_ANA) being used for the next DA window (black line), allowing the calculation of new corrected parameters at the next window’s termination.
3.3. Sensitivity of the River Depth to the Roughness Coefficient, Kstr
The sensitivity of the IBSA/MODCOU simulated river depth to a perturbation of the roughness coefficient, Kstr, is illustrated in Figure 4, for one unique grid cell, with typical conditions of a large rectangular plain section of the lower Garonne river. This test case is mono-dimensional, without the need to analyze the consequences of the effect of the Kstr perturbation on the upstream and downstream river depths. Discharge, Q, width, W, and bed slope, So, are equal to 500 m3 s−1, 150 m, and 0.0005 m m−1, respectively. The Kstr values vary between 20 and 40 m1/3 s−1. Figure 4 shows that for a difference of Kstr equal to 5 m1/3 s−1 (between 25 and 30 m1/3 s−1), the river depth variation is about 32 cm. For a difference of 1 m1/3 s−1 (between 25 and 26 m1/3 s−1), the river depth variation is about 6.5 cm. It means that an error of one Strickler coefficient equal to xb − xt = 1 m1/3 s−1 is related to an error of one river depth, H(xb) − H(xt) = 6.5 cm, xt and H(xt) being the true Strickler coefficient and the true river depth. This result must be confirmed on the scale of the Garonne river under various hydrological conditions. In this present idealized test case considering one unique grid cell, the impact of a perturbation of Kstr on the water level is not shown for downstream river grid cells. The results presented in Section 4 allow the study of how changes in the Strickler coefficient values impact the flood dynamics on the full river network of the Garonne catchment.
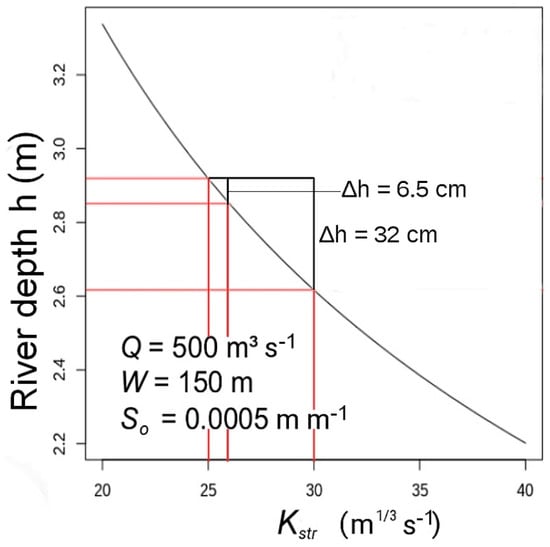
Figure 4.
River depth, h, as a function of the roughness coefficient, Kstr, for a large rectangular river channel, with geomorphological parameters and a discharge value typical of large plain rivers.
In order to verify that the model is close to linearity, we undertook an experiment on a river reach located in the downstream Garonne river: Tonneins (see Figure 1). This reach is representative of the river flows in the plain areas. The study was set up over a period of 6 weeks (between the 15th October and 30th November 1999) with a reference Kstr value of 30 m1/3 s−1. The chosen period experienced strong climate variability with dry and wet periods, allowing the analysis of different ranges of discharge in the selected reach. We imposed four different perturbations to the reference Kstr value and quantified the impact on the left balance term of Equation (4) (averaged value over the full period of study, by considering a daily time step). Table 1 shows that by comparing the four different perturbations, the linear approximation is only valid for small perturbations. In addition, it appears that the model is not symmetric. Hence, it is important to limit the perturbations to +5%, and to impose a maximum increment of 1.5 m1/3 s−1, in order to avoid any instability of the DA system. Table 1 shows that for a perturbation of +/−20%, the system is not at all linear.

Table 1.
Impact of the relative and absolute perturbation of the Kstr reference coefficient on the river depths, h (cm).
3.4. Data Assimilation Experiment Setting
3.4.1. SWOT-Like Observations Generation and Their Processing
The methodology to generate SWOT-like observations has only been very briefly shown in Figure 3 (blue boxes). It is described in more detail in the following paragraphs.
SWOT data are generated using the simple methodology used in previous studies [12,13]. First, SWOT orbit ground tracks crossing the study domain are selected. For each orbit, polygons of SWOT swaths are created. These polygons are used to select all model pixels that lie in these swaths’ polygons, for each observation time during a 21-day repeat period. Then, this pixel’s selection is replicated for all repeat cycles (i.e., 21-day time spans) during the whole study time period. Then, for all observation times and all selected pixels, a noise on water depth is simply added to the reference simulation water depths (SIM_TRUE) to generate SWOT-like data. For the three first experiments, the instrument noise is a white noise with a 10 cm standard deviation, for all selected pixels. A less simplistic additive noise on water depth is computed for the last experiment (see Section 4.4).
With this methodology, all pixels within the river network that lies in the swath polygons could be potentially observed. Yet, SWOT is conceived to observe rivers wider than 100 m (requirement) and could even observe rivers wider than 50 m (goal). To take this limitation into account, only river portions that were wider than 50 m were considered in this study. Furthermore, the 10 cm accuracy on water elevation is only met after aggregating SWOT data over 1 km2 [10]. That is why Strickler coefficients, Kstr, and river depths, h, from the reference simulation are aggregated over 10 km reaches (5 to 10 RAPID grid cells) to meet this requirement, before adding the noise on water depths. The aggregation is operated by averaging the values in the considered grid cells, with a weighting proportional to their length (1 or 2 km). The area of each reach varies from 0.5 to 2 km², knowing that the computed width varies from 50 m to 200 m. A total of 165 reaches (Figure 5a) were constituted. Over the study domain in our experimental set-up, reaches were observed between one and four times per repeat period (Figure 5b).
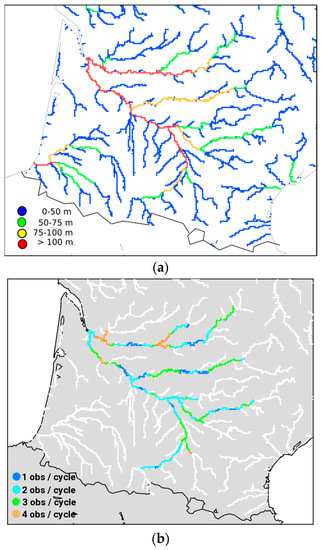
Figure 5.
(a) River widths computed in the DA platform over the Garonne catchment, considering three river width classes where virtual SWOT observations are assimilated; (b) SWOT observation number for a 21-day cycle for every 10-km reaches of the Garonne catchment.
Many sources of errors (orbit errors, SAR interferometry processing errors, impact of the surrounding topography and vegetation, delays induced by the crossing of the atmosphere by the electromagnetic wave) are therefore not considered, as the corresponding errors are not Gaussian.
3.4.2. Description of the Variables Used in the DA Platform
In the DA platform, windows with a duration of 2 to 42 days were tested, as a function of the conditions imposed in the chosen DA experiment (see Section 4). The background vector, xb, contains the 165 Strickler coefficient values for each river reach. The vector, H(xb), contains the 165 river depths simulated by the model for each river reach. The observation vector, yo, contains the p SWOT observations by a DA window. If two examples are taken with five river reaches: p = 10 when these five reaches are observed two times during a DA window, or more complicated: p = 20 when the first reach is observed two times, the second reach is observed three times, and the third, fourth, and fifth reaches are observed five times during the window. It presents a sum of 10 SWOT observations in the first example, and 20 observations in the second. The p value is then a function of the number of SWOT passes across the catchment during one DA window, and of the number of rivers reaches observed during one pass of the satellite. The Jacobian matrix, H, contains the sensitivity of the 165 simulated river depths with a 5% perturbation of the p Strickler coefficients located in the p observed reaches. The value of +5% was chosen due to Sub-Section 3.3 (see also Table 1), having a minor impact on the Δh value calculated in Equation (4), for a typical large plain river. The observation error matrix, R, and the background error matrix, B, are diagonal: R contains the errors of the p river depth observations, associated with p diagonal terms. B contains the errors of the 165 background Strickler coefficients, associated with 165 diagonal terms. According to Sub-Section 3.3, in order to avoid problems of non-linearity, we decided to limit the limitation of increment to 1 m1/3 s−1 in each experiment. The different variables of the Extended Kalman Filter equation (Equation (2)) and their dimension are described in Table 2.

Table 2.
Synthetic description of the variables used in the assimilation equations (symbol, description, and dimension). The p value corresponds to the number of SWOT observations during a DA window.
3.4.3. Description of the Data Assimilation Experiments
We set-up four different DA experiments (Table 3): The goal was to analyze whether the a priori values, xb, of the Strickler coefficient could converge to a stable value and tend to the truth, xt, through the assimilation windows, and if the simulated river depth, H(xb), could be well estimated and tend to the true depth, H(xt). The DA configuration in the first experiment was the same as in previous works related to SWOT DA [13]. In the three following experiments, more realistic experiments were then set up in the DA platform. In the experiments, n° 1, 2 and 4, the chosen period of study was 1995–1998, and 1995–2001 in the experiment, n° 3, three further years were needed to get a full convergence of the system. We will show that the period of study of this third experiment is longer, due to a longer convergence time of the system. During 1995 to 2001, wet and dry periods were observed. The strong climate variability of these years had a direct impact on the discharge: We therefore conclude that it was a good idea to have selected these years for our test case. It allowed us to analyze a wide range of discharge signals. In the following paragraphs, a short description of all four experiments is proposed and synthesized in Table 3.

Table 3.
Synthetic description of the four SWOT DA experiments.
In the first experiment, we assimilated river depths over 48 h duration windows, across a period of three years. The choice of this duration was based on one main argument: The duration corresponds to the time taken by the water to flow from the upstream to the downstream section of the Garonne river observed by SWOT, i.e., from Saint-Gaudens to Bordeaux (see Figure 1). This means that by using a window duration of 48 h, a roughness coefficient perturbation at Saint-Gaudens impacts all river reaches located downstream (until Bordeaux) during this window duration. It was decided that the experiment will commence with a background vector, xb, initialized with values equal to 25 m1/3 s−1. This value corresponded to the averaged reference Strickler coefficient, xt, in the catchment. Each diagonal term, σB2, of the model error matrix, B, contained values equal to the variance of all the xb parameters around the truth, xt, with a minimum value of (1.5 m1/3 s−1)2. Each diagonal term, σR2, of the observation error matrix, R, contained values equal to (10 cm)2.
In the second experiment, we assimilated data over 48 h duration windows by perturbing the amount of runoff and drainage produced by ISBA (increasing or decreasing the production with a bias of ±10%), and tested the impact on the convergence through the assimilation windows. It is important to represent well the atmospheric forcing: In DA, an error of quantification or repartition of precipitation will have a direct impact on the convergence of the parameters to correct, and thus on the quality of the river flow simulation. In this way, it is important to quantify the impact of a forcing error in ISBA on the convergence of the Strickler coefficients. It was decided that the experiment should start with a background vector, xb, initialized with values equal to the reference Strickler parameters on which a Gaussian centered noise, σxb, of 5 m1/3 s−1 was added. Each diagonal term, σB2, of the model error matrix, B, contained values equal to the variance of all the xb parameters around the truth, xt. A minimum value of (1.5 m1/3 s−1)2 was imposed in the DA platform. Note that σxb was always equal to σB when σB ≥ 1.5 m1/3 s−1, and σxb ≤ σB when σB = 1.5 m1/3 s−1. Each diagonal term, σR2, of the observation error matrix, R, contained values equal to (10 cm)2.
In the third experiment, river depth differences were assimilated over a 42-day duration window in the model, considering that the satellite would not observe river depths, but, instead, open water surface elevations. A solution for the use of water surface elevation in our system was to assimilate the water surface elevation difference, δh, between two consecutive observations, which was equal to the river depth difference. In order to assimilate δh in the model, two or more river depth observations in one DA window were required. One can imagine two different scenarios:
- In a DA window, there are zero or one river depth observations: It is impossible to assimilate a δh term; and
- In a DA window, there are n observations (n ≥ 2): It is possible to assimilate n − 1 δh terms.
To respect the case, n° 2, for all reaches of the Garonne basin, we decided to extend the assimilation window to 42 days, to be sure that at least two observations were present for each reach in the assimilation window. It was decided to start the experiment with a background vector, xb, initialized with values equal to the reference Strickler parameters on which a Gaussian centered noise, σxb, of 5 m1/3 s−1 was added. Each diagonal term, σB2, of the model error matrix, B, contained values equal to the variance of all the xb parameters around the truth, xt. A minimum value of (2.12 m1/3 s−1)2 was imposed in the DA platform. Each diagonal term, σR2, of the observation error matrix, R, contained values equal to (14.1 cm)2.
In the fourth experiment, we increased the realism of the SWOT error measurement, by implementing time-and-space variable errors of observation: Each diagonal term, σR2, of the observation error matrix, R, contained values varying for every reach at each DA window. Data were assimilated over a 48 h duration window. The decision was made to start the experiment with a background vector, xb, initialized with values equal to the reference Strickler parameters on which a Gaussian centered noise, σxb, of 5 m1/3 s−1 was added. Each diagonal term, σB2, of the model error matrix, B, contained values equal to the variance of all the xb parameters around the truth, xt. A minimum value of (1.5 m1/3 s−1)2 was imposed in the DA platform.
Note that the common criterion for the comparison of these four different DA experiments is the quality of the convergence of the Strickler coefficients, Kstr, to the truth, xt. The convergence time of the Kstr is irrelevant for the comparison between the four experiments, because the duration of the DA windows, the first guess, xb, of the Kstr at the beginning of the experiment, and the attribution of the diagonal terms in the R and B matrices vary in function to the experiment.
4. Results
4.1. Assimilation of River Depths (Experiment 1)
We decided in this first DA experiment to impose a minimum value of the diagonal terms, σB2, in the B matrix to (1.5 m1/3 s−1)2: When the values are too low (<(1 m1/3 s−1)2), the convergence of the terms (xb − xt) to the truth, xt, is complicated, because the analysis is closer to the background than the observation (for the EKF, there are fewer uncertainties in the background than in the observation). This limitation criterion thus improves the convergence of the terms (xb − xt) to the truth, xt. Concerning the value of the increment (xa − xb), when no limitation is imposed, the values of the terms (xb – xt) of the DA system are very high in the first windows (between −40 to +70 m1/3 s−1), and the convergence time is about 800 days. When a limitation of increment of 5 m1/3 s−1 is imposed, the values of the terms (xb – xt) of the DA system during the early windows are between -40 and +30m1/3 s−1until 100 days of assimilation, and the convergence to the truth occurs after 240 days. In the current experiment illustrated in Figure 6, the majority of the Kstr values converge to the truth after 700 days of assimilation, considering a limitation of increment fixed to 1 m1/3 s−1. We consider that the Strickler coefficient convergence to the truth, xt, is reached when the standard deviation, σxb, between all (xb − xt) values is equal or lower than 1 m1/3 s−1.
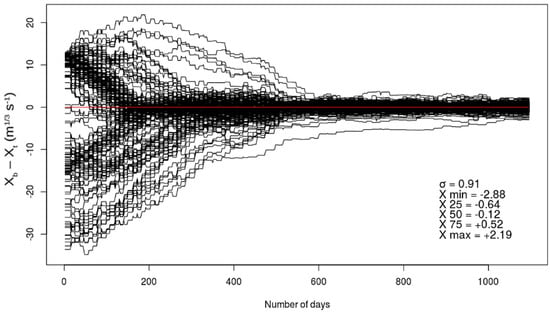
Figure 6.
Temporal evolution (1 August 1995 to 31 July 1998) of the difference between the a priori control vector (xb) and the true control vector (xt) of the Strickler coefficients in the DA system. The 165 black curves represent the value (xb − xt) at all 165 reaches defined over the Garonne catchment. The red horizontal line is equivalent to a zero difference between xb and xt. After 3 years (i.e., 548 48 h-assimilation windows), we represent the standard deviation, σxb, between the 165 values (xb − xt) in the basin. The X terms represent, from top to bottom, the minimum value, the 1st quartile, the 2nd quartile, the median, the 3rd quartile, and the maximum value of (xb − xt) at the end of the experiment (day n° 1096).
In Figure 7, we show the time evolution of the simulated and the true river depth for the reaches of Lamagistère (a) and Bergerac (b) located, respectively, in the downstream Garonne and Dordogne river (see Figure 1). We have chosen these two reaches, firstly because they are representative of plain rivers where SWOT will provide observations, and secondly because their initial Strickler coefficient in the DA system is far from the truth, xt.
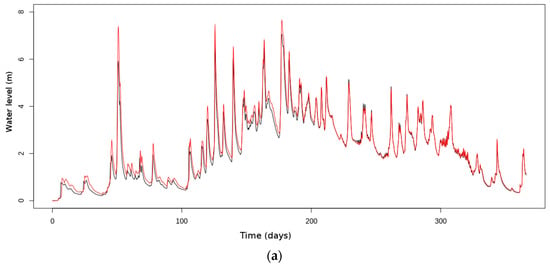
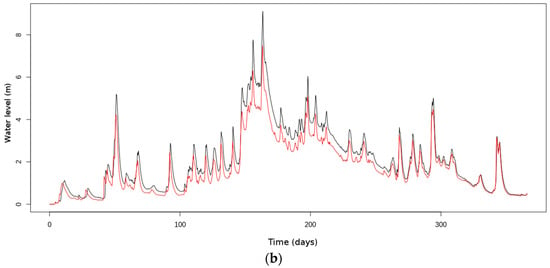
Figure 7.
Temporal evolution of the river depth at Lamagistère (a) and Bergerac (b), over the period of 1 August 1995 to 31 July 1996. Black curves correspond to the truth and red curves are the result from the assimilation of the river depth.
At Lamagistère, the initial value was 25 m1/3 s−1, while the true value was 38.7 m1/3 s−1. The simulated river depth, H(xb), before SWOT data assimilation was then higher than the true river depth H(xt), with a positive difference of about 20 cm in normal flow, and more than 80 cm during flood periods. The average true river depth, H(xt), over the full period of study (365 days) was equal to 2.11 m, with peak values up until 7.5 m. Furthermore, at the beginning of the experiment, the river flow velocity at Lamagistère and upstream was too low (due to low xb values compared to xt): The temporal delay between the river depth time series before assimilation and the true time series was negative (with about one day of delay).
At Bergerac, the case was the opposite: We started the experiment with a Strickler coefficient value higher than the truth, xt (positive difference of 7.5 m1/3 s−1), which was equal to 17.5 m1/3 s−1: The relative difference between the first xb value and xt was equal to +42.9%. The simulated river depth, H(xb), before SWOT data assimilation was then lower than the true river depth, H(xt), with a negative difference of 20–30 cm in normal flow, and more than 1 m during flood periods. The average true river depth, H(xt), over the full period of study (365 days) was equal to 2.10 m, with peak values up to 9 m. Furthermore, at the beginning of the experiment, the river flow velocity at Bergerac and upstream was too high (due to high xb values compared to xt): The delay between the river depth time series before assimilation and the true time series was positive (with about one day of advance).
For Lamagistère and Bergerac after 365 days of SWOT data assimilation, both the phasing and signals between H(xb) and H(xt) were improved: The time difference between the arrival of one H(xb) peak and one H(xt) peak was less than 3 h, and the difference between H(xb) and H(xt) was inferior to 10 cm for every discharge regime.
4.2. Assimilation of River Depths, in case of Atmospheric Forcing Biases (Experiment 2)
In this experiment, we propose two different scenarios. In the first (a), the water produced by ISBA (runoff + drainage) is decreased by 10%. In the second scenario (b), the water produced by ISBA is increased by 10%. The main goal of the experiment is to analyze what the impact of these errors on the Strickler coefficient convergence is. The effect of the over-production of water in the river is the following: The DA system will tend to increase the Kstr values to decrease the river depth. The effect of an under-production of water in the river is the opposite: The DA system will decrease the Kstr values to increase the river depth. The illustration in Figure 8 shows that after about 1000 days of assimilation, the Strickler coefficient values converge to a stable state, but differ from the true xt with an average bias of −1.56 m1/3 s−1 in scenario (a), and an average bias of +1.83 m1/3 s−1 in scenario (b). For a water production bias of +10% or −10%, we showed that the impact on the terms (xb − xt) at the end of the DA experiment was inferior to 2 m1/3 s−1, having a minor impact on the flow velocity (phasing delay of 3 h at Tonneins between the “true” hydrograph and the “analyzed” hydrograph).
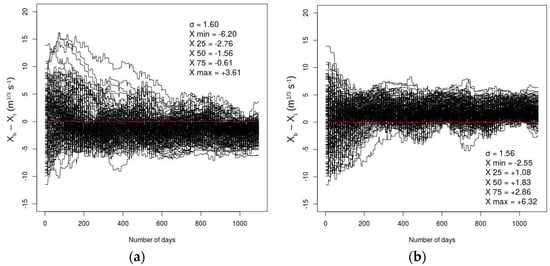
Figure 8.
Temporal evolution (1 August 1995 to 31 July 1998) of the difference between the a priori control vector (xb) and the true control vector (xt) of the Strickler coefficients in the DA system. Scenario (a) represents a −10% perturbation of water produced by ISBA, and scenario (b) represents a +10% perturbation. The 165 black curves represent the value (xb − xt) of all 165 reaches defined over the Garonne catchment. The red horizontal line is equivalent to a zero difference between xb and xt. After 3 years (i.e., 548 48 h-assimilation windows), we represent the standard deviation, σxb, between the 165 values (xb − xt) in the basin. The X terms represent from top to bottom the minimum value, the 1st quartile, the 2nd quartile, the median, the 3rd quartile, and the maximum value of (xb − xt) at the end of the experiment (day n° 1096).
4.3. Assimilation or River Depth Differences (Experiment 3)
In previous experiments, only observed river depths have been considered. To obtain river depths from SWOT surface elevations, it is required to know a priori the river bathymetry, or at least to get some estimates of the river bed elevation. To overcome this stringent assumption, assimilation of river elevation differences (equal to river depths differences) is tested in this experiment.
The variance of the observation error for two consecutive observations, ht and ht+1, follows Equation (5):
Assuming that two consecutive observation errors are not correlated and that the SWOT error is 10 cm (standard deviation), cov(ht, ht+1) = 0 and the observation error (Var(ht+1 − ht))1/2 thus becomes σR = 14.1 cm.
To keep the same ratio between the diagonal terms, σR and σB (see Equation (6)), of the two matrix, R and B (as the experiments detailed in the Section 4.1 and Section 4.2), the minimum value of σB is now fixed to 2.12 m1/3 s−1. This value is calculated from the diagonal terms, σB, equal to 1.5 m1/3 s−1 in the B matrix used in the two previous experiments. We show in Figure 9 the temporal evolution of the terms (xb − xt) for all reaches in the basin.
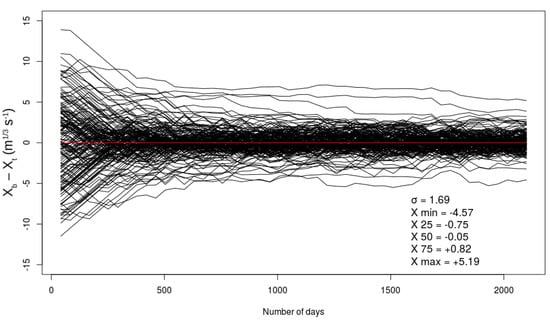
Figure 9.
Temporal evolution (1 August 1995 to 15 April 2001) of the difference between the a priori control vector (xb) and the true control vector (xt) of the Strickler coefficients in the DA system. The 165 black curves represent the value (xb − xt) at all 165 reaches defined over the Garonne catchment. The red horizontal line is equivalent to a zero difference between xb and xt. After 5 years (i.e., 50 42 day-assimilation windows), we represent the standard deviation, σxb, between the 165 values (xb − xt) in the basin. The X terms represent from top to bottom the minimum value, the 1st quartile, the 2nd quartile, the median, the 3rd quartile, and the maximum value of (xb − xt) at the end of the experiment (day n° 2100).
After 15 DA windows (2 years or 750 days), the majority of the Strickler coefficients in the DA system converged to the truth, xt. The convergence of four reaches occur more slowly: One plausible hypothesis is that the observation error is on average larger than for the other reaches, driven by the random Gaussian noise, σR, which can be lower or higher than 14.1 cm across the full study period. There are only 50 DA windows in this experiment, and the impact of σR on the convergence of xb is different for one given reach after these 50 windows, when the experiment is remade. After 50 windows or 2100 days of assimilation, the standard deviation, σxb, of all (xb − xt) terms is about 1.70 m1/3 s−1: This value is bigger than the σxb value presented in the first experiment (Section 4.1), because the diagonal terms, σR2 and σB2, imposed in the observation error matrix, R, and the model error matrix, B, are more significant.
4.4. Assimilation of River Depths Considering More Realistic SWOT Errors (Experiment 4)
In this experiment, the diagonal terms, σR, in the observation error matrix, R, vary in space and time (at each DA window). The total error (taking into account the variable and constant errors averaged in time and space) should be equal to 10 cm, and is composed of systematic and non-systematic errors [10]. The non-systematic errors are random and Gaussian, and the systematic errors are constant (see Section 3.1). We are able to approximate by a very simple method the different sources of instrumental error contributing to the changing of the SWOT error measurement values in space and time. Four factors with an impact on the diagonal term values, σR, of the observation error matrix, R, are introduced, allowing σR to vary at each time step and for every river reach. The first three factors (non-systematic source of errors) are: The surface of the reach, the SWOT look angle, and the radar water surface roughness. The calculation of these simple instrumental-like errors is based on previous works [34]. The last factor having an impact on the σR of the R matrix is the wet-troposphere error (systematic source of errors). This error is estimated in this study by the intra-day variability of water content in the troposphere. There are other sources of errors, more difficult to quantify, but they should have a lower impact on the total error budget at the reach scale: They are the ionosphere signal, the dry troposphere signal, the orbit radial component, and the KaRIn random and systematic errors after cross-over corrections. Table 4 summarizes the SWOT error budget [35], after averaging a 1 km² area [10]. It is important to note that all the equations used to calculate these different sources of instrumental errors are greatly simplified, the more realistic and complex full radar equations are not used in our study. The main goal of this fourth experiment is to take into account errors of measurement more realistic than simple Gaussian errors of 10 cm, but it is important to keep in mind that these errors are simplified compared to the detailed error budget calculated by the SWOT simulator used by the JPL and the CNES (see [36]).

Table 4.
SWOT error measurement allocation [35], after averaging over a 1 km² area [10]. The left column represents the error component, and the right column represents the values of these errors.
4.4.1. SWOT Instrumental Error along the Swath
The SWOT error measurement is linked to the surface of the observed reach: It is a non-systematic source of error. When several raw SWOT radar images are averaged over a bigger area, the error decreases with the squared root of the number of raw SWOT radar images [10]. The surface of the reach is proportional to the width, W. When the river width decreases, the error increases because the observed surface by the satellite is lower. Furthermore, the measurement errors increase with the look angle of the satellite because the surface of the raw SWOT radar image is not the same: 70 m × 5 m for the far range image, and 10 m × 5 m for the near range image (see Section 3.1). These measurement errors then vary along the swath. Based on previous works developping a simple algorithm for calculating the sensitivity of the measurement error as a function of the river width and the look angle of the satellite [34], the SWOT look angle will vary from 0.6° to 4.3°, corresponding, respectively, to the inner and outer board of each swath.
The roughness of the open water surface will determine the amount of energy reflected to the satellite and will thus impact SWOT’s error budget. In our case study, the roughness is simulated very simply, considering that it depends only on the wind velocity, and was previously validated over the ocean domain only (see [34]). Even if the important complexity of these sources of errors is not considered well, the goal for our study is to consider the main processes and to understand how the measurement errors vary along the swath. In Figure 10, we show the sensitivity of the error we considered in our study to the wind speed near the water surface, considering a river reach 10 km long and 100 m wide. Over the full period of 1 August 1995–31 July 1998, 75% of the wind speed values are between 0 and 3 m s−1. Wind speed values higher than 8 m s−1 are rare, representing about 1% of all wind speed values over the study period. The wind speeds correspond to SAFRAN reanalysis data at 10 m (3-h time step) averaged over a 10 min period.
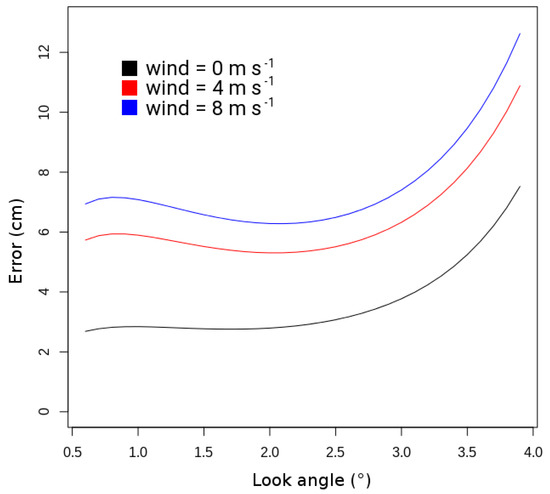
Figure 10.
SWOT error measurement as a function of the look angle for a wind speed of 0 m s−1, 4 m s−1, or 8 m s−1.
4.4.2. The Intra-Day Variability of Water Content in the Troposphere: Impact on the SWOT Error of Measurement
According to previous works [35], the estimation of the wet troposphere error is about 4 cm (Table 4). Water content changes in the troposphere have a direct impact on the velocity of electromagnetic waves. Numerical atmospheric models are able to produce a correction of the wet troposphere error. The water content simulated by models in the atmosphere, however, also shows an error. Several studies have looked at the impact of errors in meteorological model outputs or in in situ observations concerning the representation of water content in the troposphere [37,38]: These errors of the atmospheric state should be considered to determine the error on the measured open water surface elevation. We would like to base our study on previous works showing that it is more difficult to quantify the water content in a transition meteorological period than during a stable period [39]: We have defined a transition period equivalent to an interval of time with an important variability of the troposphere state, and a stable period equivalent to an interval of time with a low variability of the troposphere state. The variable chosen to describe this temporal variability is the water content, and the chosen interval of time is 24 h: This time value is well representative of the meteorological variability, especially in summer with important changes of the troposphere state during a full 24-h period (important contrasts between day and night). The SAFRAN reanalysis data of water content (g kg−1) at 10 m (3-h time step) are used to calculate intra-day variances Vi (g kg−1)2 across the study period 1 August 1995–31 July 1998. Considering the 165 river reaches of the DA platform over the full study period, a simple relationship between the intra-day variance of water content, Vi, and the SWOT error measurement, σR, is set up: The greater Vi, the greater the measurement error. We would like to build a linear relationship between Vi and σR. Once the relationship between Vi and σR is established, one can attribute a SWOT error measurement error, σR, at each time step for every river reach of the catchment. The slope of the function linking Vi and σR is equal to 6.67 cm/(g kg−1)2. This relationship is based on the assumption that the spatial and temporal averaged wet troposphere error is equal to 4.0 cm (see Table 4), and that the full spatio-temporal SAFRAN reanalysis data distribution of water content is well-known in each river grid cell of the catchment. Eighty percent of the Vi values range between 0 and 1 (g kg−1)2. Values higher than 3 (g kg−1)2 are rare, representing about 1% of all Vi values over the full study period.
4.4.3. SWOT DA Experiment Using Realistic Errors of Measurement
Considering the sensitivity of the SWOT measurement error to the two described errors in Section 4.4.1 and Section 4.4.2, it is possible to conduct this last experiment with slightly more realistic errors. The observation error matrix, R, is built considering the two sources of errors described in Section 4.4.1 and Section 4.4.2: Each term, σR, varies at each time step of the experiment for every river reach, and the spatio-temporal average of σR over the full period of the study and domain is equal to 10 cm. After 365 days of assimilation, the majority of the parameters converges to the truth, xt, with a standard deviation of ~1 m1/3 s−1. During the DA windows n° 259 and 448, and 518 and 896 days of assimilation, the standard deviation, σxb, between all (xb − xt) values decreases, respectively, to 0.76 and 0.79 m1/3 s−1 (Figure 11). To understand these low values, we analyzed the temporal evolution of the Vi variable over the full study period: It showed that during the winter months the values of Vi are equal to 0.5 (g kg−1)2 on average (the days 518 and 896 of this experiment are in the winter season), and 1.5 (g kg−1)2 on average during the summer months. The low values of Vi during the winter season lead to low SWOT error measurements, σR, and then to a better convergence of the Kstr values to the truth, xt. The convergence time of this DA experiment is around 600 days when the xb values of each reaches convergence at the truth, xt.
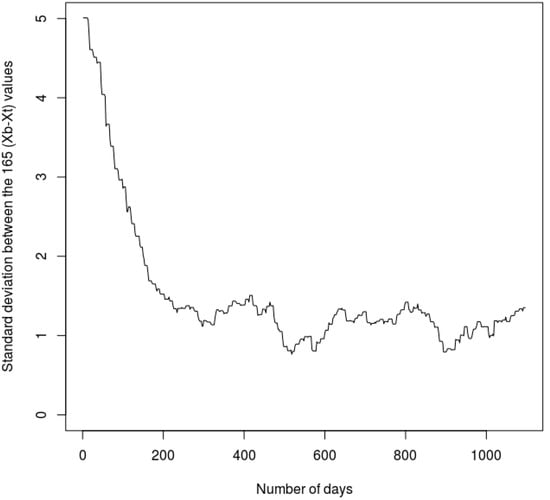
Figure 11.
Temporal evolution of the standard deviation, σ, between the 165 (xb − xt) terms, over the 1 August 1995–31 July 1998 period.
5. Conclusion and Perspectives
This study is a contribution to the building of a DA scheme over the Garonne basin within the framework of the SWOT mission. More precisely, the objective of this study was to evaluate the ability of a regional hydrometeorological model to assimilate synthetic SWOT river depths in the Garonne catchment, and to correct the Strickler roughness coefficient, Kstr, of the river bed.
In every experiment, we showed the ability of the DA system to calibrate the Kstr parameter around the known truth. In the first experiment, we showed that the parameters converge to the truth after ~2 years, with an average error of ±1 m1/3 s−1, and with an associated average error on river depths of ±5 cm. The choice of the maximum increment value (the difference between the analysis, xa, and the a priori value of the Strickler coefficient, xb) has an impact on the time of convergence. In the second experiment, we showed the importance of the atmospheric forcing and its impact on the convergence of the Kstr parameters. An error of ±10% water produced by ISBA led to an error of ±1.5 m1/3 s−1, but had a minor impact on the river flows. The impact of greater errors on the discharge phasing should be taken in consideration. The third experiment illustrated the interest of assimilating the difference of river depths instead of absolute open surface water elevations that are equivalent to river depths in our study. The bathymetry elevation is unknown in RAPID, and the satellite will not provide measurements of river depths. The duration of a DA window should be equal to 42 days, in order to be sure that every reach is observed at least two times during one DA window. The quality of the convergence (±1.69 m1/3 s−1) was slightly lower in comparison with the first experiment, but the time of convergence was equivalent (~2 years). In the last experiment, we proposed the introduction of more realistic SWOT error measurements varying in time and space, which depended on the surface of the observed reach, the look angle of the satellite, the surface water roughness, and the intra-day variability of the water content in the troposphere. The impact of the last factor seems to play an important role: The convergence was on average better during the winter months than during the summer months, because of a low temporal variability of the troposphere water content.
Several points concerning data assimilation in the context of the SWOT mission could be explored. The four main ones are as follows:
5.1. The Choice of the Data Assimilation Method and the Experimental Design
The main goal of each presented experiment in Section 4 was to calibrate the Strickler coefficients to converge them to the truth, in the context of twin experiments. The choice of the EKF requires the use of the hydrological river routing model, RAPID, in the domain of the linearity. It has its limitations: The perturbation of the parameters we want to correct (roughness coefficient) should be small, and they require limited increment values (a maximum difference between the first guess, xb, and the analysis, xa, calculated by the DA system). Other methods, such as the Ensemble Kalman Filter (EnKF) [40], could be tested to see whether it is possible to reduce the convergence time of the parameters, or to decrease the standard deviation, σxb, around the truth, xt, at the end of one given DA experiment. In our study, we assumed that the model is linear: We should use it in the domain of linearity by imposing small perturbations to the parameter to correct. The EnKF can be used in the domain of non-linearity and could be tested. It has gained popularity because of its simple conceptual formulation and relatively easy implementation, requiring no derivation of a tangent linear operator or adjoint equations, and no integrations backward in time [40]. Concerning the description of the different variables and data assimilation experiments described in Section 3.4, another way in which to build the experimental design could be proposed: One important one is the testing of what the impact is on different lengths of river reaches on the convergence of the Strickler coefficients in all four DA experiments, the SWOT error measurement being directly linked to the length of the reaches. Another point is the attribution of the different parameters used in the DA platform: Choice of the DA window duration, threshold of the increment (xa − xb) limitation, and attribution of the model error matrix. The choice of the attribution of the first a priori value, xb, at the beginning of each experiment also plays an important role, having a direct impact on the time of convergence of the Strickler coefficients. The study period can present a more or less spatial and temporal variability of precipitation reaching the surface, impacting directly the flood dynamics in the river network, and thus the increment term (xa − xb), which depends on the discharge regime. All these factors shortly described could have different impacts on the convergence of the system.
5.2. Choice of the Observation to Assimilate and the Parameter to Correct
In the study, we decided to assimilate synthetic SWOT river depths in order to calibrate the roughness coefficient of the river bed in the Garonne catchment. The possibility to assimilate river widths or water surface bed slopes should be investigated. In our work, we considered that the river channel geometry is rectangular and that the width is thus constant in time in each river grid cell. In reality, the amplitudes of the river width between summer (low discharge) and winter (high discharge) can be several tens of meters. The implementation of a trapezoidal geometry should be investigated, in order to take into account the temporal variability of the river width. Furthermore, instead of a parameter calibration, one could propose the correction of the state of prognostic variables in RAPID (initial water volumes in the river reach) or in ISBA (soil water content), or the correction of the description of the atmospheric forcing SAFRAN. The assimilation of discharge over France in ISBA/MODCOU was proposed in order to correct the initial value of the soil moisture [41]. This kind of study could also be realized with synthetic river depths instead of discharge. The correction of prognostic variables instead of parameters could lead to significant advances for operational hydrology, such as the monitoring of water resources and better representation of floods on a regional scale.
5.3. Assimilation of River Depths Considering More Realistic Meteorological and SWOT Errors
In the last proposed DA experiment (Section 4.4), we decided to set up a more realistic scheme, leading to a better representation of the SWOT error measurements. Several points can be considered. The dependence of the error to the reach surface is well established [10], but other factors could have an important impact on the measurement error, like the presence of topography and/or vegetation around the reach, or the orientation of the reach compared to the azimuthal direction of the satellite: The area of the SWOT raw radar image is not the same as a function of the propagation direction of the satellite, and it will be therefore possible to aggregate more or fewer raw radar images over a 1 km² water area; only the non-systematic errors are impacted by this last factor. They should be taken into account in order to better quantify the measurement error. However, to do so, a more complex SWOT simulator is required: The high-resolution SWOT hydrology simulator (https://swot.jpl.nasa.gov/) will allow a better quantification of the error than in the present study. This simulator is currently used at fine spatial and temporal scales in comparison with those used in this study. It would be interesting to test whether it works on a regional or global scale or, based on the results from this simulator, whether it will be possible to parametrize SWOT errors in a more realistic way than what was achieved in this study.
Concerning the wet tropospheric signal, the chosen criterion was the intra-day variability, Vi, of the water content at 10 m. We showed that this variability is greater in summer than in winter, and proposed that the associated measurement error is proportional to Vi. We assumed in this way that it is more difficult to represent variable states than stable states of the troposphere in the time. This hypothesis needs more investigation by considering carefully the synoptic weather situation. For example, important changes of water content due to a warm or cold front (case A) are more difficult to represent than the diurnal temporal evolution of the water content in a homogeneous synoptic situation (case B), because there may be uncertainties about the arrival time of the front: A Vi value of 1 (g kg−1)2 could therefore be more difficult to estimate in case A than the same Vi value during case B.
Finally, it was shown that meteorological input errors impact the determination of the Strickler coefficients. Further efforts are needed to evaluate the impact of meteorological errors in the hydrological model, by, e.g., replacing data from the high quality SAFRAN analysis by ouput from meteorological models.
5.4. Extension of SWOT DA in Other Catchments of the World
The main perspective of this study was to extend the assimilation of SWOT observations not only across the Garonne basin, but all over the world where observations are available. The initial decision to use SRTM 90 m [26] as a DEM (Digital Elevation Model) will make this operation possible. Finally, the use of real satellite data (e.g., altimetry nadir JASON-2/-3, ENVISAT or SARAL, Sentinel-3) could be tested over big river basins, such as the Amazon or the Congo basin, and will allow inter-comparisons between actual experiments and our SWOT twin experiments.
Finally, it would be valuable to build an OSSE to compare benefits of assimilating current nadir altimetry mission(s), for example, Jason-3, Sentinel-3A/B, SARAL, and/or CryoSat-2, to the benefits of assimilating SWOT data. It was shown that across 12 in situ stations along the Po river (Italy), the average root mean squared error of CryoSat-2 compared with hourly water level observations was 38 cm [7], this value being comparable to the SWOT error measurements used in this study. Furthermore, they showed the strong interest to use satellite products to cover the gaps due to the spacing of in situ measurements. Our study should be completed by providing more quantitative information on the specific added value of SWOT compared to current missions.
Author Contributions
Hydrological modelling: V.H., E.M. and A.B., Assimilation technique: S.R., A.B. and S.B., Experiment design: E.M., A.B., and S.R., Realistic SWOT errors: S.B. and V.H., Original draft preparation: V.H., Review and editing: E.M., S.B., S.R. and A.B., Funding acquisition: A.B. and E.M.
Funding
The PhD of Vincent Häfliger was co-funded by CNES and Météo-France. The work was supported by the TOSCA program of CNES, in the framework of the SWOT mission preparation.
Acknowledgments
The authors wish to thank Vanessa Pedinotti and Charlotte Emery for scientific discussion, methods and assimilation code transfer, Thierry Morel for continuous support with respect to the Open-Palm software, and two anonymous reviewers who helped to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT mission and Its capabilities for land hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Biancamaria, S.; Andreadis, K.M.; Durand, M.; Clark, E.A.; Rodríguez, E.; Mognard, N.M.; Alsdorf, D.E.; Lettenmaier, D.P.; Oudin, Y. Preliminary characterization of SWOT hydrology error budget and global capabilities. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 6–19. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Lawrence Dingman, S.; Vorosmarty, C.J.; Bolster, C.H.; Congalton, R.G. Evaluating the potential for measuring river discharge from space. J. Hydrol. 2003, 278, 17–38. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Berge-Nguyen, M.; Gennero, M.C.; Nino, F.; Del Rio, R.A.; Cazenave, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Seyoum, W.M. Characterizing water storage trends and regional climate influence using GRACE observation and satellite altimetry data in the Upper Blue Nile River Basin. J. Hydrol. 2018, 556, 274–284. [Google Scholar] [CrossRef]
- Santos da Silva, J.; Calmant, S.; Seyler, F.; Corrêa Rotunno Filho, O.; Cochonneau, G.; João Mansur, W. Water levels in the Amazon basin derived from the ERS2 and ENVISAT radar altimetry missions. Remote Sens. Environ. 2010, 114, 2160–2181. [Google Scholar] [CrossRef]
- Schneider, R.; Tarpanelli, A.; Nielsen, K.; Madsen, H.; Bauer-Gottwein, P. Evaluation of multi-mode CryoSat-2 altimetry data over the Po River against in situ data and a hydrodynamic model. Adv. Water Resour. 2018, 112, 17–26. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Pavelsky, P.; Durand, M.; Andreadis, K.M.; Beighley, R.E.; Paiva, R.C.D.; Allen, G.H.; Miller, Z.F. Assessing the potential global extent of SWOT river discharge observations. J. Hydrol. 2014, 519, 1519–1525. [Google Scholar] [CrossRef]
- Rodríguez, E.; Surface Water and Ocean Topography (SWOT). Science Requirements Document, JPL Docment D-61923. 2016. [Google Scholar]
- Zaitchik, B.F.; Rodell, M.; Reichle, R.H. Assimilation of GRACE Terrestrial Water Storage Data into a Land Surface Model: Results for the Mississippi River Basin. J. Hydrometeorol. 2008, 9, 535–548. [Google Scholar] [CrossRef]
- Biancamaria, S.; Durand, M.; Andreadis, K.M.; Bates, P.D.; Boone, A.; Mognard, N.M.; Rodríguez, E.; Alsdorf, D.E.; Lettenmaier, D.P.; Clark, E.A. Assimilation of virtual wide swath altimetry to improve Arctic river modeling. Remote Sens. Environ. 2011, 115, 373–381. [Google Scholar] [CrossRef]
- Pedinotti, V.; Ricci, S.; Biancamaria, S.; Mognard, N. Assimilation of satellite data to optimize large scale hydrological model parameters: A case study for the SWOT mission. Hydrol. Earth Syst. Sci. 2014, 18, 4485–4507. [Google Scholar] [CrossRef]
- Häfliger, V.; Martin, E.; Boone, A.; Habets, F.; David, C.H.; Garambois, P.A.; Roux, H.; Ricci, S.; Berthon, L.; Thévenin, A. Evaluation of Regional-Scale River Depth Simulations Using Various Routing Schemes within a Hydrometeorological Modeling Framework for the Preparation of the SWOT Mission. J. Hydrometeorol. 2015, 16, 1821–1842. [Google Scholar] [CrossRef]
- Caballero, Y.; Voirin-Morel, S.; Habets, F.; Noilhan, J.; Le Moigne, P.; Lehenaff, A.; Boone, A. Hydrological sensitivity of the Adour-Garonne river basin to climate change. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Noilhan, J.; Planton, S. A simple parameterization of land surface processes for meteorological models. Mon. Weather Rev. 1989, 117, 536–549. [Google Scholar] [CrossRef]
- Masson, V.; Le Moigne, P.; Martin, E.; Faroux, S.; Alias, A.; Alkama, R.; Belamari, S.; Barbu, A.; Boone, A.; Bouyssel, F.; et al. The SURFEX v7.2 land and ocean surface platform for coupled or offline simulation of earth surface variables and fluxes. Geosci. Model Dev. 2013, 6, 929–960. [Google Scholar] [CrossRef]
- Faroux, S.; Kaptué Tchuenté, A.T.; Roujean, J.-L.; Masson, V.; Martin, E.; Le Moigne, P. ECOCLIMAP-II/Europe: A twofold database of ecosystems and surface parameters at 1 km resolution based on satellite information for use in land surface. meteorological and climate models. Geosci. Model Dev. 2013, 6, 563–582. [Google Scholar] [CrossRef]
- Quintana-Seguí, P.; Le Moigne, P.; Durand, Y.; Martin, E.; Habets, F. Analysis of near-surface atmospheric variables: Validation of the SAFRAN analysis over France. Appl. Meteorol. Clim. J. 2008, 47, 92–107. [Google Scholar] [CrossRef]
- Boone, A.; Masson, V.; Meyers, T.; Noilhan, J. The influence of the inclusion of soil freezing on simulations by a soil–vegetation–atmosphere transfer scheme. Appl. Meteorol. J. 2000, 39, 1544–1569. [Google Scholar] [CrossRef]
- Decharme, B.; Boone, A.; Delire, C.; Noilhan, J. Local evaluation of the interaction between Soil Biosphere Atmosphere soil multilayer diffusion scheme using four pedotransfer functions. Geophys. Res. J. 2011, 116. [Google Scholar] [CrossRef]
- Decharme, B.; Martin, E.; Faroux, S. Reconciling soil thermal and hydrological lower boundary conditions in land surface models. Geophys. Res. Atmos. J. 2013, 118, 7819–7834. [Google Scholar] [CrossRef]
- Ledoux, E.; Girard, G.; Villeneuve, J.P. Proposition d’un modèle couplé pour la simulation conjointe des écoulements de surface et des écoulements souterrains sur un bassin hydrologique. La Houille Blanche 1984, 1–2, 101–110. [Google Scholar] [CrossRef]
- David, C.H.; Habets, F.; Maidment, D.R.; Yang, Z.-L. RAPID applied to the SIM France model. Hydrol. Proess. 2011, 25, 3412–3425. [Google Scholar] [CrossRef]
- David, C.H.; Maidment, D.R.; Niu, G.Y.; Yang, Z.L.; Habets, F.; Eijkhout, V. River network routing on the NHDPlus dataset. J. Hydrometeorol. 2011, 12, 913–934. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodríguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Decharme, B.; Alkama, R.; Douville, H.; Becker, M.; Cazenave, A. Global Evaluation of the ISBA−TRIP Continental Hydrological System. Part II: Uncertainties in River Routing Simulation Related to Flow Velocity and Groundwater Storage. Hydrometeorol. J. 2010, 11, 601–617. [Google Scholar] [CrossRef]
- Alkama, R. Global evaluation of the ISBA-TRIP continental hydrological system. Part I: Comparison to GRACE terrestrial water storage estimates and in situ river discharges. J. Hydrometeorol. 2010, 11, 583–600. [Google Scholar] [CrossRef]
- Pedinotti, V.; Boone, A.; Decharme, B.; Crétaux, J.F.; Mognard, N.; Panthou, G.; Papa, F.; Tanimou, B.A. Evaluation of the ISBA-TRIP continental hydrological system over the Niger basin using in situ and satellite derived datastes. Hydrol. Earth Syst. Sci. 2012, 16, 1745–1773. [Google Scholar] [CrossRef]
- Bouttier, F.; Courtier, P. Data Assimilation Concepts and Methods; ECMWF Lecture Note: Reading, UK, 1999. [Google Scholar]
- Buis, S.; Piacentini, A.; Déclat, D. PALM: A Computational framework for assembling high performance computing applications. Concurr. Comput. Pract. Exp. 2006, 18, 247–262. [Google Scholar] [CrossRef]
- Fouilloux, A.; Piacentini, A. The PALM Project: MPMD Paradigm for an Oceanic Data Assimilation Software. Comput. Sci. 1999, 1685, 1423–1430. [Google Scholar]
- Barthélémy, S.; Ricci, S.; Rochoux, M.C.; Le Pape, E.; Thual, O. Ensemble-based data assimilation for operational flood forecasting—On the merits of state estimation for 1D hydrodynamic forecasting through the example of the “Adour Marine” river. J. Hydrol. 2017, 552, 210–224. [Google Scholar] [CrossRef]
- Enjolras, V.; Vincent, P.; Souyris, J.-C.; Rodríguez, E.; Phalippou, L.; Cazenave, A. Performances study of interferometric radar altimeters: From the instrument to the global mission definition. Sensors 2006, 6, 164–192. [Google Scholar] [CrossRef]
- Brown, S.; Obligis, E. SWOT Wet Tropospheric Correction Working Group Report. In Proceedings of the 3rd SWOT Science Defintion Team Meeting, Washington, DC, USA, 14–16 January 2014. [Google Scholar]
- Fernandez, D.E. SWOT Project, Mission Performance and Error Budget, JPL Document D-79084. 2017. [Google Scholar]
- Cimini, D.; Pierdicca, N.; Pichelli, E.; Ferretti, R.; Mattioli, V.; Bonafoni, S.; Montopoli, M.; Perissin, D. On the accuracy of integrated water vapor observations and the potential for mitigating electromagnetic path delay error in InSAR. Atmos. Meas. Tech. 2012, 5, 1015–1030. [Google Scholar] [CrossRef]
- Ning, T.; Elgered, G.; Willen, U.; Johansson, J.M. Evaluation of the atmospheric water vapor content in a regional climate model using ground-based GPS measurements. J. Geophys. Res. Atmos. 2013, 118, 329–339. [Google Scholar] [CrossRef]
- Flentje, H.; Dörnbrack, A.; Fix, A.; Ehret, G.; Holm, E. Evaluation of ECMWF water vapour fields by airborne differential absorption lidar measurements: A case study between Brazil and Europe. Atmos. Chem. Phys. 2007, 7, 5033–5042. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter: Theoritical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Thirel, G.; Martin, E.; Mahfouf, J.-F.; Massart, S.; Ricci, S.; Habets, F. A past discharge assimilation system for ensemble streamflow forecasts over France—Part 1: Description and validation of the assimilation system. Hydrol. Earth Syst. Sci. 2010, 14, 1623–1637. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).