Spatial Variabilities of Runoff Erosion and Different Underlying Surfaces in the Xihe River Basin
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.3. SWAT Model
2.3.1. Model Construction
2.3.2. Sensitivity Analysis and Parameter Calibration
2.4. Runoff Erosion Ability Index
2.5. Geographically Weighted Regression Model
3. Results
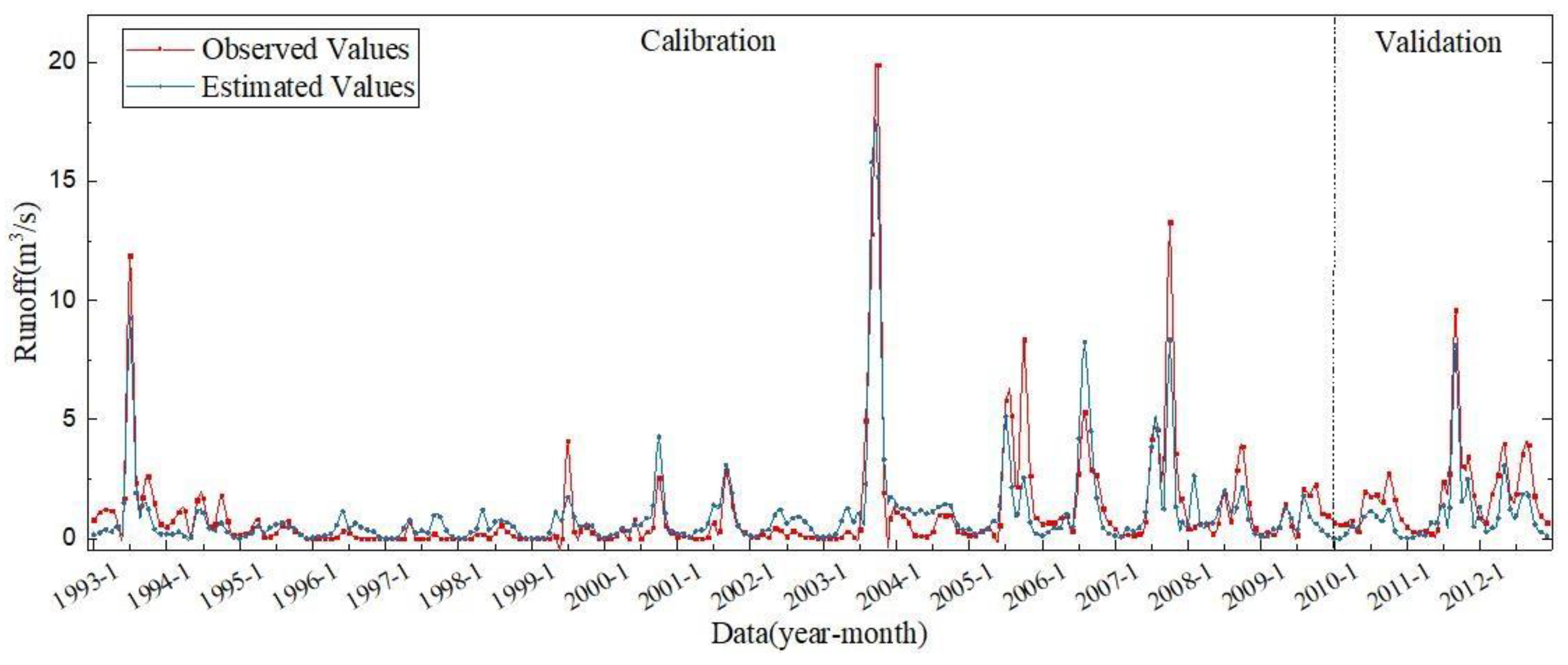
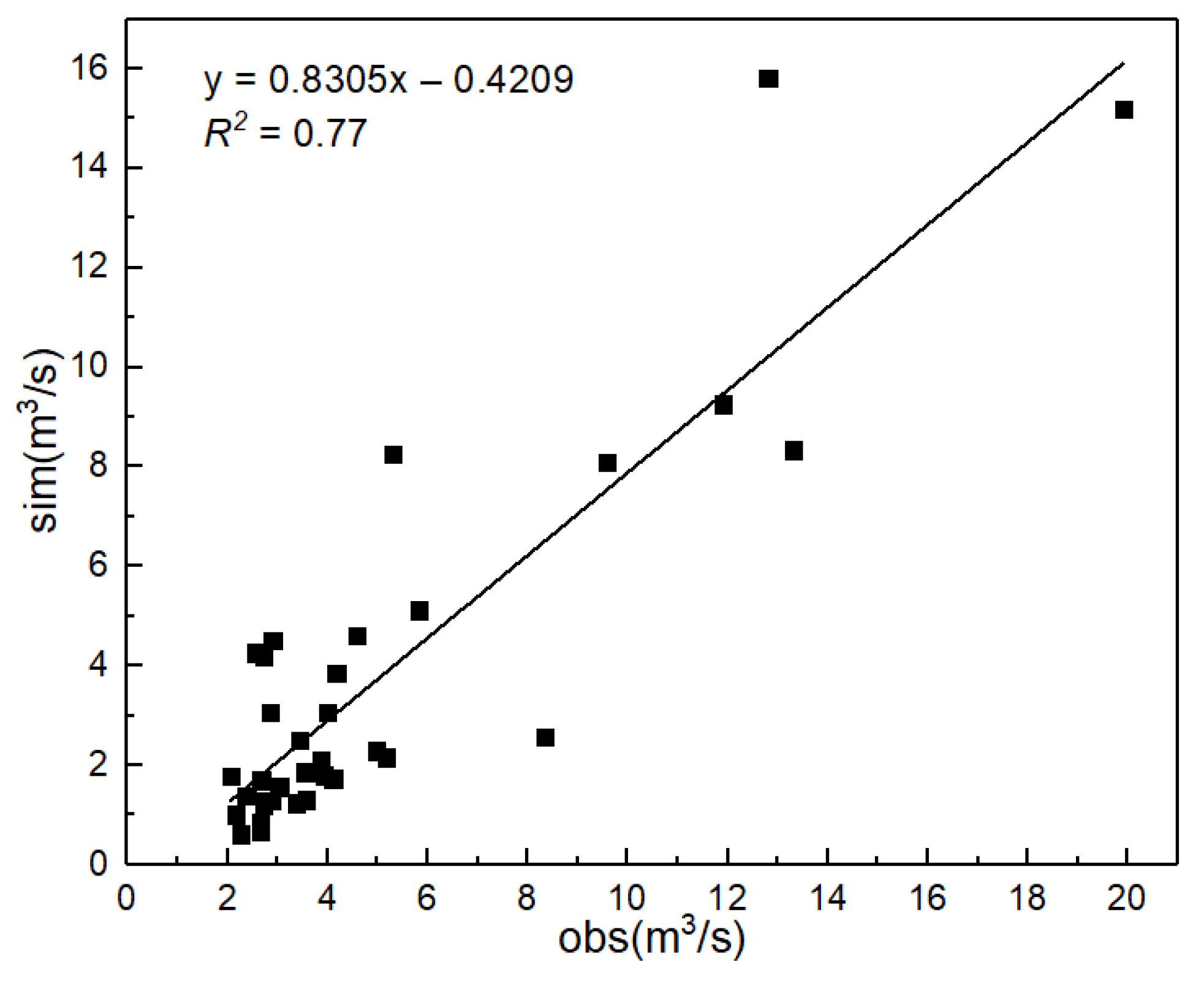
3.1. The SWAT Model Runoff Calibration and Verification
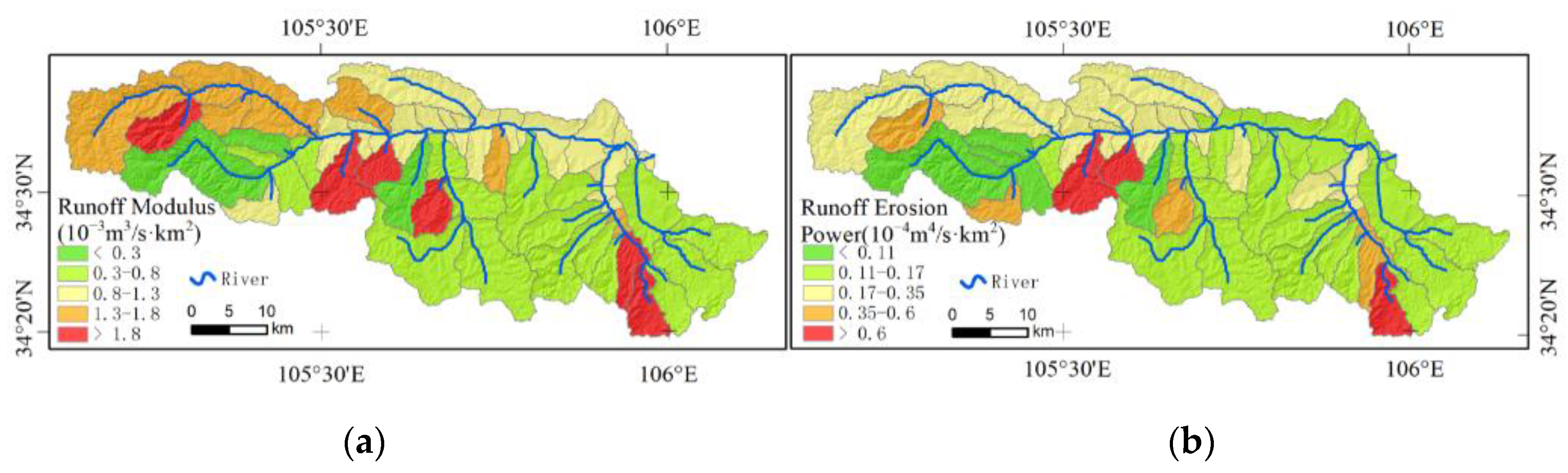
3.2. Spatial Pattern of Runoff Erosion Capacity
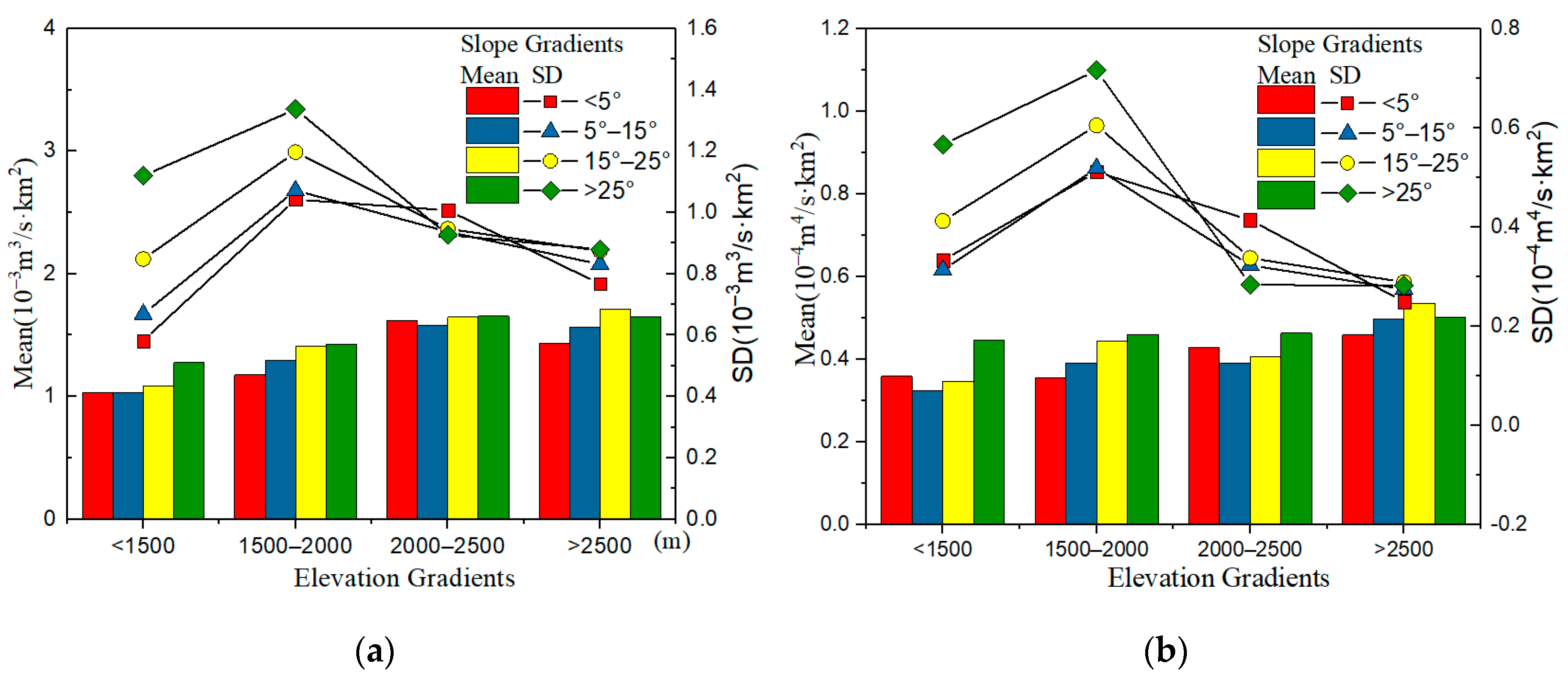
3.3. Gradient Analysis of Runoff Erosion Capacity and Topographic Factors
3.4. Relationship between Runoff Erosion Capacity and Vegetation Factors
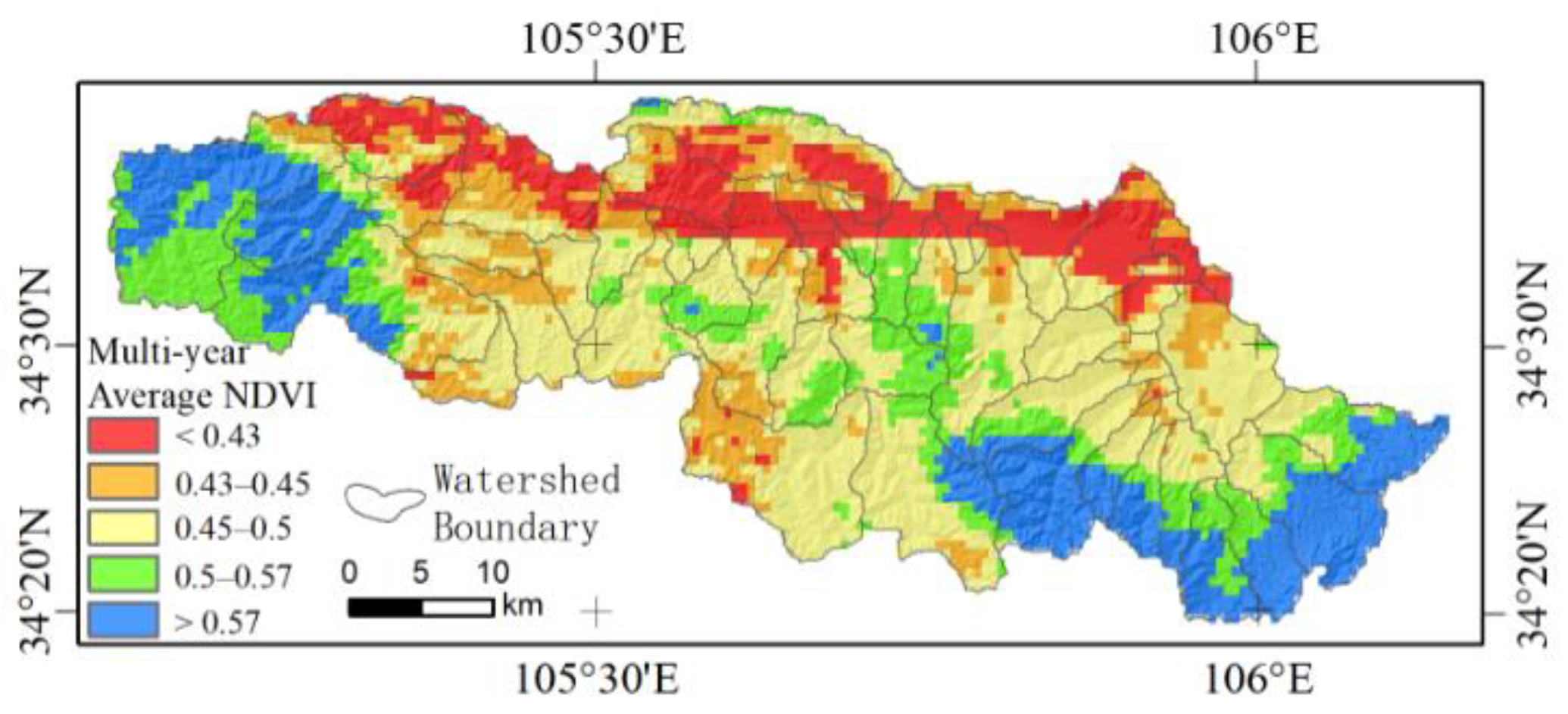
3.4.1. Vegetation Coverage in the Basin
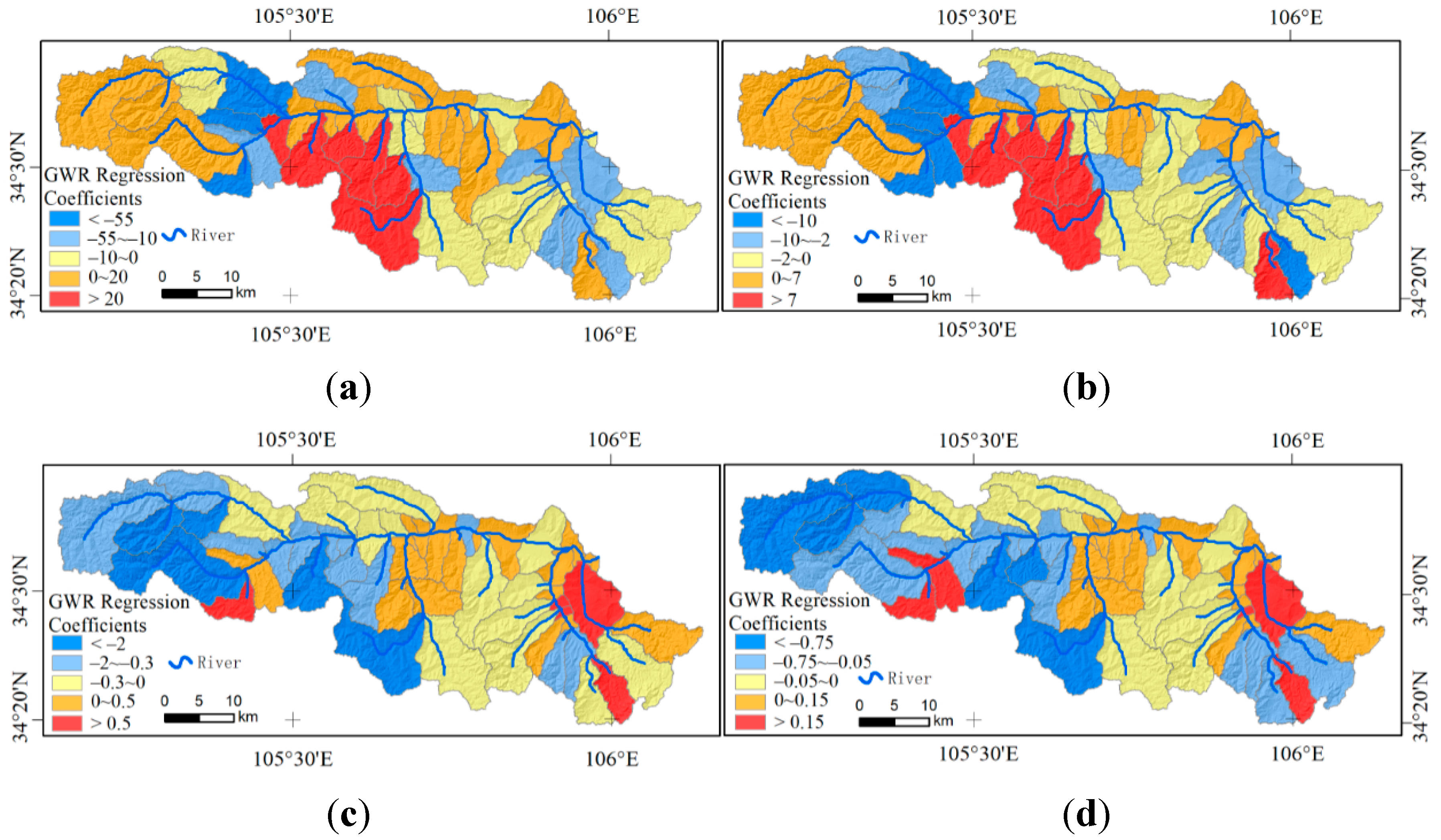
3.4.2. Spatial Correlation with Vegetation Index
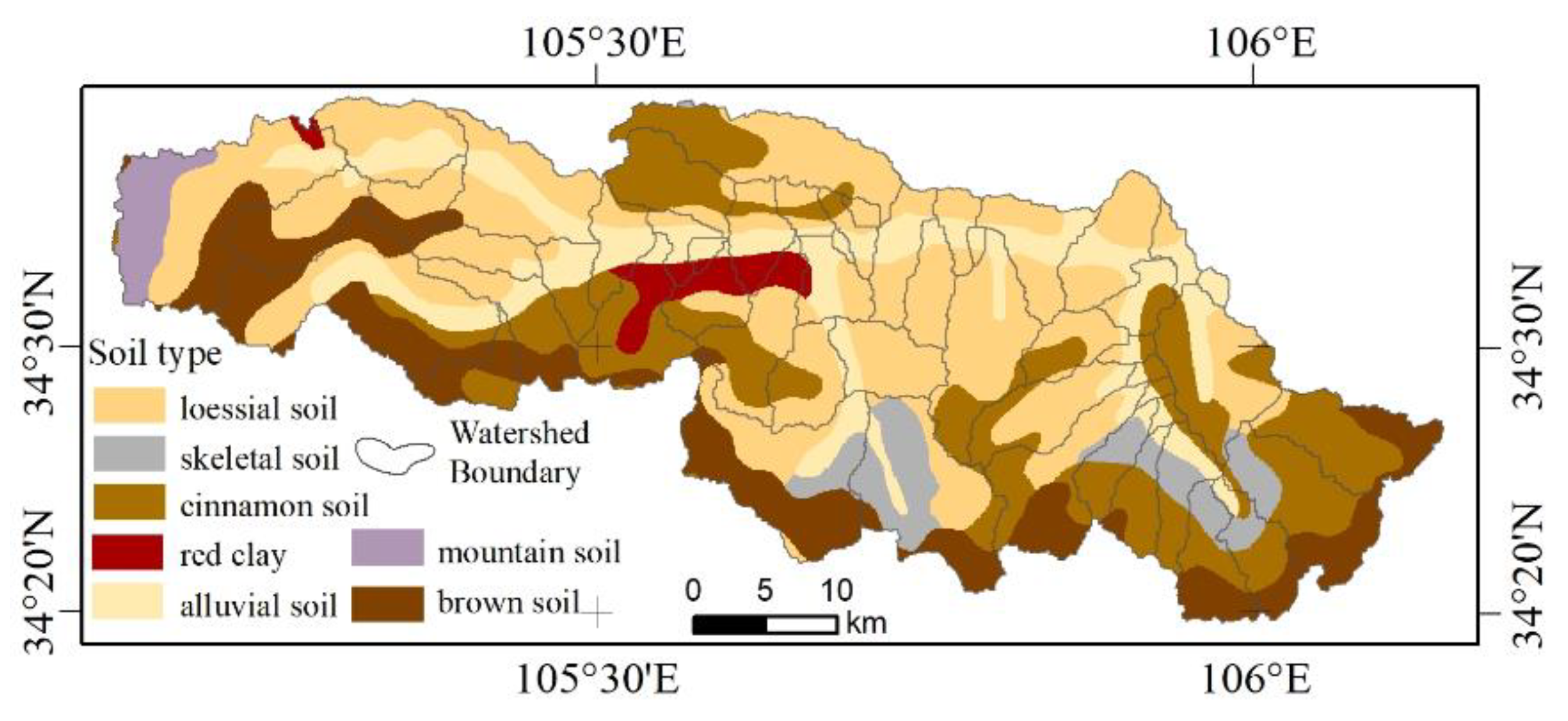
3.5. Spatial Variability of Runoff Erosion Capacity and Soil Factors
4. Discussion
5. Conclusions
- The SWAT model has a good applicability in the arid Xihe River Basin in the Loess Plateau. The spatial pattern of runoff erosion capacity in the Xihe River Basin has the following characteristics: strong in the north, weak in the south, strong in the west, and weak in the east. Approximately 13% of the total area of the basin is prone to runoff erosion.
- The runoff modulus increases with the increase of elevation and slope. Surface vegetation coverage (NDVI) is closely related to the runoff erosion capacity. However, not all areas with high vegetation coverage have weak runoff erosion capacity, indicating that merely increasing vegetation coverage cannot improve soil erosion in the areas where runoff erosion capacity is positively correlated with NDVI. The correlation between runoff erosion capacity and stable soil infiltration rate is mainly negative (accounting for 73.8% of total area). However, compared with other factors, the influence of soil factor on runoff erosion capacity is smaller. The red clay and mountain soil in this region have strong runoff erosion capacities, while the alluvial soil has a weak runoff erosion capacity.
- In the upper reaches of the Xihe River, topographic factors such as elevation and slope gradient are the dominant factors affecting the runoff erosion. In the northern part of the basin, the runoff erosion is strong due to the low coverage of vegetation. In the middle reaches of the basin, the land is mainly used for cultivation, strong runoff is caused by the combination of topographic fluctuations and land use. Since runoff erosion is strong in this region, farming shall be replaced with forest and grass learning from adjacent sub-basins to reduce the soil erosion. In the downstream area, the runoff erosion is weak due to lower altitude, small topographic fluctuation, good vegetation coverage, and good soil infiltration.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ellison, W.D. Soil erosion studies—Part I. Agric. Eng. 1947, 28, 145–146. [Google Scholar]
- Keesstra, S.D.; Temme, A.; Schoorl, J.M.; Visser, S.M. Evaluating the hydrological component of the new catchment-scale sediment delivery model LAPSUS-D. Geomorphology 2014, 212, 97–107. [Google Scholar] [CrossRef]
- Rodrigo-Comino, J.; Davis, J.; Keesstra, S.D.; Cerda, A. Updated Measurements in Vineyards Improves Accuracy of Soil Erosion Rates. Agron. J. 2018, 110, 411–417. [Google Scholar] [CrossRef]
- Keesstra, S.; Mol, G.; de Leeuw, J.; Okx, J.; de Cleen, M.; Visser, S. Soil-related sustainable development goals: Four concepts to make land degradation neutrality and restoration work. Land 2018, 7, 133. [Google Scholar] [CrossRef]
- Keesstra, S.; Nunes, J.P.; Saco, P.; Parsons, T.; Poeppl, R.; Masselink, R.; Cerda, A. The way forward: Can connectivity be useful to design better measuring and modelling schemes for water and sediment dynamics? Sci. Total Environ. 2018, 644, 1557–1572. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; An, N.; Yin, Y.; Cheng, F.; Dong, S. Relationship between spatio-temporal dynamaics of soil and water loss and NDVI of the small basins in the middle reaches of Lancang River based on SWAT model. J. Soil Water Conserv. 2016, 30, 62–67. [Google Scholar]
- Sun, J.; Yu, D.; Shi, X.; Gu, Z.; Zhang, W.; Yang, H. Comparision of between LAI and VFC in relationship with siol erosion in the red soil hilly region of south China. Acta Pedol. Sin. 2010, 47, 1060–1066. [Google Scholar]
- Wang, G.; Zhang, C.; Liu, J.; Wei, J.; Xue, H.; Li, T. Analyses on the variation of vegetation coverage and water sediment reduction in the rich and coarse sediment area of the Yellow River basin. J. Sediment Res. 2006, 2, 10–16. [Google Scholar]
- Patovvary, S.; Sarma, A.K. GIS-Based Estimation of Soil Loss from Hilly Urban Area Incorporating Hill Cut Factor into RUSLE. Water Resour. Manag. 2018, 32, 1–13. [Google Scholar] [CrossRef]
- Qin, W.; Guo, Q.; Cao, W.; Yin, Z.; Yan, Q.; Shan, Z.; Zheng, F. A new RUSLE slope length factor and its application to soil erosion assessment in a Loess Plateau watershed. Soil Tillage Res. 2018, 182, 10–24. [Google Scholar] [CrossRef]
- Hu, G.; Song, H.; Shi, X.; Zhang, M.; Liu, X.; Zhang, X. Soil erosion characteristics based on RUSLE in the Wohushan Reservoir Watershed. Sci. Geogr. Sin. 2018, 38, 610–617. [Google Scholar]
- Li, D.; Yang, J.; Li, W.; Zhu, C. Evaluating the sensitivity of soil erosion in the Yili River valley based on GIS and USLE. Chin. J. Ecol. 2016, 35, 942–951. [Google Scholar]
- Liao, Y.; Zhuo, M.; Xie, J.; Wei, G.; Guo, T.; Xie, Z.; Li, D. Variations in vegetation cover factors and their influence on USLE and RUSLE. Acta Ecol. Sin. 2017, 37, 1987–1993. [Google Scholar]
- Peng, S.; Yang, K.; Hong, L.; Xv, Q.; Huang, Y. Spatio-temporal evolution analysis of soil erosion based on USLE model in Dianchi Basin. Trans. Chin. Soc. Agric. Eng. 2018, 34, 138–146. [Google Scholar]
- Thomas, J.; Joseph, S.; Thrivikramji, K.P. Assessment of soil erosion in a tropical mountain river basin of the southern Western Ghats, India using RUSLE and GIS. Geosci. Front. 2018, 9, 893–906. [Google Scholar] [CrossRef]
- Mondal, A.; Khare, D.; Kundu, S. A comparative study of soil erosion modelling by MMF, USLE and RUSLE. Geocarto Int. 2018, 33, 89–103. [Google Scholar] [CrossRef]
- Mehra, M.; Singh, C.K. Spatial analysis of soil resources in the Mewat district in the semiarid regions of Haryana, India. Environ. Dev. Sustain. 2018, 20, 661–680. [Google Scholar] [CrossRef]
- Bhowmik, M.; Das, N.; Das, C.; Ahmed, I.; Debnath, J. Bank material characteristics and its impact on river bank erosion, West Tripura district, Tripura, North-East India. Curr. Sci. 2018, 115, 1571–1576. [Google Scholar] [CrossRef]
- Thomas, J.; Joseph, S.; Thrivikramji, K.P. Assessment of soil erosion in a monsoon-dominated mountain river basin in India using RUSLE-SDR and AHP. Hydrol. Sci. J. 2018, 63, 542–560. [Google Scholar] [CrossRef]
- Guo, H.; Hu, Q.; Jiang, T. Annual and seasonal streamflow responses to climate and land-cover changes in the Poyang Lake basin, China. J. Hydrol. 2008, 355, 106–122. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.-Z.; Zhang, X.-C.; Zheng, F.-L. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Feng, C.; Mao, D.; Zhou, H.; Cao, Y.; Hu, G. Impacts of climate and land use changes on runoff in the Lianshui basin. J. Glaciol. Geocryol. 2017, 39, 395–406. [Google Scholar]
- Hou, W.; Gao, J.; Dai, E.; Peng, T.; Wu, S.; Wang, H. The runoff generation simulation and its spatial variation analysisin Sanchahe basin as the south source of Wujiang. Acta Geogr. Sin. 2018, 73, 1268–1282. [Google Scholar]
- Li, S.; Wei, H.; Liu, Y.; Ma, W.; Gu, Y.; Peng, Y.; Li, C. Runoff prediction for Ningxia Qingshui River Basin under scenarios of climate and land use changes. Acta Ecol. Sin. 2017, 37, 1252–1260. [Google Scholar]
- Da Silva, V.D.R.; Silva, M.T.; De Souza, E.P. Influence of land use change on sediment yield: A case study of the sub-middle of the Sao Francisco River basin. Eng. Agric. 2016, 36, 1005–1015. [Google Scholar] [CrossRef]
- Jeziorska, J.; Niedzielski, T. Applicability of TOPMODEL in the mountainous catchments in the upper Nysa Kodzka river basin (SW Poland). Acta Geophys. 2018, 66, 203–222. [Google Scholar] [CrossRef]
- Wang, S.-P.; Zhang, Z.-Q.; Ge, S.; Strauss, P.; Guo, J.-T.; Yao, A.-K.; Tang, Y. Assessing Hydrological Impacts of Changes in Land Use and Precipitation in Chaohe Watershed Using MIKESHE Model. J. Ecol. Rural Environ. 2012, 28, 320–325. [Google Scholar]
- Reis, M.; Aladag, I.A.; Bolat, N.; Dutal, H. Using Geoweep model to determine sediment yield and runoff in the Keklik watershed in Kahramanmaras, Turkey. Sumar. List 2017, 141, 563–569. [Google Scholar]
- Xu, H.; Xu, C.-Y.; Saelthun, N.R.; Xu, Y.; Zhou, B.; Chen, H. Entropy theory based multi-criteria resampling of rain gauge networks for hydrological modelling—A case study of humid area in southern China. J. Hydrol. 2015, 525, 138–151. [Google Scholar] [CrossRef]
- Lv, L.; Peng, Q.; Guo, Y.; Liu, Y.; Jiang, Y. Runoff simulation of Dongjiang River Basin based on the soil and water assessment tool. J. Nat. Resour. 2014, 29, 1746–1757. [Google Scholar]
- Yuan, Y.; Zhnag, Z.; Meng, J. Impact of changes in land use and climate on the runoff in Liuxihe Watershed based on SWAT model. Chin. J. Appl. Ecol. 2015, 26, 989–998. [Google Scholar]
- Zhao, A.; Liu, X.; Zhu, X.; Pan, Y.; Li, Y. Spatiotemporal patterns of droughts based on SWAT model for the Weihe River Basin. Prog. Geogr. 2015, 34, 1156–1166. [Google Scholar]
- Hao, F.H.; Zhang, X.S.; Yang, Z.F. A distributed non-point source pollution model: Calibration and validation in the Yellow River basin. J. Environ. Sci. 2004, 16, 646–650. [Google Scholar]
- Xu, H.; Taylor, R.G.; Xu, Y. Quantifying uncertainty in the impacts of climate change on river discharge in sub-catchments of the Yangtze and Yellow River Basins, China. Hydrol. Earth Syst. Sci. 2011, 15, 333–344. [Google Scholar] [CrossRef]
- Zuo, D.; Xu, Z.; Yao, W.; Jin, S.; Xiao, P.; Ran, D. Assessing the effects of changes in land use and climate on runoff and sediment yields from a watershed in the Loess Plateau of China. Sci. Total Environ. 2016, 544, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Shivhare, N.; Rahul, A.K.; Omar, P.J.; Chauhan, M.S.; Gaur, S.; Dikshit, P.K.S.; Dwivedi, S.B. Identification of critical soil erosion prone areas and prioritization of micro-watersheds using geoinformatics techniques. Ecol. Eng. 2018, 121, 26–34. [Google Scholar] [CrossRef]
- Yesuf, H.M.; Assen, M.; Alamirew, T.; Melesse, A.M. Modeling of sediment yield in Maybar gauged watershed using SWAT, northeast Ethiopia. Catena 2015, 127, 191–205. [Google Scholar] [CrossRef]
- Duru, U.; Arabi, M.; Wohl, E.E. Modeling stream flow and sediment yield using the SWAT model: A case study of Ankara River basin, Turkey. Phys. Geogr. 2018, 39, 264–289. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, C.; Huang, Y. The theory of SWAT model and its application in Heihe Basin. Prog. Geogr. 2003, 22, 79–86. [Google Scholar]
- Chen, C.; Zhang, Y.; Xiang, Y.; Wang, L. Study on runoff responses to land use change in Ganjiang Basin. J. Nat. Resour. 2014, 29, 1758–1769. [Google Scholar]
- Zhang, D.; Zhang, W.; Zhu, L.; Zhu, Q. Improvement and application of SWAT—A physically based, distributed hydrological model. Sci. Geogr. Sin. 2005, 25, 434–440. [Google Scholar]
- Golden, H.E.; Sander, H.A.; Lane, C.R.; Zhao, C.; Price, K.; D’Amico, E.; Christensen, J.R. Relative effects of geographically isolated wetlands on streamflow: A watershed-scale analysis. Ecohydrology 2016, 9, 21–38. [Google Scholar] [CrossRef]
- Haregeweyn, N.; Tsunekawa, A.; Poesen, J.; Tsubo, M.; Meshesha, D.T.; Fenta, A.A.; Nyssen, J.; Adgo, E. Comprehensive assessment of soil erosion risk for better land use planning in river basins: Case study of the Upper Blue Nile River. Sci. Total Environ. 2017, 574, 95–108. [Google Scholar] [CrossRef] [PubMed]
- Muenich, R.L.; Kalcic, M.; Scavia, D. Evaluating the Impact of Legacy P and Agricultural Conservation Practices on Nutrient Loads from the Maumee River Watershed. Environ. Sci. Technol. 2016, 50, 8146–8154. [Google Scholar] [CrossRef] [PubMed]
- Sarrazin, F.; Pianosi, F.; Wagener, T. Global Sensitivity Analysis of environmental models: Convergence and validation. Environ. Model. Softw. 2016, 79, 135–152. [Google Scholar] [CrossRef]
- Hu, S.; Cao, M.; Qiu, H.; Song, J.; Wu, J.; Gao, Y.; Li, J.; Sun, K. Applicability evaluation of CFSR climate datafor hydrologic simulation: A case study in the Bahe River Basin. Acta Geogr. Sin. 2016, 71, 1571–1586. [Google Scholar]
- Li, Y.; Chang, J.; Wang, Y.; Jin, W.; Bai, X. Spatiotemporal responses of runoff to land use change in Wei River Basin. Trans. Chin. Soc. Agric. Eng. 2016, 32, 232–238. [Google Scholar]
- Lai, Z.; Li, S.; Li, C.; Nan, Z.; Yu, W. Improvement and applications of SWAT model in the upper-middle Heihe River Basin. J. Nat. Resour. 2013, 28, 1404–1413. [Google Scholar]
- Ruan, H.; Zou, S.; Lu, Z.; Yang, D.; Xiong, J.; Yin, Z. Coupling SWAT and RIEMS to simulate mountainous runoff in the upper reaches of the Heihe River basin. J. Glaciol. Geocryol. 2017, 39, 384–394. [Google Scholar]
- Yu, W. Improvement and Application of SWAT Hydrologic Model in Mountainous Upper Heihe River Basin. Master’s Thesis, Nanjing Normal University, Nanjing, China, 2012. [Google Scholar]
- Gong, J.; Li, Z.; Li, P.; Reng, Z.; Yang, Y.; Han, L.; Tang, S.; Sun, Q. Spatial distribution of runoff erosion power based on SWAT Model in Yanhe River Basin. Trans. Chin. Soc. Agric. Eng. 2017, 33, 120–126. [Google Scholar]
- Li, J.; Zhou, Z. Landscape pattern and hydrological processes in Yanhe River basin of China. Acta Geogr. Sin. 2014, 69, 933–944. [Google Scholar]
- Zhao, C. Runoff Response to Land Use Change in the Yan River Using SWAT Model. Master’s Thesis, Research Center of Soil and Water Conservation and Ecological Environmen, Chinese Academy of Sciences and Ministry of Education, Beijing, China, 2015. [Google Scholar]
- Yang, H.; Xv, C. Effect of LUCC on runoff of three representative watersheds in Dongjiang River Basin. J. Lake Sci. 2011, 23, 991–996. [Google Scholar]
- Jun, G. Study on Runoff and Sediment Variation and Spatial Distribution of Erosion Energy in Wudinghe Watershed. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2018. [Google Scholar]
- Ke, L.; Zhan, L.; Hua, J.; Sheng, C. Study on a comparison of runoff erosion power and rainfall erosivity for single rainstorm event under different spatial scales. J. Northwest A F Univ. 2009, 37, 204–208. [Google Scholar]
- Wheeler, D.C. Simultaneous coefficient penalization and model selection in geographically weighted regression: The geographically weighted lasso. Environ. Plan. A 2009, 41, 722–742. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Ajaaj, A.A.; Mishra, A.K.; Khan, A.A. Evaluation of Satellite and Gauge-Based Precipitation Products through Hydrologic Simulation in Tigris River Basin under Data-Scarce Environment. J. Hydrol. Eng. 2019, 24, 18. [Google Scholar] [CrossRef]
- Tang, X.P.; Zhang, J.Y.; Wang, G.Q.; Yang, Q.L.; Yang, Y.Q.; Guan, T.S.; Liu, C.S.; Jin, J.L.; Liu, Y.L.; Bao, Z.X. Evaluating Suitability of Multiple Precipitation Products for the Lancang River Basin. Chin. Geogr. Sci. 2019, 29, 37–57. [Google Scholar] [CrossRef]
- Lyu, L.T.; Wang, X.R.; Sun, C.Z.; Ren, T.T.; Zheng, D.F. Quantifying the Effect of Land Use Change and Climate Variability on Green Water Resources in the Xihe River Basin, Northeast China. Sustainability 2019, 11, 338. [Google Scholar] [CrossRef]
- Nunes, H.G.G.C.; Sousa, A.M.L.D.; Santos, J.T.S.D. Simulation of Flow in the Capim River (PA) using the SWAT Model. Floresta e Ambiente 2019, 26, e20160171. [Google Scholar] [CrossRef]
- Qiao, P.; Lei, M.; Yang, S.; Yang, J.; Zhou, X.; Dong, N.; Guo, G. Development of a model to simulate soil heavy metals lateral migration quantity based on SWAT in Huanjiang watershed, China. J. Environ. Sci. (China) 2019, 77, 115–129. [Google Scholar] [CrossRef]
| Parameters | Physical Meanings | Sensitivity Order | Parameter Adjustment Method | Calibration Range | Optimum Calibration Value |
|---|---|---|---|---|---|
| ESCO | Compensation coefficient of soil evaporation | 1 | V | 0.1~0.9 | 0.864 |
| CN2_AGRL | SCS Runoff Curve Value of Cultivated Land | 2 | R | −0.5~0.5 | −0.129 |
| GWQMN | Runoff coefficient of shallow groundwater | 3 | V | 0~5000 | 0.696 |
| CN2_URLD | SCS Runoff Curve Value of Construction Land | 4 | R | −0.5~0.5 | 0.0516 |
| CANMX | Maximum canopy interception | 5 | V | 0~100 | 9.1697 |
| ALPHA_BNK | Reservoir Coefficient of Main Channel | 6 | V | 0~0.8 | 0.3746 |
| CN2_WATR | SCS Runoff Curve Value of Water | 7 | R | −0.5~0.5 | 0.164 |
| SOL_AWC | Available Water Content of Surface Soil | 8 | V | 0~1 | 0.568 |
| CN2_FRSD | SCS Runoff Curve Value of Forest Land | 9 | R | −0.5~0.5 | −0.1139 |
| SOL_K | Saturated hydraulic conductivity of soil | 10 | V | 0~10 | 5.367 |
| GW_DELAY | Hysteresis coefficient of groundwater | 11 | V | 0~500 | 159.107 |
| CN2_PAST | SCS Runoff Curve Value of Grassland | 12 | R | −0.5~0.5 | 0.1028 |
| SOL_BD | Surface soil bulk density | 13 | V | 0.9~2.5 | 1.766 |
| ALPHA_BF | Base flow regression coefficient | 14 | V | 0~1 | 0.852 |
| CN2_SWRN | SCS Runoff Curve Value in Bare Land | 15 | R | −0.5~0.5 | −0.003 |
| Function | Description |
|---|---|
| Runoff modulus refers to the runoff generated per unit area of a river basin in a unit time, , in m3/s·km2. | |
| Annual runoff erosion power combines runoff depth H and peak discharge Qm, , in m4/s·km2. | |
| The maximum monthly flow modulus, , in m3/s·km2. | |
| The average flow depth of the annual flow, Hyear, in mm. |
| Soiltype | Runoff Module | Runoff Erosion Power | ||
|---|---|---|---|---|
| Max | Mean | Max | Mean | |
| loessial soil | 2.746 | 1.003 | 0.826 | 0.200 |
| skeletal soil | 4.830 | 1.009 | 2.254 | 0.318 |
| cinnamon soil | 4.830 | 1.068 | 2.254 | 0.292 |
| red clay | 2.740 | 1.790 | 0.826 | 0.480 |
| alluvial soil | 2.830 | 0.960 | 2.254 | 0.198 |
| mountain soil | 1.680 | 1.680 | 0.318 | 0.340 |
| brown soil | 4.834 | 0.980 | 2.254 | 0.297 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Yao, Z.; Liu, W.; Lv, X.; Ma, M. Spatial Variabilities of Runoff Erosion and Different Underlying Surfaces in the Xihe River Basin. Water 2019, 11, 352. https://doi.org/10.3390/w11020352
Wang N, Yao Z, Liu W, Lv X, Ma M. Spatial Variabilities of Runoff Erosion and Different Underlying Surfaces in the Xihe River Basin. Water. 2019; 11(2):352. https://doi.org/10.3390/w11020352
Chicago/Turabian StyleWang, Ning, Zhihong Yao, Wanqing Liu, Xizhi Lv, and Mengdie Ma. 2019. "Spatial Variabilities of Runoff Erosion and Different Underlying Surfaces in the Xihe River Basin" Water 11, no. 2: 352. https://doi.org/10.3390/w11020352
APA StyleWang, N., Yao, Z., Liu, W., Lv, X., & Ma, M. (2019). Spatial Variabilities of Runoff Erosion and Different Underlying Surfaces in the Xihe River Basin. Water, 11(2), 352. https://doi.org/10.3390/w11020352





