Abstract
Effective and accurate water demand prediction is an important part of the optimal scheduling of a city water supply system. A novel deep architecture model called the continuous deep belief echo state network (CDBESN) is proposed in this study for the prediction of hourly urban water demand. The CDBESN model uses a continuous deep belief network (CDBN) as the feature extraction algorithm and an echo state network (ESN) as the regression algorithm. The new architecture can model actual water demand data with fast convergence and global optimization ability. The prediction capacity of the CDBESN model is tested using historical hourly water demand data obtained from an urban waterworks in Zhuzhou, China. The performance of the proposed model is compared with those of ESN, continuous deep belief neural network, and support vector regression models. The correlation coefficient (r2), normalized root-mean-square error (NRMSE), and mean absolute percentage error (MAPE) are adopted as assessment criteria. Forecasting results obtained in the testing stage indicate that the CDBESN model has the largest r2 value of 0.995912 and the smallest NRMSE and MAPE values of 0.027163 and 2.469419, respectively. The prediction accuracy of the proposed model clearly outperforms those of the models it is compared with due to the good feature extraction ability of CDBN and the excellent feature learning ability of ESN.
1. Introduction
Precise short-term prediction of urban water demand provides guidance for the planning and management of water resources and plays an important role in the economic operation of a water supply system. Therefore, various water demand prediction models, such as support vector regression (SVR) [1,2], random forests regression [3], artificial neural network (ANN) [4], Markov chain model [5], and hybrid models [6,7,8,9], have been widely developed in the past few decades. Research regarding water demand prediction generally focuses on methods involving ANN, which are nonparametric data-driven approaches applicable for building nonlinear mapping from input to output variables for estimating nonlinear continuous functions with an arbitrary accuracy [10].
For example, Jain et al. [11] compared ANNs, a time series model, and a regression model for the weekly water demand prediction of the Indian Institute of Technology in Kanpur, India, and found that the ANNs outperformed the two other methods. Adamowski [12] applied an ANN model to forecast peak daily urban water demands and achieved a high prediction accuracy. Bennett et al. [13] used an ANN model to predict the residential water end-use demand and confirmed that the ANN model is a useful predictive tool. Al-Zahrani and Abo-Monasar [14] developed a hybrid approach of a time series model and ANNs to forecast the daily water demand of Al-Khobar City. The hybrid approach provided better prediction than single ANN or time series models. Although the ANN model has a favorable performance for water demand prediction, the use of ANN still suffers from some disadvantages, including the difficulty associated with selecting optimal network parameters, a high propensity for becoming trapped in local minima, and a poor global search capability. These difficulties may lead to specific problems, such as overfitting.
The deep belief network (DBN) model, which was proposed by Hinton et al. [15], is a deep learning algorithm based on a probability generative model. Unlike the ANN model, DBN effectively avoids overfitting problems with a distinctive unsupervised training method. A DBN model has many hidden layers that are constructed by the stacking of numerous restricted Boltzmann machines (RBMs). A DBN extracts the latent features of the training dataset by using a greedy layer-wise unsupervised learning method. Specifically, layer-by-layer independent training is implemented to pre-train the initial network weights, with each layer acquiring the features of the previous layer; finally, the network returns the features of the training sample. Following independent training, the weights are fine-tuned using a back-propagation (BP) learning algorithm to achieve a powerful nonlinear expressive capacity. In recent years, the DBN model has been successfully applied in many fields, such as natural language understanding [16], image classification [17,18], fault diagnosis [19], financial prediction [20], load prediction [21], and flow prediction [22,23]. Moreover, DBN models have demonstrated remarkable potential for time series prediction [24]. Kuremoto et al. [25] developed a DBN model with three layers applied to predict time series. Qin et al. [26] developed a combined approach based on DBN and an autoregressive integrated moving average model for red tide time series prediction. Xu et al. [27] constructed a continuous deep belief neural network (CDBNN) to forecast a daily water demand time series. However, DBN or CDBNN models that use BP learning algorithms to adjust parameters have slow convergence and easily fall into local optima, thereby resulting in an unsatisfactory prediction accuracy [28,29].
A new recurrent neural network model called the echo state network (ESN), which was proposed by Jeager et al. [30,31,32], has a large, sparse, recursively connected reservoir and a linear output. The reservoir serves as an echo for storing historical information. The input and the internal connection weights of the reservoir remain unchanged after the initial setting. Only the output weight must be solved by the linear regression method. Therefore, training the ESN model becomes a task of linear regression. The learning algorithm is simple, the calculation speed is fast, and the solution is unique and globally optimal; moreover, the algorithm shows an excellent performance in nonlinear time series modeling and prediction [33,34,35]. Sun et al. [29] introduced the ESN algorithm to a DBN and proposed the deep belief echo state network model for time series forecasting. However, the DBN model composed of RBMs can only reconstruct symmetric analog data [36]. Actual water demand data are continuous; therefore, an advanced deep learning architecture is needed for effectively forecasting the urban water demand.
In this study, a hybrid deep architecture continuous deep belief ESN (CDBESN) model, which is composed of continuous DBN (CDBN) and ESN models, is proposed and applied to forecast the hourly urban water demand. In this new architecture, the CDBN model in the bottom layer is used to extract features of the original water demand data, and the ESN model in the top layer is adopted for feature regression. This method can process real continuous data and also avoid the local optimum and slow convergence caused by BP learning algorithms.
The rest of this paper is organized as follows. Section 2 details the methodology of the CDBN, ESN, and CDBESN models. Section 3 presents the study area, data, and the performance evaluation indexes. Section 4 discusses the CDBESN model, forecasting results, and comparisons with other models. Finally, Section 5 explains the conclusions.
2. Methodology
2.1. Continuous Deep Belief Network
Chen and Murray found that an RBM with binary random units can only reconstruct symmetric analog data, and they developed a continuous RBM (CRBM) [36] with visible and hidden layer units with a continuous state, thereby enabling the CRBM to process real continuous data. Multiple CRBMs are used to stack a CDBN model, which can deal with continuous data and be used to extract features from original water demand data. The structure of the CDBN model is shown in Figure 1.
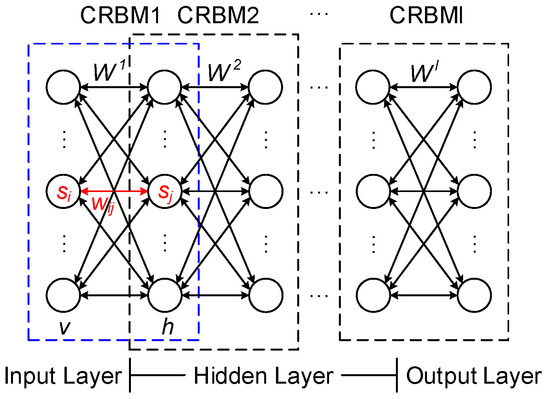
Figure 1.
CDBN model structure.
In Figure 1, a typical CDBN model is stacked by using l CRBMs, which present an input or visible layer, an output layer, and l−1 hidden layers. Here, Wl represents the weight matrix of the layers l and l−1. A typical CRBM model is marked by blue dashed lines in Figure 1, which is constructed from a hidden layer h and a visible layer v. Symmetric connections of the weight matrix exist between the two layers, but no such connections are present within a layer.
For a CRBM, sj and si denote the states of the hidden layer unit j and the visible layer unit i, respectively; moreover, wij denotes the interconnected weights of the units j and i. A group of samples is randomly chosen as input data, and the update rule of the states sj of the hidden layer unit is given as follows:
with
where stands for a Gaussian unit with unit variance and a zero mean, denotes a constant, and represents a sigmoid function with asymptotes at and . The noise-control parameters controls the slope of the sigmoid function and thus the nature of the stochastic behavior of the unit [36].
is used to compute the states of visible layer units:
with
where, as before, , , and represent a Gaussian unit, a sigmoid function, and noise-control parameters, respectively.
is used to compute the states of the hidden layer units:
After minimizing contrastive divergence [37], algorithms are introduced into the CRBM as a simple training rule, the weights and the parameters and are updated as follows:
where and stand for the learning rates of the weights and noise-control parameters, respectively; and represent the states of a single-step sample of the hidden layer unit and the visible layer unit , respectively; and denotes the average value of the training dataset.
The next training process is carried out after the change of the weight matrix is minimal or the preset maximum training time is achieved. Such conditions indicate that the current CRBM training is completed, and its outputs are used as the inputs of the following CRBM. The aforementioned training process is repeated until all CRBMs of the CDBN model are trained completely, and the training of the CDBN model is ended.
2.2. Echo State Network
The ESN model is a novel large-scale recurrent neural network, whose core is a reservoir layer consisting of numerous randomly generated and sparsely connected neurons [29]. The structure of the ESN model is shown in Figure 2. In the figure, the ESN model consists of an input layer, an output layer, and a reservoir layer. Here, Win represents the weight matrix of the input layer, W is the internal weight matrix of the reservoir, Wo is the weight matrix of the output layer, and Wb is the feedback weight matrix. The values of Win, W, and Wb are randomly produced during the initialization process and cannot be changed after generation. Only the value of Wo must be adjusted during the training process of the reservoir.
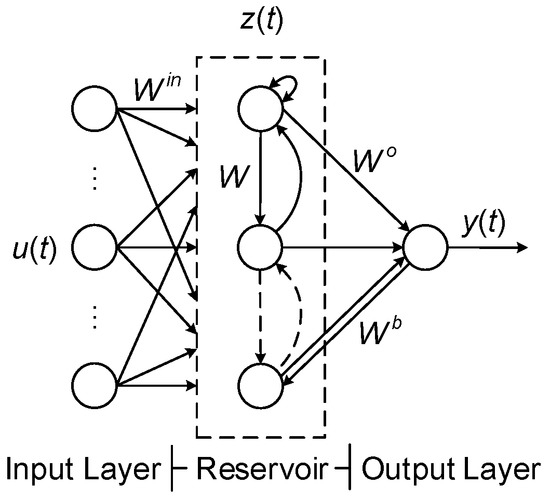
Figure 2.
ESN model structure.
, , and denote the numbers of the input, reservoir, and output units, respectively. The input vector , state connection vector , and output vector can be expressed as follows:
The reservoir state and network output at time are updated in accordance with the following rules:
where and are the activation functions of the reservoir and output, respectively. In this study, is selected as the hyperbolic tangent, and is the identity function.
To eliminate the influence of the random initial states of the reservoir, a small number of the reservoir states are abandoned. Moreover, the rest states of the reservoir are collected into a matrix and used as corresponding desired target outputs into a target output matrix . Then, the output weight matrix is computed using a linear regression approach by minimizing the target function of error between the network output and the desired output , which is given by:
where stands for the Euclidean norm. The weight matrix of the output layer can typically be computed using the Moore–Penrose-inversion method:
where is the generalized inverse of .
At this point, ESN training is completed, and the model can be used for specific problems, such as time series modeling.
2.3. CDBESN Model
The CDBN and ESN models are integrated to construct a new deep architecture CDBESN model for the prediction of hourly urban water demand. The structure of the CDBESN model is shown in Figure 3. The model consists of a CDBN with l CRBMs in the bottom layer and ESN in the top layer. Accordingly, the learning process of the CDBESN model includes two stages: feature extraction and regression.
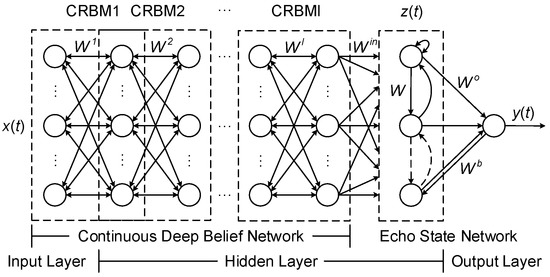
Figure 3.
CDBESN model structure.
In the first stage, a CDBN model is trained in a greedy layer-by-layer unsupervised learning approach and applied to learn the potential nonlinear feature of the original hourly urban water demand data. The output states of the last CRBMs in the CDBN model are the most representative features learned from the hourly water demand data. In the second stage, these features learned by the CDBN model are used as the input of the ESN model for regression. Finally, the trained CDBESN model can be applied for the prediction of hourly water demand.
3. Application Example
3.1. Study Area and Data Collection
In this study, 7800 hourly water demand data were collected from an urban waterworks of Zhuzhou, China from 1 January 2016 to 21 November 2016. The waterworks has a capacity of 15,000 m3/h, and supplies water to about 600,000 urban residents and factories in that region with an area of about 500 km2. The original hourly water demand data were divided into two parts: 84% of the data (the first 6552 hourly data, from 1 January 2016 to 30 September 2016) were used to train the CDBESN model, and the remaining 16% were applied for the testing dataset. Figure 4 shows the original hourly water demand records obtained from the urban waterworks.
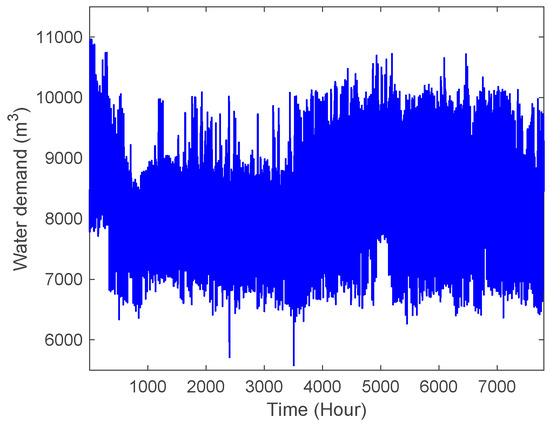
Figure 4.
Original hourly water demand data from 1 January 2016 to 21 November 2016.
3.2. Performance Index
In the experiments, the correlation coefficient (r2), normalized root mean-square error (NRMSE), and mean absolute percentage error (MAPE) were employed to measure the prediction accuracy of the hourly urban water demand forecasting model. The respective equations were defined as follows:
where and are the actual data and prediction data, respectively; and are the means of the actual data and prediction data, respectively; and is the number of prediction data. describes the linearity between the actual data and prediction data, NRMSE signifies the total accuracy of the prediction, and MAPE represents an unbiased estimator for assessing the predictive ability of a model. A large and small NRMSE and MAPE values indicate that the model has superior predictive capability.
4. Results and Discussions
4.1. CDBESN Modeling
The modeling process of CDBESN selects the optimal parameters of the CDBN and ESN models. The numbers of input layer units, hidden layers, and hidden layer units are the major parameters in the CDBN architecture. Currently, no mature theory guides the selection of the numbers of input layer units, hidden layers, and hidden layer units. Thus, an experiment was conducted to determine the three parameters in this study. The numbers of input layer units ranged from 3 to 10, which corresponds to the number of actual historical data related to the prediction data. The numbers of hidden layer units were set to 5, 10, 15, 20, and 25, and the numbers of hidden layers were set to vary from 1 to 3. The update approach and initial values of wij in Equation (1) need to be set. A set of random initial values of wij was used in the first CRBM, and the weight matrix was constantly adjusted until it reached stability. Then, the next CRBM’s weight matrix was initialized by using the previously trained CRBM’s weight matrix, and layer-wise training was performed until all CRBMs were trained completely. Fixed values of the parameters θmin and θmax in Equations (2) and (4) were adopted, and set to be the minimum and maximum values of the original hourly water demand data, respectively. The constant σ in Equations (3) and (5), the learning rates ηw in Equation (6), ηa in Equations (7) and (8), and the noise-control parameters aj and ai in Equations (7) and (8), respectively, were determined by utilizing the fivefold cross-validation strategy and were also considered.
The output states of the last CRBM in the CDBN model were used as the input states of the ESN model. Single-step prediction was utilized, and the ESN model with one output unit was set. The weight matrixes Win, W, and Wb were randomly initialized and remained constant until the ESN training was complete. The relevant optimal parameters of the reservoir were determined by the grid search method and fivefold cross-validation method.
The three evaluation criteria (r2, NRMSE, and MAPE) were used to assess the learning performance of the CDBESN model with different parameters and select the parameters with the best learning performance. According to the method described above, the optimal architecture of the CDBN is 10–5–10; that is, 10 input layer units, 5 units in the first hidden layer, and 10 units in the second hidden layer. The optimal parameters of the ESN are the reservoir units N = 1000, the spectral radius λ = 0.9, and the leaking rate α = 0.3. The results of three performance indexes of the CDBESN model for the hourly water demand prediction in the training stage are r2 = 0.995753, NRMSE = 0.027649, and MAPE = 2.354166.
4.2. Prediction and Results
Figure 5 depicts the prediction results of the hourly water demand data by the proposed CDBESN model in the training stage. As shown in the Figure 5a, the prediction data can accurately follow the changes of the actual hourly water demand data. Figure 5b plots the correlations between the prediction data and the actual data for the training data. Evidently, the prediction data are in good agreement with the actual data. Figure 6 presents the forecasting results of the proposed CDBESN in the testing stage. Figure 6a shows the periodicity and trends of the prediction and actual hourly water demand data are successfully matched. As displayed in Figure 6b, the correlations between the prediction data and the actual data in the testing stage show good agreement. This match further confirms that the CDBESN model has a satisfactory feature extraction ability and prediction performance. The three performance indexes of the CDBESN for the hourly water demand prediction in the testing stage are r2 = 0.995912, NRMSE = 0.027163, and MAPE = 2.469419.
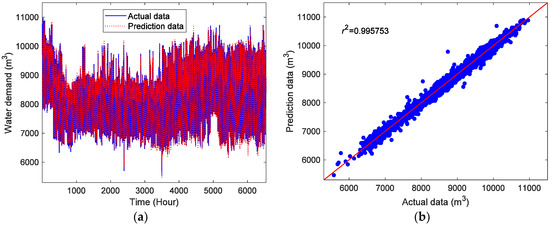
Figure 5.
Forecasting results and scatter plots by the CDBESN model for the training data: (a) Shows the forecasting results, and (b) shows the scatter plots.
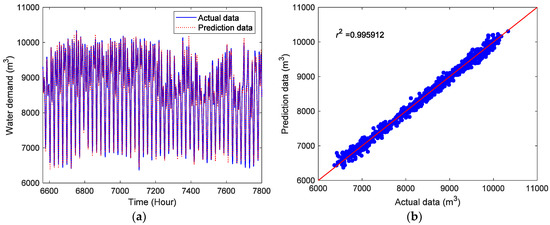
Figure 6.
Forecasting results and scatter plots by the CDBESN model for the testing data: (a) Shows the forecasting results, and (b) shows the scatter plots.
4.3. Comparison Experiment
The predictive ability of the CDBESN model was further evaluated by comparisons with the corresponding performance of the ESN, CDBNN, and SVR models using the same dataset. The ESN model is introduced in Section 2.2, and the numbers of input, reservoir, and output units, as well as the values of the spectral radius, were similarly set to those of the ESN in the CDBESN model. The CDBNN model [27], which consists of CDBN and BP neural networks, uses the same modeling method as the CDBN in the CDBESN model to select the numbers of units and hidden layers. The sigmoid activation function is applied to all hidden layers, and the linear transfer function to the output layer. The BP algorithm is used to adjust the parameters. Finally, the structure of the CDBNN is set to 8–15–10–1. The SVR model is widely applied for water demand forecasting [1]. The insensitive loss function and kernel function are selected by using the particle swarm optimization algorithm, and the inputs utilized are similar to those in the CDBESN model.
Figure 7 plots the forecasting results of the hourly water demand with the ESN, CDBNN, and SVR models in the testing stage. Figure 7a,c,e show the prediction data and actual data of the hourly water demand using the ESN, CDBNN, and SVR models, respectively. Figure 7b,d,f present the scatter plots of the prediction data and actual data with the ESN, CDBNN, and SVR models, respectively. Notably, the ESN, CDBNN, and SVR models follow the trends of the actual hourly water demand data. However, the values of r2 shown in the figure reveal that the CDBESN model slightly outperforms the comparison models in predicting the hourly water demand during the testing stage.
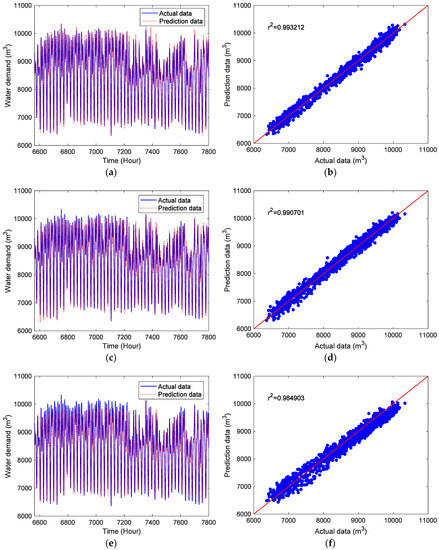
Figure 7.
Prediction results and scatter plots of the hourly water demand in the testing stage using different models: (a) and (b) for ESN, (c) and (d) for CDBNN, and (e) and (f) for SVR.
The performance evaluation indexes r2, NRMSE, and MAPE are employed to estimate the forecasting performances of the ESN, CDBNN, and SVR models by using the same testing dataset, as shown in Table 1. The CDBESN model has the best predictive performance, having the largest r2 value and the smallest NRMSE and MAPE values among all models. Compared with the ESN, CDBNN, and SVR models, the proposed CDBESN model shows increases in r2 of approximately 0.27%, 0.53%, and 1.12%; reductions in NRMSE of 21.91%, 33.28%, and 55.05%; and reductions in MAPE of 25.18%, 36.20%, and 56.55%. The CDBESN approach also has a higher prediction accuracy than the other comparison models in predicting the hourly water demand during the testing stage, partly because of the excellent feature extraction capabilities of the CDBN model and the good regression performance of ESN model in the new deep learning architecture.

Table 1.
Forecasting results of the CDBESN, ESN, CDBNN, and SVR models in the testing stage.
5. Conclusions
In this study, a new CDBESN model is proposed for the prediction of the original hourly urban water demand. The model is constructed by integrating a CDBN-based feature extraction model and an ESN-based regression model. The CDBN model is a stack of multiple CRBMs with continuous state values, which can deal with actual hourly water demand data. The ESN model replaces the BP algorithm of the traditional CDBN model for regression, and can thus effectively overcome the local optimum and slow convergence of the classical BP learning algorithm. The original hourly water demand records obtained from an urban waterworks in Zhuzhou, China are adopted to exploit the proposed CDBESN model. The forecasting performance of the CDBESN model is compared with those of the ESN, CDBNN, and SVR models. Three performance evaluation indexes, namely, r2, NRMSE, and MAPE, are used to estimate the forecasting performances of these models. The empirical results show that the proposed CDBESN model more accurately predicts the hourly urban water demand of the urban waterworks in Zhuzhou, China than the other models. The excellent performance of the proposed CDBESN model is due to the powerful feature extraction capacity of the CDBN model and the good feature regression ability of the ESN model.
Author Contributions
Y.X. designed the research and wrote this paper; J.Z., Z.L., and X.Z. provided professional guidance; and H.T. performed the data collection for this paper.
Funding
This work was supported in part by the National Natural Science Foundation of China (61573299), the Science and Technology Plan Project of Hunan Province (2016TP1020), the Natural Science Foundation of Hunan Province (2017JJ2011, 2017JJ3315), and the Research Project of the Education Department of Hunan Province (17A031).
Acknowledgments
The author would like to thank the anonymous reviewers and editors for their precious suggestions, which have greatly helped to improve the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Msiza, I.S.; Nelwamondo, F.V.; Marwala, T. Artificial neural networks and support vector machines for water demand time series forecasting. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2007; pp. 638–643. [Google Scholar]
- Candelieri, A.; Soldi, D.; Archetti, F. Short-term forecasting of hourly water consumption by using automatic metering readers data. Procedia Eng. 2015, 119, 844–853. [Google Scholar] [CrossRef]
- Chen, G.; Long, T.; Xiong, J.; Bai, Y. Multiple random forests modelling for urban water consumption forecasting. Water Resour. Manag. 2017, 31, 1–15. [Google Scholar] [CrossRef]
- Adamowski, J.; Karapataki, C. Comparison of multivariate regression and artificial neural networks for peak urban water-demand forecasting: Evaluation of different ann learning algorithms. J. Hydrol. Eng. 2010, 15, 729–743. [Google Scholar] [CrossRef]
- Gagliardi, F.; Alvisi, S.; Kapelan, Z.; Franchini, M. A probabilistic short-term water demand forecasting model based on the markov chain. Water 2017, 9, 507. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, P.; Li, C.; Xie, J.; Wang, Y. A multi-scale relevance vector regression approach for daily urban water demand forecasting. J. Hydrol. 2014, 517, 236–245. [Google Scholar] [CrossRef]
- Candelieri, A. Clustering and support vector regression for water demand forecasting and anomaly detection. Water 2017, 9, 224. [Google Scholar] [CrossRef]
- Brentan, B.M.; Luvizotto, E., Jr.; Herrera, M.; Izquierdo, J.; Pérez-García, R. Hybrid regression model for near real-time urban water demand forecasting. J. Comput. Appl. Math. 2017, 309, 532–541. [Google Scholar] [CrossRef]
- Shabani, S.; Candelieri, A.; Archetti, F.; Naser, G. Gene expression programming coupled with unsupervised learning: A two-stage learning process in multi-scale, short-term water demand forecasts. Water 2018, 10, 142. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.A.; Soyer, R.; Roberson, J.A. Urban water demand forecasting: Review of methods and models. J. Water Resour. Plan. Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Jain, A.; Kumar Varshney, A.; Chandra Joshi, U. Short-term water demand forecast modelling at IIT Kanpur using artificial neural networks. Water Resour. Manag. 2001, 15, 299–321. [Google Scholar] [CrossRef]
- Adamowski, J.F. Peak daily water demand forecast modeling using artificial neural networks. J. Water Resour. Plan. Manag. 2008, 134, 119–128. [Google Scholar] [CrossRef]
- Bennett, C.; Stewart, R.A.; Beal, C.D. Ann-based residential water end-use demand forecasting model. Expert Syst. Appl. 2013, 40, 1014–1023. [Google Scholar] [CrossRef]
- Al-Zahrani, M.A.; Abo-Monasar, A. Urban residential water demand prediction based on artificial neural networks and time series models. Water Resour. Manag. 2015, 29, 3651–3662. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Sarikaya, R.; Hinton, G.E.; Deoras, A. Application of deep belief networks for natural language understanding. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 778–784. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–spatial classification of hyperspectral data based on deep belief network. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Zhao, Z.; Jiao, L.; Zhao, J.; Gu, J.; Zhao, J. Discriminant deep belief network for high-resolution sar image classification. Pattern Recognit. 2017, 61, 686–701. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhang, H.; Liang, T. Electric locomotive bearing fault diagnosis using novel convolutional deep belief network. IEEE Trans. Ind. Electron. 2017, 65, 2727–2736. [Google Scholar] [CrossRef]
- Zheng, J.; Fu, X.; Zhang, G. Research on exchange rate forecasting based on deep belief network. Neural Comput. Appl. 2017. [Google Scholar] [CrossRef]
- Fu, G. Deep belief network based ensemble approach for cooling load forecasting of air-conditioning system. Energy 2018, 148, 269–282. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, Z.; Xie, J.; Li, C. Daily reservoir inflow forecasting using multiscale deep feature learning with hybrid models. J. Hydrol. 2016, 532, 193–206. [Google Scholar] [CrossRef]
- Bai, Y.; Sun, Z.; Zeng, B.; Deng, J.; Li, C. A multi-pattern deep fusion model for short-term bus passenger flow forecasting. Appl. Soft Comput. 2017, 58, 669–680. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Long, Z.; Chen, Y. A novel dual-scale deep belief network method for daily urban water demand forecasting. Energies 2018, 11, 1068. [Google Scholar] [CrossRef]
- Kuremoto, T.; Kimura, S.; Kobayashi, K.; Obayashi, M. Time series forecasting using a deep belief network with restricted boltzmann machines. Neurocomputing 2014, 137, 47–56. [Google Scholar] [CrossRef]
- Qin, M.; Li, Z.; Du, Z. Red tide time series forecasting by combining arima and deep belief network. Knowledge-Based Syst. 2017, 125, 39–52. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Long, Z.; Lv, M. Daily urban water demand forecasting based on chaotic theory and continuous deep belief neural network. Neural Process. Lett. 2018. [Google Scholar] [CrossRef]
- Ding, S.; Su, C.; Yu, J. An optimizing bp neural network algorithm based on genetic algorithm. Artif. Intell. Rev. 2011, 36, 153–162. [Google Scholar] [CrossRef]
- Sun, X.; Li, T.; Li, Q.; Huang, Y.; Li, Y. Deep belief echo-state network and its application to time series prediction. Knowledge-Based Syst. 2017, 130, 17–29. [Google Scholar] [CrossRef]
- Jaeger, H. The “Echo State” Approach to Analysing and Training Recurrent Neural Networks—With an Erratum Note; GMD Report 148; German National Research Center for Information Technology: Bonn, Germany, 2001. [Google Scholar]
- Jaeger, H. Short Term Memory in Echo State Networks; GMD Report 152; German National Research Center for Information Technology: Bonn, Germany, 2002. [Google Scholar]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef]
- Jaeger, H.; Lukoševičius, M.; Popovici, D.; Siewert, U. Optimization and applications of echo state networks with leaky- integrator neurons. Neural Netw. 2007, 20, 335–352. [Google Scholar] [CrossRef]
- Lun, S.-X.; Yao, X.-S.; Qi, H.-Y.; Hu, H.-F. A novel model of leaky integrator echo state network for time-series prediction. Neurocomputing 2015, 159, 58–66. [Google Scholar] [CrossRef]
- Chouikhi, N.; Ammar, B.; Rokbani, N.; Alimi, A.M. Pso-based analysis of echo state network parameters for time series forecasting. Appl. Soft Comput. 2017, 55, 211–225. [Google Scholar] [CrossRef]
- Chen, H.; Murray, A. A continuous restricted Boltzmann machine with a hardware- amenable learning algorithm. In Proceedings of the 12th International Conference on Artificial Neural Networks, Madrid, Spain, 28–30 August 2002; pp. 358–363. [Google Scholar]
- Hinton, G.E. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002, 14, 1771–1800. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).