Dynamic Modeling of Sediment Budget in Shihmen Reservoir Watershed in Taiwan
Abstract
1. Background
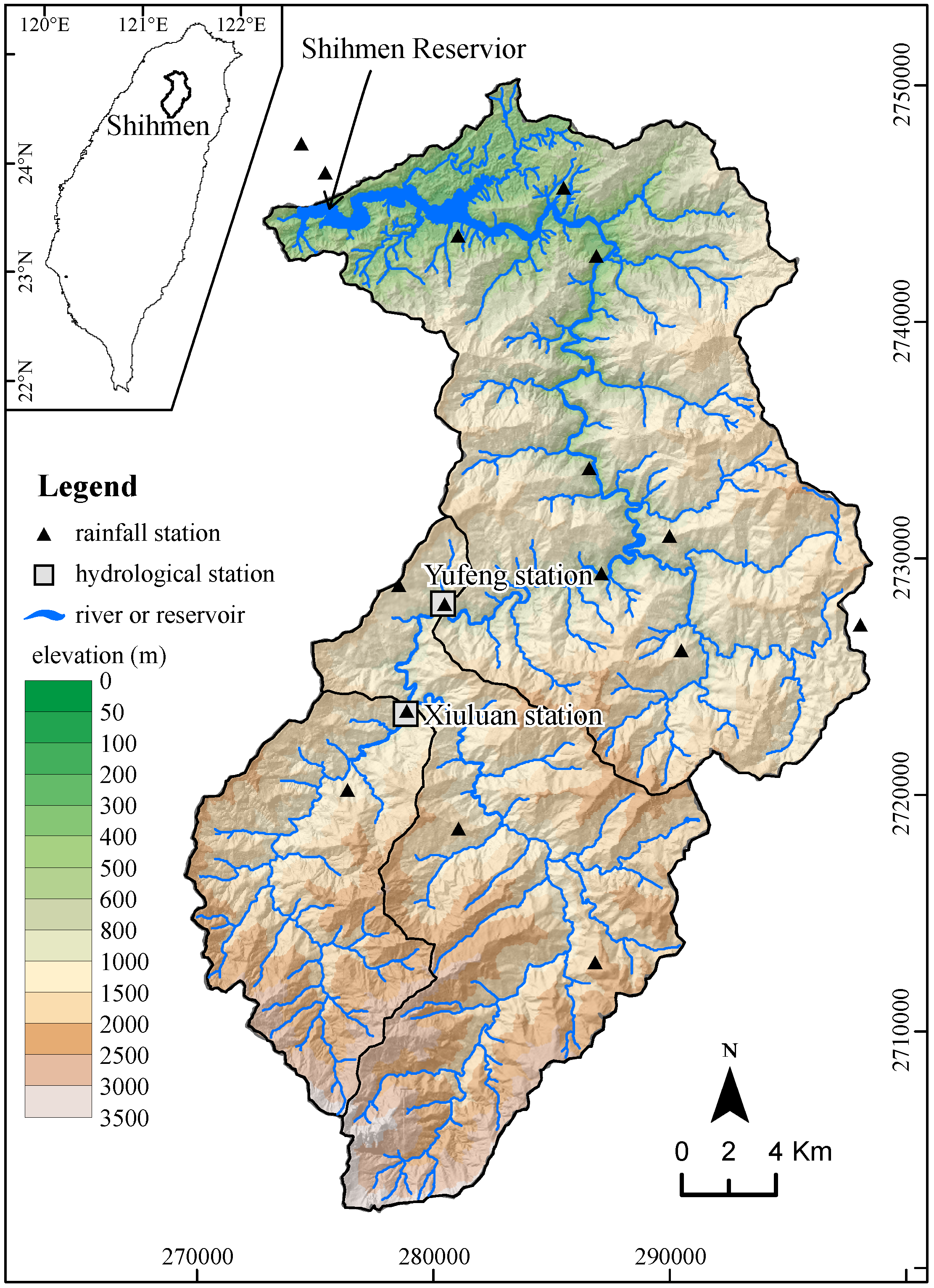
2. Study Area—Shihmen Reservoir Watershed
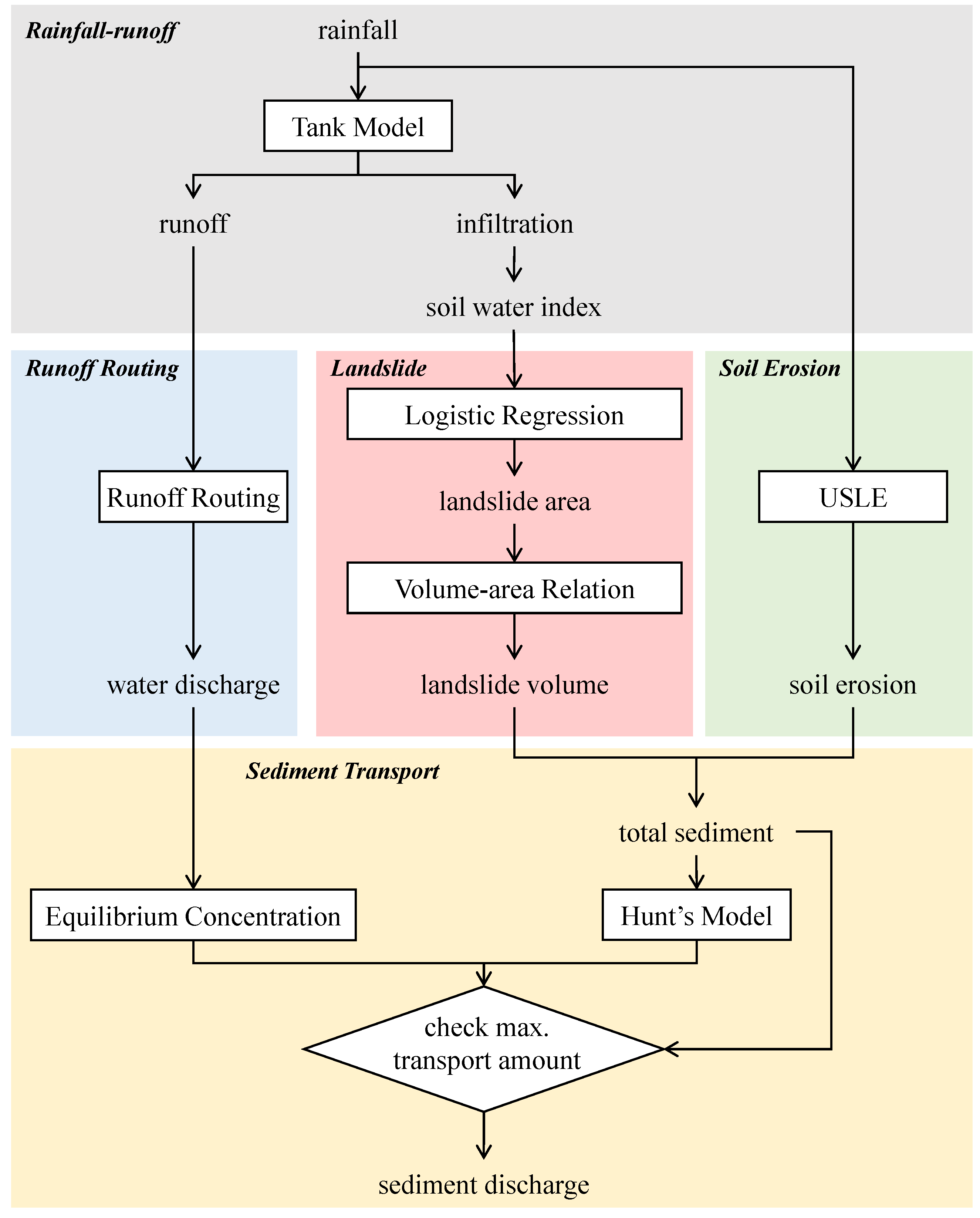
3. Introduction to GSPTM
3.1. Rainfall–Runoff Model
3.2. Sediment Production Prediction
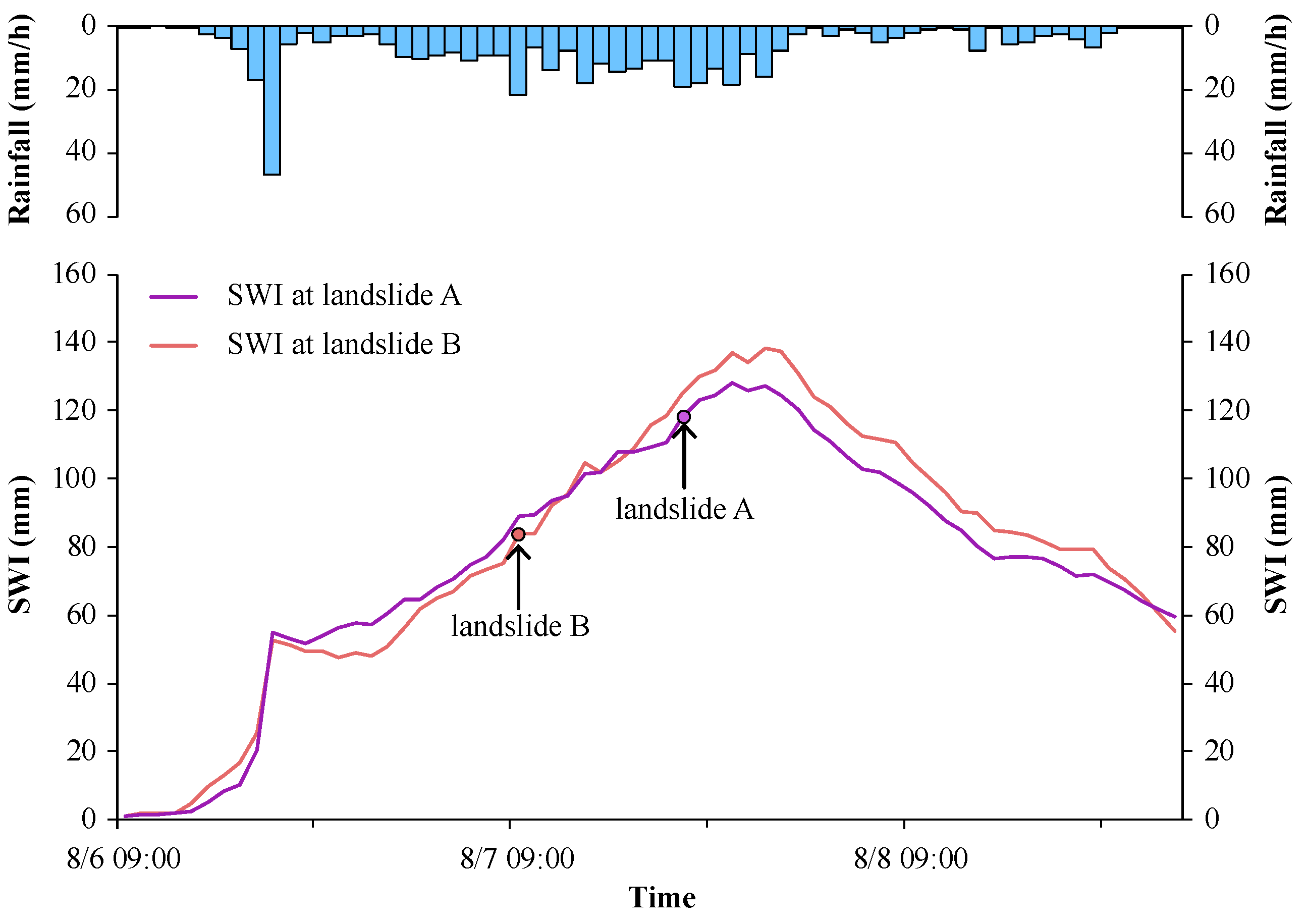
3.2.1. Landslide Model
3.2.2. Soil Erosion Prediction
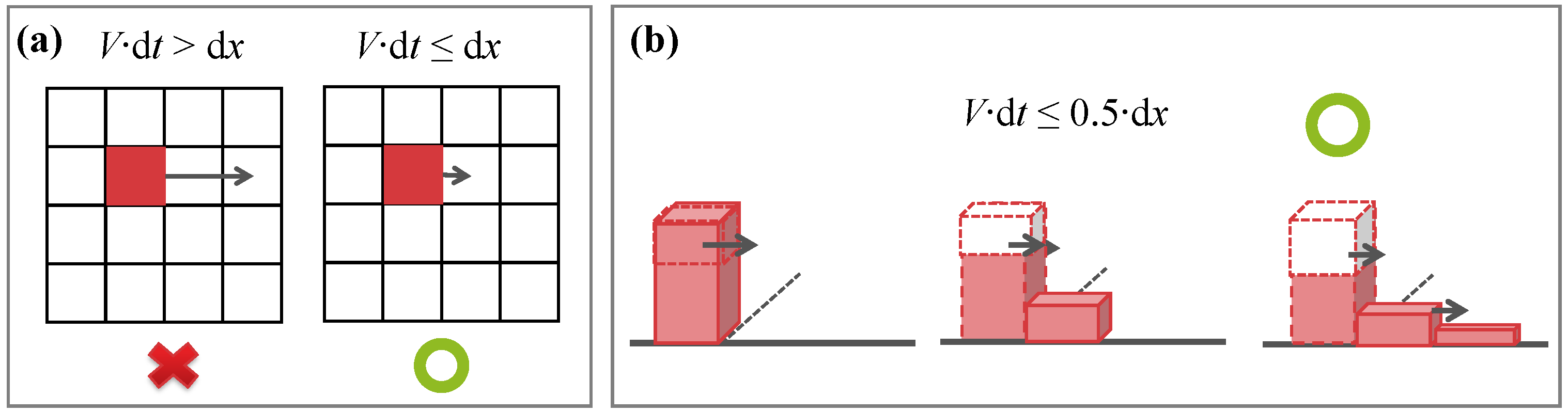
3.3. Mass Movement Simulation
3.4. Runoff Simulation
3.5. Sediment Transport
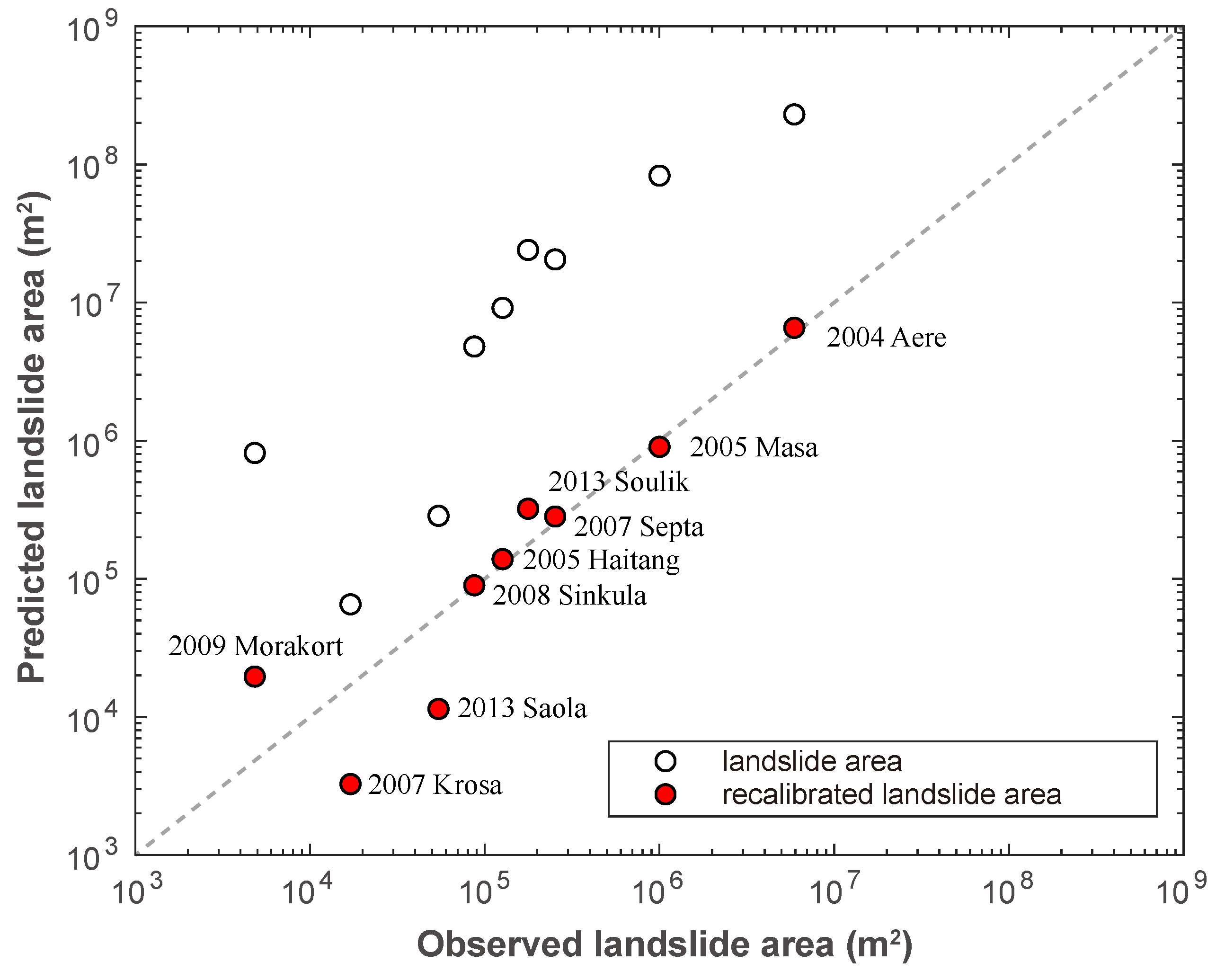
3.6. Model Verification and Performance Elevation
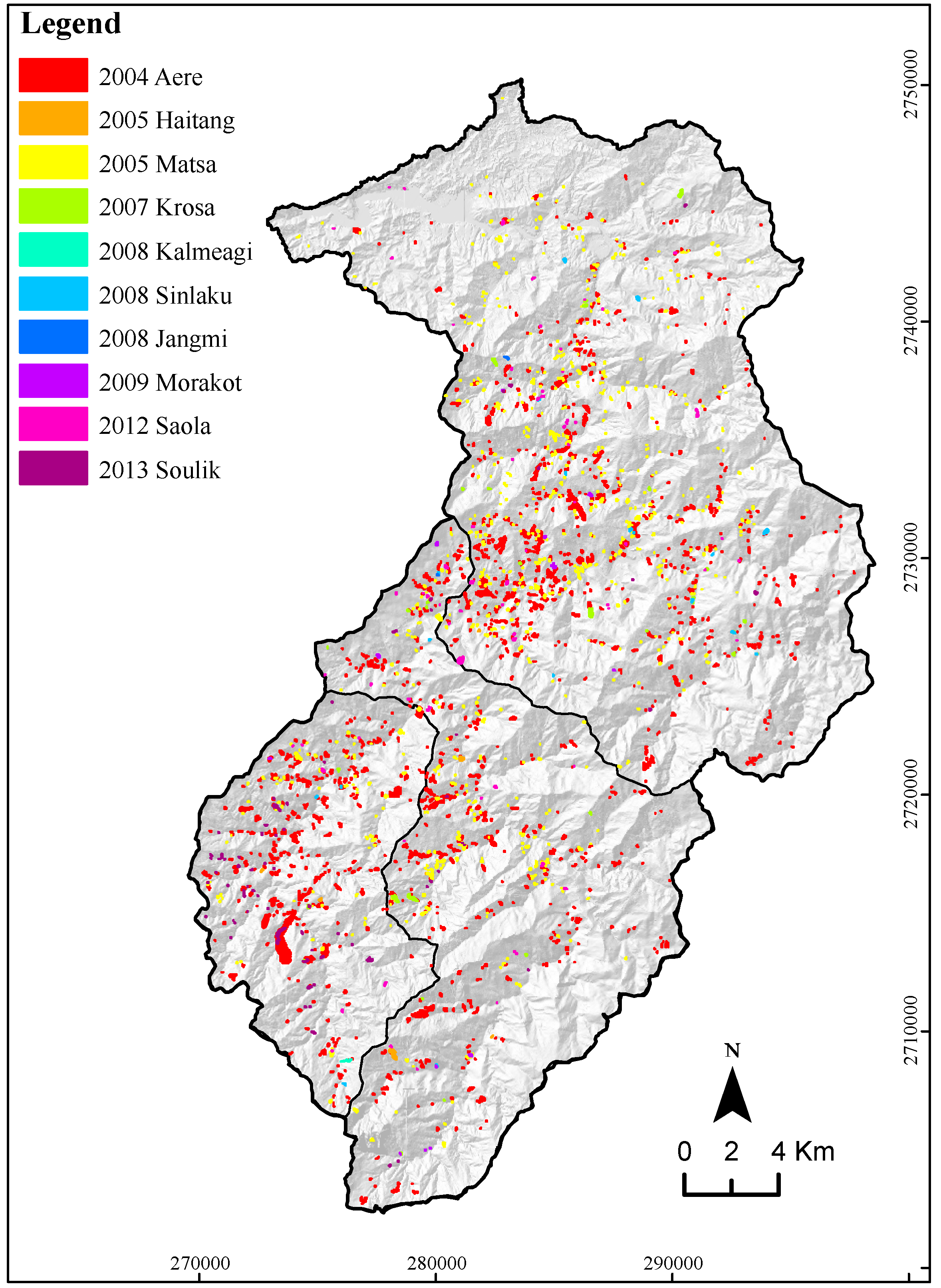
4. Result and Discussion—Reconstruction of Typhoon Morakot Event
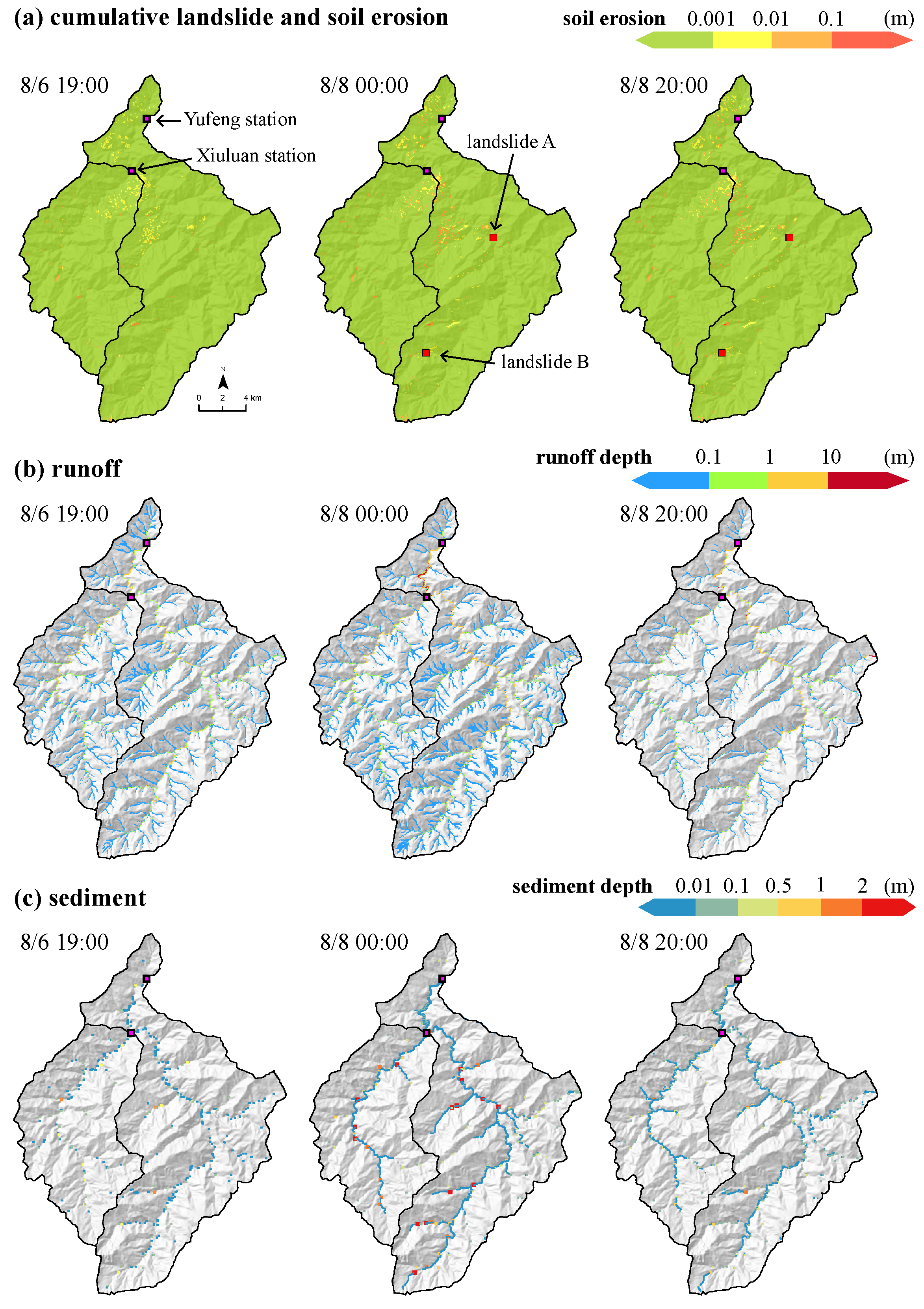
4.1. Mass Production by Landslide and Soil Erosion
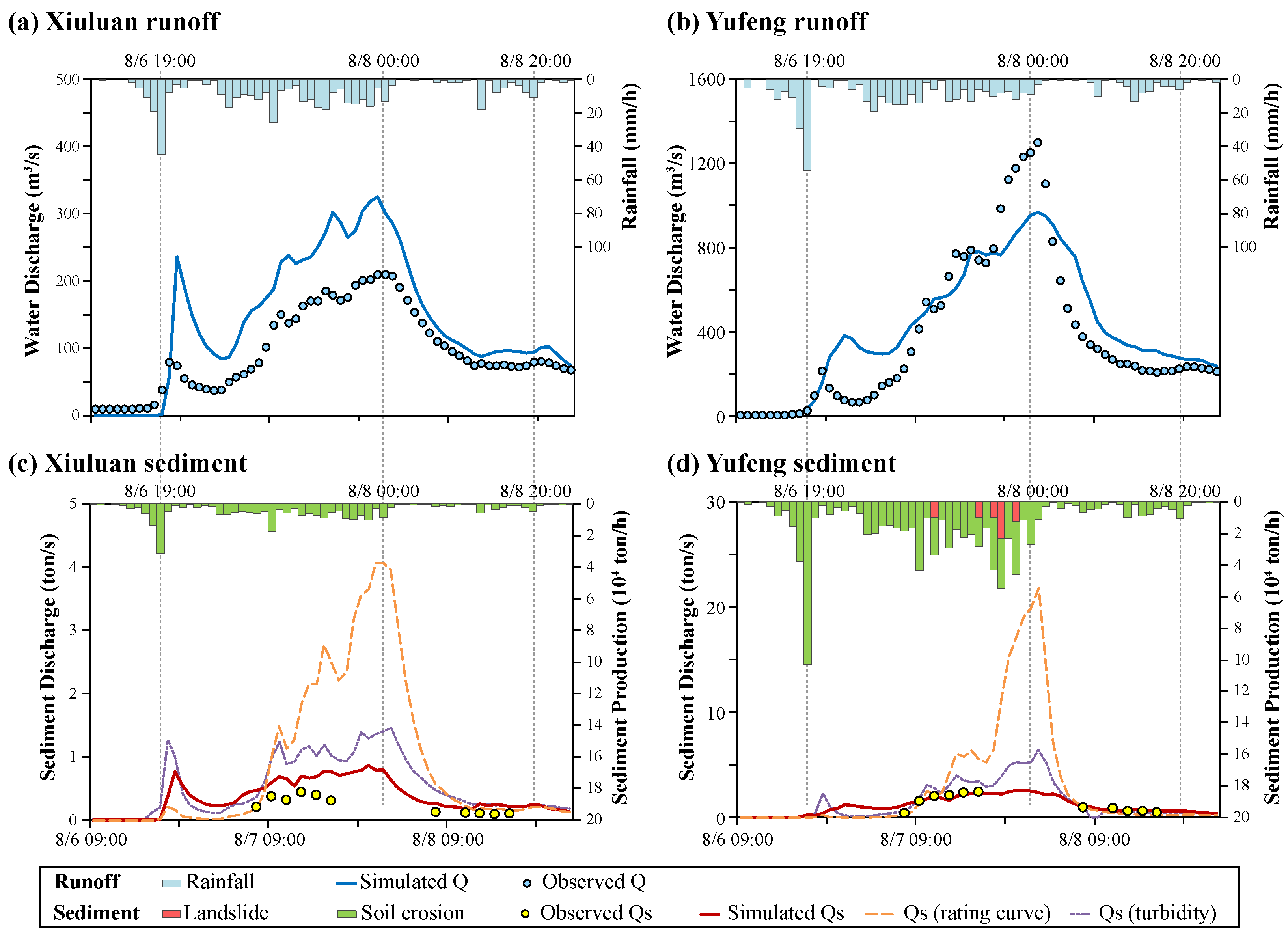
4.2. Sediment Transport Condition
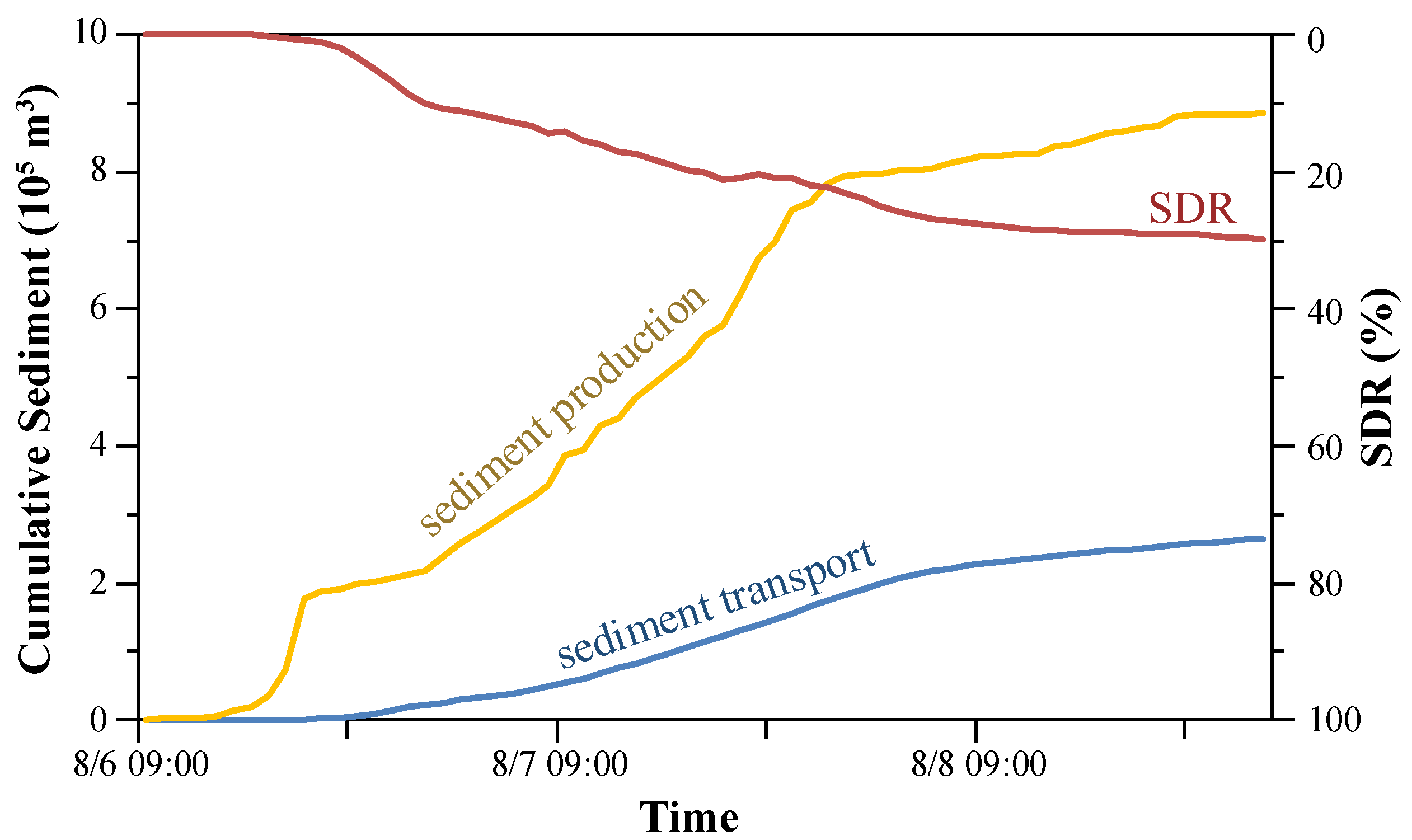
4.3. Sediment Delivery Condition
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dadson, S.J.; Hovius, N.; Chen, H.; Dade, W.B.; Lin, J.C.; Hsu, M.L.; Lin, C.W.; Horng, M.J.; Chen, T.C.; Milliman, J.; et al. Earthquake-triggered increase in sediment delivery from an active mountain belt. Geology 2004, 32, 733–736. [Google Scholar] [CrossRef]
- Kao, S.J.; Lee, T.Y.; Milliman, J.D. Calculating highly fluctuated suspended sediment fluxes from mountainous rivers in Taiwan. Terr. Atmos. Ocean. Sci. 2005, 16, 653. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, Y.; Lee, H. The budget of sediment supply and removal triggered by typhoon tainfall in the Kaoping river basin. In Proceedings of the 2013 APEC Typhoon Symposium, Taipei, Taiwan, 21–23 October 2013; pp. 21–23. [Google Scholar]
- Chen, Y.C.; Chang, K.T.; Lee, H.Y.; Chiang, S.H. Average landslide erosion rate at the watershed scale in southern Taiwan estimated from magnitude and frequency of rainfall. Geomorphology 2015, 228, 756–764. [Google Scholar] [CrossRef]
- Dong, J.J.; Lai, P.J.; Chang, C.P.; Yang, S.H.; Yeh, K.C.; Liao, J.J.; Pan, Y.W. Deriving landslide dam geometry from remote sensing images for the rapid assessment of critical parameters related to dam-breach hazards. Landslides 2014, 11, 93–105. [Google Scholar] [CrossRef]
- Lin, G.W.; Chen, H.; Petley, D.N.; Horng, M.J.; Wu, S.J.; Chuang, B. Impact of rainstorm-triggered landslides on high turbidity in a mountain reservoir. Eng. Geol. 2011, 117, 97–103. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Gao, Y.; Annandale, G.W.; Morris, G.L.; Jiang, E.; Zhang, J.; Cao, Y.; Carling, P.; Fu, K.; Guo, Q.; et al. Sustainable sediment management in reservoirs and regulated rivers: Experiences from five continents. Earths Future 2014, 2, 256–280. [Google Scholar] [CrossRef]
- Wang, H.W.; Kondolf, M.; Tullos, D.; Kuo, W.C. Sediment management in Taiwan’s reservoirs and barriers to implementation. Water 2018, 10, 1034. [Google Scholar] [CrossRef]
- Brunner, G.W. HEC-RAS 5.0 Users Manual; US Army Corps of Engineers, Institute for Water Resources, Hydrologic Engineering Center: Washington, DC, USA, 2016. [Google Scholar]
- Lee, H.Y.; Lin, Y.T.; Chiu, Y.J. Quantitative estimation of reservoir sedimentation from three typhoon events. J. Hydrol. Eng. 2006, 11, 362–370. [Google Scholar] [CrossRef]
- Krysanova, V.; Arnold, J.G. Advances in ecohydrological modelling with SWAT—A review. Hydrol. Sci. J. 2008, 53, 939–947. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Larry, W. Applied Hydrology; MacGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Brutsaert, W. Hydrology: An Introduction; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Sayama, T.; McDonnell, J.J. A new time-space accounting scheme to predict stream water residence time and hydrograph source components at the watershed scale. Water Resour. Res. 2009, 45, W07401. [Google Scholar] [CrossRef]
- Sayama, T.; Ozawa, G.; Kawakami, T.; Nabesaka, S.; Fukami, K. Rainfall–runoff–inundation analysis of the 2010 Pakistan flood in the Kabul River basin. Hydrol. Sci. J. 2012, 57, 298–312. [Google Scholar] [CrossRef]
- Chae, B.G.; Park, H.J.; Catani, F.; Simoni, A.; Berti, M. Landslide prediction, monitoring and early warning: A concise review of state-of-the-art. Geosci. J. 2017, 21, 1033–1070. [Google Scholar] [CrossRef]
- Wu, Y.H.; Liu, K.F.; Chen, Y.C. Comparison between FLO-2D and Debris-2D on the application of assessment of granular debris flow hazards with case study. J. Mt. Sci. 2013, 10, 293–304. [Google Scholar] [CrossRef]
- Wu, Y.H.; Liu, K.F. The Influence of Countermeasure on Debris Flow Hazards with Numerical Simulation. In Landslide Science for a Safer Geoenvironment; Sassa, K., Canuti, P., Yin, Y., Eds.; Springer: Cham, Switzerland, 2014; pp. 473–478. [Google Scholar]
- Han, Z.; Chen, G.; Li, Y.; Xu, L.; Zheng, L.; Zhang, Y. A new approach for analyzing the velocity distribution of debris flows at typical cross-sections. Nat. Hazards 2014, 74, 2053–2070. [Google Scholar] [CrossRef]
- Liu, K.F.; Wei, S.C.; Wu, Y.H. The influence of accumulated precipitation on debris flow hazard area. In Landslide Science for a Safer Geoenvironment; Springer: Berlin, Germany, 2014; pp. 45–50. [Google Scholar]
- Iverson, R.M.; George, D.L. A depth-averaged debris-flow model that includes the effects of evolving dilatancy. I. Physical basis. Proc. R. Soc. A 2014, 470, 20130819. [Google Scholar] [CrossRef]
- George, D.L.; Iverson, R.M. A depth-averaged debris-flow model that includes the effects of evolving dilatancy. II. Numerical predictions and experimental tests. Proc. R. Soc. A 2014, 470, 20130820. [Google Scholar] [CrossRef]
- Han, Z.; Chen, G.; Li, Y.; Tang, C.; Xu, L.; He, Y.; Huang, X.; Wang, W. Numerical simulation of debris-flow behavior incorporating a dynamic method for estimating the entrainment. Eng. Geol. 2015, 190, 52–64. [Google Scholar] [CrossRef]
- Papanicolaou, A.T.N.; Elhakeem, M.; Krallis, G.; Prakash, S.; Edinger, J. Sediment transport modeling review—Current and future developments. J. Hydraul. Eng. 2008, 134, 1–14. [Google Scholar] [CrossRef]
- Iverson, R.M.; Ouyang, C. Entrainment of bed material by Earth-surface mass flows: Review and reformulation of depth-integrated theory. Rev. Geophys. 2015, 53, 27–58. [Google Scholar] [CrossRef]
- Alatorre, L.; Beguería, S.; García-Ruiz, J. Regional scale modeling of hillslope sediment delivery: A case study in the Barasona Reservoir watershed (Spain) using WATEM/SEDEM. J. Hydrol. 2010, 391, 109–123. [Google Scholar] [CrossRef]
- Easton, Z.M.; Fuka, D.R.; White, E.D.; Collick, A.S.; Biruk Ashagre, B.; McCartney, M.; Awulachew, S.B.; Ahmed, A.A.; Steenhuis, T.S. A multi basin SWAT model analysis of runoff and sedimentation in the Blue Nile, Ethiopia. Hydrol. Earth Syst. Sci. 2010, 14, 1827–1841. [Google Scholar] [CrossRef]
- Liu, K.F.; Wu, Y.H.; Chen, Y.C.; Chiu, Y.J.; Shih, S.S. Large-scale simulation of watershed mass transport: A case study of Tsengwen reservoir watershed, southwest Taiwan. Nat. Hazards 2013, 67, 855–867. [Google Scholar] [CrossRef]
- Kabir, M.A.; Dutta, D.; Hironaka, S. Estimating sediment budget at a river basin scale using a process-based distributed modelling approach. Water Resour. Manag. 2014, 28, 4143–4160. [Google Scholar] [CrossRef]
- Okada, K. Soil water index. Sokkojihou 2002, 69, 67–100. [Google Scholar]
- Osanai, N.; Shimizu, T.; Kuramoto, K.; Kojima, S.; Noro, T. Japanese early-warning for debris flows and slope failures using rainfall indices with Radial Basis Function Network. Landslides 2010, 7, 325–338. [Google Scholar] [CrossRef]
- Chen, S.; Tsai, C.; Chen, C.; Chen, M. Soil Water Index applied as a debris flow warning-reference based on a tank model. J. Chin. Soil Water Conserv. 2013, 44, 31–43. [Google Scholar]
- Ishihara, Y.; Kobatake, S. Runoff model for flood forecasting. Bull. Disaster Prev. Res. Inst. 1979, 29, 27–43. [Google Scholar]
- Chen, Y.C.; Chang, K.T.; Chiu, Y.J.; Lau, S.M.; Lee, H.Y. Quantifying rainfall controls on catchment-scale landslide erosion in Taiwan. Earth Surf. Proc. Land. 2013, 38, 372–382. [Google Scholar] [CrossRef]
- Williams, J.; Berndt, H. Sediment yield prediction based on watershed hydrology. Trans. ASAE 1977, 20, 1100–1104. [Google Scholar] [CrossRef]
- Hunt, B. Newtonian fluid mechanics treatment of debris flows and avalanches. J. Hydraul. Eng. ASCE 1994, 120, 1350–1363. [Google Scholar] [CrossRef]
- Yeh, T.T. Simulation on the Rainfall–Runoff Process in Shihmen Watershed. Master’s Thesis, National Central University, Taoyuan, Taiwan, 2003. [Google Scholar]
- Takahashi, T. Debris flow. Annu. Rev. Fluid Mech. 1981, 13, 57–77. [Google Scholar] [CrossRef]
- Water Resource Agency. Hydrological Yearbook, 2008 Part I: Rainfall; Technical Report; Water Resource Agency, Ministry of Economic Affair: Taipei, Taiwan, 2009. [Google Scholar]
- Northern Region Water Resource Office. Evaluation of Morphological Effects in Downstream River due to Sediment Venting and Replenishment from the Shihmen Reservoir, Taoyuan; Technical Report; Water Resources Agency, Ministry of Economic Affairs: Taipei, Taiwan, 2014. [Google Scholar]
- Tsai, Z.X.; You, G.J.Y.; Lee, H.Y.; Chiu, Y.J. Modeling the sediment yield from landslides in the Shihmen Reservoir watershed, Taiwan. Earth Surf. Proc. Land. 2013, 38, 661–674. [Google Scholar] [CrossRef]
- Saito, H.; Matsuyama, H. Catastrophic landslide disasters triggered by record-breaking rainfall in Japan: Their accurate detection with Normalized Soil Water Index in the Kii Peninsula for the year 2011. Sci. Online Lett. Atmos. 2012, 8, 81–84. [Google Scholar] [CrossRef]
- Chen, C.W.; Oguchi, T.; Hayakawa, Y.S.; Saito, H.; Chen, H.; Lin, G.W.; Wei, L.W.; Chao, Y.C. Sediment yield during typhoon events in relation to landslides, rainfall, and catchment areas in Taiwan. Geomorphology 2018, 303, 540–548. [Google Scholar] [CrossRef]
- Menard, S. Applied Logistic Regression Analysis; Sage: Thousand Oaks, CA, USA, 2002; Volume 106. [Google Scholar]
- Chang, K.T.; Chiang, S.H.; Hsu, M.L. Modeling typhoon-and earthquake-induced landslides in a mountainous watershed using logistic regression. Geomorphology 2007, 89, 335–347. [Google Scholar] [CrossRef]
- Chang, K.T.; Chiang, S.H. An integrated model for predicting rainfall-induced landslides. Geomorphology 2009, 105, 366–373. [Google Scholar] [CrossRef]
- Chan, H.C.; Chen, P.A.; Lee, J.T. Rainfall-induced landslide susceptibility using a rainfall–runoff model and logistic regression. Water 2018, 10, 1354. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Larsen, I.J.; Montgomery, D.R.; Korup, O. Landslide erosion controlled by hillslope material. Nat. Geosci. 2010, 3, 247. [Google Scholar] [CrossRef]
- Liu, Y.H.; Li, D.H.; Chen, W.; Lin, B.S.; Seeboonruang, U.; Tsai, F. Soil erosion modeling and comparison using slope units and grid cells in Shihmen reservoir watershed in northern Taiwan. Water 2018, 10, 1387. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Rainfall energy and its relationship to soil loss. Eos Trans. Am. Geophys. Union 1958, 39, 285–291. [Google Scholar] [CrossRef]
- Yang, S.; Jan, C.; Huang, C.; Tseng, K. Application of hourly rainfall data to estimate the rainfall erosion index. J. Chin. Soil Water Conserv. 2010, 41, 189–199. [Google Scholar]
- Lin, C.Y.; Lin, W.T.; Chou, W.C. Soil erosion prediction and sediment yield estimation: The Taiwan experience. Soil Tillage Res. 2002, 68, 143–152. [Google Scholar] [CrossRef]
- McCool, D.; Brown, L.; Foster, G.; Mutchler, C.; Meyer, L. Revised slope steepness factor for the Universal Soil Loss Equation. Trans. ASAE 1987, 30, 1387–1396. [Google Scholar] [CrossRef]
- Hsieh, Z.; Wang, M. An Atlas Major Soils of Taiwan; Soil Survey and Testing Center, National Chung Hsing University: Taichung, Taiwan, 1991. [Google Scholar]
- Lee, C. Soil and Water Conservation Handbook; Soil and Water Conservation Bureau: Nantou, Taiwan, 2017. [Google Scholar]
- Chiang, S.H.; Chang, K.T.; Mondini, A.C.; Tsai, B.W.; Chen, C.Y. Simulation of event-based landslides and debris flows at watershed level. Geomorphology 2012, 138, 306–318. [Google Scholar] [CrossRef]
- Wu, Y.H.; Liu, K.F. Formulas for calibration of rheological parameters of bingham fluid in couette rheometer. J. Fluids Eng. 2015, 137, 041202. [Google Scholar] [CrossRef]
- Tarboton, D.G. A new method for the determination of flow directions and upslope areas in grid digital elevation models. Water Resour. Res. 1997, 33, 309–319. [Google Scholar] [CrossRef]
- Yang, T.H.; Chen, Y.C.; Chang, Y.C.; Yang, S.C.; Ho, J.Y. Comparison of different grid cell ordering approaches in a simplified inundation model. Water 2015, 7, 438–454. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Leopold, L.B.; Wolman, M.G.; Miller, J.P. Fluvial Processes in Geomorphology; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Tsai, Y.F.; Shieh, C.L. Experimental and numerical studies on the morphological similarity of debris-flow fans. J. Chin. Inst. Eng. 1997, 20, 629–642. [Google Scholar] [CrossRef]
- Northern Region Water Resource Office. Artificial and Automatic Monitoring for Water Quality at Shihmen Reservoir and Watershed, Taoyuan; Technical Report; Water Resources Agency, Ministry of Economic Affairs: Taipei, Taiwan, 2014. [Google Scholar]
- Walling, D.E. The sediment delivery problem. J. Hydrol. 1983, 65, 209–237. [Google Scholar] [CrossRef]
- Shen, C.W.; Liu, S.H.; Chen, Y.C.; Chiu, Y.J.; Liu, K.F. Budget of landslide-induced sediment for the watersheds in Taiwan—A case study in pre- and post typhoon Morakot periods. J. Taiwan Agric. Eng. 2016, 62, 23–42. [Google Scholar]
| Attribute (unit) | Variable | Coefficient b | Standard Error of the Mean (%) | Wald | p-Value |
|---|---|---|---|---|---|
| elevation (m) | 8.0 × | 0.000 | 106.810 | 0.000 | |
| inclination () | 0.058 | 0.002 | 554.326 | 0.000 | |
| aspect sine (-) | 0.076 | 0.028 | 7.211 | 0.007 | |
| aspect cosine (-) | −0.45 | 0.028 | 274.032 | 0.000 | |
| longitudinal curvature (m) | −1.84 | 0.710 | 6.740 | 0.009 | |
| planar curvature (m) | −1.67 | 0.684 | 5.942 | 0.015 | |
| topographic wetting index (m) | 0.25 | 0.016 | 245.940 | 0.000 | |
| distance to river (km) | −9.0 × | 0.000 | 58.786 | 0.000 | |
| distance to ridge (km) | 5.0 × | 0.000 | 27.411 | 0.000 | |
| distance to road (km) | 4.0 × | 0.000 | 8.967 | 0.003 | |
| geological category | 1.0 | 0.000 | 106.810 | 0.000 | |
| soil water index (m) | 0.00657 | 0.000 | 985.196 | 0.000 | |
| constant (-) | −7.534 | 0.275 | 695.069 | 0.000 |
| Category | Value | Category | Value |
|---|---|---|---|
| Erhchiu formation (Eh) | −0.297 | Kangkou formation (Kk) | −1.008 |
| Tapu Formation (Tp) | 1.271 | Tsuku Formation (Tu) | −0.175 |
| Mushan Form (Ms) | 0.237 | Terrace Deposits (t) | −2.302 |
| Paling Form (Pl) | 0.714 | Piling Shale (Pi) | 0.000 |
| Peiliao Formation (Pe) | 0.136 | Shihti Formation (St) | −0.058 |
| Szeleng Sandstone (Ss) | −0.158 | Hsitsun Formation (Ht) | −0.300 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-C.; Wu, Y.-H.; Shen, C.-W.; Chiu, Y.-J. Dynamic Modeling of Sediment Budget in Shihmen Reservoir Watershed in Taiwan. Water 2018, 10, 1808. https://doi.org/10.3390/w10121808
Chen Y-C, Wu Y-H, Shen C-W, Chiu Y-J. Dynamic Modeling of Sediment Budget in Shihmen Reservoir Watershed in Taiwan. Water. 2018; 10(12):1808. https://doi.org/10.3390/w10121808
Chicago/Turabian StyleChen, Yi-Chin, Ying-Hsin Wu, Che-Wei Shen, and Yu-Jia Chiu. 2018. "Dynamic Modeling of Sediment Budget in Shihmen Reservoir Watershed in Taiwan" Water 10, no. 12: 1808. https://doi.org/10.3390/w10121808
APA StyleChen, Y.-C., Wu, Y.-H., Shen, C.-W., & Chiu, Y.-J. (2018). Dynamic Modeling of Sediment Budget in Shihmen Reservoir Watershed in Taiwan. Water, 10(12), 1808. https://doi.org/10.3390/w10121808







