Open Channel Sluice Gate Scouring Parameters Prediction: Different Scenarios of Dimensional and Non-Dimensional Input Parameters
Abstract
1. Introduction
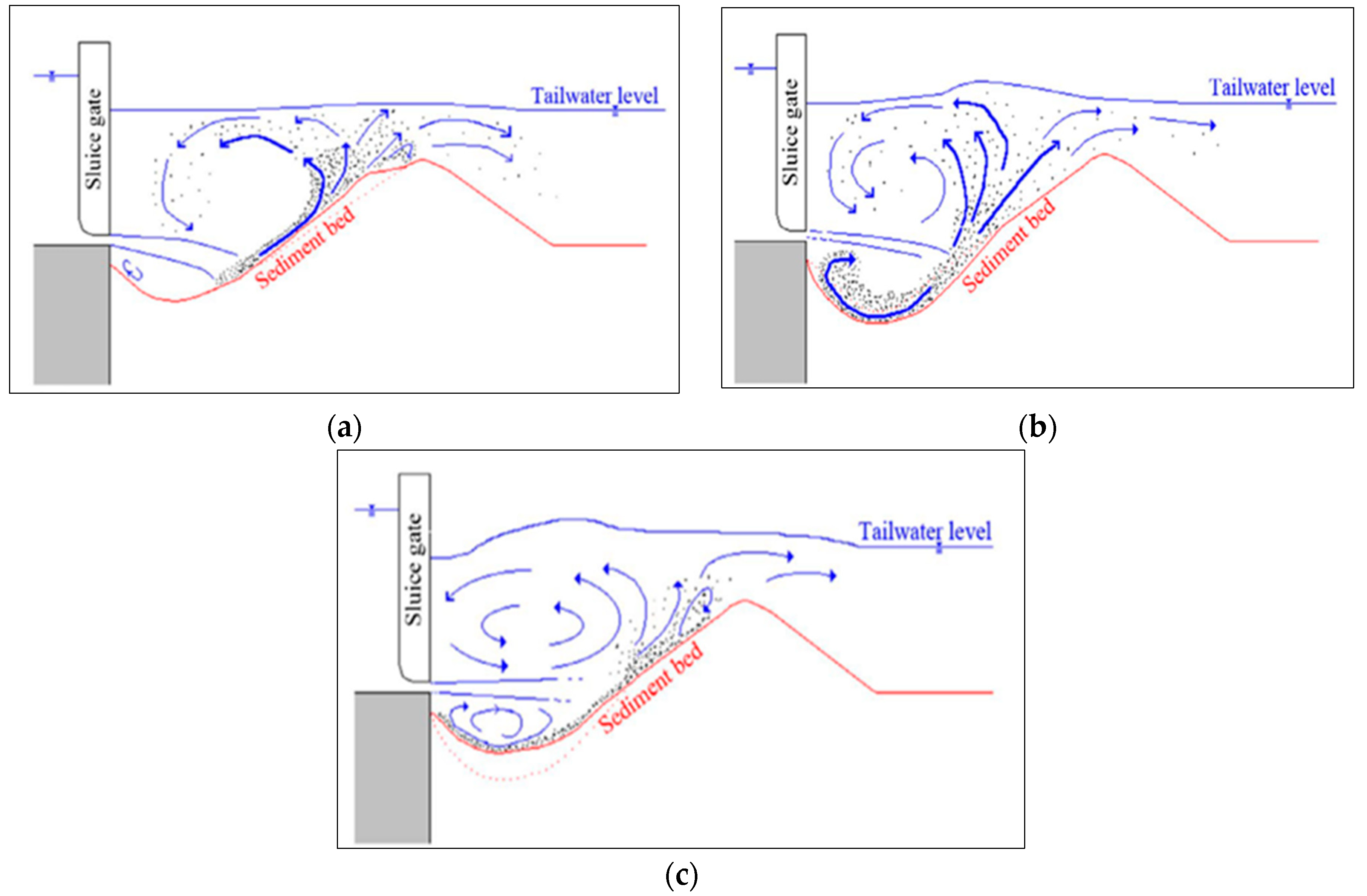
2. Laboratory Experiment of Scouring in Sluice Gate
3. Description of the Models
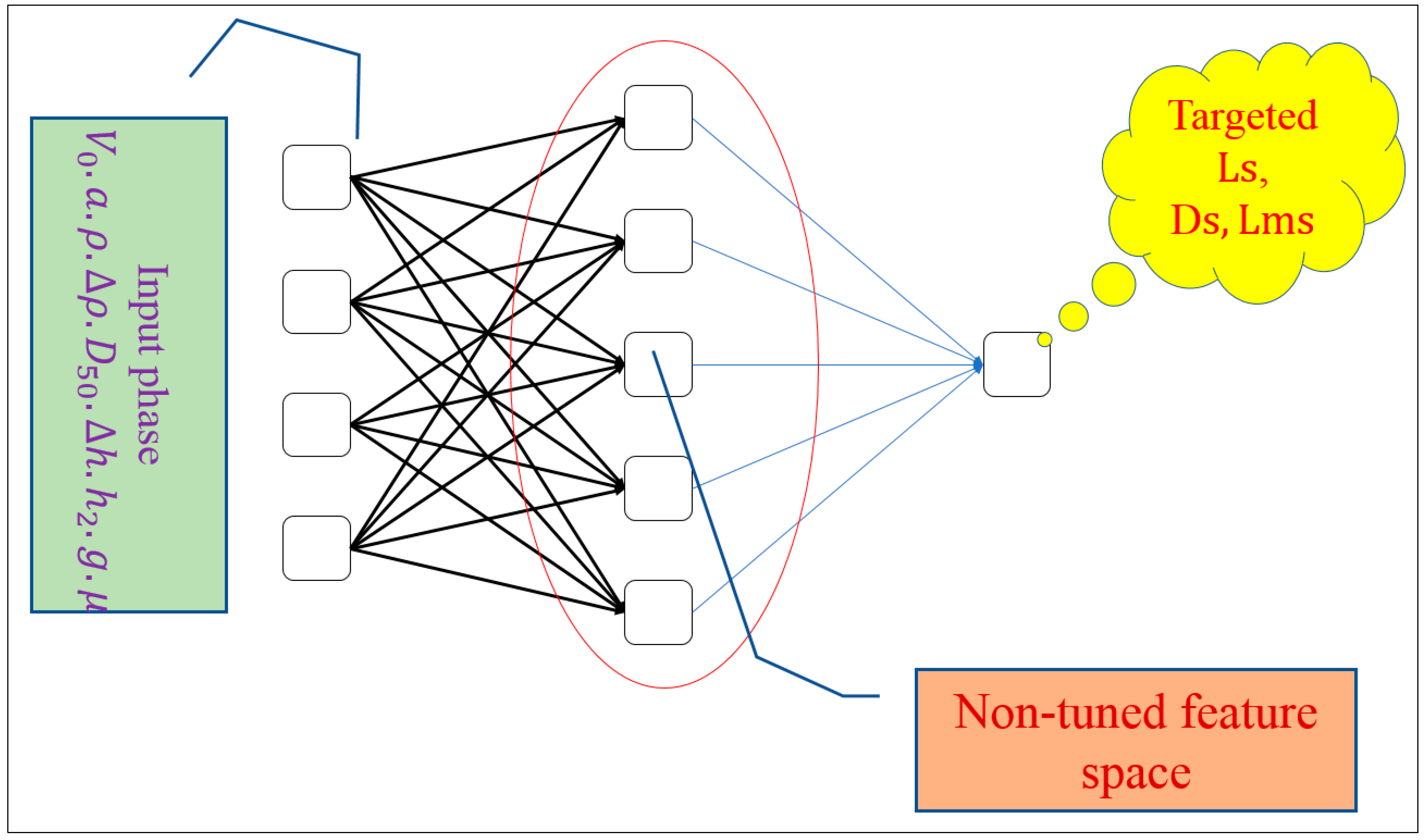
3.1. Extreme Learning Machine (ELM) Model
3.2. Multivariate Adaptive Regression Spline
3.3. Model Development
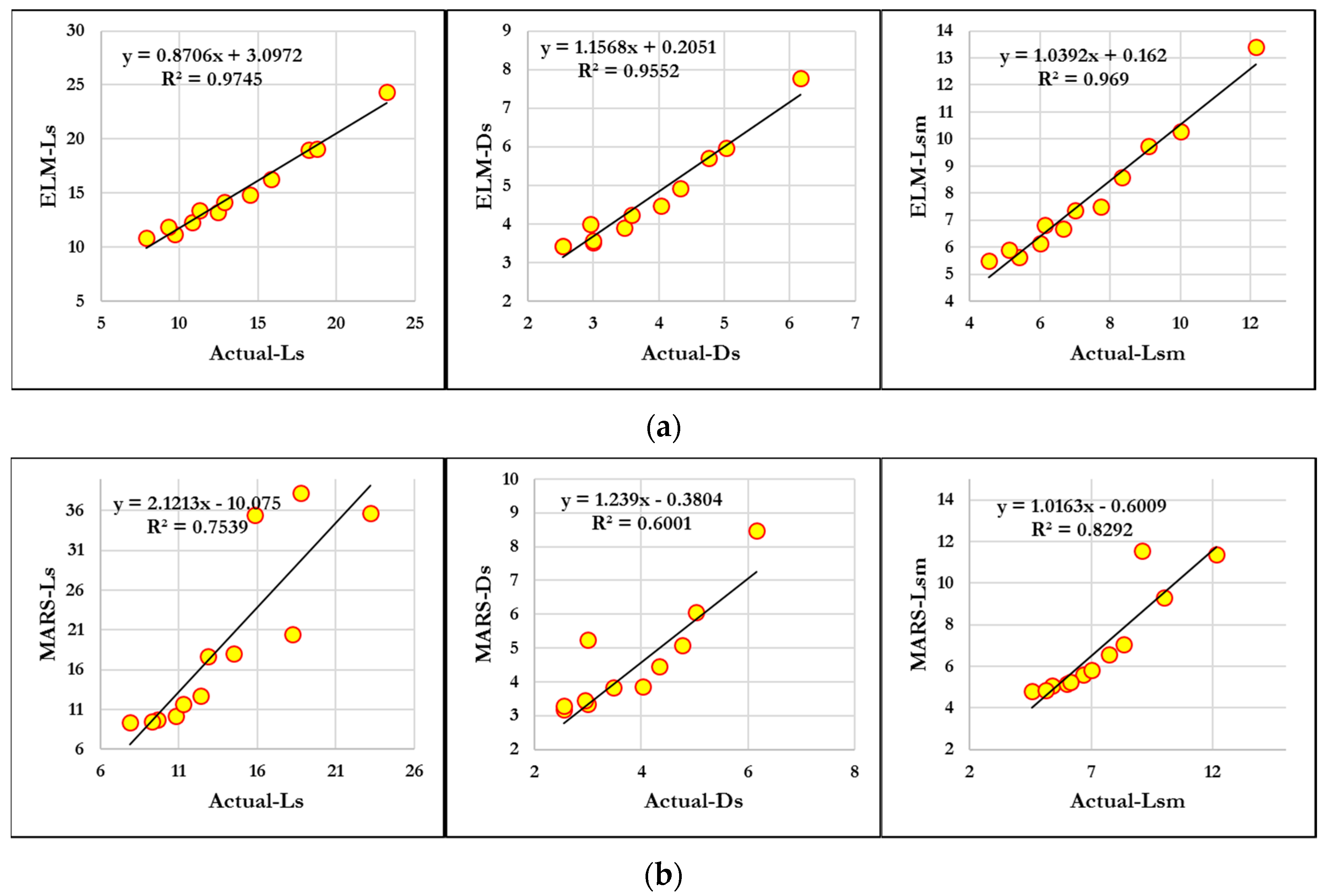
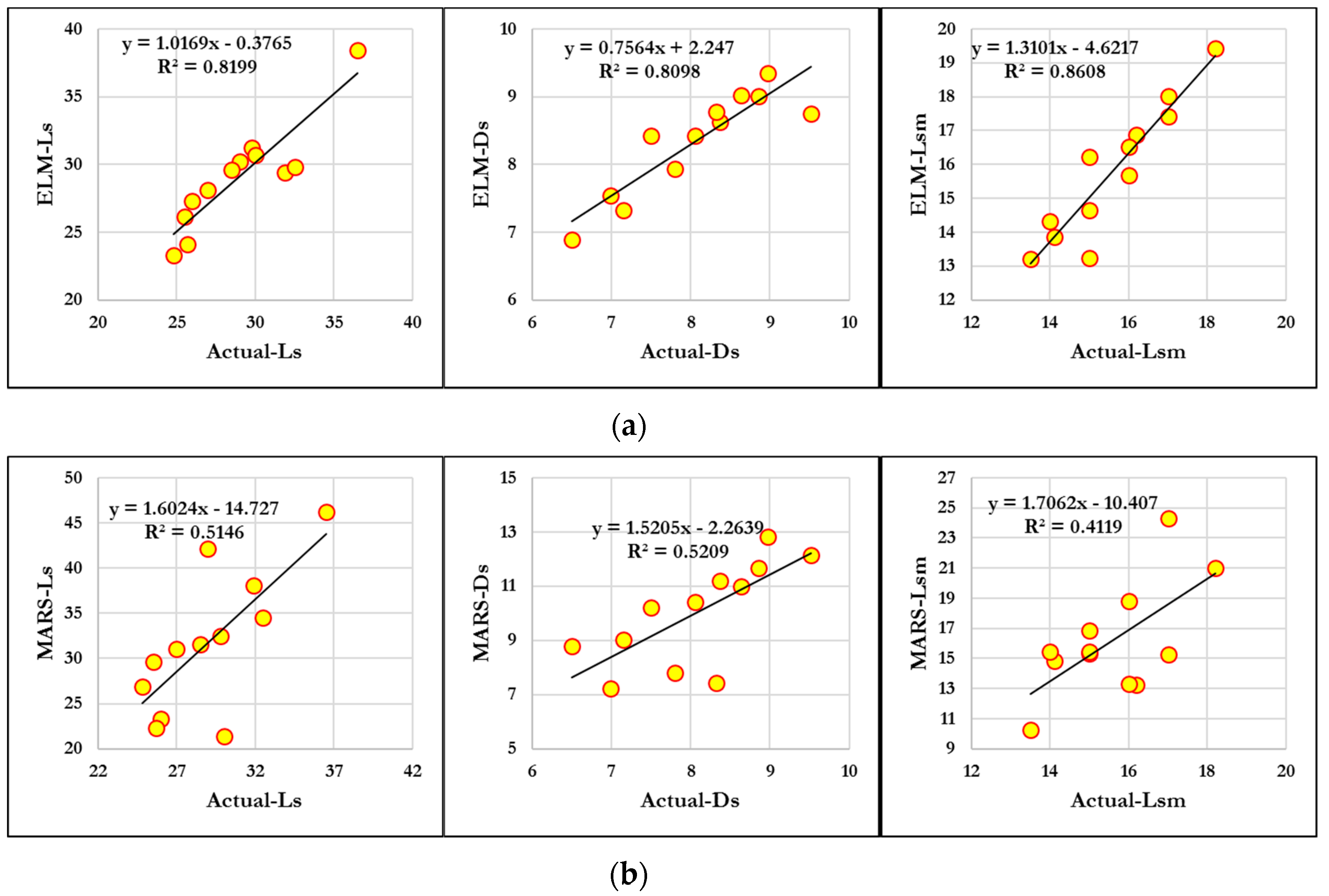
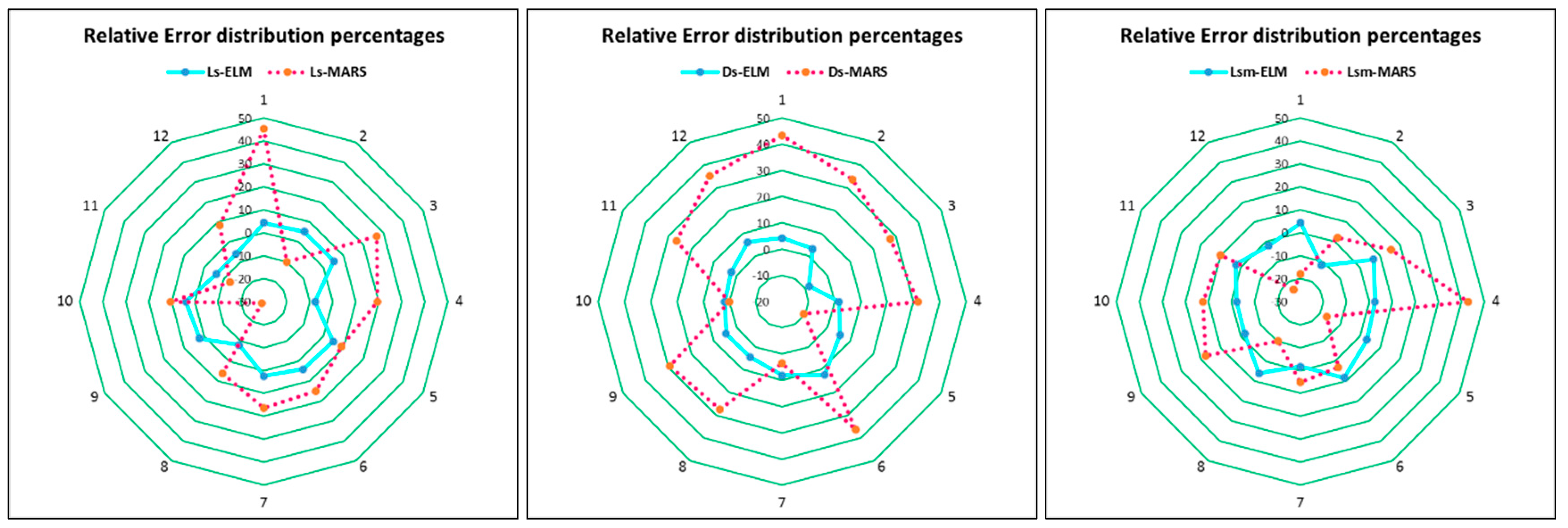
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ali, H.M.; El Gendy, M.M.; Mirdan, A.M.H.; Ali, A.A.M.; Abdelhaleem, F.S.F. Minimizing downstream scour due to submerged hydraulic jump using corrugated aprons. Ain Shams Eng. J. 2014, 5, 1059–1069. [Google Scholar] [CrossRef]
- Novák, P.; Moffat, A.; Nalluri, C.; Narayanan, R. Hydraulic Structures, 4th ed.; Taylor & Francis: New York, NY, USA, 2007. [Google Scholar]
- Sharafati, A.; Yasa, R.; Azamathulla, H.M. Assessment of Stochastic Approaches in Prediction of Wave-Induced Pipeline Scour Depth. J. Pipeline Syst. Eng. Pract. 2018, 9, 4018024. [Google Scholar] [CrossRef]
- Simons, D.B.; Senturk, F. Sediment Transport Technology; Water Resources Publications: Fort Collins, CO, USA, 1976. [Google Scholar]
- Lim, S.Y.; Yu, G. Scouring downstream of sluice gate. In Proceedings of the First International Conference on Scour of Foundations, ICSF-1, College Station, TX, USA, 17–20 November 2002. [Google Scholar]
- Carstens, M.R. Similarity laws for localized scour. J. Hydraul. Div. 1966, 92, 13–36. [Google Scholar]
- Abrahim, H.I. Flume Study of Scour Length Downstream of Regulators with Variable Block Sizes; University of Baghdad: Baghdad, Iraq, 1978. [Google Scholar]
- Chatterjee, S.S.; Ghosh, S.N. Submerged Horizontal Jet over Erodible Bed. J. Hydraul. Div. 1980, 106, 1765–1782. [Google Scholar]
- Hassan, N.M.K.N.; Narayanan, R. Local Scour Downstream of an Apron. J. Hydraul. Eng. 1985, 111, 1371–1385. [Google Scholar] [CrossRef]
- Aderibigbe, O.; Rajaratnam, N. Effect of sediment gradation on erosion by plane turbulent wall jets. J. Hydraul. Eng. 1998, 124, 1034–1042. [Google Scholar] [CrossRef]
- Grimaldi, C.; Gaudio, R.; Calomino, F.; Cardoso, A.H. Countermeasures against local scouring at bridge piers: slot and combined system of slot and bed sill. J. Hydraul. Eng. 2009, 135, 425–431. [Google Scholar] [CrossRef]
- Kells, J.A.; Balachandar, R.; Hagel, K.P. Effect of grain size on local channel scour below a sluice gate. Can. J. Civ. Eng. 2001, 451, 440–451. [Google Scholar] [CrossRef]
- Uyumaz, A.; Altunkaynak, A.; Özger, M. Fuzzy Logic Model for Equilibrium Scour Downstream of a Dam’s Vertical Gate. J. Hydraul. Eng. 2006, 132, 1069–1075. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Deo, M.C.; Deolalikar, P.B. Alternative neural networks to estimate the scour below spillways. Adv. Eng. Softw. 2008, 39, 689–698. [Google Scholar] [CrossRef]
- Shenouda, B.; Abdel-rahim, G.A.; Ali, K.A.; Izumi, N. Prediction of Scour Downstream Regulators Using ANNs. Int. J. Hydraul. Eng. 2013, 2, 1–13. [Google Scholar]
- Guven, A.; Gunal, M. Prediction of Scour Downstream of Grade-Control structures using neural networks. J. Hydraul. Eng. 2008, 134, 1656–1660. [Google Scholar] [CrossRef]
- Guven, A. A multi-output descriptive neural network for estimation of scour geometry downstream from hydraulic structures. Adv. Eng. Softw. 2011, 42, 85–93. [Google Scholar] [CrossRef]
- Azamathulla, M.; Ghani, A.A.; Zakaria, N.; Lai, S.; Chang, C.; Leow, C.; Abuhasan, Z. Genetic programming to predict ski-jump bucket spill-way scour. J. Hydrodyn. Ser. B 2008, 20, 477–484. [Google Scholar] [CrossRef]
- Azamathulla, H.M. Gene-expression programming to predict scour at a bridge abutment. J. Hydroinform. 2012, 14, 324–331. [Google Scholar] [CrossRef]
- Guven, A.; Azamathulla, H.M. Gene-expression programming for flip-bucket spillway scour. Water Sci. Technol. 2012, 65, 1982–1987. [Google Scholar] [CrossRef]
- Mesbahi, M.; Talebbeydokhti, N.; Hosseini, S.; Afzali, S. Gene-expression programming to predict the local scour depth at downstream of stilling basins. Sci. Iran. Trans A Civil Eng. 2016, 23, 102. [Google Scholar] [CrossRef]
- Onen, F. Prediction of Scour at a Side-Weir with GEP, ANN and Regression Models. Arab. J. Sci. Eng. 2014, 39, 6031–6041. [Google Scholar] [CrossRef]
- Goel, A.; Pal, M. Application of support vector machines in scour prediction on grade-control structures. Eng. Appl. Artif. Intell. 2009, 22, 216–223. [Google Scholar] [CrossRef]
- Sharafi, H.; Ebtehaj, I.; Bonakdari, H.; Zaji, A.H. Design of a support vector machine with different kernel functions to predict scour depth around bridge piers. Nat. Hazards 2016, 84, 2145–2162. [Google Scholar] [CrossRef]
- Goyal, M.K.; Ojha, C.S.P. Estimation of Scour Downstream of a Ski-Jump Bucket Using Support Vector and M5 Model Tree. Water Resour. Manag. 2011, 25, 2177–2195. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Lim, S.Y. Application of improved neuro-fuzzy GMDH to predict scour depth at sluice gates. Earth Sci. Inform. 2015, 8, 187–196. [Google Scholar] [CrossRef]
- Najafzadeh, M. Neuro-fuzzy GMDH based particle swarm optimization for prediction of scour depth at downstream of grade control structures. Eng. Sci. Technol. Int. J. 2015, 18, 42–51. [Google Scholar] [CrossRef]
- Najafzadeh, M. Neuro-fuzzy GMDH systems based evolutionary algorithms to predict scour pile groups in clear water conditions. Ocean Eng. 2015, 99, 85–94. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Tafarojnoruz, A.; Lim, S.Y. Prediction of local scour depth downstream of sluice gates using data-driven models. ISH J. Hydraul. Eng. 2017, 23, 195–202. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Macdougall, R.K. Erosion by Plane Wall Jets with Minimum Tailwater. J. Hydraul. Eng. 1983, 109, 1061–1064. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- Sanikhani, H.; Deo, R.C.; Yaseen, Z.M.; Eray, O.; Kisi, O. Non-tuned data intelligent model for soil temperature estimation: A new approach. Geoderma 2018, 330, 52–64. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Li, J.; Salim, R.D.; Aldlemy, M.S.; Abdullah, J.M.; Yaseen, Z.M. Fiberglass-Reinforced Polyester Composites Fatigue Prediction Using Novel Data-Intelligence Model. Arab. J. Sci. Eng. 2018. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Deo, R.C.; Hilal, A.; Abd, A.M.; Bueno, L.C.; Salcedo-Sanz, S.; Nehdi, M.L. Predicting compressive strength of lightweight foamed concrete using extreme learning machine model. Adv. Eng. Softw. 2018, 115, 112–125. [Google Scholar] [CrossRef]
- Bhat, A.U.; Merchant, S.S.; Bhagwat, S.S. Prediction of Melting Points of Organic Compounds Using Extreme Learning Machines. Ind. Eng. Chem. Res. 2008, 47, 920–925. [Google Scholar] [CrossRef]
- Soria-Olivas, E.; Gómez-Sanchis, J.; Martín, J.D.; Vila-Francés, J.; Martínez, M.; Magdalena, J.R.; Serrano, A.J. BELM: Bayesian extreme learning machine. IEEE Trans. Neural Netw. 2011, 22, 505–509. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Allawi, M.F.; Yousif, A.A.; Jaafar, O.; Hamzah, F.M.; El-Shafie, A. Non-tuned machine learning approach for hydrological time series forecasting. Neural Comput. Appl. 2016, 30, 1–13. [Google Scholar] [CrossRef]
- Hou, M.; Zhang, T.; Weng, F.; Ali, M.; Al-Ansari, N.; Yaseen, Z. Global solar radiation prediction using hybrid online sequential extreme learning machine model. Energies 2018, 11, 3415. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Butte, N.F.; Wong, W.W.; Adolph, A.L.; Puyau, M.R.; Vohra, F.A.; Zakeri, I.F. Validation of Cross-Sectional Time Series and Multivariate Adaptive Regression Splines Models for the Prediction of Energy Expenditure in Children and Adolescents Using Doubly Labeled Water. J. Nutr. 2010, 140, 1516–1523. [Google Scholar] [CrossRef]
- Sephton, P. Forecasting recessions: Can we do better on MARS? Review 2001, 83, 39–49. [Google Scholar] [CrossRef]
- Yaseen, Z.; Kisi, O.; Demir, V. Enhancing Long-Term Streamflow Forecasting and Predicting using Periodicity Data Component: Application of Artificial Intelligence. Water Resour. Manag. 2016, 30, 4125–4151. [Google Scholar] [CrossRef]
- Sharda, V.N.; Prasher, S.O.; Patel, R.M.; Ojasvi, P.R.; Prakash, C. Performance of Multivariate Adaptive Regression Splines (MARS) in predicting runoff in mid-Himalayan micro-watersheds with limited data. Hydrol. Sci. J. 2008, 53, 1165–1175. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T.C. Multivariate adaptive regression splines and neural network models for prediction of pile drivability. Geosci. Front. 2014, 7, 45–52. [Google Scholar] [CrossRef]
- Craven, P.; Wahba, G. Smoothing noisy data with spline functions—Estimating the correct degree of smoothing by the method of generalized cross-validation. Numer. Math. 1978, 31, 377–403. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Application of the Artificial Neural Network model for prediction of monthly Standardized Precipitation and Evapotranspiration Index using hydrometeorological parameters and climate indices in eastern Australia. Atmos. Res. 2015, 161–162, 65–81. [Google Scholar] [CrossRef]
- Tao, H.; Diop, L.; Bodian, A.; Djaman, K.; Ndiaye, P.M.; Yaseen, Z.M. Reference evapotranspiration prediction using hybridized fuzzy model with firefly algorithm: Regional case study in Burkina Faso. Agric. Water Manag. 2018, 208, 140–151. [Google Scholar] [CrossRef]
- Choi, S.U.; Choi, B.; Lee, S. Prediction of local scour around bridge piers using the ANFIS method. Neural Comput. Appl. 2017, 28, 335–344. [Google Scholar] [CrossRef]
- Ayoubloo, M.K.; Etemad-Shahidi, A.; Mahjoobi, J. Evaluation of regular wave scour around a circular pile using data mining approaches. Appl. Ocean Res. 2010, 32, 34–39. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2018, 569, 387–408. [Google Scholar] [CrossRef]


| Bed Material Samples | Geometric Standard Deviation | Mean Diameter (mm) |
|---|---|---|
| A | 2 | 0.345 |
| B | 3.51 | 0.6309 |
| C | 3.79 | 1.31 |
| Predicted Value | SI | MAPE | RMSE | MAE | RMSRE | R |
|---|---|---|---|---|---|---|
| 0.0482 | 0.0219 | 0.6611 | 0.2366 | 0.0691 | 0.98 | |
| 0.0961 | 0.0393 | 0.3634 | 0.1430 | 0.0995 | 0.97 | |
| 0.0349 | 0.0128 | 0.2563 | 0.0871 | 0.0391 | 0.97 |
| Predicted Value | SI | MAPE | RMSE | MAE | RMSRE | R |
|---|---|---|---|---|---|---|
| 0.2760 | 0.0580 | 3.7876 | 0.9721 | 0.2171 | 0.86 | |
| 0.1375 | 0.0454 | 0.5201 | 0.1654 | 0.1420 | 0.77 | |
| 0.0631 | 0.0223 | 0.4637 | 0.1673 | 0.0589 | 0.90 |
| Predicted Value | SI | MAPE | RMSE | MAE | RMSRE | R |
|---|---|---|---|---|---|---|
| 0.0232 | 0.0090 | 0.6724 | 0.2637 | 0.0225 | 0.90 | |
| 0.0249 | 0.0093 | 0.2008 | 0.0742 | 0.0253 | 0.89 | |
| 0.0230 | 0.0080 | 0.3590 | 0.1257 | 0.0227 | 0.92 |
| Predicted Value | SI | MAPE | RMSE | MAE | RMSRE | R |
|---|---|---|---|---|---|---|
| 0.0902 | 0.0312 | 2.6107 | 0.9213 | 0.0867 | 0.71 | |
| 0.1232 | 0.0456 | 0.9925 | 0.3717 | 0.1207 | 0.72 | |
| 0.0804 | 0.0266 | 1.2525 | 0.4236 | 0.0772 | 0.64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousif, A.A.; Sulaiman, S.O.; Diop, L.; Ehteram, M.; Shahid, S.; Al-Ansari, N.; Yaseen, Z.M. Open Channel Sluice Gate Scouring Parameters Prediction: Different Scenarios of Dimensional and Non-Dimensional Input Parameters. Water 2019, 11, 353. https://doi.org/10.3390/w11020353
Yousif AA, Sulaiman SO, Diop L, Ehteram M, Shahid S, Al-Ansari N, Yaseen ZM. Open Channel Sluice Gate Scouring Parameters Prediction: Different Scenarios of Dimensional and Non-Dimensional Input Parameters. Water. 2019; 11(2):353. https://doi.org/10.3390/w11020353
Chicago/Turabian StyleYousif, Ali A., Sadeq Oleiwi Sulaiman, Lamine Diop, Mohammad Ehteram, Shamsuddin Shahid, Nadhir Al-Ansari, and Zaher Mundher Yaseen. 2019. "Open Channel Sluice Gate Scouring Parameters Prediction: Different Scenarios of Dimensional and Non-Dimensional Input Parameters" Water 11, no. 2: 353. https://doi.org/10.3390/w11020353
APA StyleYousif, A. A., Sulaiman, S. O., Diop, L., Ehteram, M., Shahid, S., Al-Ansari, N., & Yaseen, Z. M. (2019). Open Channel Sluice Gate Scouring Parameters Prediction: Different Scenarios of Dimensional and Non-Dimensional Input Parameters. Water, 11(2), 353. https://doi.org/10.3390/w11020353










