How does PTF Interpret Soil Heterogeneity? A Stochastic Approach Applied to a Case Study on Maize in Northern Italy
Abstract
1. Introduction
- (i)
- Evaluating to what extent the variability of the soil hydraulic properties parameters is reflected in the hydrological processes observed at the field scale. To do that, a preliminary analysis of the sensitivity of a physically-based agro-hydrological model to the measured variability of both water retention and hydraulic conductivity parameters will be carried out. This analysis will be based on a stream tube approach used in a stochastic (Monte Carlo) framework;
- (ii)
- Evaluating the effectiveness of selected PTFs in reproducing the field scale hydrological pattern described by the measured hydraulic properties through using independent and spatially distributed information (Normalized Difference Vegetation Index ‒ NDVI) as data quality control.
2. Materials and Methods
2.1. Study Area
2.2. Hydraulic Properties
2.3. Evaluation of PTFs’ Performance
2.4. Soil-Plant-Atmosphere Model
2.5. Monte Carlo Simulations
2.6. Remote Sensing Data
- An NDVI map at high resolution from a visible RGB and near IR Quickbird image for 21 July 2004 (spatial resolution 2.4 m).
- NDVI maps derived from free Landsat 5 TM and Landsat OLI-8 scenes Collection 1 Level-2 on-Demand—path 193–194/row 28–29—at spatial resolution of 30 m, atmospherically corrected [50,51], including a cloud, shadow, water, and snow mask produced using CFMASK [52], as well as a per-pixel saturation mask for years 2009, 2010, 2013, 2014, 2015, 2016, 2017, and 2018 ranging from 1 to 25 July, in order to strengthen our assumptions on the relationship between NDVI and hydraulic properties. The selection of these layers (years and periods) was done considering their availability, the need to observe NDVI data within July as was done for 2004, and the presence of masking clouds during specific days.
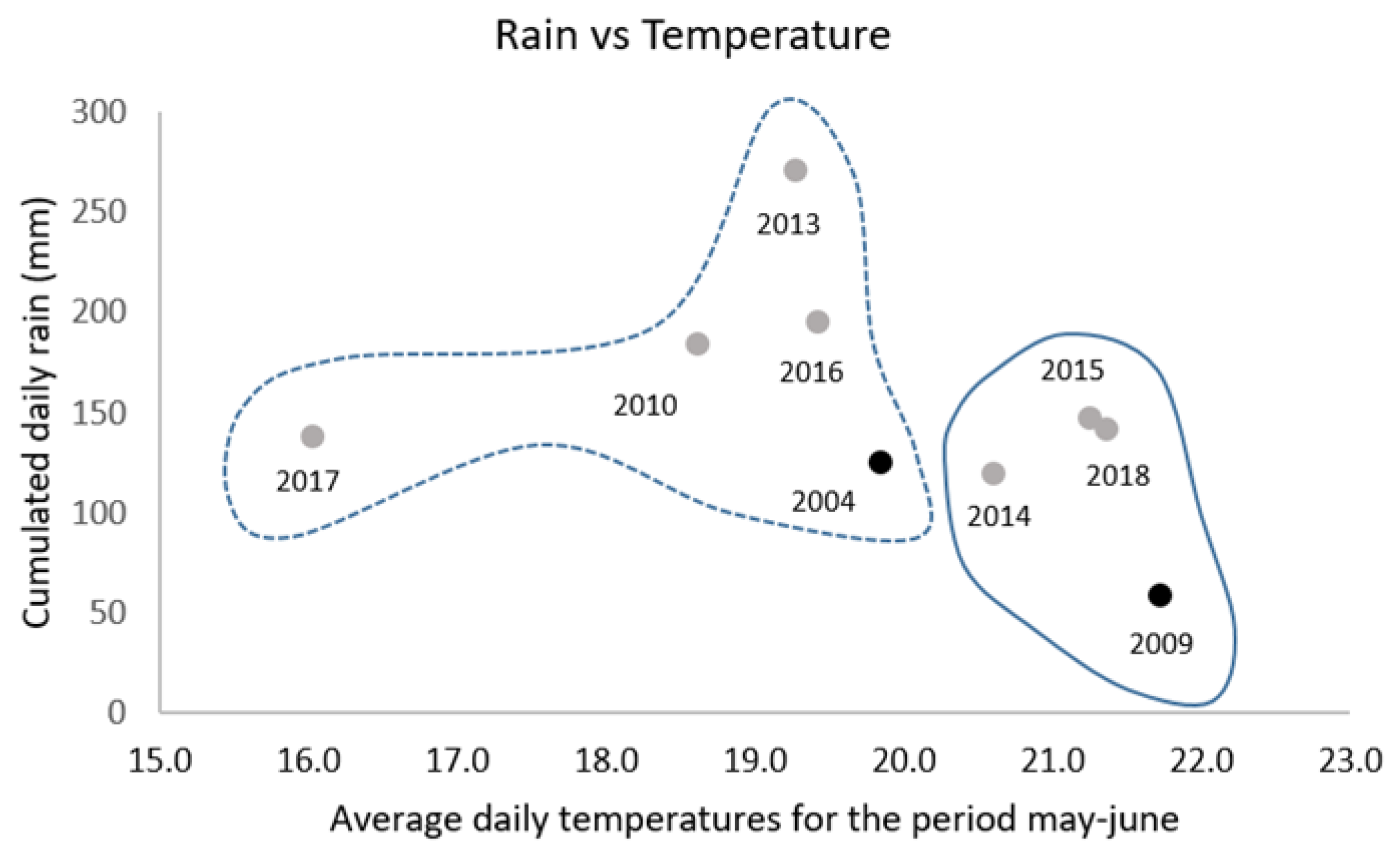
2.7. Climate Data
3. Results
3.1. Variability of Soil Hydraulic Properties
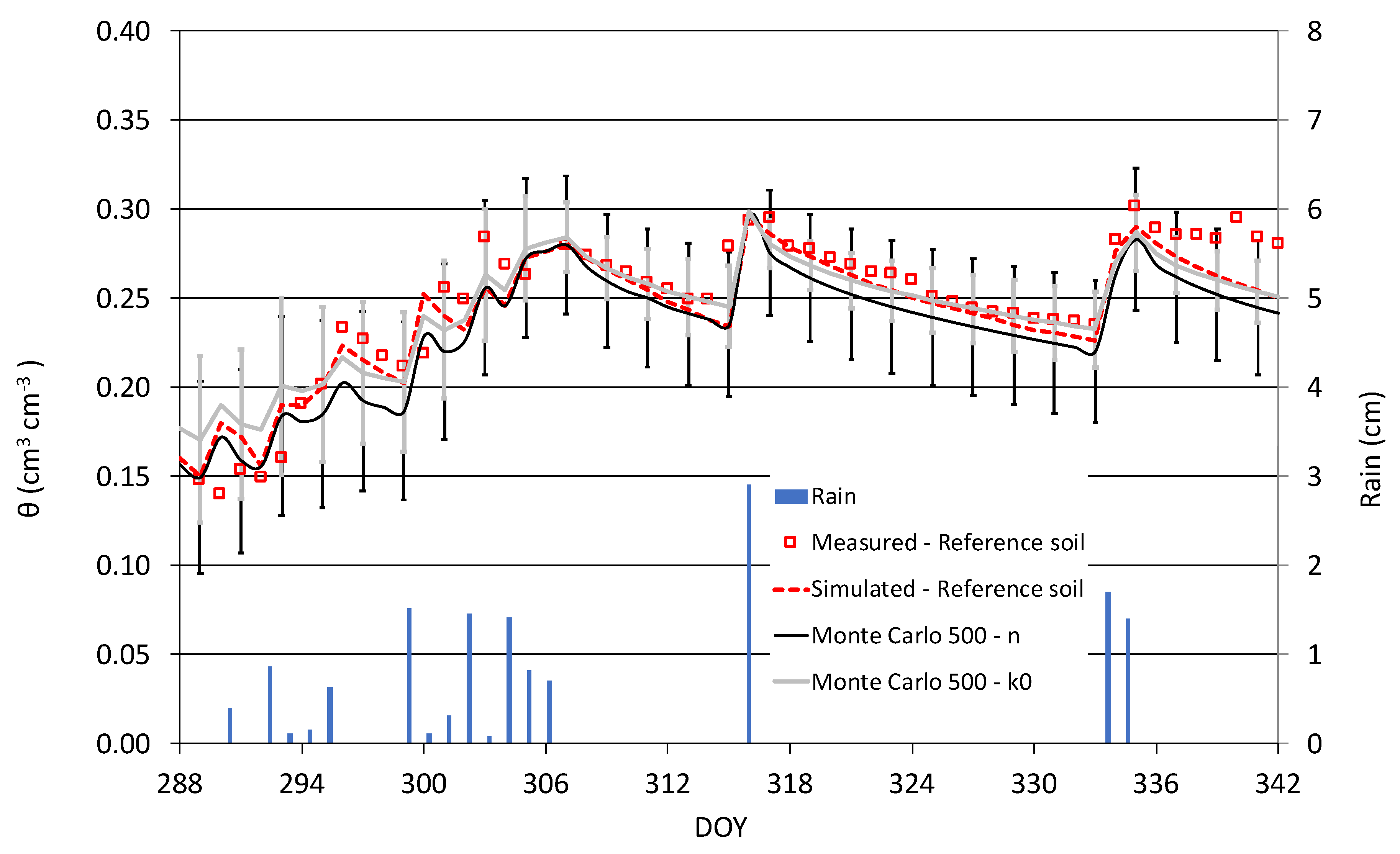
3.2. Model Validation
3.3. Predictive Capability of PTFs
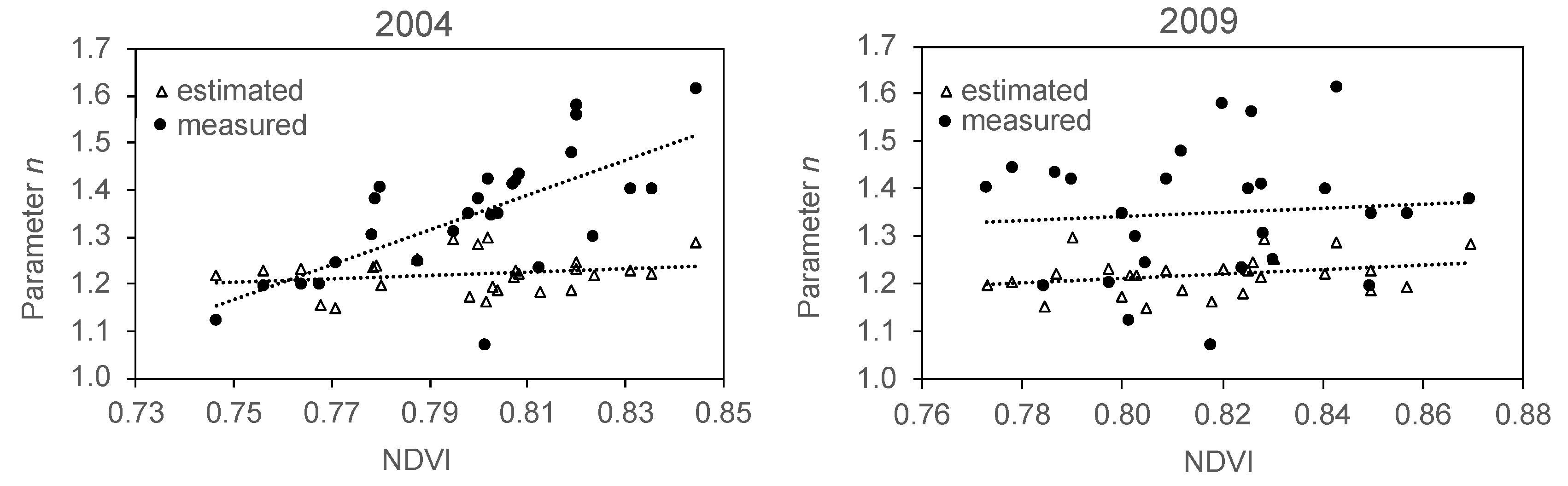
3.4. Soundness of PTF Estimations Based on NDVI Data
4. Discussion
4.1. Variability of Soil Hydraulic Properties Parameters and its Impact on the Process under Study
4.2. Effectiveness of PTFs in Representing the Actual Variability of Hydraulic Properties and its Impact on the Process under Study
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bonfante, A.; Basile, A.; Langella, G.; Manna, P.; Terribile, F. Soil science solutions for advancing SDG 2 towards resilient agriculture. In Soil and Sustainable Development Goals; Schweizerbart Science Publishers: Stuttgart, Germany, 2018; p. 196. ISBN 978-3-510-65425-3. [Google Scholar]
- Terribile, F.; Agrillo, A.; Bonfante, A.; Buscemi, G.; Colandrea, M.; D’Antonio, A.; De Mascellis, R.; De Michele, C.; Langella, G.; Manna, P. A web-based spatial decision supporting system for land management and soil conservation. Solid Earth 2015, 6, 903. [Google Scholar] [CrossRef]
- Dane, J.H.; Topp, G.C. (Eds.) Methods of Soil Analysis: Part 4 Physical Methods; SSSA Book Series; Soil Science Society of America: Madison, WI, USA, 2002; ISBN 978-0-89118-893-3. [Google Scholar]
- Basile, A.; Ciollaro, G.; Coppola, A. Hysteresis in soil water characteristics as a key to interpreting comparisons of laboratory and field measured hydraulic properties. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil Moisture for Hydrological Applications: Open Questions and New Opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Montzka, C.; Moradkhani, H.; Weihermüller, L.; Franssen, H.-J.H.; Canty, M.; Vereecken, H. Hydraulic parameter estimation by remotely-sensed top soil moisture observations with the particle filter. J. Hydrol. 2011, 399, 410–421. [Google Scholar] [CrossRef]
- Valdes-Abellan, J.; Pachepsky, Y.; Martinez, G. Obtaining soil hydraulic parameters from soil water content data assimilation under different climatic/soil conditions. Catena 2018, 163, 311–320. [Google Scholar] [CrossRef]
- Nimmo, J.R. Modeling structural influences on soil water retention. Soil Sci. Soc. Am. J. 1997, 61, 712–719. [Google Scholar] [CrossRef]
- Pachepsky, Y.A.; Rawls, W.J. Soil structure and pedotransfer functions. Eur. J. Soil Sci. 2003, 54, 443–452. [Google Scholar] [CrossRef]
- Romano, N.; Palladino, M. Prediction of soil water retention using soil physical data and terrain attributes. J. Hydrol. 2002, 265, 56–75. [Google Scholar] [CrossRef]
- Van Looy, K.; Bouma, J.; Herbst, M.; Koestel, J.; Minasny, B.; Mishra, U.; Montzka, C.; Nemes, A.; Pachepsky, Y.A.; Padarian, J.; et al. Pedotransfer Functions in Earth System Science: Challenges and perspectives. Rev. Geophys. 2017, 55, 1199–1256. [Google Scholar] [CrossRef]
- Merdun, H. Pedotransfer functions for point and parametric estimations of soil water retention curve. Plant Soil Environ. 2006, 52, 321. [Google Scholar] [CrossRef]
- Pachepsky, Y.A.; Rawls, W.J. Accuracy and reliability of pedotransfer functions as affected by grouping soils. Soil Sci. Soc. Am. J. 1999, 63, 1748–1757. [Google Scholar] [CrossRef]
- Donatelli, M.; Wösten, J.H.M.; Belocchi, G. Methods to evaluate pedotransfer functions. Dev. Soil Sci. 2004, 30, 357–411. [Google Scholar]
- Schaap, M.G.; Nemes, A.; van Genuchten, M.T. Comparison of Models for Indirect Estimation of Water Retention and Available Water in Surface Soils. Vadose Zone J. 2004, 3, 1455–1463. [Google Scholar] [CrossRef]
- Calzolari, C.; Ungano, F.; Busoni, E. The SINA project in the Padano-Veneto basin. In Proceedings of the International Congress Soil Vulnerability and Sensitivity, Florence, Italy, 18–21 October 2000; pp. 287–307. [Google Scholar]
- Leonaviciute, N. Predicting soil bulk and particle densities by pedotransfer functions from existing soil data in Lithuania. Geografijos Metraštis 2000, 33, 317–330. [Google Scholar]
- Van Alphen, B.J.; Booltink, H.W.G.; Bouma, J. Combining pedotransfer functions with physical measurements to improve the estimation of soil hydraulic properties. Geoderma 2001, 103, 133–147. [Google Scholar] [CrossRef]
- Wagner, B.; Tarnawski, V.R.; Hennings, V.; Müller, U.; Wessolek, G.; Plagge, R. Evaluation of pedo-transfer functions for unsaturated soil hydraulic conductivity using an independent data set. Geoderma 2001, 102, 275–297. [Google Scholar] [CrossRef]
- Yang, J.; Greenwood, D.J.; Rowell, D.L.; Wadsworth, G.A.; Burns, I.G. Statistical methods for evaluating a crop nitrogen simulation model, N_ABLE. Agric. Syst. 2000, 64, 37–53. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Bannink, M.H.; De Gruijter, J.J.; Bouma, J. A procedure to identify different groups of hydraulic conductivity and moisture retention curves for soil horizons. J. Hydrol. 1986, 86, 133–145. [Google Scholar] [CrossRef]
- Vereecken, H.; Diels, J.; Van Orshoven, J.; Feyen, J.; Bouma, J. Functional evaluation of pedotransfer functions for the estimation of soil hydraulic properties. Soil Sci. Soc. Am. J. 1992, 56, 1371–1378. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15(7), 1–25. [Google Scholar] [CrossRef]
- Hardelauf, H.; Javaux, M.; Herbst, M.; Gottschalk, S.; Kasteel, R.; Vanderborght, J.; Vereecken, H. PARSWMS: A Parallelized Model for Simulating Three-Dimensional Water Flow and Solute Transport in Variably Saturated Soils. Vadose Zone J. 2007, 6, 255–259. [Google Scholar] [CrossRef]
- Dagan, G.; Neuman, S.P. Subsurface Flow and Transport: A Stochastic Approach; Cambridge University Press: Cambridge, UK, 2005; ISBN 0521020093. [Google Scholar]
- Hopmans, J.; Stricker, J. Stochastic analysis of soil water regime in a watershed. J. Hydrol. 1989, 105, 57–84. [Google Scholar] [CrossRef]
- Mallants, D.; Mohanty, B.P.; Jacques, D.; Feyen, J. Spatial variability of hydraulic properties in a multi-layered soil profile. Soil Sci. 1996, 161, 167–181. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, D. Stochastic analysis of transient flow in heterogeneous, variably saturated porous media. Vadose Zone J. 2002, 1, 137–149. [Google Scholar] [CrossRef]
- Coppola, A.; Basile, A.; Comegna, A.; Lamaddalena, N. Monte Carlo analysis of field water flow comparing uni-and bimodal effective hydraulic parameters for structured soil. J. Contam. Hydrol. 2009, 104, 153–165. [Google Scholar] [CrossRef] [PubMed]
- Coppola, A.; Dragonetti, G.; Comegna, A.; Lamaddalena, N.; Caushi, B.; Haikal, M.A.; Basile, A. Measuring and modeling water content in stony soils. Soil Tillage Res. 2013, 128, 9–22. [Google Scholar] [CrossRef]
- Manna, P.; Basile, A.; Bonfante, A.; De Mascellis, R.; Terribile, F. Comparative Land Evaluation approaches: An itinerary from FAO framework to simulation modelling. Geoderma 2009, 150, 367–378. [Google Scholar] [CrossRef]
- Ente Regionale per i Servizi all’Agricoltura e alle Foreste (ERSAF). Suoli e Paesaggi Della Provincia di Lodi; Regione Lombardia: Milano, Italy, 2004. [Google Scholar]
- Gee, G.W.; Or, D. 2.4 Particle-size analysis. Methods of soil analysis. Part 2002, 4, 255–293. [Google Scholar]
- Reynolds, W.D.; Elrick, D.E. The soil solution phase. Falling head soil core (tank) method. In Methods of Soil Analysis; SSSA Book Ser. Dane, J.K., Topp, G.C., Eds.; SSSA: Madison, WI, USA, 2002; Volume 5, pp. 809–812. [Google Scholar]
- Dane, J.H.; Hopmans, J. Water retention and storage. In Methods of Soil Analysis; SSSA Book Ser. Dane, J.K., Topp, G.C., Eds.; SSSA: Madison, WI, USA, 2002; Volume 5, pp. 671–720. [Google Scholar]
- Schaap, M.G.; Leij, F.J.; Van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Coppola, A.; Comegna, A.; Dragonetti, G.; Dyck, M.; Basile, A.; Lamaddalena, N.; Kassab, M.; Comegna, V. Solute transport scales in an unsaturated stony soil. Adv. Water Resour. 2011, 34, 747–759. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils 1. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Vogel, T. SWM II: Numerical Model of Two-Dimensional Flow in a Variably Saturated Porous Medium; Res. Rep. 87; Agricultural Univ Wageningen: Wageningen, The Netherlands, 1987. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef]
- Feddes, R.A.; Raats, P.A.C. Parameterizing the Soil–Water–Plant Root System. Unsaturated-Zone Modeling: Progress, Challenges, Applications; Kluwer Academic Publisher: Dordrecht, The Netherlands, 2004; Volume 6, pp. 95–141. [Google Scholar]
- Kroes, J.G.; van Dam, J.C.; Groenendijk, P.; Hendriks, R.F.A.; Jacobs, C.M.J. SWAP Version 3.2: Theory Description and User Manual; Alterra Rep. 1649; Alterra: Wageningen, the Netherlands, 2008. [Google Scholar]
- Bonfante, A.; Basile, A.; Acutis, M.; De Mascellis, R.; Manna, P.; Perego, A.; Terribile, F. SWAP, CropSyst and MACRO comparison in two contrasting soils cropped with maize in Northern Italy. Agric. Water Manag. 2010, 97, 1051–1062. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Greant Plains with ERTS: Proceedings of the Earth Resources Technology Satellite Symposium NASA SP-351; NASA: Washington, DC, USA, 1973; Volume 1, pp. 309–317.
- Wang, J.; Rich, P.M.; Price, K.P.; Kettle, W.D. Relations between NDVI and tree productivity in the central Great Plains. Int. J. Remote Sens. 2004, 25, 3127–3138. [Google Scholar] [CrossRef]
- Prabhakara, K.; Hively, W.D.; McCarty, G.W. Evaluating the relationship between biomass, percent groundcover and remote sensing indices across six winter cover crop fields in Maryland, United States. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 88–102. [Google Scholar] [CrossRef]
- LANDSAT 4-7 SURFACE REFLECTANCE (LEDAPS) PRODUCT GUIDE, Version 1.0 December 2018. Available online: https://landsat.usgs.gov/sites/default/files/documents/ledaps_product_guide.pdf (accessed on 1 February 2019).
- LANDSAT 8 SURFACE REFLECTANCE CODE (LASRC) PRODUCT GUIDE, Version 1.0 December 2018. Available online: https://landsat.usgs.gov/sites/default/files/documents/lasrc_product_guide.pdf (accessed on 1 February 2019).
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4–7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Terribile, F.; Coppola, A.; Langella, G.; Martina, M.; Basile, A. Potential and limitations of using soil mapping information to understand landscape hydrology. Hydrol. Earth Syst. Sci. 2011, 15, 3895–3933. [Google Scholar] [CrossRef]
- Van Genuchten, M.; Leij, F.; Yates, S. The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils; Tech. Report 1991, EPA/600/2-91/065. 93pp., R.S. Kerr Environ. Res. Lab., U.S.; Environmental Protection Agency: Ada, OK, USA.
- Wang, P.; Tartakovsky, D.M. Probabilistic predictions of infiltration into heterogeneous media with uncertain hydraulic parameters. Int. J. Uncertain. Quantif. 2011, 1, 35–47. [Google Scholar] [CrossRef]
- Chirico, G.B.; Medina, H.; Romano, N. Functional evaluation of PTF prediction uncertainty: An application at hillslope scale. Geoderma 2010, 155, 193–202. [Google Scholar] [CrossRef]
- Deng, H.; Ye, M.; Schaap, M.G.; Khaleel, R. Quantification of uncertainty in pedotransfer function-based parameter estimation for unsaturated flow modeling. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Liao, K.; Xu, S.; Wu, J.; Zhu, Q. Uncertainty analysis for large-scale prediction of the van Genuchten soil-water retention parameters with pedotransfer functions. Soil Res. 2014, 52, 431–442. [Google Scholar] [CrossRef]
- Lei, W.-J.; Tang, X.-Y.; Reid, B.J.; Zhou, X.-Y. Spatial distribution of soil hydraulic parameters estimated by pedotransfer functions for the Jialing River Catchment, Southwestern China. J. Mt. Sci. 2016, 13, 29–45. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.; Zaradny, J. Simulation of Field Water Use and Crop Yield; Pudoc for the Centre for Agricultural Publishing and Documentation: Wageningen, The Netherlands, 1978; ISBN 978-90-220-0676-4. [Google Scholar]


| θs | α | n | k0 (cm d−1) | Clay (%) | Silt (%) | Sand (%) | |
|---|---|---|---|---|---|---|---|
| Mean | 0.42 | 0.02 | 1.32 | 486 | 16.4 | 34.0 | 49.6 |
| Standard deviation | 0.06 | 0.02 | 0.10 | 897 | 3.8 | 7.1 | 8.5 |
| Coefficient of variation (%) | 13.9 | 109 | 7.74 | 185 | 23.0 | 20.8 | 17.1 |
| Type of distribution (n: normal; Log-n: Lognormal) | n | Log-n | n | Log-n | n | n | n |
| Root Mean Error (RME) | Root Mean Square Error (RMSE) | Model Efficiency (EF) | |
|---|---|---|---|
| HYPRES | 0.09 | 5.51 | −1.56 |
| VERECKEEN | −2.86 | 5.47 | −1.25 |
| ROSETTA | −7.03 | 5.76 | −2.56 |
| Hydraulic Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| Estimated | Measured | |||||||
| Years | θs | k0 (cm/d) | α (1/cm) | n | θs | k0 (cm/d) | α (1/cm) | n |
| 2004 | 0.16 | 0.15 | 0.03 | 0.04 | 0.13 | 0.04 | 0.30 * | 0.48 ** |
| 2009 | 0.00 | 0.04 | 0.00 | 0.09 | 0.05 | 0.09 | 0.01 | 0.01 |
| 2010 | 0.00 | 0.04 | 0.01 | 0.11 | 0.00 | 0.02 | 0.18 * | 0.22 * |
| 2013 | 0.15 | 0.02 | 0.08 | 0.04 | 0.02 | 0.18 | 0.40 ** | 0.32 ** |
| 2014 | 0.08 | 0.02 | 0.01 | 0.04 | 0.16 | 0.08 | 0.00 | 0.01 |
| 2015 | 0.18 | 0.02 | 0.06 | 0.00 | 0.02 | 0.62 ** | 0.18 | 0.03 |
| 2016 | 0.01 | 0.00 | 0.08 | 0.04 | 0.01 | 0.03 | 0.32 ** | 0.48 ** |
| 2017 | 0.00 | 0.00 | 0.08 | 0.00 | 0.02 | 0.08 | 0.26 ** | 0.31 ** |
| 2018 | 0.00 | 0.00 | 0.04 | 0.05 | 0.09 | 0.00 | 0.17 * | 0.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basile, A.; Bonfante, A.; Coppola, A.; De Mascellis, R.; Falanga Bolognesi, S.; Terribile, F.; Manna, P. How does PTF Interpret Soil Heterogeneity? A Stochastic Approach Applied to a Case Study on Maize in Northern Italy. Water 2019, 11, 275. https://doi.org/10.3390/w11020275
Basile A, Bonfante A, Coppola A, De Mascellis R, Falanga Bolognesi S, Terribile F, Manna P. How does PTF Interpret Soil Heterogeneity? A Stochastic Approach Applied to a Case Study on Maize in Northern Italy. Water. 2019; 11(2):275. https://doi.org/10.3390/w11020275
Chicago/Turabian StyleBasile, Angelo, Antonello Bonfante, Antonio Coppola, Roberto De Mascellis, Salvatore Falanga Bolognesi, Fabio Terribile, and Piero Manna. 2019. "How does PTF Interpret Soil Heterogeneity? A Stochastic Approach Applied to a Case Study on Maize in Northern Italy" Water 11, no. 2: 275. https://doi.org/10.3390/w11020275
APA StyleBasile, A., Bonfante, A., Coppola, A., De Mascellis, R., Falanga Bolognesi, S., Terribile, F., & Manna, P. (2019). How does PTF Interpret Soil Heterogeneity? A Stochastic Approach Applied to a Case Study on Maize in Northern Italy. Water, 11(2), 275. https://doi.org/10.3390/w11020275











