Laboratory Experiments of Drainage, Imbibition and Infiltration under Artificial Rainfall Characterized by Image Analysis Method and Numerical Simulations
Abstract
:1. Introduction
2. Materials and Methods
2.1. The 2D Flow Tank and Porous Media
2.2. Image Acquisition and Instruments Used to Take Direct Measurements
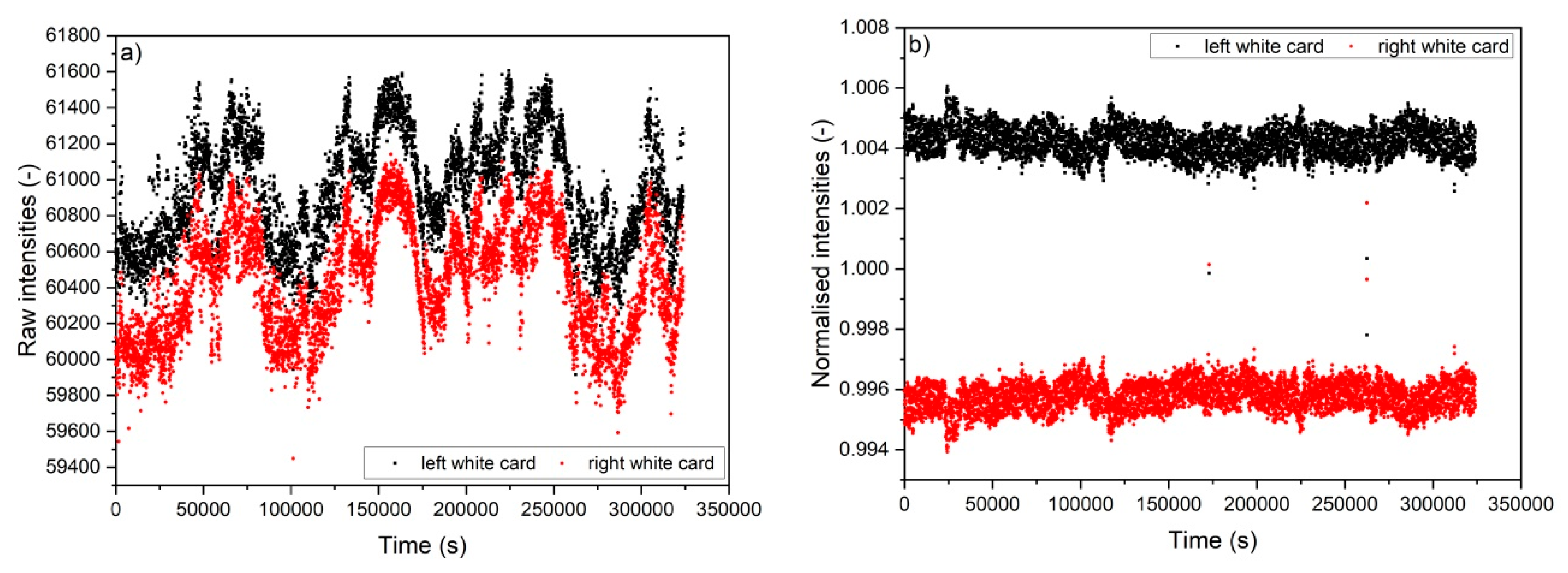
2.3. Method Dealing with Photometric Procedure
- Importing the images, converting to 16-bit .tiff images and extracting their information.
- Selecting the color space (global, RGB or HSB image stacking).
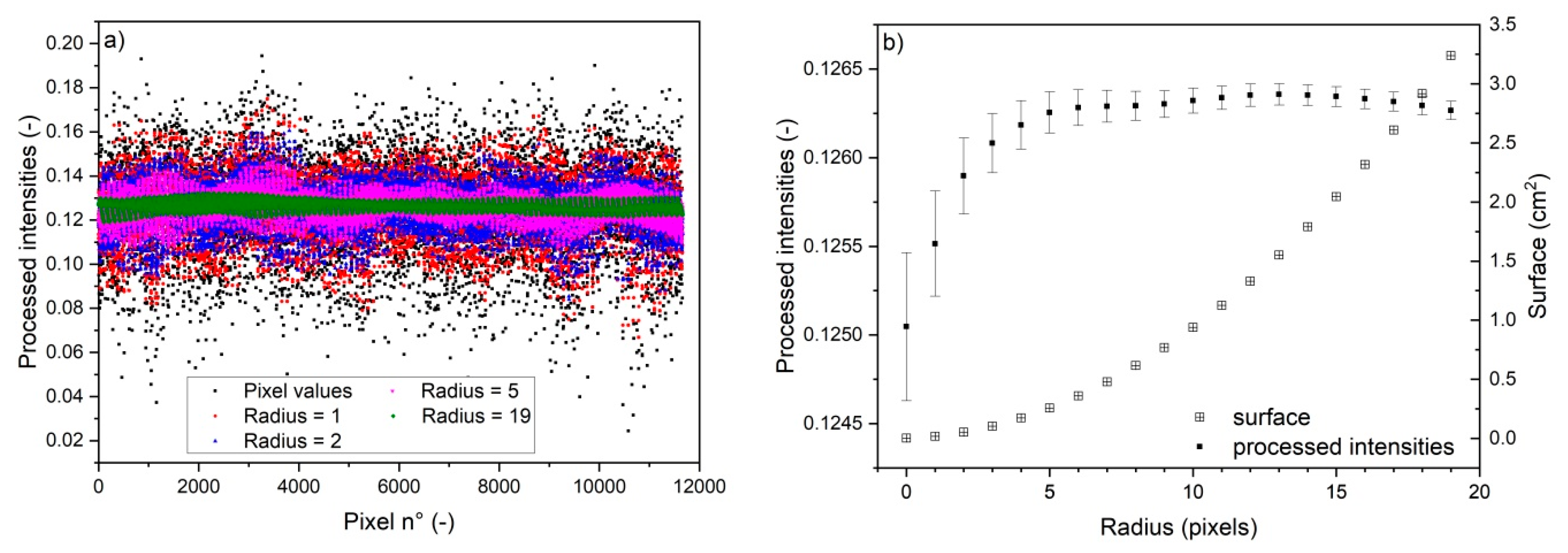
- Applying a median filter with a radius value of 5. The intensity of the pixel located at position on the picture taken at time t as .
- Normalizing the pre-processed image to get . The minimum and maximum intensity values ( and ) are measured for each picture and allow us to normalize the picture according to the following equation:
- Obtaining through background subtraction:
- Obtaining through the insertion of a measurement zone.
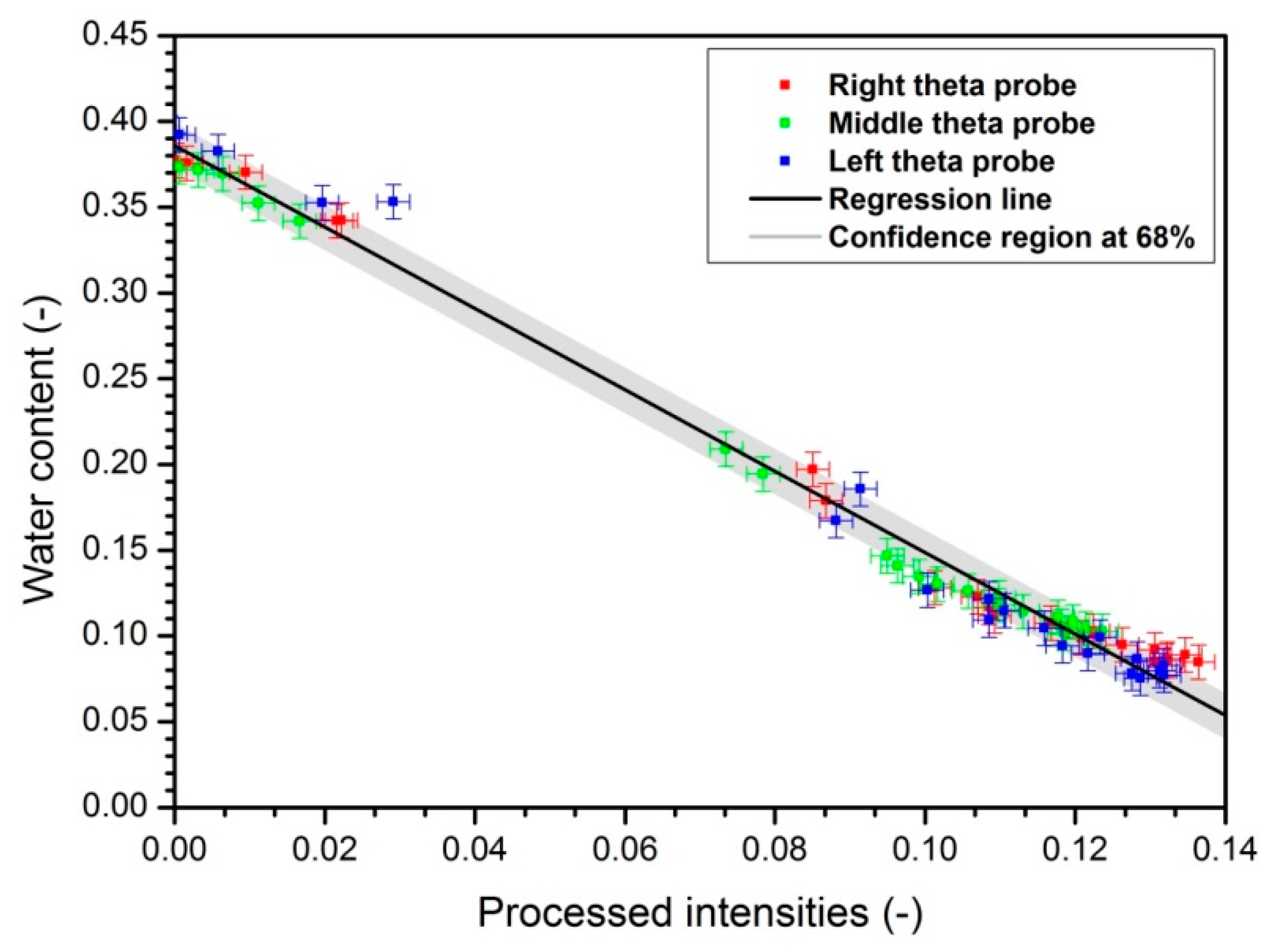
- Obtaining through image calibration:
- Converting processed intensities to water contents to construct moisture maps.
- Computing the error of the estimated water content:
2.4. Numerical Method for Variably Saturated Flow Modelling
3. Results and Discussion
3.1. First Experiment: Simple Drainage–Imbibition Cycle
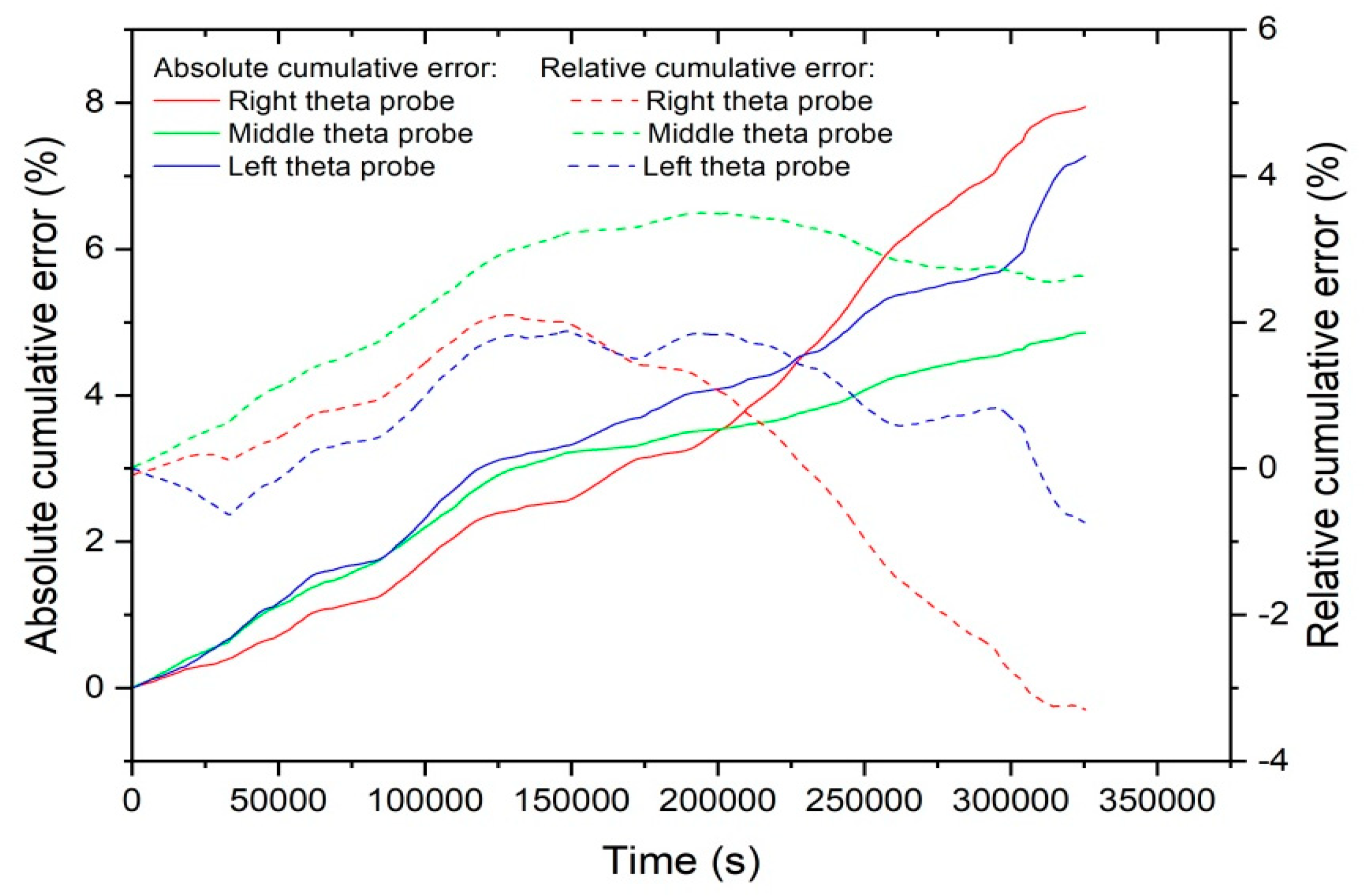
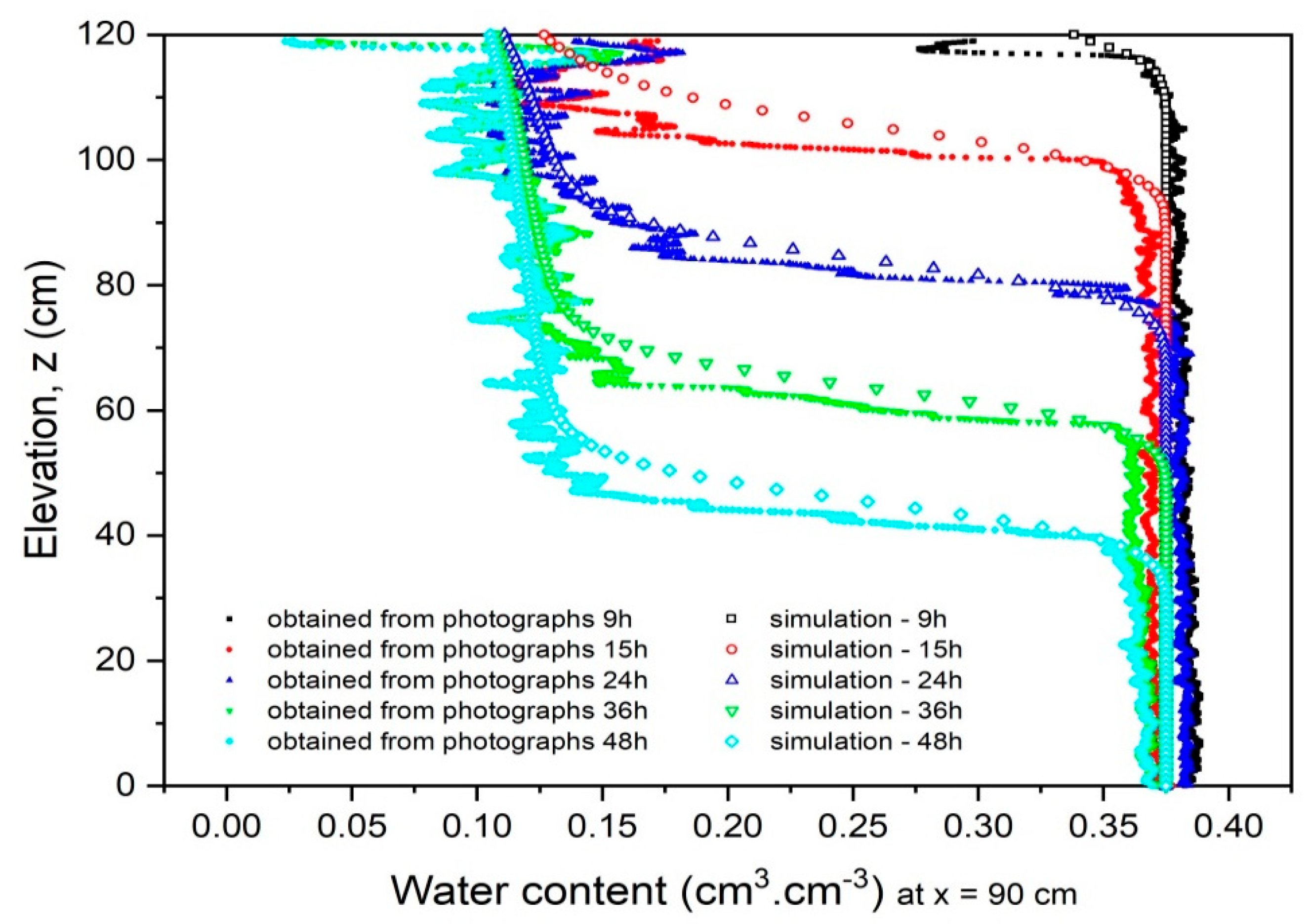
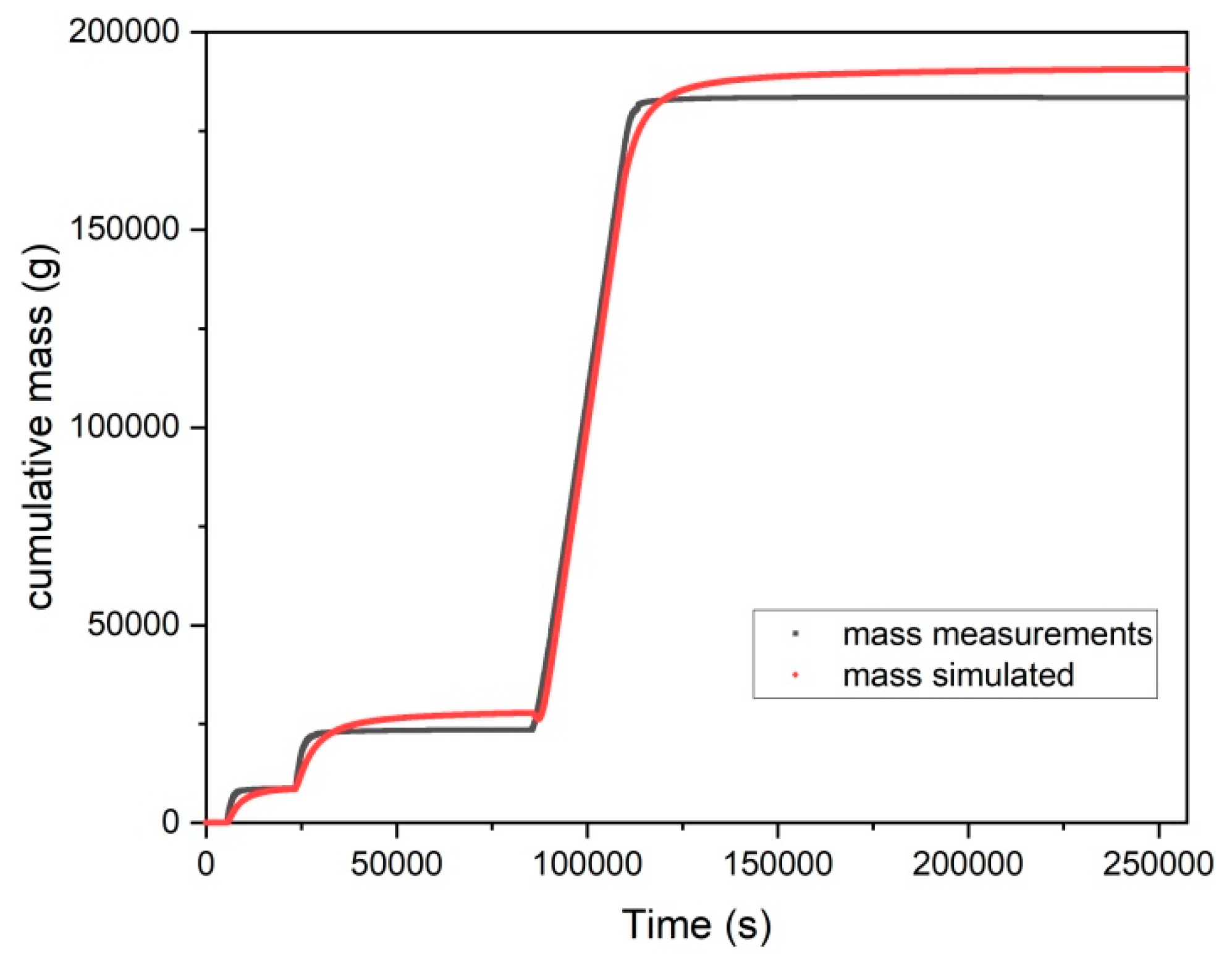
3.2. Second Experiment: Drainage–Rainfall Infiltration–Drainage–Imbibition Cycle
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Corwin, D.L.; Hopmans, J.; de Rooij, G.H. From Field- to Landscape-Scale Vadose Zone Processes: Scale Issues, Modeling, and Monitoring. Vadose Zone J. 2006, 5, 129–139. [Google Scholar] [CrossRef]
- Fleckenstein, J.H.; Krause, S.; Hannah, D.M.; Boano, F. Groundwater-surface water interactions: New methods and models to improve understanding of processes and dynamics. Adv. Water Resour. 2010, 33, 1291–1295. [Google Scholar] [CrossRef]
- Harter, T.; Hopmans, J.W. Role of vadose-zone flow processes in regional-scale hydrology: Review, opportunities and challenges. In Unsaturated-Zone Modelling: Progress, Challenges and Applications; Feddes, R.A., de Rooij, G.H., van Dam, J.C., Eds.; Springer: Dordrecht, The Netherlands, 2004; Volume 8, pp. 179–208. [Google Scholar]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Or, D.; Smets, B.F.; Wraith, J.M.; Dechesne, A.; Friedman, S.P. Physical constraints affecting bacterial habitats and activity in unsaturated porous media—A review. Adv. Water Resour. 2007, 30, 1505–1527. [Google Scholar] [CrossRef]
- Rivett, M.O.; Wealthall, G.P.; Dearden, R.A.; McAlary, T.A. Review of unsaturated-zone transport and attenuation of volatile organic compound (VOC) plumes leached from shallow source zones. J. Contam. Hydrol. 2011, 123, 130–156. [Google Scholar] [CrossRef] [PubMed]
- Leong, E.C.; Rahardjo, H. Review of Soil-Water Characteristic Curve Equations. J. Geotech. Geoenviron. 1997, 123, 1106–1117. [Google Scholar] [CrossRef]
- Malaya, C.; Sreedeep, S. Critical Review on the Parameters Influencing Soil-Water Characteristic Curve. J. Irrig. Drain. Eng. 2012, 138, 55–62. [Google Scholar] [CrossRef]
- Steefel, C.I.; Appelo, C.A.J.; Arora, B.; Jacques, D.; Kalbacher, T.; Kolditz, O.; Lagneau, V.; Lichtner, P.C.; Mayer, K.U.; Meeussen, J.C.L.; et al. Reactive transport codes for subsurface environmental simulation. Computat. Geosci. 2015, 19, 445–478. [Google Scholar] [CrossRef]
- Gargiulo, G.; Bradford, S.A.; Simunek, J.; Ustohal, P.; Vereecken, H.; Klumpp, E. Bacteria Transport and Deposition under Unsaturated Flow Conditions: The Role of Water Content and Bacteria Surface Hydrophobicity. Vadose Zone J. 2008, 7, 406–419. [Google Scholar] [CrossRef] [Green Version]
- Dobriyal, P.; Qureshi, A.; Badola, R.; Hussain, S.A. A review of the methods available for estimating soil moisture and its implications for water resource management. J. Hydrol. 2012, 458–459, 110–117. [Google Scholar] [CrossRef]
- Ochsner, T.E.; Cosh, M.H.; Cuenca, R.H.; Dorigo, W.A.; Draper, C.S.; Hagimoto, Y.; Kerr, Y.H.; Njoku, E.G.; Small, E.E.; Zreda, M.; et al. State of the Art in Large-Scale Soil Moisture Monitoring. Soil Sci. Soc. Am. J. 2013, 77, 1888–1919. [Google Scholar] [CrossRef] [Green Version]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil Moisture Measurement for Ecological and Hydrological Watershed-Scale Observatories: A Review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- Romano, N. Soil moisture at local scale: Measurements and simulations. J. Hydrol. 2014, 516, 6–20. [Google Scholar] [CrossRef]
- Susha Lekshmi, S.L.; Singh, D.N.; Shojaei Baghini, M. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar]
- Vereecken, H.; Huisman, J.A.; Bogena, H.; Vanderborght, J.; Vrugt, J.A.; Hopmans, J.W. On the value of soil moisture measurements in vadose zone hydrology: A review. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Duygu, B.M.; Akyürek, Z. Using Cosmic-Ray Neutron Probes in Validating Satellite Soil Moisture Products and Land Surface Models. Water 2019, 11, 1362. [Google Scholar] [CrossRef]
- Zhou, L.; Yu, D.; Wang, Z.; Wang, X. Soil Water Content Estimation Using High-Frequency Ground Penetrating Radar. Water 2019, 11, 1036. [Google Scholar] [CrossRef]
- Blonquist, J.M.; Jones, S.B.; Robinson, D.A. Standardizing Characterization of Electromagnetic Water Content Sensors. Vadose Zone J. 2005, 4, 1059–1069. [Google Scholar] [CrossRef]
- Jones, S.B.; Blonquist, J.M., Jr.; Robinson, D.A.; Rasmussen, V.P.; Or, D. Standardizing Characterization of Electromagnetic Water Content Sensors: Part 1. Methodology. Vadose Zone J. 2005, 4, 1048–1058. [Google Scholar] [CrossRef] [Green Version]
- Robinson, D.A.; Gardner, C.M.K.; Cooper, J.D. Measurement of relative permittivity in sandy soils using TDR, capacitance and theta probes: Comparison, including the effects of bulk soil electrical conductivity. J. Hydrol. 1999, 223, 198–211. [Google Scholar] [CrossRef]
- Vaz, C.M.P.; Jones, S.; Meding, M.; Tuller, M. Evaluation of Standard Calibration Functions for Eight Electromagnetic Soil Moisture Sensors. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Belfort, B.; Weill, S.; Lehmann, F. Image analysis method for the measurement of water saturation in a two-dimensional experimental flow tank. J. Hydrol. 2017, 550, 343–354. [Google Scholar] [CrossRef] [Green Version]
- Oostrom, M.; Dane, J.H.; Wietsma, T.W. A Review of Multidimensional, Multifluid, Intermediate-Scale Experiments: Flow Behavior, Saturation Imaging, and Tracer Detection and Quantification. Vadose Zone J. 2007, 6, 610–637. [Google Scholar] [CrossRef]
- Goswami, R.R.; Clement, T.P. Laboratory-scale investigation of saltwater intrusion dynamics. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Konz, M.; Ackerer, P.; Meier, E.; Huggenberger, P.; Zechner, E.; Gechter, D. On the measurement of solute concentrations in 2-D flow tank experiments. Hydrol. Earth Syst. Sci. 2008, 12, 727–738. [Google Scholar] [CrossRef] [Green Version]
- Konz, M.; Ackerer, P.; Huggenberger, P.; Veit, C. Comparison of light transmission and reflection techniques to determine concentrations in flow tank experiments. Exp. Fluids 2009, 47, 85–93. [Google Scholar] [CrossRef] [Green Version]
- Konz, M.; Younes, A.; Ackerer, P.; Fahs, M.; Huggenberger, P.; Zechner, E. Variable-density flow in heterogeneous porous media — Laboratory experiments and numerical simulations. J. Contam. Hydrol. 2009, 108, 168–175. [Google Scholar] [CrossRef]
- McNeil, J.D.; Oldenborger, G.A.; Schincariol, R.A. Quantitative imaging of contaminant distributions in heterogeneous porous media laboratory experiments. J. Contam. Hydrol. 2006, 84, 36–54. [Google Scholar] [CrossRef]
- Oostrom, M.; Hayworth, J.S.; Dane, J.H.; Güven, O. Behavior of dense aqueous phase leachate plumes in homogeneous porous media. Water Resour. Res. 1992, 28, 2123–2134. [Google Scholar] [CrossRef]
- Oostrom, M.; Dane, J.H.; Güven, O.; Hayworth, J.S. Experimental investigation of dense solute plumes in an unconfined aquifer model. Water Resour. Res. 1992, 28, 2315–2326. [Google Scholar] [CrossRef]
- Rahman, M.A.; Jose, S.C.; Nowak, W.; Cirpka, O.A. Experiments on vertical transverse mixing in a large-scale heterogeneous model aquifer. J. Contam. Hydrol. 2005, 80, 130–148. [Google Scholar] [CrossRef] [PubMed]
- Schincariol, R.A.; Schwartz, F.W. An experimental investigation of variable density flow and mixing in homogeneous and heterogeneous media. Water Resour. Res. 1990, 26, 2317–2329. [Google Scholar] [CrossRef]
- Schincariol, R.A.; Herderick, E.E.; Schwartz, F.W. On the application of image analysis to determine concentration distributions in laboratory experiments. J. Contam. Hydrol. 1993, 12, 197–215. [Google Scholar] [CrossRef]
- Simmons, C.T.; Pierini, M.L.; Hutson, J.L. Laboratory Investigation of Variable-Density Flow and Solute Transport in Unsaturated–Saturated Porous Media. Transp. Porous Media 2002, 47, 215–244. [Google Scholar] [CrossRef]
- Swartz, C.H.; Schwartz, F.W. An experimental study of mixing and instability development in variable-density systems. J. Contam. Hydrol. 1998, 34, 169–189. [Google Scholar] [CrossRef]
- Van Geel, P.J.; Sykes, J.F. Laboratory and model simulations of a LNAPL spill in a variably-saturated sand, 1. Laboratory experiment and image analysis techniques. J. Contam. Hydrol. 1994, 17, 1–25. [Google Scholar] [CrossRef]
- Wildenschild, D.; Jensen, K.H. Laboratory investigations of effective flow behavior in unsaturated heterogeneous sands. Water Resour. Res. 1999, 35, 17–27. [Google Scholar] [CrossRef]
- Hoa, N.T. A new method allowing the measurement of rapid variations of the water content in sandy porous media. Water Resour. Res. 1981, 17, 41–48. [Google Scholar] [CrossRef]
- Persson, M. Estimating Surface Soil Moisture from Soil Color Using Image Analysis. Vadose Zone J. 2005, 4, 1119–1122. [Google Scholar] [CrossRef]
- Yoshimoto, N.; Orense, R.P.; Tanabe, F.; Kikkawa, N.; Hyodo, M.; Nakata, Y. Measurement of degree of saturation on model ground by digital image processing. Soils Found. 2011, 51, 167–177. [Google Scholar] [CrossRef]
- Cremer, C.J.M.; Schuetz, C.; Neuweiler, I.; Lehmann, P.; Lehmann, E.H. Unstable Infiltration Experiments in Dry Porous Media. Vadose Zone J. 2017, 16. [Google Scholar] [CrossRef]
- Conrad, S.H.; Glass, R.J.; Peplinski, W.J. Bench-scale visualization of DNAPL remediation processes in analog heterogeneous aquifers: Surfactant floods and in situ oxidation using permanganate. J. Contam. Hydrol. 2002, 58, 13–49. [Google Scholar] [CrossRef]
- Gerhard, J.I.; Kueper, B.H. Capillary pressure characteristics necessary for simulating DNAPL infiltration, redistribution, and immobilization in saturated porous media. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Abdul, A.S.; Gillham, R.W. Laboratory Studies of the Effects of the Capillary Fringe on Streamflow Generation. Water Resour. Res. 1984, 20, 691–698. [Google Scholar] [CrossRef]
- Abdul, A.S.; Gillham, R.W. Field studies of the effects of the capillary fringe on streamflow generation. J. Hydrol. 1989, 112, 1–18. [Google Scholar] [CrossRef]
- Hills, R.G.; Wierenga, P.J.; Hudson, D.B.; Kirkland, M.R. The Second Las Cruces Trench Experiment: Experimental Results and Two-Dimensional Flow Predictions. Water Resour. Res. 1991, 27, 2707–2718. [Google Scholar] [CrossRef]
- Stauffer, F.; Dracos, T. Experimental and numerical study of water and solute infiltration in layered porous media. J. Hydrol. 1986, 84, 9–34. [Google Scholar] [CrossRef]
- Stephens, D.B.; Heermann, S. Dependence of anisotropy on saturation in a stratified sand. Water Resour. Res. 1988, 24, 770–778. [Google Scholar] [CrossRef]
- Tidwell, V.C.; Glass, R.J. X ray and visible light transmission for laboratory measurement of two-dimensional saturation fields in thin-slab systems. Water Resour. Res. 1994, 30, 2873–2882. [Google Scholar] [CrossRef]
- Vauclin, M.; Khanji, D.; Vachaud, G. Experimental and numerical study of a transient, two-dimensional unsaturated-saturated water table recharge problem. Water Resour. Res. 1979, 15, 1089–1101. [Google Scholar] [CrossRef]
- Yeh, T.-C.J.; Harvey, D.J. Effective unsaturated hydraulic conductivity of layered sands. Water Resour. Res. 1990, 26, 1271–1279. [Google Scholar] [CrossRef]
- Beydoun, H.; Lehmann, F. Expériences de drainage et estimation de paramètres en milieu poreux non saturé. Comptes Rendus Geosci. 2006, 338, 180–187. [Google Scholar] [CrossRef]
- DiCarlo, D.A. Stability of gravity-driven multiphase flow in porous media: 40 Years of advancements. Water Resour. Res. 2013, 49, 4531–4544. [Google Scholar] [CrossRef]
- Hincapié, I.; Germann, P. Gravity-Driven Viscous Flow in Sand Boxes Assessed with Neutron Radiography. Vadose Zone J. 2009, 8, 891–901. [Google Scholar] [CrossRef] [Green Version]
- Pfletschinger, H.; Engelhardt, I.; Piepenbrink, M.; Königer, F.; Schuhmann, R.; Kallioras, A.; Schüth, C. Soil column experiments to quantify vadose zone water fluxes in arid settings. Environ. Earth Sci. 2012, 65, 1523–1533. [Google Scholar] [CrossRef]
- Sililo, O.T.N.; Tellam, J.H. Fingering in Unsaturated Zone Flow: A Qualitative Review with Laboratory Experiments on Heterogeneous Systems. Groundwater 2000, 38, 864–871. [Google Scholar] [CrossRef]
- Noh, S.J.; An, H.; Kim, S.; Kim, H. Simulation of soil moisture on a hillslope using multiple hydrologic models in comparison to field measurements. J. Hydrol. 2015, 523, 342–355. [Google Scholar] [CrossRef]
- Vanderborght, J.; Kasteel, R.; Herbst, M.; Javaux, M.; Thiéry, D.; Vanclooster, M.; Mouvet, C.; Vereecken, H. A Set of Analytical Benchmarks to Test Numerical Models of Flow and Transport in Soils. Vadose Zone J. 2005, 4, 206–221. [Google Scholar] [CrossRef]
- Gaskin, G.J.; Miller, J.D. Measurement of Soil Water Content Using a Simplified Impedance Measuring Technique. J. Agric. Eng. Res. 1996, 63, 153–159. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Belfort, B.; Younes, A.; Fahs, M.; Lehmann, F. On equivalent hydraulic conductivity for oscillation–free solutions of Richard’s equation. J. Hydrol. 2013, 505, 202–217. [Google Scholar] [CrossRef]
- Fahs, M.; Younes, A.; Lehmann, F. An easy and efficient combination of the Mixed Finite Element Method and the Method of Lines for the resolution of Richards’ Equation. Environ. Modell. Softw. 2009, 24, 1122–1126. [Google Scholar] [CrossRef]
- Russ, J.C. The Image Processing Handbook; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Gimmi, T.; Ursino, N. Mapping Material Distribution in a Heterogeneous Sand Tank by Image Analysis. Soil Sci. Soc. Am. J. 2004, 68, 1508–1514. [Google Scholar] [CrossRef]
- Almhdie, A.; Rozenbaum, O.; Lespessailles, E.; Jennane, R. Image processing for the non-destructive characterization of porous media. Application to limestones and trabecular bones. Math. Comput. Simul. 2014, 99, 82–94. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.; Schwartz, F.W. Determining concentration fields of tracer plumes for layered porous media in flow-tank experiments. Hydrogeol. J. 1999, 7, 236–240. [Google Scholar] [CrossRef]
- Kaestner, A.; Lehmann, E.; Stampanoni, M. Imaging and image processing in porous media research. Adv. Water Resour. 2008, 31, 1174–1187. [Google Scholar] [CrossRef]

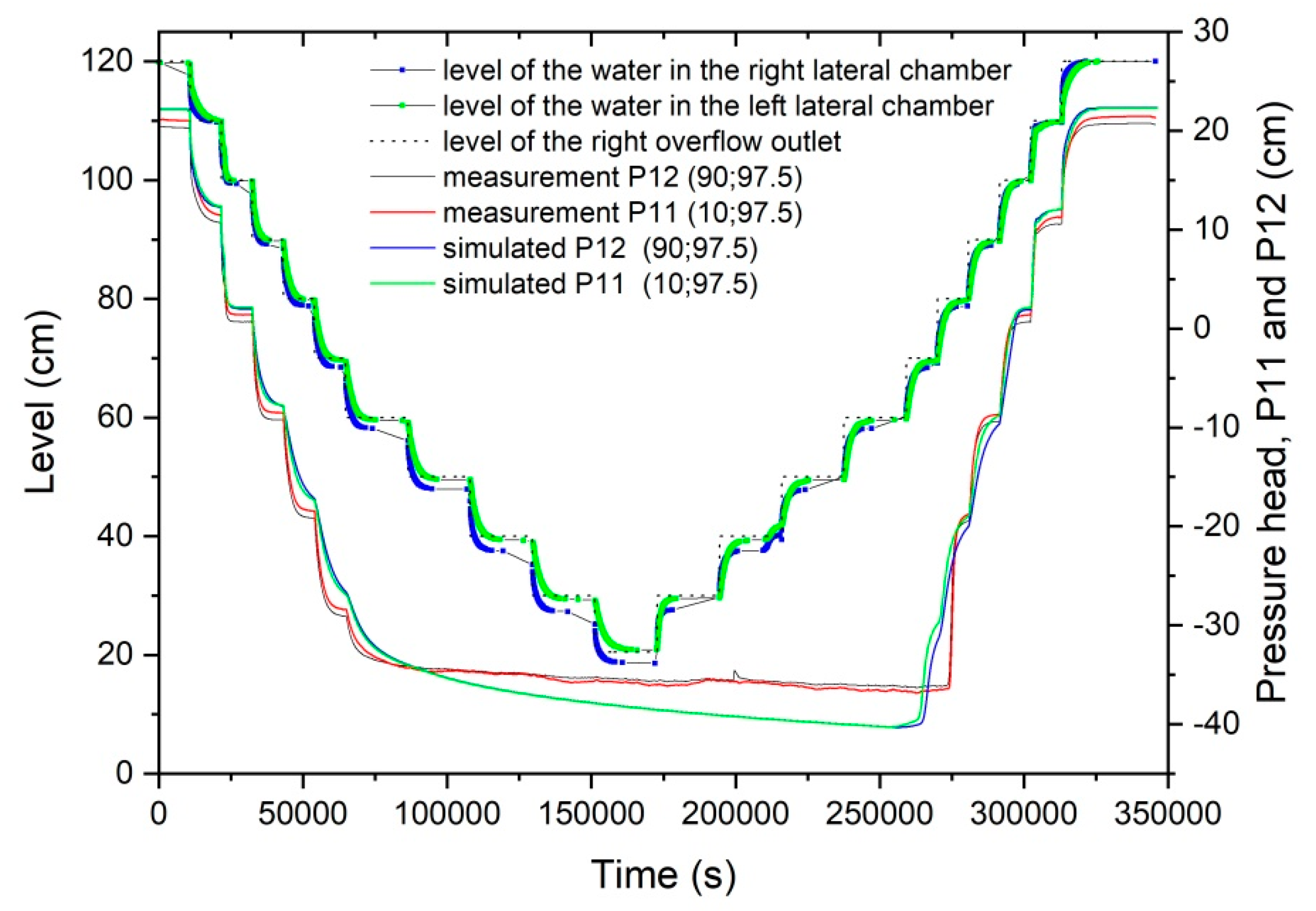
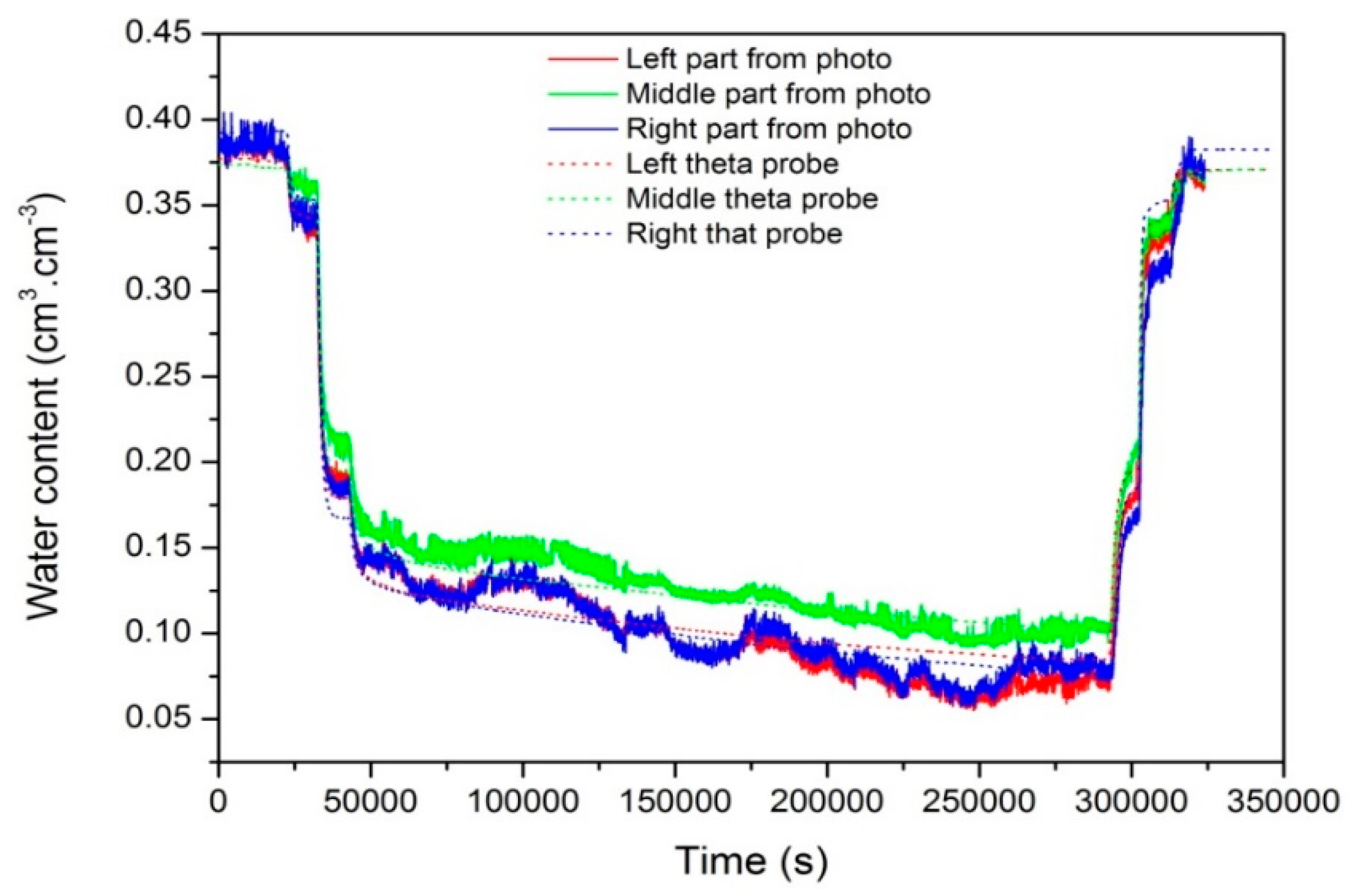

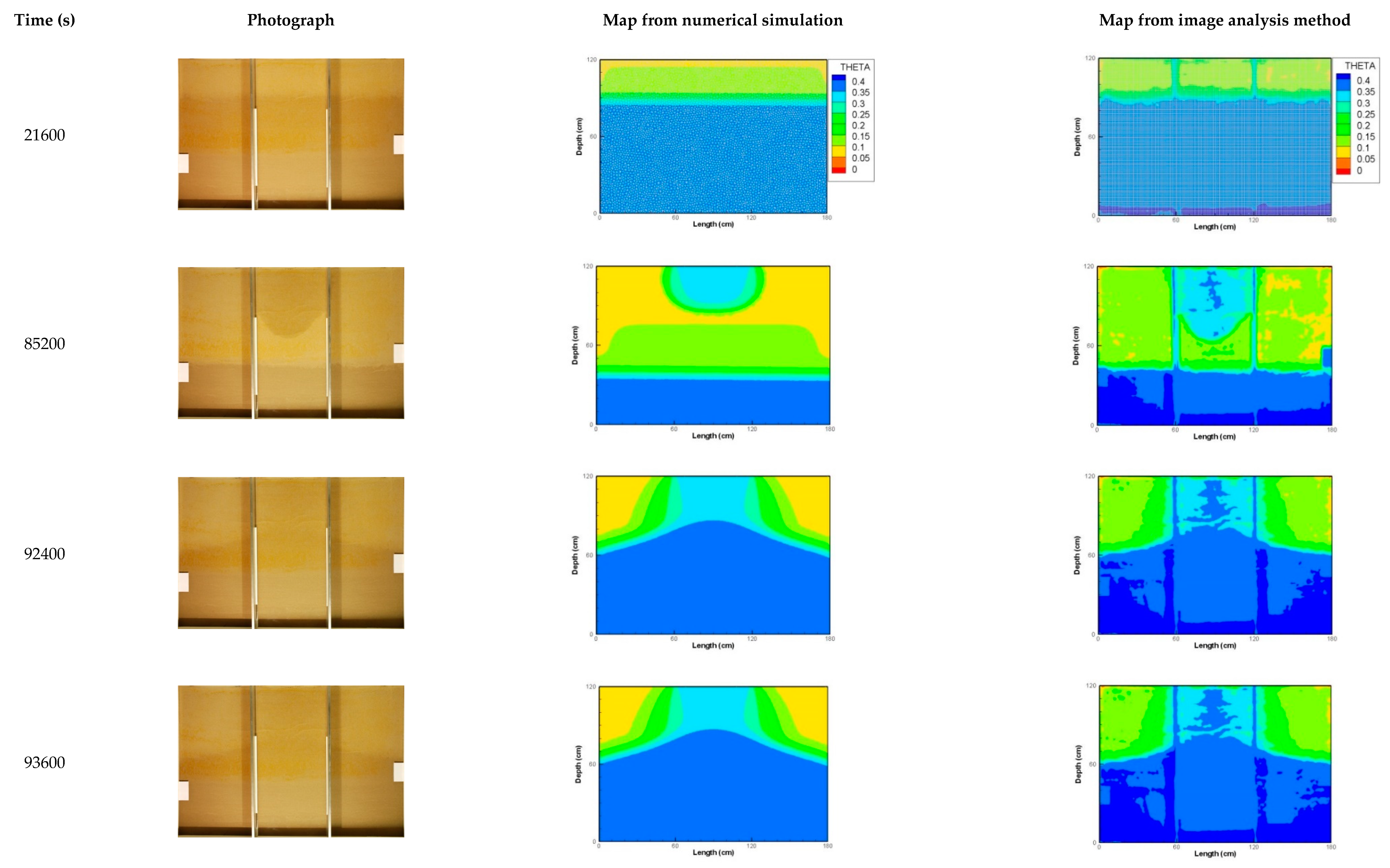
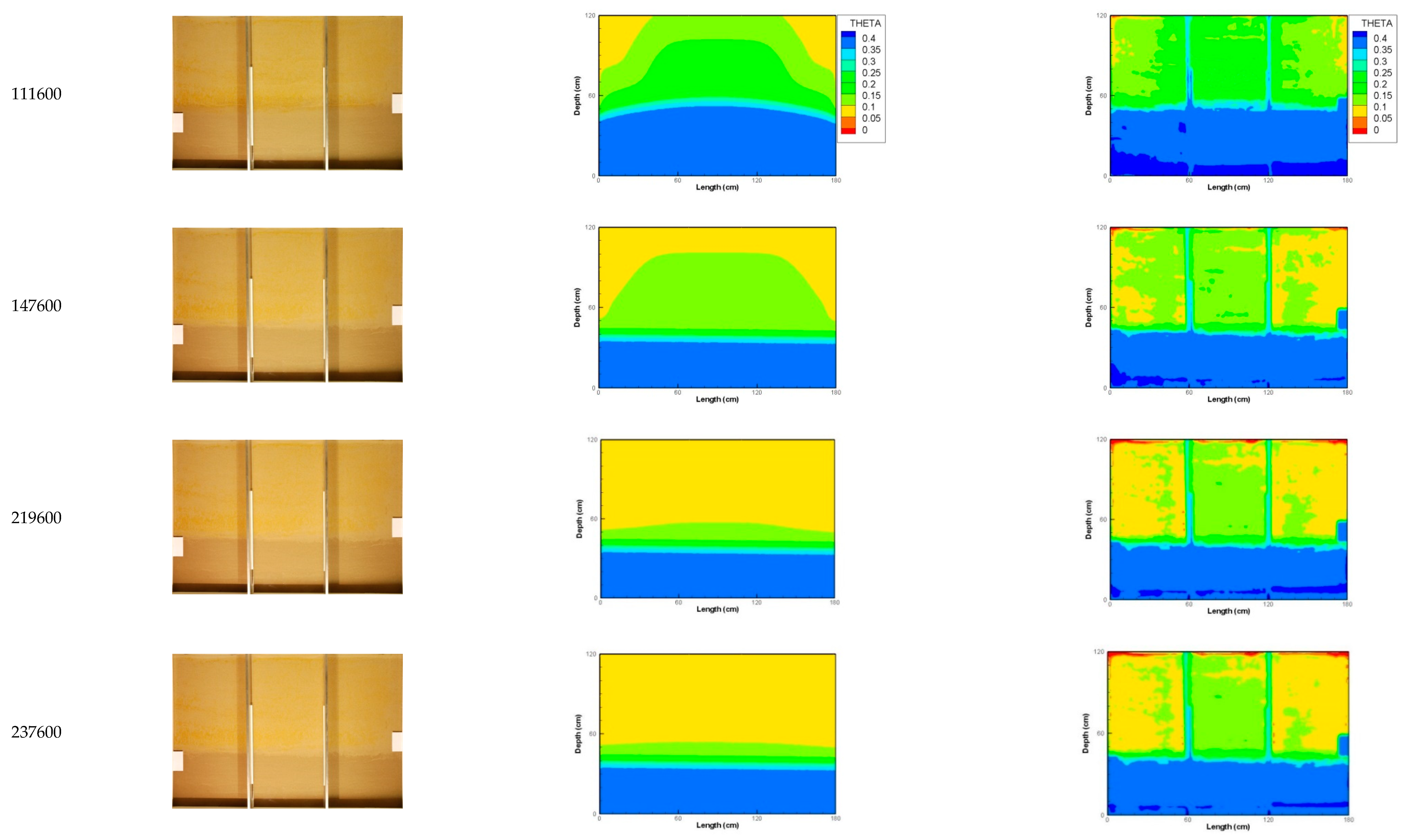
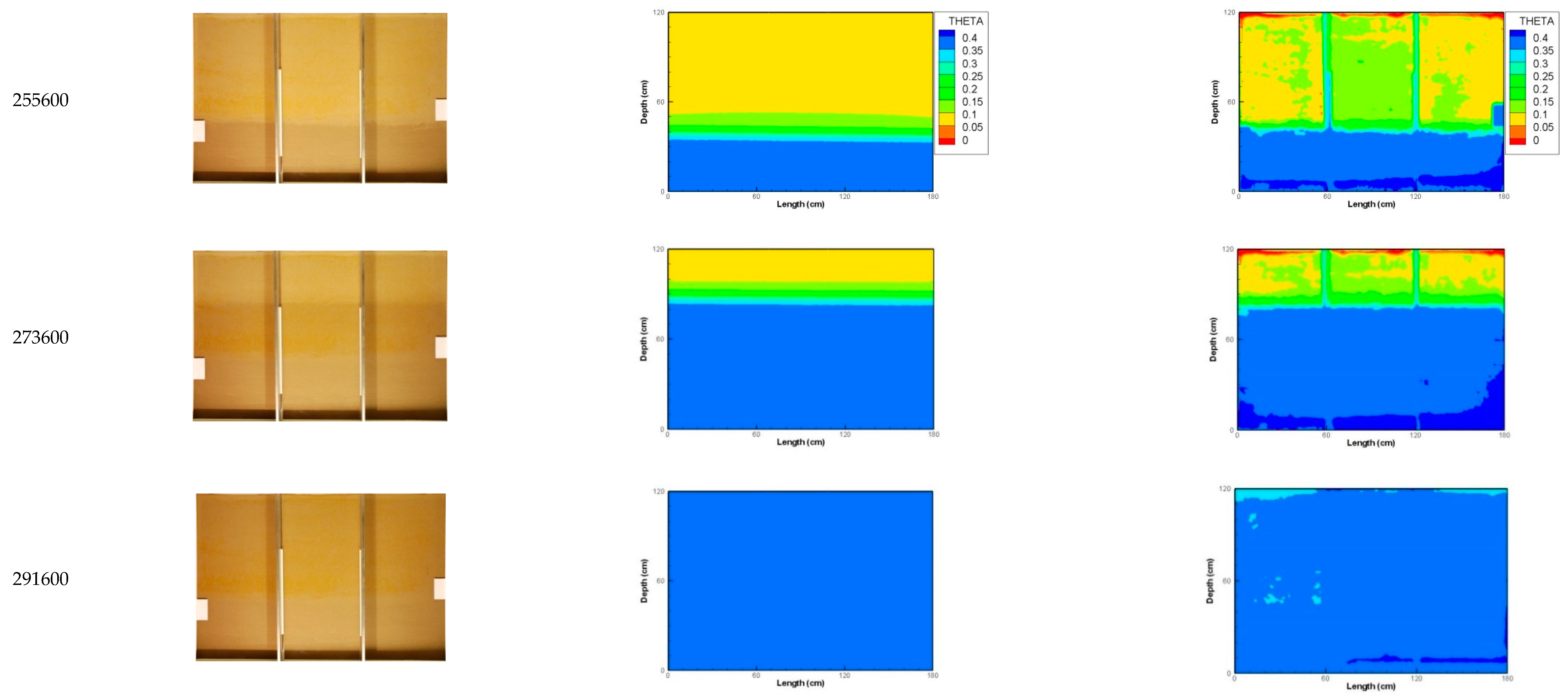
| 1st Experiment: Simple Drainage–Imbibition Cycle | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Right overflow outlet displacement (cm) | −10 | −10 | −10 | −10 | −10 | −10 | −10 | −10 | −10 | −9.5 | 9.5 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| step duration (h) | 3 | 3 | 3 | 3 | 3 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 3 | 3 | 3 | 3 | 3 | 3 |
| Elapsed time at the end of the step (h) | 6 | 9 | 12 | 15 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 75 | 78 | 81 | 84 | 87 | 90 |
| 2nd experiment: drainage–rainfall–drainage–imbibition cycle | ||||||||||||||||||||
| description | Waiting time | Both overflow outlets displacement (cm) | Constant rainfall | Waiting time | Both overflow outlets displacement (cm) | |||||||||||||||
| details | fully saturated | −50 | −48.5 | - | Partially saturated | 48.5 | 49 | 1 | ||||||||||||
| step duration (h) | 1.5 | 5 | 17 | 7 | 41 | 5 | 4 | 1 | ||||||||||||
| Elapsed time at the end of the step (h) | 1.5 | 6.5 | 23.5 | 30.5 | 71.5 | 76.5 | 80.5 | 81.5 | ||||||||||||
| Parameter | Value | Standard Error |
|---|---|---|
| 0.3859 | 0.003 | |
| −2.373 | 0.031 | |
| r² | 0.989 | |
| −8.674 10−5 | ||
| 0.00013 | 0.01151 | |
| 4.77 10−6 | 0.002184 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belfort, B.; Weill, S.; Fahs, M.; Lehmann, F. Laboratory Experiments of Drainage, Imbibition and Infiltration under Artificial Rainfall Characterized by Image Analysis Method and Numerical Simulations. Water 2019, 11, 2232. https://doi.org/10.3390/w11112232
Belfort B, Weill S, Fahs M, Lehmann F. Laboratory Experiments of Drainage, Imbibition and Infiltration under Artificial Rainfall Characterized by Image Analysis Method and Numerical Simulations. Water. 2019; 11(11):2232. https://doi.org/10.3390/w11112232
Chicago/Turabian StyleBelfort, Benjamin, Sylvain Weill, Marwan Fahs, and François Lehmann. 2019. "Laboratory Experiments of Drainage, Imbibition and Infiltration under Artificial Rainfall Characterized by Image Analysis Method and Numerical Simulations" Water 11, no. 11: 2232. https://doi.org/10.3390/w11112232
APA StyleBelfort, B., Weill, S., Fahs, M., & Lehmann, F. (2019). Laboratory Experiments of Drainage, Imbibition and Infiltration under Artificial Rainfall Characterized by Image Analysis Method and Numerical Simulations. Water, 11(11), 2232. https://doi.org/10.3390/w11112232






