Well Rate and Placement for Optimal Groundwater Remediation Design with A Surrogate Model

Abstract

A new surrogate-assisted optimization formulation for groundwater remediation design was developed. A stationary Eulerian travel time model was used in lieu of a conservative solute transport model. The decision variables of the management model are well locations and their flow rates. The objective function adjusts the residence time distribution between all pairs of injection-production wells in the remediation system. This goal is achieved by using the Lorenz coefficient as an effective metric to rank the relative efficiency of many remediation policies. A discrete adjoint solver was developed to provide the sensitivity of the objective function with respect to changes in decision variables. The quality management model was checked with simple solutions and then applied to hypothetical two- and three-dimensional test problems. The performance of the simulation-optimization approach was evaluated by comparing the initial and optimal remediation designs using an advective-dispersive solute transport simulator. This study shows that optimal designs simultaneously delay solute transport breakthrough at pumping wells and improve the sweep efficiency leading to smaller cleanup times. Well placement optimization in heterogeneous porous media was found to be more important than well rate optimization. Additionally, optimal designs based on two-dimensional models were found to be more optimistic suggesting a direct use of three-dimensional models in a simulation-optimization framework. The computational budget was drastically reduced because the proposed surrogate-based quality management model is generally cheaper than one single solute transport simulation. The introduced model could be used as a fast, but first-order, approximation method to estimate pump-and-treat capital remediation costs. The results show that physically based low-fidelity surrogate models are promising computational approaches to harness the power of quality management models for complex applications with practical relevance.

1. Introduction

Simulation-based optimization (S/O) approaches are increasingly used to support water resources management, policy analysis, economics and decision-making. They result from a coupling between a physically based model, such as groundwater flow or solute/energy transport and an optimization search algorithm [1,2,3,4]. The optimization engine iteratively updates decision variables to minimize a given objective function under a set of equality and inequality constraints to meet a desired policy. The primary outcome from the management model is a set of optimally designed variables, such as external stresses and the corresponding value of the objective function. Practical engineering applications of mathematical groundwater management models include a pump-and-treat (P&T) systems design [5,6,7,8,9,10,11], sustainable coastal aquifer management [12,13,14], planning of surface and groundwater supply systems [15,16], the identification of unknown pollution sources [17,18], geothermal reservoir engineering [19,20] and pressure buildup management via brine extraction in geological CO₂ storage [21], among others.

After many decades of research, groundwater quality management models have many bottlenecks preventing their mainstream use [4]. While groundwater flow management models have advanced significantly, this is not the case for existing S/O approaches based on solute transport models. Practitioners are facing major challenges to turn their existing groundwater quality models, whose complexity increases over time, into effective water resources management tools. Indeed, even with the affordability of state-of-the-art computational resources, rigorous optimization workflows are prohibitively expensive. Mathematical groundwater quality management based on solute transport models requires a large number of forward iterations before finding an optimal, or near-optimal, solution. This issue is critical as there is clearly a recent shift towards global optimization methods requiring a lengthy iterative process [4,6,7,8,10,11,22]. Model complexity relates to the problem dimension, the size of the discrete problem, the total number of injection and pumping wells, the strength of the geological control, and nature of the flow and solute transport processes. As a single S/O iteration performance depends on model complexity, many alternative solutions have been sought in the past. Replacing a discrete finite-difference or finite-element model with a simple analytical solution or a cheaper alternative as the analytical element method are popular examples. These techniques have been used to prevent seawater intrusion in coastal aquifers [12] and to contain pollution by P&T systems [7]. However, these alternatives rely on many assumptions preventing their general applicability to real-world problems. In particular, the assessment of the subsurface aquifer heterogeneity impacts on decision variables cannot be achieved, leading to possibly false optimal designs. It has been shown that physical and chemical heterogeneities chiefly impact optimal remediation design, costs and cleanup times [23]. A class of approaches based on surrogates of groundwater models have been the focus of recent developments [24,25]. The role of a surrogate model in an optimization framework is to drive the whole process towards the optimal solution, even if the intermediate iterates are not accurate. Therefore, the overall computational budget of the S/O loop would drop to an acceptable level for processing complex applications with practical relevance.

There are three broad categories of surrogate models currently developed for the water resources engineering problems. These belong either to response surface models (or metamodels) [26], projection-based models [27,28], and physically based low-fidelity models [29,30]. Metamodels are intensive data-driven techniques because the surrogate model is constructed from many simulations with the complex model. This database is used to train the surrogate with techniques, such as deep learning algorithms [19,31]. A recent review [24] critically analyzed the current progress in response to surface surrogates and concluded that many shortcomings persist against their adoption for practical groundwater applications. In particular, there are little-developed community skills to validate the constructed metamodels. In addition, the efforts to construct and train response surface models may offset their claimed computational savings. Consequently, low-fidelity surrogates are promising alternatives because they circumvent many limitations of the surface response surrogates [24,25]. Indeed, when qualitatively compared to metamodels, they are less biased to the parametric sampling methodology. Hence, they are more reliable to search the unexplored regions of the decision variables space during optimization. Moreover, a physically based surrogate model is a sound alternative for groundwater modeling practitioners because the underlying principles are easier to explain and understand. This facilitates their acceptance by practicing engineers, water resources managers and stakeholders.

Most existing S/O approaches in the literature use simplified groundwater models, such as, those relying on the two-dimensional Dupuit-Forchhemeir assumption. Frequently, there are no further assessments of how these assumptions would affect the effectiveness of the optimal design. This is of high relevance to heterogeneous aquifers with spatially distributed parameters. Simplifying the realism of these formations may lead to far than optimal solutions for quality management models [32]. The available computational budget often falls short to accomplish the lengthy number of solute transport iterates before convergence of the S/O loop. To cope with this fundamental limitation, this paper introduces a physically based surrogate model to streamline the use of quality management models for complex aquifer systems. The key idea is to replace the solute transport model with a grid-based advective travel time model [33]. This method could be considered as a new model reduction technique, which is explored herein for the first time to the authors’ best knowledge. This is mainly reflected by approximating the transient concentration dynamics with a lumped steady-state travel time. The purpose of this work is not to compare the merits of the introduced surrogate-based approach versus metamodels or other alternatives for P&T optimal design, but rather to examine the applicability of this approach to this class of problems and develop guidelines for its appropriate formulation.

Previous investigations have demonstrated the importance of considering the well placement in the framework of an S/O design. For instance, [6] indicated that when considering PT remediation in heterogeneous aquifers, well placement optimization is more important than optimizing the pumping rate. In the presented S/O algorithm, well positions are implicit decision variables of the problem. Avoiding explicit inclusion of well placement constraints into the problem formulation leads to enhanced robustness when using gradient-based optimization techniques [6,31]. This is because explicit inclusion of well locations as decision variables produces discontinuous derivatives leading to convergence difficulties.

In this work, a new formulation of the objective function is proposed. A specific choice is made to counteract adverse effects of the physical heterogeneity distribution on the P&T system performance. In heterogeneous porous media, long residence times result from the occurrence of elongated streamlines possibly connecting badly placed well pairs and/or connected boundary conditions. This is manifest in early breakthrough and late tailing of the pollutant at pumping wells. The residence time between all injection-pumping well pairs in the remediation system need to be adjusted by manipulating the flow filed. Therefore, the objective function was formulated to narrow the streamlines’ length distribution in the aquifer, as would be the case for an otherwise ideal homogeneous displacement. To facilitate the analysis, the Lorenz coefficient was used as a metric to rank the dynamic heterogeneity for several designs.

The following section presents the fundamental concepts of the surrogate based groundwater quality management model developed in this paper. The different steps of the algorithm implementation are described. Next, the model is evaluated to predict solutions to one- and two-dimensional configurations. Then, demonstrative test problems of increasing complexity illustrate the effectiveness of the developed S/O approach. In particular, the performances of the optimal P&T system design were systematically validated. This is achieved by a comparative analysis based on two solute transport simulations implemented with the initial and optimal decision variables, respectively. Prospective conclusions and recommendations close the paper.

2. Simulation-Optimization Approach

The goal of a solute transport solver in the context of a S/O approach is not to accurately capture the dynamics of the solute plume, but rather to guide the optimization search towards a descent direction in the parameters space. For this purpose, this study advocates that a transient solute transport simulation may not be necessary at all. In this work the use of a simpler steady-state surrogate model is investigated to efficiently process an S/O loop. An aggressive reduction of the computational cost favors the development of tools, which are easy to plug in interactive engineering workflows. Therefore, the complex groundwater flow and solute transport models would be transformed into more valuable tools guiding water resources quality management.

2.1. Problem Formulation

This study hypothesizes that solute transport dynamics for an optimal P&T system design involving a heterogeneous aquifer should be as close as possible to a piston-like displacement in an ideal homogeneous aquifer system. Therefore, a quantitative measure expressing how far a solute transport displacement deviates from an ideal displacement needs to be introduced. For this purpose, the concepts of flow and storage capacity are used to express the objective function of the optimization problem [34]. This dynamic heterogeneity measure is a generalization of the flow capacity—storage capacity diagram developed in the reservoir engineering literature [35,36]. This diagram was proposed for layered porous media with uniform aquifer properties in each model layer. The static measures of heterogeneity are related to permeability and porosity distributions of the aquifer sediments. Meanwhile, dynamic measures depend also on the streamlines’ length distribution and the well pattern geometry [34].

The aquifer storage capacity, $\mathsf{\Phi }$, is the cumulative pore volume as a function of increasing travel time $\tau$ [L]:

$$\mathsf{\Phi }\left(\tau \right)={{\displaystyle \int }}_0^{\tau }\phi \left(x\left(s\right)\right)ds$$

(1)

where $\phi$ is the aquifer porosity distribution [-] and $x\left(\tau \right)$ represents all streamlines whose total travel time equal $\tau$. This is equivalent to the volume fraction of all streamlines that breakthrough at time $\tau$.

The aquifer flow capacity, F is the cumulative flow rate as a function of increasing travel time:

$$F\left(\tau \right)={{\displaystyle \int }}_0^{\tau }\frac{\phi \left(x\left(s\right)\right)}{s}ds$$

(2)

$F\left(\tau \right)$ represents the fractional flow rate at time $\tau$, which is defined as the fraction of the injected fluid to that being produced. The difference between the actual flow capacity, F, and that for the ideal displacement (i.e. when F = Φ) gives rise, after normalizing (i.e., dividing $\mathsf{\Phi }\left(\tau \right)$ and $F\left(\tau \right)$ by their values at infinite time, respectively), to the so-called Lorenz coefficient, L [34]:

$$L\left(\tau \right)=2{{\displaystyle \int }}_0^1\left(F\left(\mathsf{\Phi }\right)-\mathsf{\Phi }\right)d\mathsf{\Phi }$$

(3)

The Lorenz coefficient is a quantitative measure of the dynamic heterogeneity in the aquifer system. It is graphically interpreted as twice the net difference between the integrals of the actual F (Φ) curve and the linear straight-line F = Φ for ideal tracer displacement as illustrated in Figure 1. Consequently, F is bounded between zero and one. When L is close to zero, the solute displacement is considered to be homogeneous or ideal. As L increases, the dynamic aquifer heterogeneity becomes more pronounced. This coefficient constitutes, therefore, a useful metric upon which to compare and rank the response of a heterogeneous aquifer to different stresses, well patterns or boundary conditions.

Notably, the ratio $d\mathsf{\Phi }/\mathrm{dF}$ defines a dimensionless time quantity representing the pore volume injected in the aquifer and later denoted by PVI. The key idea behind the proposed algorithm in this paper is to optimize the P&T system design including the flow rates and well placements to minimize the Lorenz coefficient. By doing so, the streamline length distribution, in the aquifer, is narrowed to simultaneously prevent the early breakthrough and late tailing of the solute at all pumping wells. This results in shorter cleanup times and less injected pore volumes in order to meet a target cleanup concentration. Another merit of this formulation lies in its ability to eliminate stagnant areas through judicious redistribution of the flow filed to flush the contaminants towards pumping wells. This behavior is further discussed and demonstrated in some test problems presented in this paper.

The objective function of the optimization problem is given, therefore, for a total number of N_i injection wells and N_p pumping wells as:

$$\mathrm{Minimize}L\left(h,\tau \right)$$

(4)

Subject to:

$${{\displaystyle \sum }}_{i\in I}{Q}_i={{\displaystyle \sum }}_{p\in P}{Q}_p$$

(5)

$$Q_i^{min}<Q_i<Q_i^{max}$$

(6)

$$s_i<s_i^{max}$$

(7)

It is noted that the objective function (Equation (4)) depends implicitly on the groundwater head distribution, h(x) [L]. The first equality constraint imposes an equal total flow rate for injection and pumping wells, where I and P are the indices sets of injection and pumping wells, respectively given that N_w = N_I + N_P is the total number of wells. The first inequality constraint limits the flow rate of any well between the prescribed minimal and maximal thresholds. The last inequality constraint states that the drawdown at well number i, s_i [L], is not allowed to exceed a prescribed maximum. For an injection well, the drawdown is replaced by a water table rise, which should not exceed the prescribed value. The last constrain may be omitted for confined and leaky aquifers.

The evaluation of the objective function requires a numerical solution of a forward problem. An adjoint state method was used to evaluate the gradient of the objective function with respect to the travel time and the sensitivity with respect to the flow rates [37]. The forward and backward problems are described in the next subsections. During a single sweep of the S/O loop, these problems are solved sequentially.

It is noted that the S/O formulation given by Equations (4)–(7) differs from traditional single objective P&T management models formulated in the literature [5,6,7,8,9,10,11,22]. In previous works, the objective function was formulated to provide a solution that minimizes the cost function to clean up the aquifer within the remediation design timeframe. Three types of cost functions have been devised in the past including (i) the total pumping rate as a proxy for cost; (ii) operational costs related to energy consumption, water treatment, disposal and labor costs; and (iii) both operational and capital costs that include well installation and pumping costs [38]. While these formulations are well founded, they cannot necessarily lead to an optimal solution in terms of additional objectives such as cleanup performance, cleanup time and reliability. This is because the P&T remediation design problem belongs to the challenging class of multi-objective optimization problems. The techniques that implicitly incorporate objectives into the single optimization problem by transforming them into fixed constraints cannot elucidate the tradeoffs between these possibly conflicting objectives. For instance, imposing an additional constraint on the pollutant concentration to fall below a cut-off value in the aquifer or in some observation points increases the complexity of the problem considerably [38]. By ignoring this constraint, the introduced formulation does not explicitly depend on the pollutant concentration enabling the use of a physically based surrogate model. While this simultaneously improves the efficiency and robustness of the S/O problem for P&T remediation design, it inevitably entails other limitations. For instance, it prevents the applicability of this approach to other classes of groundwater remediation technologies, such as in situ bioremediation. This is because unlike P&T systems, bioremediation injection supplies chemical species (i.e., electron acceptors) needed to drive rate-limited biogeochemical reactions.

In a future version of this continuously evolving S/O framework, the author plans to consider several cost functions. Meanwhile, it is shown that the model, as formulated above, can still be useful to provide a first-order estimation of the capital costs.

2.2. The Forward Problem

The surrogate forward model involves a numerical solution of the 3D steady-state groundwater flow equation and the gridded distribution of travel time(s) in the aquifer. The steady-state groundwater flow equation for a 3D heterogeneous and anisotropic aquifer is [39]:

$$\nabla ·\left(K·\nabla h\right)+q_w\delta \left(x-x_w\right)=0$$

(8)

where $\nabla$ is the del operator; $K$ is the hydraulic conductivity tensor [L T⁻¹ ]; $h\left(x\right)$ is the hydraulic head [L]; $\delta$ is the Dirac delta function; $q_w$ is a source/sink strength term [T⁻¹] prescribed at well coordinates $x_w$ [L]. The groundwater velocity, v, [L T⁻¹] is computed using Darcy’s Law:

$$v=-K·\nabla h$$

(9)

Equation (8) is subject to Dirichlet, ${\mathsf{\Gamma }}_D$; Neumann ${\mathsf{\Gamma }}_N$; and Cauchy, ${\mathsf{\Gamma }}_C$, boundary conditions. We further subdivide the domain boundary, $\mathsf{\Gamma }$, is further subdivided into distinct zones of inflowing, outflowing and no-flow Neumann boundaries denoted by ${\mathsf{\Gamma }}_i$, ${\mathsf{\Gamma }}_O$ and ${\mathsf{\Gamma }}_{N_0}$, respectively.

The steady-state advection transport like equation governing travel time, supplemented with a Dirichlet boundary condition, is solved next as previously presented by [33]:

$$\pm v·\nabla \tau =\phi \mathrm{subject}\mathrm{to}\tau =0\mathrm{at}{\mathsf{\Gamma }}_{i/o}$$

(10)

The leading sign in front of the advection term in Equation (10) indicates the flow direction taken by a moving solute particle. In the forward direction, Equation (10) is applied to inflowing boundaries, ${\mathsf{\Gamma }}_i$, whereas outflowing boundaries, ${\mathsf{\Gamma }}_o$, have to be considered in the opposite direction. When needed, Equation (10) would be solved twice, with a standard finite difference method, to get the cell-centered values of the forward and backward travel times on a finite-difference grid. By summing these two spatial distributions, the cell-centered values of the groundwater residence time distribution are obtained.

2.3. The Backward Problem

Considering the global vector of solution unknowns $x^T=\left(h^T,{\tau }^T\right)$, this implicitly depends on the target values of well rates $Q=\left[Q_i\right]$. Next, Equation (4) is rewritten as $L\left(x\left(Q\right)\right)$ subject to constraints given by the forward model Equations (8) and (10) such that $m\left(x\left(Q\right),Q\right)=0$. The augmented Lagrange function for this problem is:

$$L_{\lambda }=L\left(x\left(Q\right)\right)+{\lambda }^{T}m\left(x\left(Q\right),Q\right)$$

(11)

The adjoint form of the above problem is given as:

$${\left(\frac{\partial m}{\partial x}\right)}^T\lambda =-{\left(\frac{\partial L}{\partial x}\right)}^T$$

(12)

The linear system of Equation (12) is solved for the Lagrange multipliers, λ. The gradient of the Lagrange function with respect to the well rates is calculated for a feasible state, x, of the system as:

$$\frac{d{L}_{\lambda }}{dQ}=\frac{dL}{dQ}+{\lambda }^T\frac{dm}{dQ}$$

(13)

As the objective function depends only on the state variable, x, the first term in the right-hand side of Equation (13) vanishes.

The forward problem is solved to obtain cell-centered groundwater heads and forward travel time as outlined above. Next, the backward problem represented by Equation (12) is solved to get the sensitivities of the objective function.

One approach to numerically approximate the Jacobian of the adjoint equation is the simpler finite difference approach for a finite and sufficiently small perturbation $\epsilon$ as:

$$\frac{\partial m}{\partial x}\approx \frac{m\left(x+\epsilon \right)-m\left(x\right)}{\epsilon }$$

(14)

A serious drawback of this approach is that a full forward simulation is necessary to compute $m\left(x+\epsilon \right)$ for every variable in the design space. Moreover, to choose the value of $\epsilon$ leading to accuracy problems is unclear. Henceforth, a high computational cost is expected when computing the Jacobian with this approach.

An efficient alternative result comes from adopting techniques borrowed from automatic differentiation (AD) to numerically compute the sensitivities [40]. AD is a set of techniques that modify the semantics of a computer program to provide sensitivities of the outputs with respect to input variations. It relies on the fact that any computer program for evaluating a numerical function can be regarded as a concatenation of elementary operations whose derivatives are known. Thus, the derivative of the output can be computed by applying the chain rule to the elemental operations. This study uses an operator overloading software approach to achieve this goal [40].

2.4. Flow Rate Optimization

A nonlinear interior-point solver was used from the MATLAB^© optimization toolbox (i.e., the fmincon algorithm) to optimize the well flow rates. This algorithm is designed for sparse large-scale linear problems. Therefore, it is best suited for problems involving a significant number of injections and/or production wells. The well rates are constrained not to fall below a prescribed small threshold (i.e., 0.1% of the upper limit in practice). Note that in the special case of a confined aquifer, a linear programming algorithm (the linprog driver function) can be used because the hydraulic head is linearly related to the flow rates. A pumping well cannot be switched to become an injection well and vice-versa. The S/O loop stops when the residual of the objective function between two successive iterations becomes smaller than a prescribed tolerance for convergence.

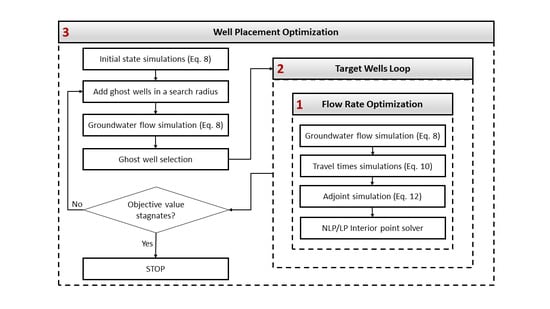
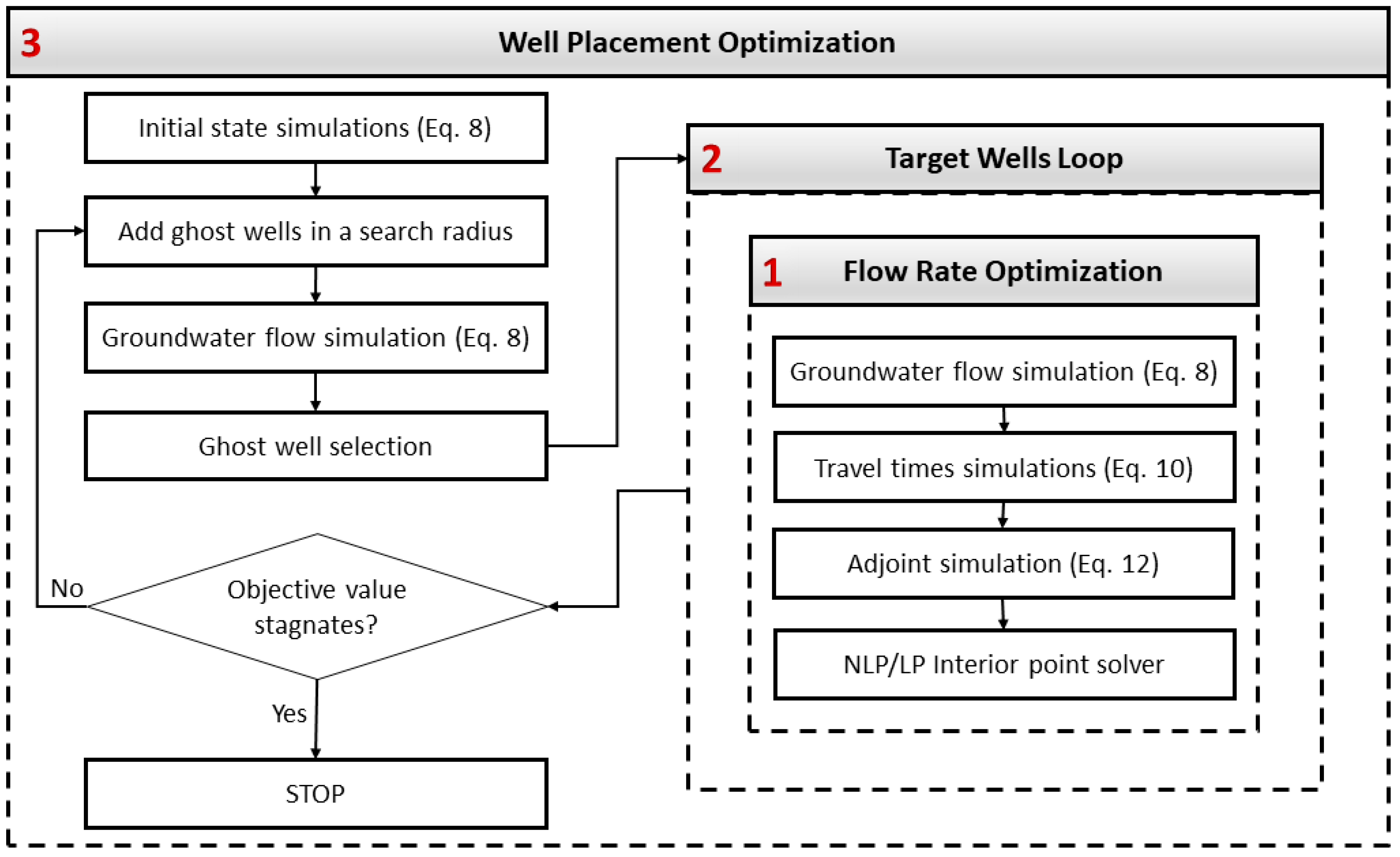
2.5. Well Placement Optimization

An important aspect of a P&T system design for a heterogeneous subsurface aquifer is well placement. In the developed S/O algorithm, well placement is not an explicit decision variable because it has been found to be inefficient [6,31]. When the shape and extent of the initial solute transport plume are known, its center of mass is a sub-optimal location for a pumping well placement [6]. The optimal location of the injection wells is not so obvious for a heterogeneous formation. Indeed, considering a homogeneous aquifer system, wells could be reasonably placed close to the plume edges. Therefore, this study seeks to optimize the positions of a prescribed number of N_i injection wells. An initial guess is the first step, and then well positions are improved by means of a grid search similar to the traversal algorithm presented by [41]. Their method consists on adding pseudo-wells, within a prescribed search radius, with a negligible flow rate close to each candidate injection well. Next, the objective function gradients of all pseudo-wells are computed and the pseudo-well with the largest gradient replaces the original well. This procedure is repeated until there is no change in all well positions. The main advantage of this approach over other alternatives [31] is its ability to determine new directions for all moving wells in only one forward and adjoint sweep. The well rates are optimized in each iteration of the well placement search algorithm. Only one well position is moving at a time to ensure capturing the optimal configuration, although this strategy slightly increases the number of forward model evaluations.

2.6. Implementation of the Surrogate-based S/O Approach

MATLAB^© was used as an integrated computational environment for prototyping, testing and analyzing the results given by the presented S/O approach. All components of the overall algorithmic sub-steps were added to an existing toolkit for groundwater data analysis, modeling, visualization and post-processing [33]. Case studies were designed by using the interactive Live Editor^© script technology enabling, not only mixing of commands and intermediate results in textual/graphical modes, but also favoring scientific reproducibility. For instance, all the results presented in this paper were generated inside a single executable notebook designed for each test problem.

Figure 2 is a simplified flowchart diagram of the surrogate-based S/O algorithm developed in this study. It shows how the different components are organized and tied together. Particularly, it depicts where the loops for optimizing the well flow rates and their placement, and how they relate, iteratively, to each other.

3. Model Evaluation

Two test problems are presented to evaluate the performance of the introduced S/O approach in this paper. They involve one- and two-dimensional problems on aquifers with two porosity zones. The simulated results were compared with the expectations derived from simple physical intuition. The model and numerical parameters used in these problems are listed in

Table 1. Model and numerical algorithm parameters used in the test problems for simulation-based optimization (S/O) evaluation.

Parameter(s)	Value(s)
Hydraulic conductivity K	10−5 m/s
Porosity ${\phi }_{low}$	20%
Porosity ${\phi }_{high}$	40%
Total flow rate Q	100 m3/day
Maximum allowed flow rate $Q_{max}$	99 m3/day
Minimum allowed flow rate $Q_{min}$	1 m3/day
S/O convergence tolerance tolopt	1%

.

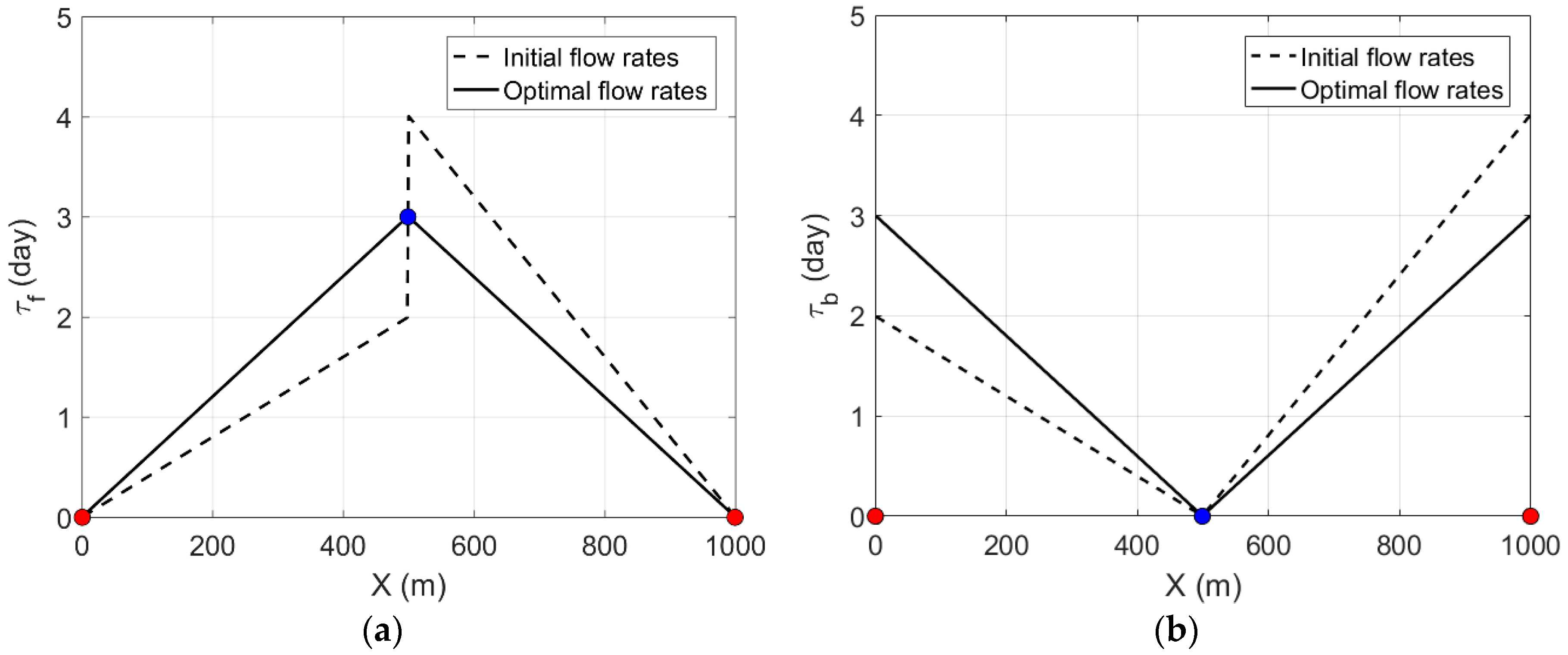
3.1. Flow Rate Optimization in a Two-zoned One-dimensional Aquifer

To test the well rate optimization component of the S/O algorithm, a 1000-m-long one-dimensional confined aquifer was considered. The two injection wells, I₁ and I₂, were placed on the left and right boundaries of the computational domain, respectively. The pumping well, P, is located in the middle at X = 500 m. The total injection flow rate, Q, was initially divided equally between I₁ and I₂. The aquifer was subdivided into two zones of low and high porosity regions at 20% and 40%, respectively. The high porosity region spans the space on the left side between I₁ and P while the remainder corresponds to the low porosity region. A uniform spatial discretization was considered into 1001 cells along the X-direction. Note that the cell at the pumping well P has an average porosity of 30 %.

Note that Equation 10 expresses a linear relationship between the porosity and the travel time. Therefore, it is expected that the forward travel time at the pumping well P of a particle released from the left at I₁ is twice that for a particle injected from well I₂. This is due to the occurrence of a higher groundwater velocity on the right side. This is exactly the double of its counterpart on the left side. Physical intuition suggests an optimal injection flow rate at I₁ to be twice of that at I₂ to maintain the forward and backward travel times equal between the two-aquifer sides. Hence, the optimal flow rate distribution would be +2Q/3 and +Q/3 for wells I₁ and I₂, respectively.

To verify these expectations, the developed S/O model was executed for this test problem. This was attained in only 15 s CPU time. Figure 3a,b illustrate the asymmetry in the forward and backward travel time profiles for the initial well design, respectively. Any particle takes 2 days to move from the right to the pumping well, while moving particles from the left side are twice as slow. On the other hand, the obtained forward and backward travel time profiles for the optimal flow rates are perfectly symmetric. The arrival time from all injection wells equals 3 days regardless of the aquifer porosity contrast in the left and right aquifer zones. This test problem illustrates the success of the introduced S/O approach in balancing the travel time between the pumping and injection wells. The simulated optimal flow rates are 66.75 m³/day and 33.25 m³/day at injection wells I₁ and I₂, respectively. Therefore, there is perfect agreement of the obtained results with suggestions derived from simple physical intuition.

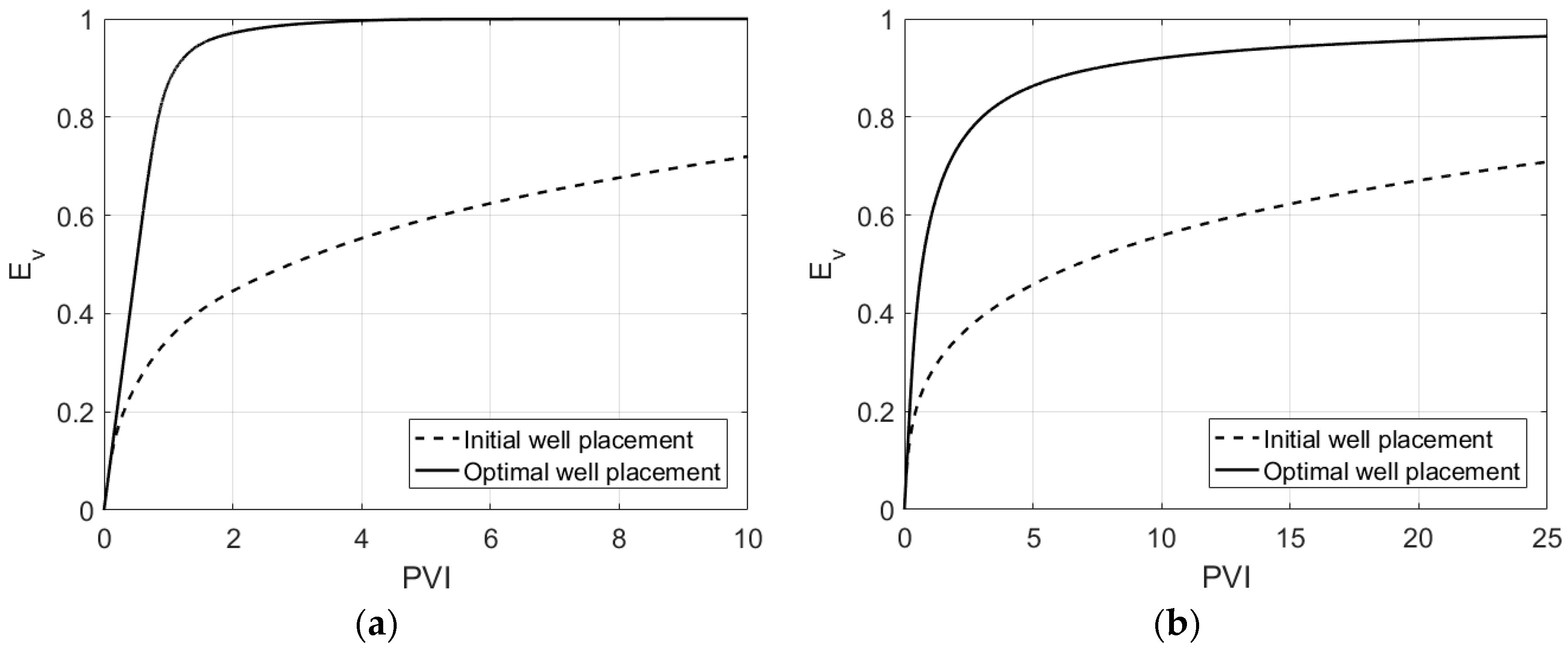
3.2. Well Placement Optimization in A Homogeneous Two-dimensional Aquifer

To test the well placement component of the S/O algorithm, a homogeneous two-dimensional confined aquifer of 1200-m extension was considered along each axis. The porosity is constant throughout the domain and equals 20%. One pumping well was placed at the domain center and four injection wells at random positions, but at an equal radial distance from the pumping well. The total injection flow rate is equally divided among all injectors I_1,...,4. A uniform spatial discretization into 60 cells on each side was considered.

Physical intuition suggests an optimal well placement of the injectors at the domain corners. Figure 4a shows the calculated moving injection well positions during the intermediate iterations. The terminations of these well paths are in close agreement with the physical intuition. The optimal well design was obtained in approximately 57 s CPU time. Figure 4b illustrates the optimization algorithm success to lower the Lorenz coefficient from a rather high initial value to a smaller one as indicated by the corresponding F (Φ) curves.

To test the sensitivity of the S/O algorithm versus the initial design, the model with a second set of initial conditions was executed. Random positions were assigned to the injection wells in each quarter of the computational domain. The flow rates satisfy the constraint Equation (5), but are not equal. The obtained solution was identical to the previous one. Indeed, Figure 5a shows that the iteratively determined moving well positions are ending up to the domain corners. Figure 5b suggests a much lower Lorenz coefficient for this second scenario. This is consistent with the fact that all injection wells are closer to their optimal positions than in the first case.

4. Results and Discussion

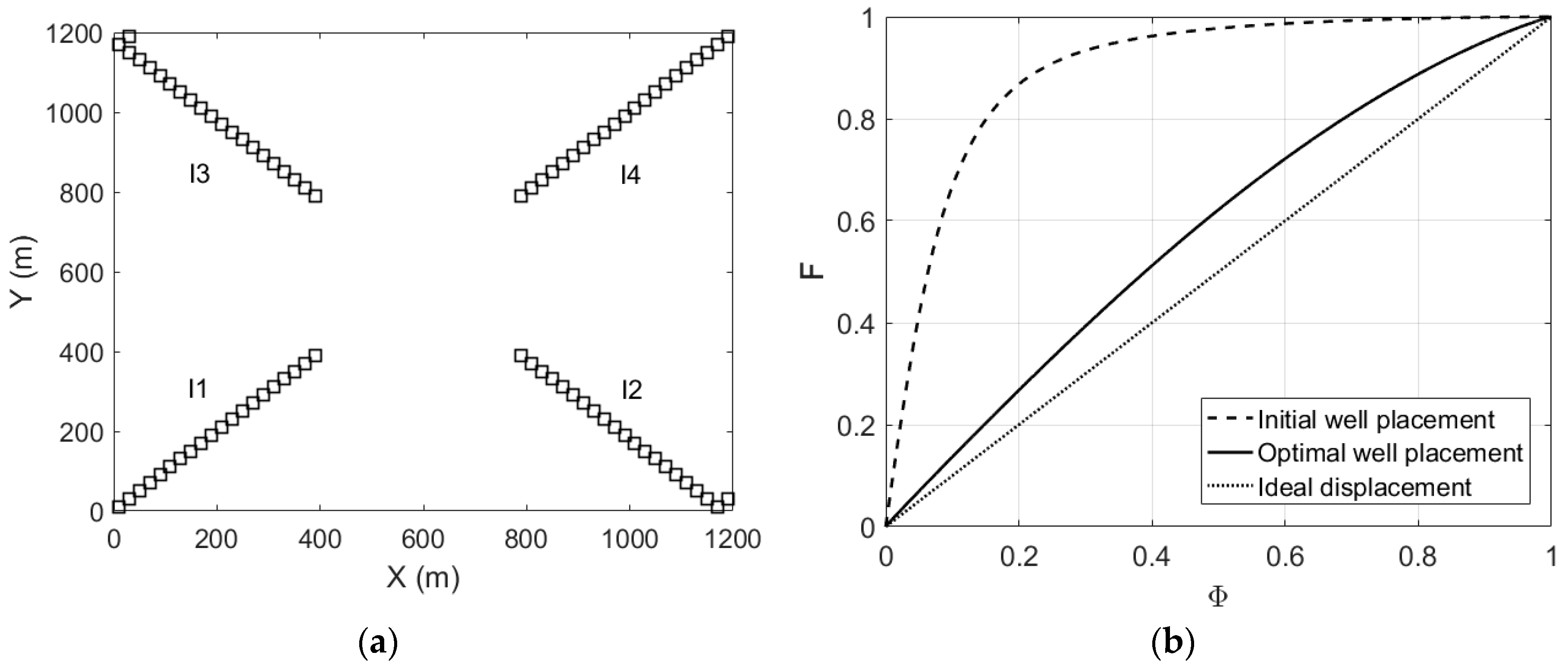
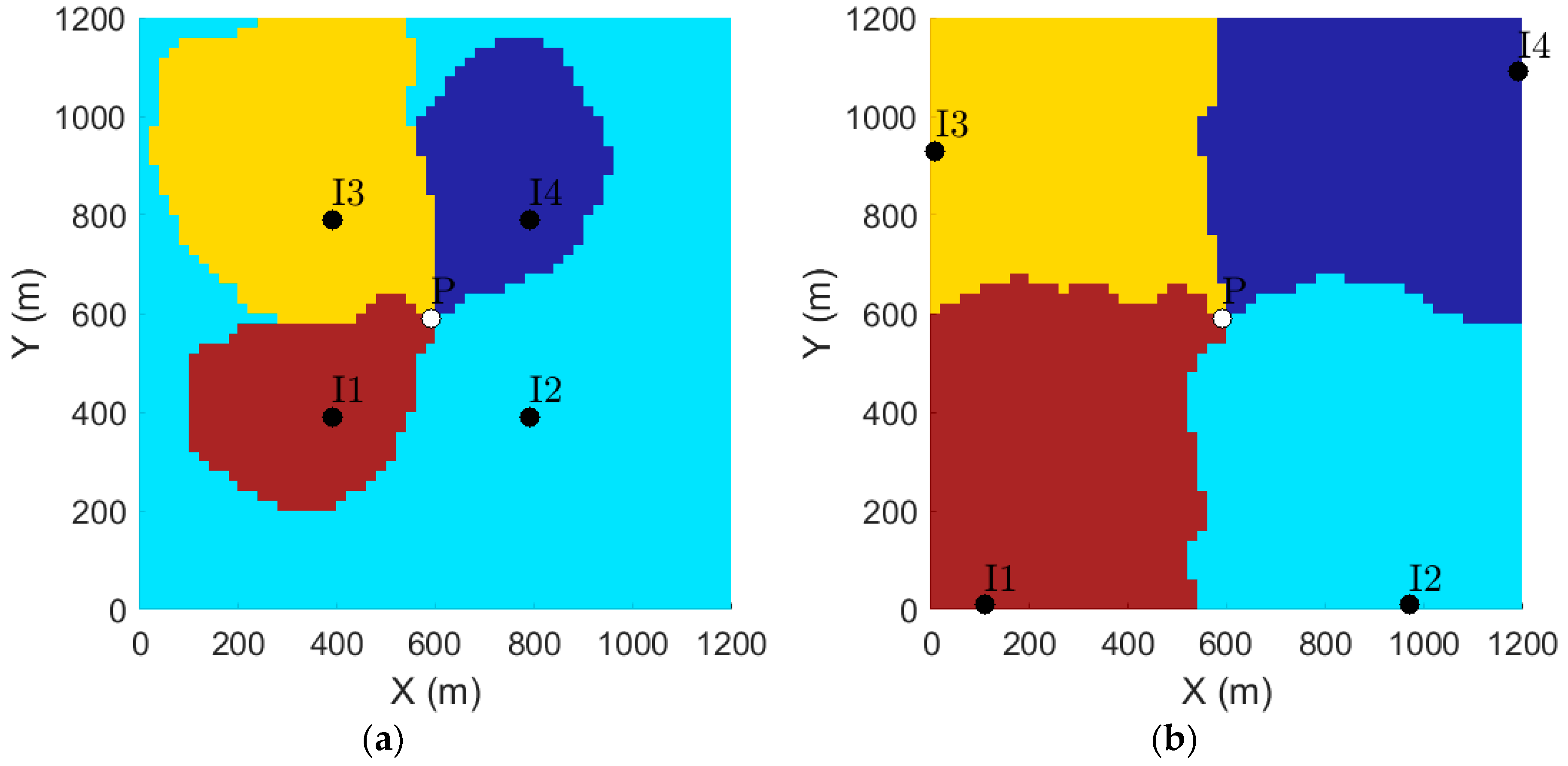
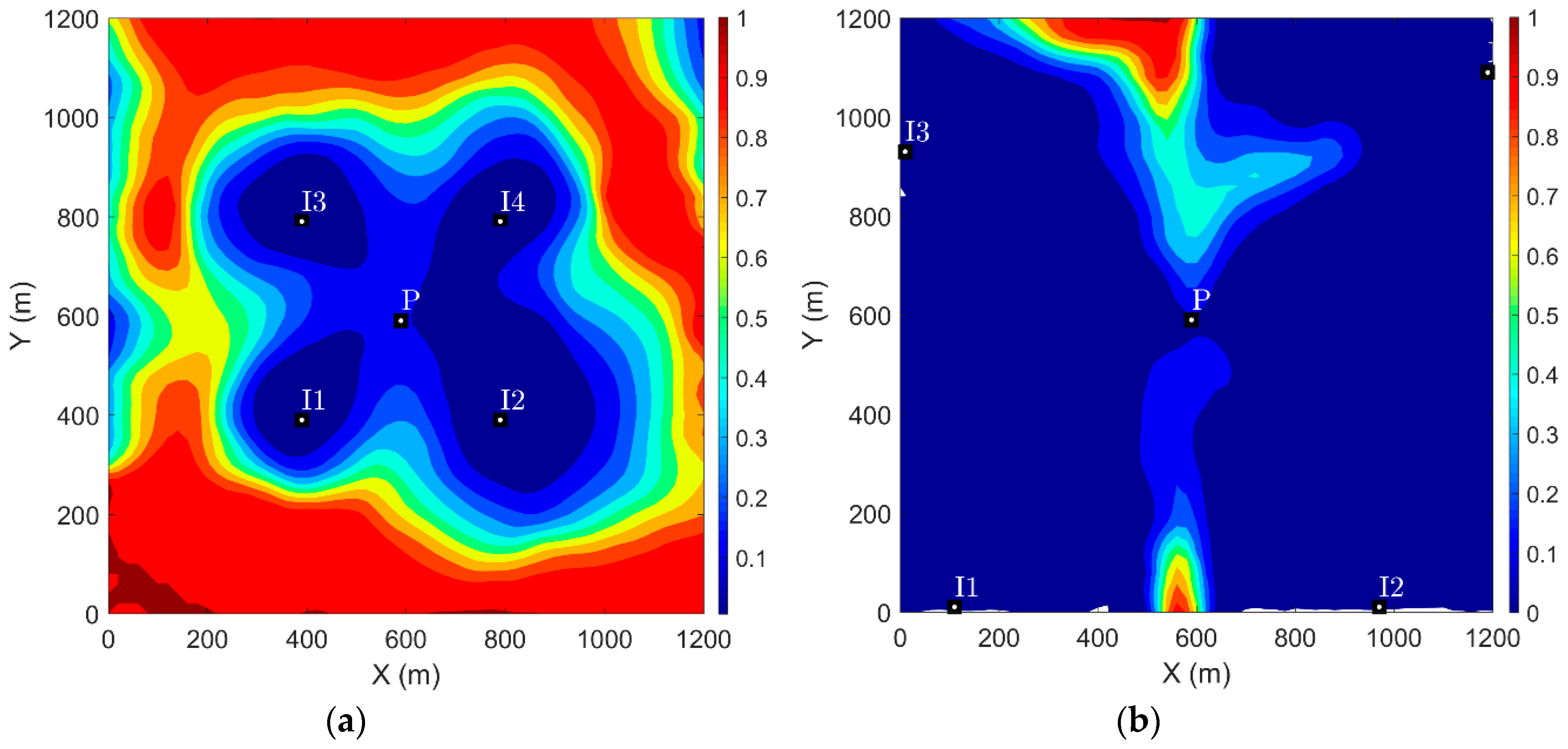
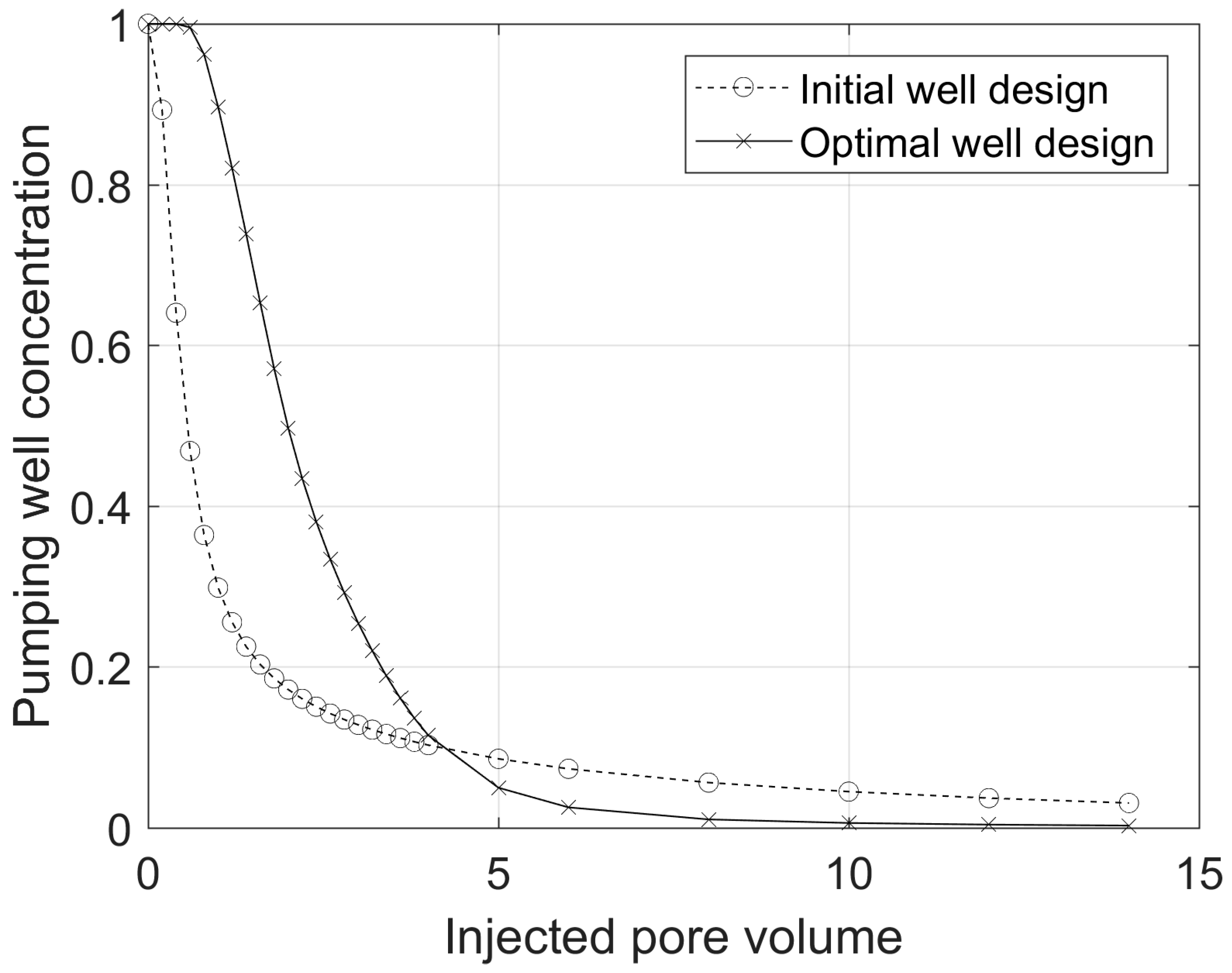
4.1. Well Rate and Placement Optimization in A Two-dimensional Heterogeneous Aquifer

A two-dimensional model of a heterogeneous confined aquifer was considered where an optimal P&T well configuration design was south. The aim is to optimize the locations of the injection wells and their rates to maximize the resident concentration breakthrough at the pumping well. The hydraulic conductivity distribution of this aquifer spans more than four orders of magnitudes ranging between 6 × 10⁻⁵ m/s and 4 × 10⁻⁹ m/s as shown in Figure 6a. The domain has a grid resolution of 60 cells on each side with a uniform spatial discretization at 20 m spacing along each direction. Figure 6b displays the correlated porosity distribution on the same grid showing values up to 38.5%. In Figure 6a, the initial position of the four injection wells, I_1,…,4, and the pumping well, P, at the domain center are equally plotted. These wells form a closed loop injection-pumping system to study the feasibility of a P&T project. One pore volume (PV) of the aquifer was injected each five years corresponding to a total injection flow rate of 54.6 m³/h. One percent hydraulic gradient was assumed from the left to the right fixed head boundaries representing the background groundwater flow. This problem is challenging for prediction from simple physical intuition. First, it is unclear how to partition the total flow rate between the four injection wells because the flow paths connecting each injector with the producer are tortuous and are mainly attracted by the most permeable pathways. Second, the initial well placement is clearly unfavorable to pollutant recovery from less permeable zones where solute transport cleanup would require long times. Therefore, an optimal design needs to consider the optimization of injection wells placement and their flow rates simultaneously.

The overall computational effort needed does not exceed 149 s, which represents a fraction of the CPU time spent for a single transient solute transport modeling simulation. Figure 6b and Figure 7b show the optimal injection wells positions as determined by the optimization search algorithm.

The Lorenz coefficient for the initial design was equal to 0.79, characterizing a very heterogeneous pollutant transport mode. L decreases for the optimal design up to 0.18 associated with a nearly homogeneous displacement mode of the solute.

Figure 7a shows the residence time distribution in log₁₀ scale highlighting the poor pollutant recovery in many areas of the domain using the initial well design. This is typically the case close to domain boundaries. Figure 7b indicates an important improvement by more than two orders of magnitude in such areas when adopting the optimal well design. The latter divides the total injection flow rate following the ratios of 25.17% for I₁, 27.81% for I₂, 17.88% for I₃ and 29.14% for I₄. Hence, the major change in allocating the injection flow rates consists of increasing that of I₄ in favor of I₃. In short, this test problem illustrates the secondary importance of well rate optimization in a heterogeneous aquifer relative to well placement.

The key differences between the initial and optimal P&T designs are better understood, analyzed and appreciated by plotting the capture zones around the injection wells [29]. Figure 8a shows that I₂ would drive polluted waters into distant areas, such as in the upper and lower left corner of the domain, before their attraction by the pumping well. This explains why travel times for the initial P&T system design are the highest in these zones. It can also be noted that the capture zones associated to I₄ and I₁ are restricted to their immediate neighborhoods. By relocating the injection wells and reallocating their flow rates according to the developed S/O algorithm, the newly obtained well capture zones as shown in Figure 8b favor pollutant displacement along the shortest possible flow paths. A striking observation is the regularity of the connection pathways between all injection and pumping wells for the optimal design despite the physical heterogeneity of the porous medium. This indicates that the flow paths and travel times are shorter in this case. The well capture zones for the optimal P&T system design are very close to what is expected for an otherwise homogeneous aquifer system. This behavior is interpreted as a decrease of the physical heterogeneity control when moving from the initial to the optimal P&T system design.

To verify the effectiveness of our S/O algorithm for this test problem, two transient solute transport simulations were conducted for post-verification. They correspond to the initial and the optimal system designs, respectively. A standard finite difference spatial discretization approach was adopted in this study [33,39,42]. It assumed a uniform unit initial resident concentration throughout the domain and a pristine state of reinjected waters. The longitudinal and transverse dispersivities are taken equal to 50 m, respectively. The molecular diffusion coefficient equals 10⁻⁹ m²/s. Each simulation lasts for a total period of 70 years corresponding to 14 reinjected PVs. Figure 9 displays the spatial distribution of the resident concentration after a period of 20 years for these two situations. In the first case, the P&T system does not succeed to drive the concentration below the drinking water standards nor to contain the pollution. The plume is removed only in the proximity of the injection wells. This configuration needs considerably longer cleanup times to attract pollution from other areas. The optimal design is more effective to contain the plume at this time level as depicted in Figure 9b. The concentration in a large portion of the aquifer volume is below the drinking water standards. In other areas, the plume is contained because it spreads locally over smaller volumes in the northern and southern domain regions.

It is noted that a single solve of the advection-dispersion equation (ADE) for this problem, until 70 years, takes approximately 445 s CPU time. The whole surrogate-based S/O model is, therefore, three times faster than a single ADE simulation. Notice that this comparison is highly biased because the S/O computer code uses an interpreted language (i.e., MATLAB^©) while the solute transport simulator is a highly optimized Fortran based code. Hence, implementing the S/O code in a high-level computer language would further improve this observed speedup. The same remark also applies to all test problems discussed in this paper.

The relative efficiency of the optimal design is confirmed by plotting the ratio of the net difference between the initial and time dependent concentration for the optimal and initial designs against the injected PV as depicted in Figure 10. The system efficiency increases rapidly at early times. It is maximal at 2.5 injected PVs, that is, after 12.5 years of injection before declining at a rather slow rate. This graph shows also the decline rates of the mean resident concentration on the aquifer. The initial design does not recover the overall resident concentration, even after a long cleanup time. The optimal design succeeds to recover 95% of the total mass after injecting 4.8 PVs. The remaining fraction is contained, however, in a small aquifer area.

The breakthrough concentration curves (BTC’s) at the pumping well station, shown in Figure 11, confirm the previous conclusions. This graph shows that the recovered concentration for the optimal design is much higher when the injected PV is below the critical point at 4.8. Notably, the BTC for the initial design is associated with a long tailing effect indicating the need for a considerably longer cleanup time.

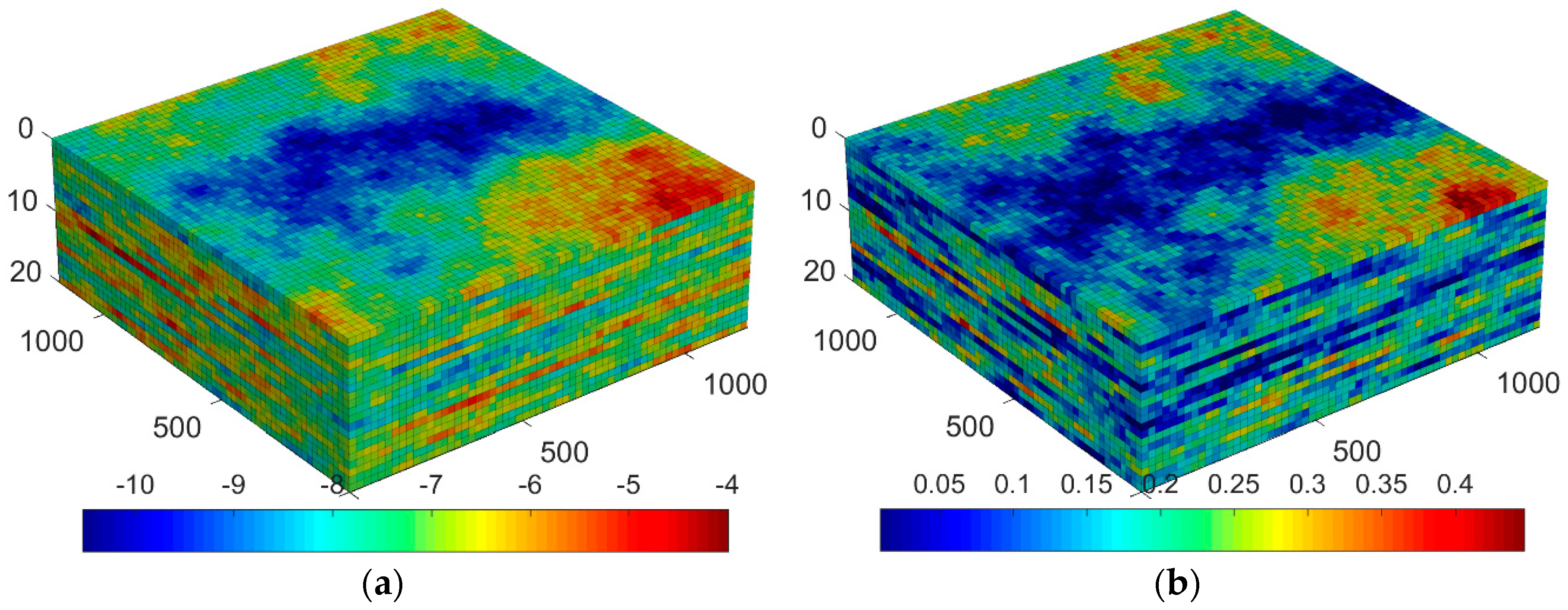
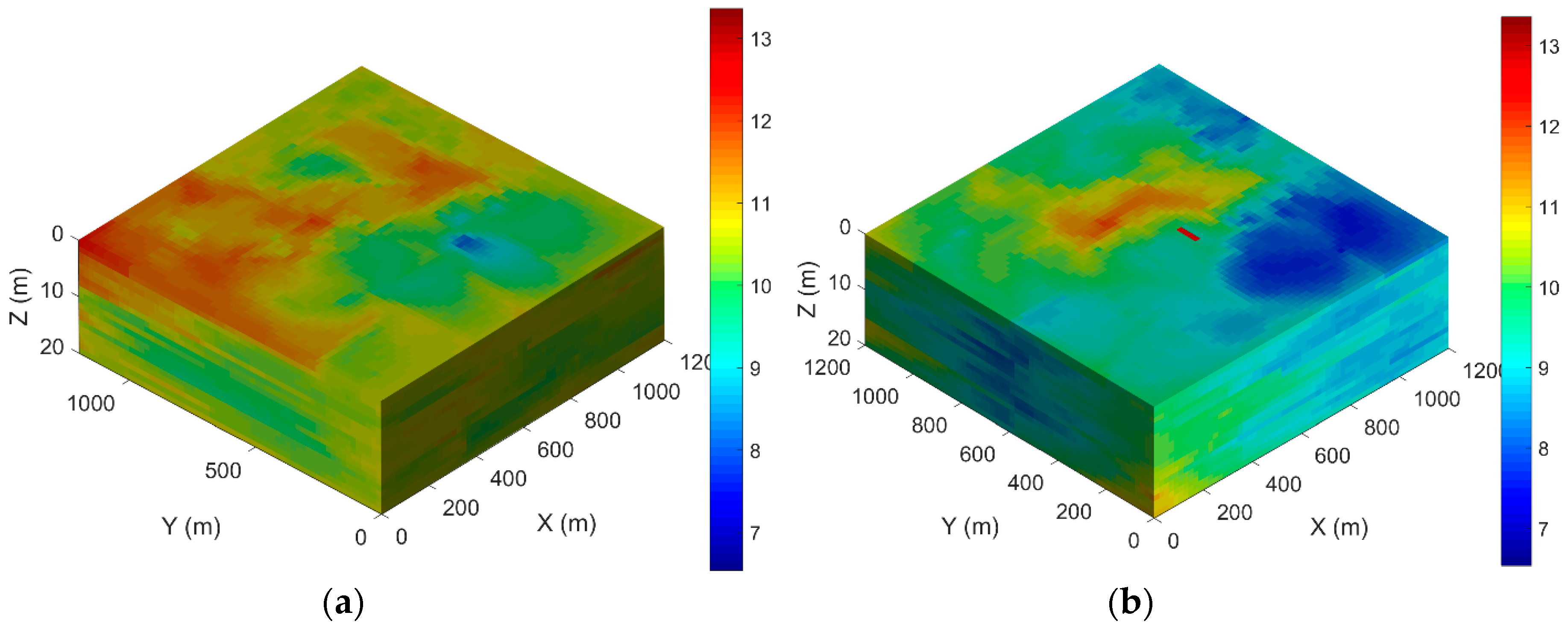
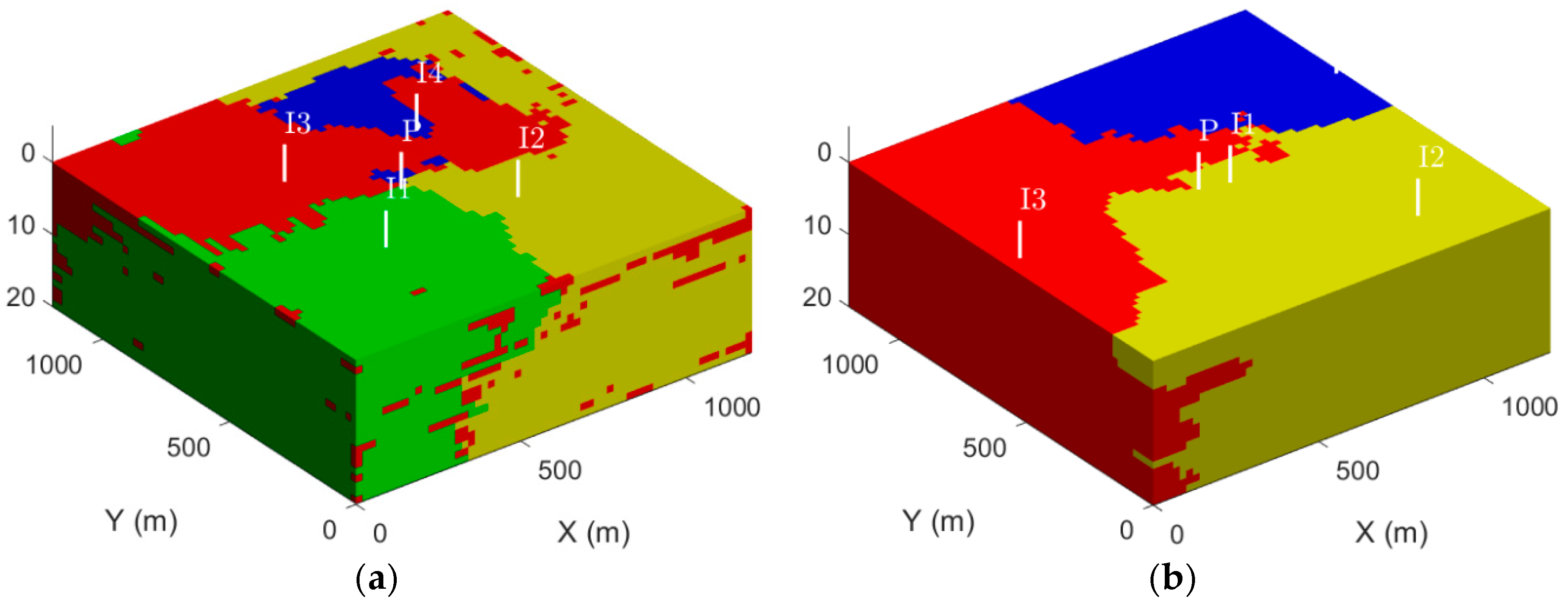
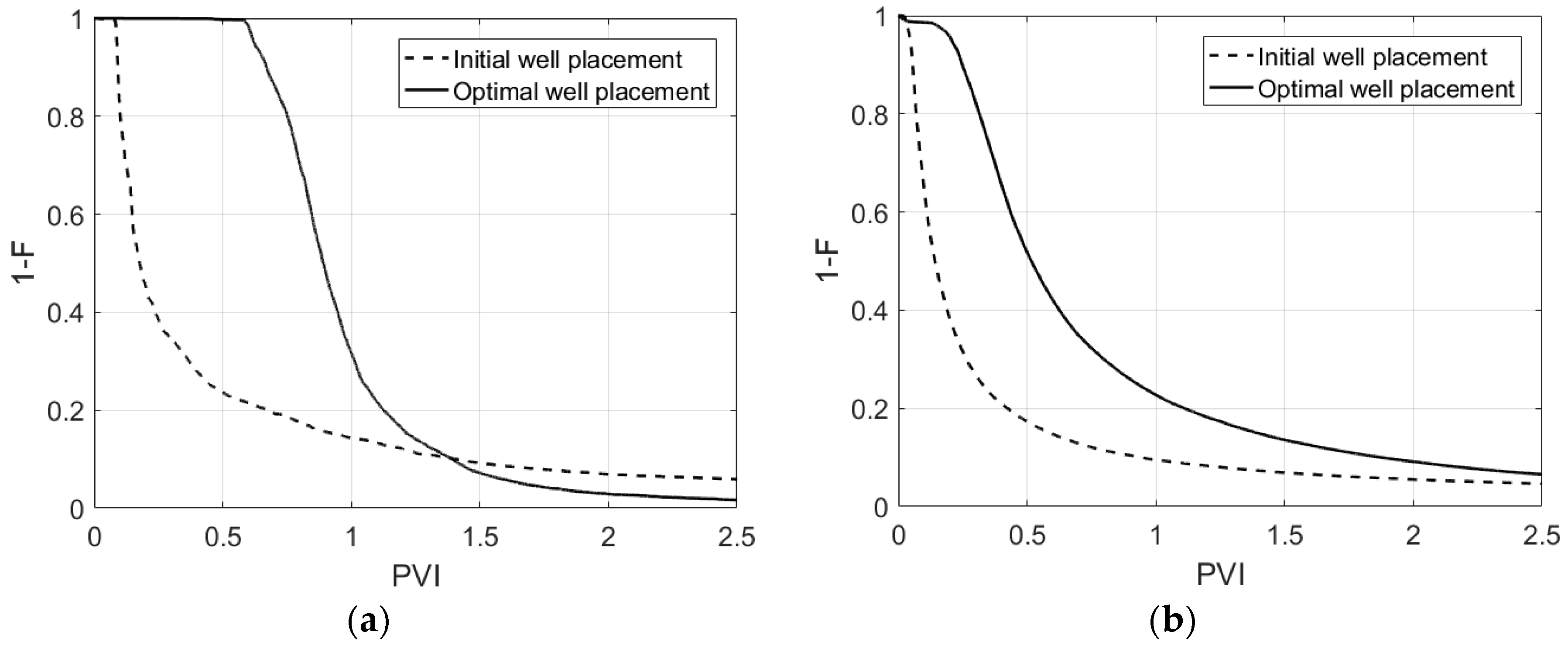
4.2. Well Rate and Placement Optimization in A Three-dimensional Heterogeneous Aquifer

A three-dimensional geological model is considered as a more challenging test problem. The hydraulic conductivity and effective porosity distributions in this aquifer are shown in Figure 12. The grid has similar horizontal size and extents to the previously discussed two-dimensional test problem. The total injection flow rate is also similar to that retained in the previous example. The model comprises 20 layers with uniform and equal unit thickness along the vertical direction. Therefore, the grid comprises 72,000 active cells. A conventional S/O approach based on a transient solute transport model is practically infeasible, for this test problem, within the available computational budget in conventional hardware.

The S/O approach, by using the travel time-based surrogate transport model, converged to the optimal well design in less than 2h CPU time, which is much less than a single run of a transient solute transport model for the same problem. Figure 13a shows the residence time distribution in log₁₀ scale, for the initial design, indicating potential aquifer zones from where pollution recovery would take very long-time scales. These areas spread laterally but also along localized positions along the aquifer depth. This is a special phenomenon mostly occurring in three-dimensional heterogeneous media, which is known as bypassing.

In the context of a P&T remediation, this phenomenon occurs in areas that do not belong to any injection well capture zone as indicated in Figure 14a (area with light grey color). Bypassing causes, very often, a marked decrease in the performances of a P&T system. Figure 13b shows that the optimal design significantly decreases residence times of injected waters almost everywhere in the aquifer. As a direct consequence, aquifer pore volume bypassing is restricted to a much smaller zone as depicted in Figure 14b. Similar to the previous test cases, the S/O algorithm succeeds to readjust the shape, volume and partitioning of injection well capture zones to meet the optimization targets.

Figure 14 shows that an optimal choice for the four injection well locations does not necessarily coincide with the traditionally adopted five-spot well pattern. While the latter could be chosen reasonably as a sub-optimal configuration for two-dimensional heterogeneous aquifers as demonstrated in the previous test problem, this is not the case for three-dimensional aquifer systems. This study interprets this because of the fundamental nature of streamlines and their topology in real three-dimensional aquifers. In two-dimensional aquifers, groundwater flow streamlines are only influenced by stretching and folding. In real space, twisting and intertwining of streamlines are additional mechanisms influencing their topology [43]. These mechanisms strongly influence the optimal injection well positions resulting in the shortest possible flow paths traveling through the entire domain. Due to the simpler groundwater flow topology in two-dimensional aquifer systems, the five-spot well pattern is a near-optimal configuration. In three-dimensional systems, the deviations to this configuration are expected as the heterogeneity and anisotropy levels of the aquifer increase.

The total injection flow rate is optimally divided among the wells following the ratios of 3.6% for I₁, 45.1% for I₂, 15.7% for I₃ and 35.6% for I₄. Hence, the major change in allocating the injection flow rates consists of increasing those of I₂ and I₄ in favor of I₁ and I₃.

Additionally, in this case, the algorithm was able to implicitly determine an optimal number of three injection wells for P&T remediation. Indeed, the pore volume and the spatial extent of the capture zone belonging to the first injector (i.e., I₁) are negligible compared to others. In addition, the optimal flow rate determined for I₁ represents less than 4% of the total flow rate. Therefore, in practice, this well is taken out from the optimal design and its flow rate is equally divided among other injection wells. Hence, although the S/O approach presented in this paper does not explicitly optimize the capital costs, they can be indirectly estimated through the selection of the optimum number of wells. Therefore, the introduced model could be used as a fast, but first-order approximation method to estimate project related capital costs for P&T groundwater remediation.

It is also instructive to compare the performances of P&T remediation designs for two- and three-dimensional systems as simplified two-dimensional settings are very often used in the literature. This results from computational limitations of the traditional S/O approaches relying on an explicit ADE model. In the following, these analyses are presented with derived proxies emulating the early and late times behavior of each P&T remediation design.

Early time behavior is best illustrated by plotting the curve of (1-F) versus $\mathrm{PVI}=d\mathsf{\Phi }/\mathrm{dF}$ which is the dimensionless pore volume injected in the aquifer. This is particularly useful to track the onset time of solute breakthrough, that is, when (1-F) just drops below 1 as illustrated in Figure 15. This graph can be used as a proxy to compare early time behavior of many P&T remediation strategies for the same site, or alternatively compare the same remediation design for different conceptual models. As stated previously, a small onset time of breakthrough is a sign of high dynamic heterogeneity of the system.

Figure 15 shows the fractional recovery plots for the heterogeneous two- and three-dimensional problems, respectively. For each problem, these curves are given for the initial and optimal well placements. It can be concluded that, as expected, the onset of solute transport breakthrough increases for the optimal P&T designs, although this is markedly more important in the case of the two-dimensional case study. This onset time is generally problem dimension dependent as illustrated here. In three-dimensional space, the probability that a few streamlines breakthrough much faster than the others is likely higher than in two-dimensional space for the same physical heterogeneity structure. Hence, two-dimensional models tend to be more optimistic on the performance of a P&T remediation design when used by any S/O approach because they underestimate the dynamic heterogeneity of the system, as it would be in 3D space.

Similarly, late time behavior could be diagnosed by plotting the sweep efficiency proxy plotting the volumetric sweep efficiency, $E_v$, versus the dimensionless pore volume injected in the aquifer. $E_v$ is the fraction of resident fluid that is displaced by the injection forces which is shown to be expressed as:

$$E_v=\left(1-F\right)PVI+\mathsf{\Phi }$$

(15)

At a given time, it represents the sum of the volume of drained flow paths (i.e., $\mathsf{\Phi }$) and the volume of flow paths being drained (i.e., $\left(1-F\right)PVI$). It is a measure of the P&T remediation design efficiency in terms of reinjected water volumes or cleanup time as previously discussed for the third test problem. Figure 16 shows these diagrams for the heterogeneous two- and three-dimensional problems, respectively. For each problem, these curves are given for the initial and optimal well placements. This study observed that, as expected, the optimal well placement improves the P&T system efficiency significantly in all cases. For the two-dimensional problem, Figure 16a indicates that, when using the optimal well design, the injection of 10 PVI will produce all the fluids in place. This correlates well with the results obtained from an ADE-based model to check the efficiency of the optimal P&T remediation design for the same problem, as discussed previously. Figure 16b shows that the efficiency rate of the optimal P&T remediation design for the three-dimensional problem is slower than that for the two-dimensional one. This correlates well with the stronger dynamic heterogeneity in the first case, as discussed earlier, and indicates the occurrence of many stagnant regions in 3D space. However, P&T might not be an appropriate remediation technology for sites presenting a high volume of such zones because mass transport in these areas is expected to be dominated by molecular diffusion. Hence, cleanup times are expected to be much longer. The merit of the introduced S/O approach is to timely predict this behavior when considering a large-scale geological model.

Here again, two-dimensional models tend to be more optimistic on the performance of a P&T remediation design because they overestimate the system sweep efficiency and consequently underestimate the cleanup time.

The Lorenz coefficient, hence the objective function, could be easily modified to account for the pollutant plume shape and concentration strength. For instance, to account for the concentration distribution, C₀, taken as initial condition prior to a S/O the objective function becomes:

$$L\left(\tau \right)=2{{\displaystyle \int }}_0^1\left(F\left(\mathsf{\Phi }\right)-\mathsf{\Phi }\right)C_{0}d\mathsf{\Phi }$$

(16)

This concentration-weighted objective function ensures that the above benefits of the proposed formulation applies only to model cells where the pollutant plume exists. This has not been taken in the provided examples because C₀ was taken equal to unity.

The weighting of the objective function as shown in Equation (16) could be easily expanded to account for other concentration-dependent measures and their cost functions.

5. Conclusions

This study introduces and evaluates a new surrogate-assisted simulation-optimization (S/O) formulation for groundwater remediation design. This proposed S/O model is highly efficient and readily applicable to complex three-dimensional groundwater problems bypassing the need to introduce further model assumptions. The following general conclusions can be drawn from this work.

• The travel time-based surrogate model provided a cheap and adequate tool to streamline the computationally demanding simulation-optimization approach for groundwater quality models.
• Owing to the stationarity of the surrogate model, computational savings are enormous. Large three-dimensional models as encountered in practice are processed timely in conventional hardware.
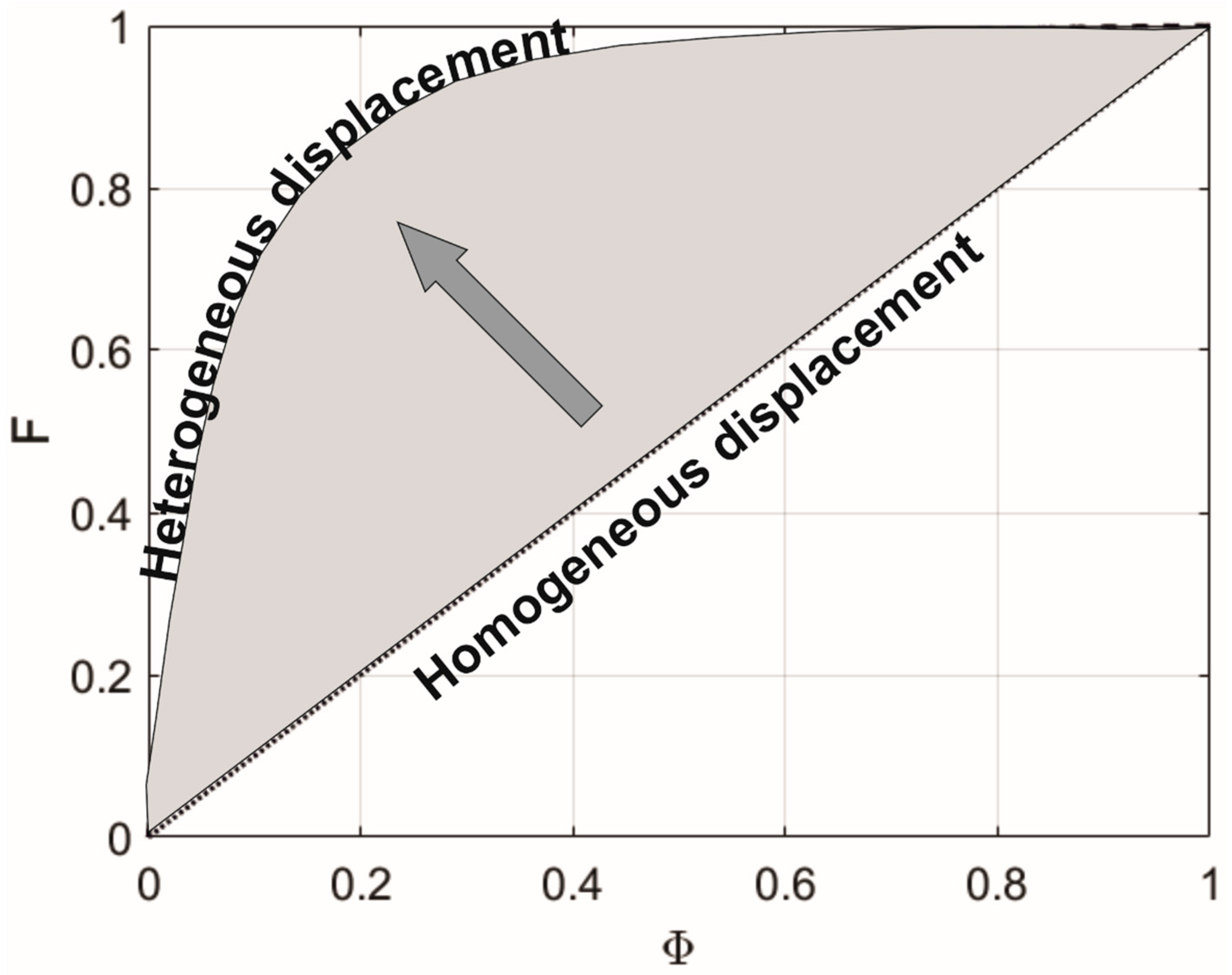
• The objective function formulation based on minimizing the Lorenz coefficient has been found effective to rank the relative efficiency of many remediation policies. The automatic differentiation method used to evaluate the objective function sensitivities contributes to the overall efficiency of the S/O model.
• This study found that well placement optimization in heterogeneous porous media is more important than well rate optimization in P&T remediation design. While this finding confirms previously published research, the merit of this work is to bring novel graphical interpretation tools facilitating the understanding of the underlying processes.
• When used in a S/O framework, two-dimensional models are optimistic on optimal P&T system performances. In general, they overestimate the delay in breakthrough at pumping wells and underestimate the cleanup time. Hence, three-dimensional models are a necessity rather than a luxury.
• Even if the project costs are not explicit components of the objective function, the introduced model could be used as a first-order approximation to estimate pump-and-treat capital remediation costs.

However, further developments and field scale-based assessments are needed to relax the limitations of the S/O model to solve problems that are more complex. The next challenge is how to appropriately set up a surrogate model that takes into account chemical and mineral heterogeneities and assess their impacts on remediation design. New global optimization algorithms would increase the S/O model robustness and ascertain that a globally optimal solution has been found. Finally, yet importantly, a user-friendly software package can enhance the model applicability for a wide audience.

The presented approach could serve as a basis to solve similar or even more complex real-world problems in geosciences, such as water allocation, geothermal heat pumps and artificial recharge management, etc., by reformulating the objective function(s), decision variables and constraints.